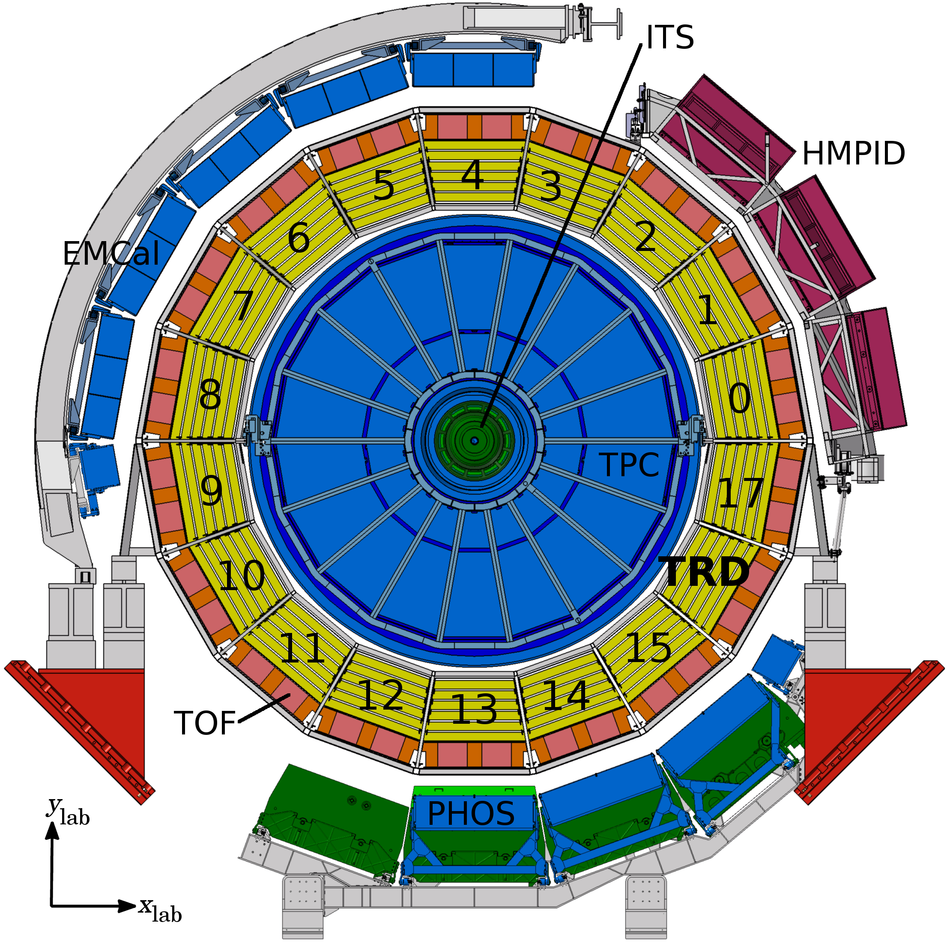
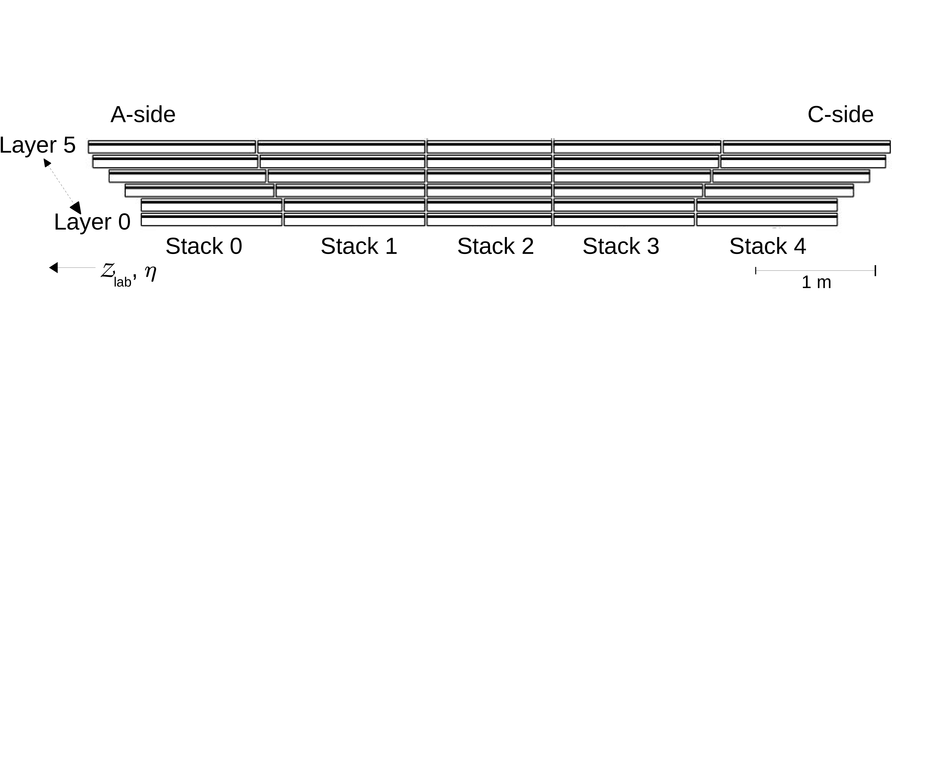
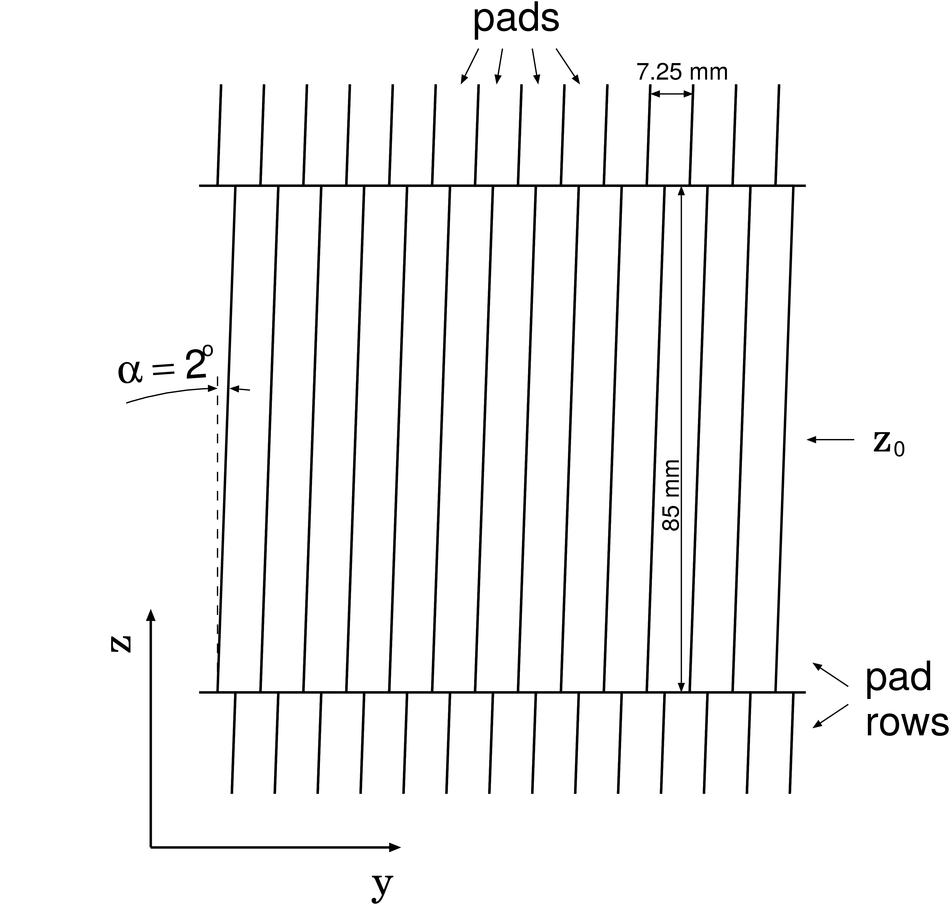
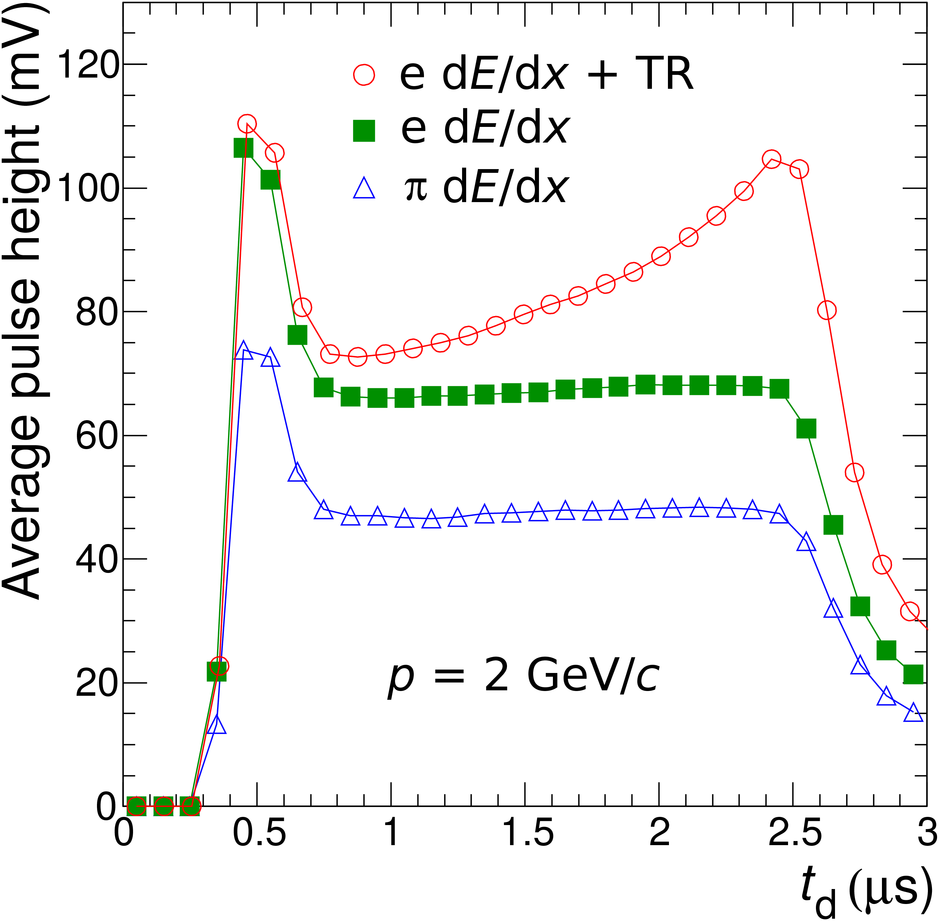
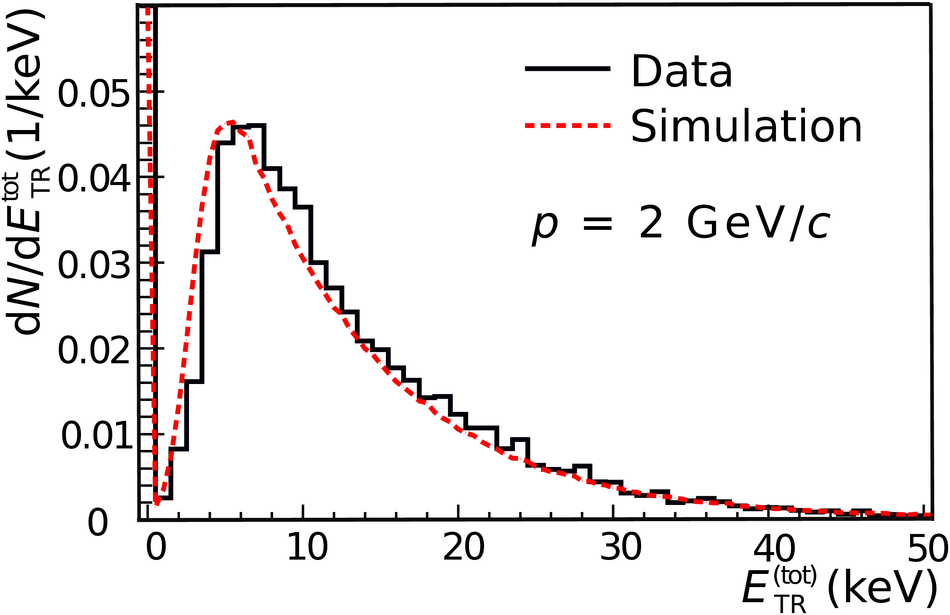
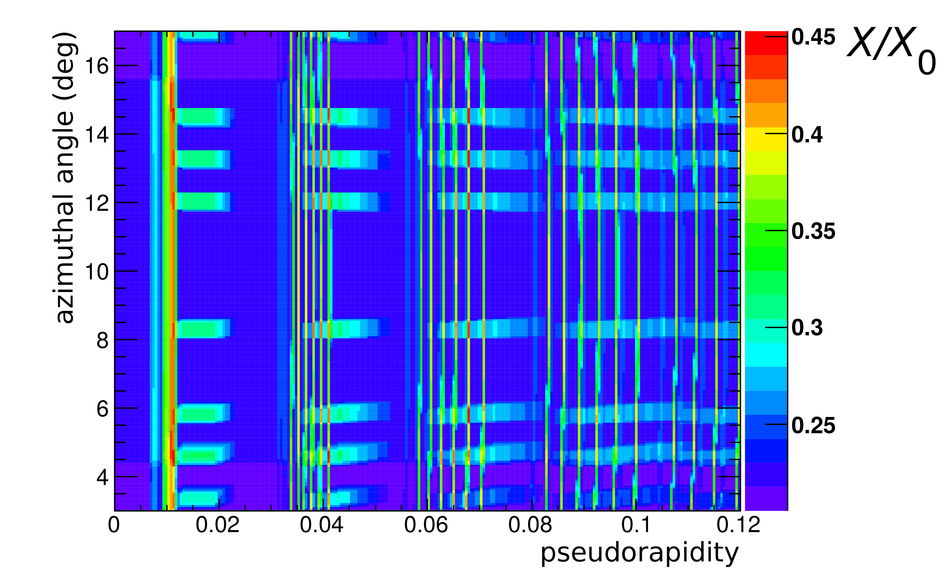
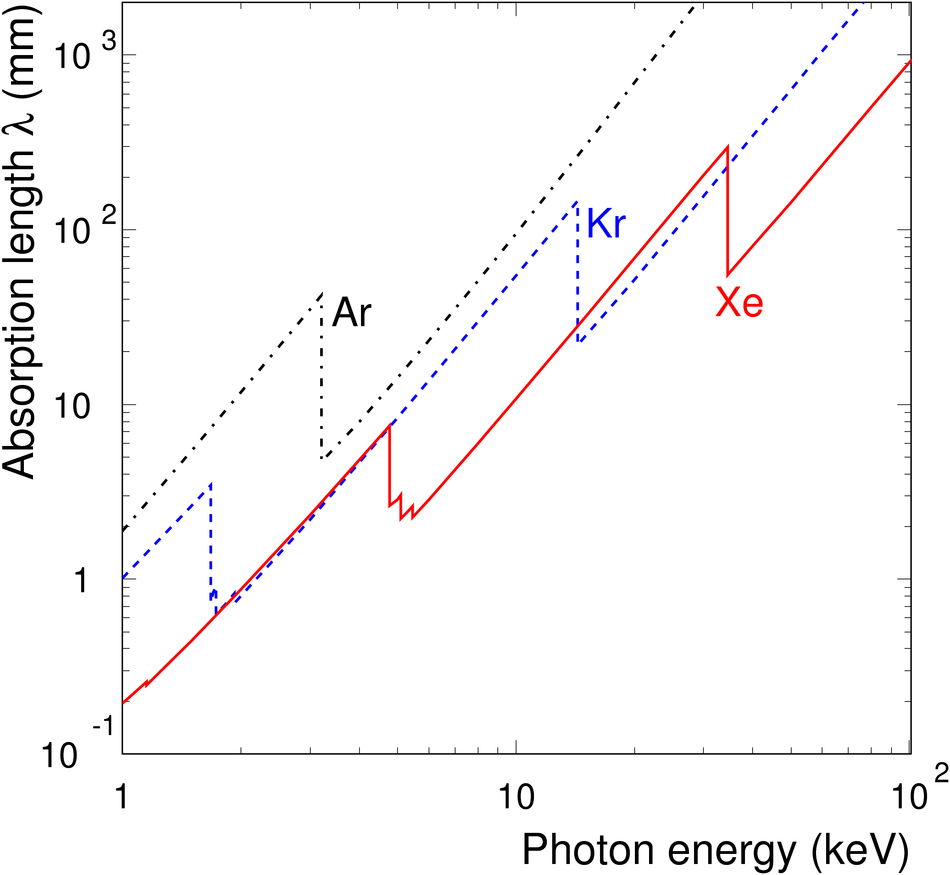
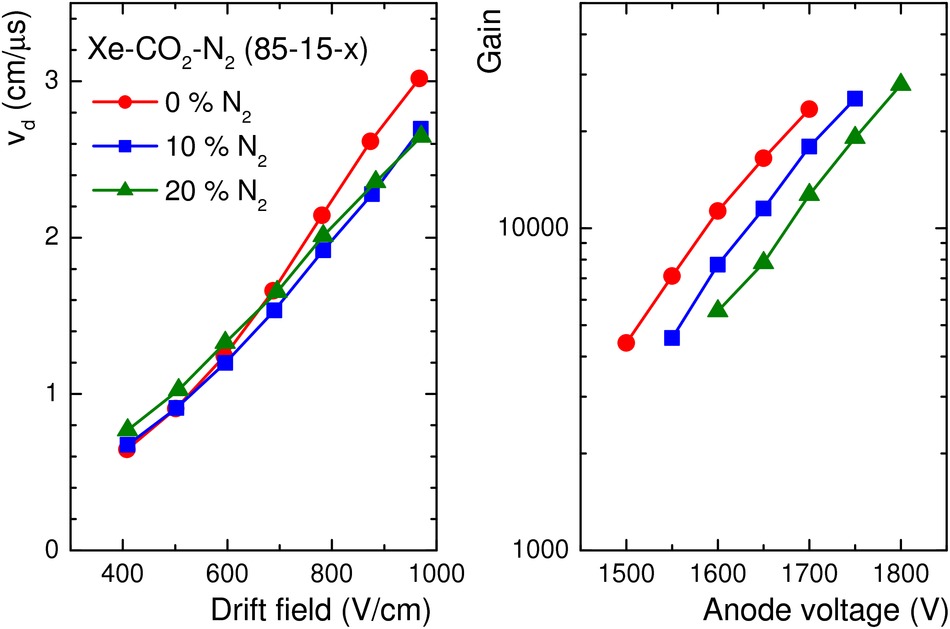
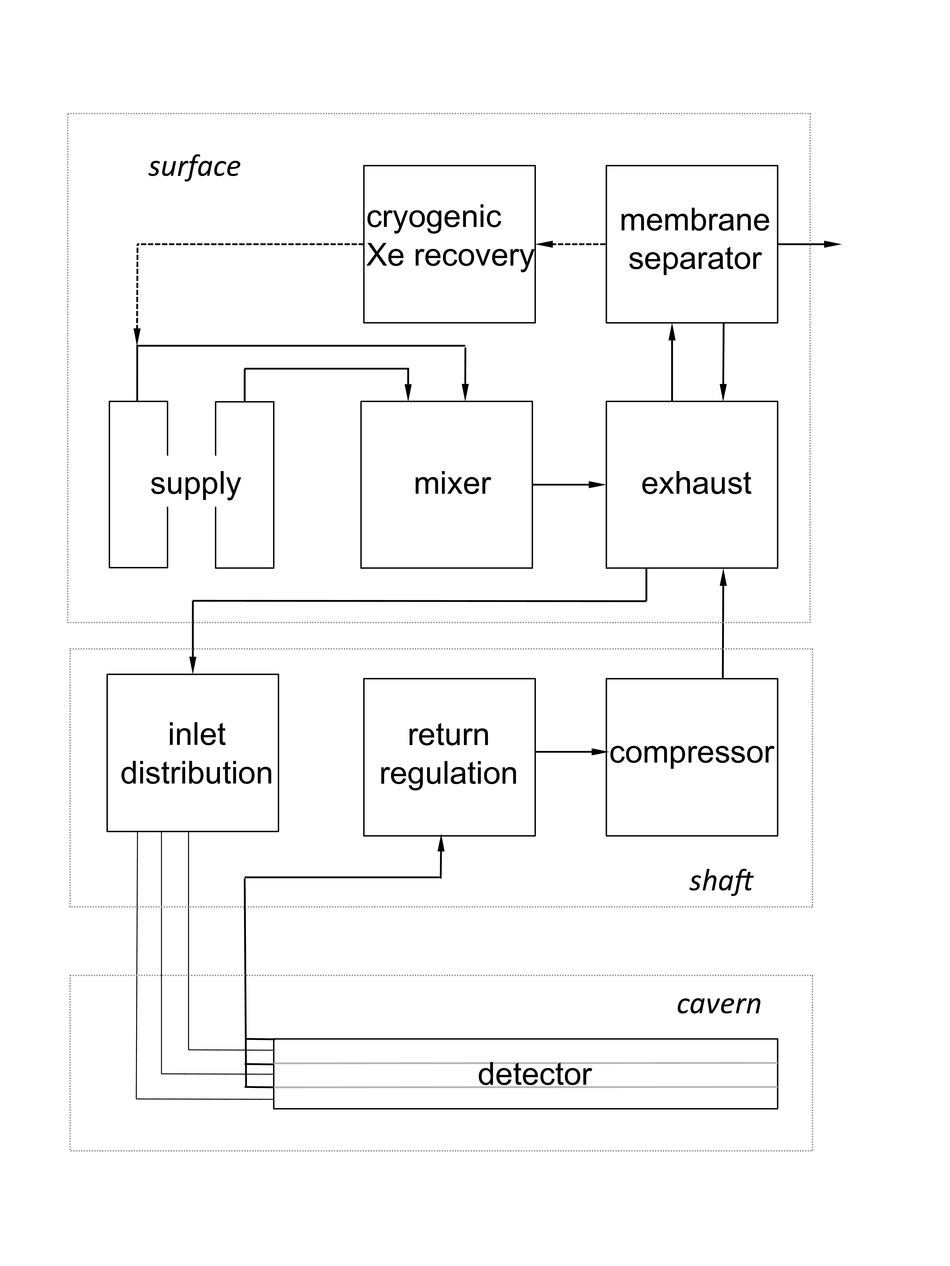
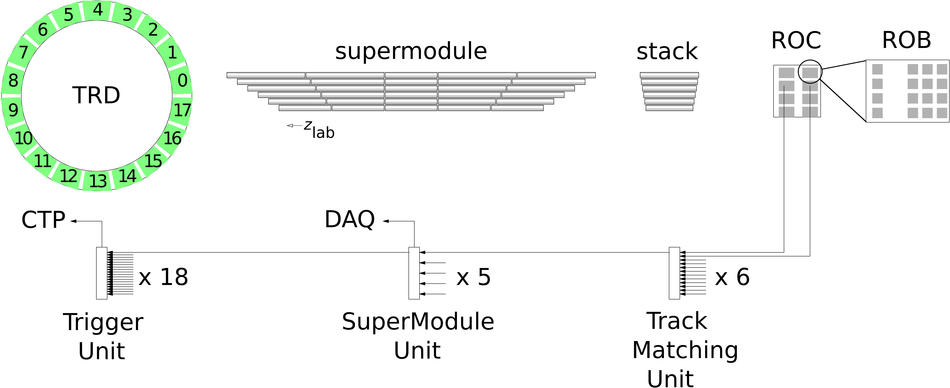
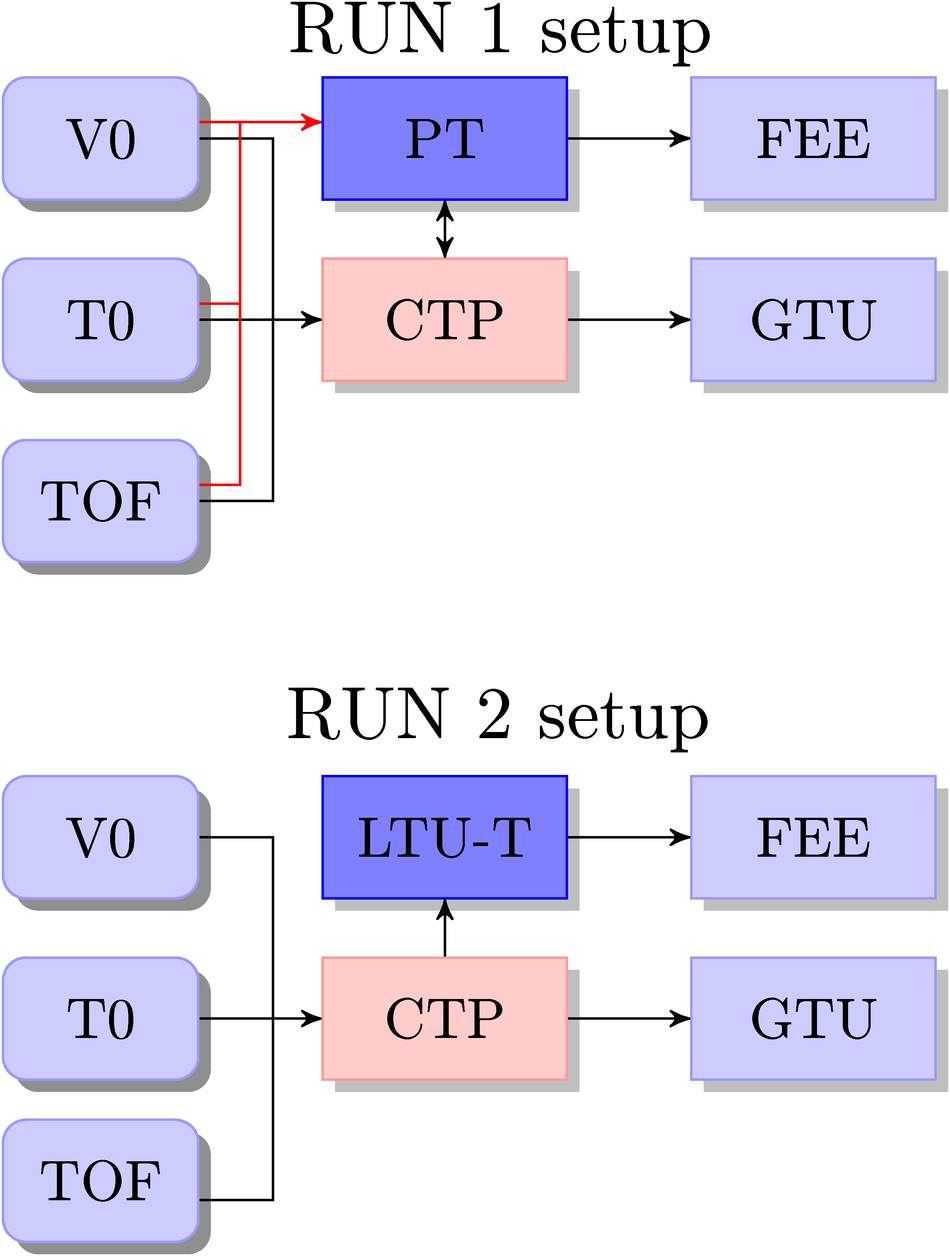
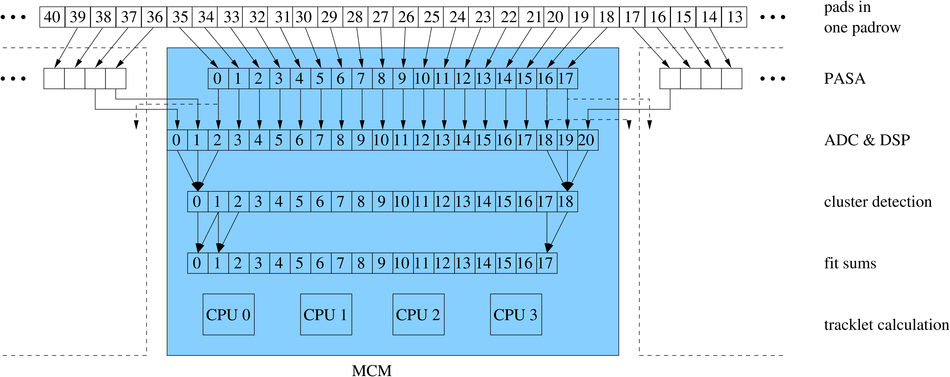
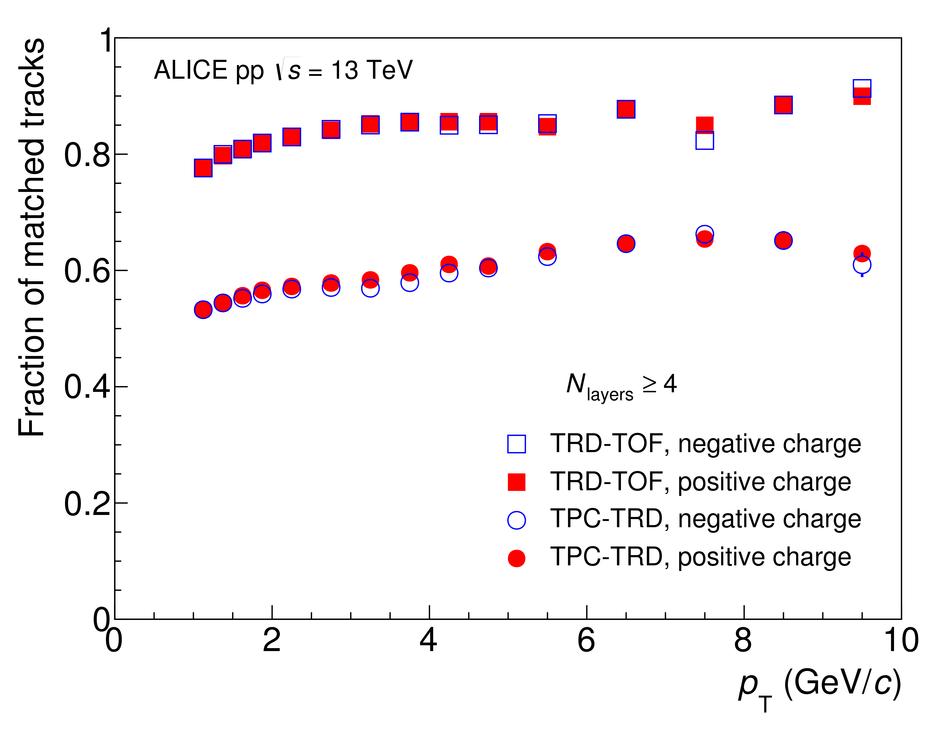
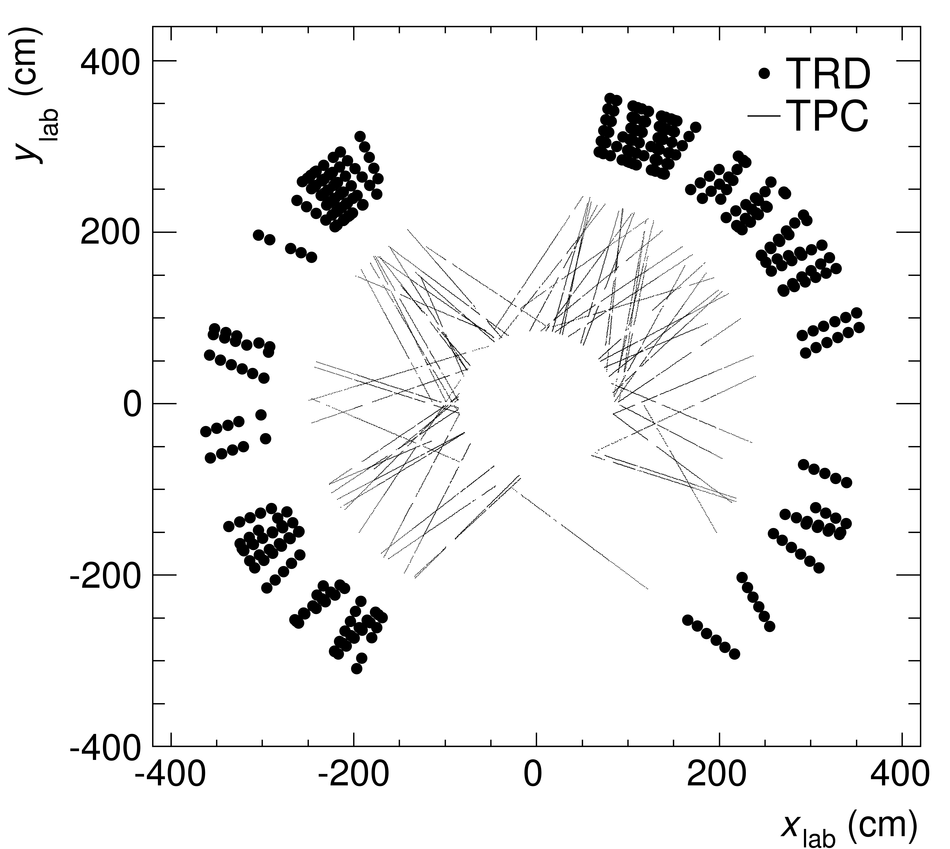
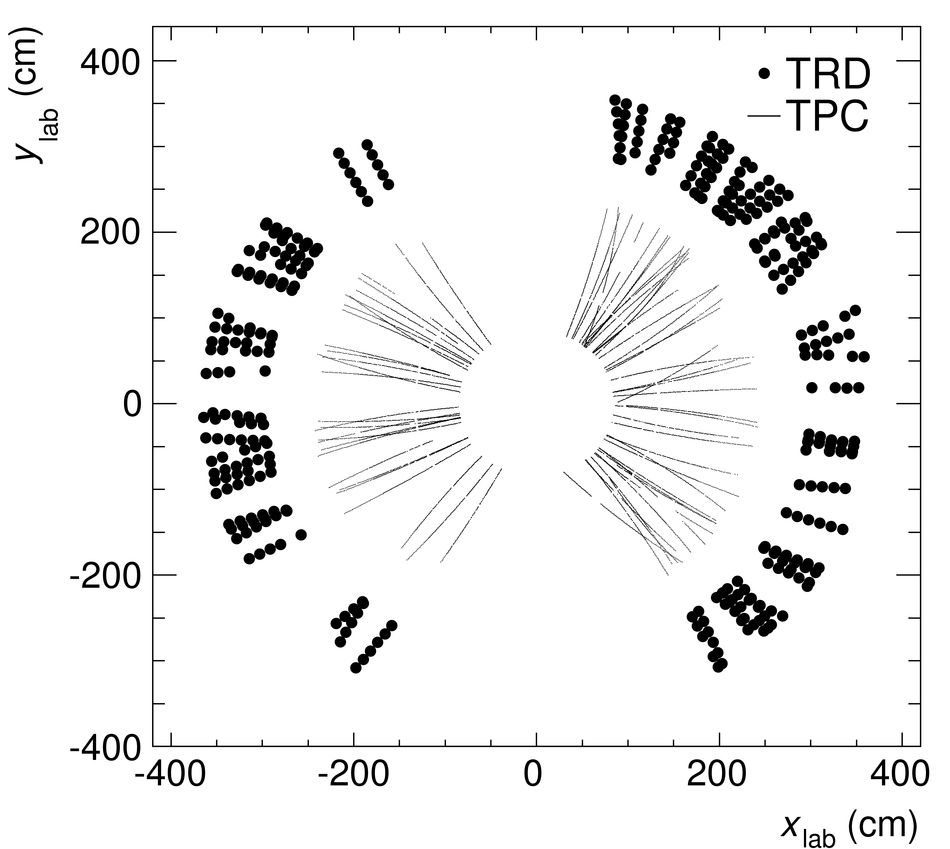
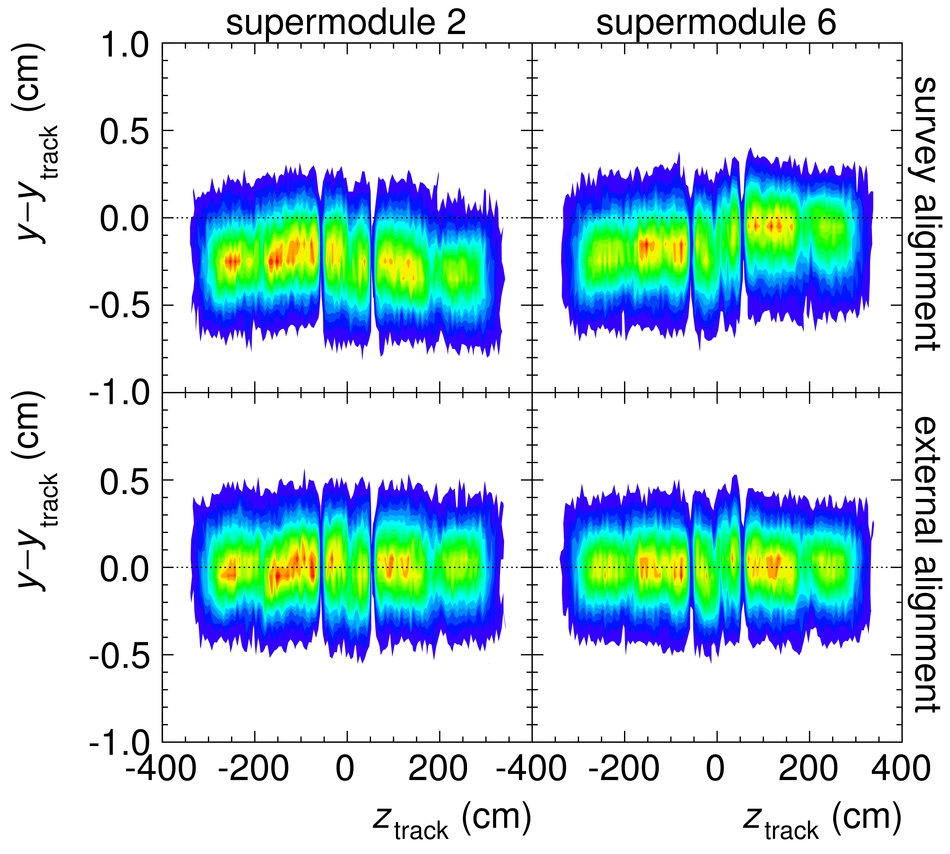
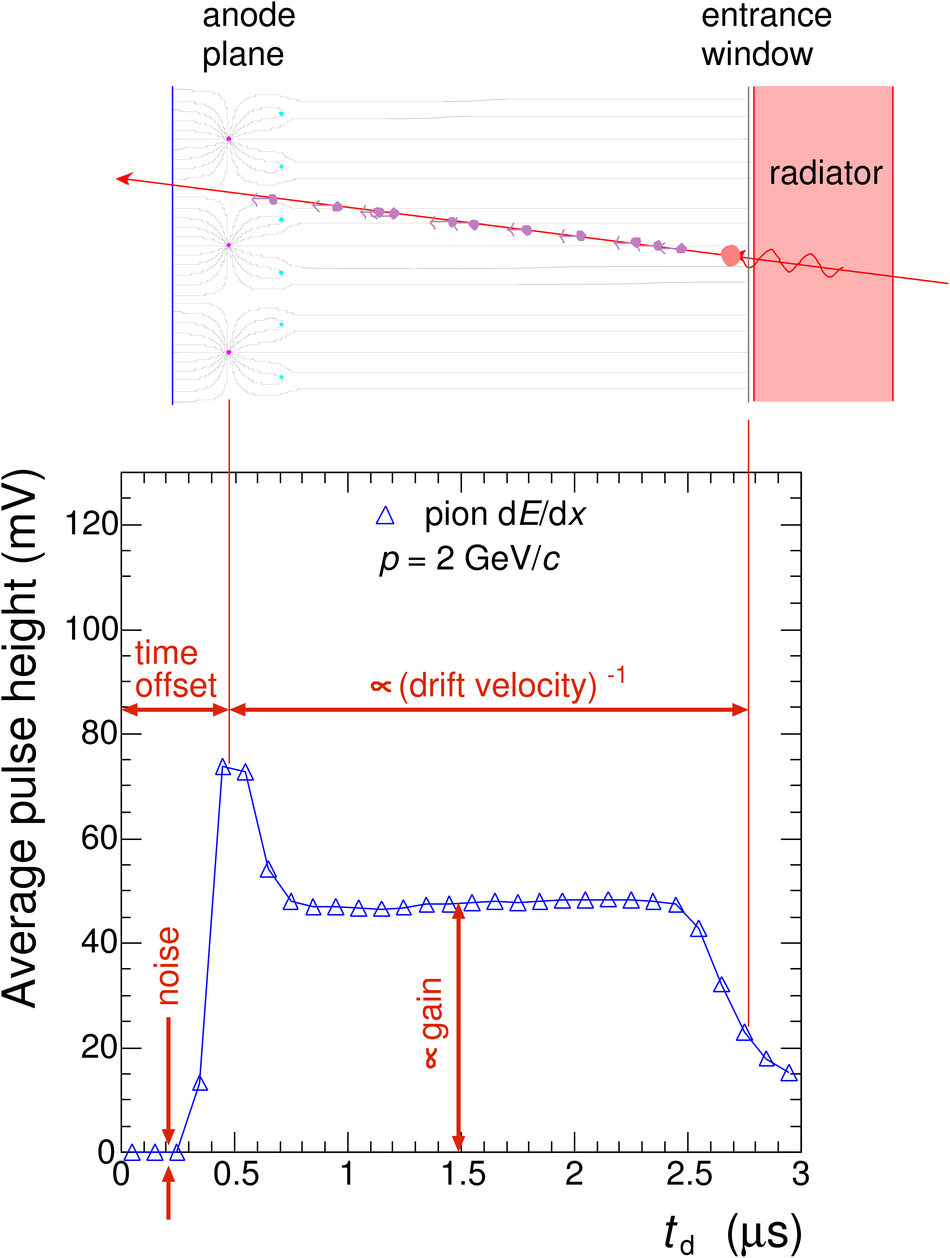
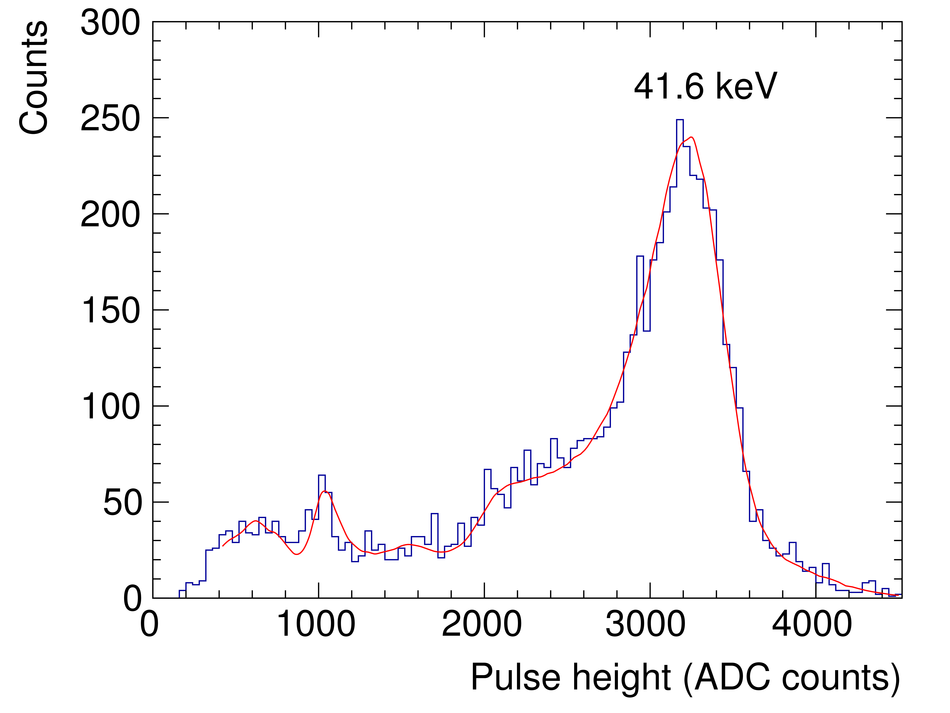
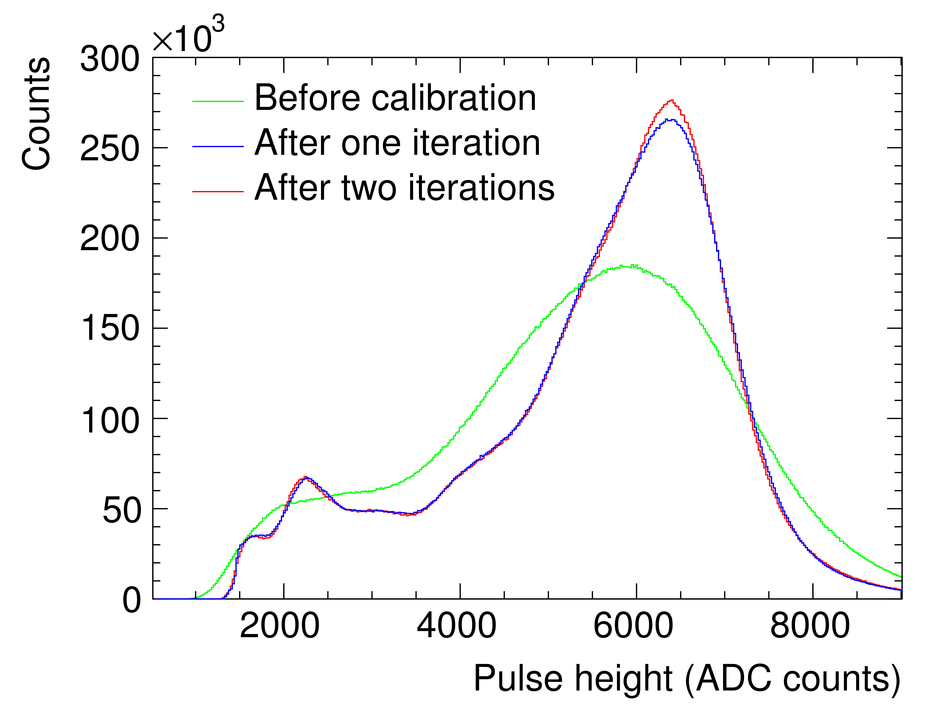
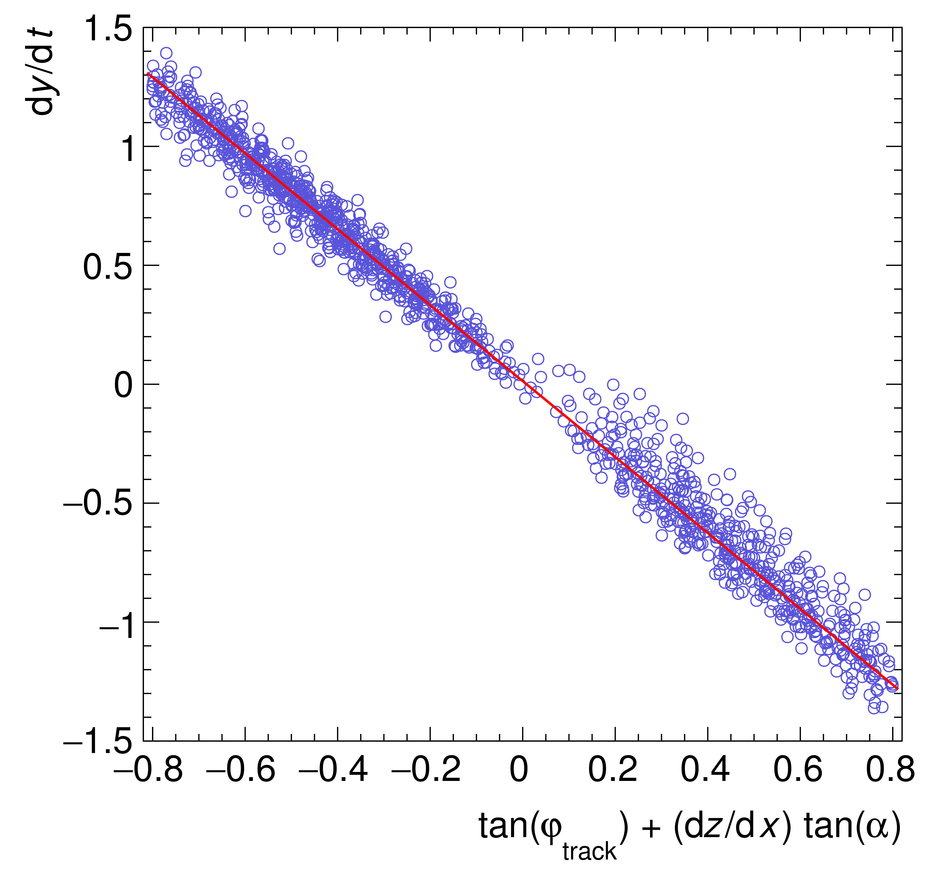
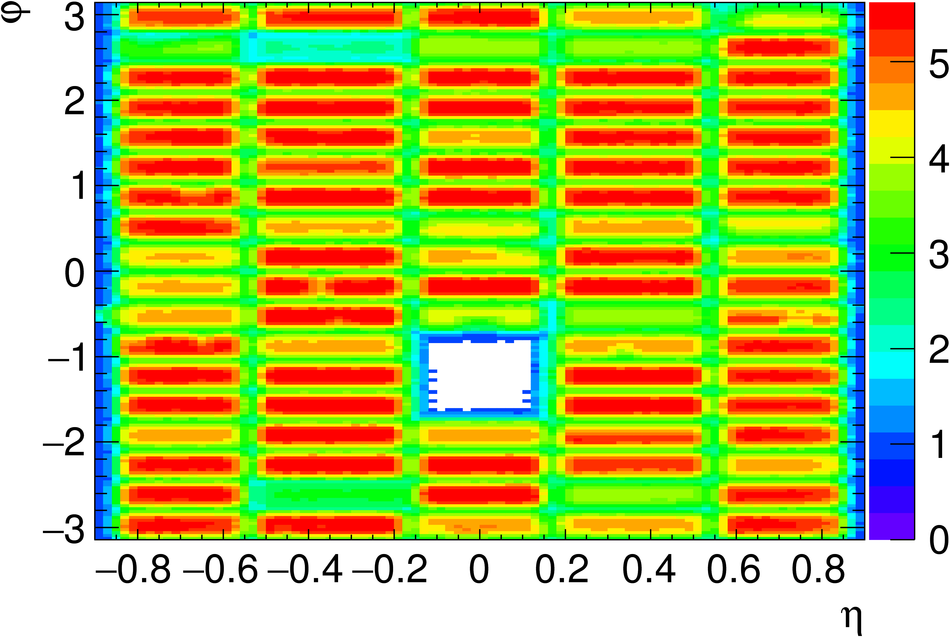
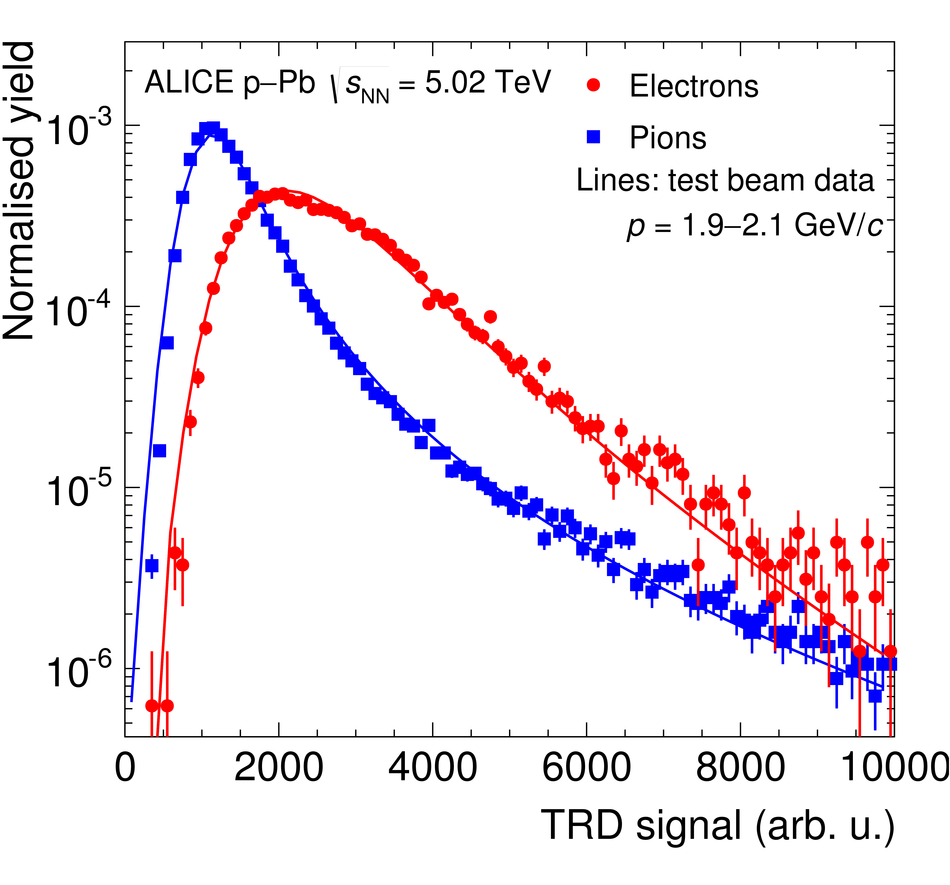
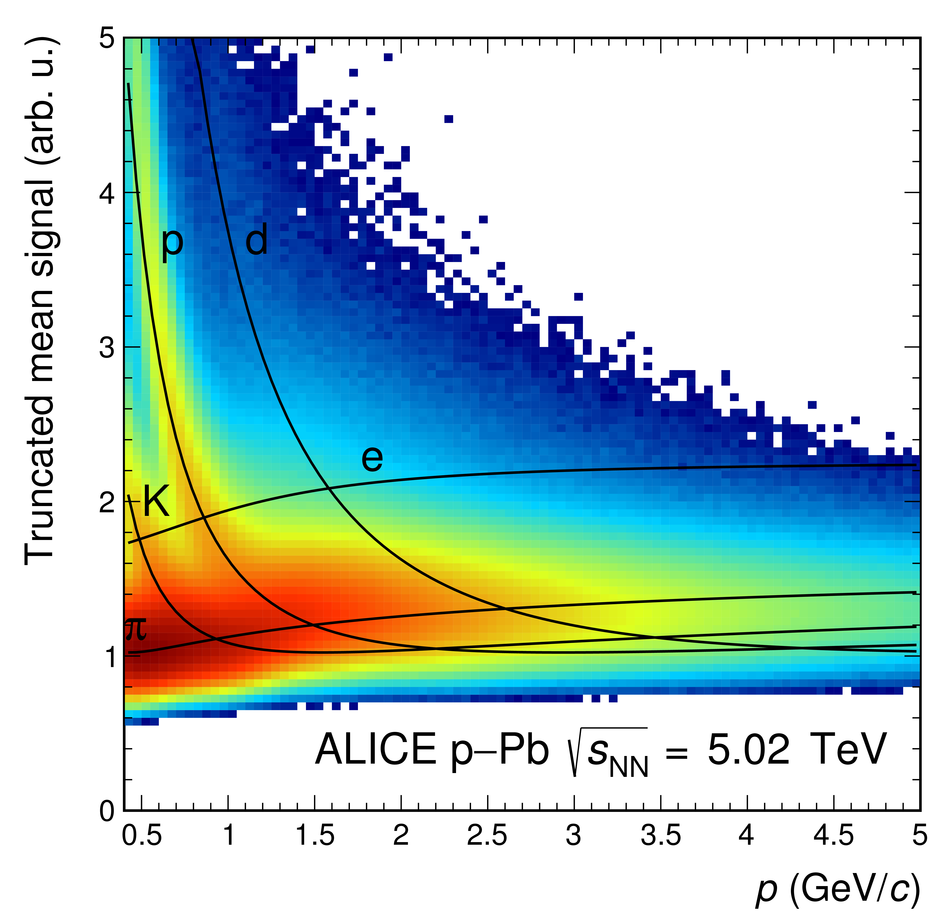
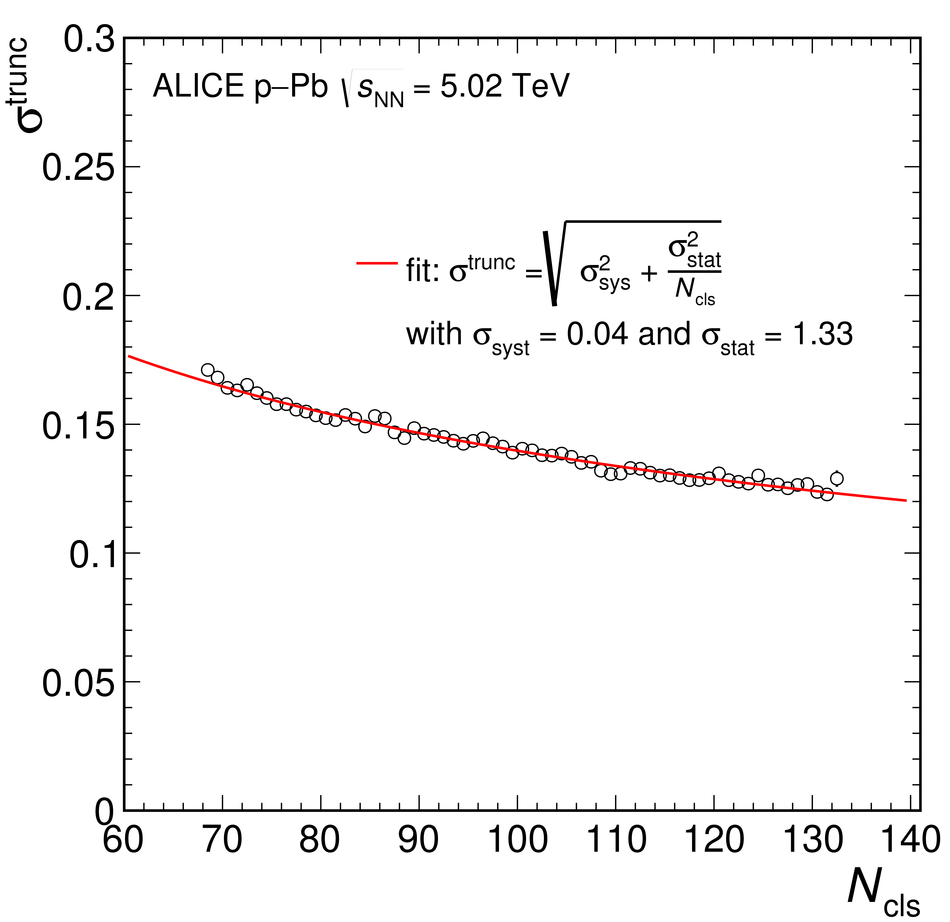
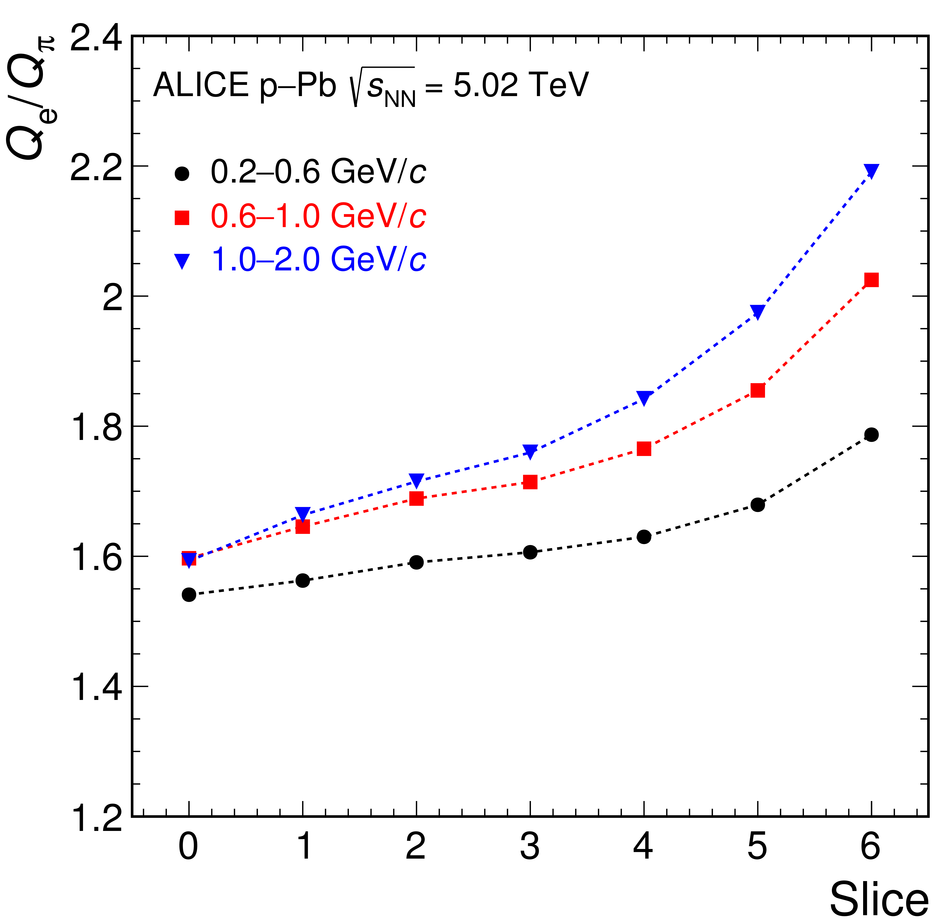
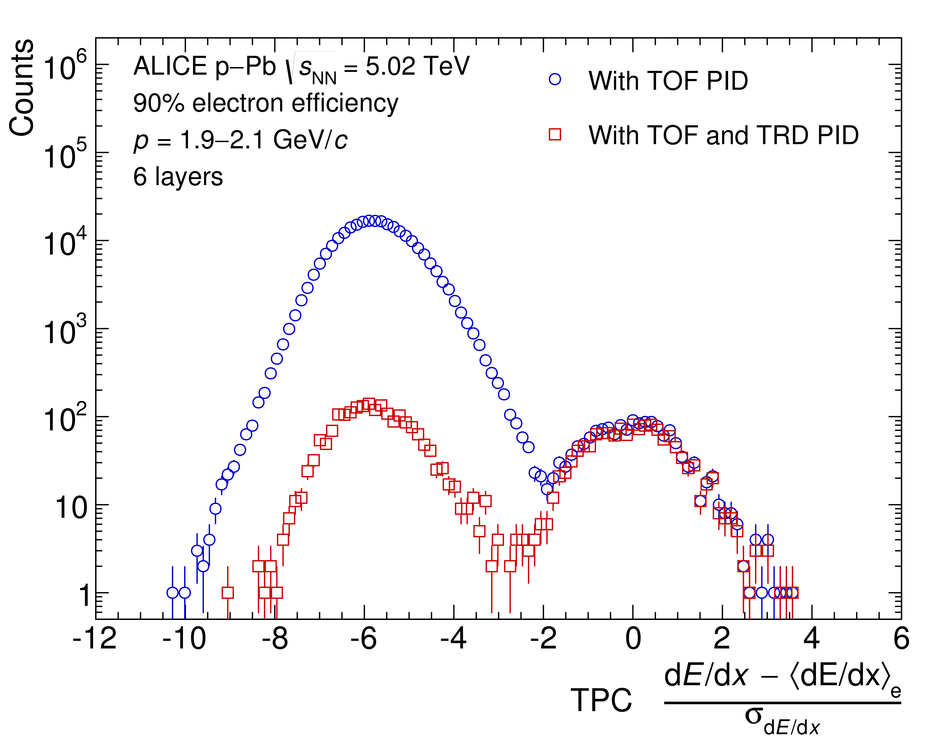
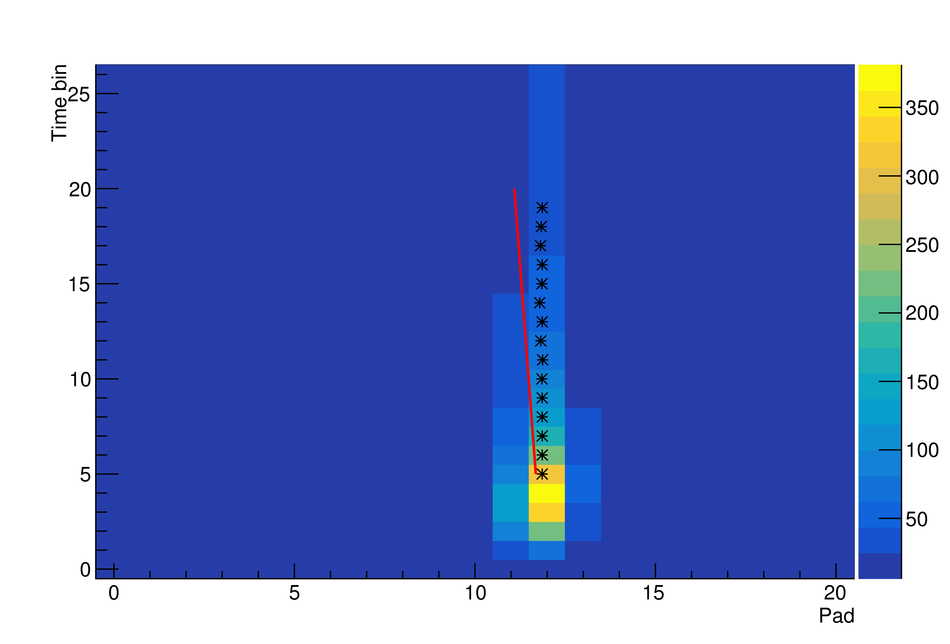
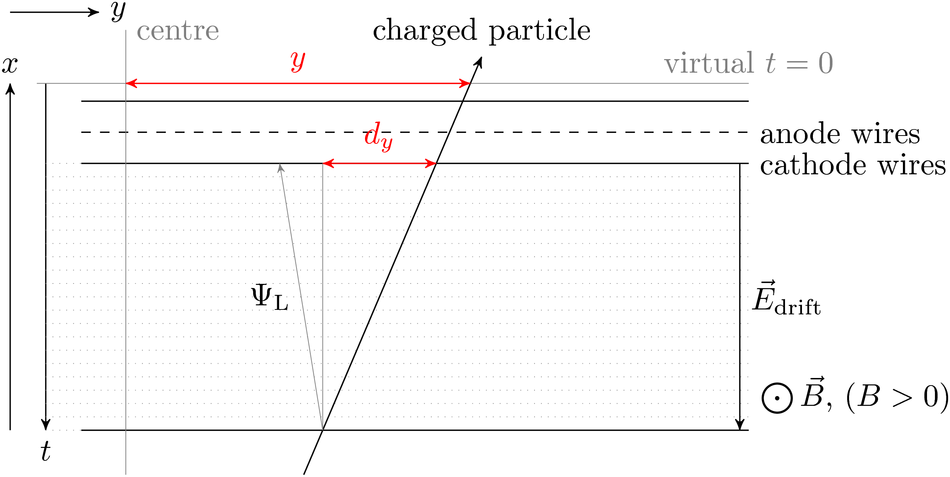
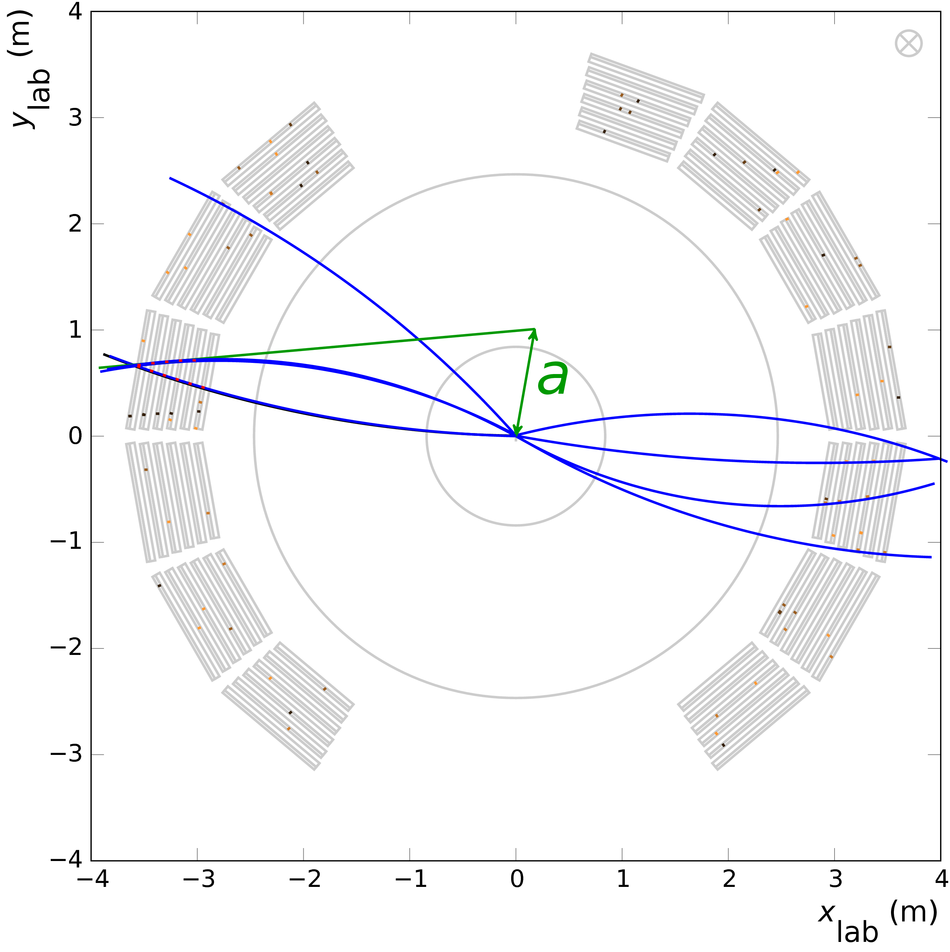
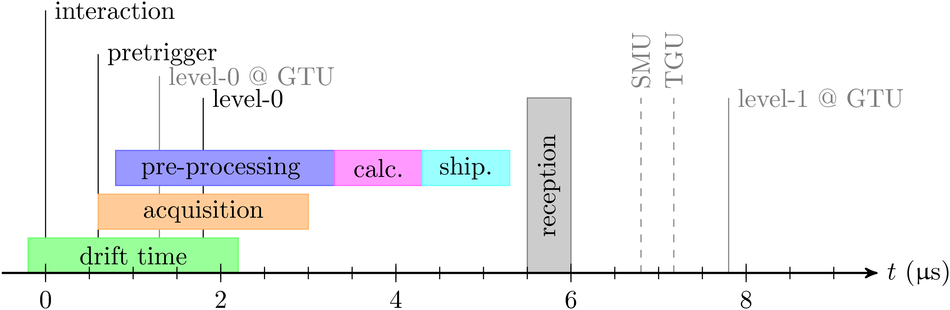
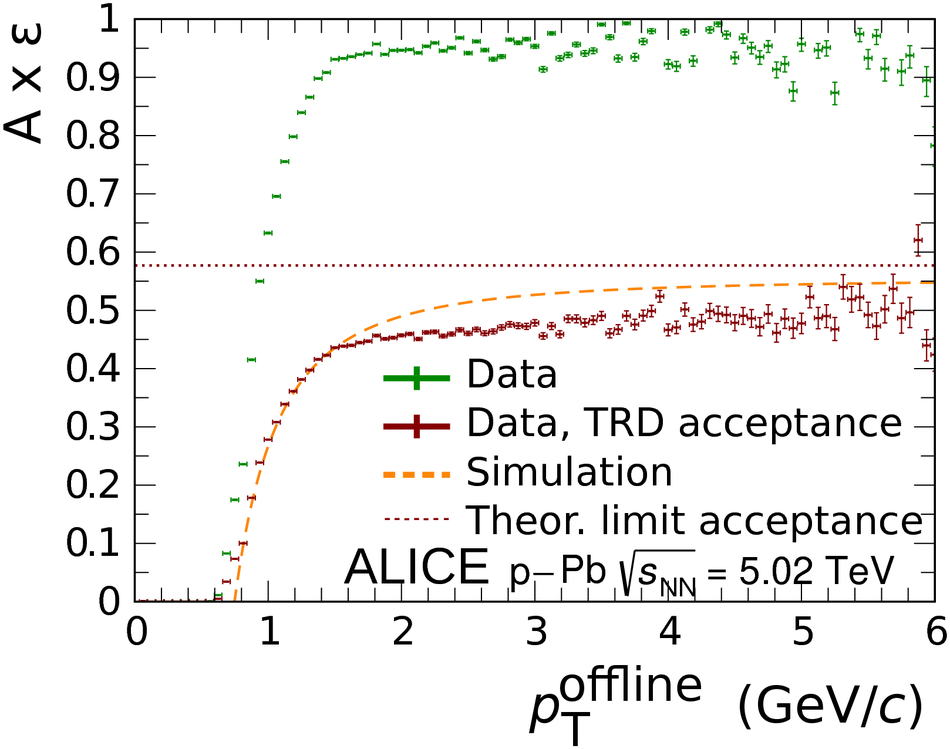
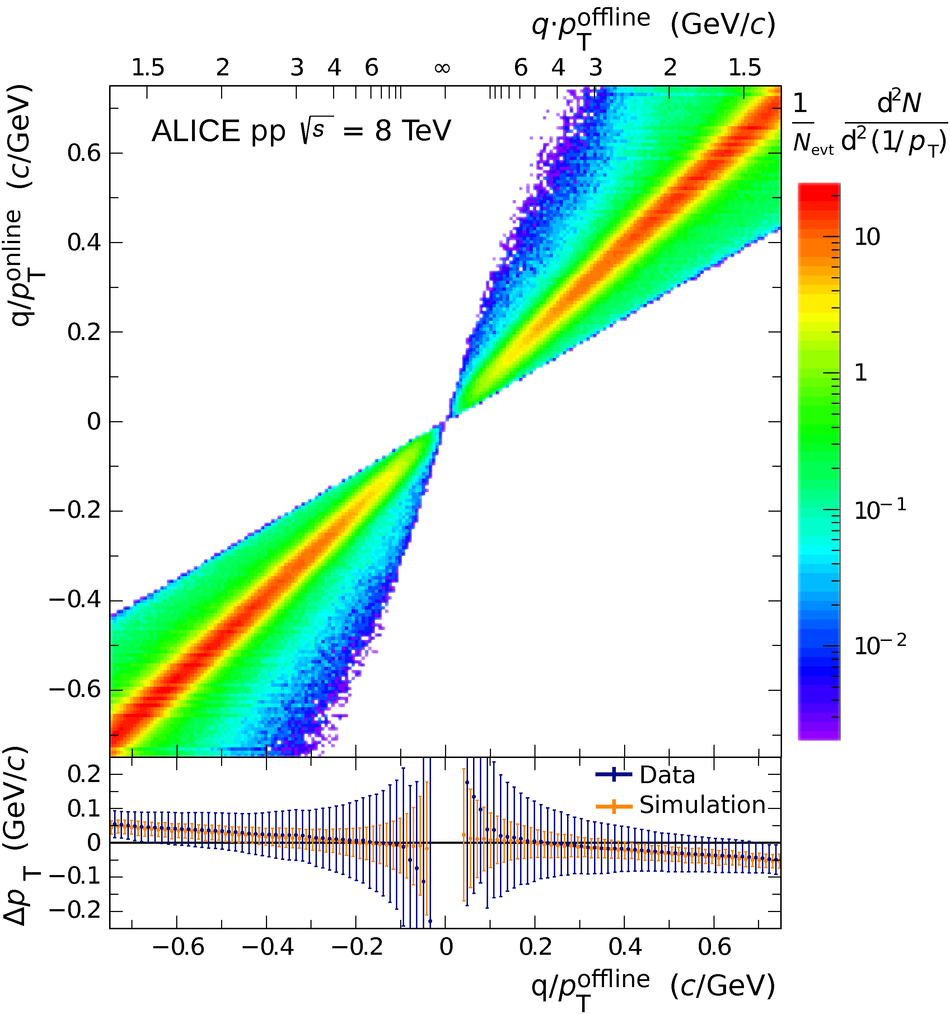
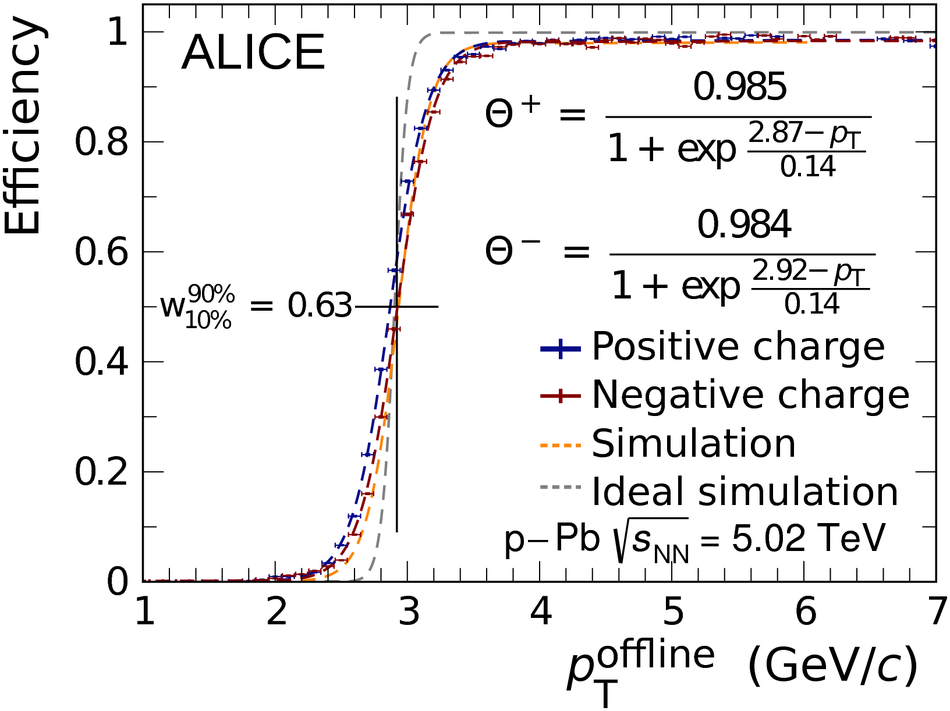
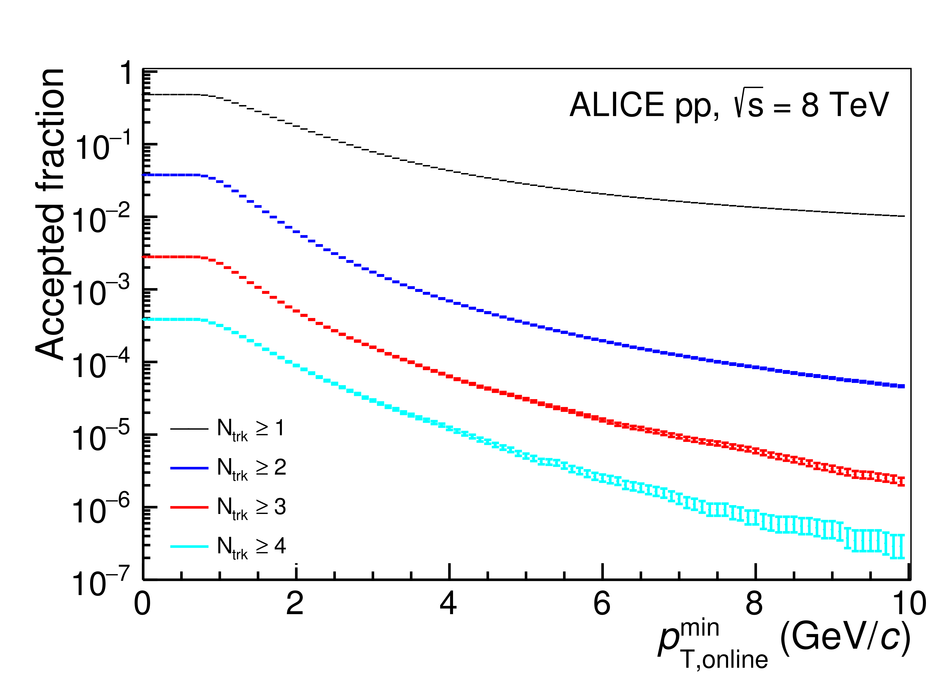
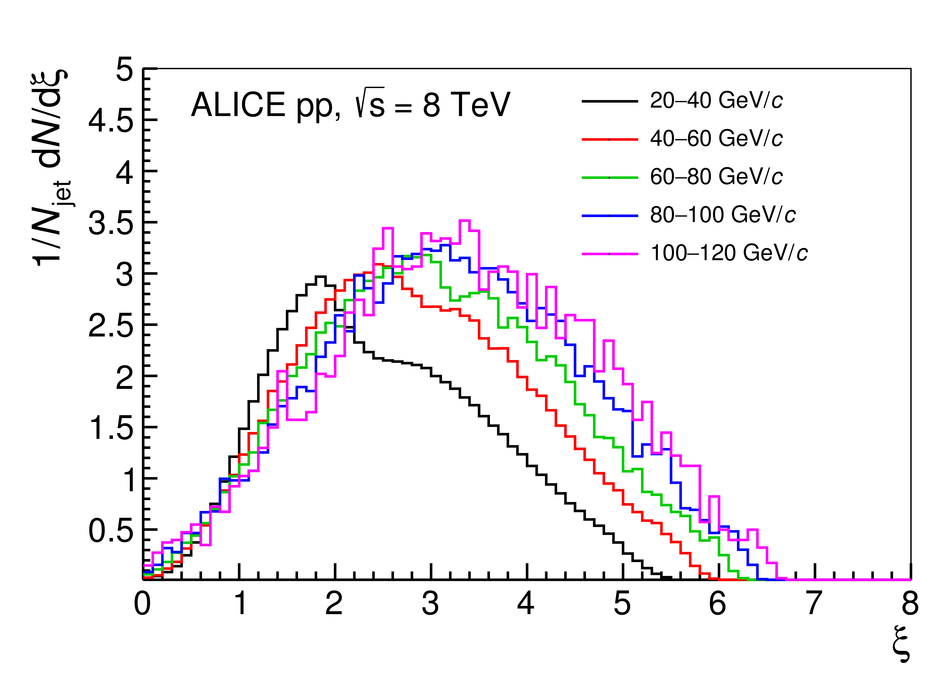
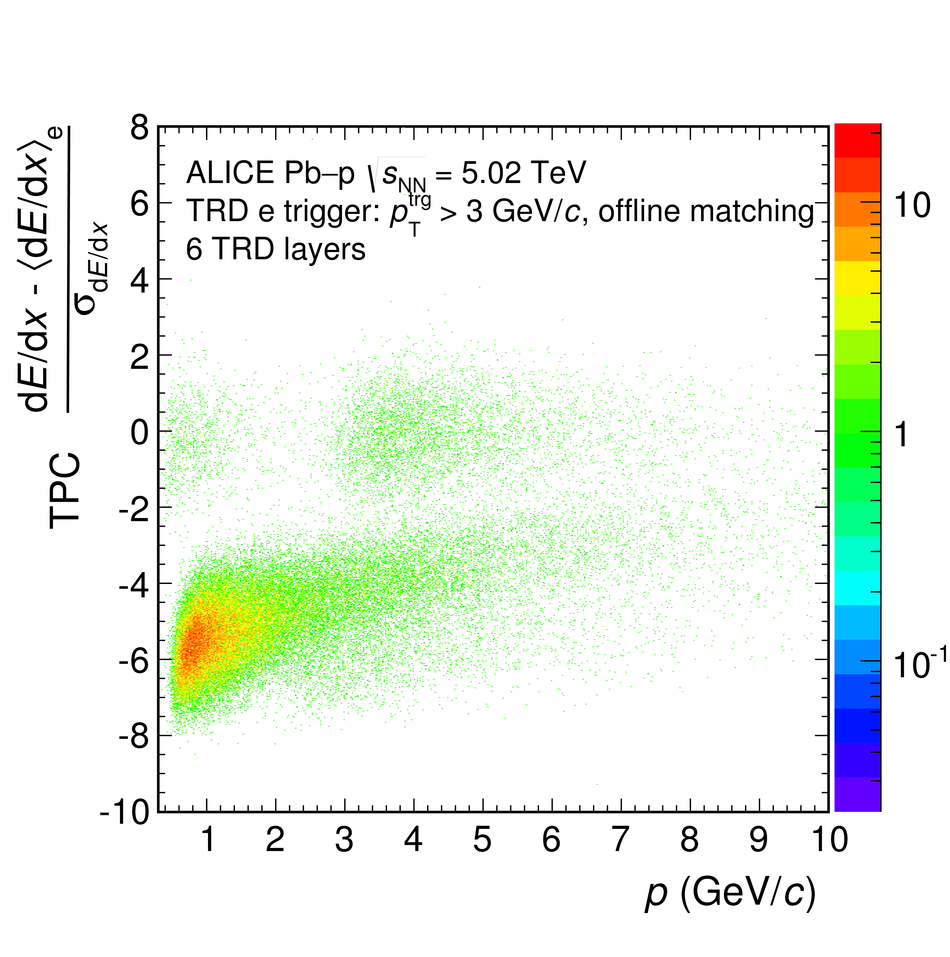
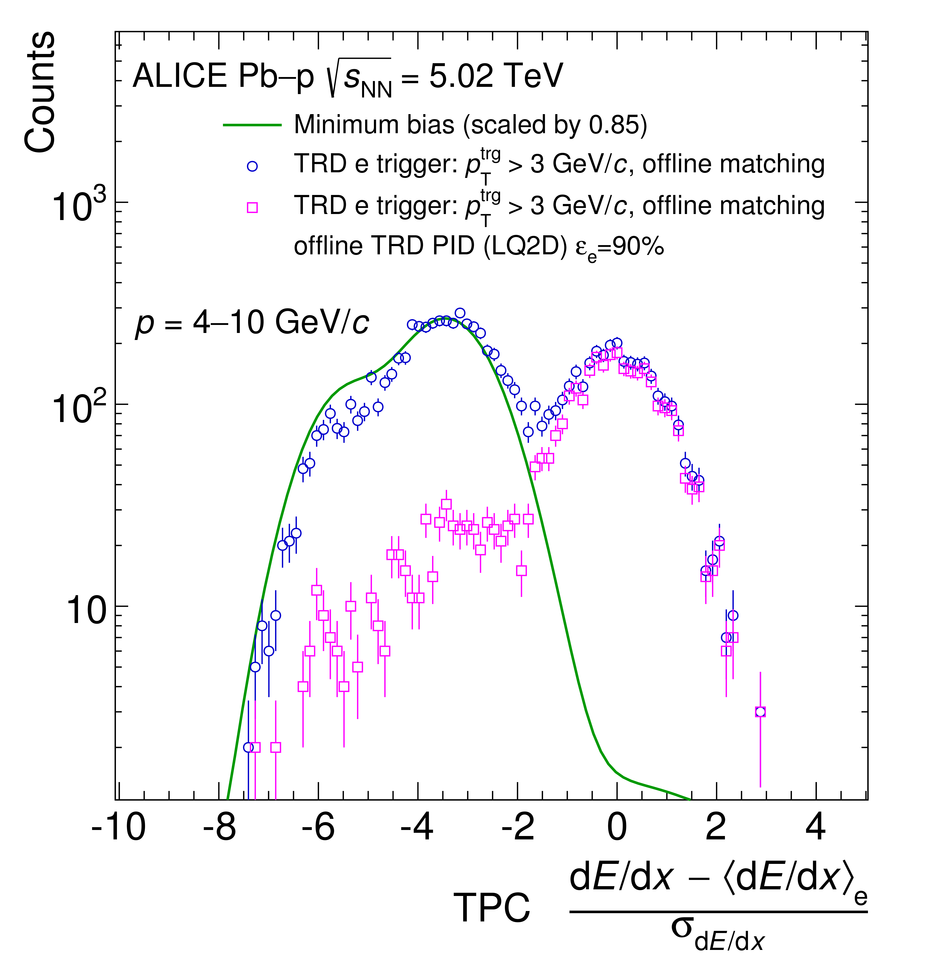
The Transition Radiation Detector (TRD) was designed and built to enhance the capabilities of the ALICE detector at the Large Hadron Collider (LHC). While aimed at providing electron identification and triggering, the TRD also contributes significantly to the track reconstruction and calibration in the central barrel of ALICE. In this paper the design, construction, operation, and performance of this detector are discussed. A pion rejection factor of up to 410 is achieved at a momentum of 1 GeV/$c$ in p-Pb collisions and the resolution at high transverse momentum improves by about 40% when including the TRD information in track reconstruction. The triggering capability is demonstrated both for jet, light nuclei, and electron selection.
Nucl. Instr. Meth. A881 (2018) 88
HEP Data
e-Print: arXiv:1709.02743 | PDF | inSPIRE
CERN-PH-EP-2017-222
Figure 1
Schematic cross-section of the ALICE detector perpendicular to the LHC beam direction (status of the detector since the start of LHC \run{2}). The central barrel detectors cover the pseudorapidity range $| \eta | \lesssim 0.9 $ and are located inside the solenoid magnet, which provides a magnetic field with strength $B$ = \SI{0.5}{\tesla} along the beam direction. |  |
Figure 2
Schematic cross-section of a TRD chamber in the $x$-$z$ plane (perpendicular to the wires) with tracks of a pion and an electron to illustrate the ionisation energy deposition and the TR contribution. The large energy deposition due to the TR photon absorption is indicated by the large red circle in the drift region. The drift lines (solid lines) are calculated with Garfield and correspond to the nominal voltage settings for chamber operation. The radiator is not drawn to scale. |  |
Figure 5
Average pulse height as a function of drift time for pionsand electrons (with and without radiator). The time axis is shown with an arbitrary offset of\SI{0.3}{\micro\second}. The measurements were performed at the CERN PS with prototype read-out chambers that were smaller in overall size (active area \SI{25}{\centi\meter} $\times$ \SI{32}{\centi\meter}) but otherwise similar in construction to that of the final detector. Figure taken from . |  |
Figure 6
Distributions of the ionisation energy loss of pions and electrons with momenta of 2\gevc. The symbols represent the measurements obtained at the CERN PS with prototype read-out chambers that were smaller in overall size (active area \SI{25}{\centi\meter} $\times$ \SI{32}{\centi\meter}) but otherwise similar in construction to that of the final detector. The lines are simulations accounting (continuous line) or not (dashed line) for the long range of $\delta$-electrons as compared to the chamber dimensions. Figure taken from . \TBD{(Replace with GEANT4 once available M.Voelkl)} |  |
Figure 9
The radiation length map in units of $X/X_{0}$ ina zoomed-in part of the active detector area as a function of the pseudorapidityand the azimuthal angle, calculated from the geometry inAliRoot (the colour scale has a suppressed zero). The positions of the MCMs and the cooling pipes are visible as hot spots. The radiation length was calculated for particles originating from the collision vertex. Therefore the cooling pipes of the six layers overlap for small, but not large $\eta$ |  |
Figure 12
Schematic view of the TRD gas system. The gas circulates in a closed loop pushed by a compressor. The flow for each supermodule is determined by the pressure set at individual pressure reducers in the inlet distribution modules. The overpressure is regulated with individual pneumatic valves at the return modules. The gas is purified at the surface and, when needed, supply gas is mixed and added to the loop. For the filling and the removing of the expensive xenon, semipermeable membranes are used to separate it from the CO$_2$. The recovered xenon can be treated in a cryogenic plant in order to remove accumulated N$_2$, prior to storage. |  |
Figure 16
Simulation of the dead time as function of the read-out rate in Pb--Pb collisions for the effective DDL bandwidth in \run{1} (DDL) and \run{2} (DDL2). The simulation assumes a 5\% L1/L0 accept ratio and no L2 rejects. The scenarios central and mix correspond to an event size of 470 kB and 310 kB per supermodule, respectively, mimicking thus different event multiplicities |  |
Figure 19
Graphical User Interface: example panel (FSM top node) representing the status in the year 2010 (i.e.\ with 10 installed TRD sectors). The FSM state of the main systems of each sector is represented by the corresponding colour; run status and alarm summary are displayed. The panel gives quick access to emergency actions and detailed monitoring panels via single mouse clicks. |  |
Figure 22
Signal produced by a positively charged particle ($\pt = 0.5\gevc$). Left: Total charge per time bin used for particle identification Right: Ionisation signal vs. pad number and time bin. The cluster positions are shown as reconstructed from the charge distribution (raw clusters) and after correction for the $E \times B$ effect (Lorentz-corr. clusters). |  |
Figure 26
Dependence of the position resolution on charge over transverse momentum for simulated tracks in the TRD (red) and in the TPC (blue), reconstructed global tracks from simulation (gray) and from \pp collisions at $\sqrt{s} = 13 \mathrm{TeV}$ (black). The label TRD-TPC indicates global tracks reconstructed with the ITS and TPC that were extrapolated to the TRD. The green line represents the theoretical value for the combined resolution of TRD and global tracks. The red line shows a parabolic fit to the corresponding points. |  |
Figure 28
Left: Cosmic-ray tracks with at least 100 TPC clusters and 5 TRD layers, recorded without magnetic field, used for the relative $r\varphi$ alignment of the TRD chambers within stacks (internal alignment). Right: Charged-particle tracks with at least 100 TPC clusters and 4 TRD layers from \pp collisions at $\sqrts=8$ TeV, used for the alignment of the TRD with respect to the TPC (external alignment). Both figures show data from 2012 (setup with 13 supermodules). |   |
Figure 29
TRD tracklet to TPC track residuals in $y$ as a function of the $z$ coordinate of the TPC track ($z_{\rm track}$)for supermodules 2 (left) and 6 (right). The colour code is linear in the number of tracks. The upper and lower panels show the situation with the survey alignment and with in addition the external alignment, respectively. The data are from a 2012 run of \pp collisions with B = $-$\SI{0.5}{\tesla}. The alignment set used for the lower plots was deduced from the same run. The internal alignment is applied in all four cases. |  |
Figure 30
Average pulse height vs.\ drift time plot (derived from Fig. \ref{fig:ph}) illustrating the main calibration parameters. For better understanding, a sketch of the chamber cross-section with field lines from Fig. \ref{fig:roccross} is shown at the top. The peak at the left and the edge on the right of the drift time spectrum correspond to the anode wires and the chamber entrance window. The temporal difference between them depends on the drift velocity. The anode-peak position defines the time offset. The mean pulse height and the pedestal width are related to the gain and the pad noise, respectively. |  |
Figure 35
Two quality-assurance plots (data from \pp collisions recorded in 2015 with all supermodules installed, tracks with at least 70 TPC clusters and $\pt>0.5$\gevc). Left: Efficiency of matching tracklets to TPC tracks. Right: Mean number of layers per track in each stack (cf.\ the discussion of inactive chambers in Section \ref{Chapterhvinbeam}). |   |
Figure 36
Total integrated charge, normalised to the tracklet length, measured in a single read-out chamber for electrons and pions in \ppb collisions at \mbox{\sqrtsnn = 5.02 TeV}, in comparison with results from test beam measurements (solid lines) . The electrons and pions from test beam measurements were scaled by one common factor to compensate the difference in gain of the two data sets. |  |
Figure 37
Most probable charge deposit signal normalised to that ofminimum ionising particles as a function of $\beta\gamma$. The data are from measurements performed in test beam runs, \pp collisions at \mbox{\sqrts = 7 TeV}, and cosmic-ray runs. Uncertainties in momentum and thus $\beta\gamma$ determination are drawn as horizontal and statistical uncertainties as vertical error bars. The shown fits correspond to the Equations \ref{equ:aleph} and \ref{equ:logistic} described in the text. |  |
Figure 42
Pion efficiency as a function of electron efficiency (left, for 6 detector layers) and as a function of the number of detector layers (right, for 90\% electron efficiency) for the various eID methods The results are compared for the momentum interval 0.9--1.1\gevc in \ppb collisions at \sqrtsnn = 5.02 TeV. The results of the truncated mean method are only shown for a minimum of 4 tracklets, where the resolution is better than 18\% (see Fig. \ref{Figure_truncmeanres}). |   |
Figure 44
Difference in units of standard deviations between the measured TPC energy loss of a given track and the expected energy loss of an electron with TOF ($\pm 3 \sigma^\mathrm{TOF}_\mathrm{e}$) and TRD (90\% electron efficiency) electron identification. The distributions are shown for tracks with a momentum of 1.9--2.1\gevc within the TRD acceptance (6 layers in the TRD) in \ppb collisions at \sqrtsnn = 5.02 TeV. |  |
Figure 46
Sketch of the tracklet reconstruction. The tracklet reconstruction in the MCMs is performed in a local coordinate system. The tracklet comprises the information on $y$, $d_y$, $z$ and PID. The magnetic and electric field and the effect of the Lorentz angle ($\Psi_{\rm L}$) are indicated as well. |  |
Figure 48
Event display showing the tracks available for the level-1 trigger from the online reconstruction (green) in comparison with helix fits to the contributing tracklets (blue). The offset $a$ from the primary vertex used as measure for $1/\pt$ is shown as well. The colour coding of the tracklets (small boxes) is according to stacks. |  |
Figure 51
Acceptance times efficiency of the global online tracking for primary tracks (Data) and tracks in the detector acceptance (Data, TRD acceptance) as function of the transverse momentum of the global offline track (trigger threshold at 2--3\gevc). The results of an ideal simulation, not considering non-operational parts of the real detector, are drawn for comparison. The dotted line shows the theoretical limit of the acceptance with $13$ out of $18$ supermodules installed during the \ppb data taking period in \run{1}. |  |
Figure 52
Top: Correlation between $1/p_\textrm{T}$ obtained from the online tracking and from a matched offline track for pp collisions at $\sqrt{s} = 8 \mathrm{TeV}$. Bottom: Difference (points) of the online and offline track \pt for data and simulation. The error bars indicate the corresponding width of the difference in $p_\textrm{T}$ |  |
Figure 53
Turn-on curve of the trigger with a \pt threshold of 3\gevc for positively and negatively charged particles in comparison to the same variable computed in simulation with a realistic detector geometry (active channels). Also shown is the corresponding distribution for an ideal detector geometry (ideal simulation, not considering misalignment). The onset is characterised by a fit with a Fermi function. |  |
Figure 54
Rejection by the level-1 trigger for requiring 1--4 tracks in any stack ($N_{\rm trk}$) above varying \pt thresholds for pp collisions at \sqrts = 8 TeV . The error bars indicate the statistical uncertainties. The distributions were obtained by counting the number of tracks in a stack above a given threshold and normalised by the number of sampled events. |  |
Figure 55
Left: \pt spectra of leading jets for the minimum-bias and triggered samples of pp collisions at \sqrts = 8 TeV . The leading jets are defined as the jets with the highest \pt in the event. Right: For comparison the \pt spectra were scaled to the same yield between 60 and 80\gevc. The spectra were re-binned to calculate the ratios. |   |
Figure 57
$n_{\sigma^\mathrm{TPC}_\mathrm{e}}$ as a function of momentum for Pb--p collisions at \mbox{\sqrtsnn = 5.02 TeV} recorded with the electron trigger (\pt threshold at 3\gevc) Electrons from photon conversions in the detector material were rejected bymatching the online track with a track in the TPC |  |
Figure 58
Electron selection for triggered data with and without the TRD offline PID (see Section \ref{Chapterpid}) in Pb--p collisions at \mbox{\sqrtsnn = 5.02 TeV}. Electrons from photon conversions in the detector material were rejected by matching the online track with a track in the TPC. The corresponding distribution for minimum-bias data, scaled to the maximum of the distribution of the triggered data sample, is shown to visualise the TRD trigger capability to enhance electrons. |  |
Figure 59
\pt spectra of identified electrons for the minimum-bias and TRD-triggered data sample of Pb--p collisions at \mbox{\sqrtsnn = 5.02 TeV}. For the result of the TRD-triggered sample, electrons from photon conversions in the detector material were rejected by matchingthe online track with a track in the TPC |  |
