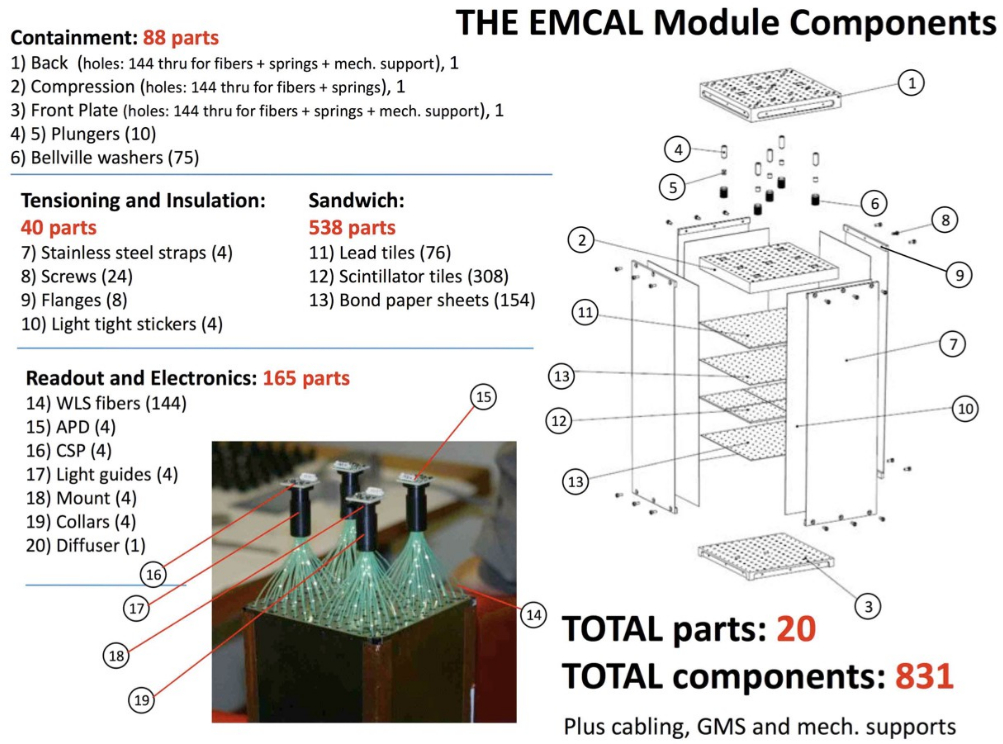
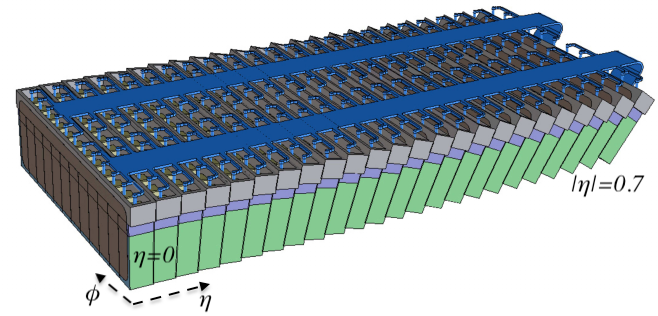
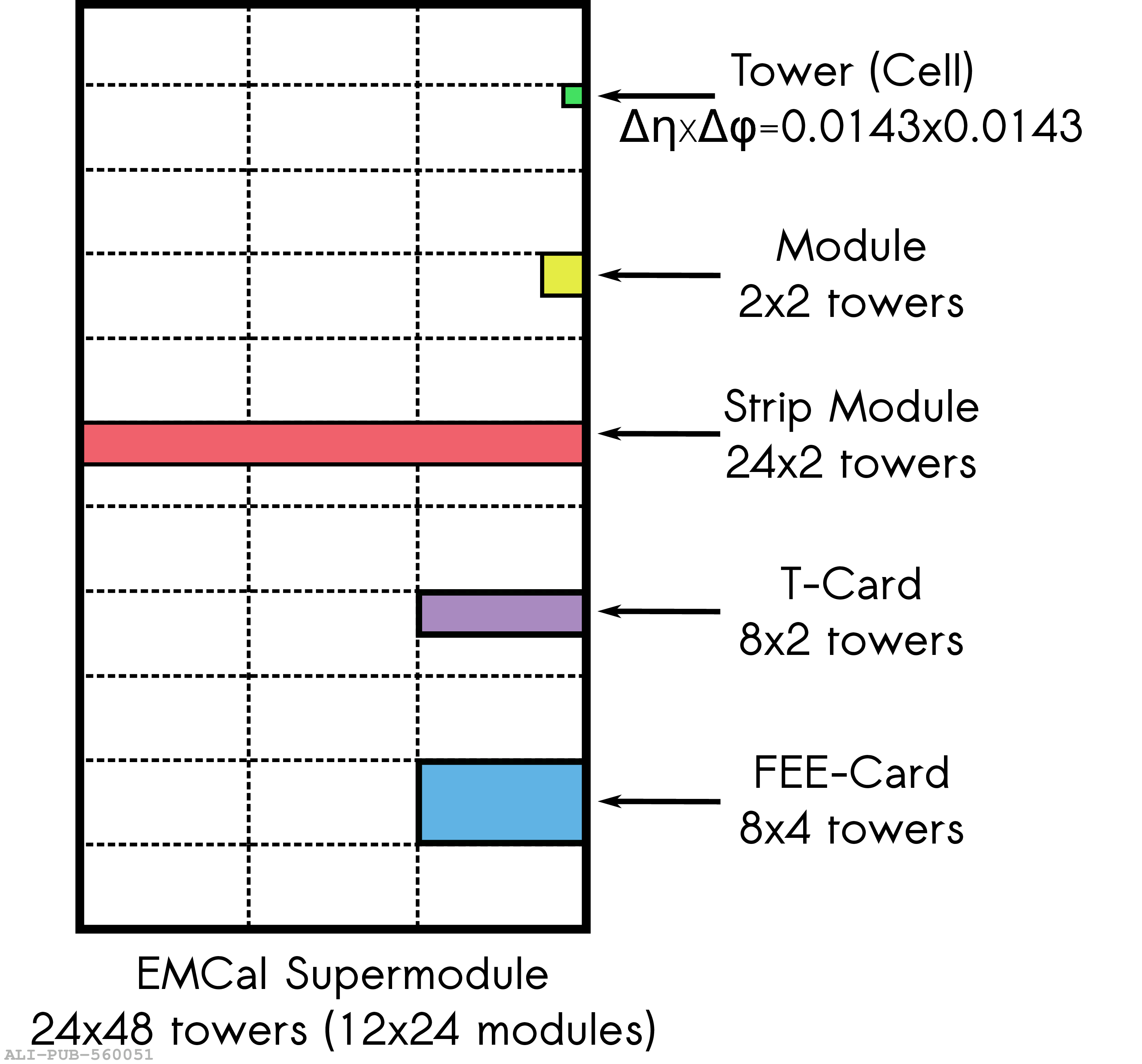
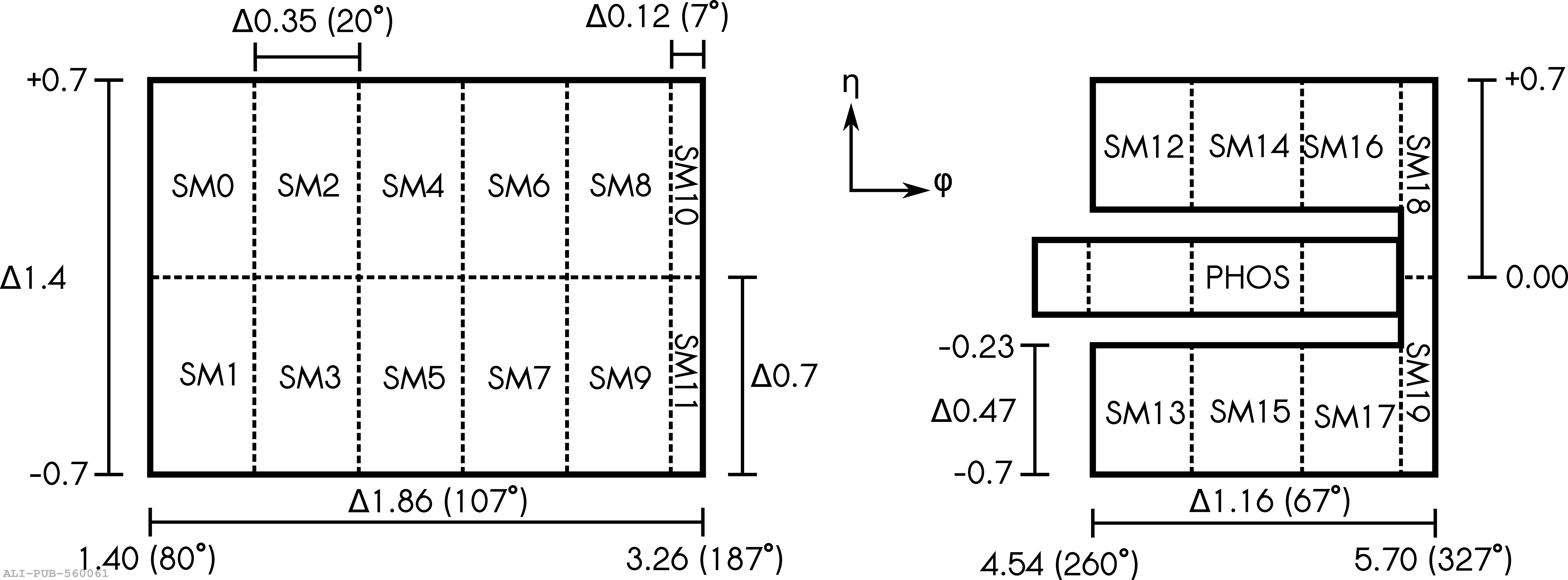
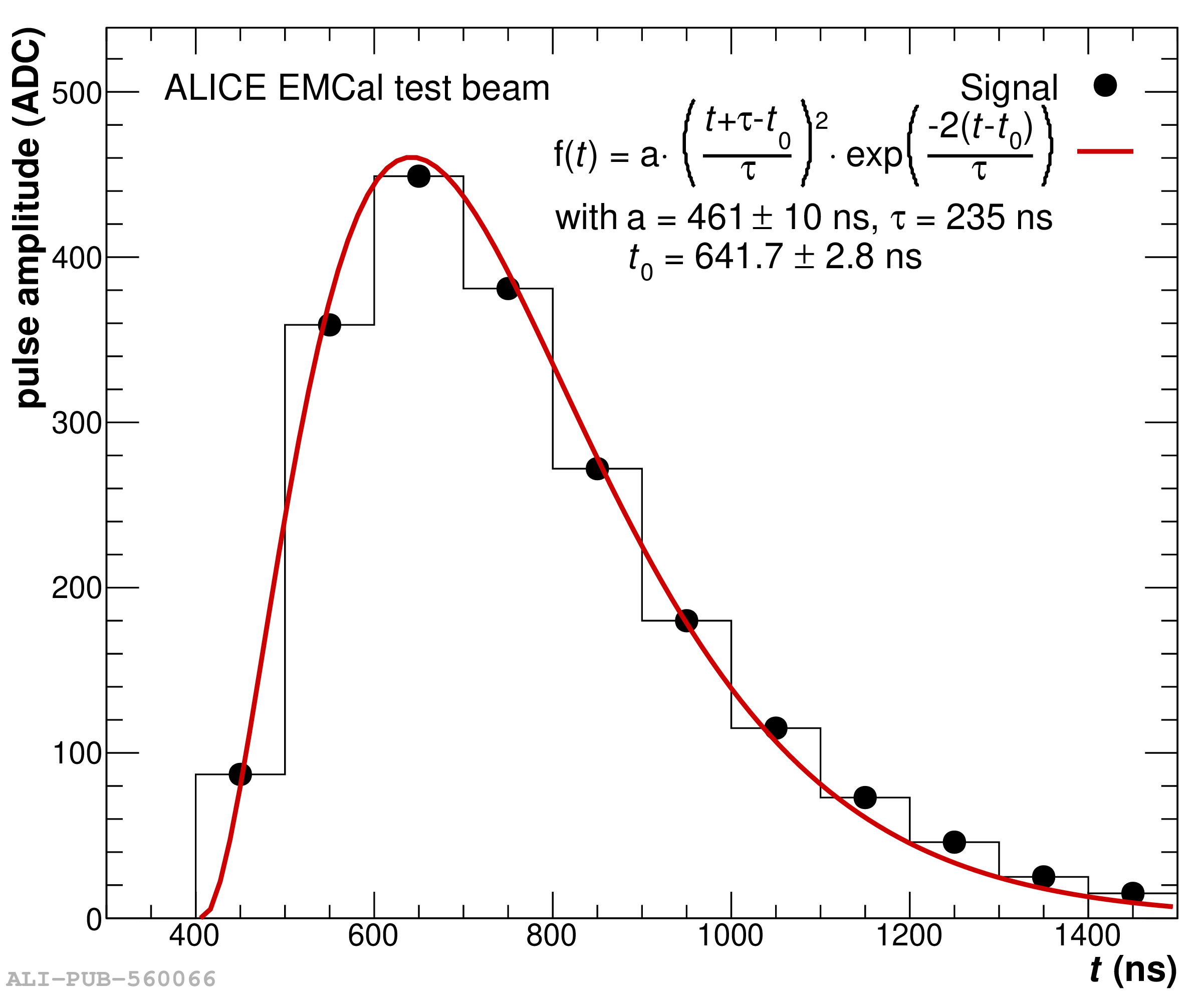
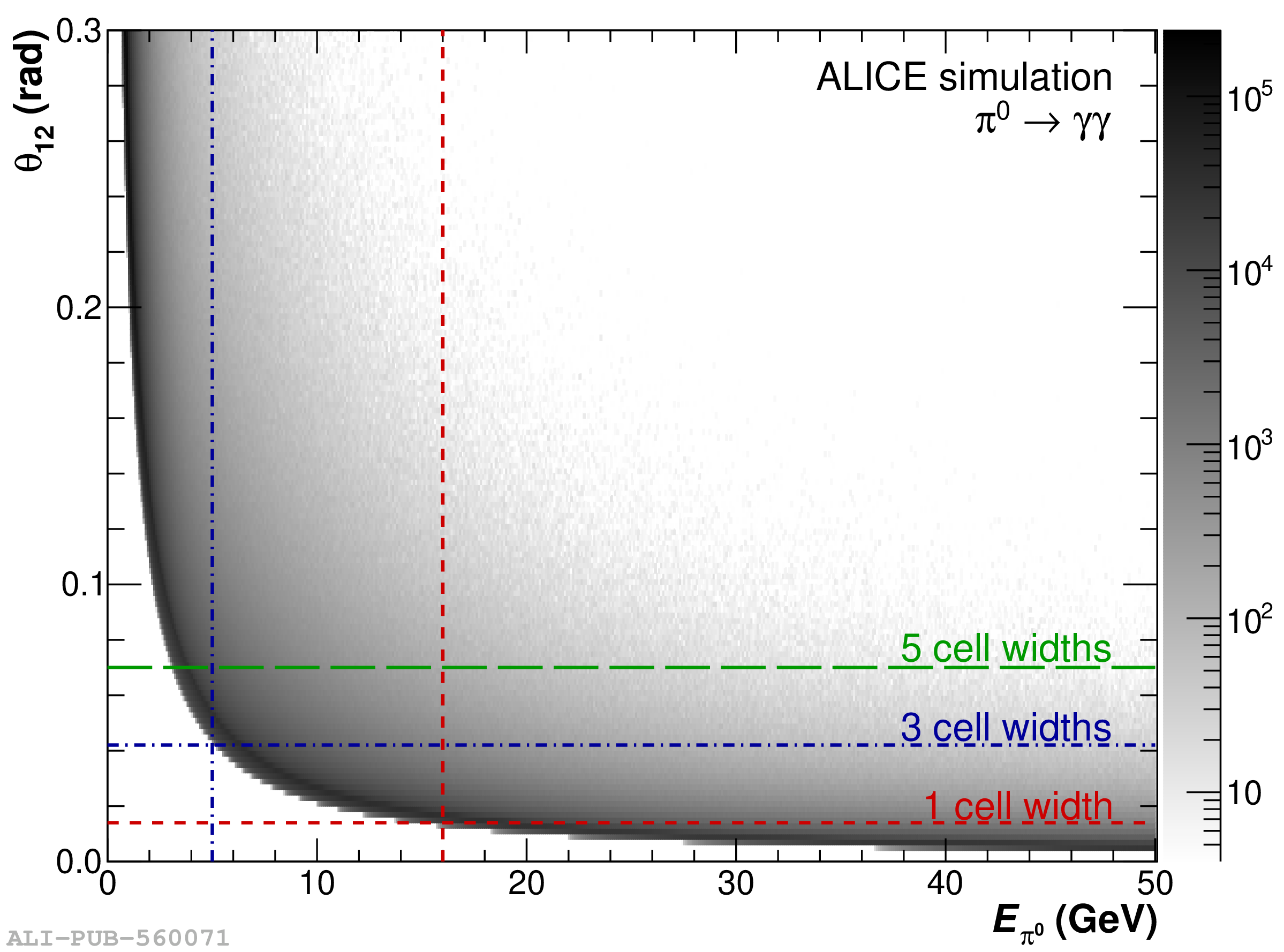
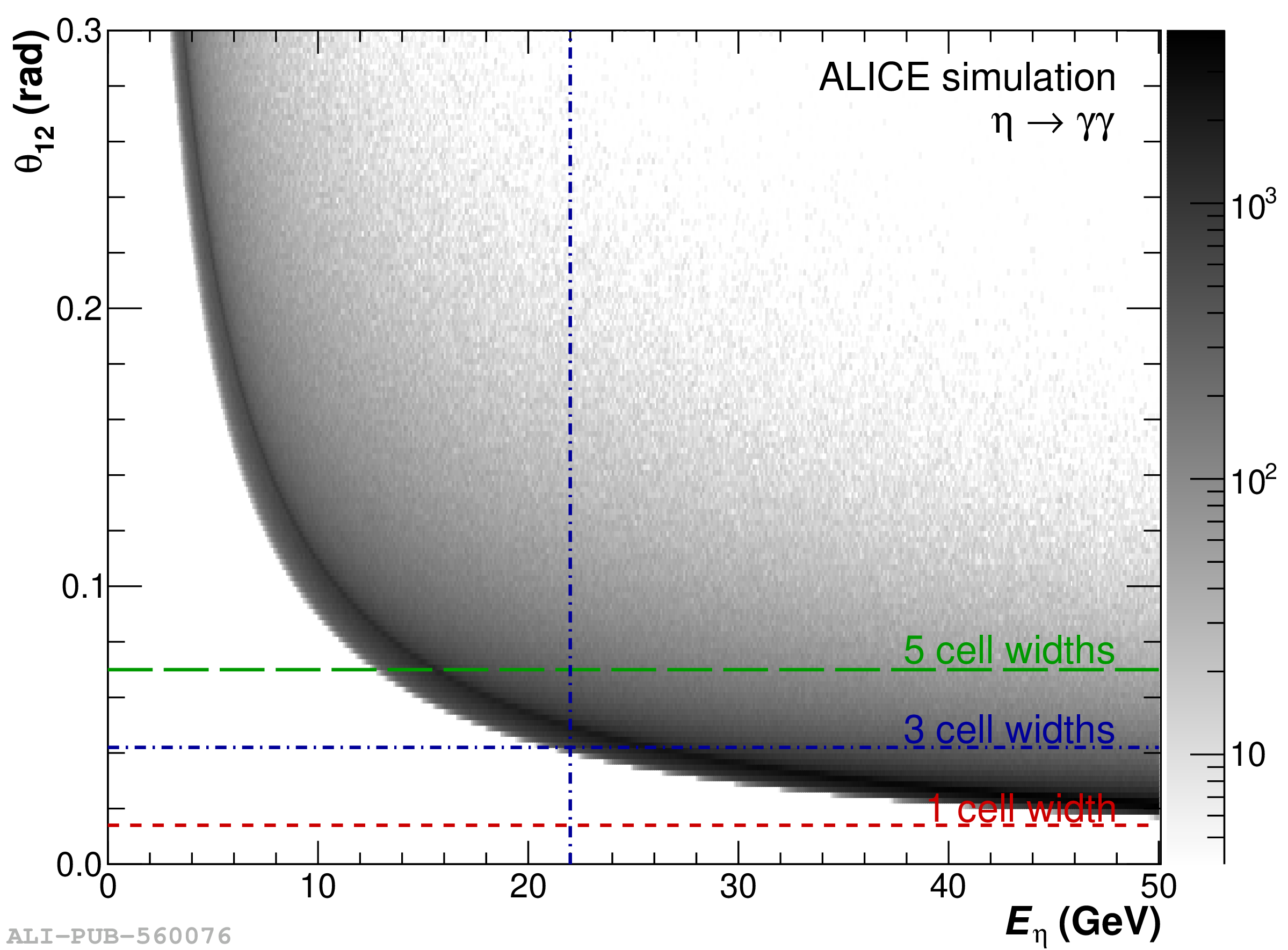
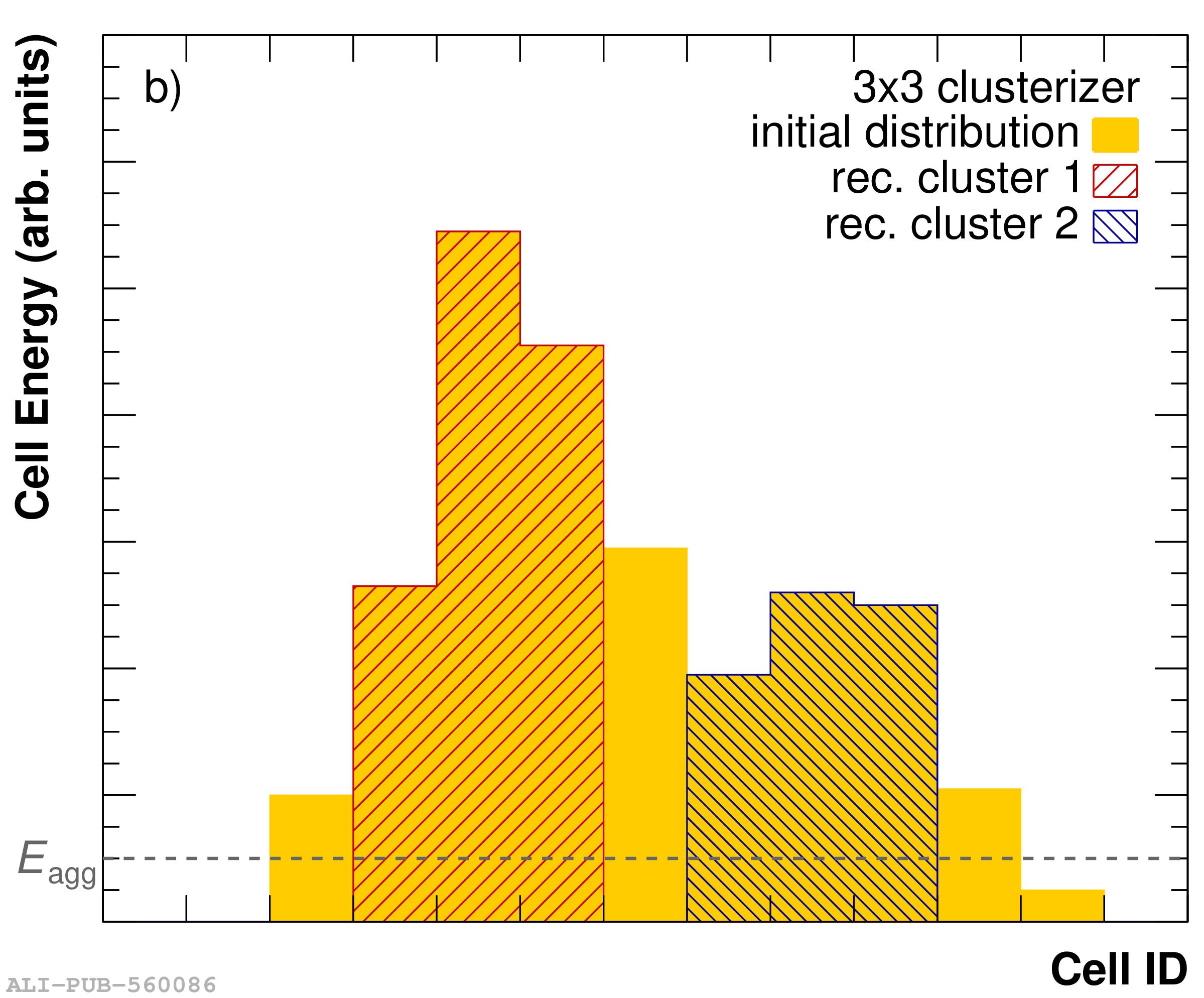
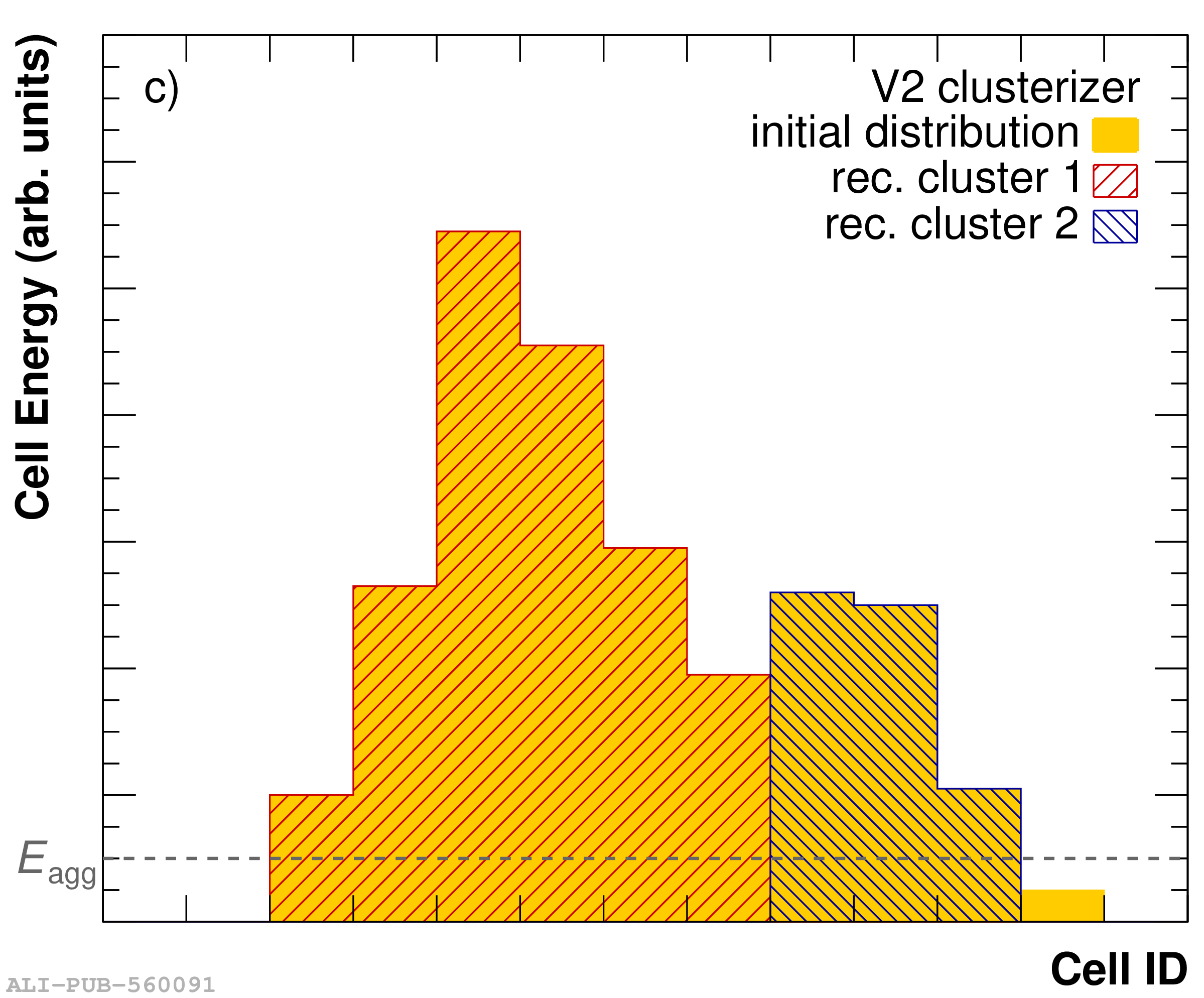
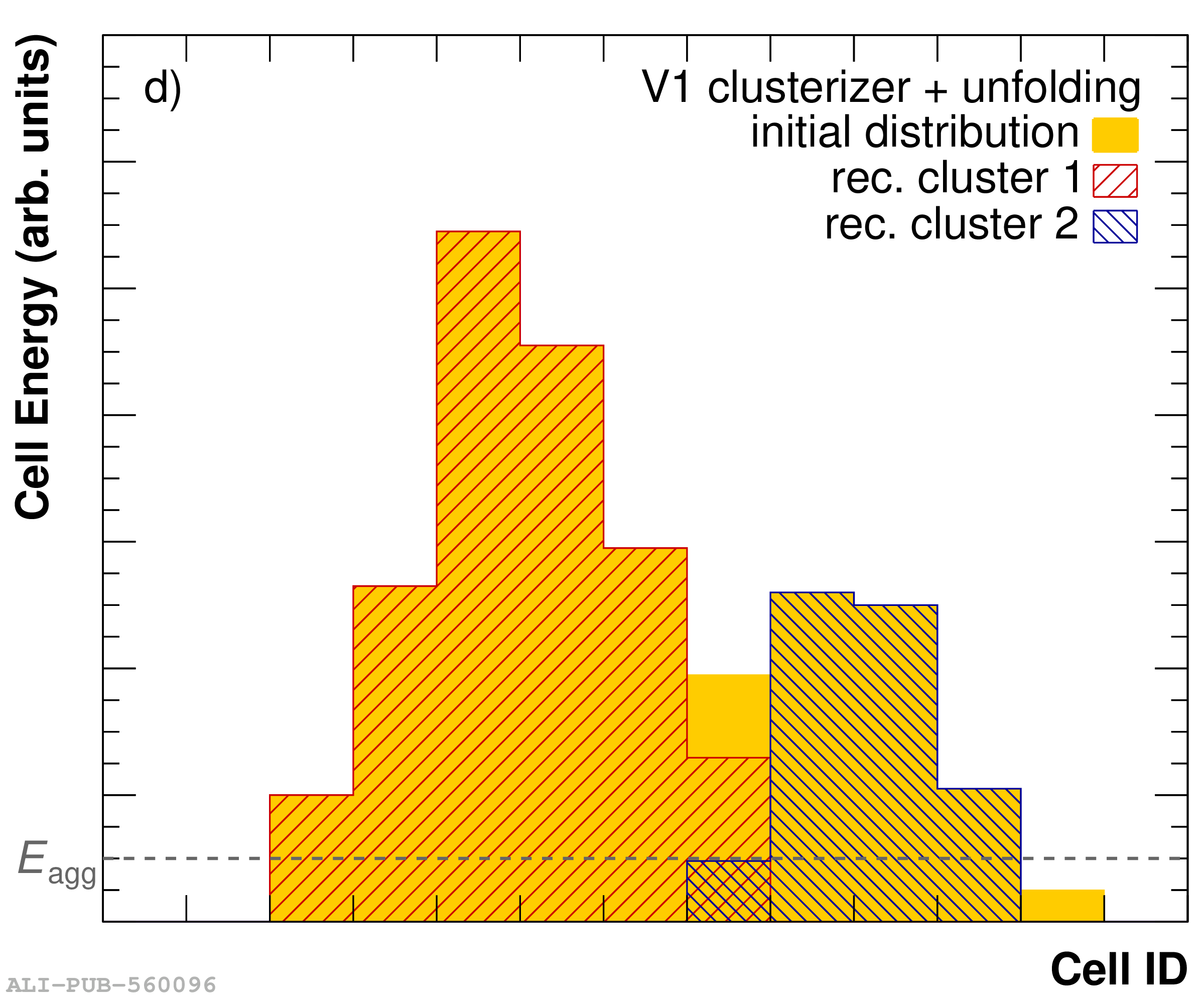
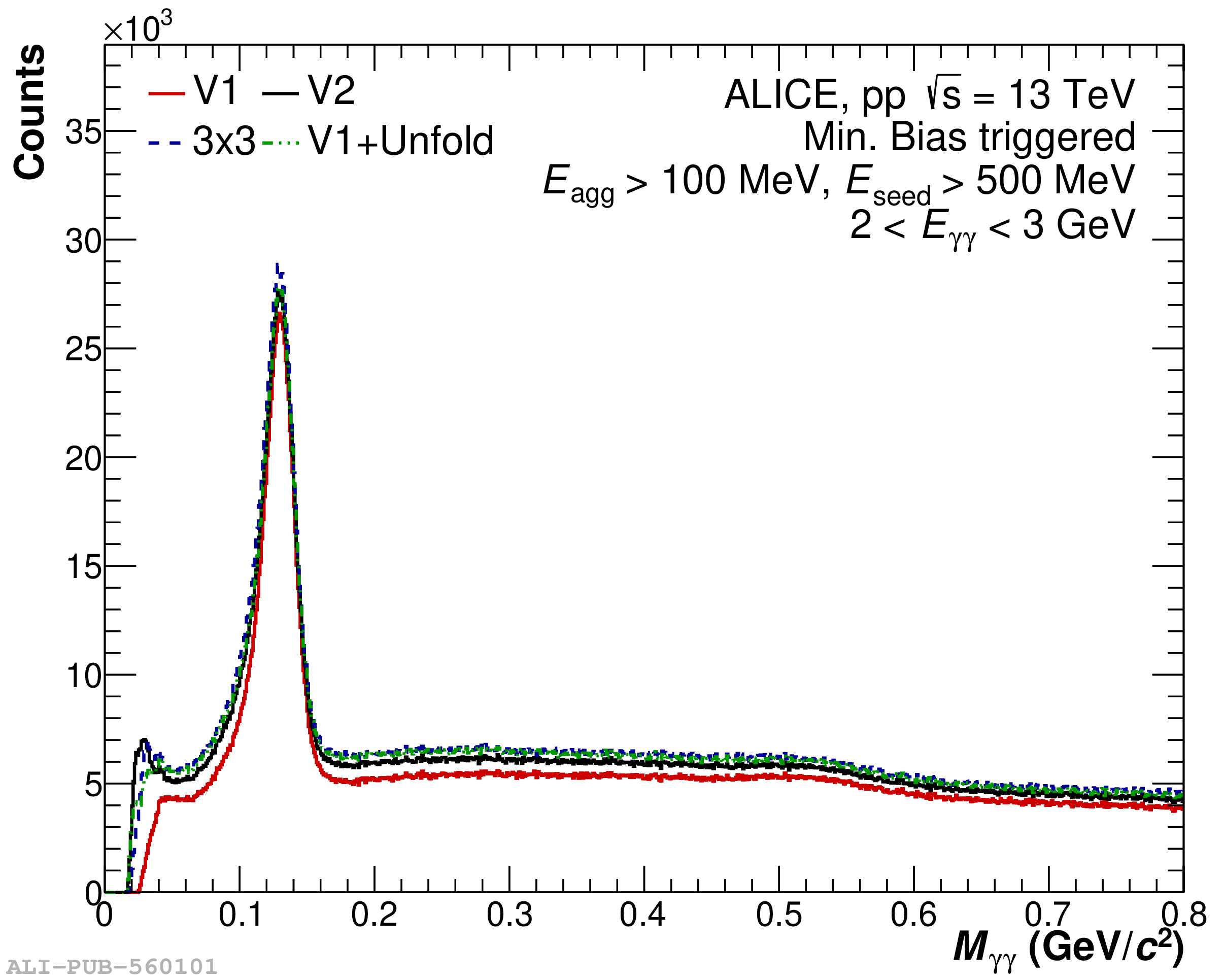
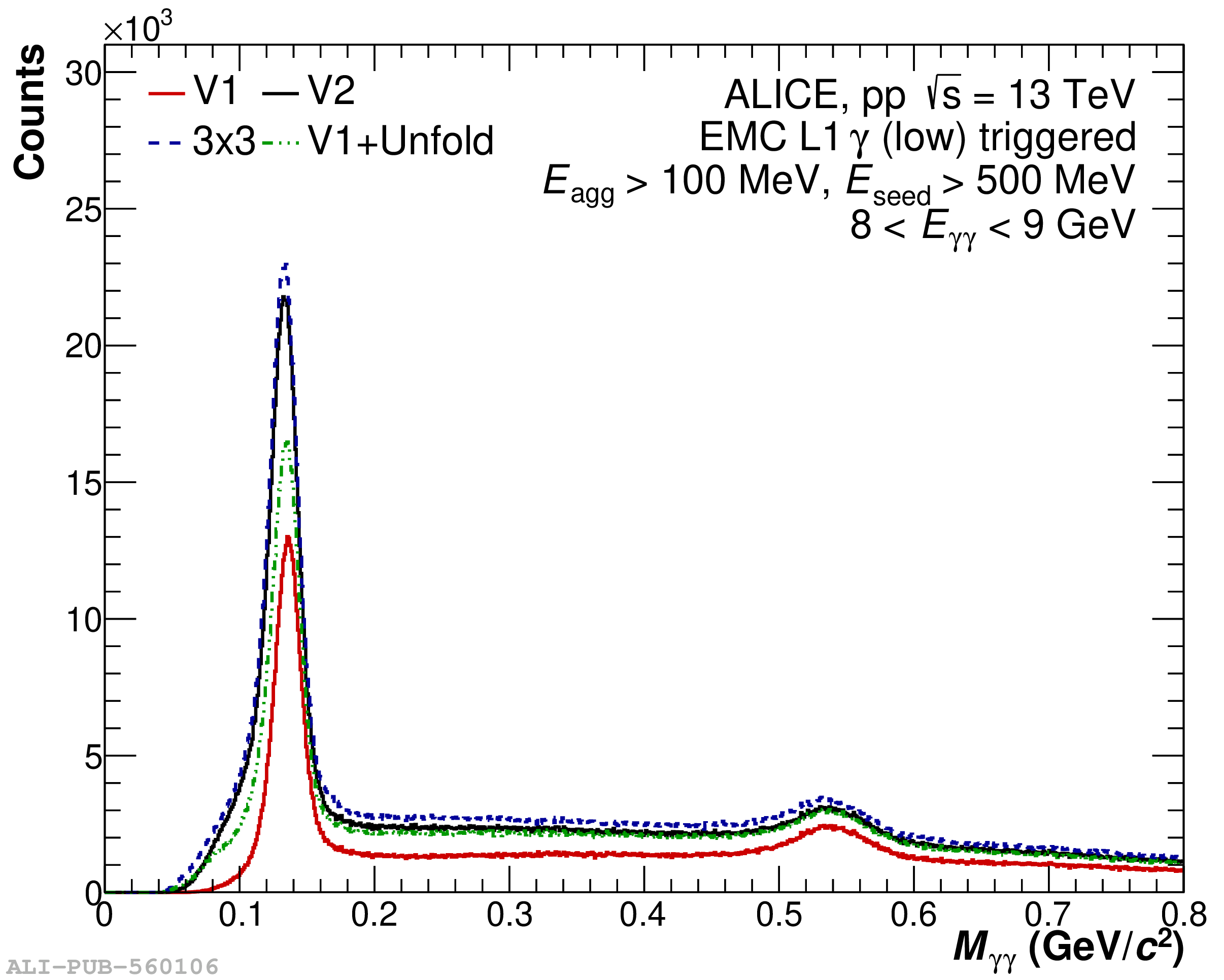
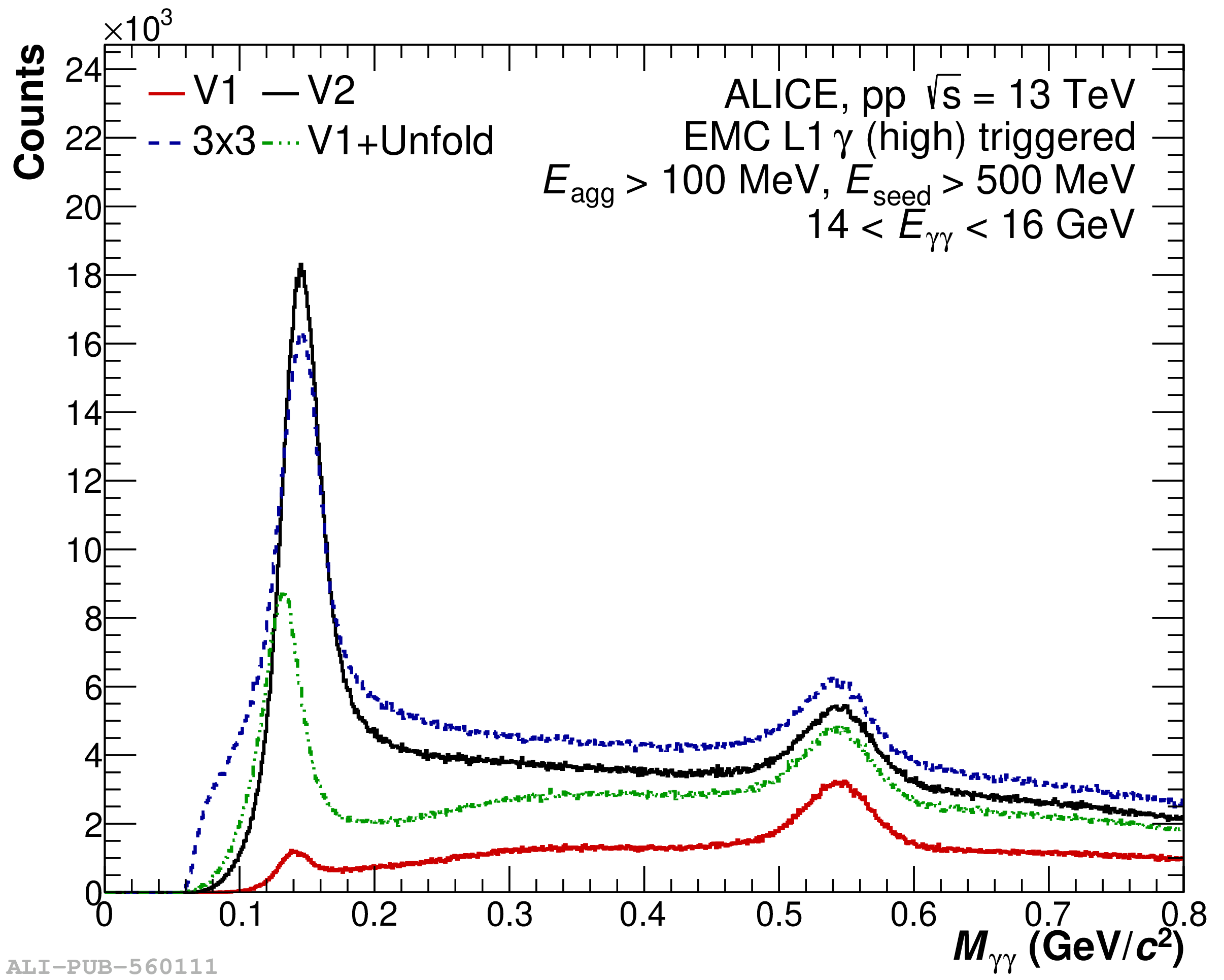
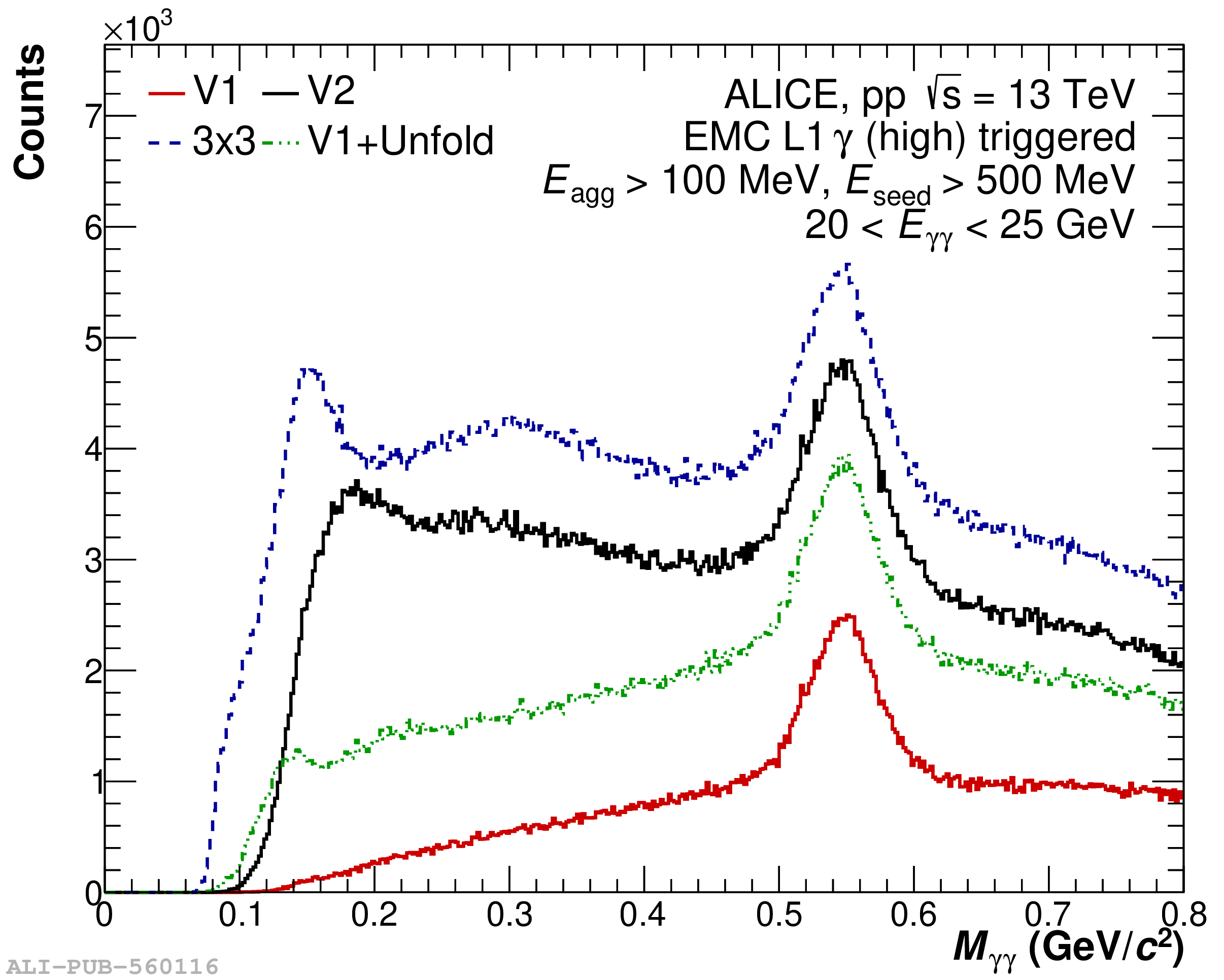
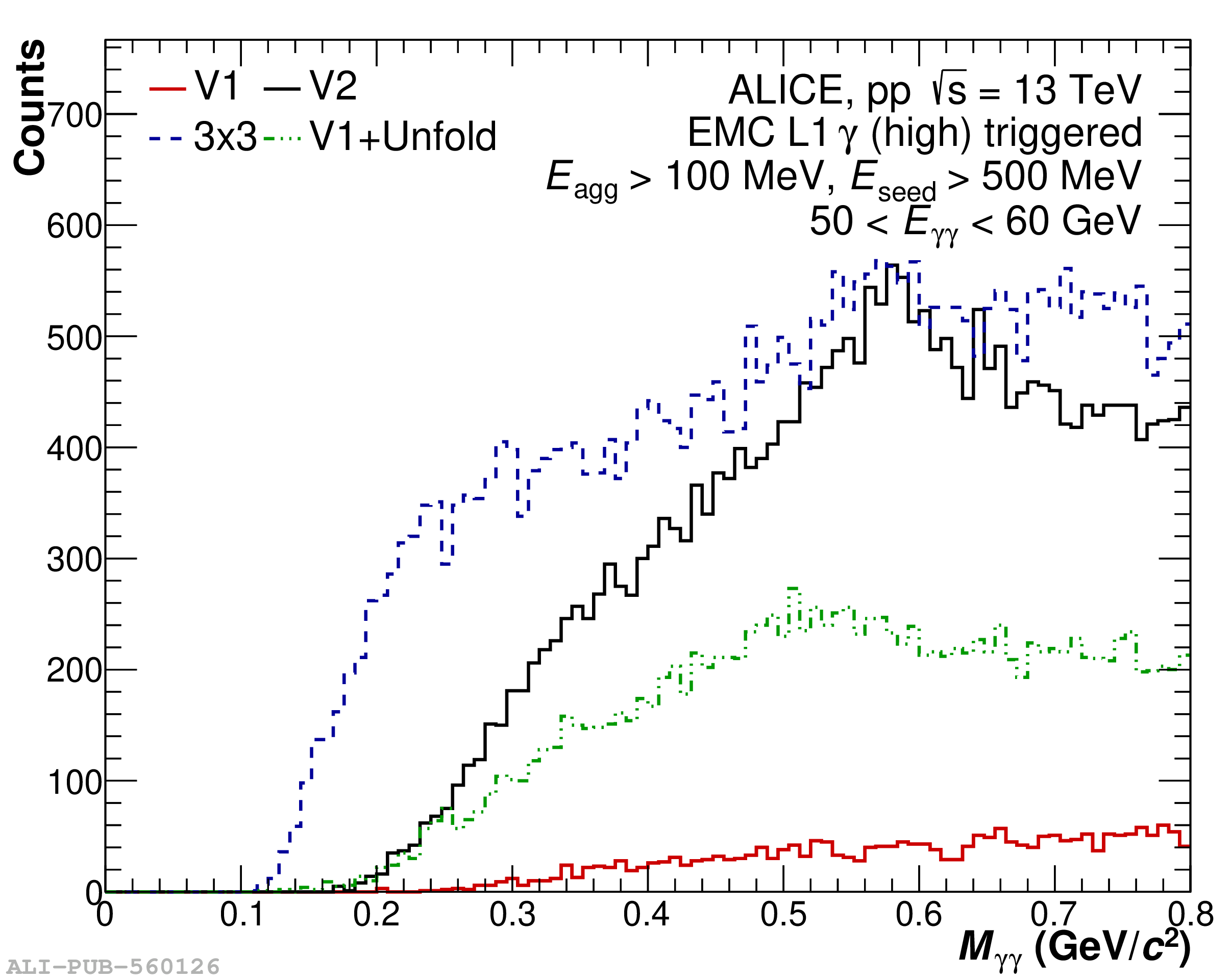
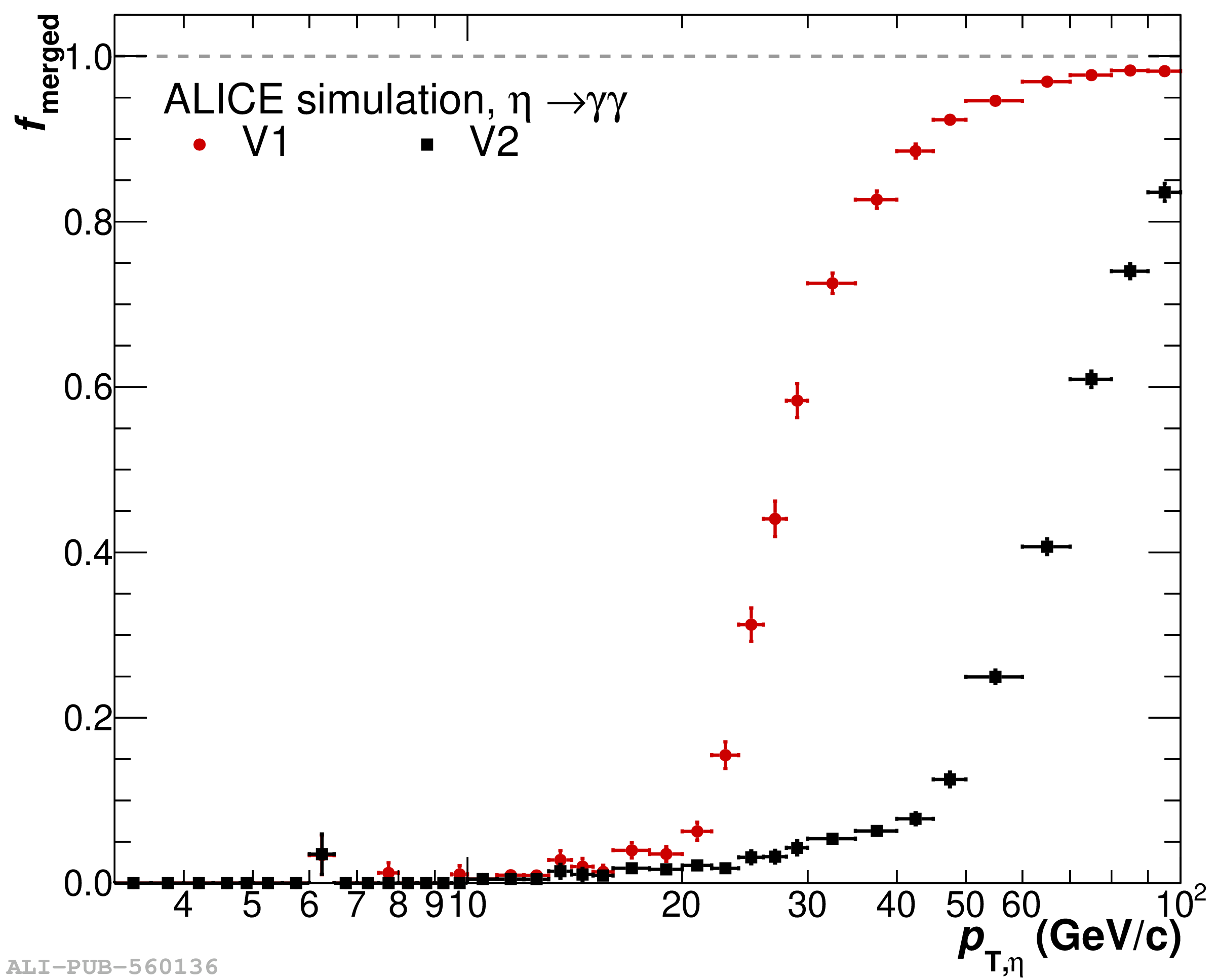
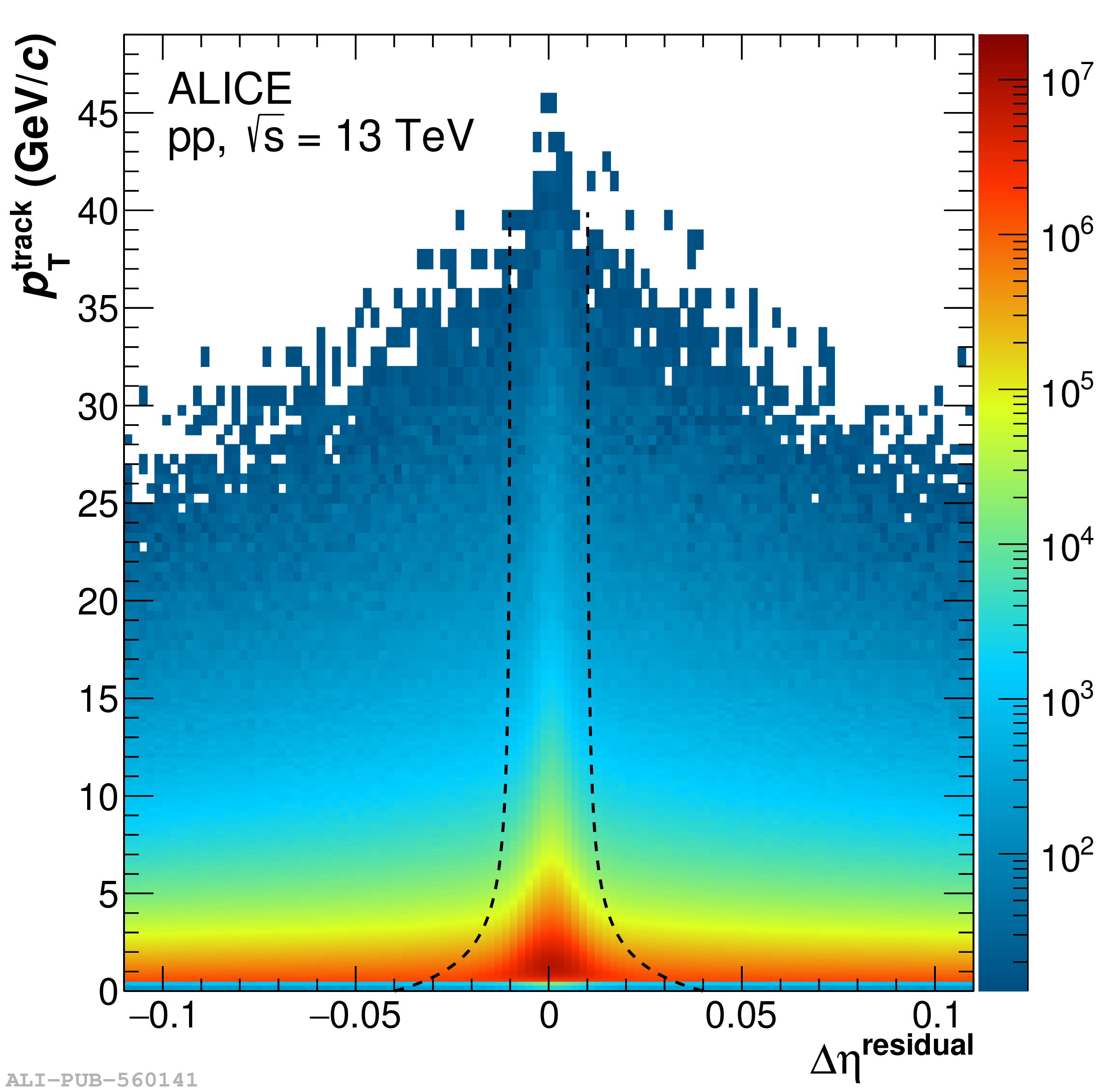
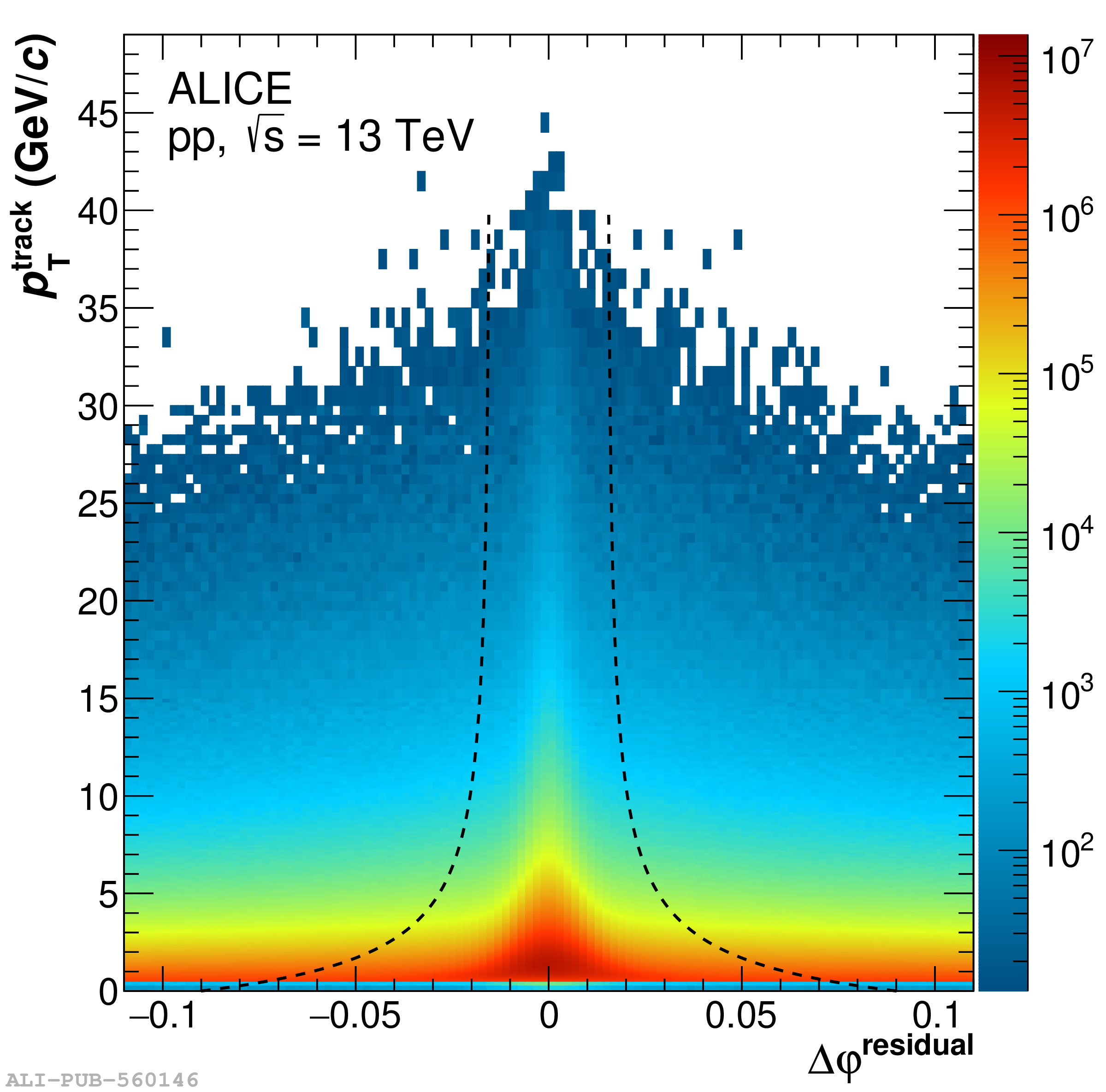
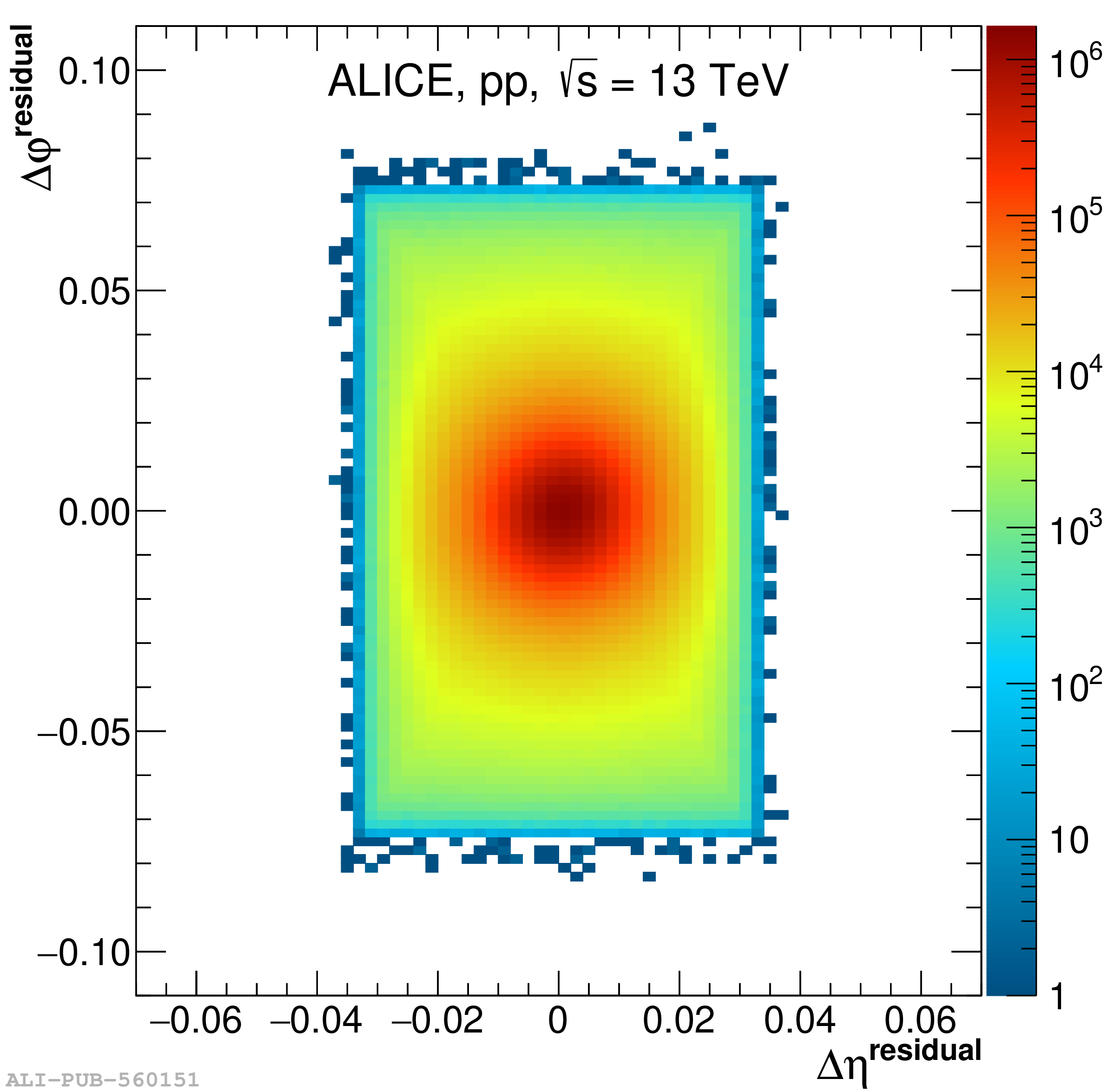
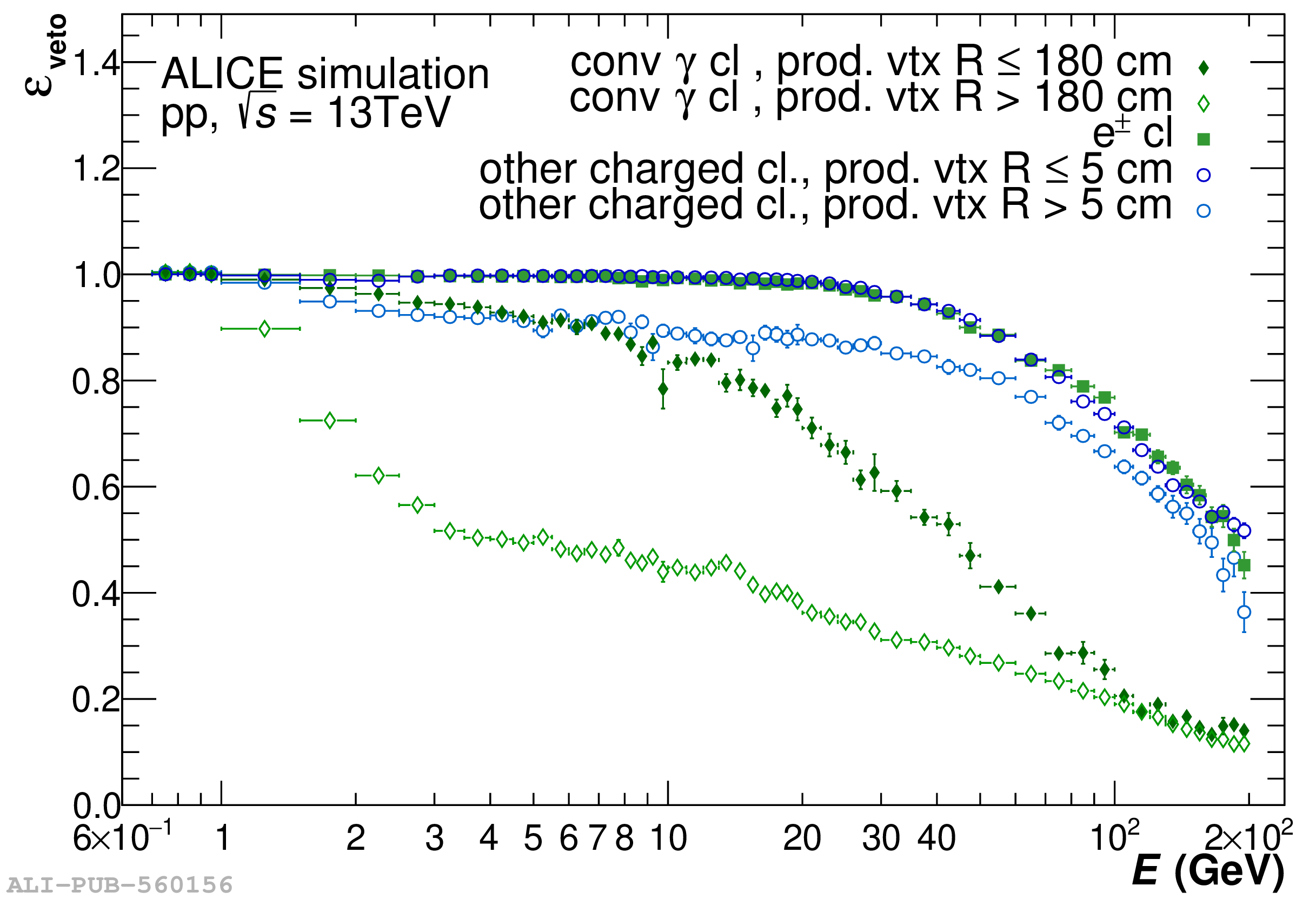
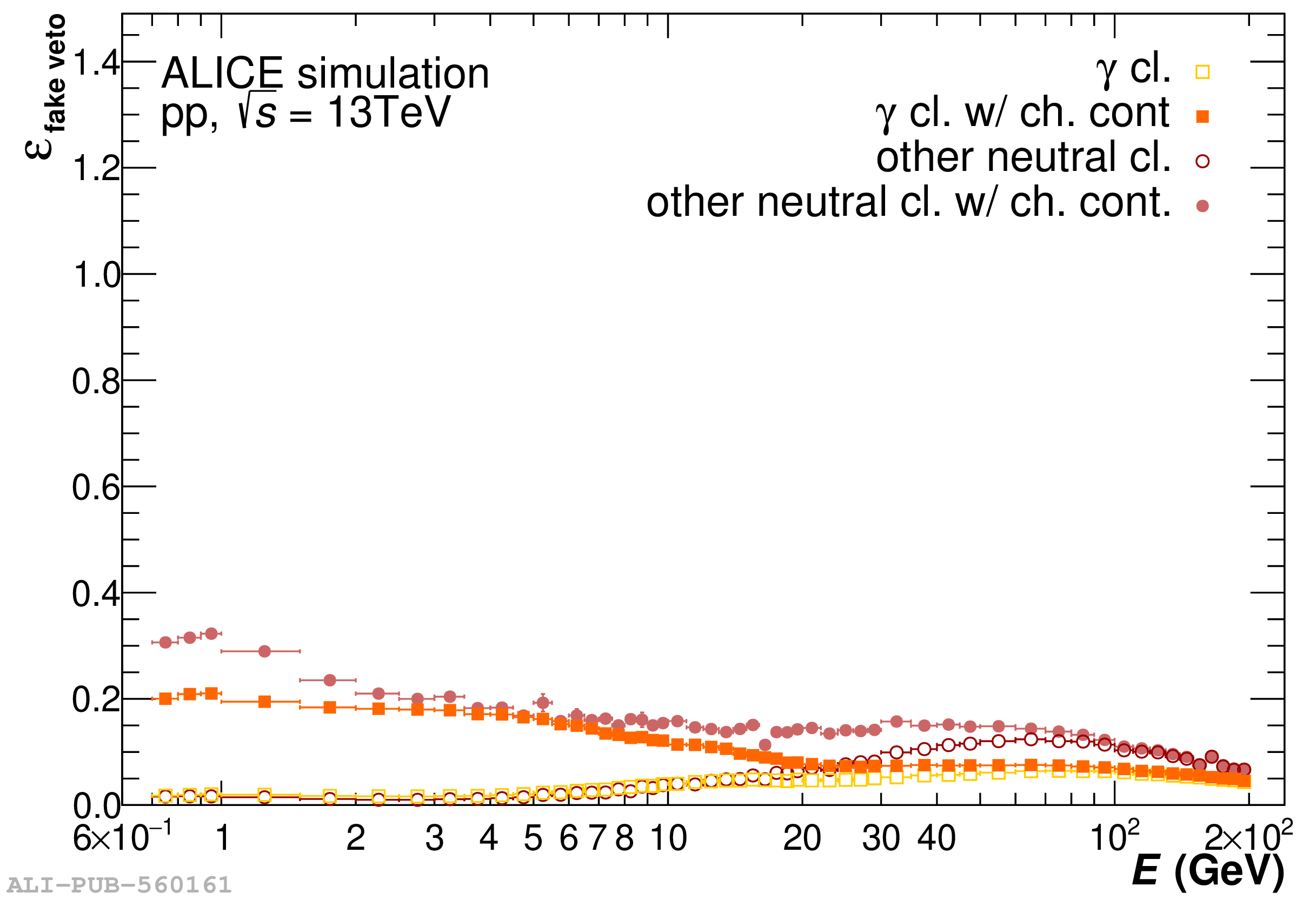
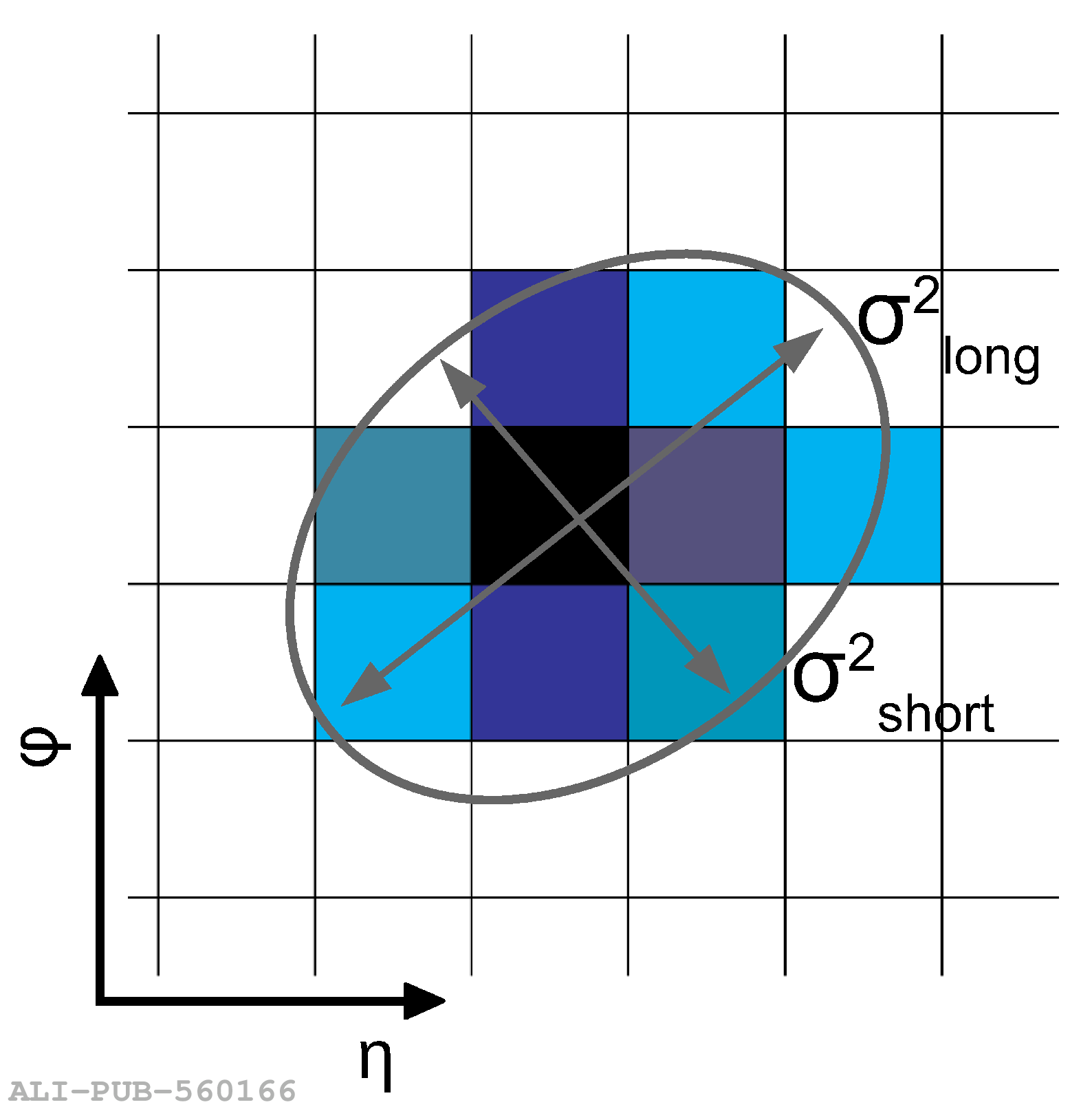
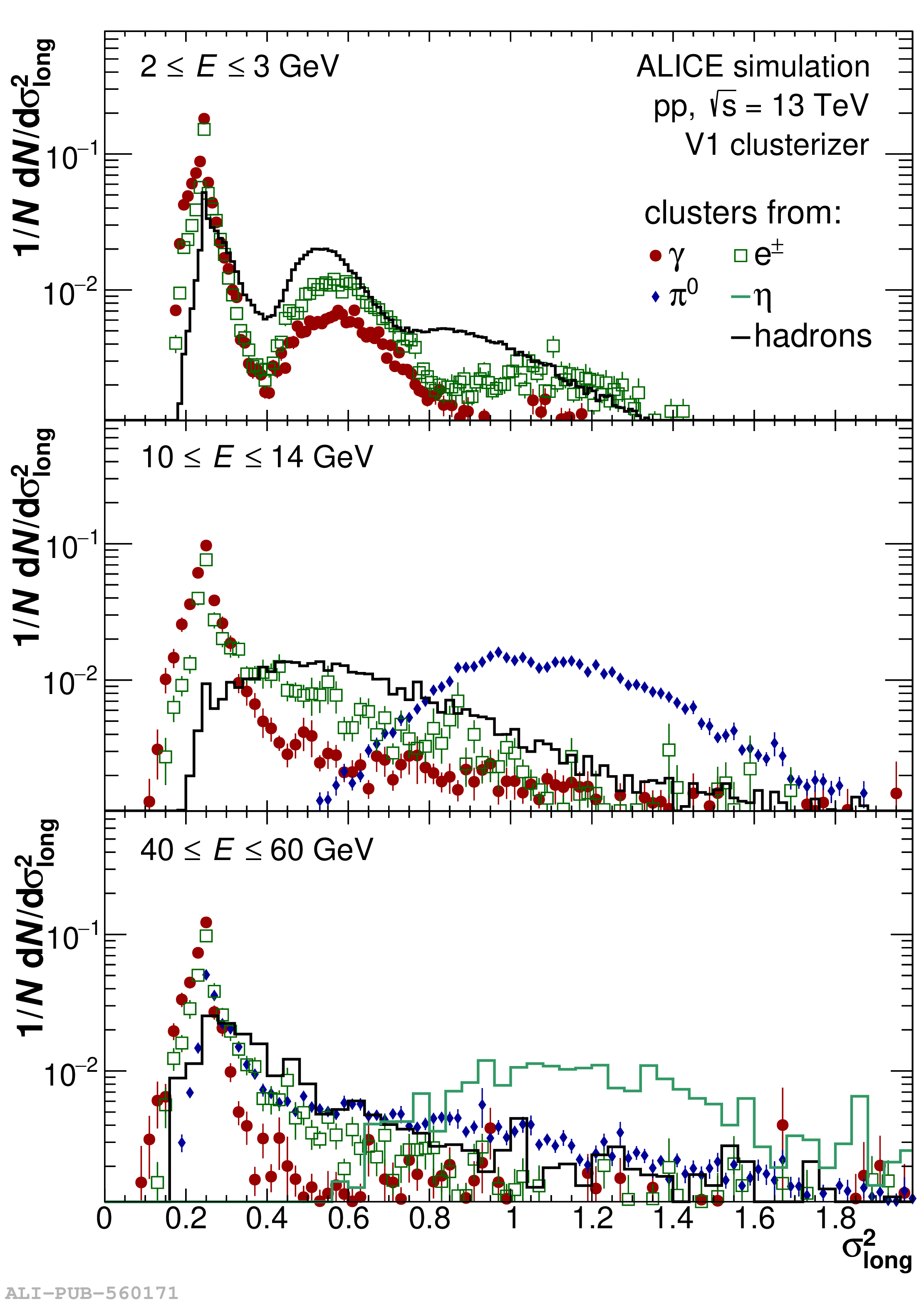
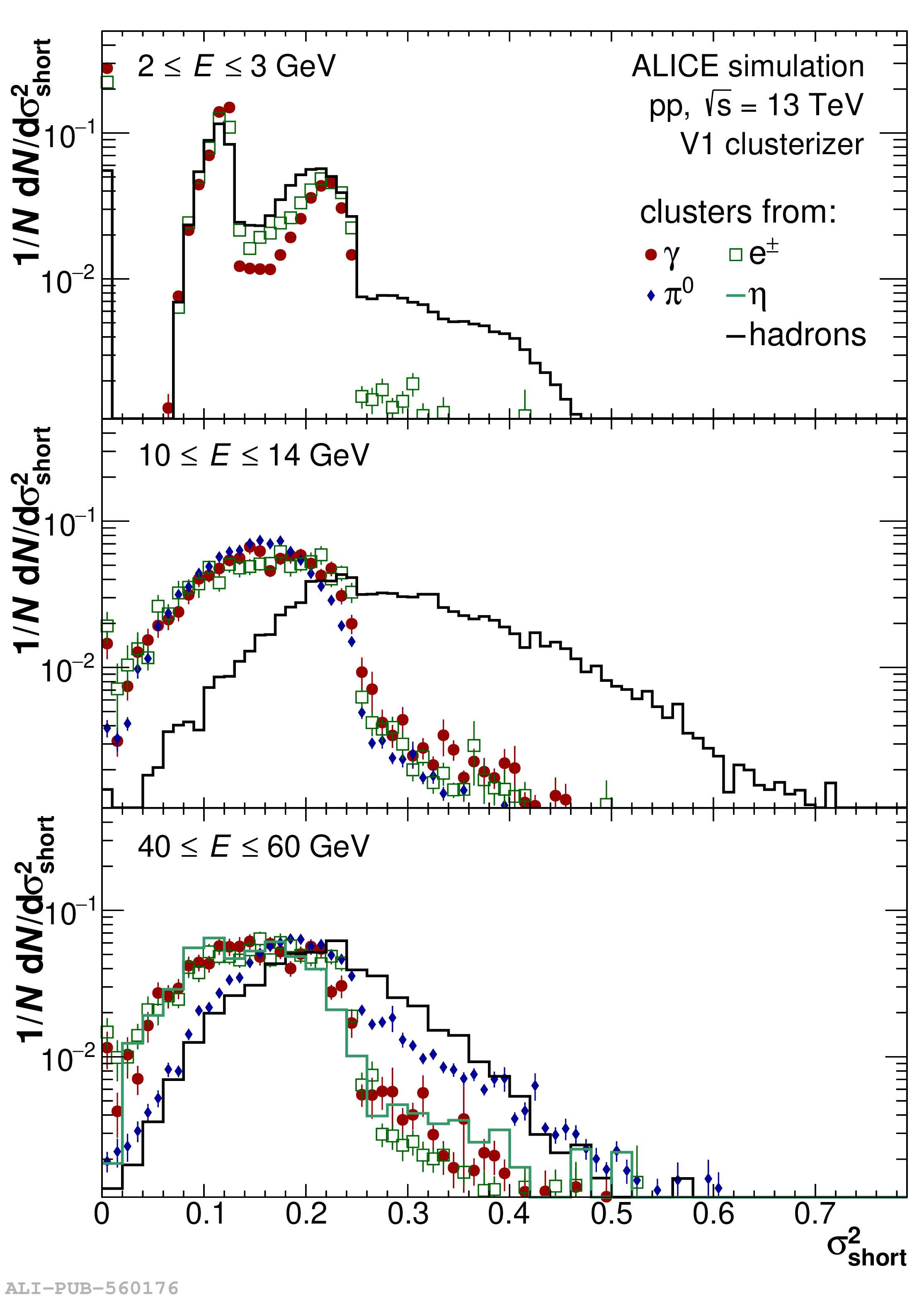
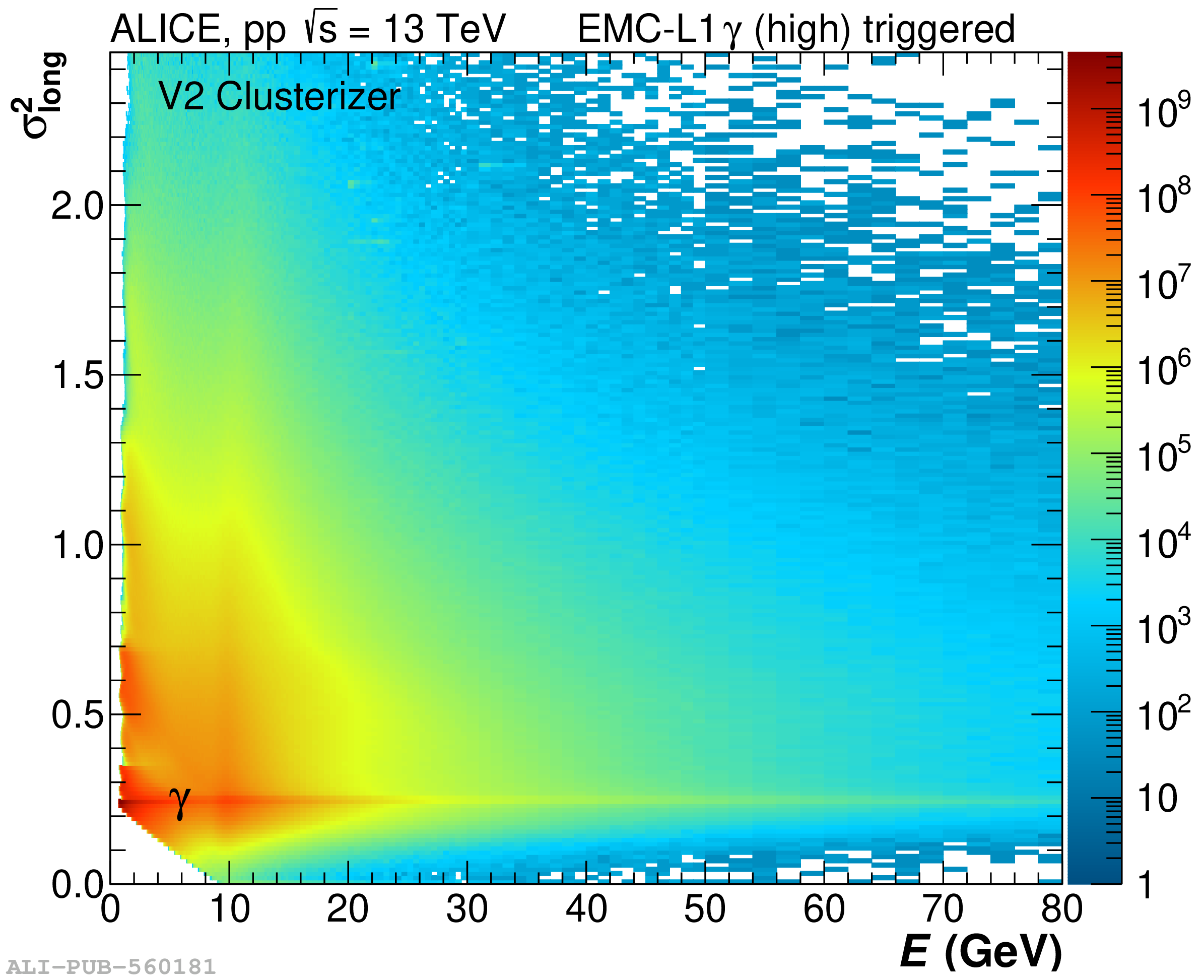
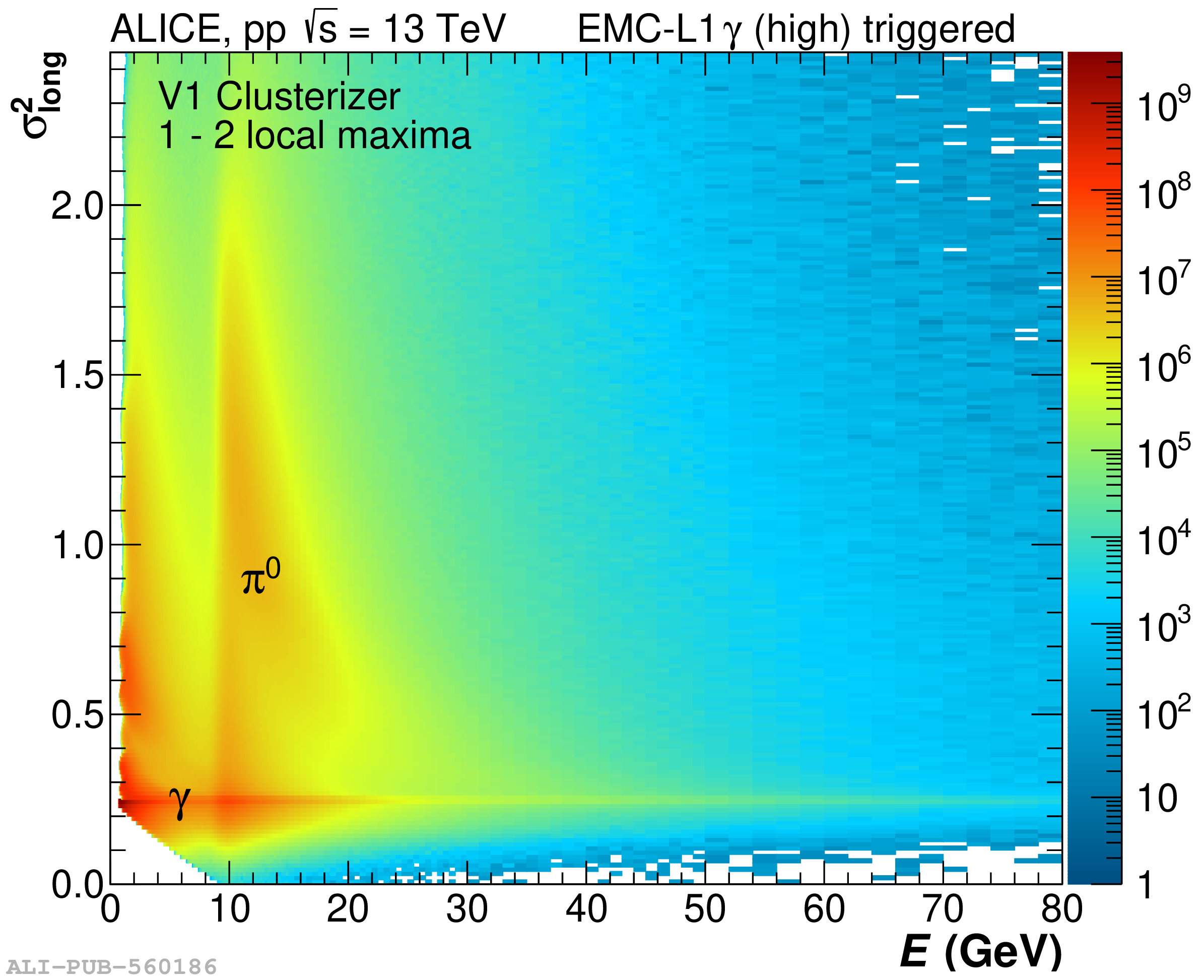
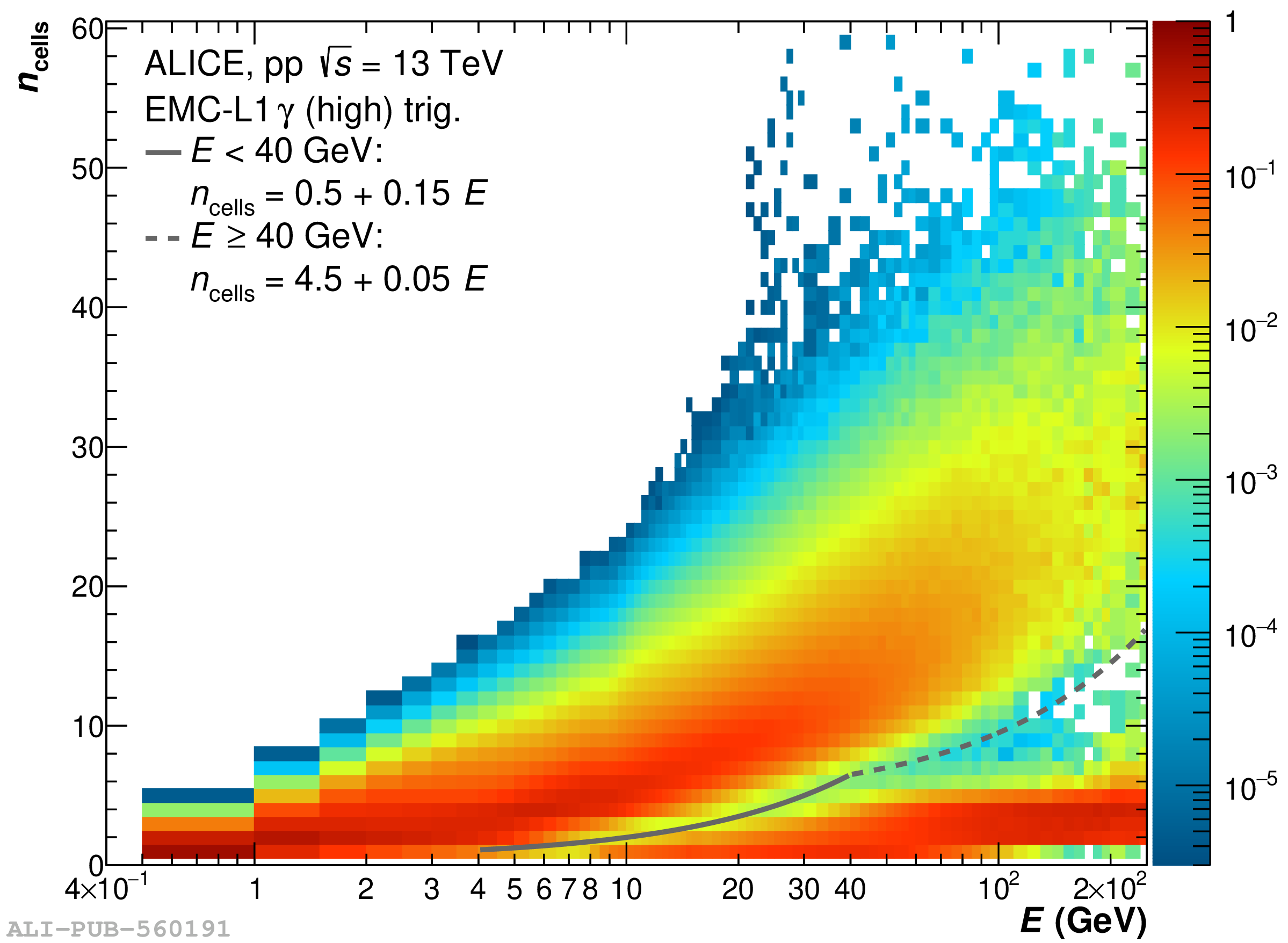
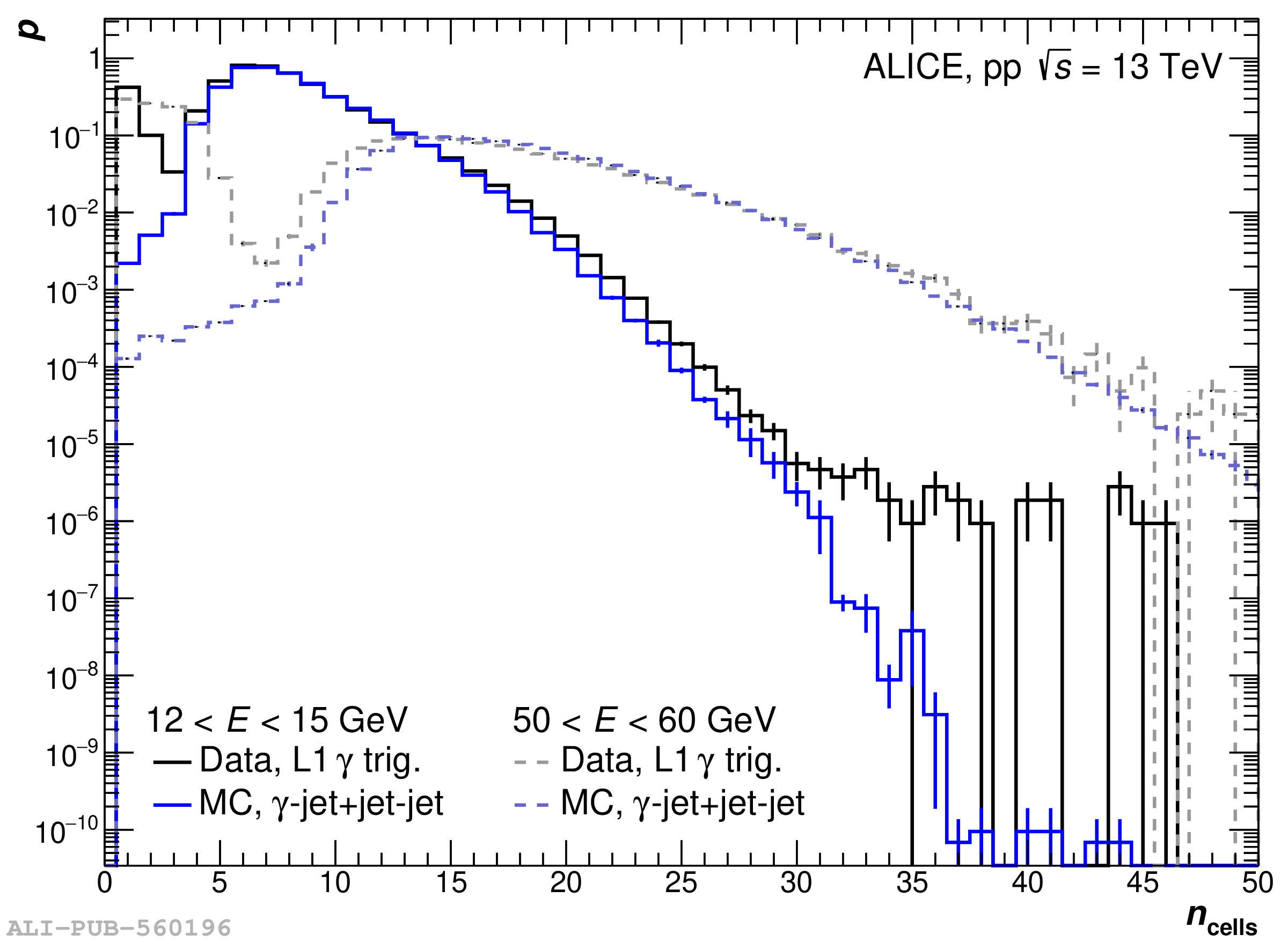
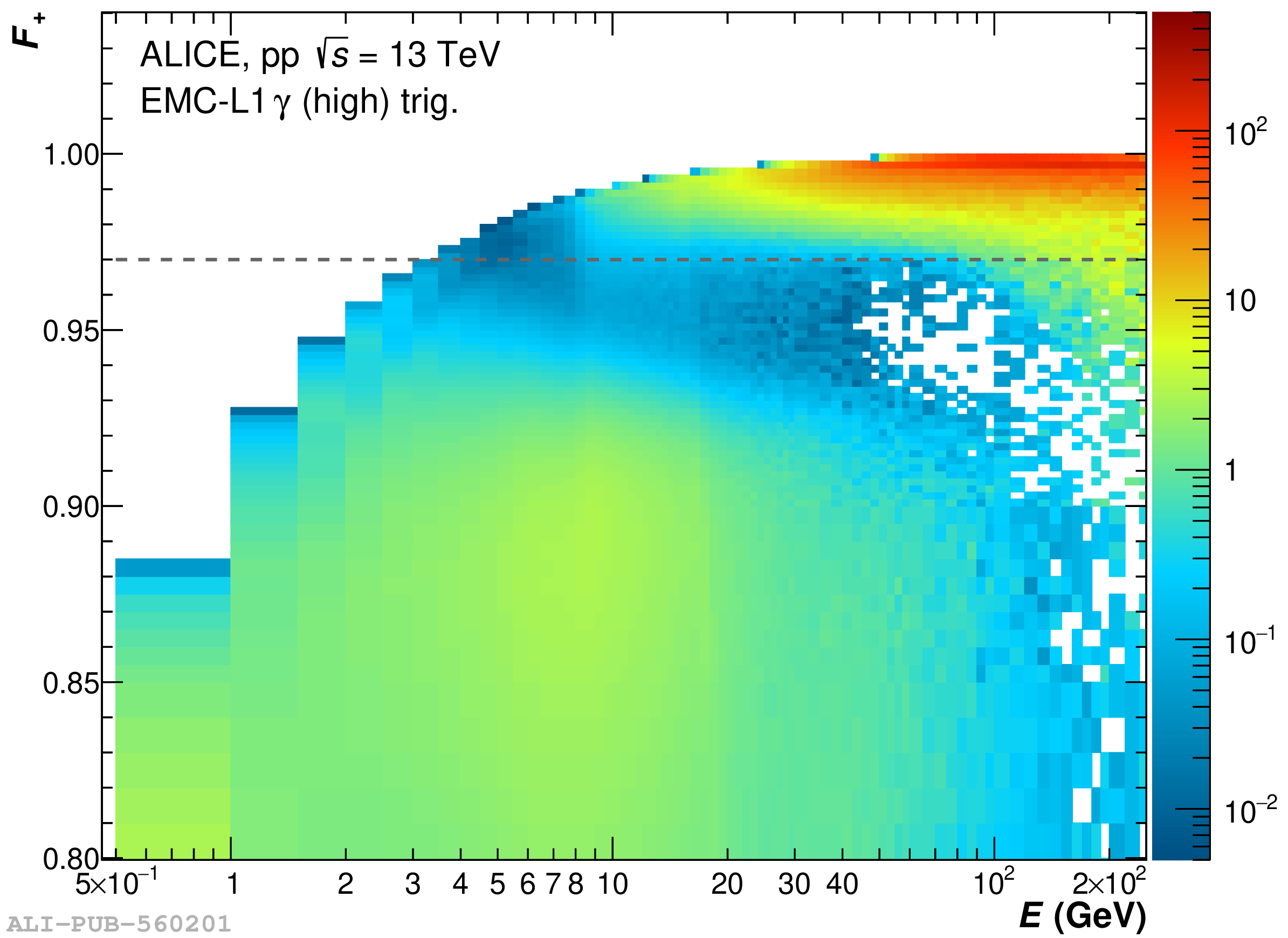
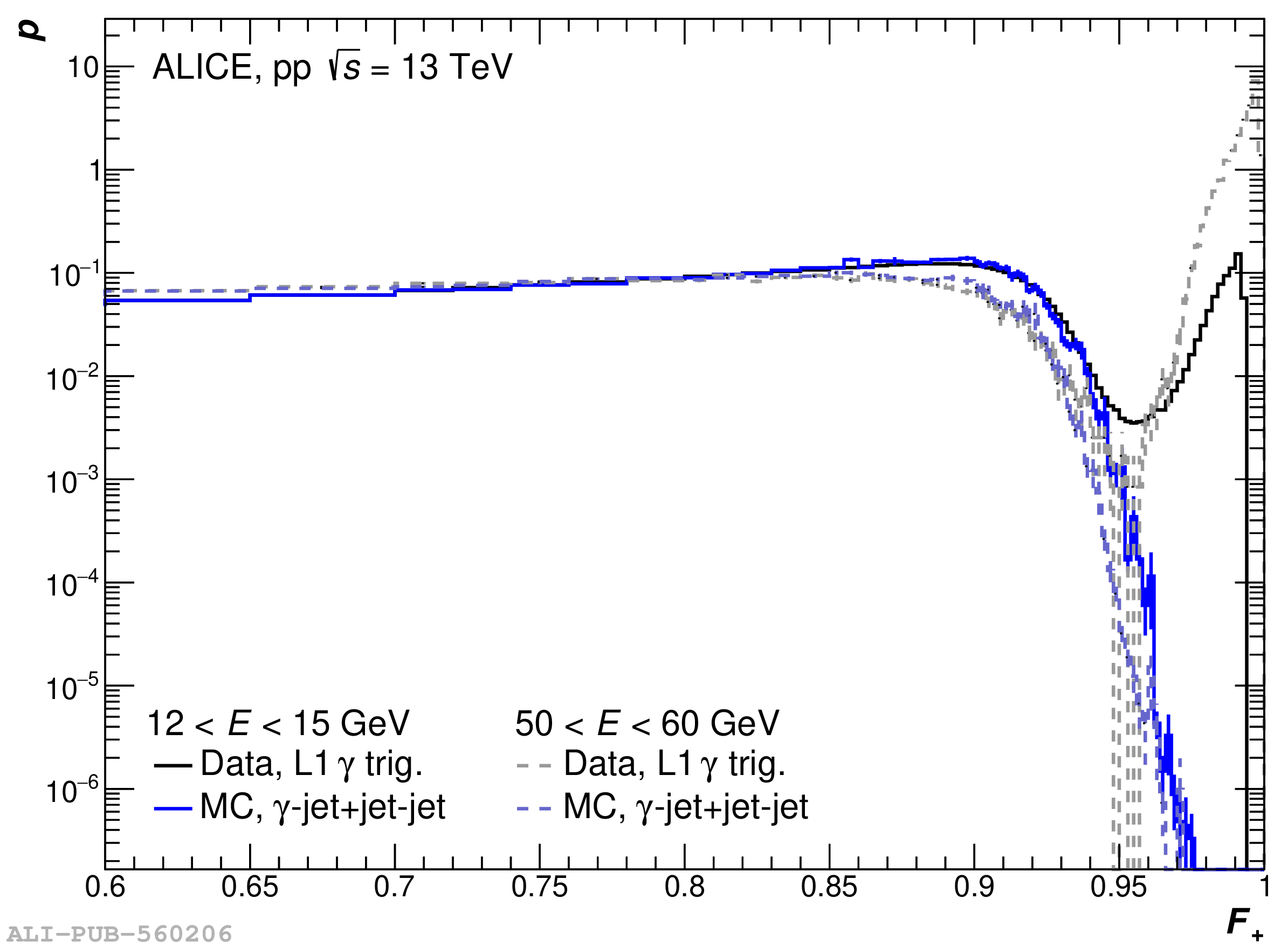
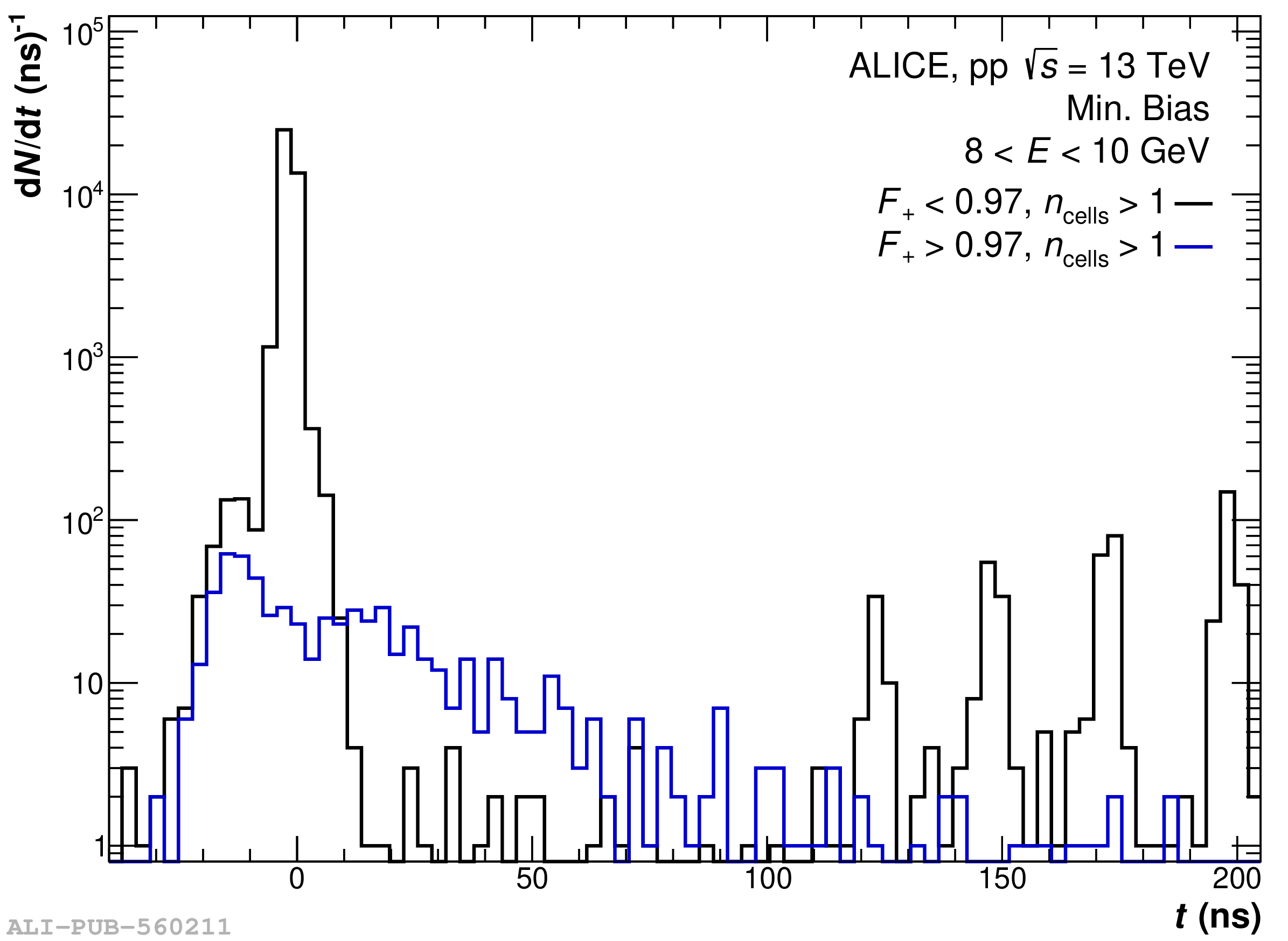
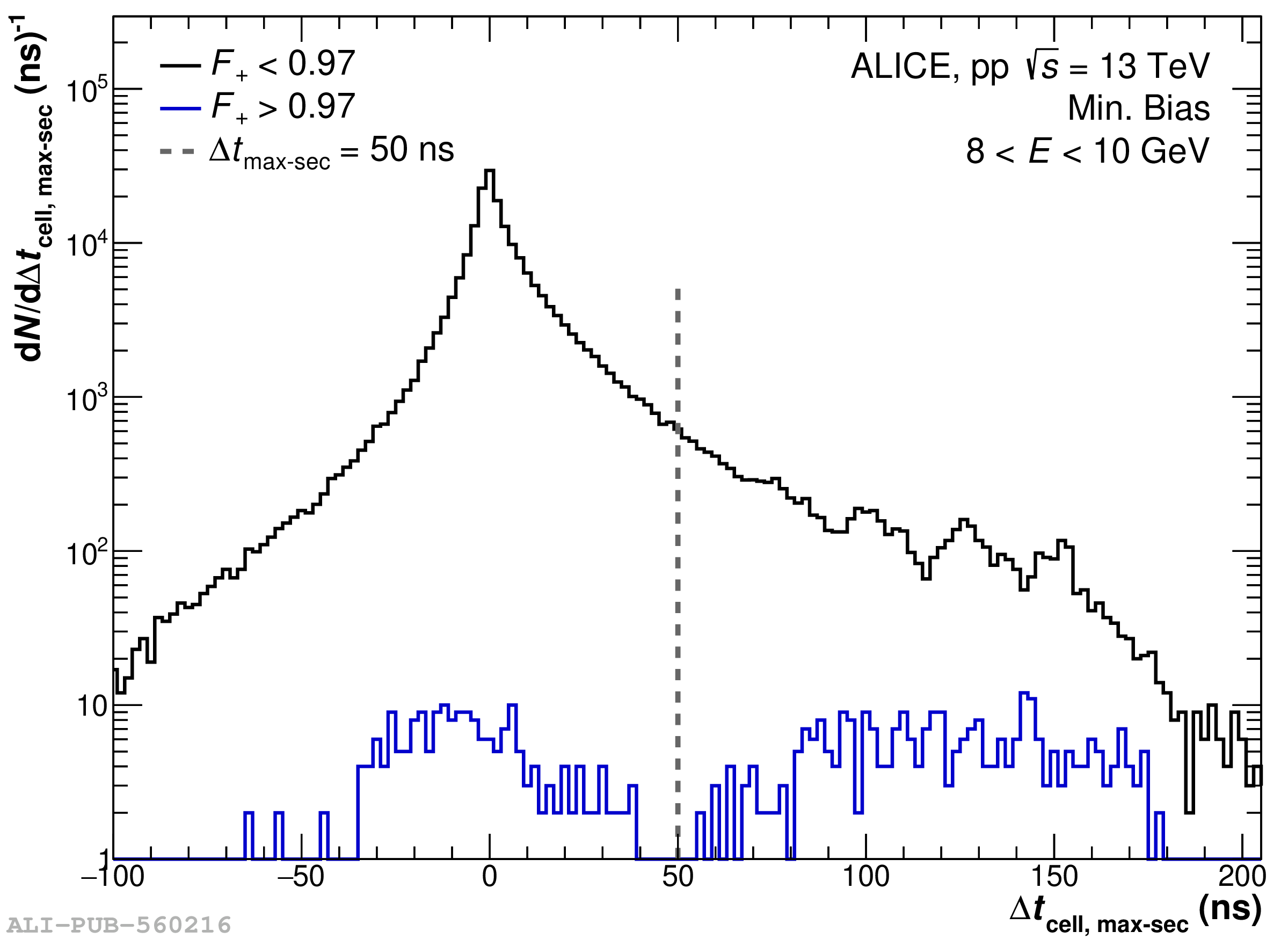
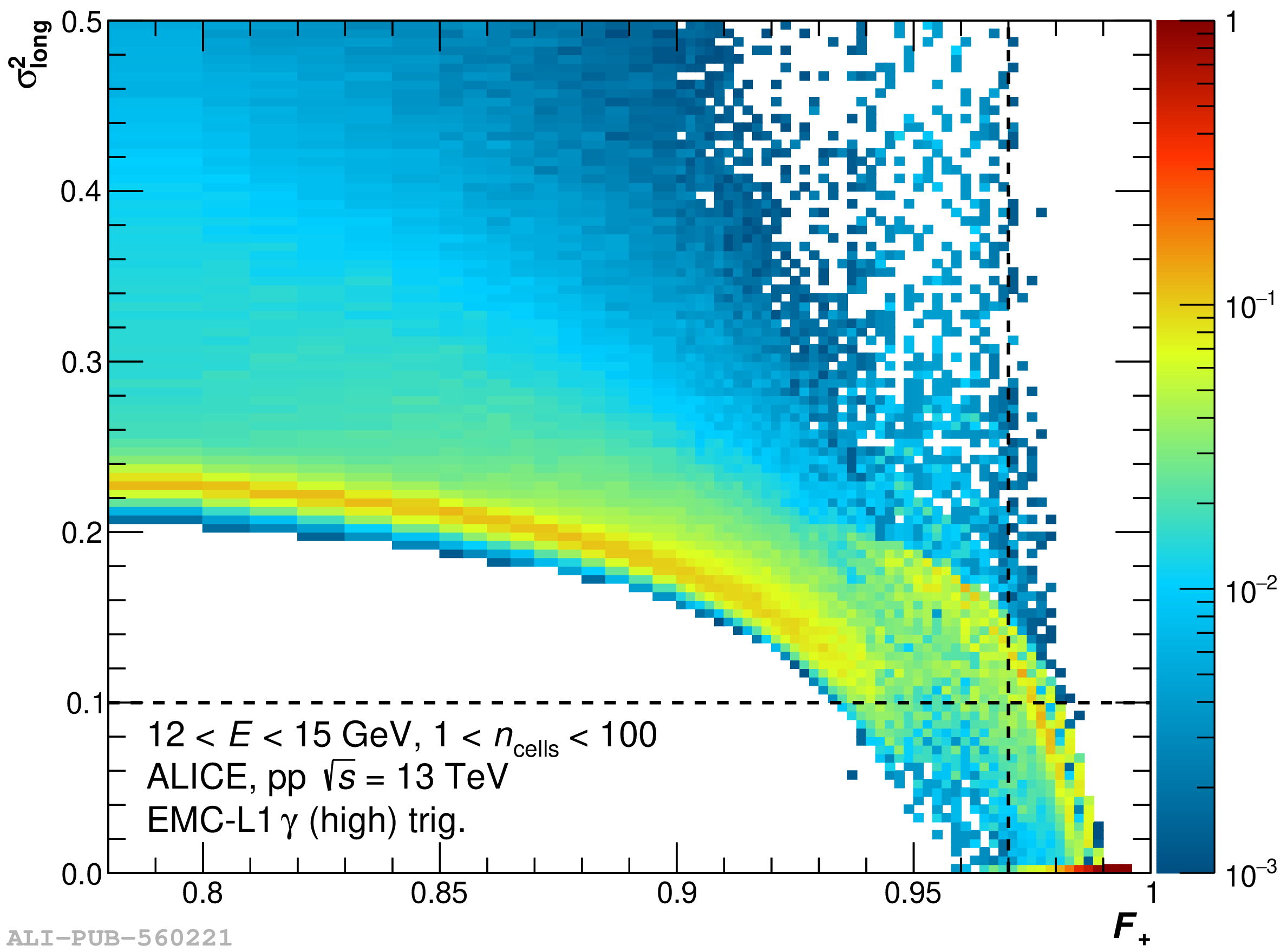
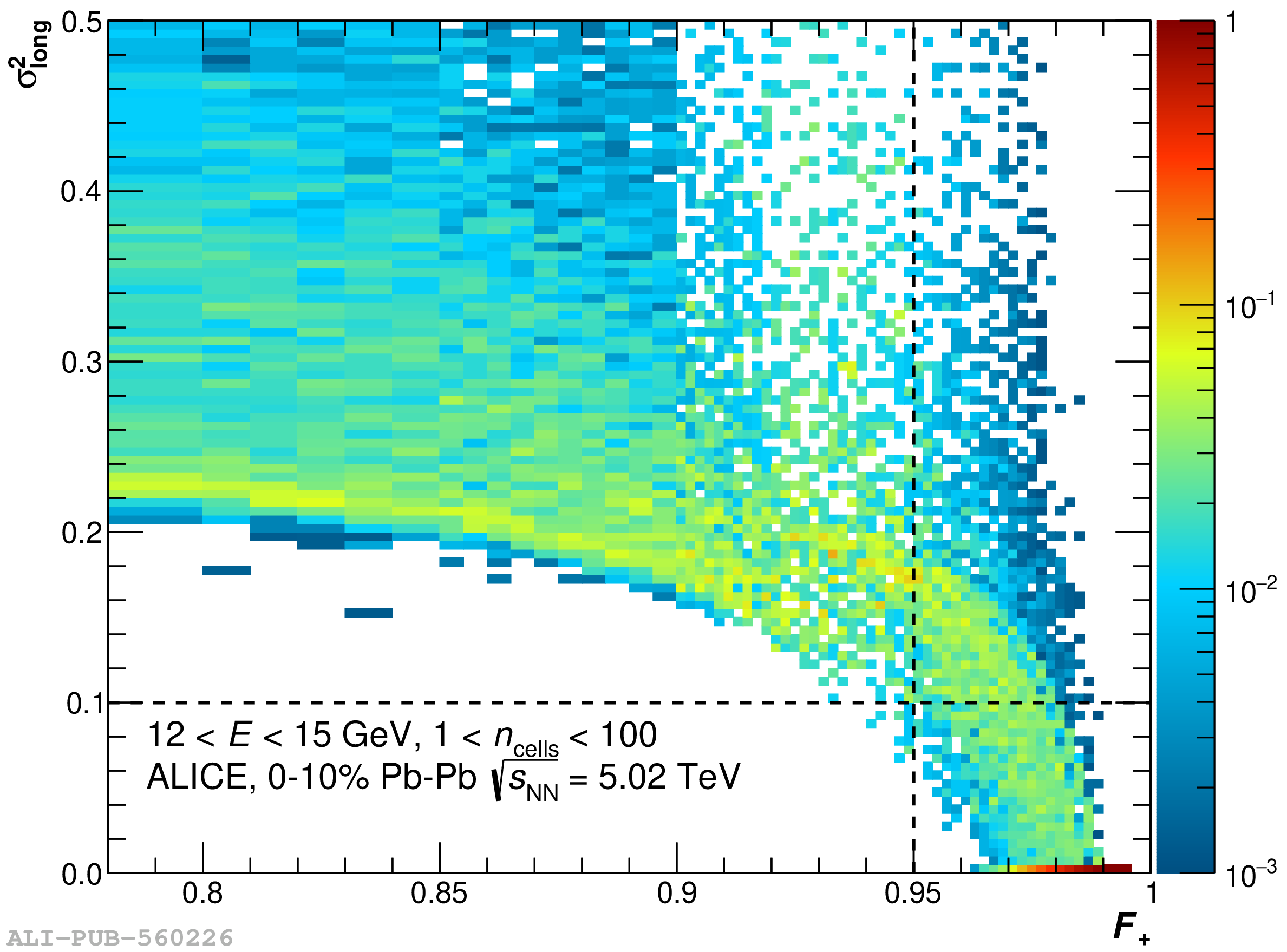
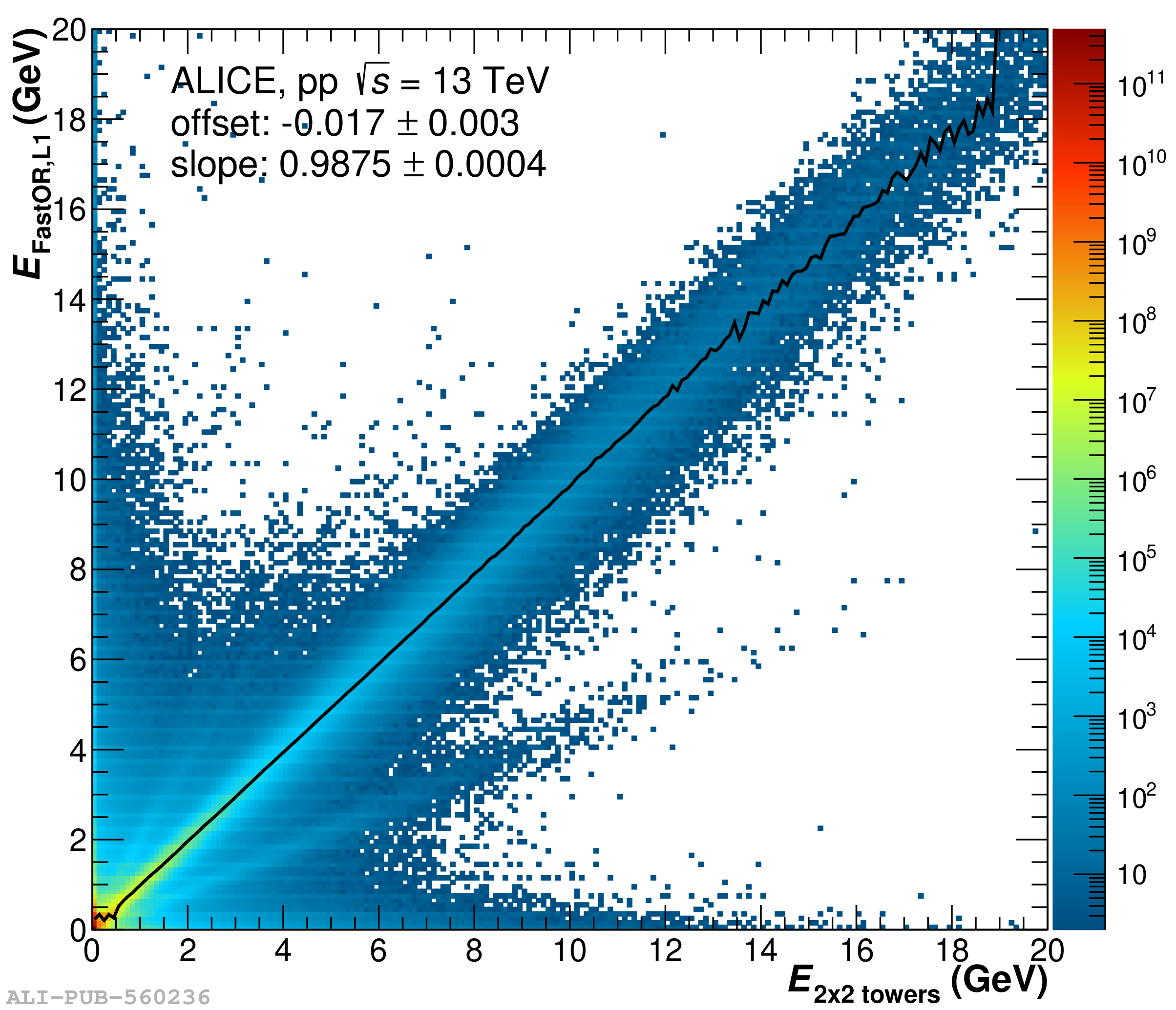
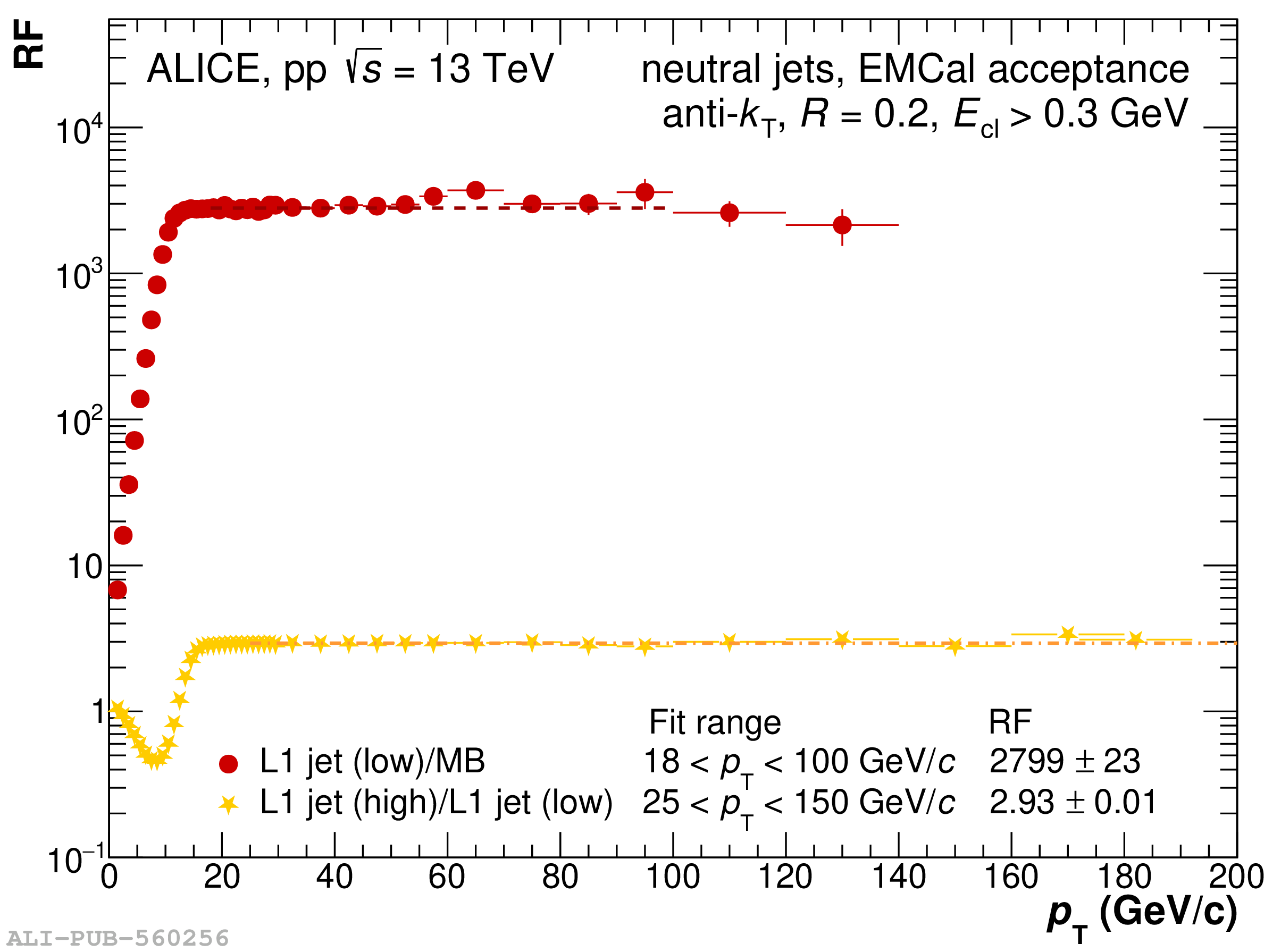
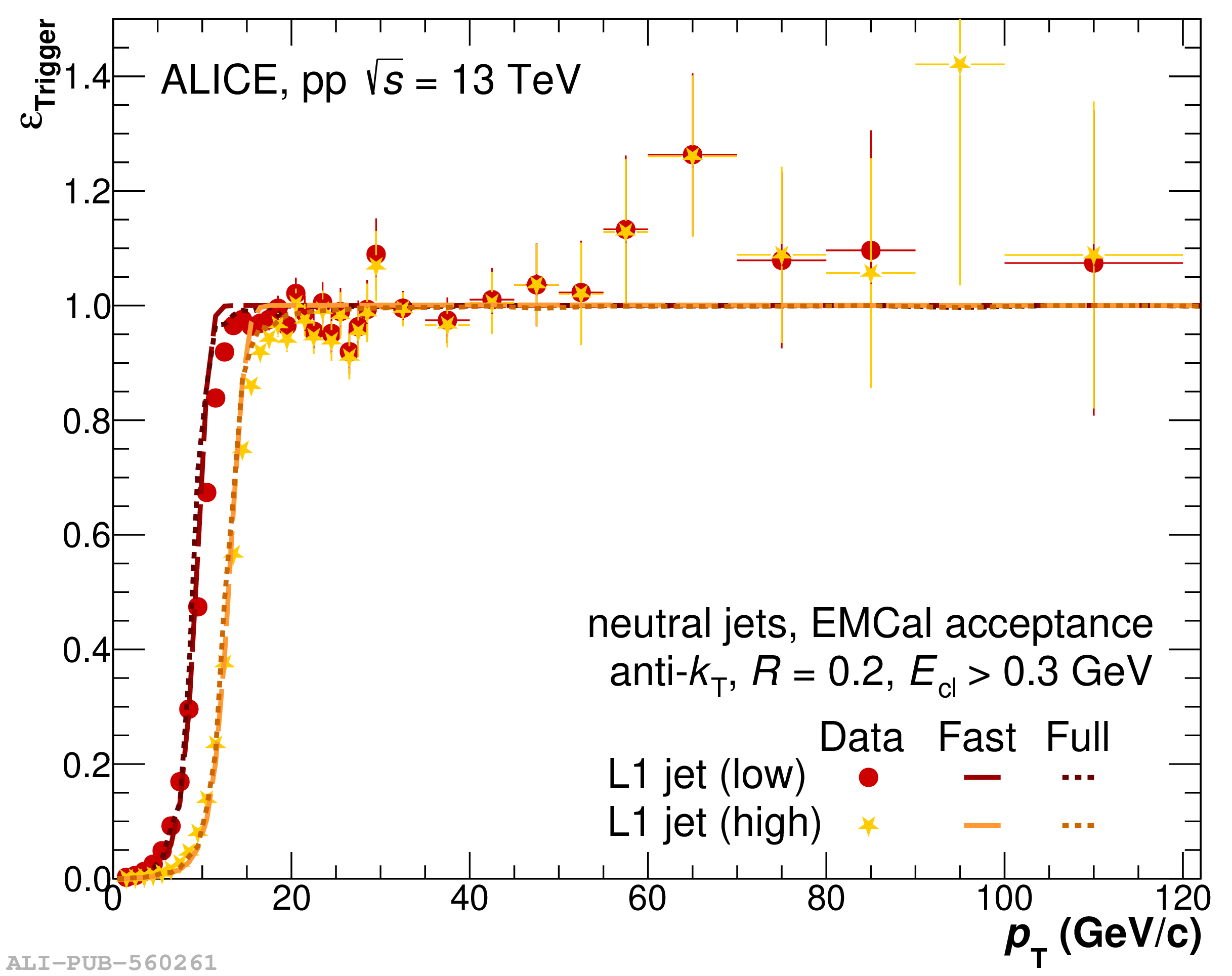
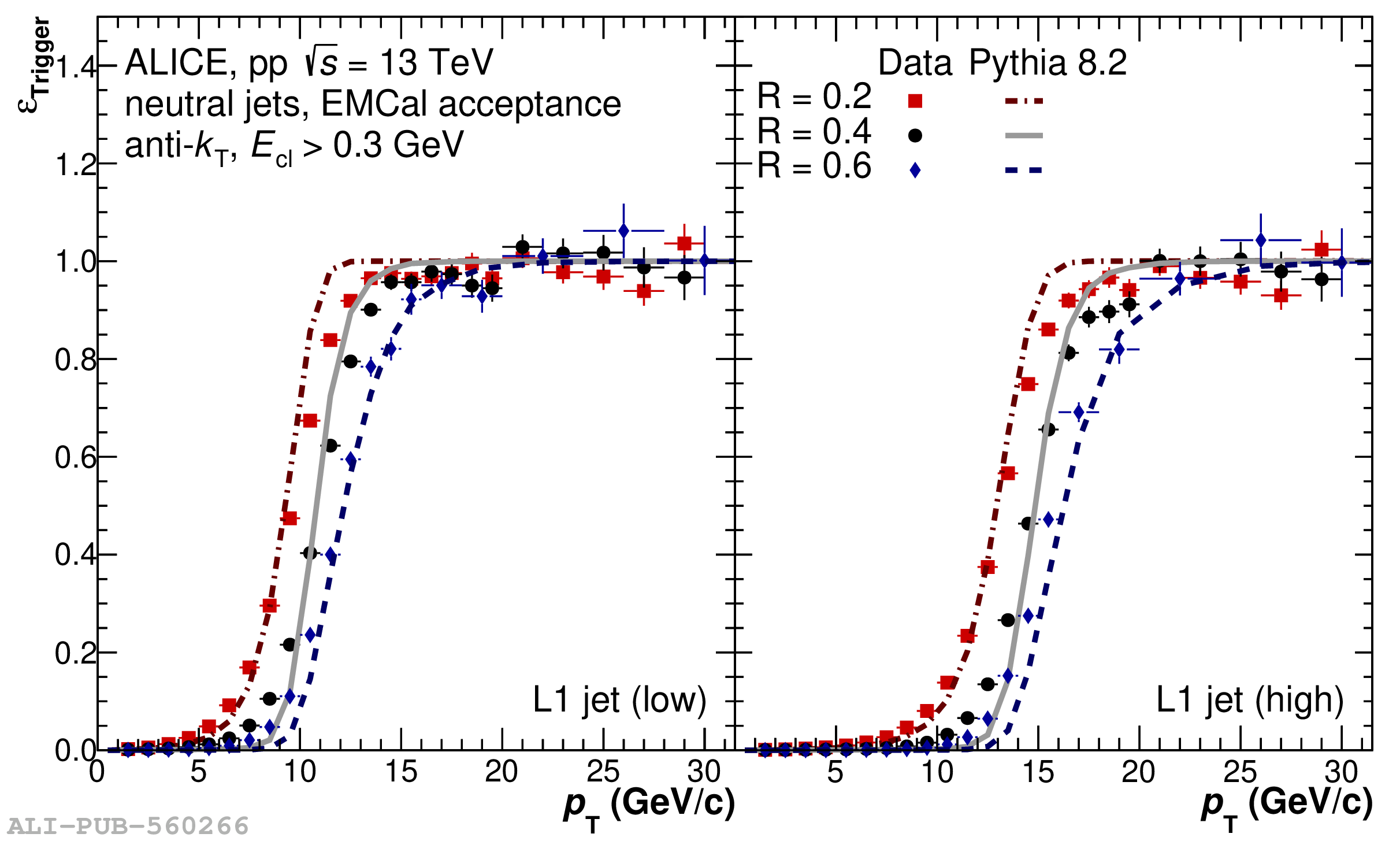
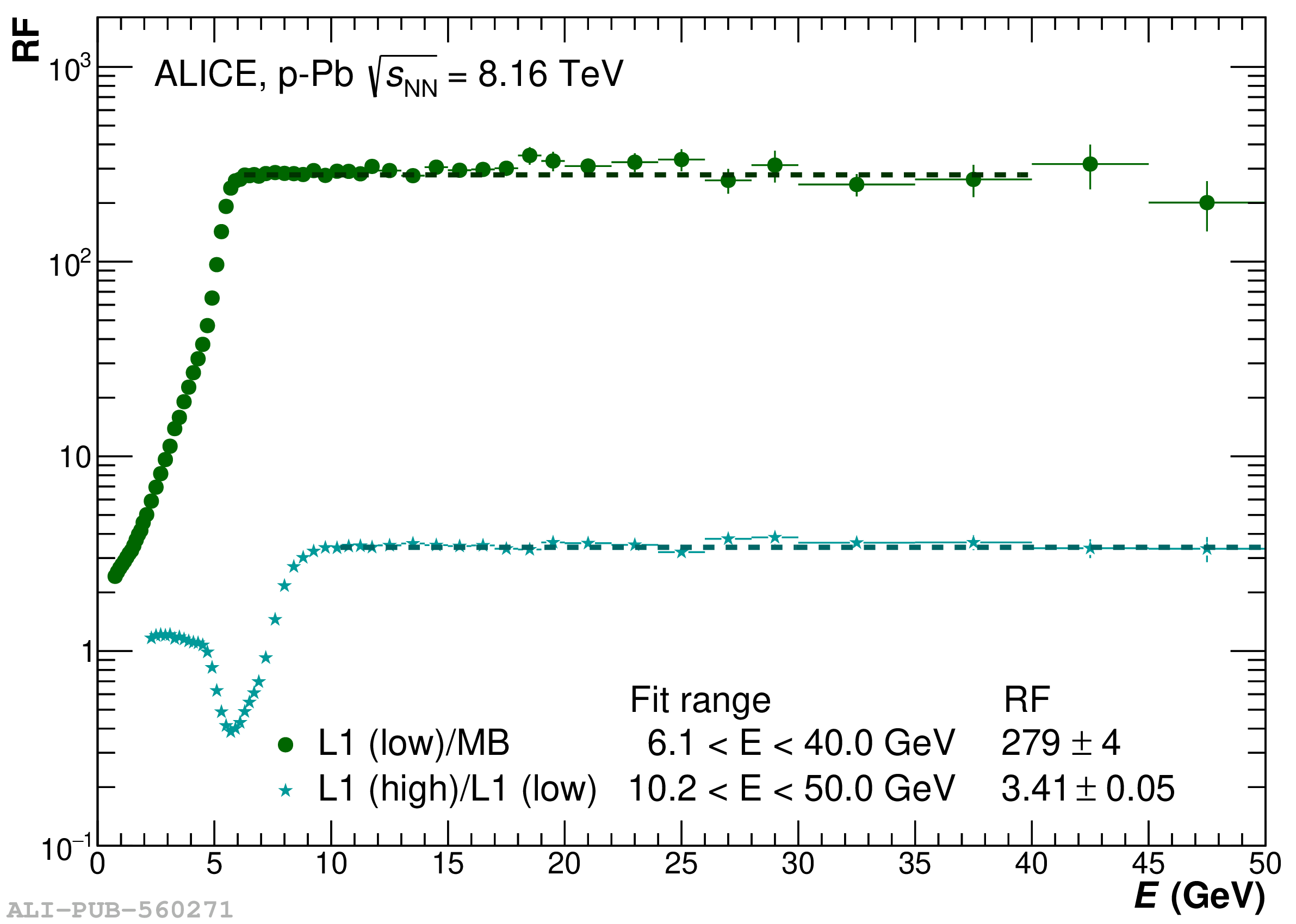
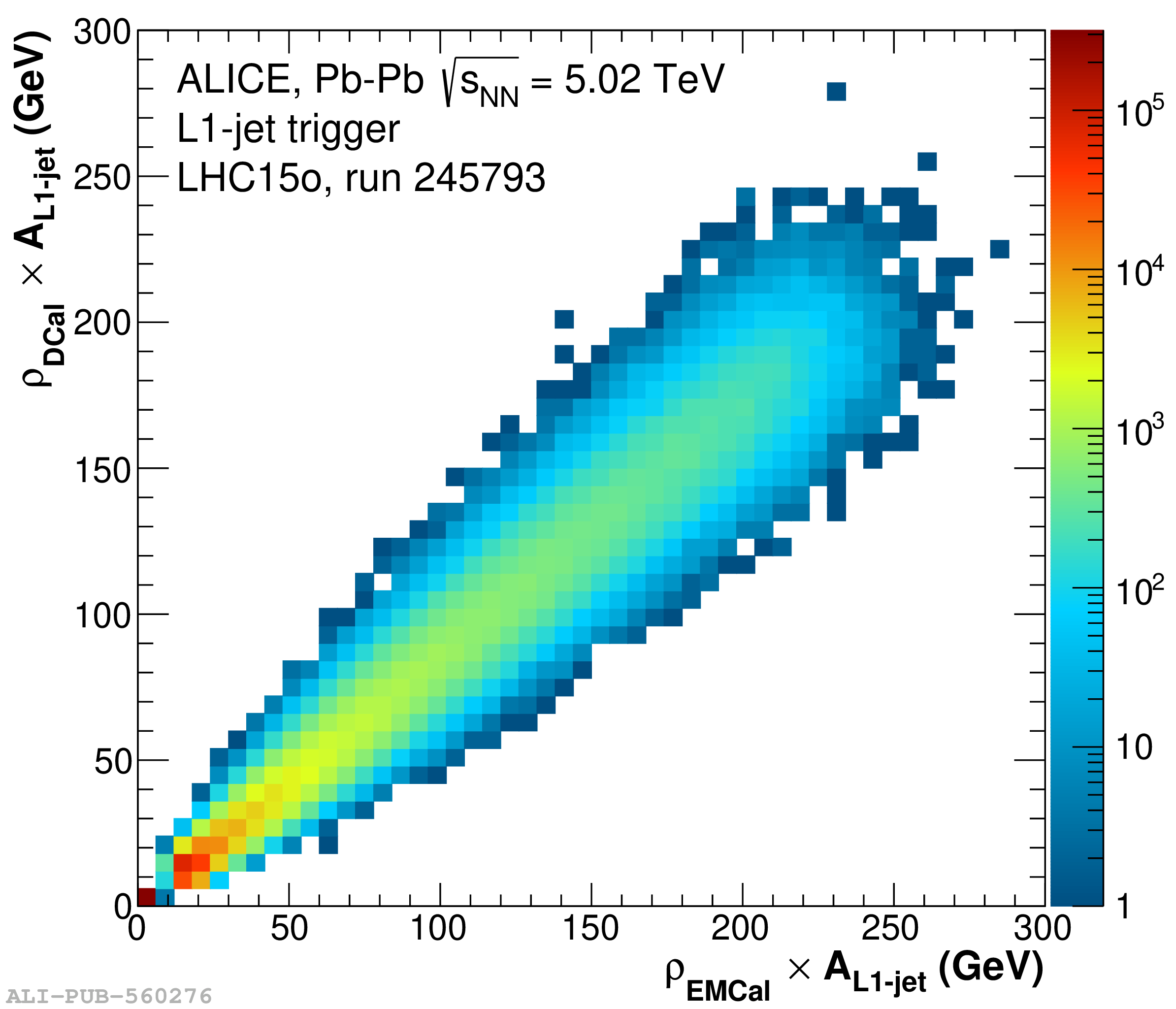
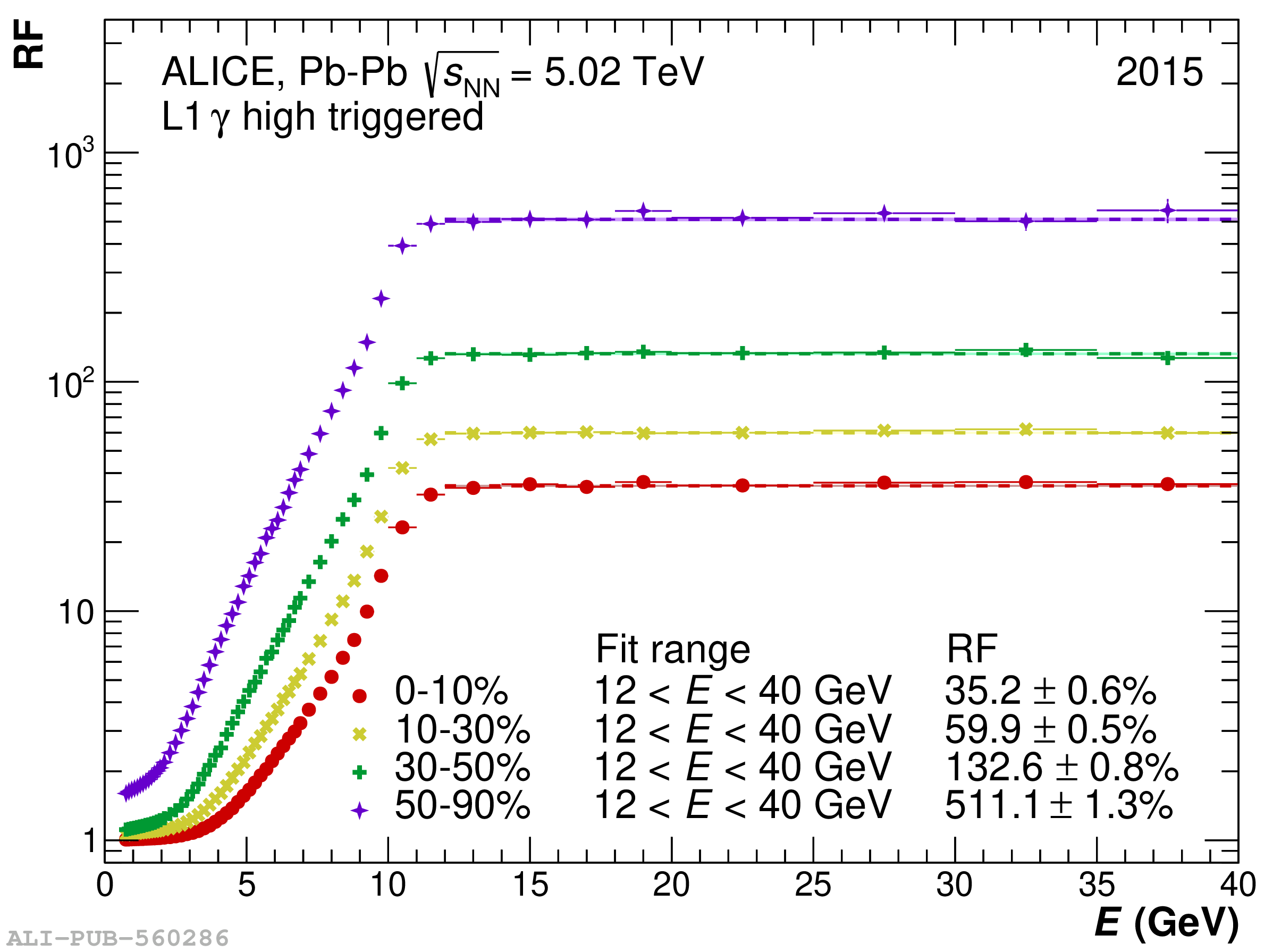
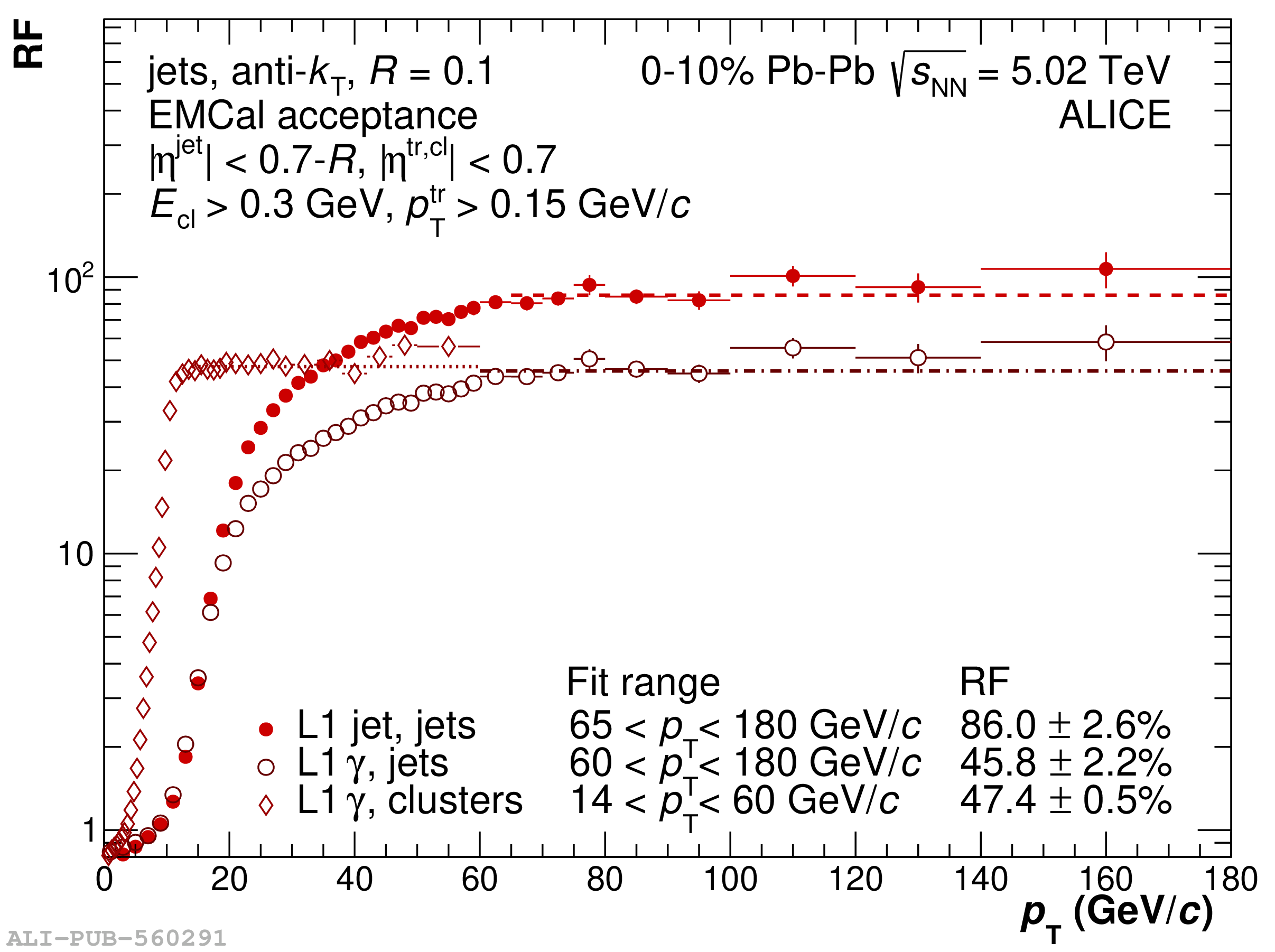
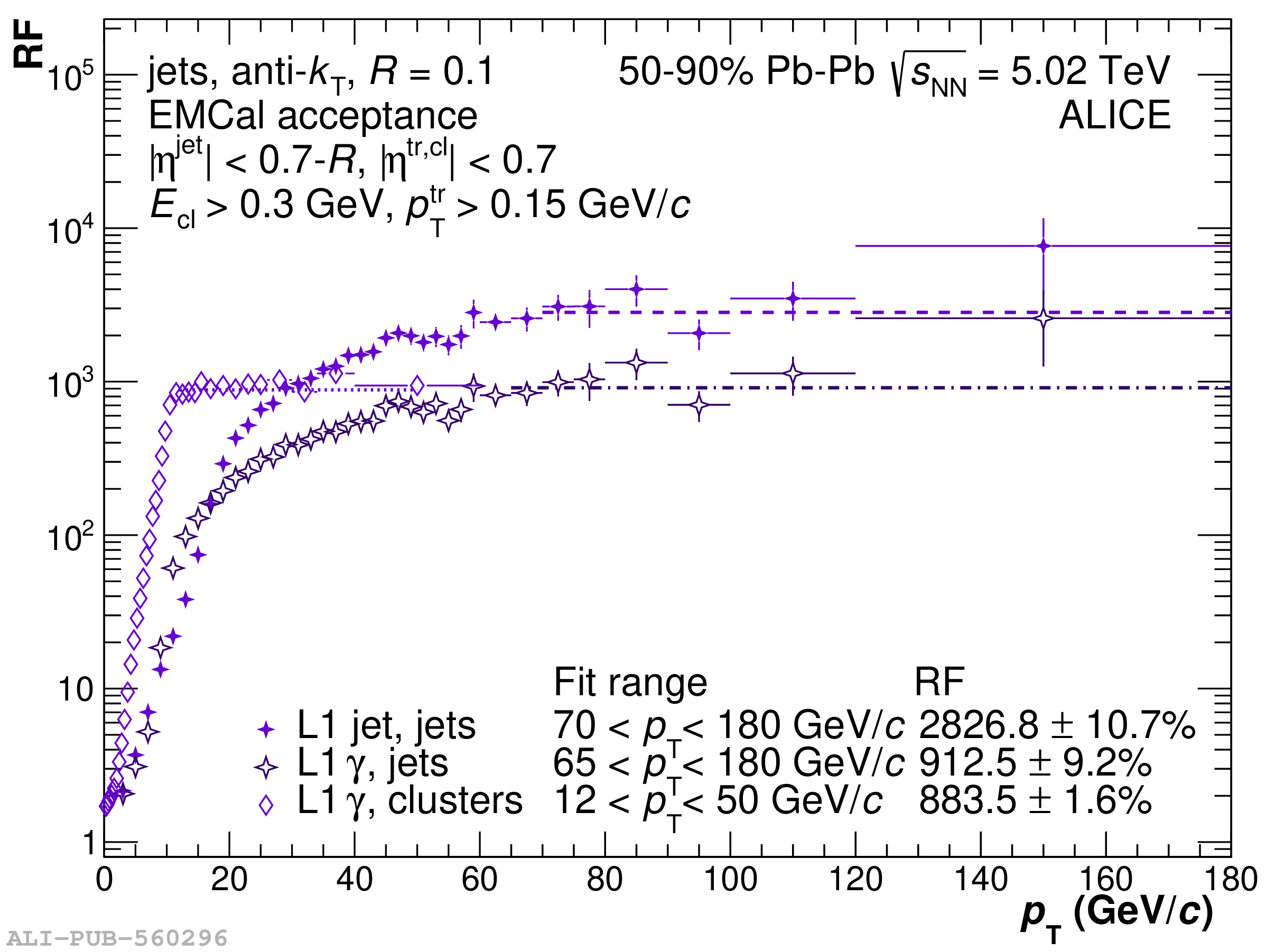
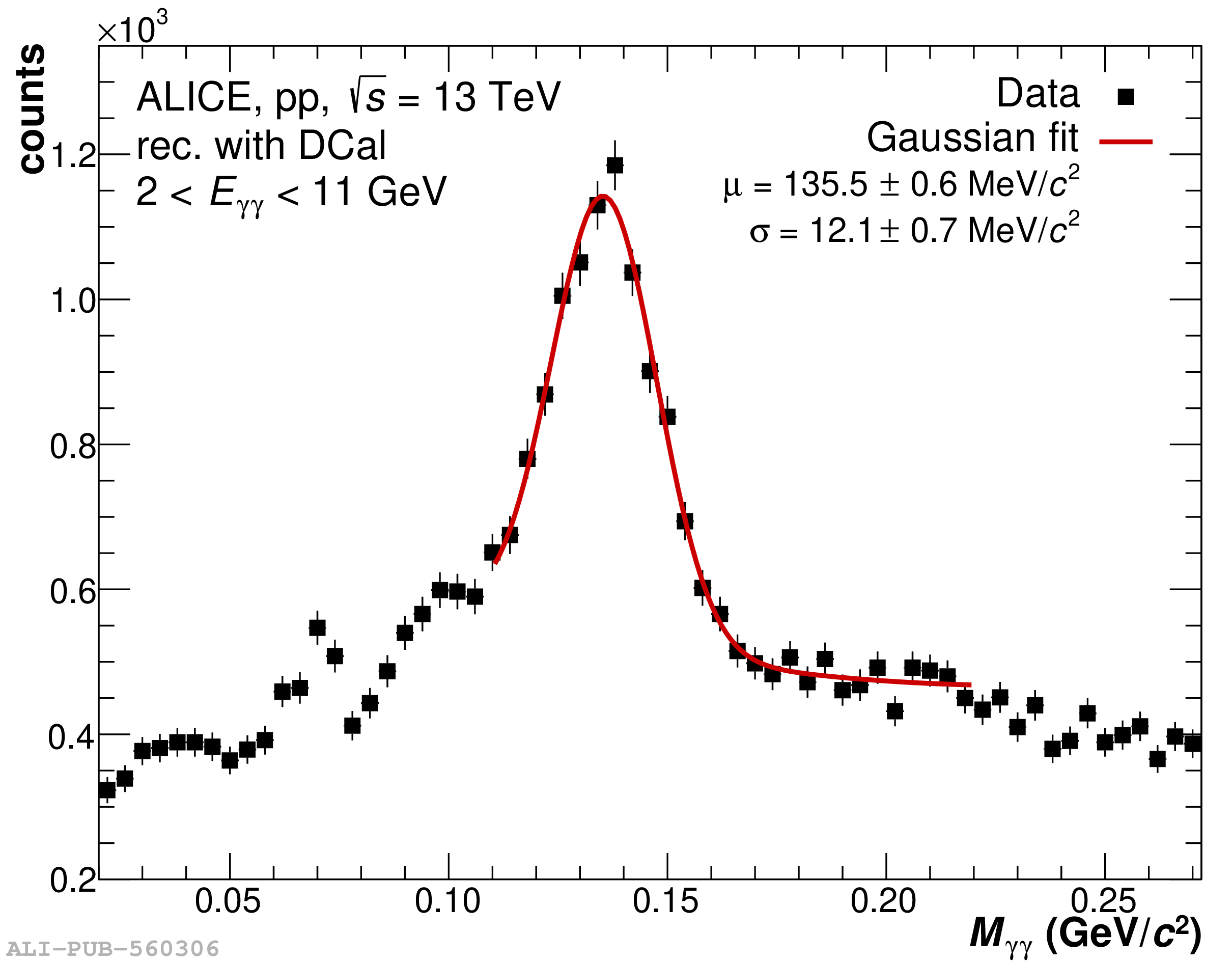
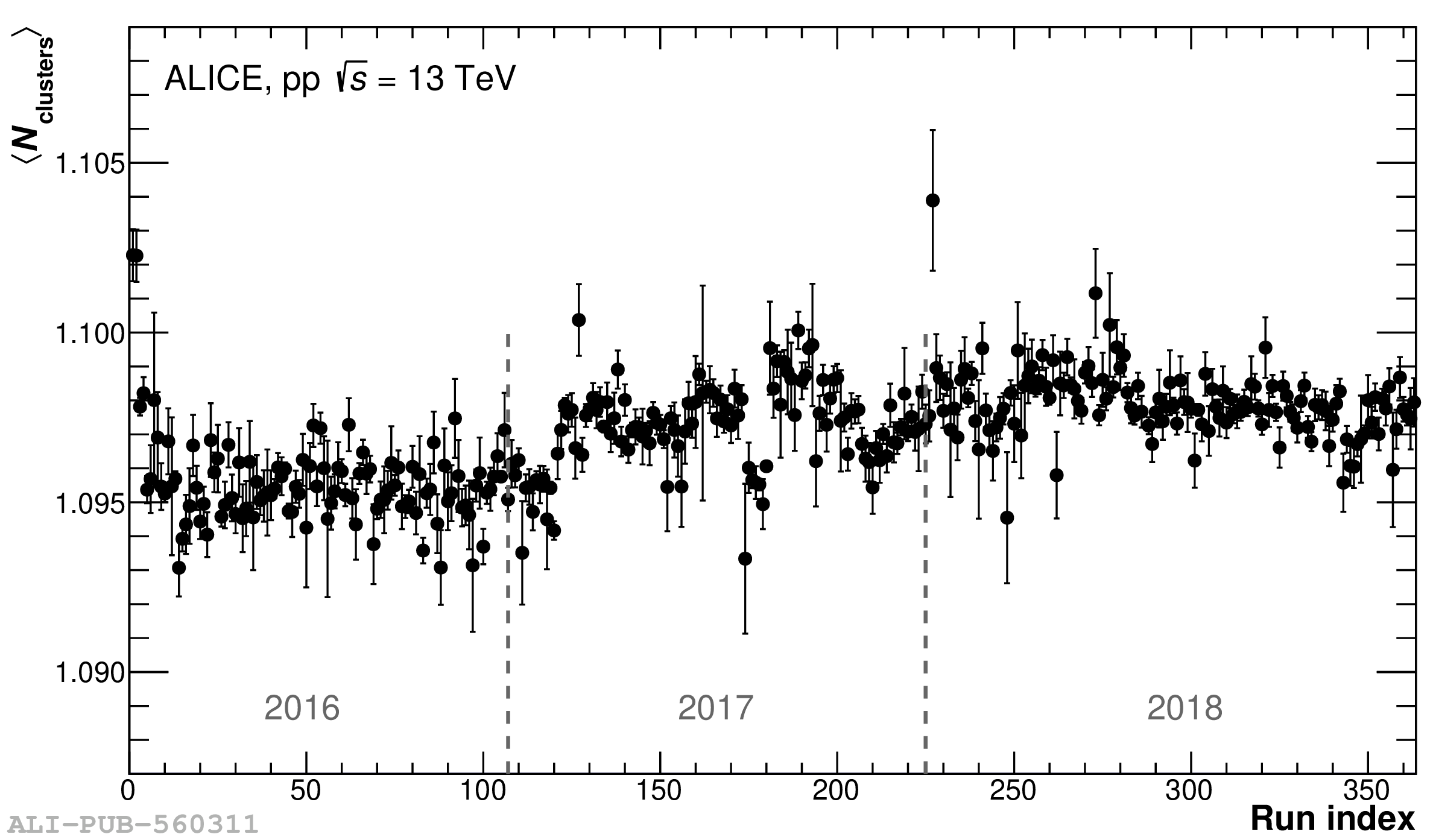
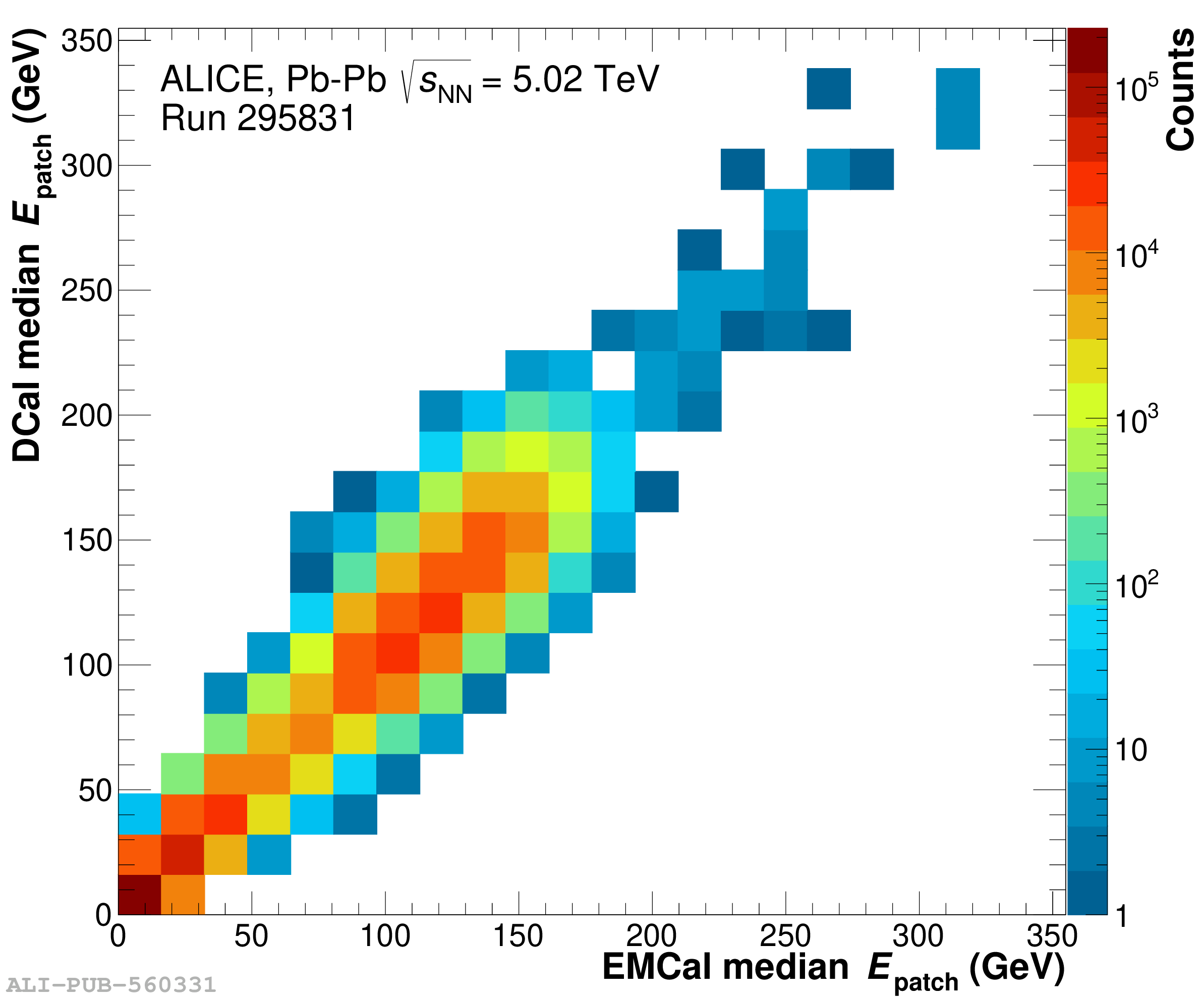
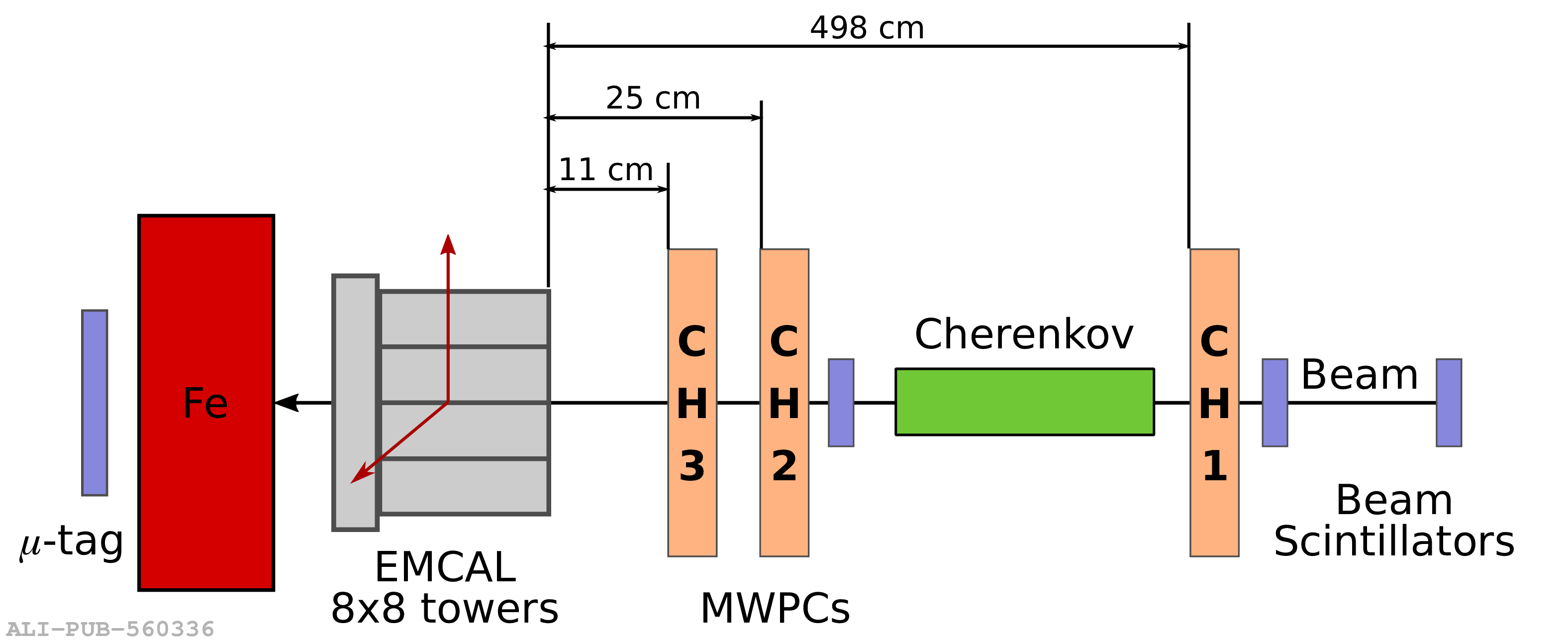
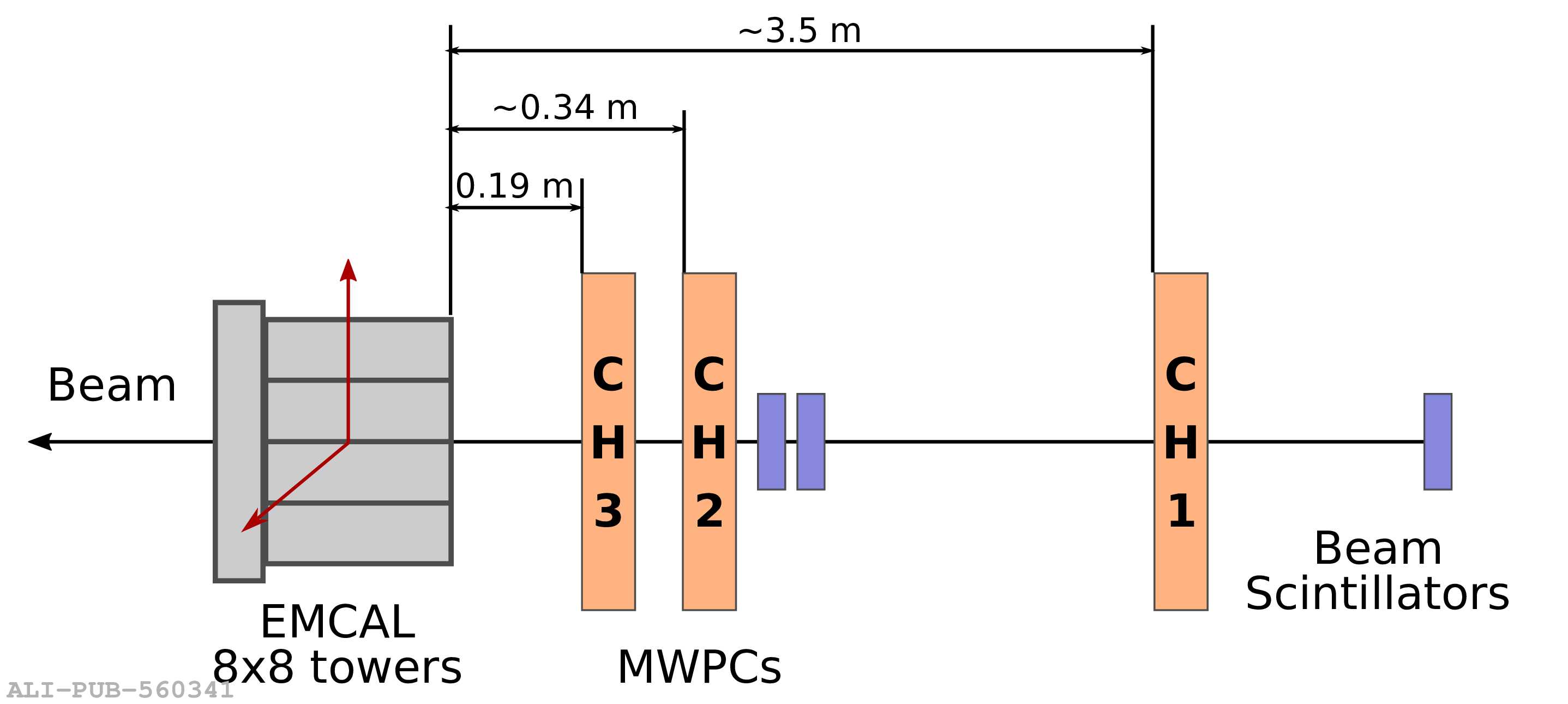
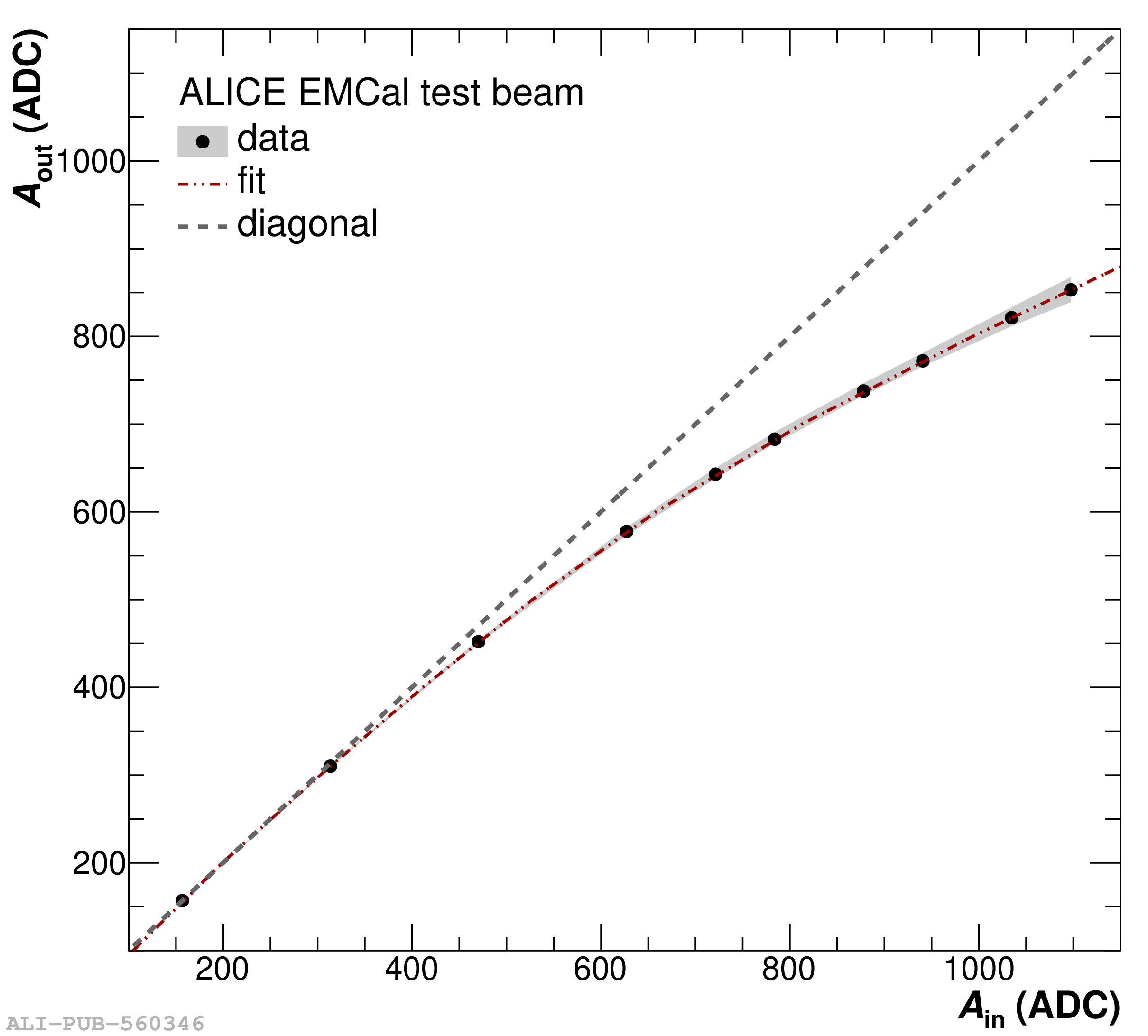
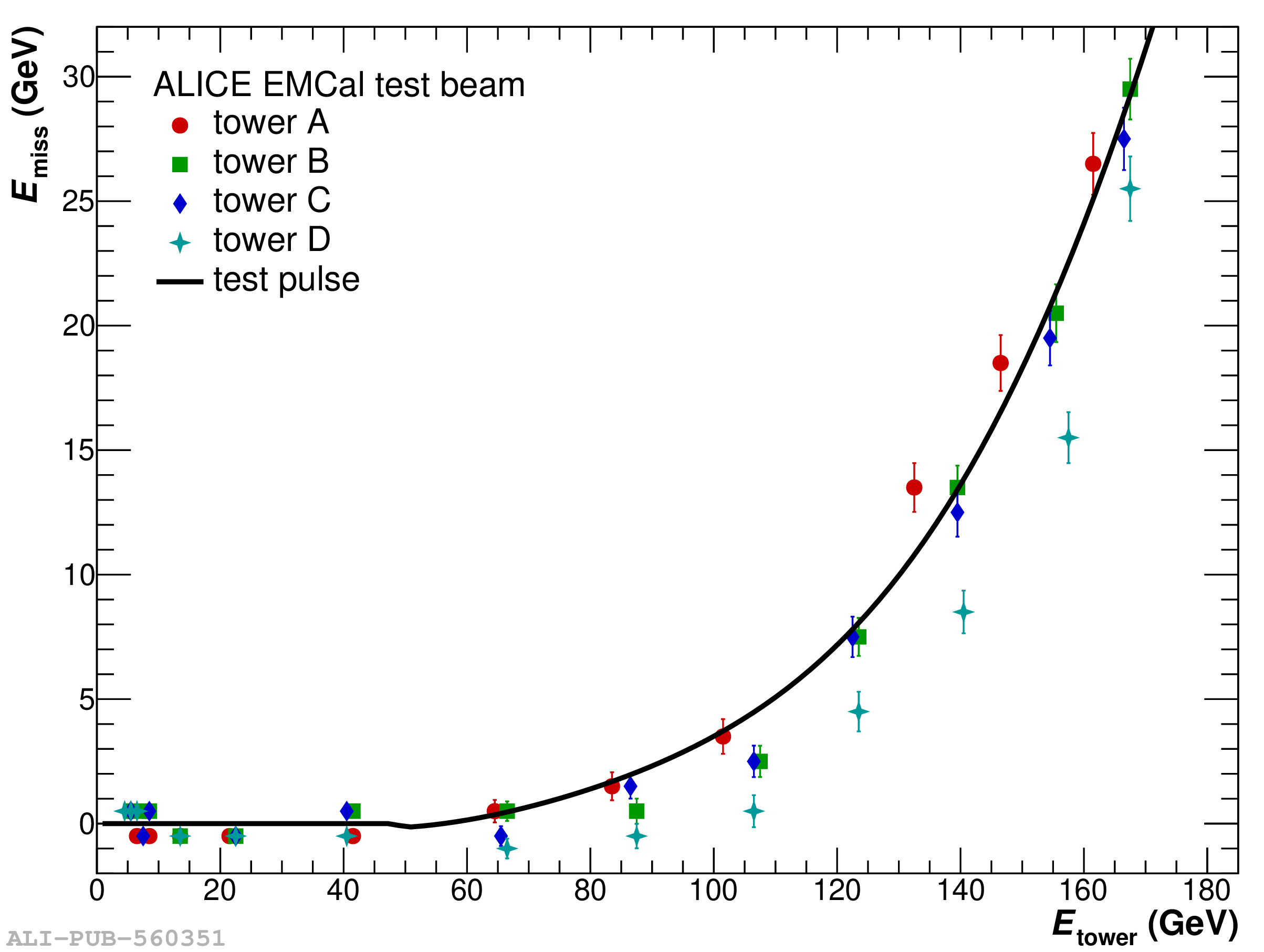
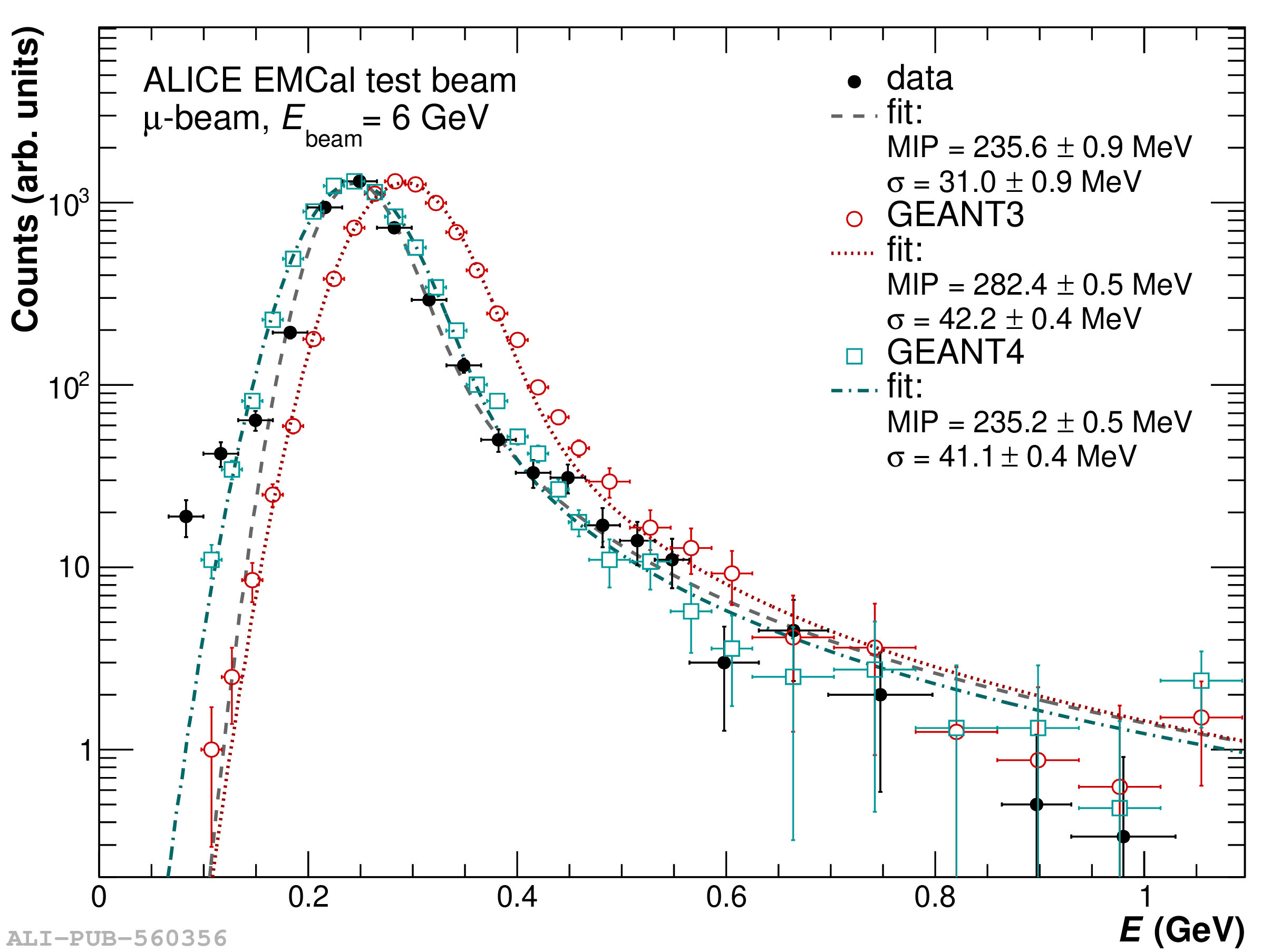
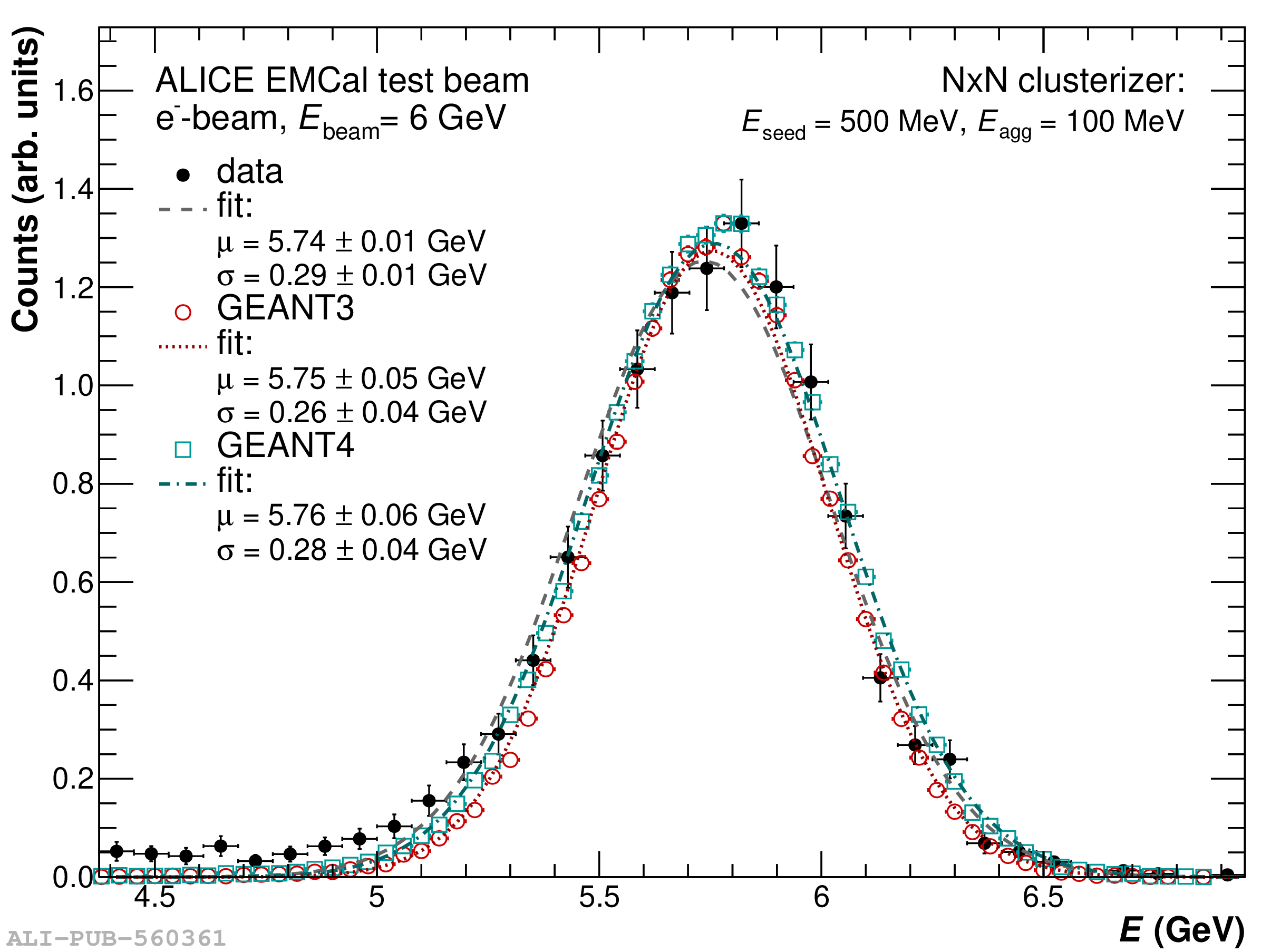
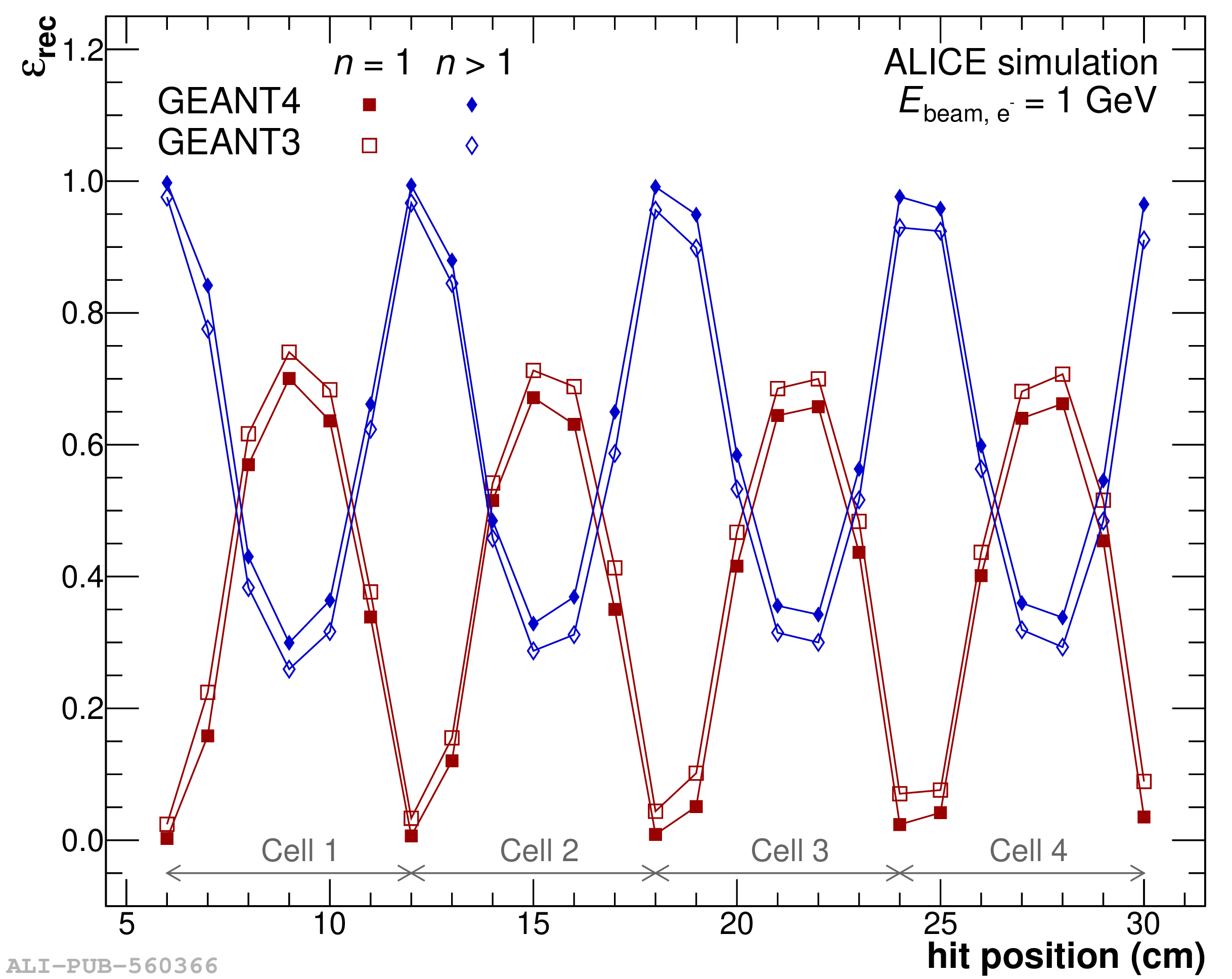
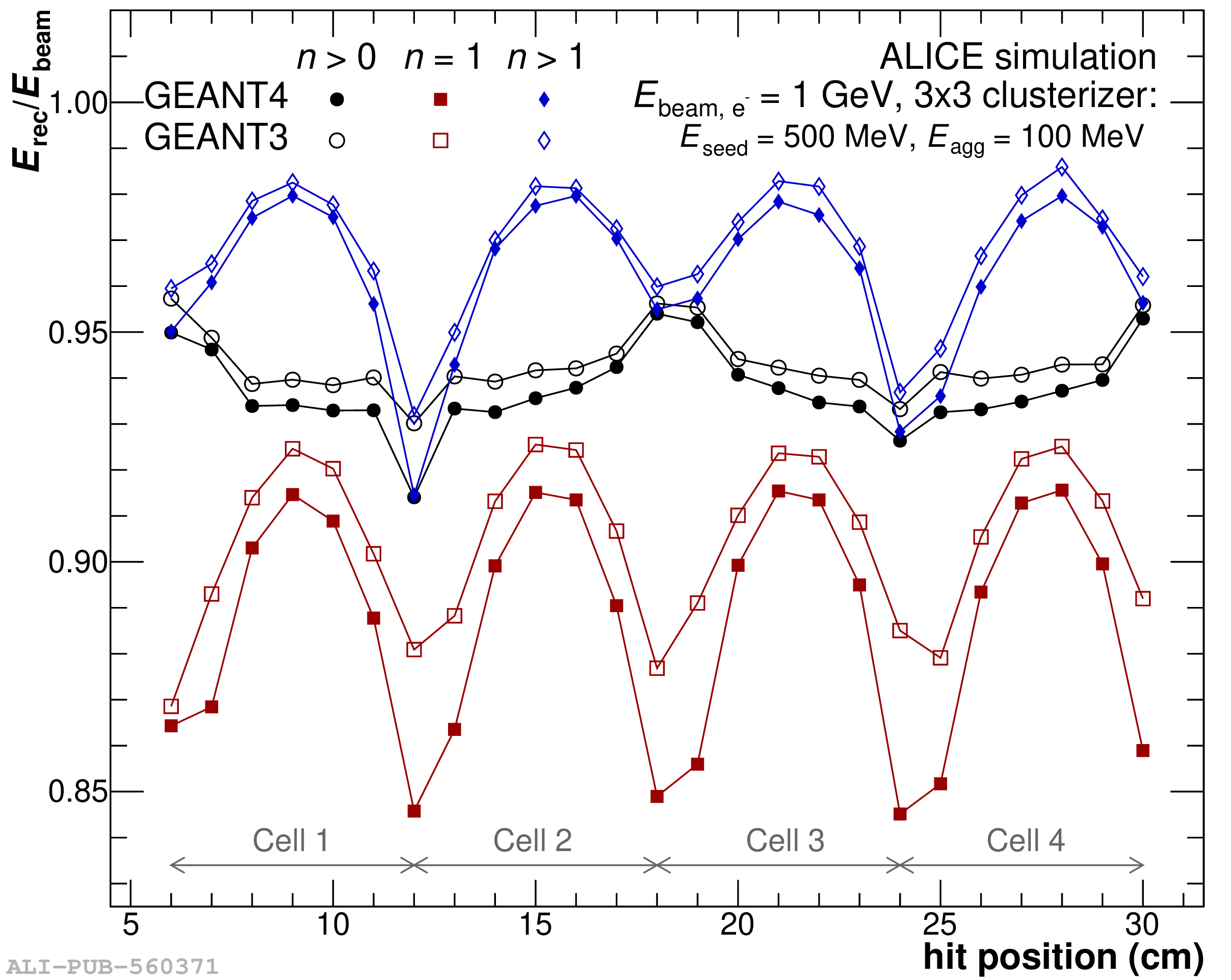
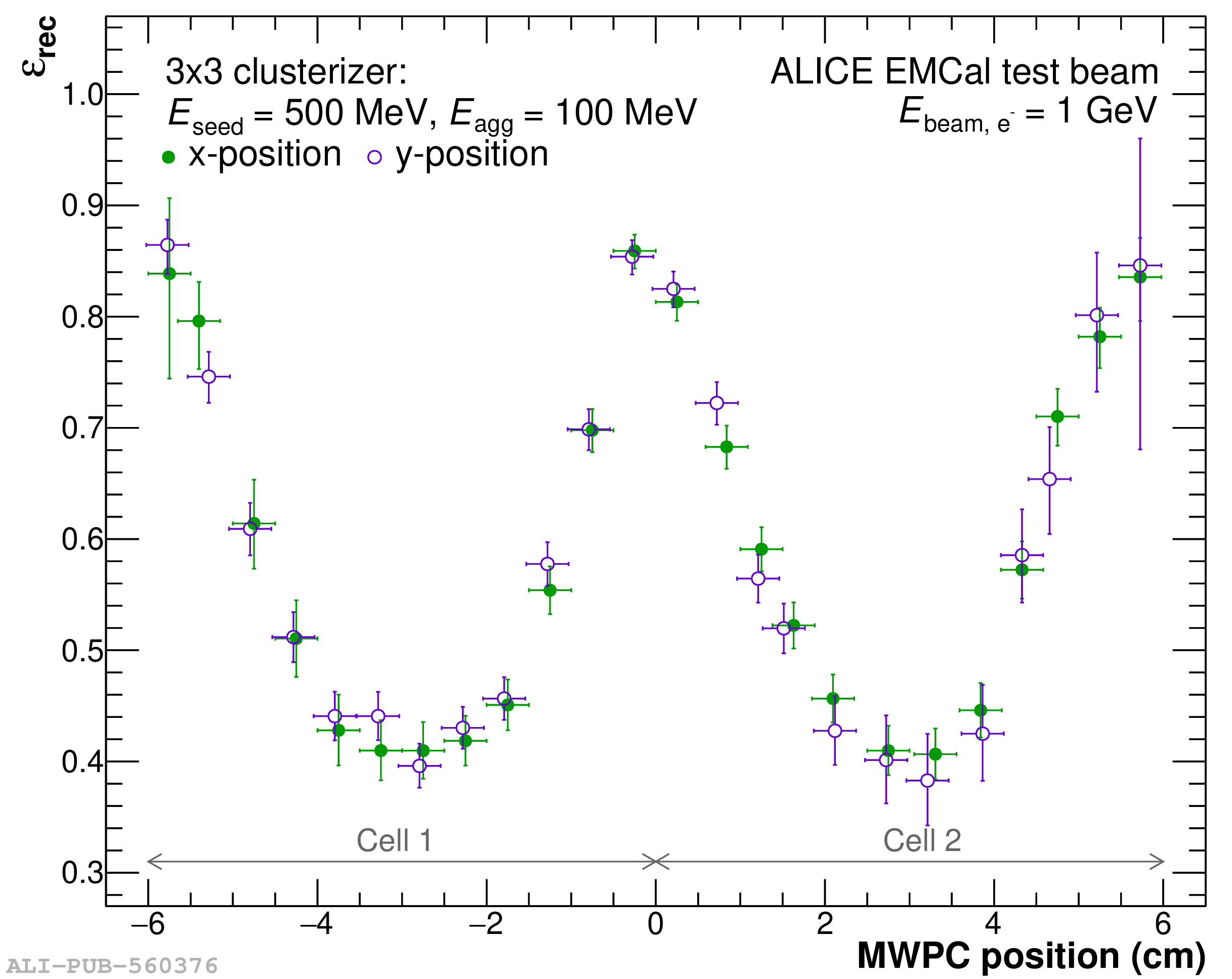
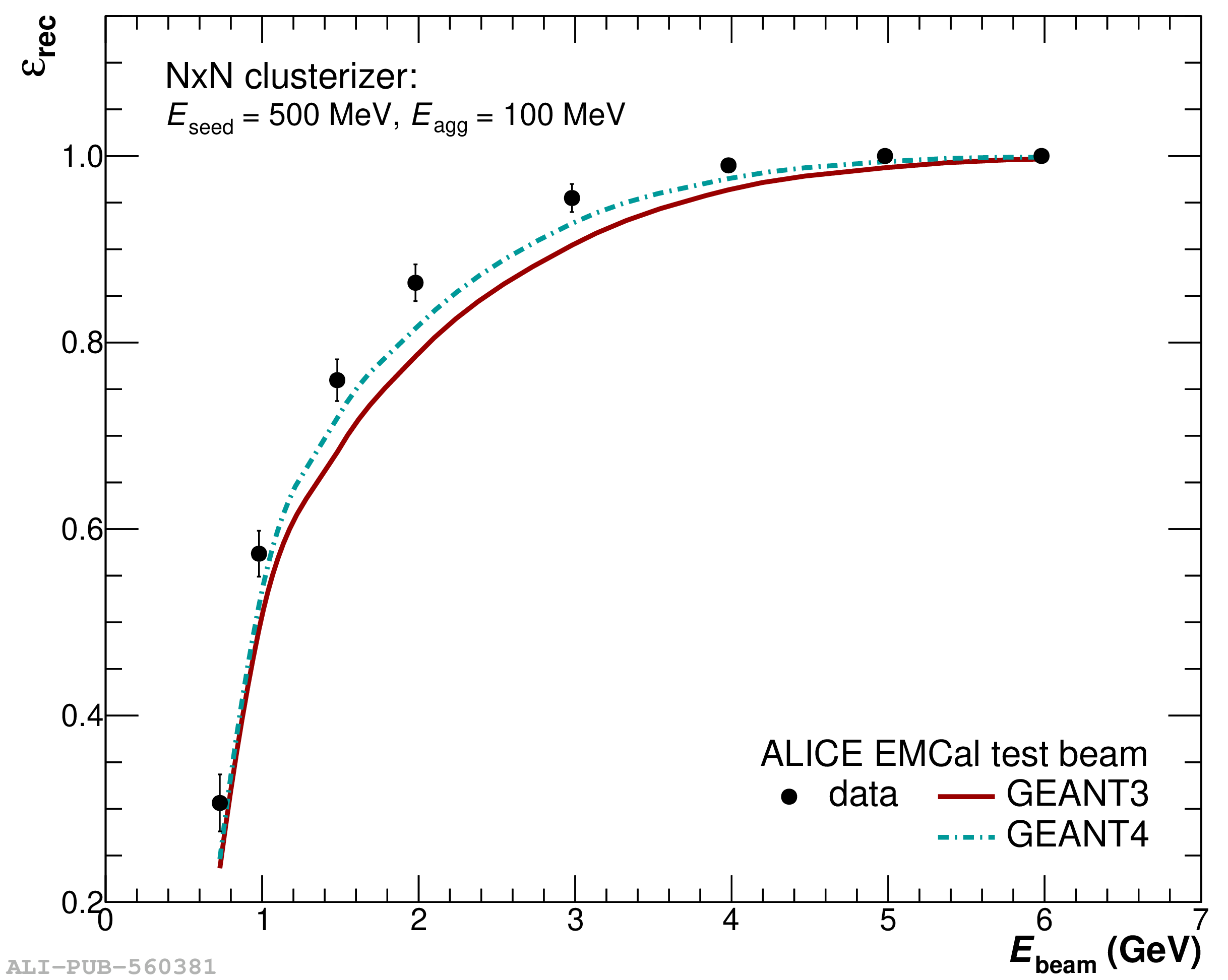
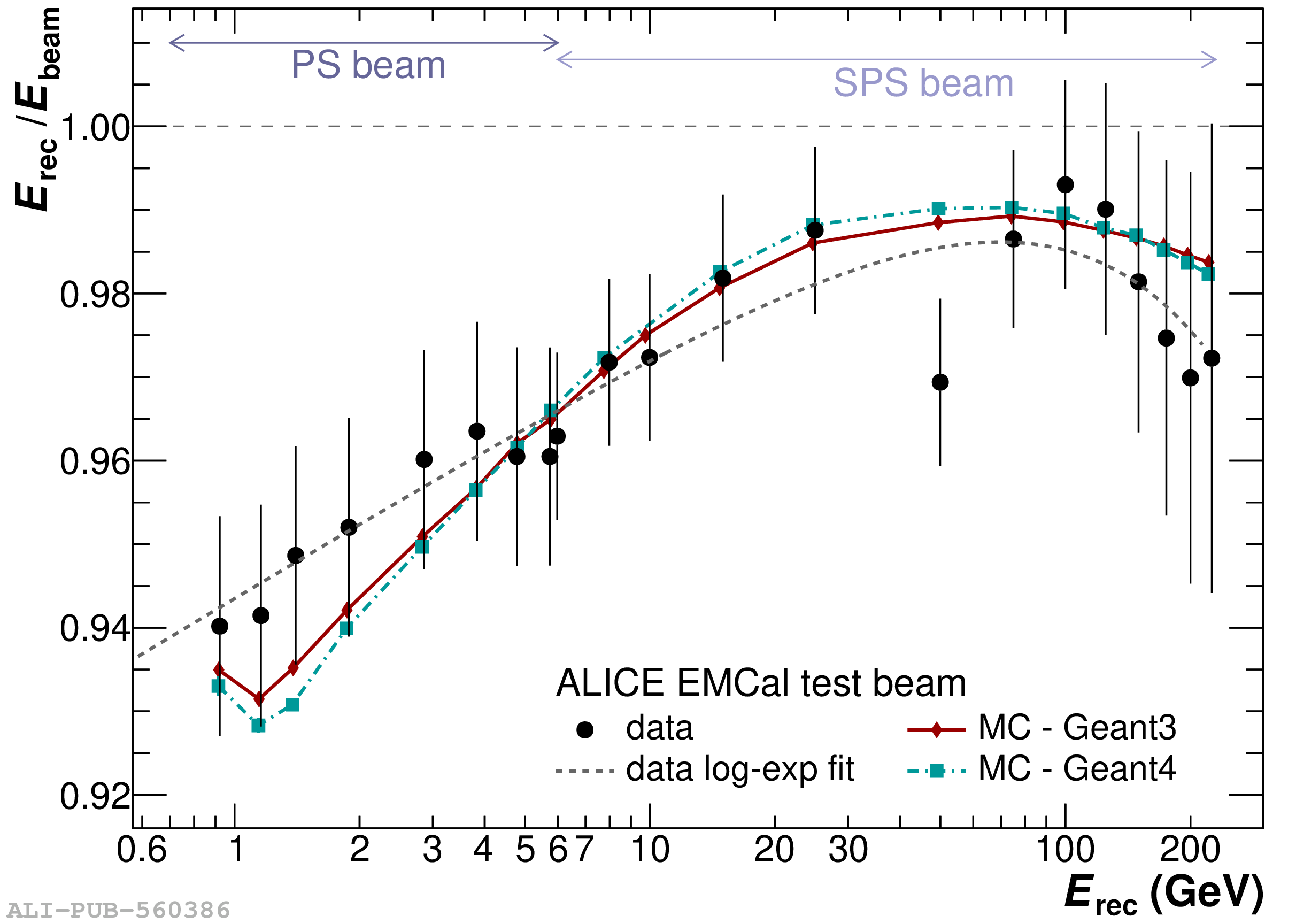
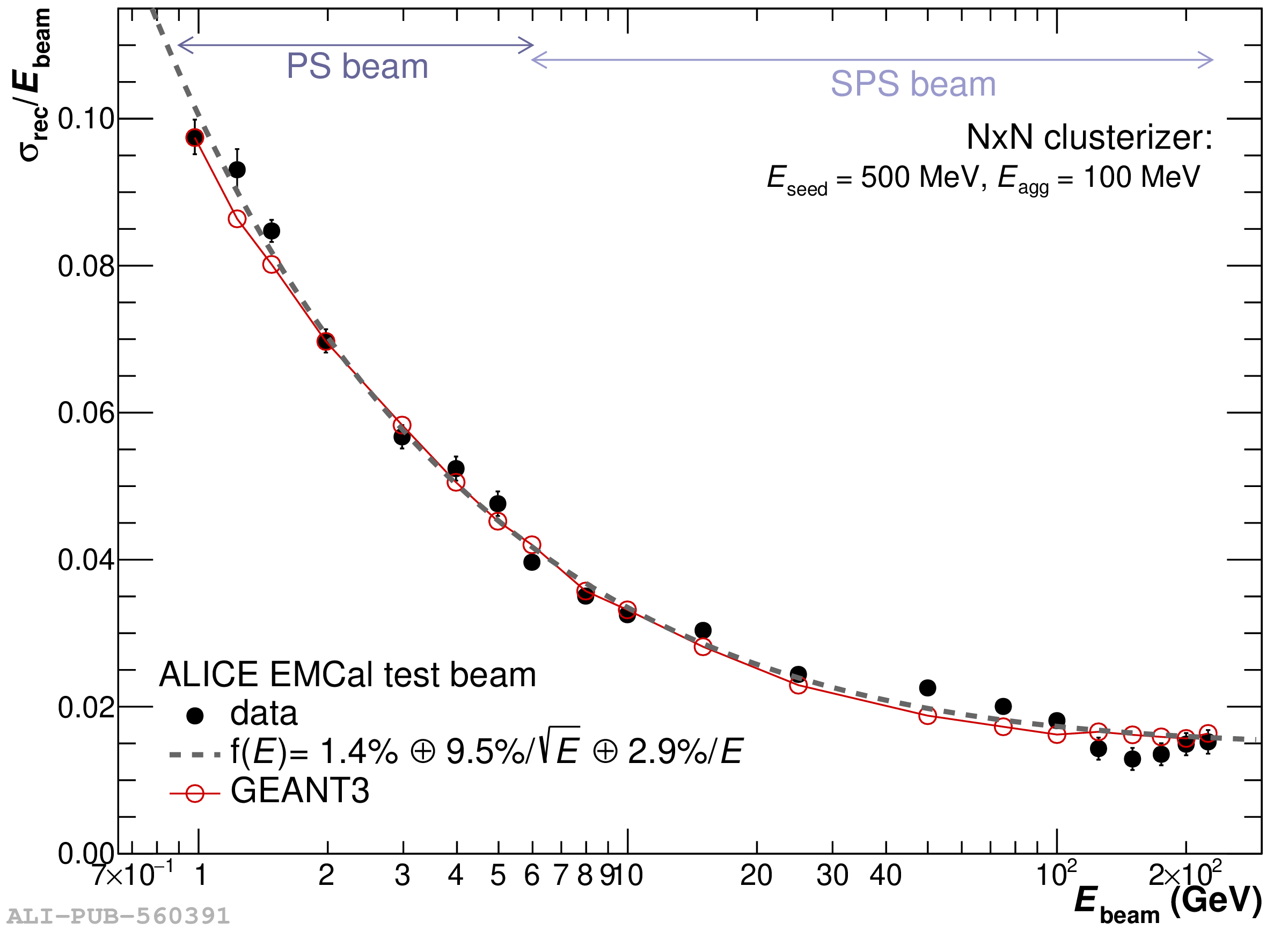
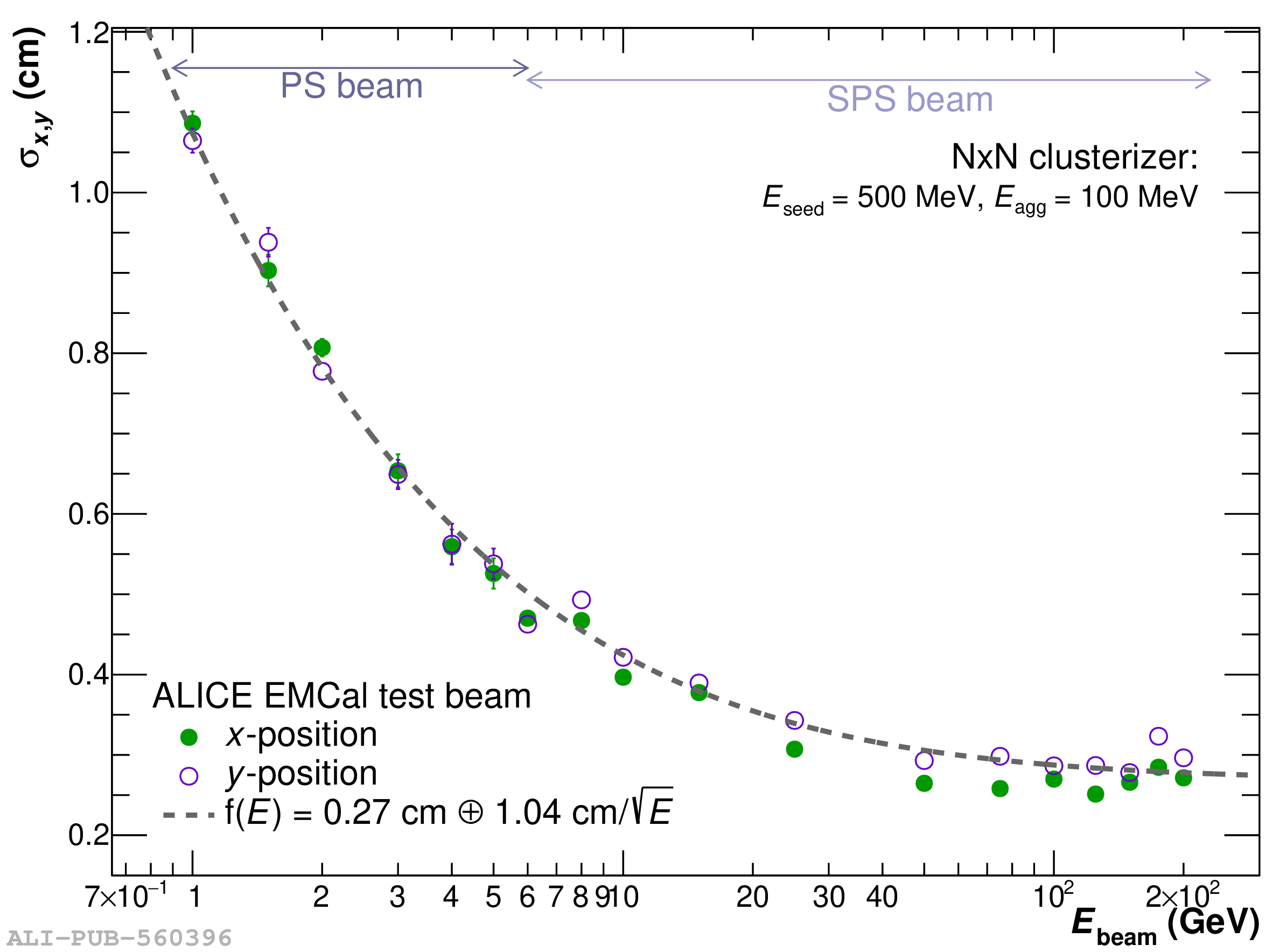
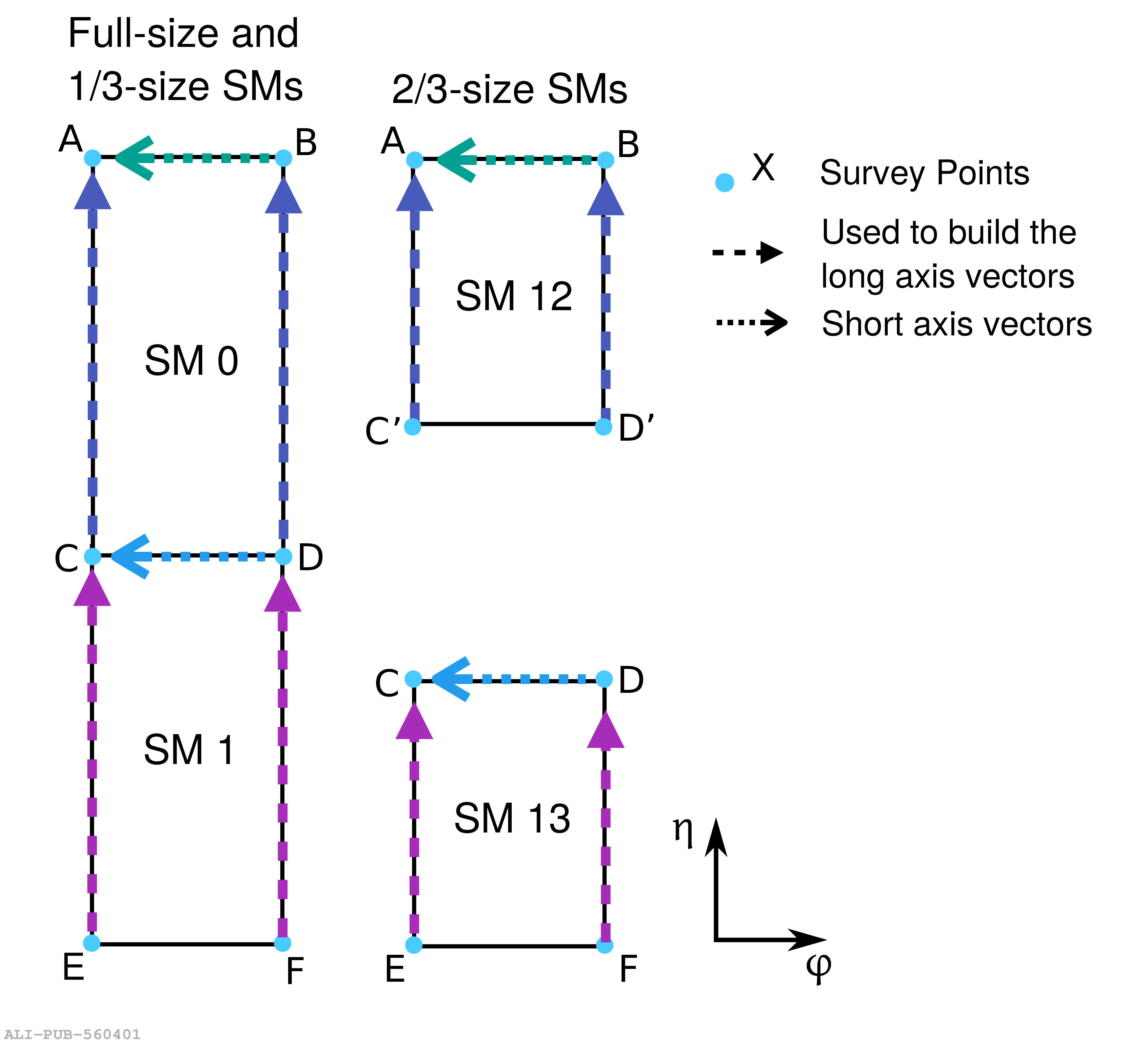
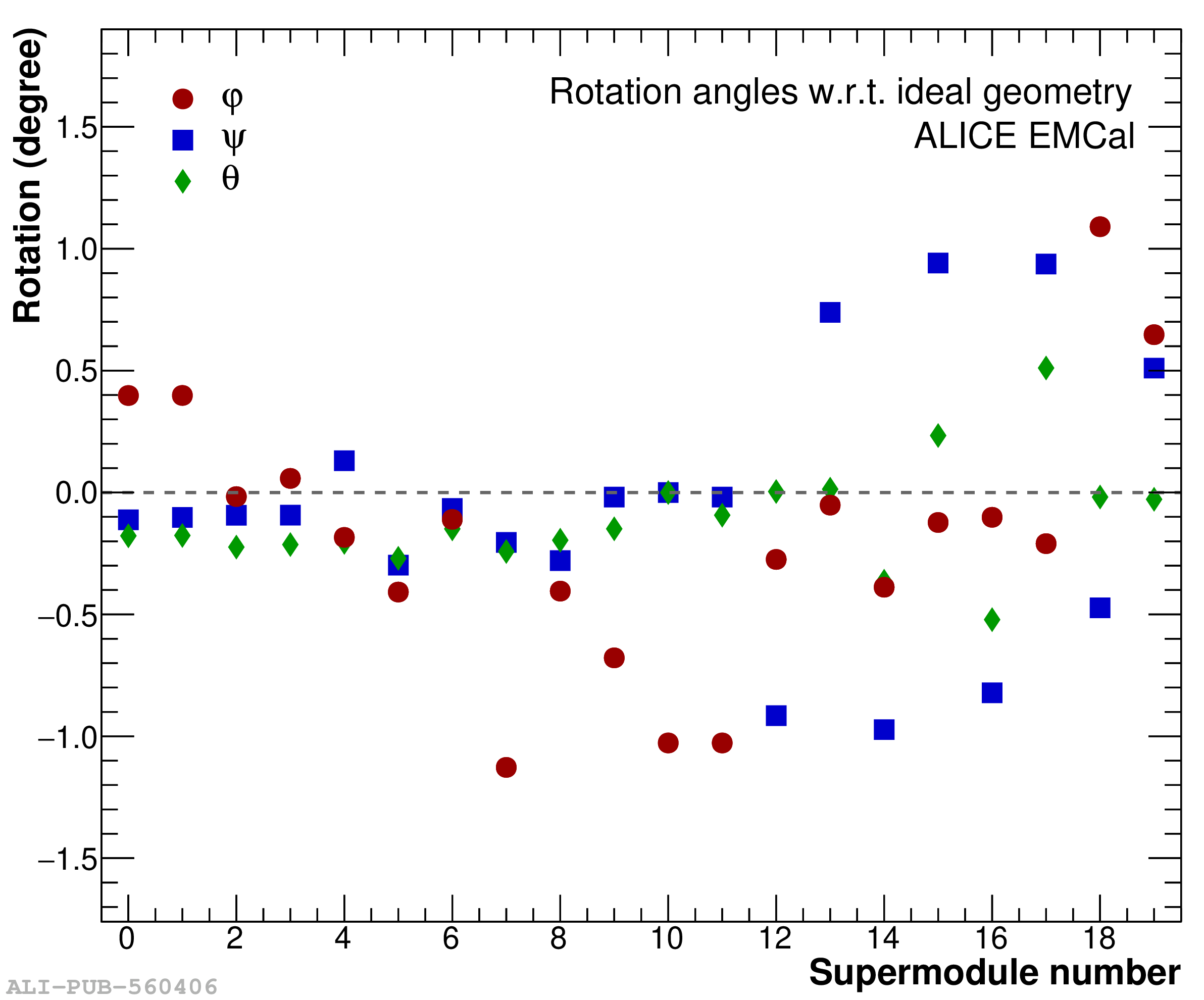
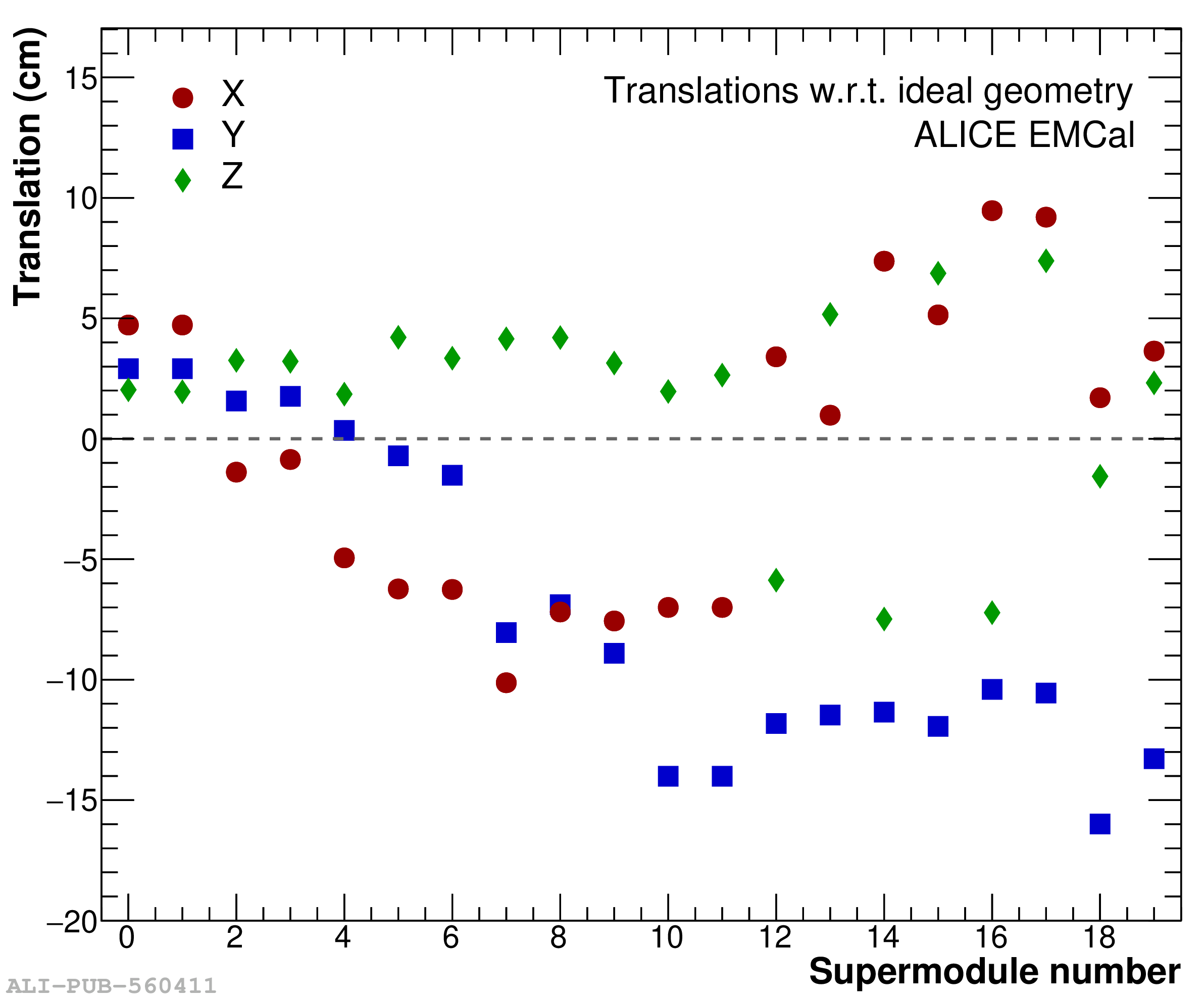
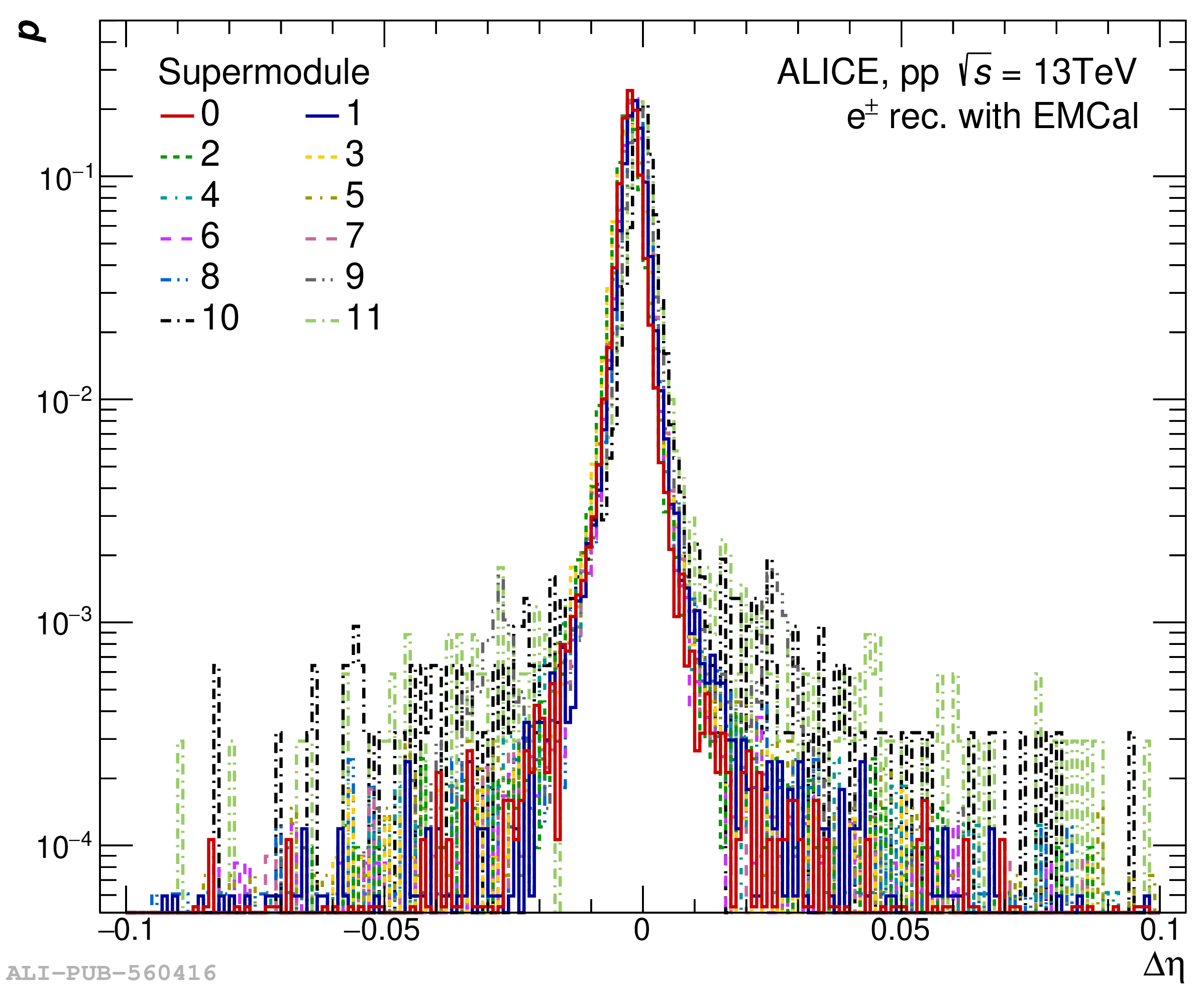
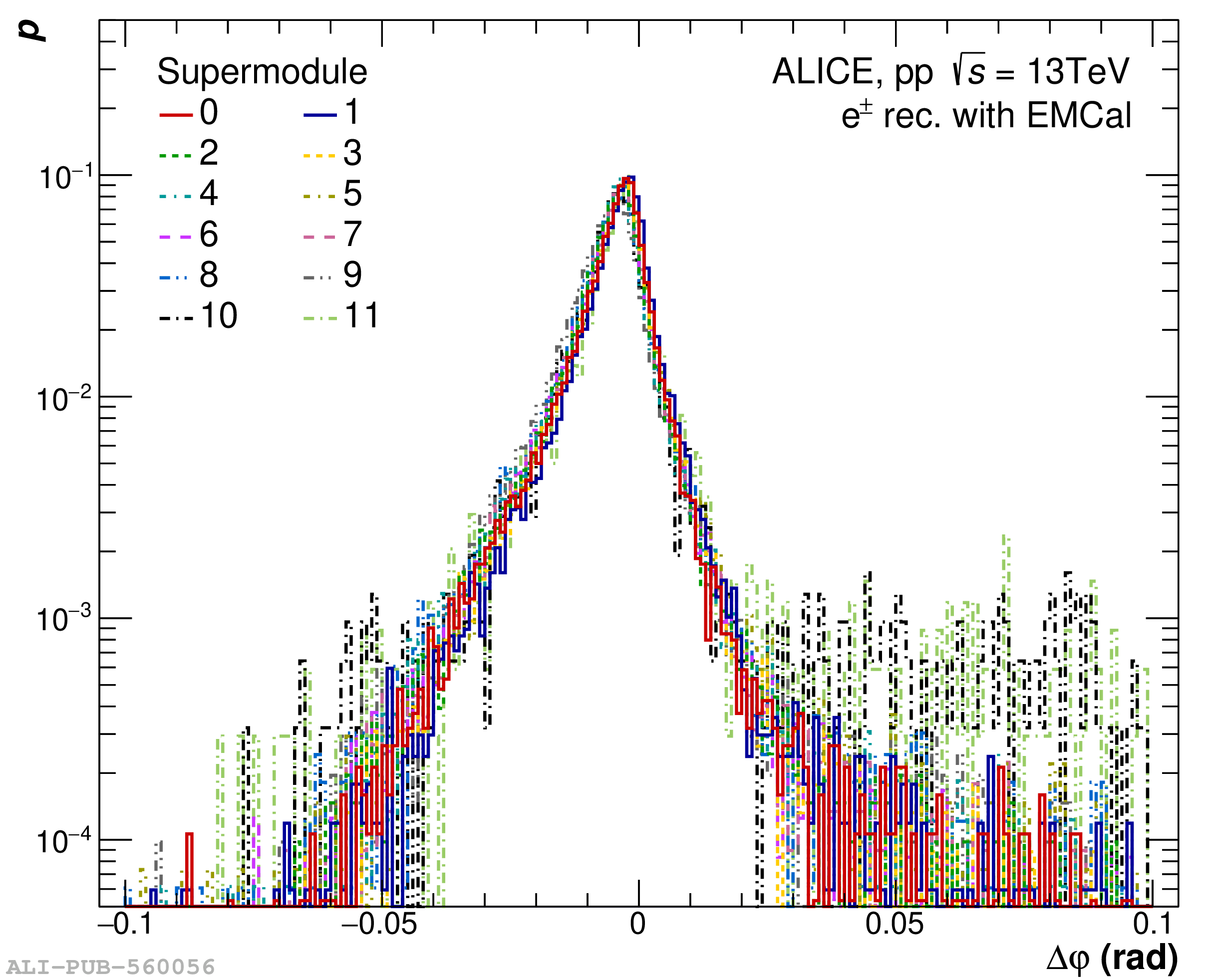
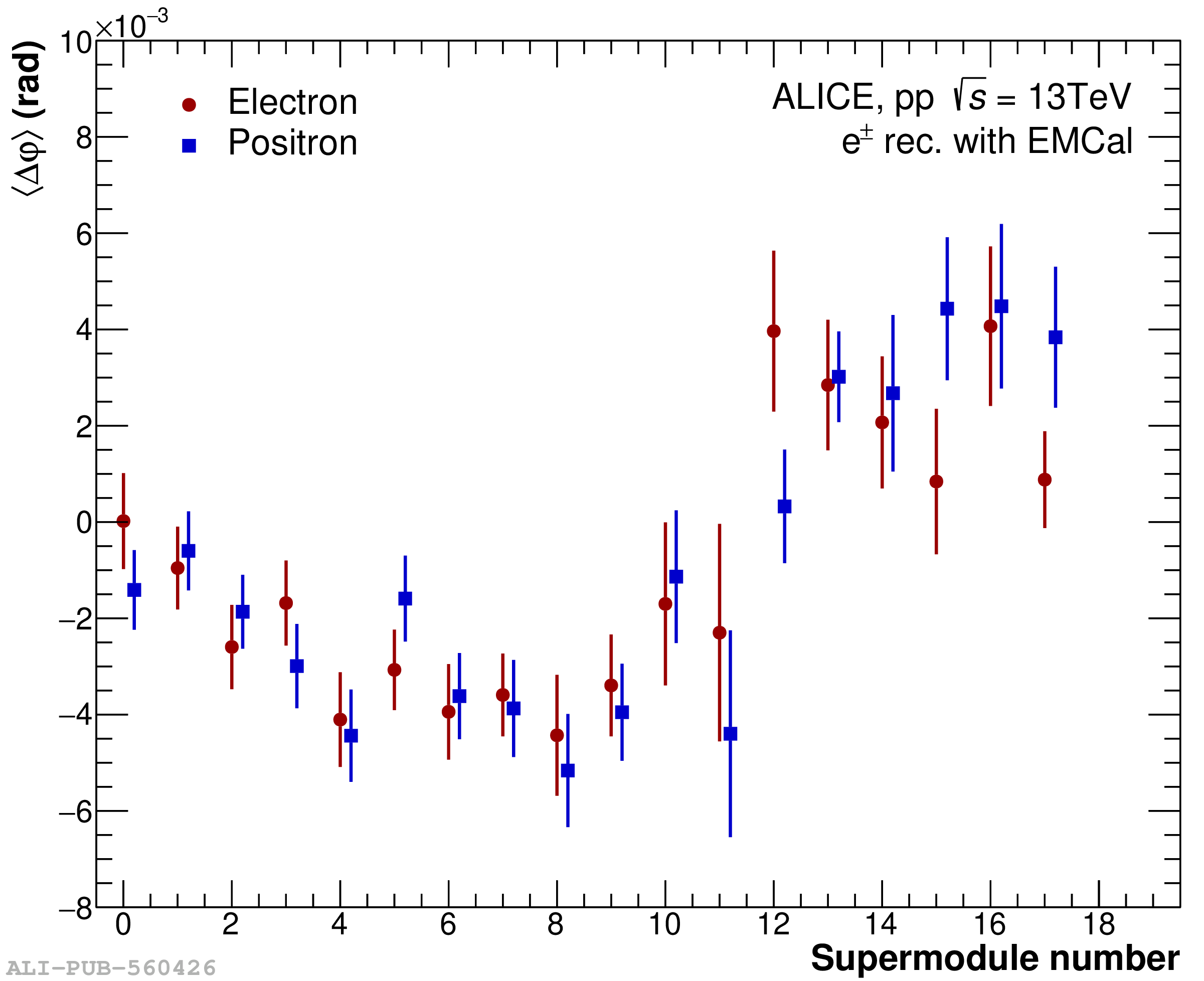
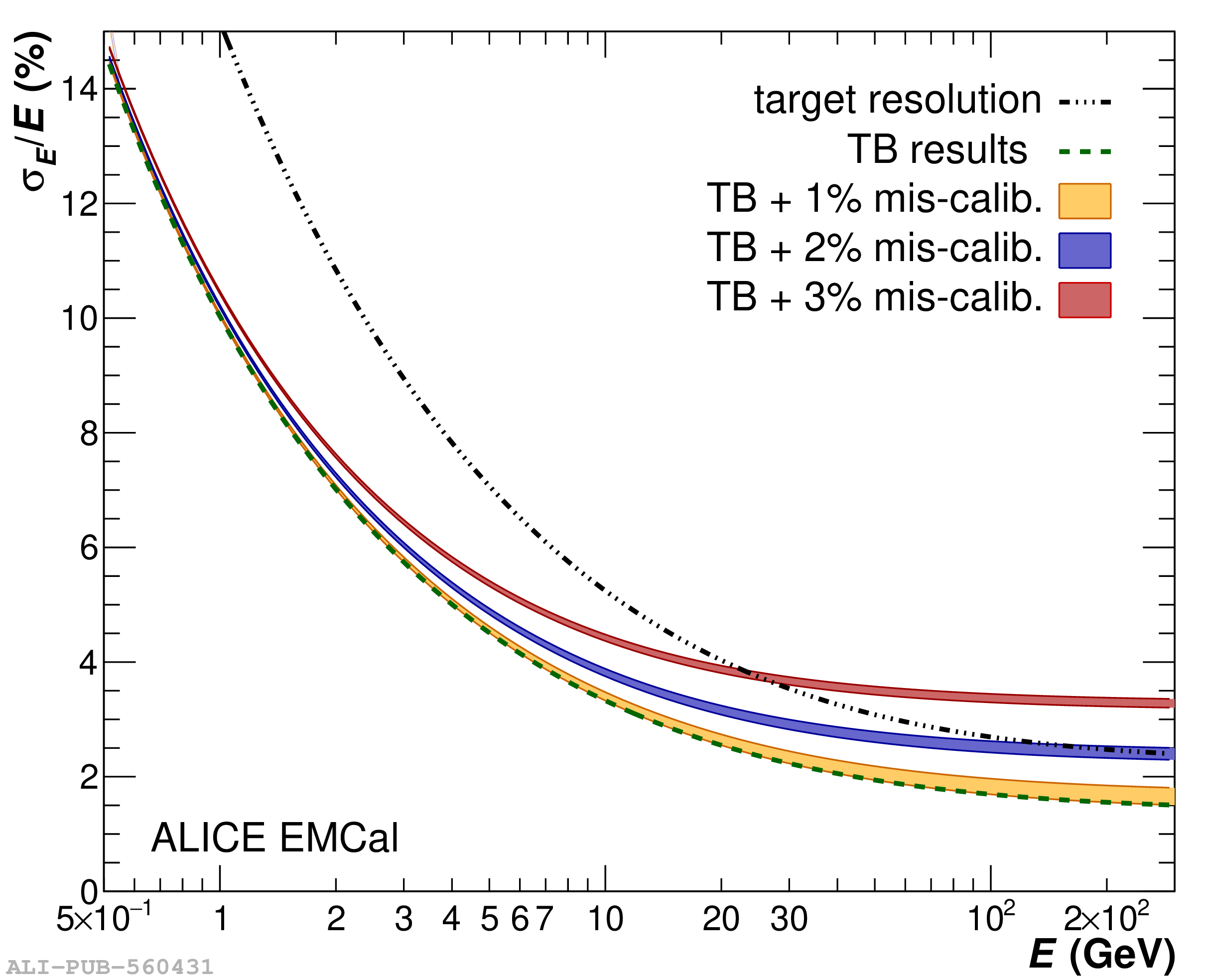
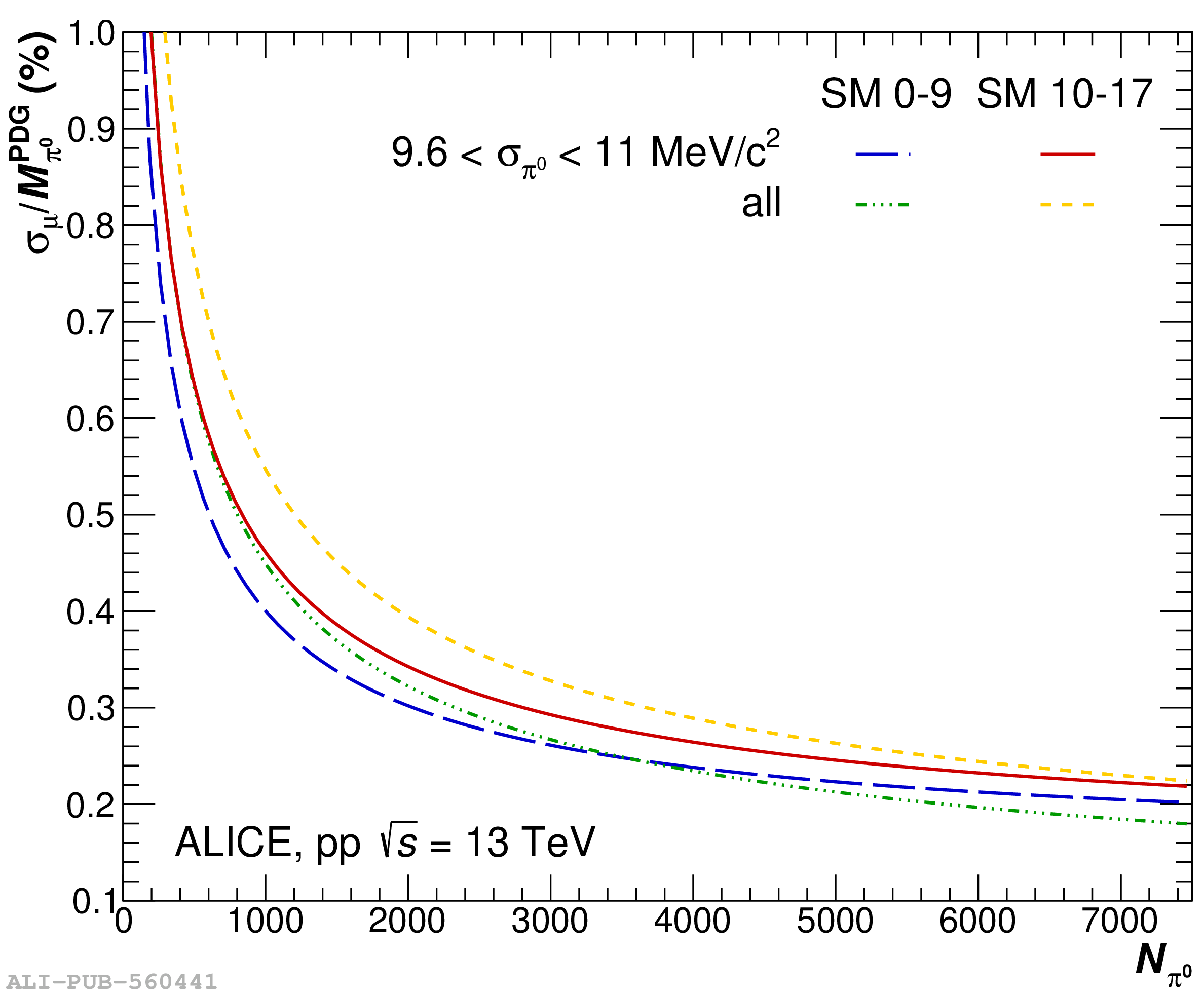
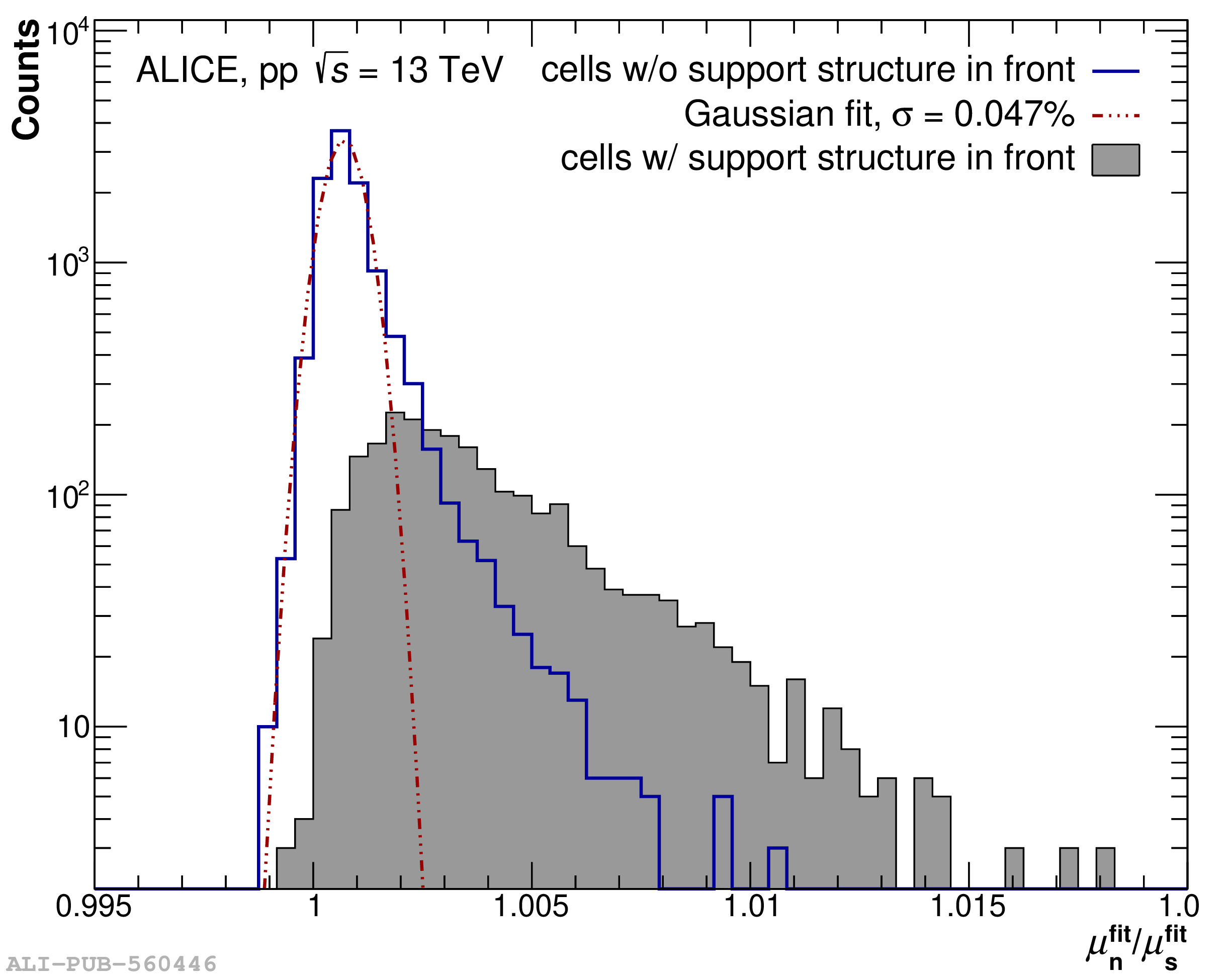
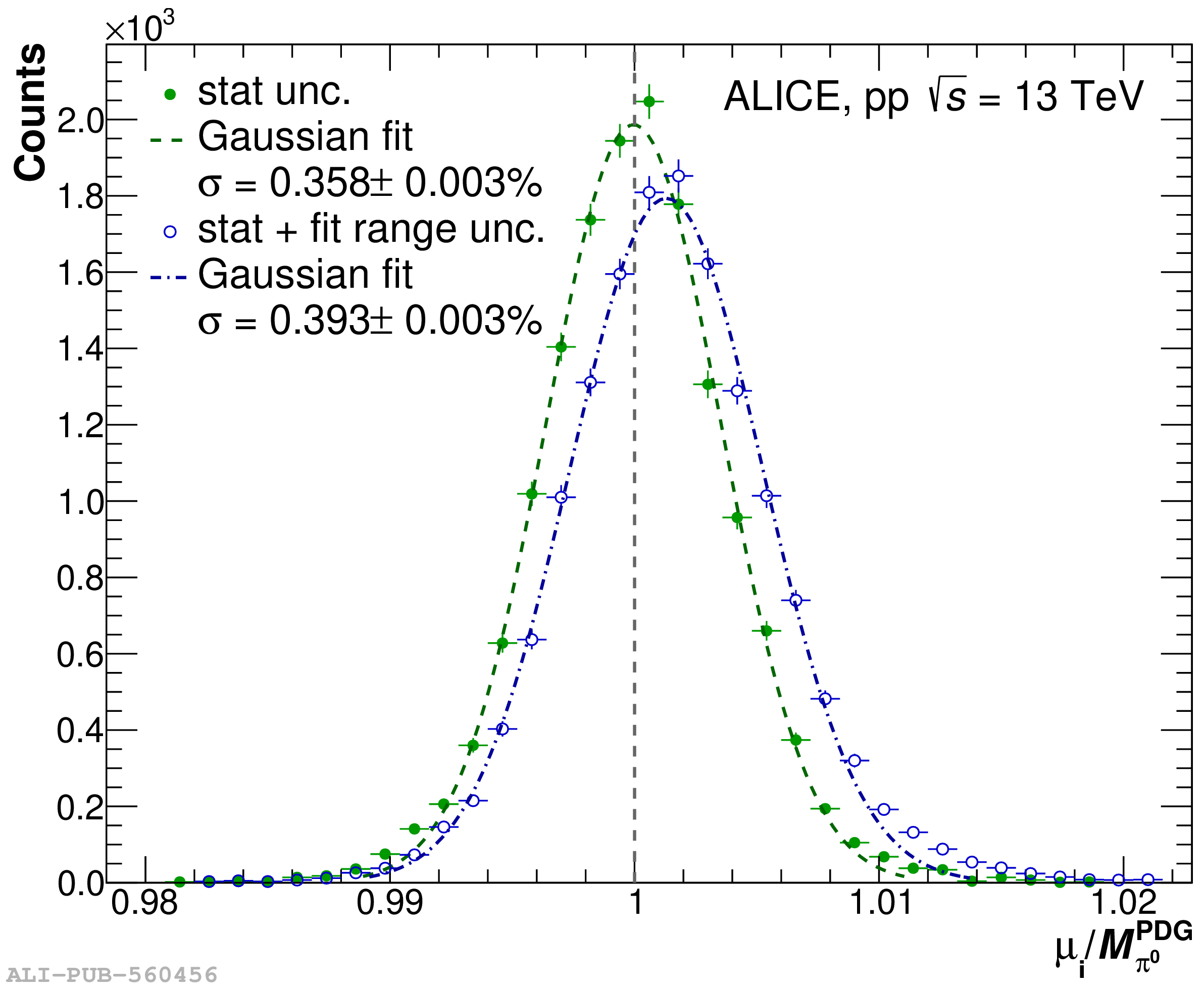
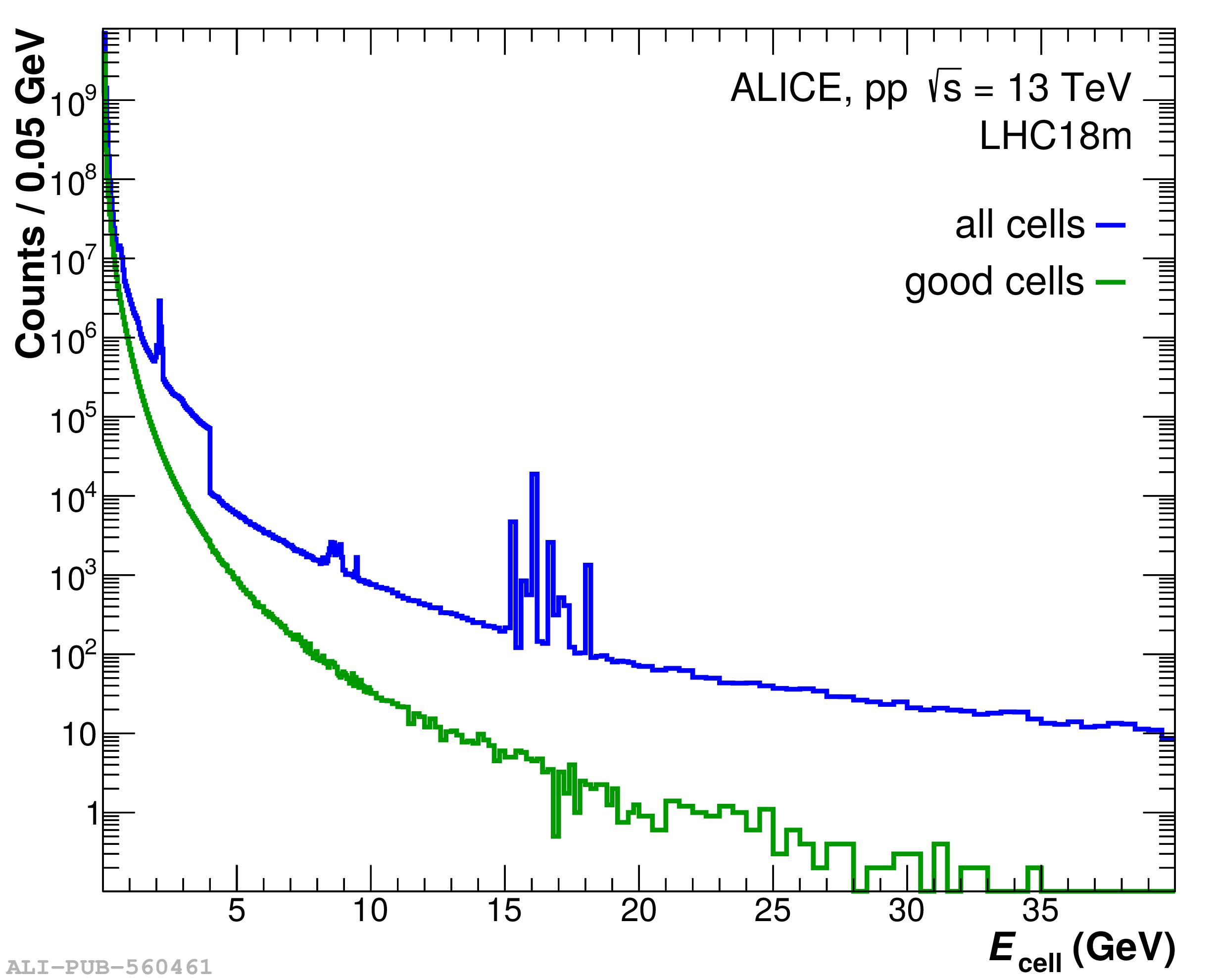
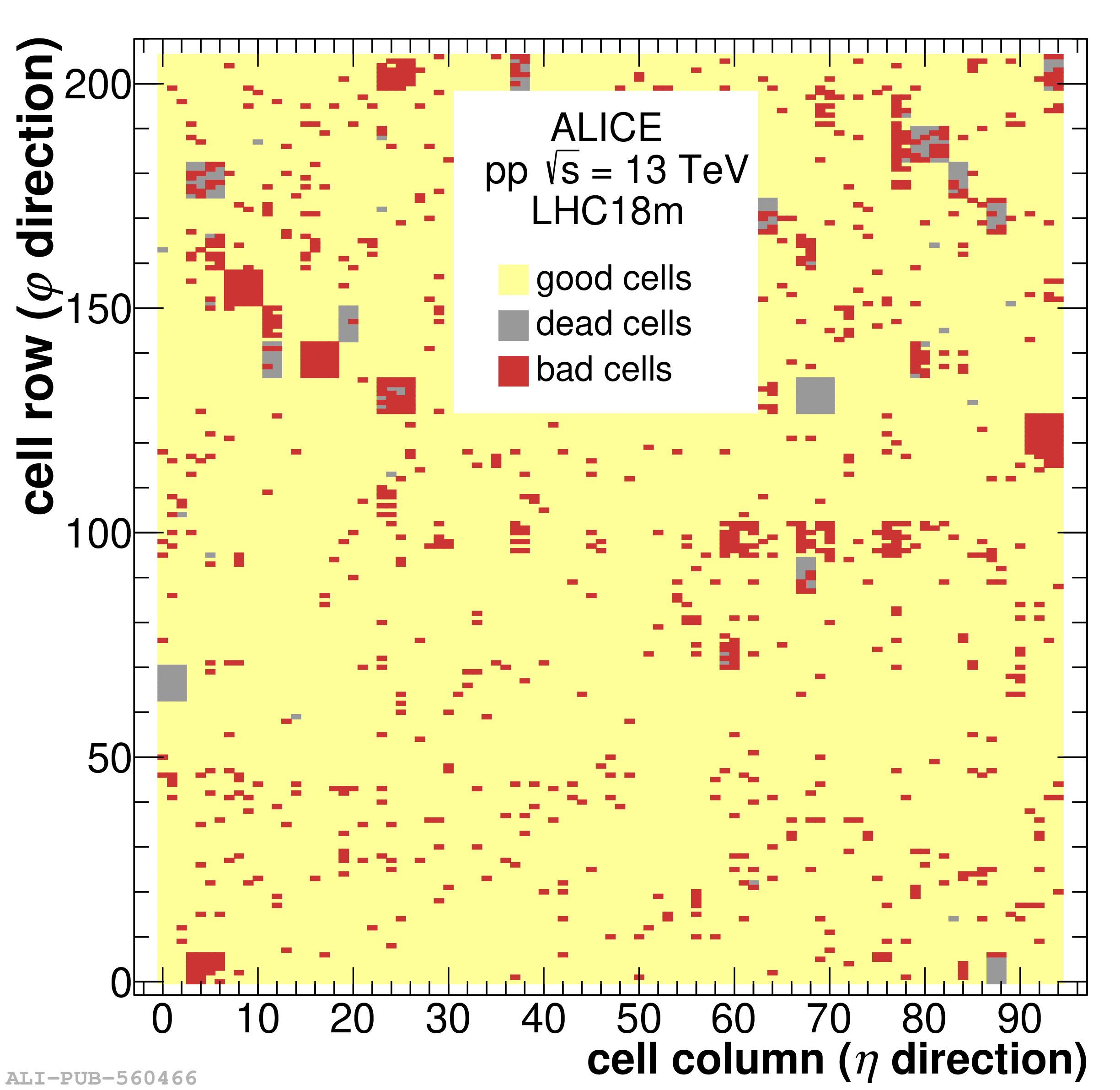
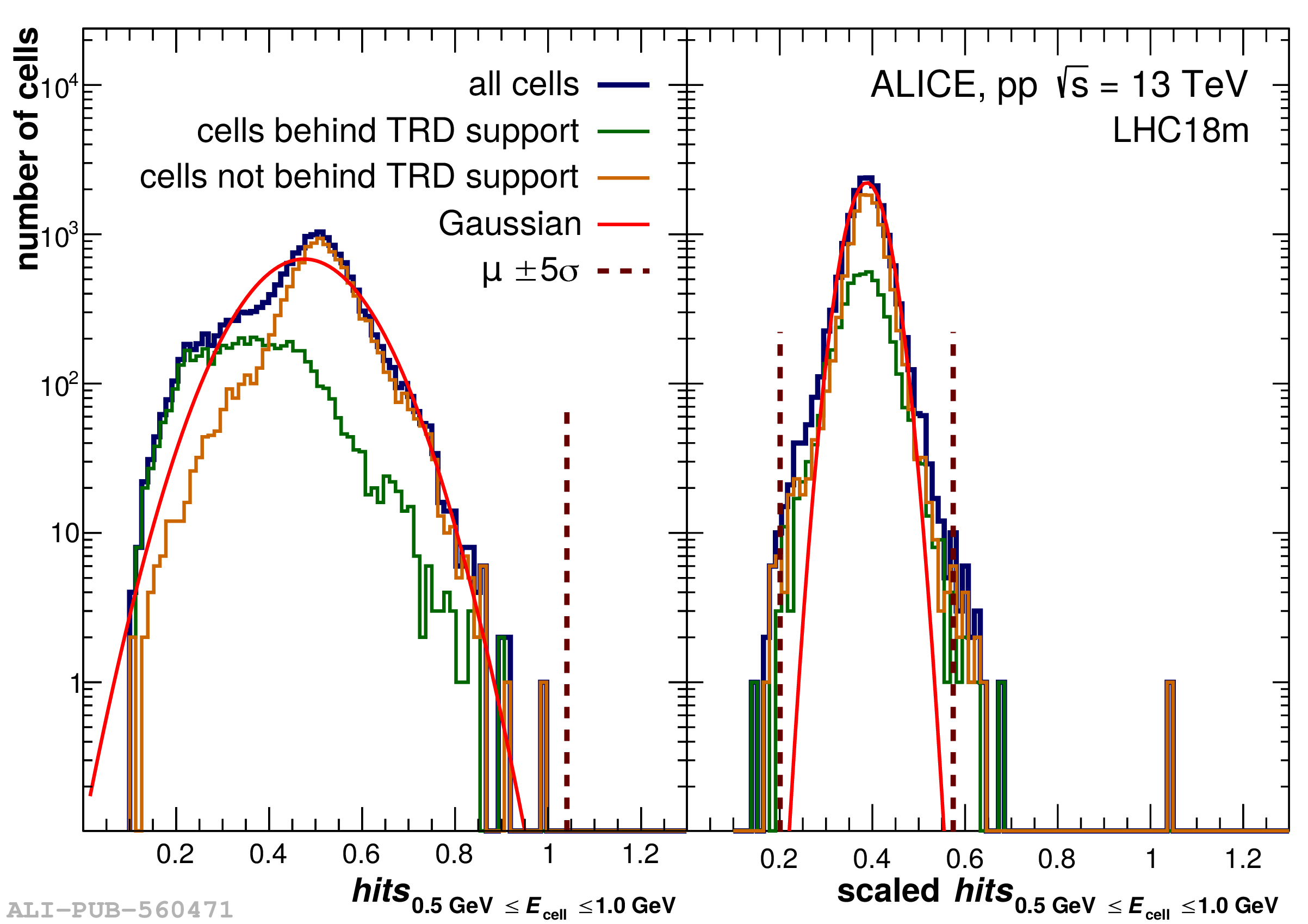
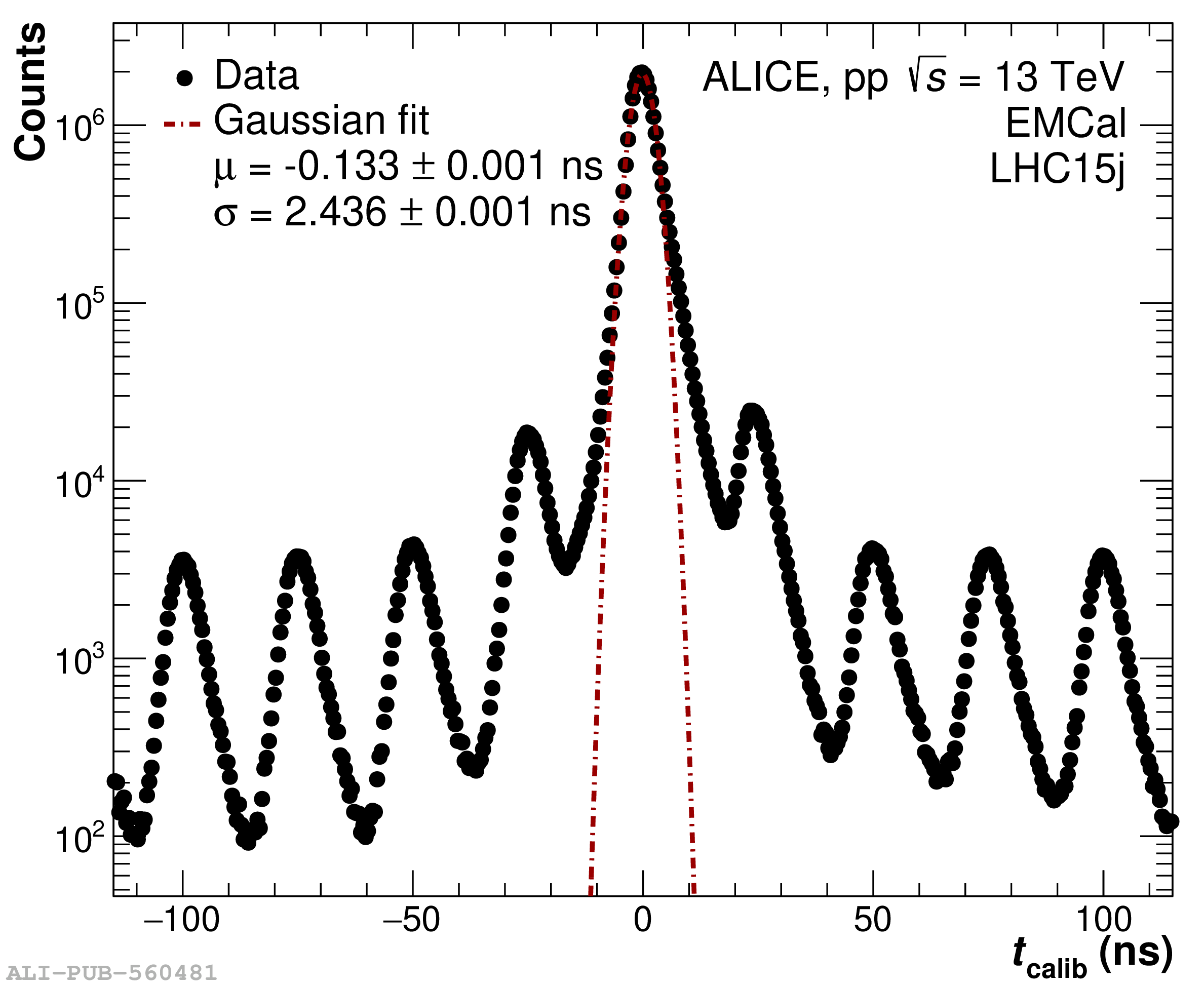
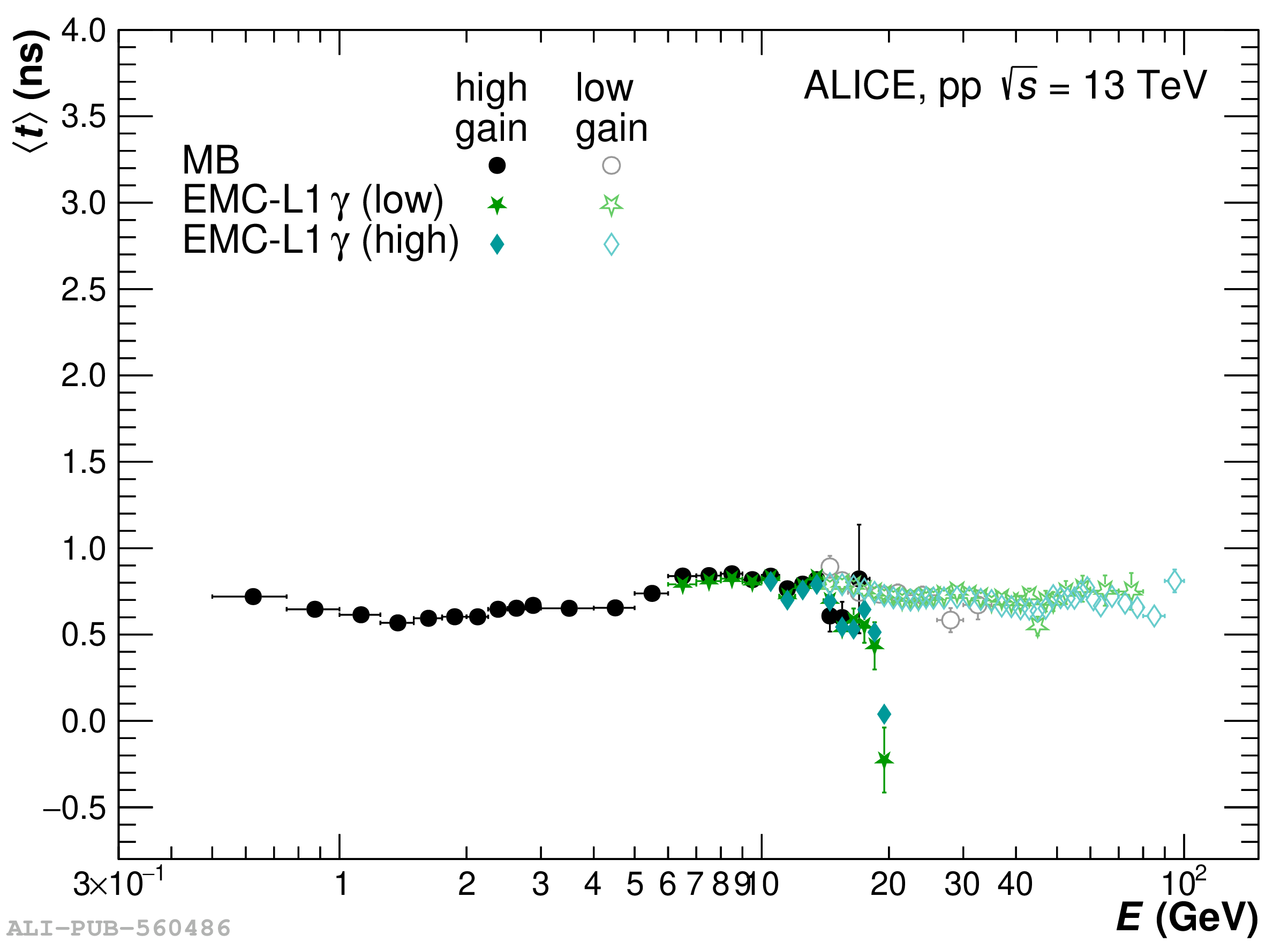
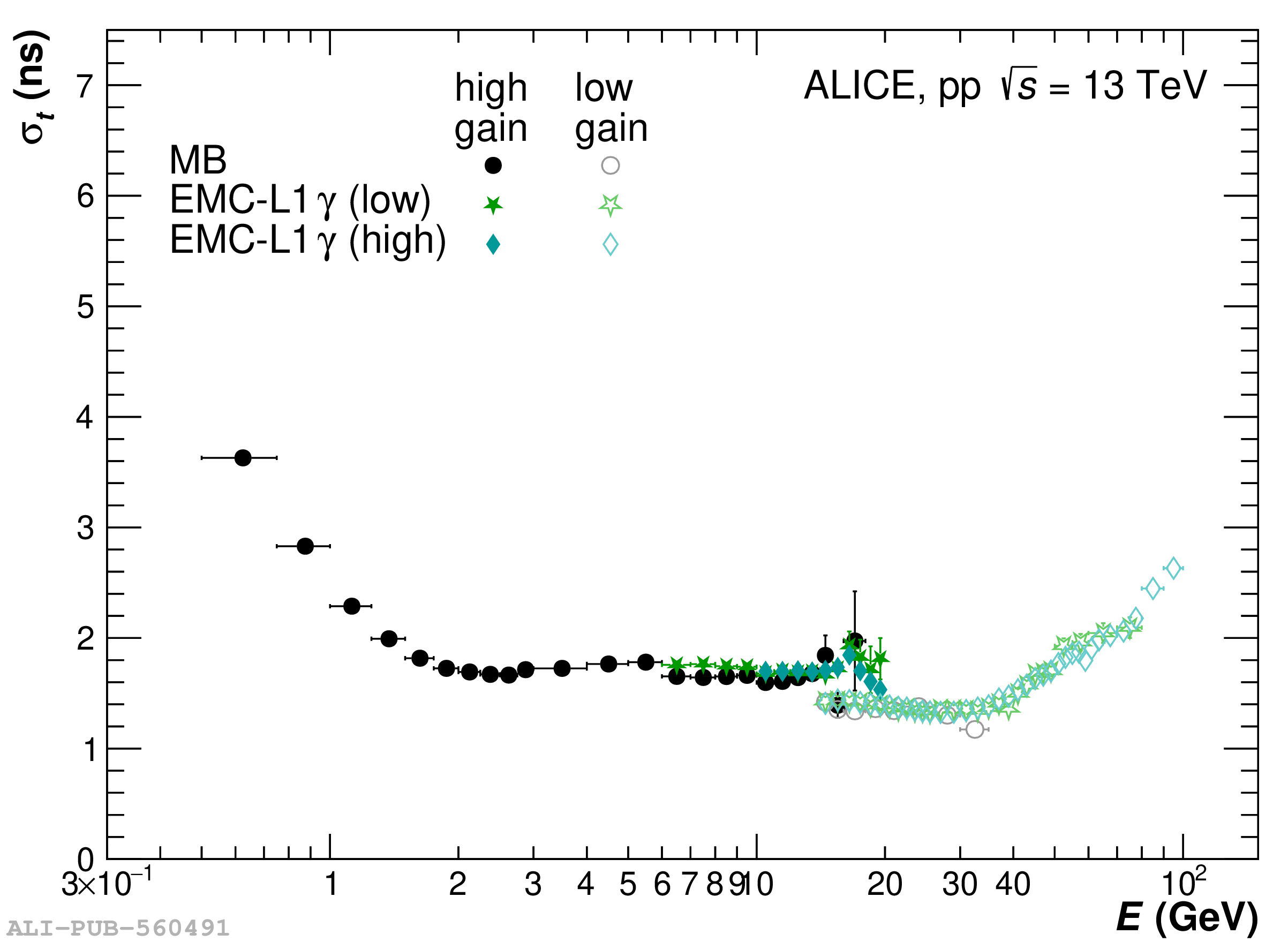
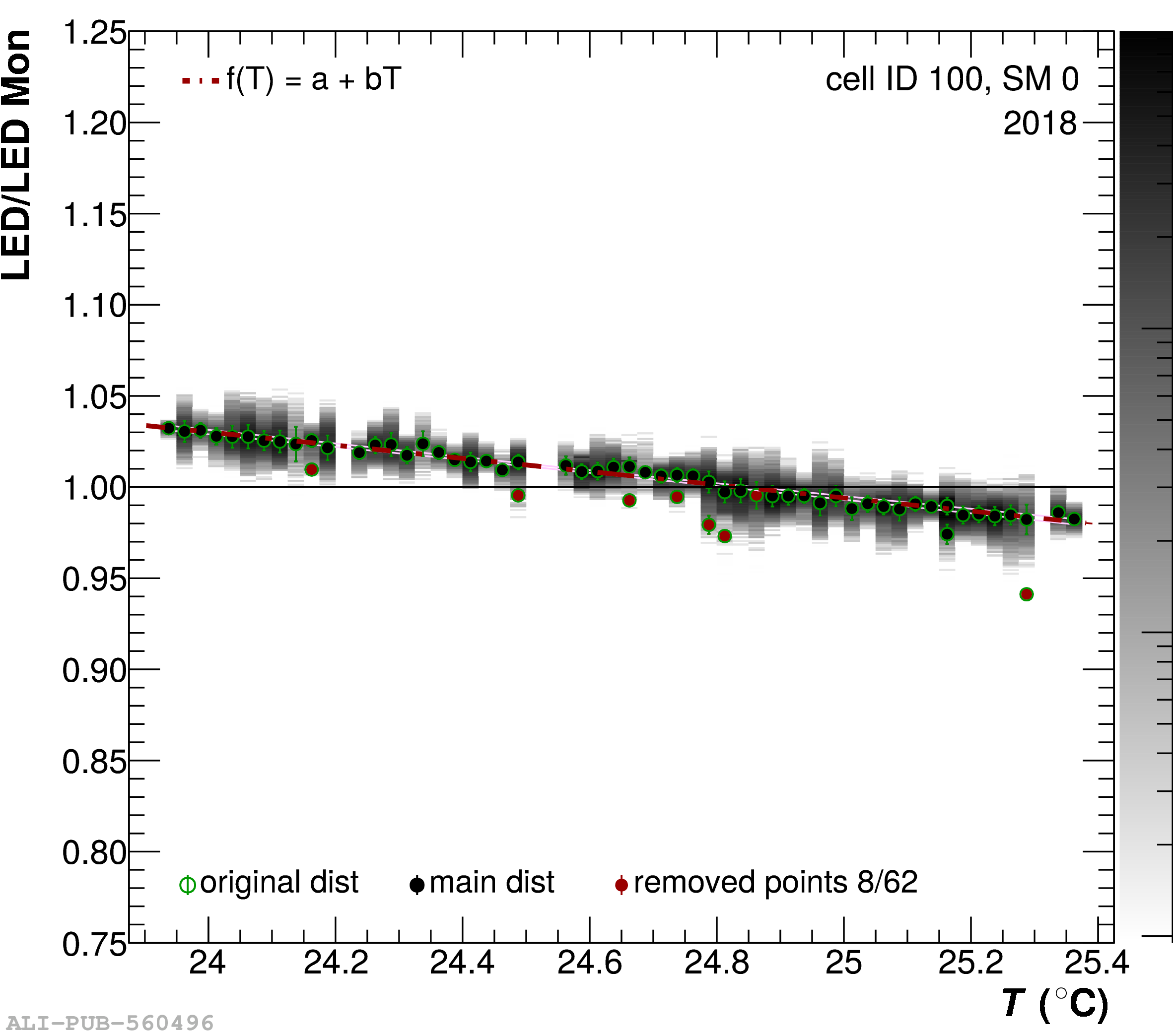
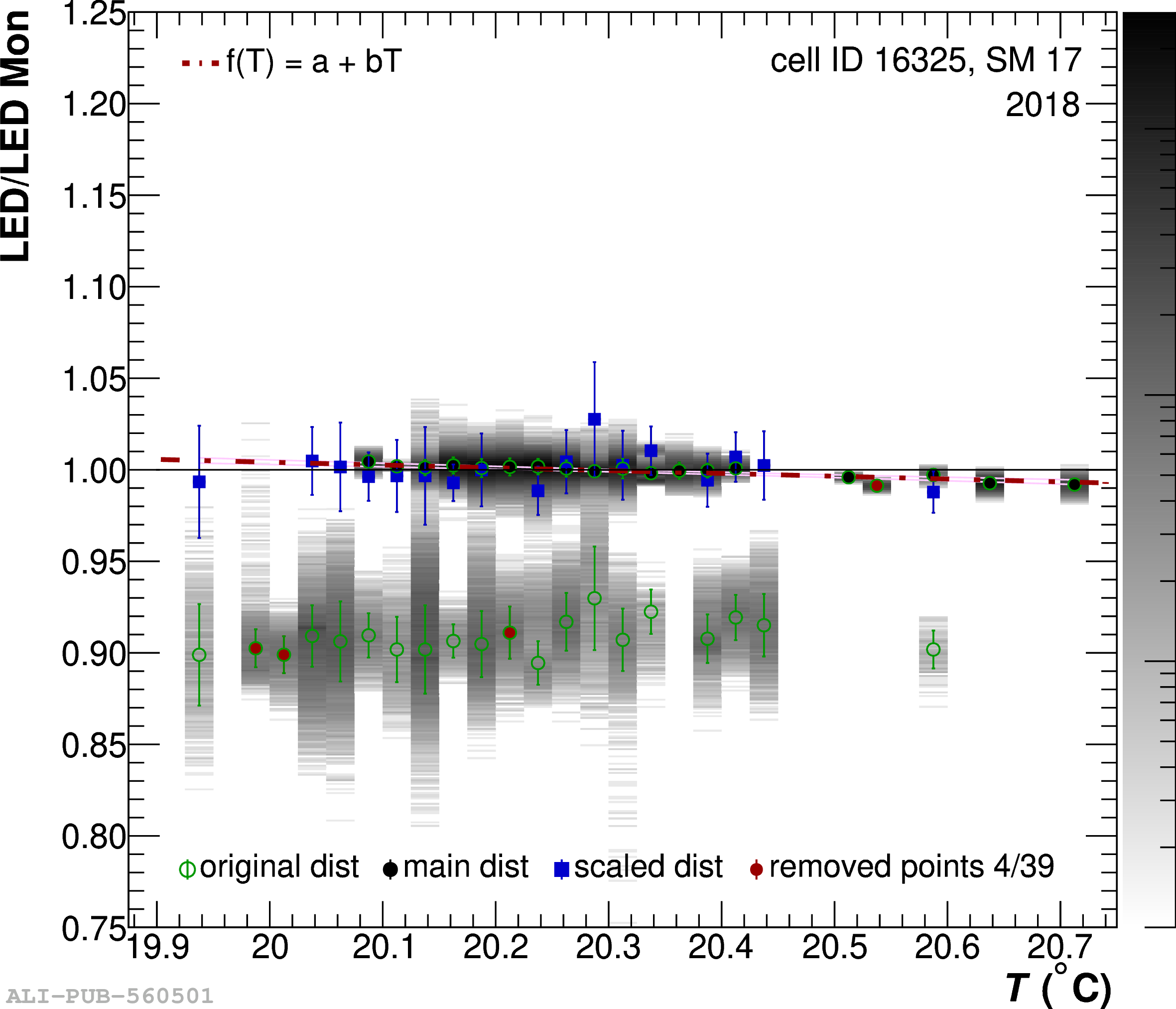
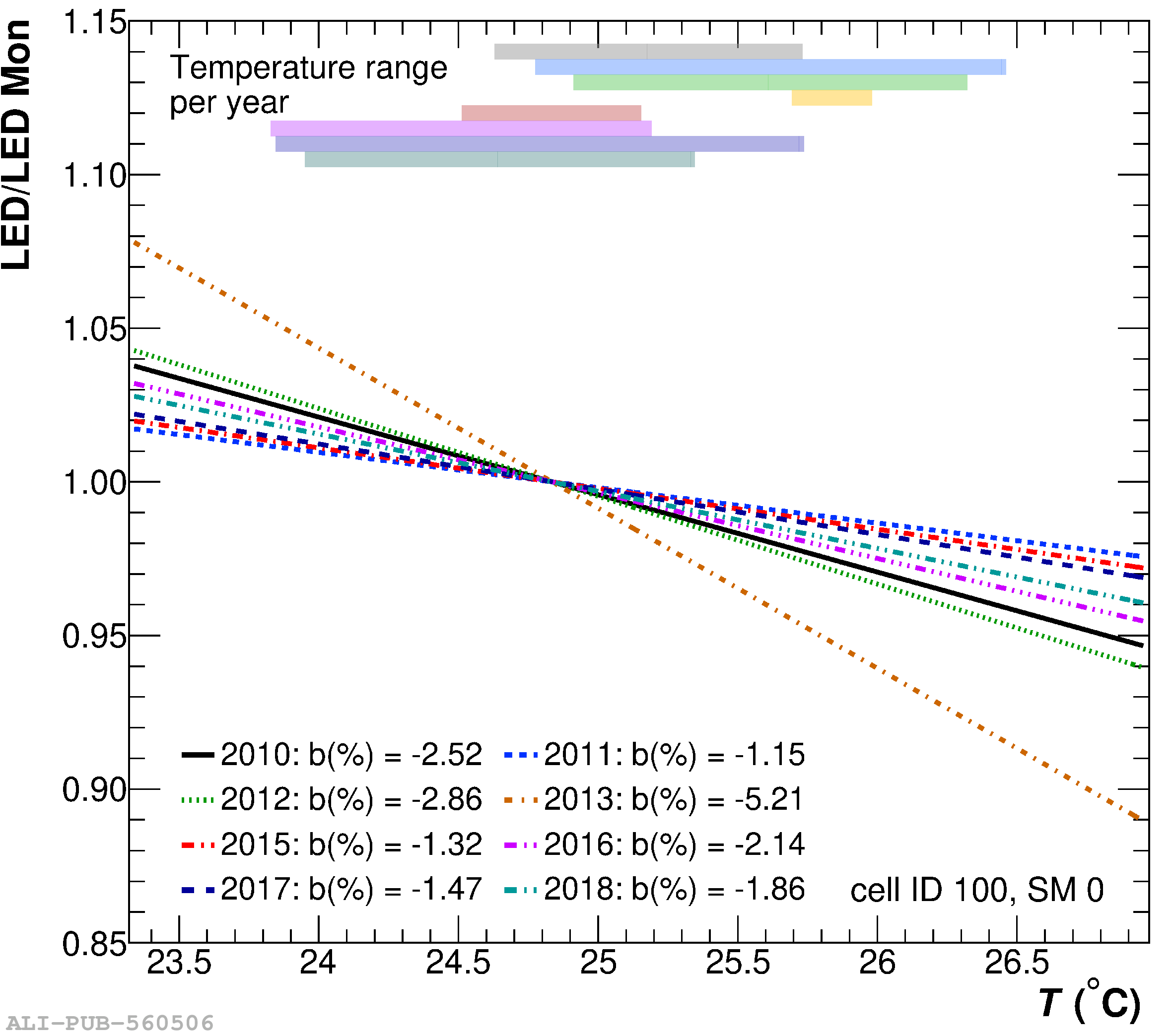
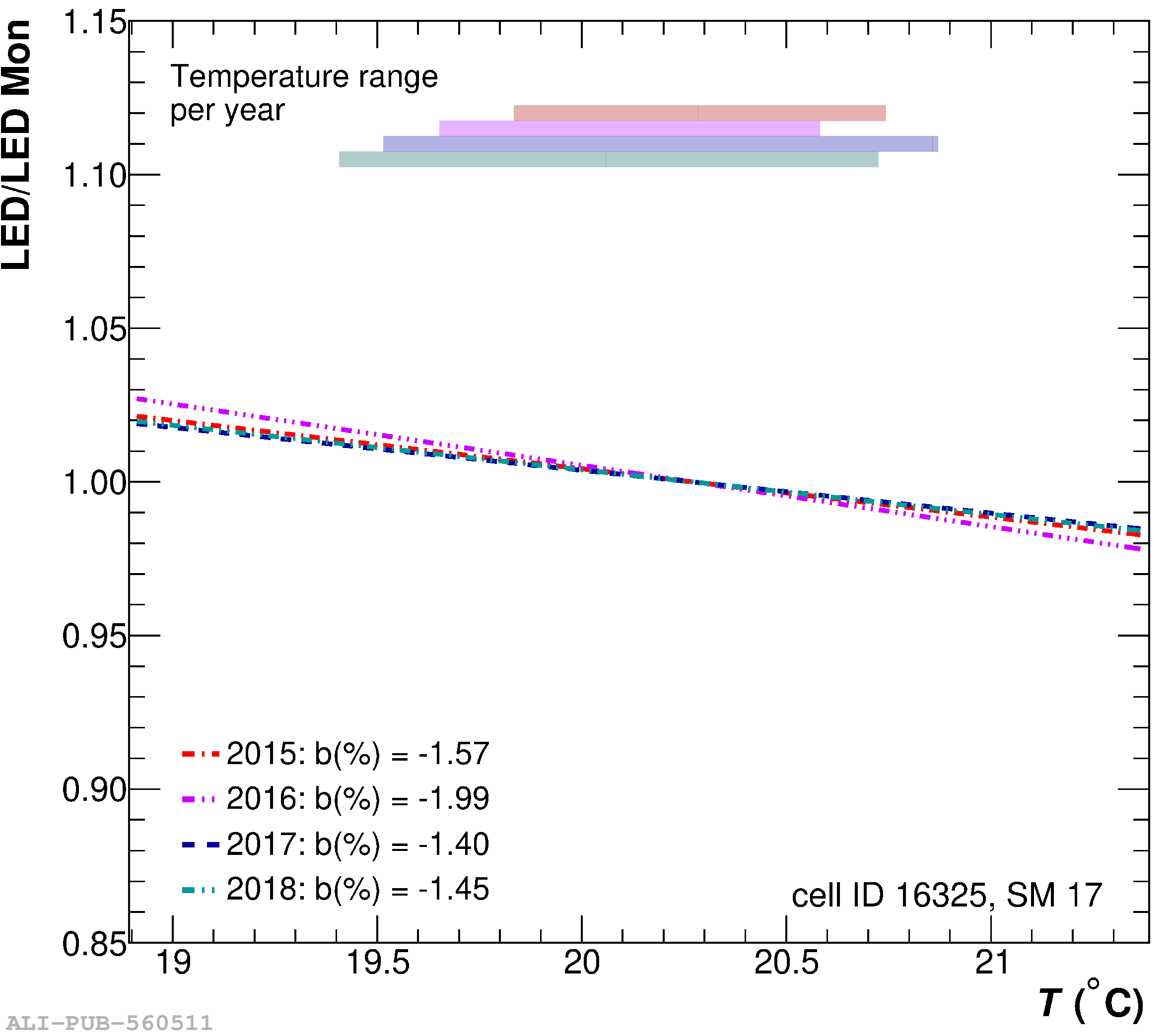
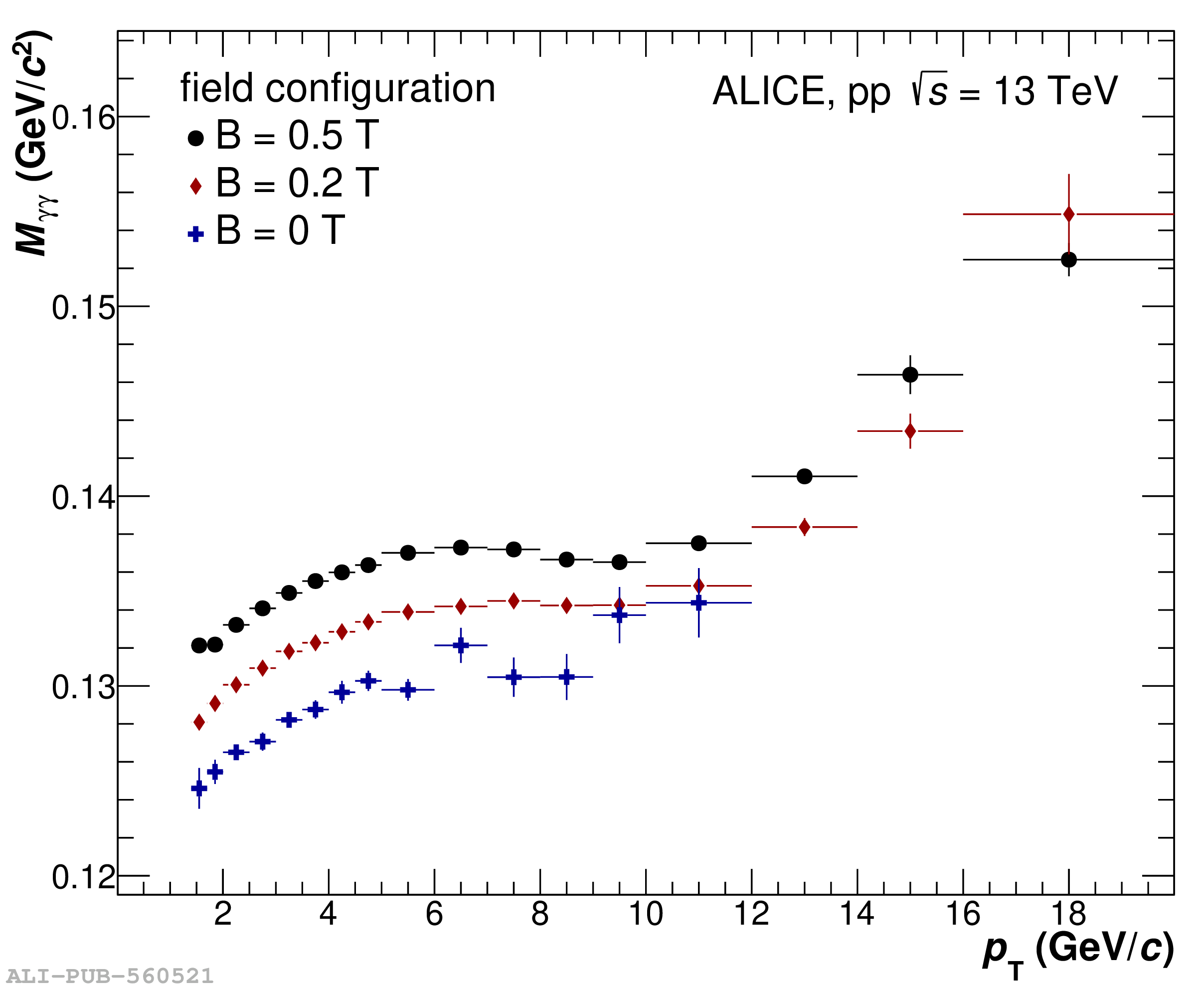
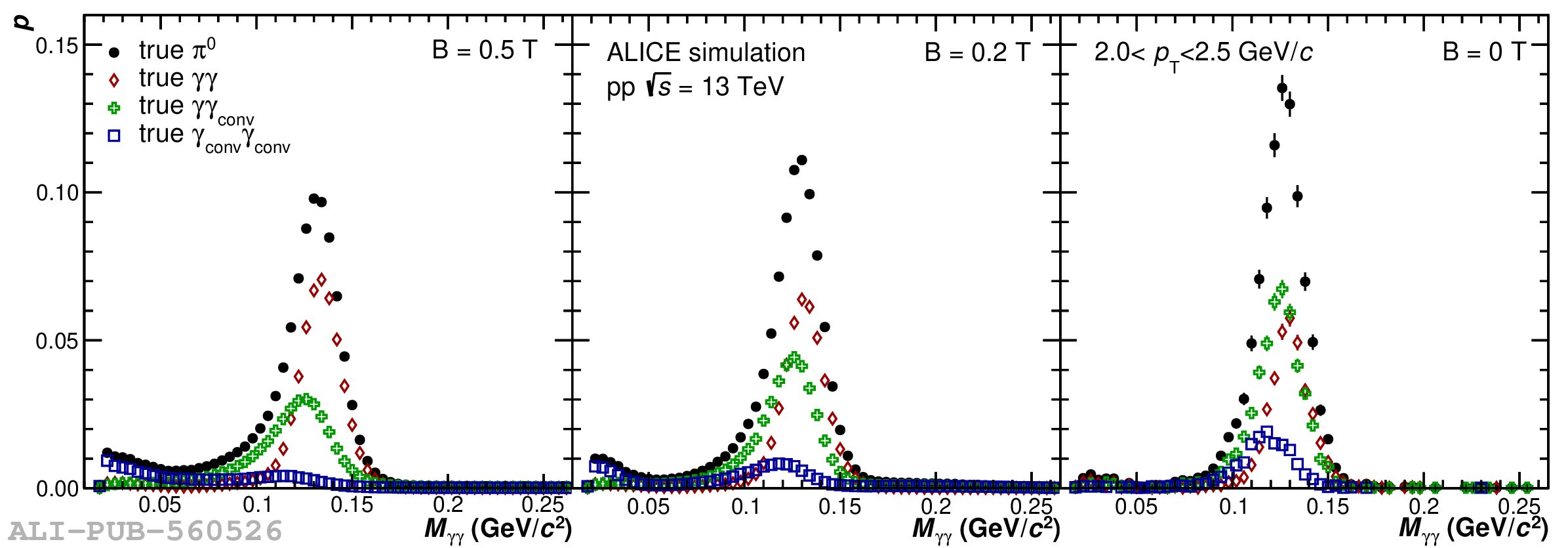
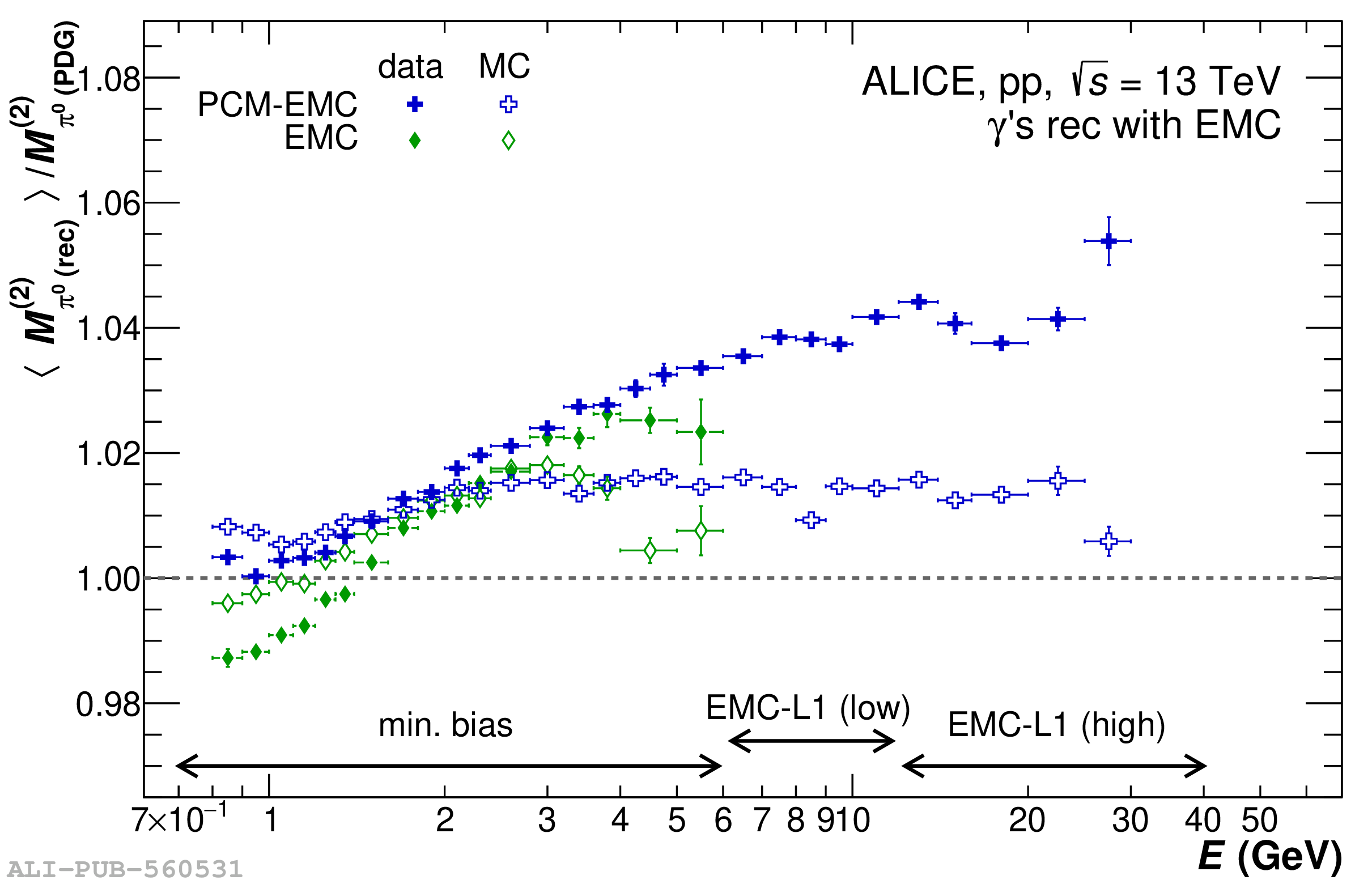
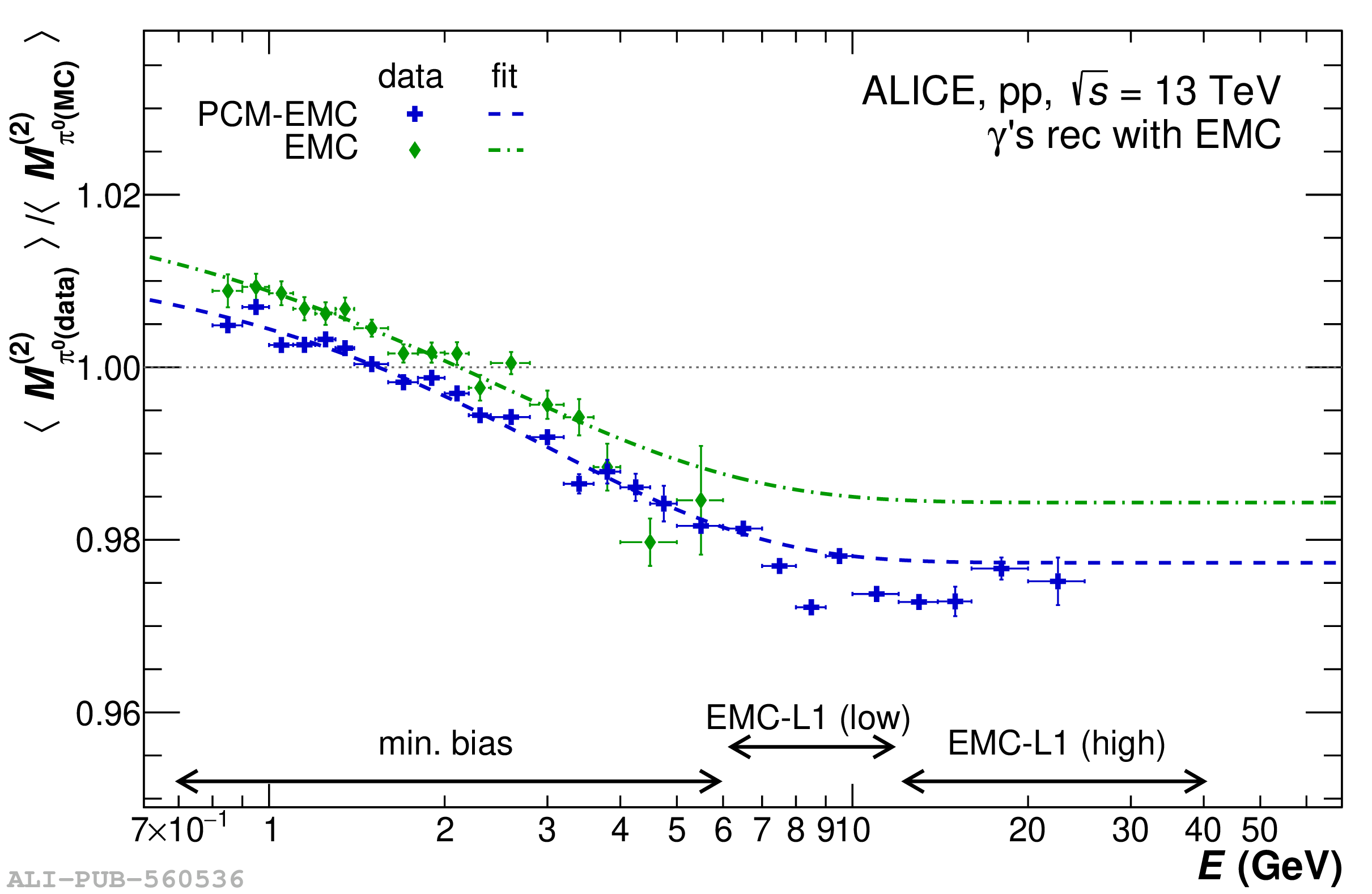
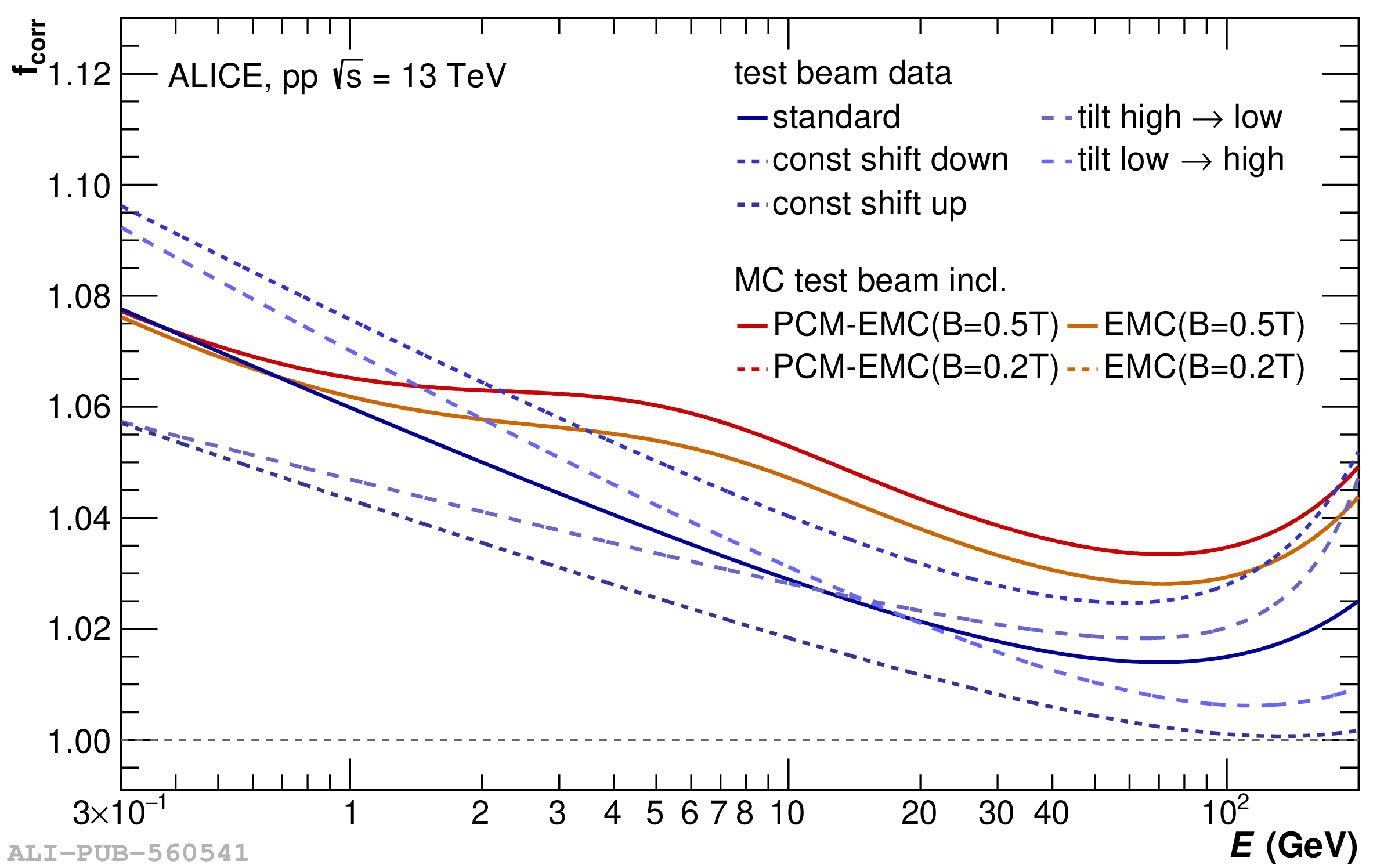
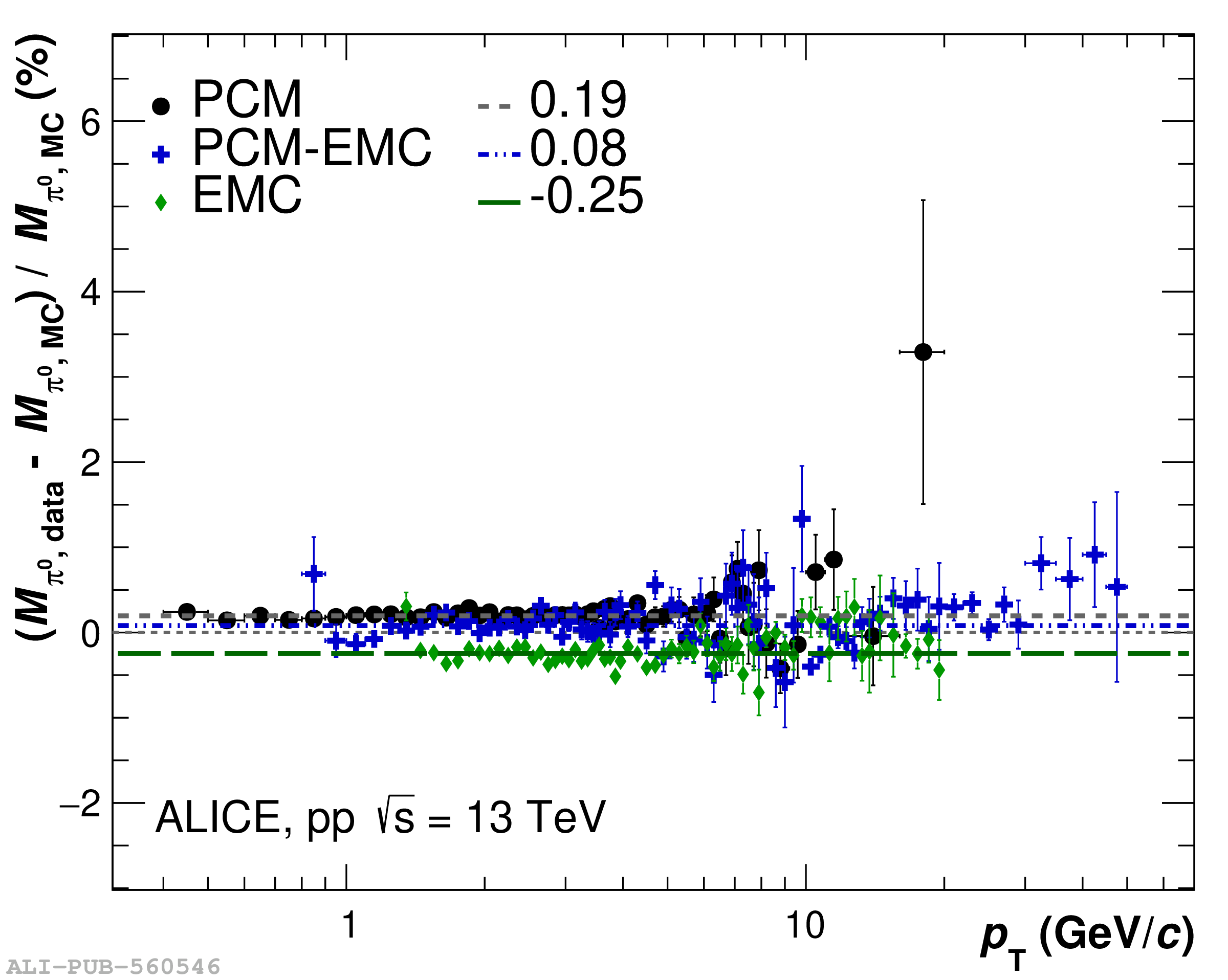
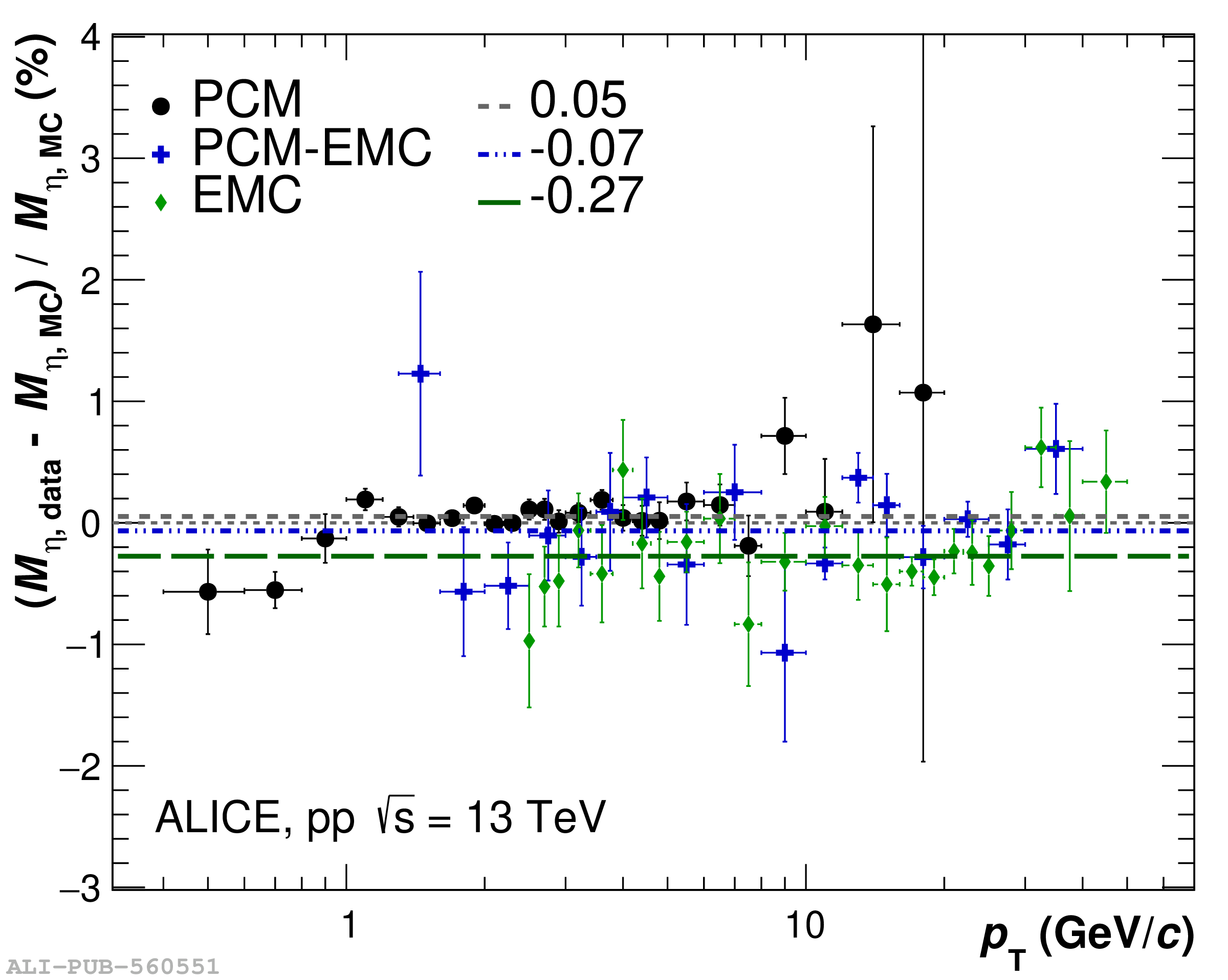
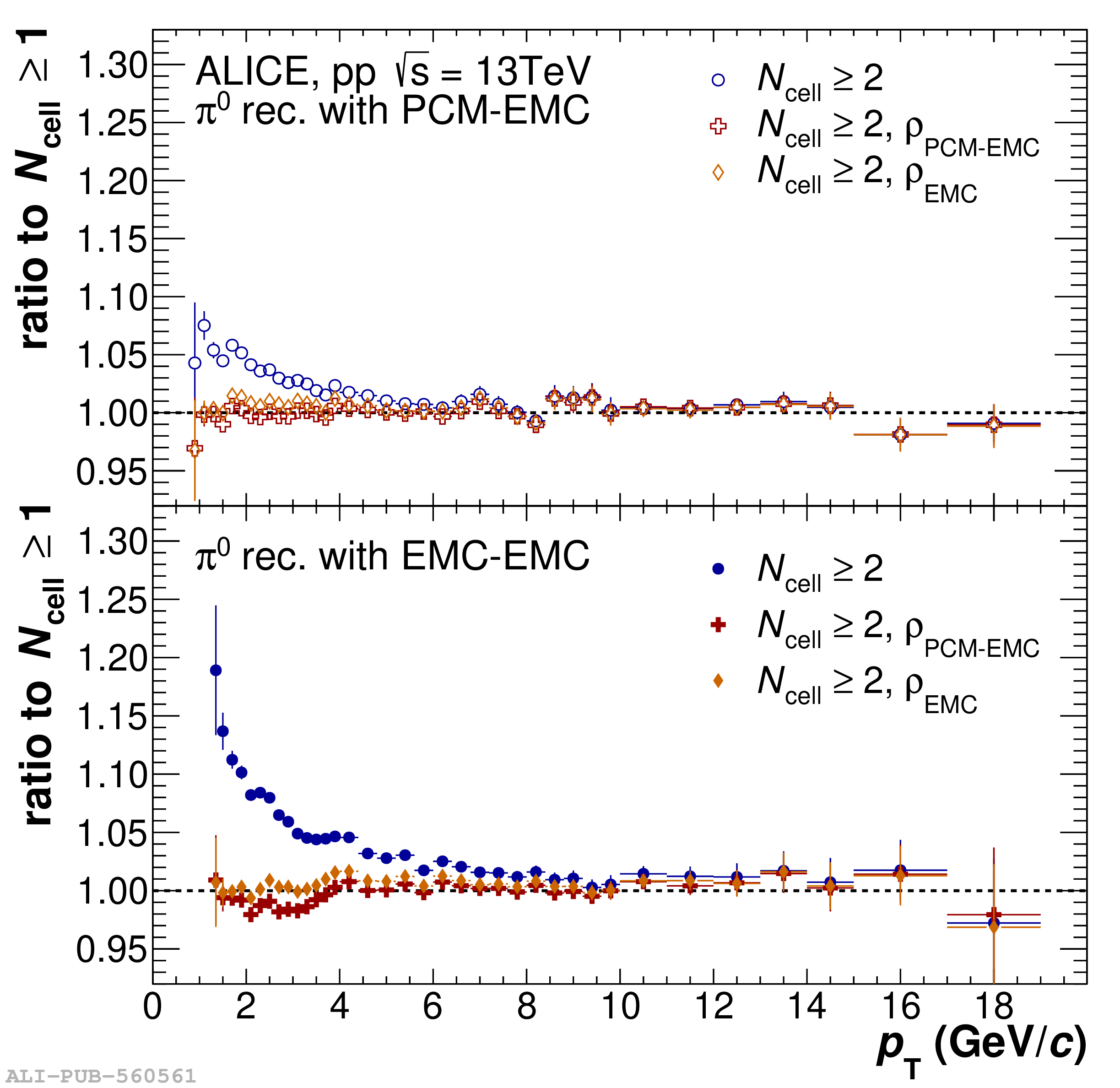
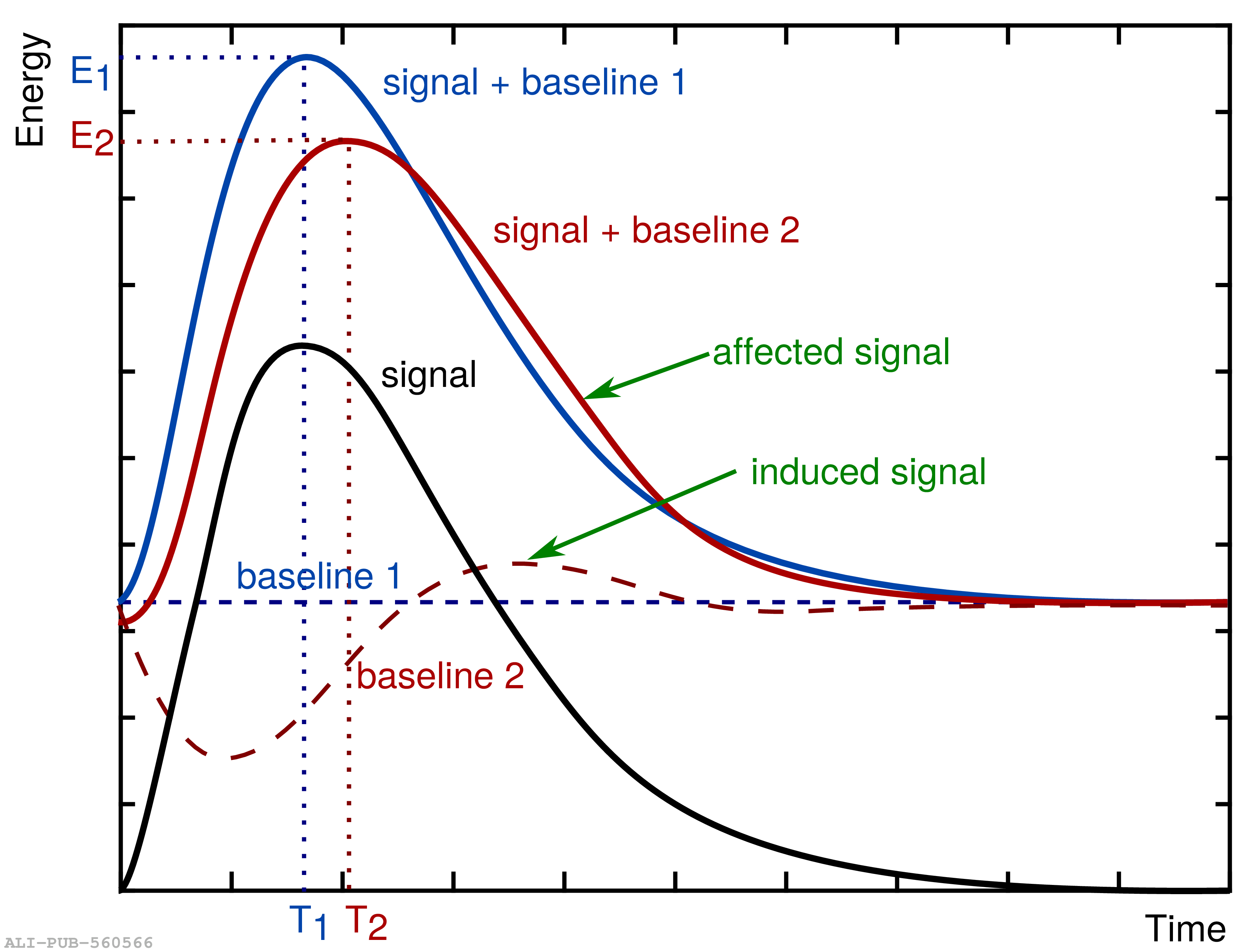
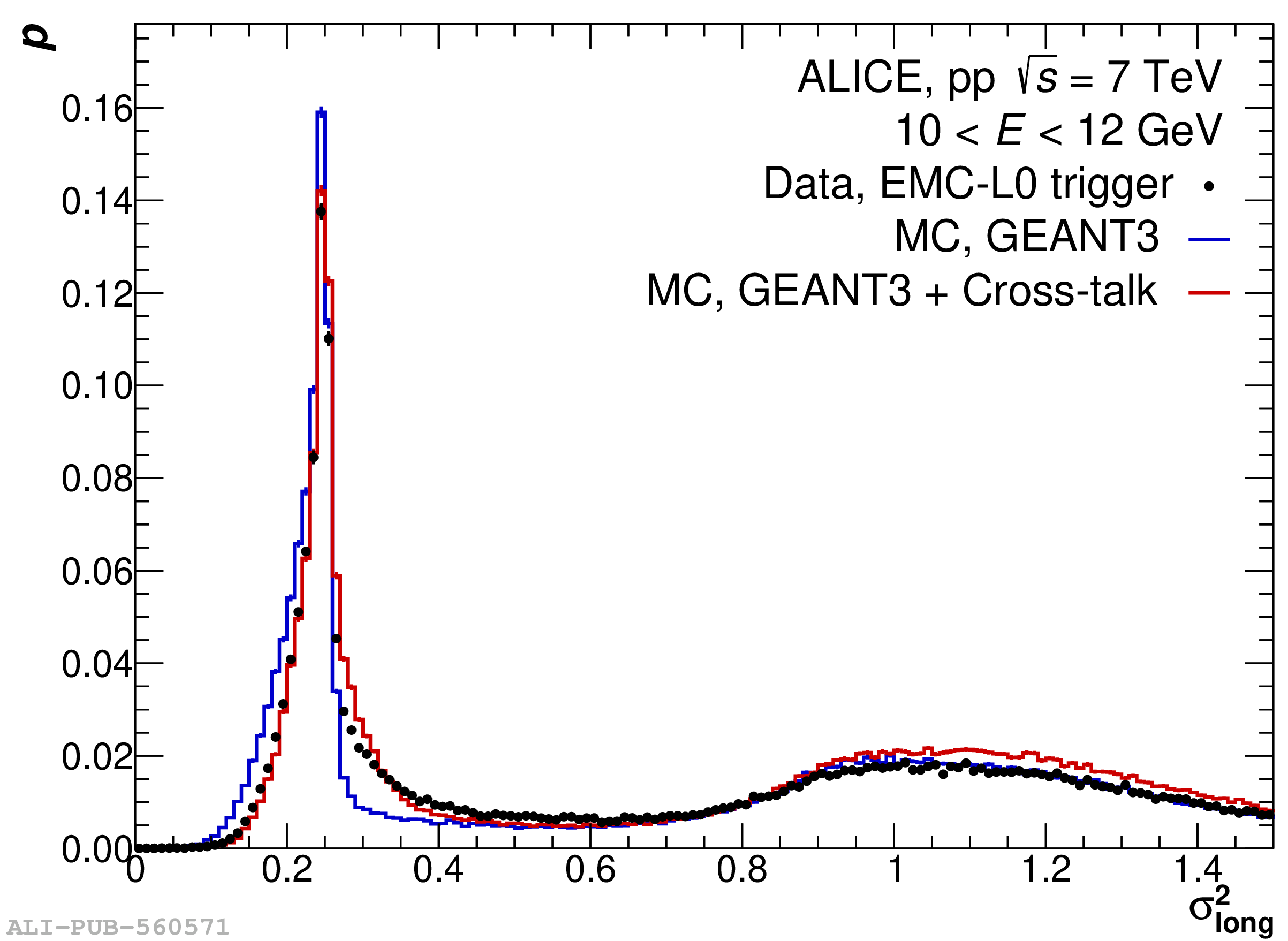
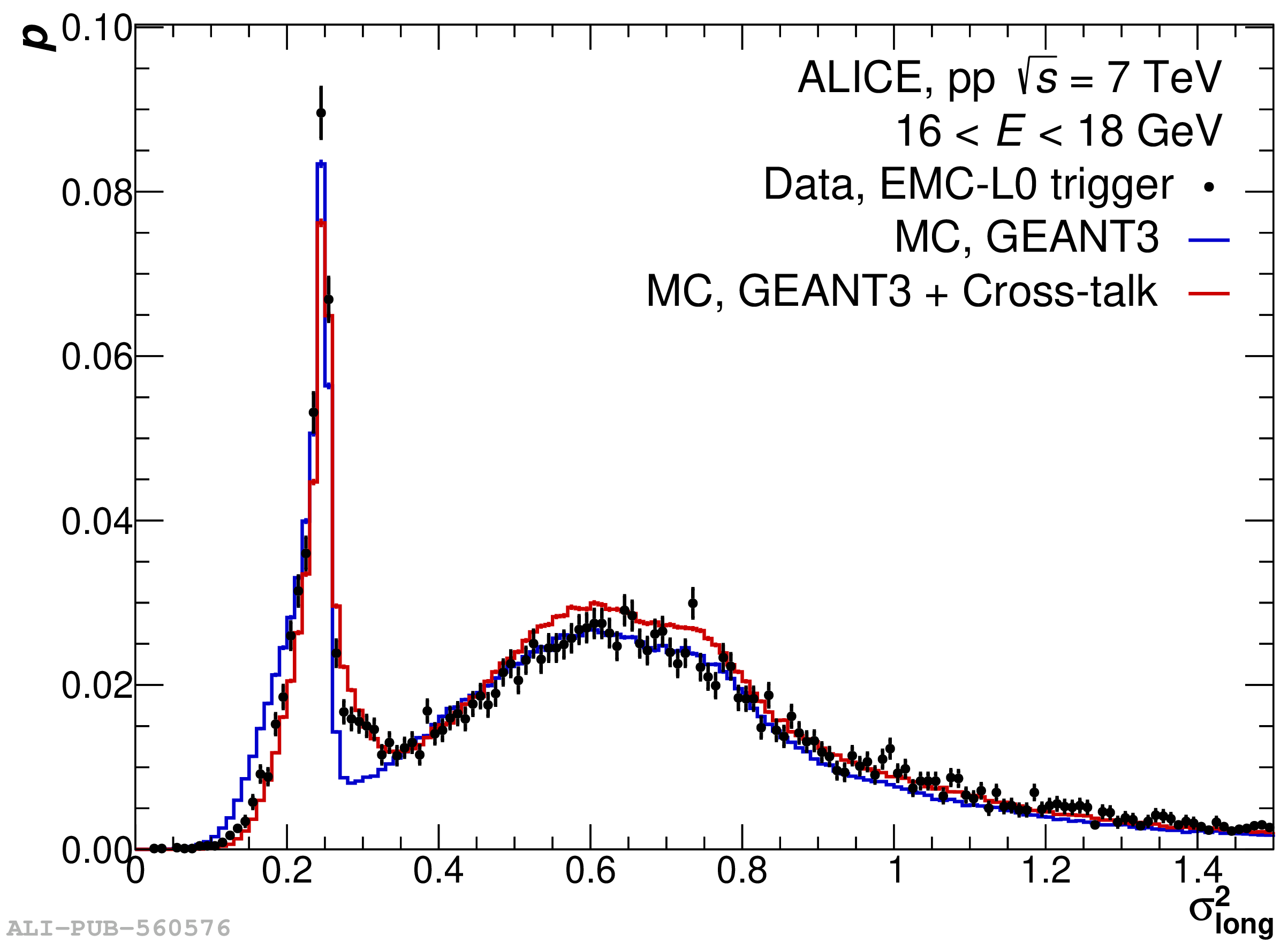
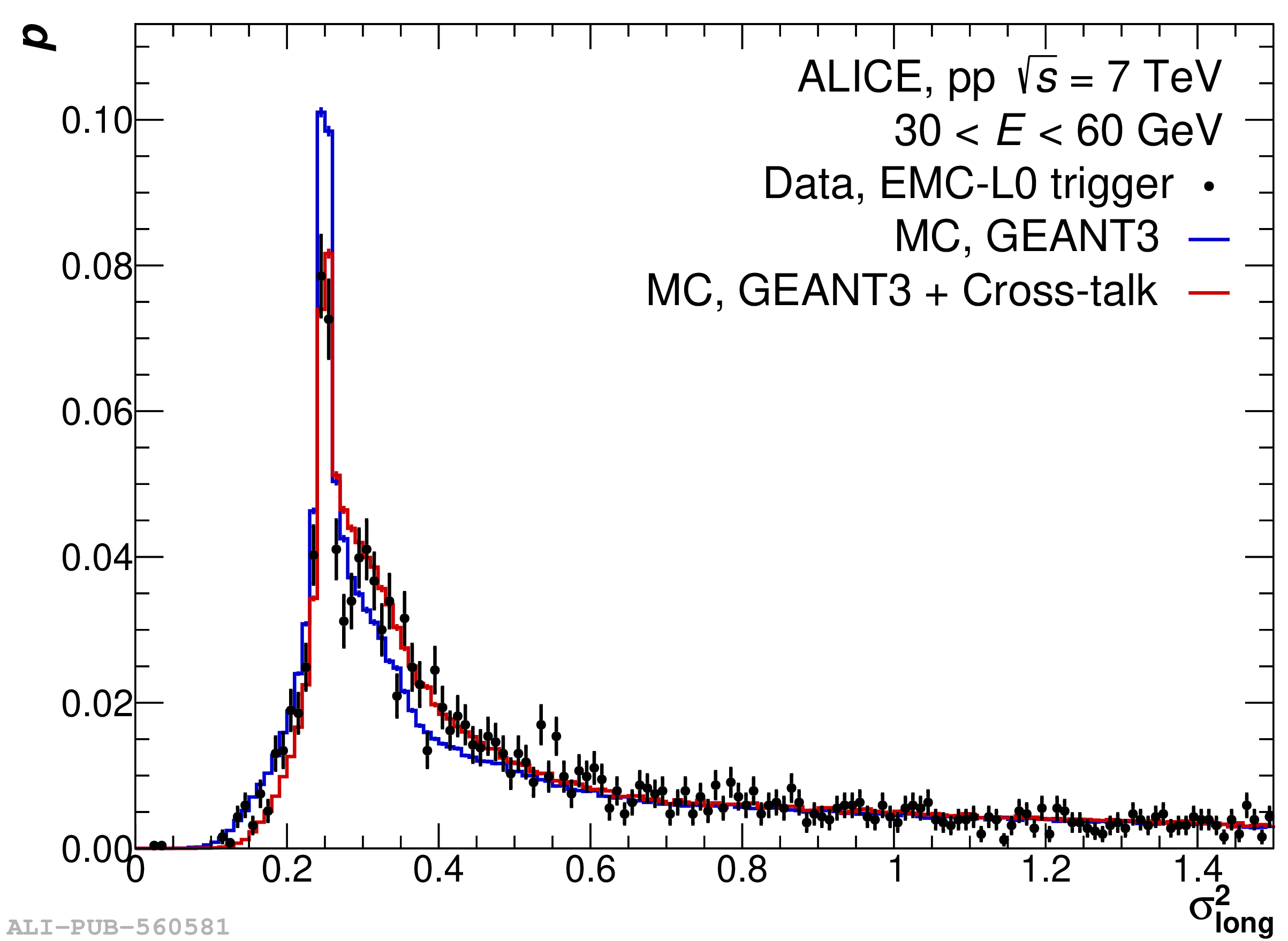
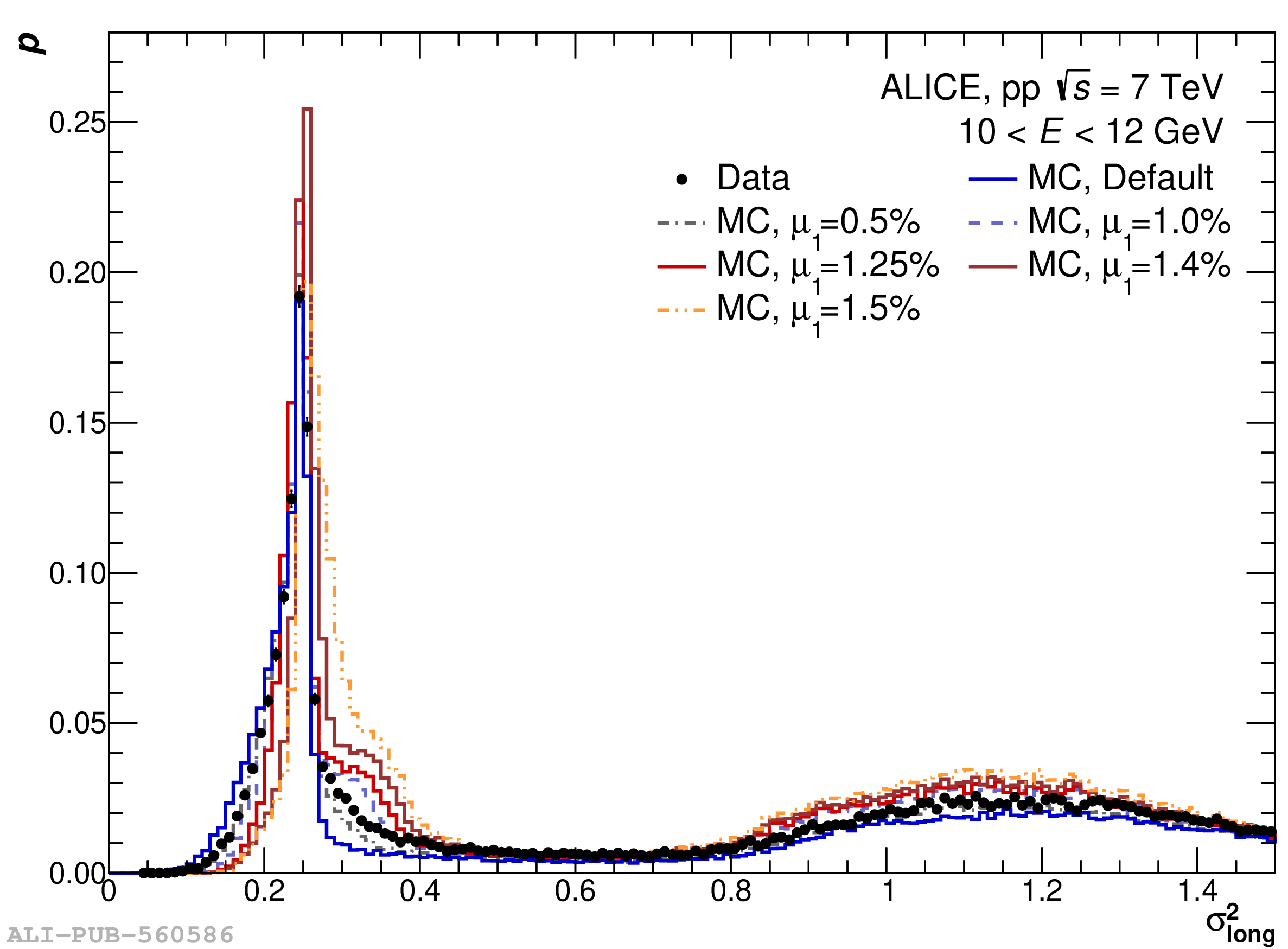
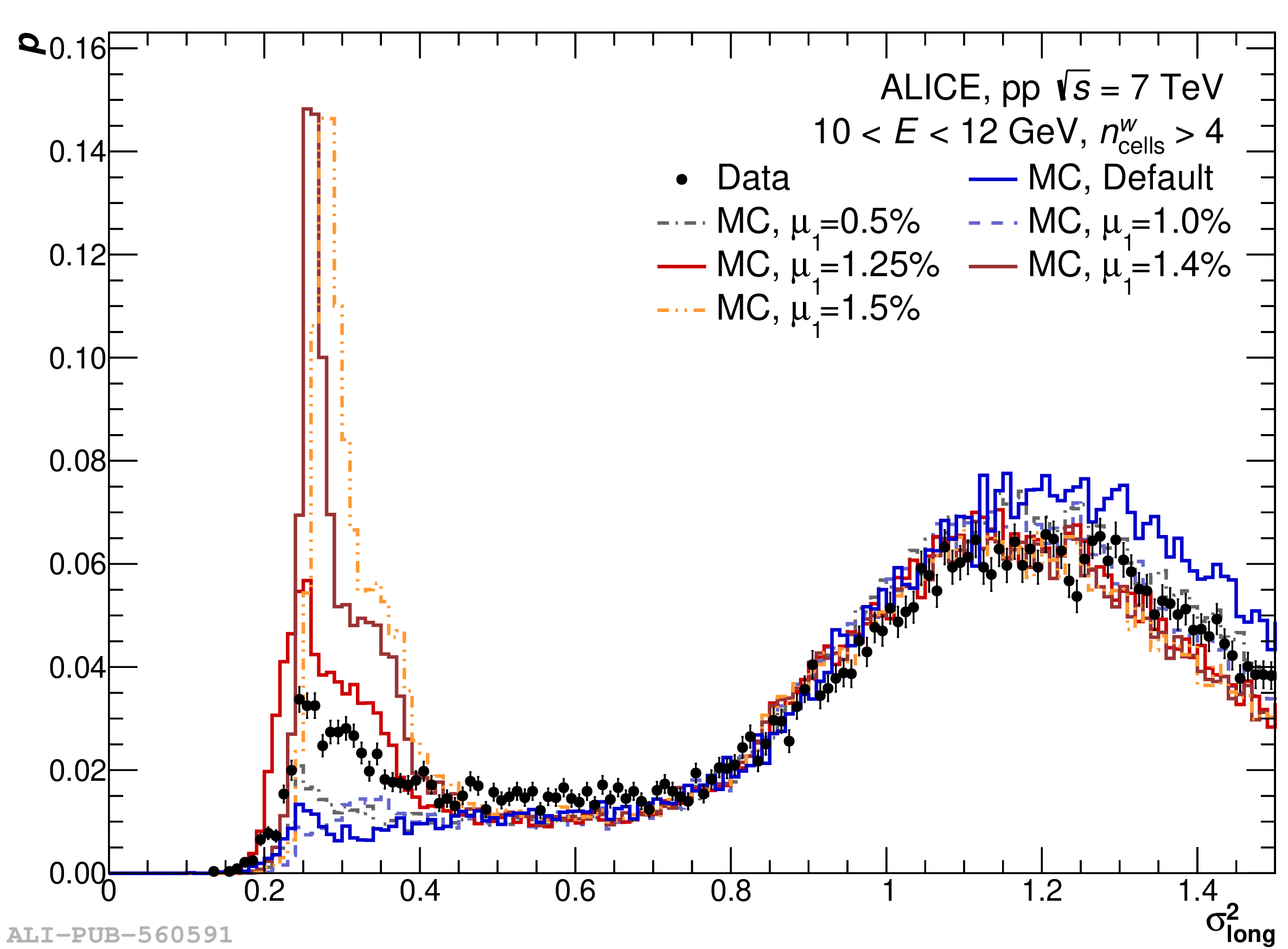
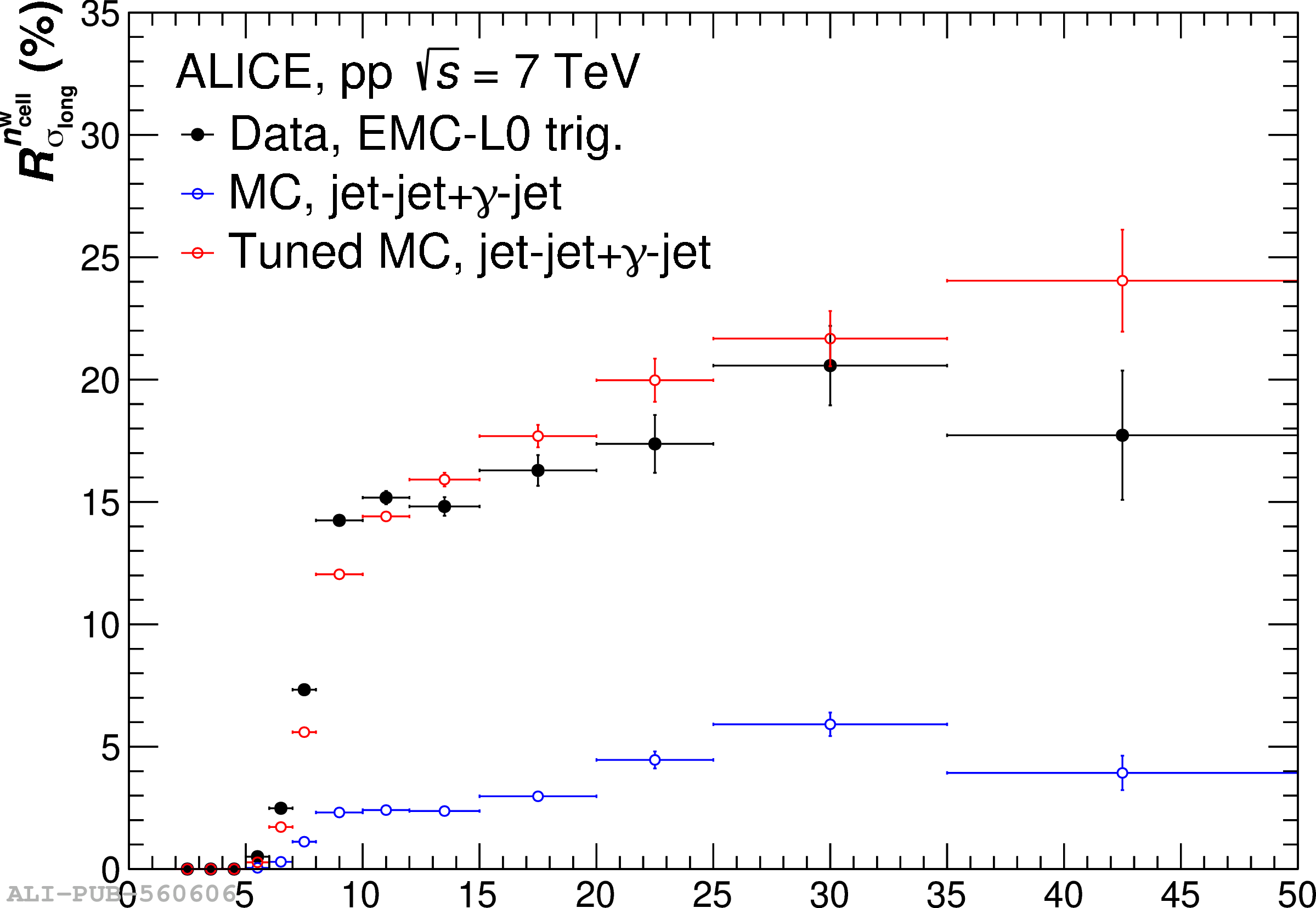
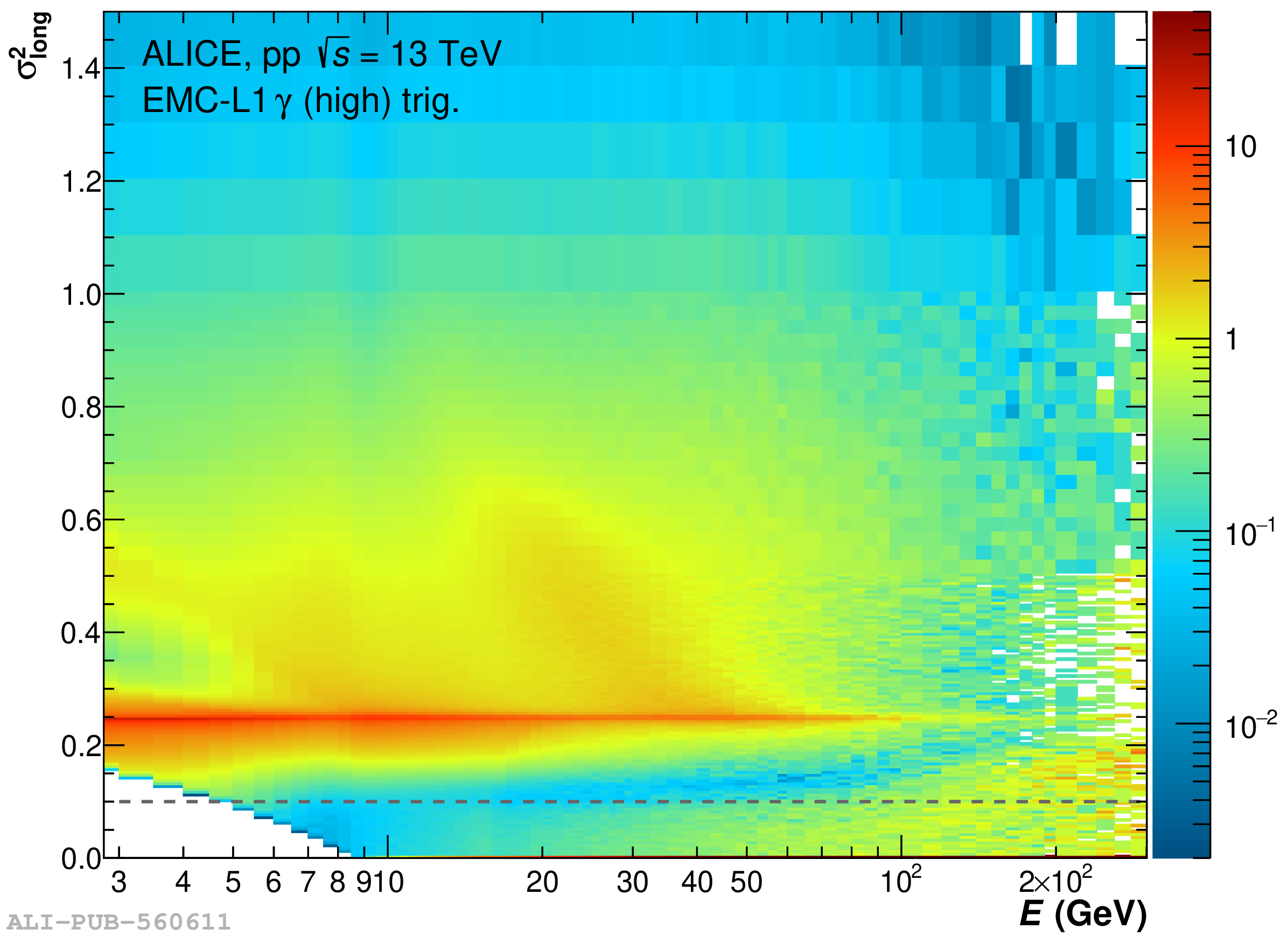
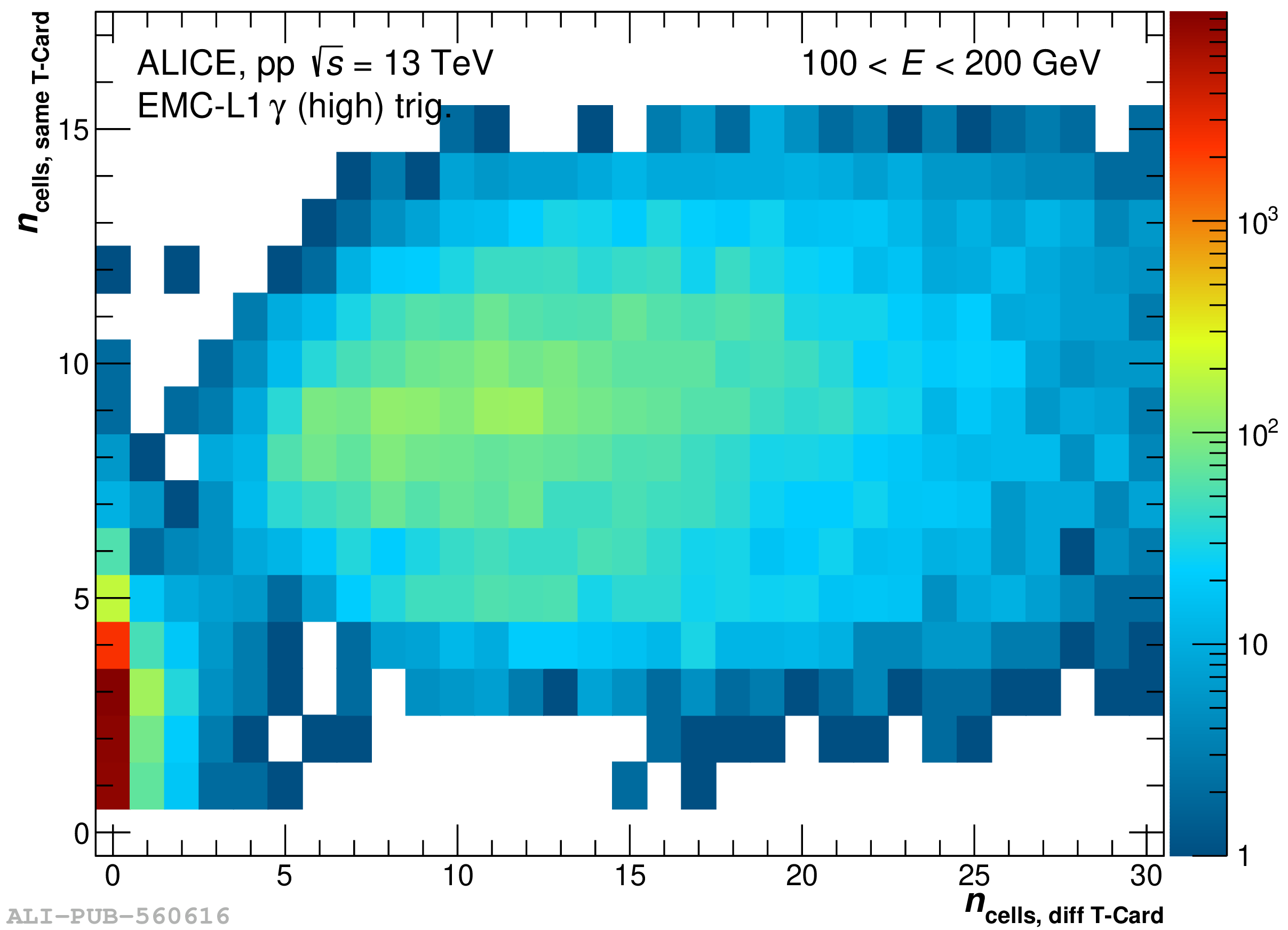
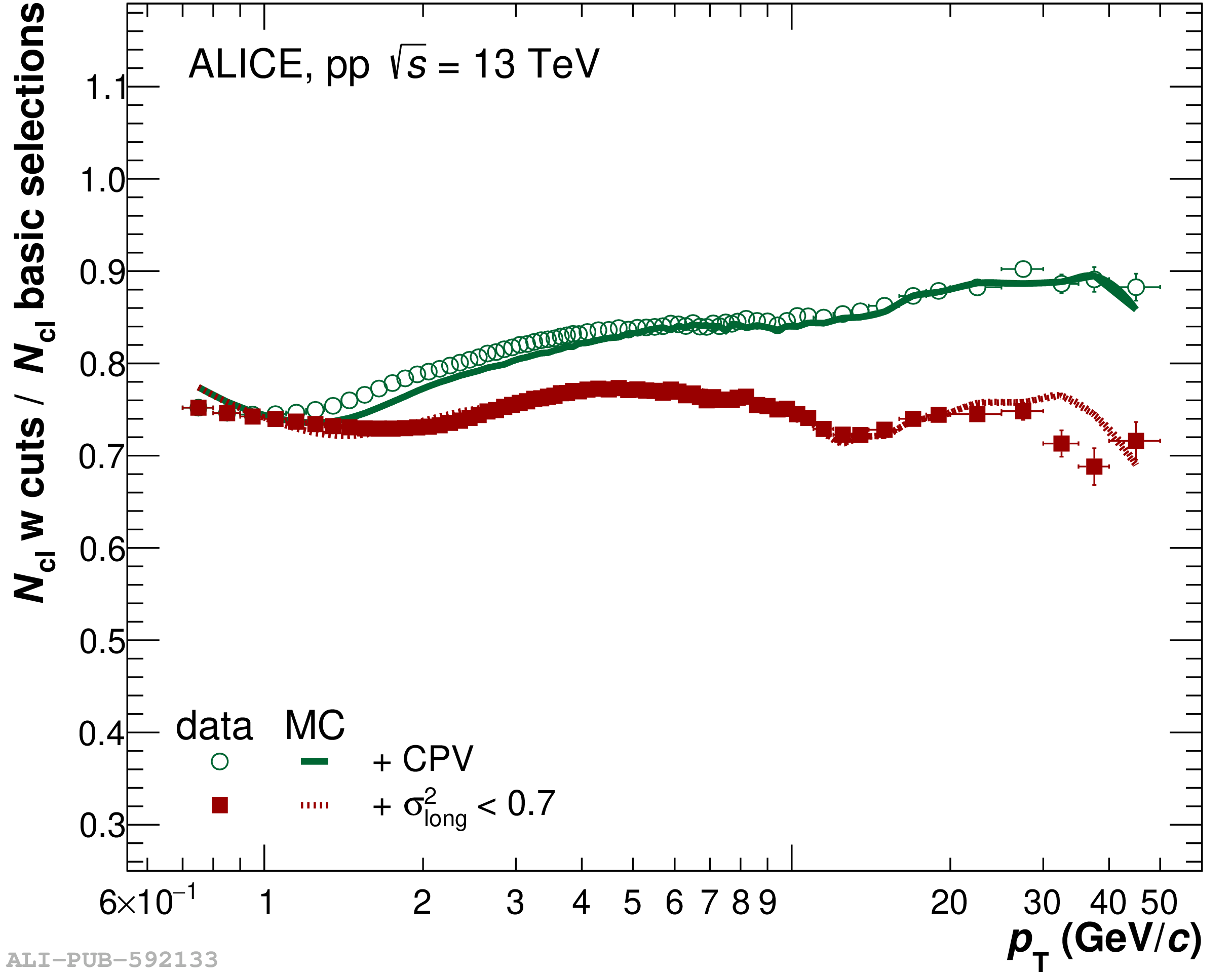
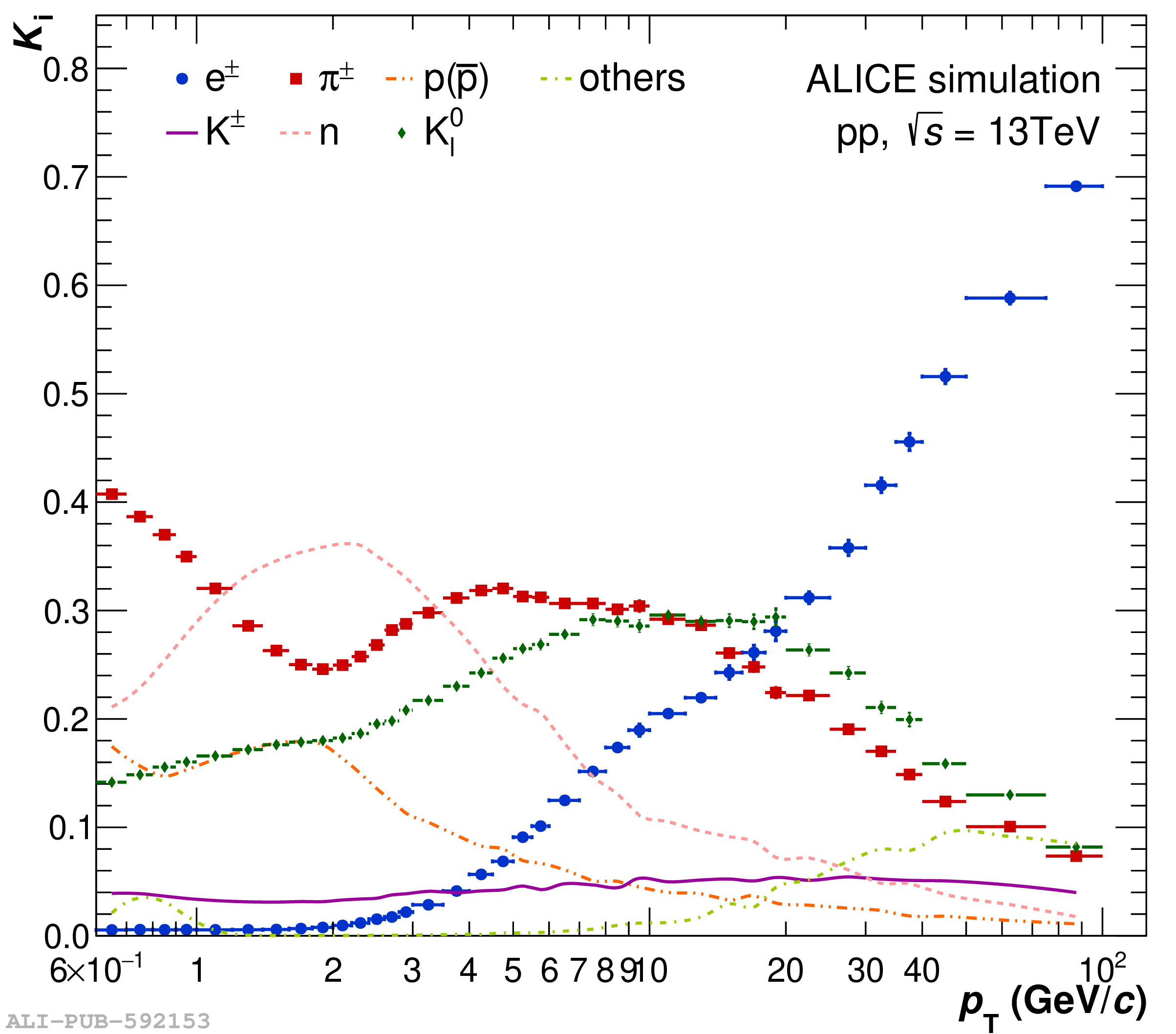
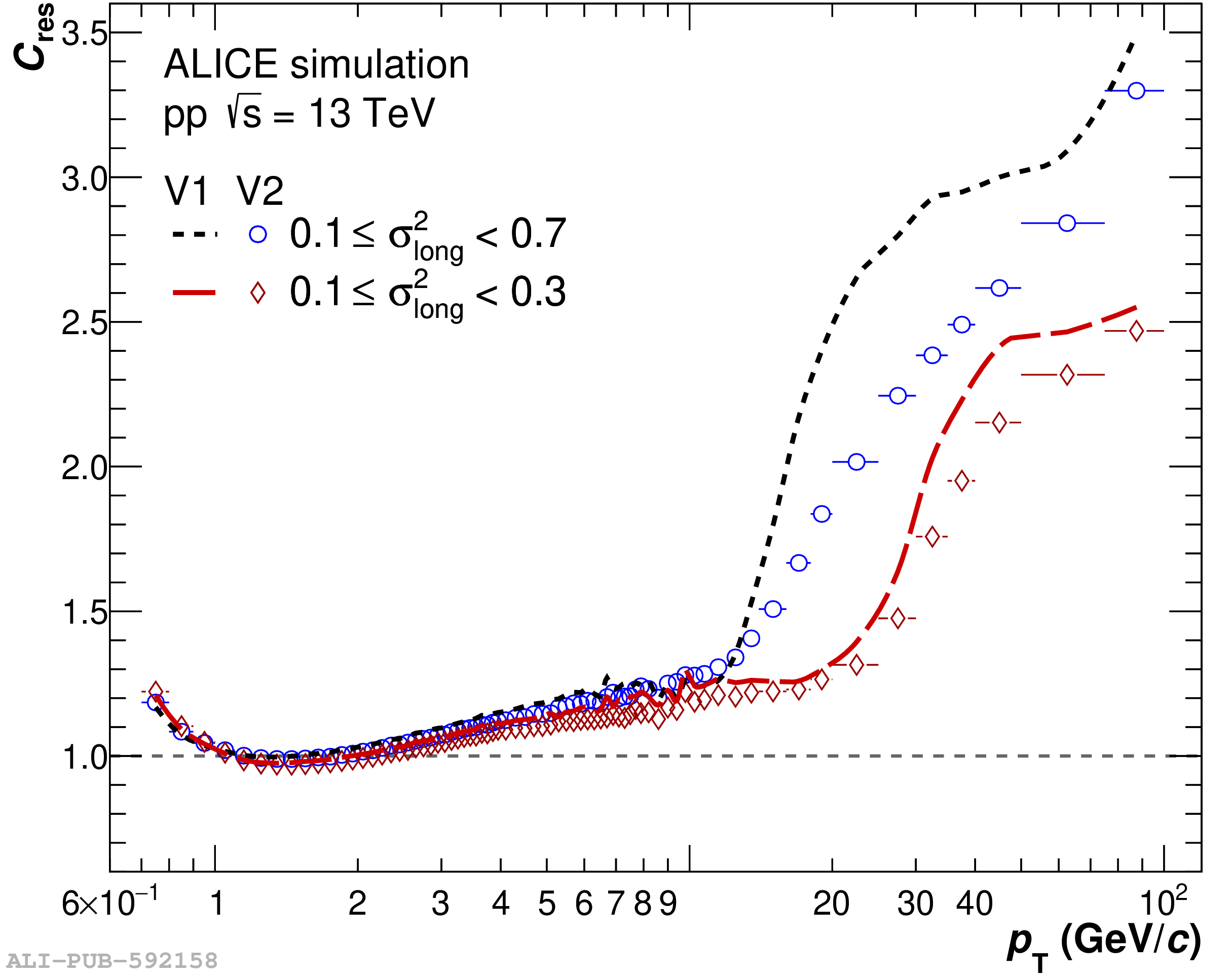
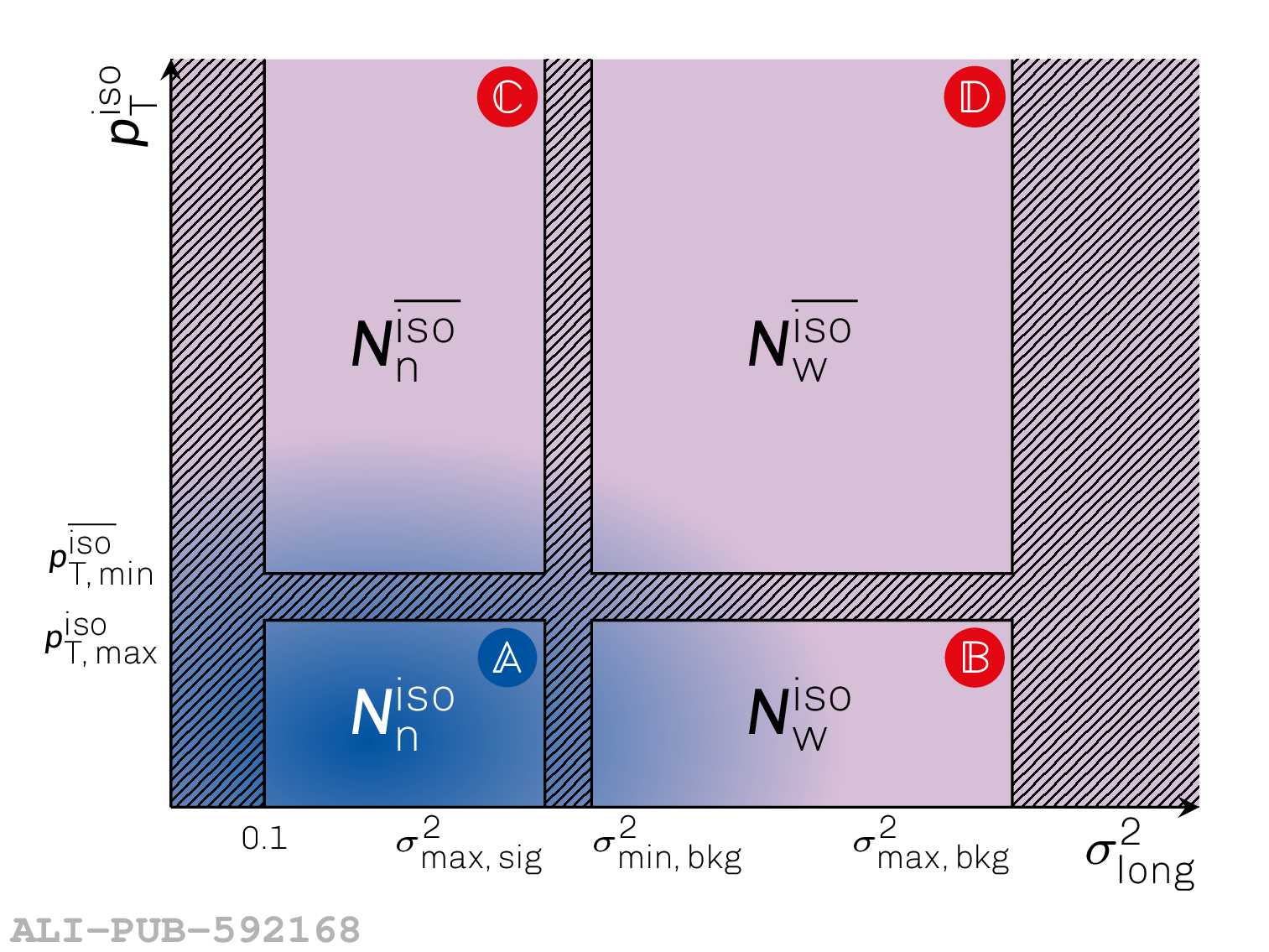
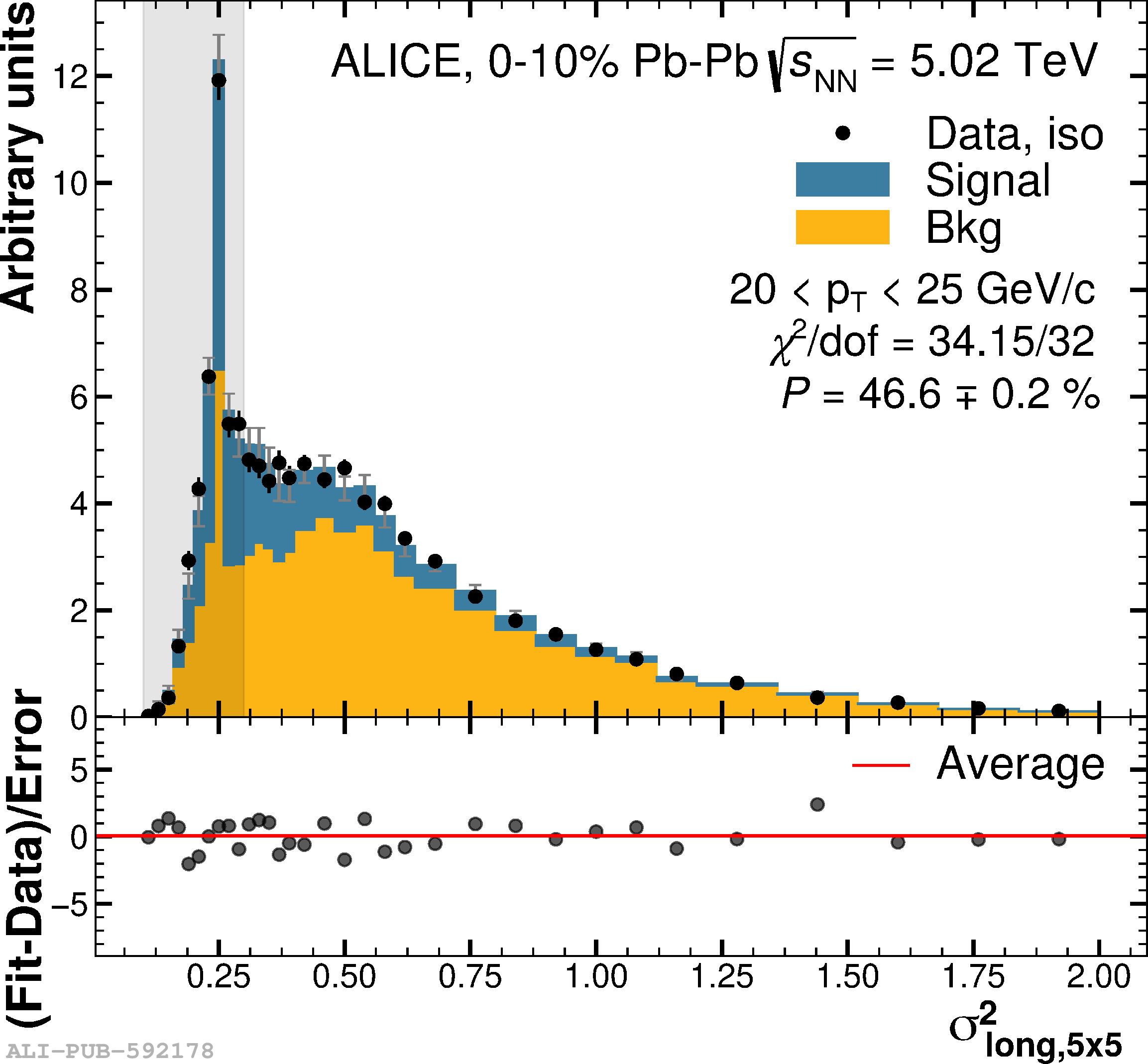
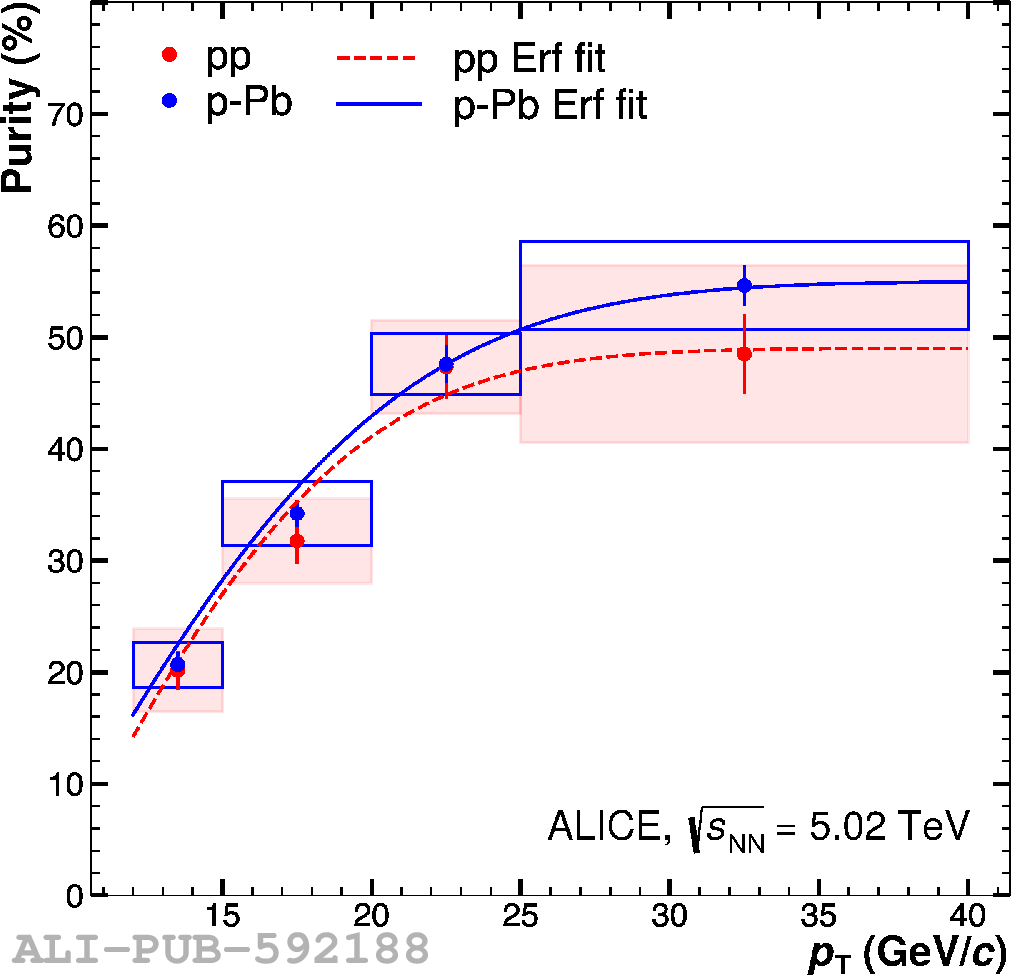
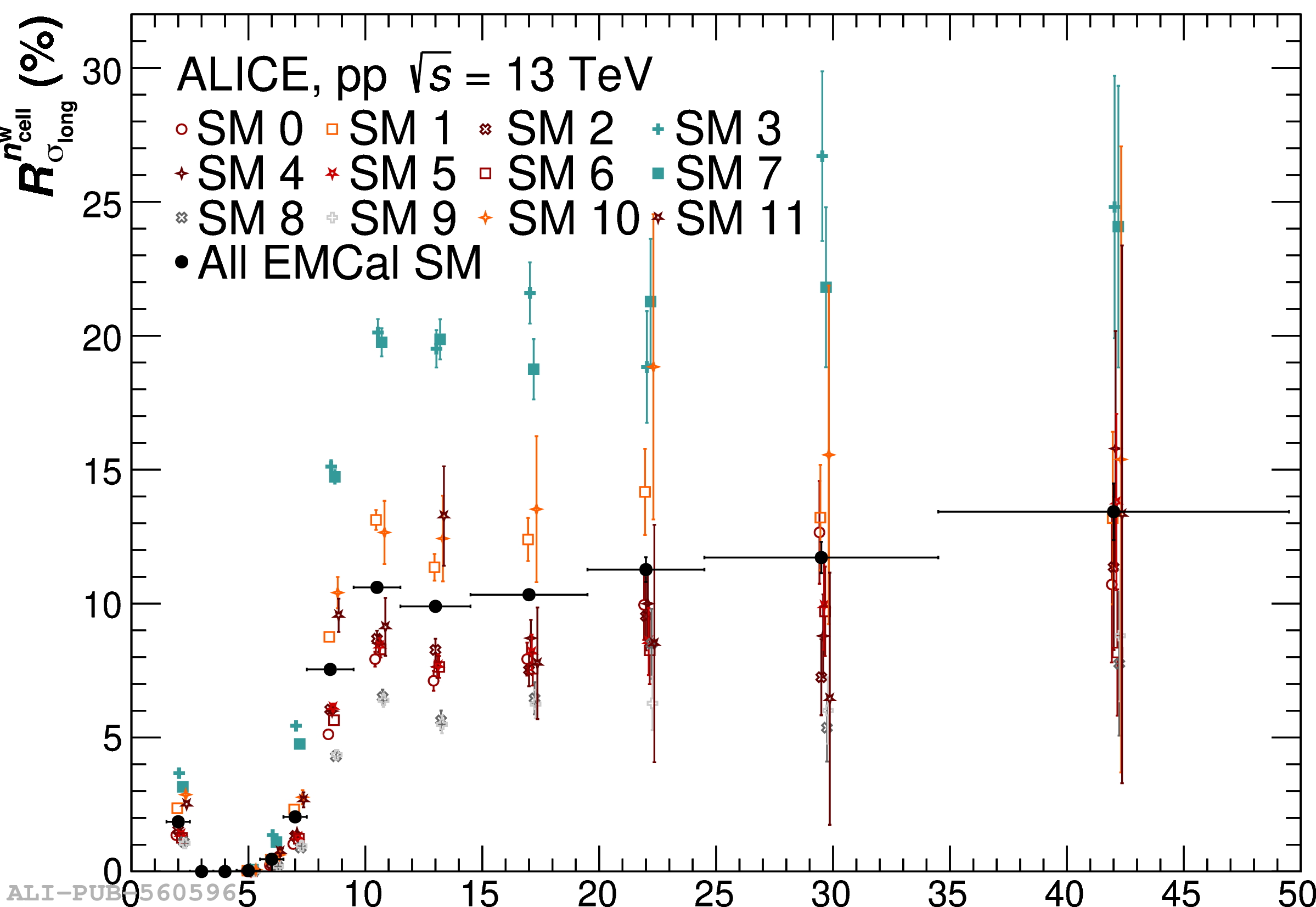The performance of the electromagnetic calorimeter of the ALICE experiment during operation in 2010-2018 at the Large Hadron Collider is presented. After a short introduction into the design, readout, and trigger capabilities of the detector, the procedures for data taking, reconstruction, and validation are explained. The methods used for the calibration and various derived corrections are presented in detail. Subsequently, the capabilities of the calorimeter to reconstruct and measure photons, light mesons, electrons and jets are discussed. The performance of the calorimeter is illustrated mainly with data obtained with test beams at the Proton Synchrotron and Super Proton Synchrotron or in proton-proton collisions at $\sqrt{s}=13$ TeV, and compared to simulations.
Accepted by: JINST
e-Print: arXiv:2209.04216 | PDF | inSPIRE
CERN-EP-2022-184
Figure group
Figure 3
Schematic view of the \gls{EMCal} full-size super modules (\glspl{SM}) illustrating the strip structure made of 24 strips.. |  |
Figure 7
Distribution of the opening angle $\theta_{12}$ of two decay photons from \piz\ (left) and $\eta$ (right) mesons decays as a function of the meson energy obtained at generator level from a \gls{MC} simulation. The horizontal lines indicate the opening angle corresponding to a width of approximately 1, 3 and 5 cells separating the two photons Two photons completely merge into one cluster if they fall below the one cell distance, while they start merging at a width of approximately 3 cells, depending on the clusterizer The colored vertical lines correspond to the energy limits where two photons could still be fully resolved using the V1 (blue) and V2 (red) clusterizers . |   |
Figure 8
Schematic comparison of different clusterization algorithms. Only one dimension is shown for simplicity Yellow boxes represent the energy in each cell. $E_\mathrm{agg}$ is the clusterization threshold as defined in the text. The different clusters are indicated by blue and red hatched areas Each panel represents a clusterization algorithm: a) V1, b) $3 \times 3$, c) V2, d) V1+unfolding.. |     |
Figure 9
Invariant mass distribution of cluster pairs in pp collisions at \sthirteen\ for different intervals of pair energy. The differently colored lines correspond to different clusterizer types, using the same aggregation $E_\mathrm{agg}=100$ MeV and seed $E_\mathrm{seed} = 500$ MeV thresholds. The lowest bin in energy uses the data sample with minimum bias trigger, while the others are obtained from the \gls{EMCal} \gls{L1} triggered data with thresholds at about $E \approx 4$ and $9$ GeV, respectively. . |       |
Figure 11
Distance between a cluster and the closest projected track in $\eta$ (left) or $\varphi$ angle (middle) versus the track momentum and for matched track-cluster pairs (right) in pp collisions at \sthirteen\ collected with the minimum bias trigger. Clusters are reconstructed using the V2 clusterizer. The black lines in the left and middle panels indicate the suggested selection criteria expressed in \Eq{Eq:TMVetoCriteria} . |    |
Figure 12
Left: cluster-veto efficiency for primary particles (dark blue open circles) and electrons (green squares) as well as conversion electrons with a production vertex below 180 cm (green closed diamonds) and above 180 cm (green open diamonds) and other secondary particles (cyan open circles) as obtained from simulations of pp collisions at \sthirteen . Right: fraction of fake track-to-cluster matches for clusters originating from photons (yellow open squares) and other neutral particles (red open circles). Additionally, the same categories are shown for clusters that have additional charged particle contributions for photon clusters (orange squares) and other neutral particles (light red circles). . |   |
Figure 14
\shshlo\ (left) and \shshsh\ (right) distributions in three energy intervals for photons, electrons, hadrons, \piz\ and $\eta$ mesons. The distributions are obtained using the V1 clusterizer from a simulation of pp collisions at \sthirteen\ performed with the \gls{PYTHIA} event generator, in which events are required to contain either two jets or a jet and a high-energy direct photon. Each distribution is normalized to its integral. A model simulating the effect of the cross talk was applied as discussed in \Sec{sec:crosstalk}. . Distributions of \shshlo\ versus cluster energy in pp collisions at \sthirteen\ triggered by the \gls{EMCal} \gls{L1} at approximately 9 GeV for the V2 (left) and V1 clusterizer (right). Each energy bin is normalized to its integral and exotic clusters were rejected (\Sec{sec:exotics}). . |     |
Figure 15
Left: number of cells as a function of the cluster energy found with the V2 clusterizer in \pp\ collisions at \sthirteen\ using the \gls{EMCal} high threshold \gls{L1} $\gamma$ trigger The region below the lines is populated by exotic clusters The distribution for each energy bin is normalized to its integral. Right: comparison of $n_{\text{cells}}$ probability distributions for measured data (black), projection of the left plot, to simulated (blue) collisions for two different cluster energy bins. Each distribution is normalized by the integral of the distribution for $n_{\rm cells}$ > 10. . |   |
Figure 16
Left: ``exoticity'' ($F_{\rm +}$) as function of the cluster energy found with the V2 clusterizer in \pp\ collisions at \sthirteen\ using the \gls{EMCal} high threshold \gls{L1} $\gamma$ trigger The region above the line is populated by exotic clusters The distributions are normalized to have an integral of unity for each energy bin. Right: comparison of $F_{+}$ probability distributions for measured data (black), projection of the left panel, and simulated (blue) collisions for two different cluster-energy intervals. Each distribution is normalized by the integral of the distribution for $F_{+}<0.85$ . |   |
Figure 17
Left: cluster time for exotic ($F_{+}>$ 0.97 and non-exotic ($F_{+}<$ 0.97) clusters. The additional peaks in the time distribution beyond $100$ ns arise from additional bunch crossings, which could not be rejected by the online Past-Future protection using the \gls{V0} detector Right: difference in time of the most and second most energetic cell in the cluster for exotic and non exotic clusters. Both distributions are obtained for V2 clusters with energy in the interval $8 < E < 10$ GeV from data taken from pp collisions at \sthirteen . |   |
