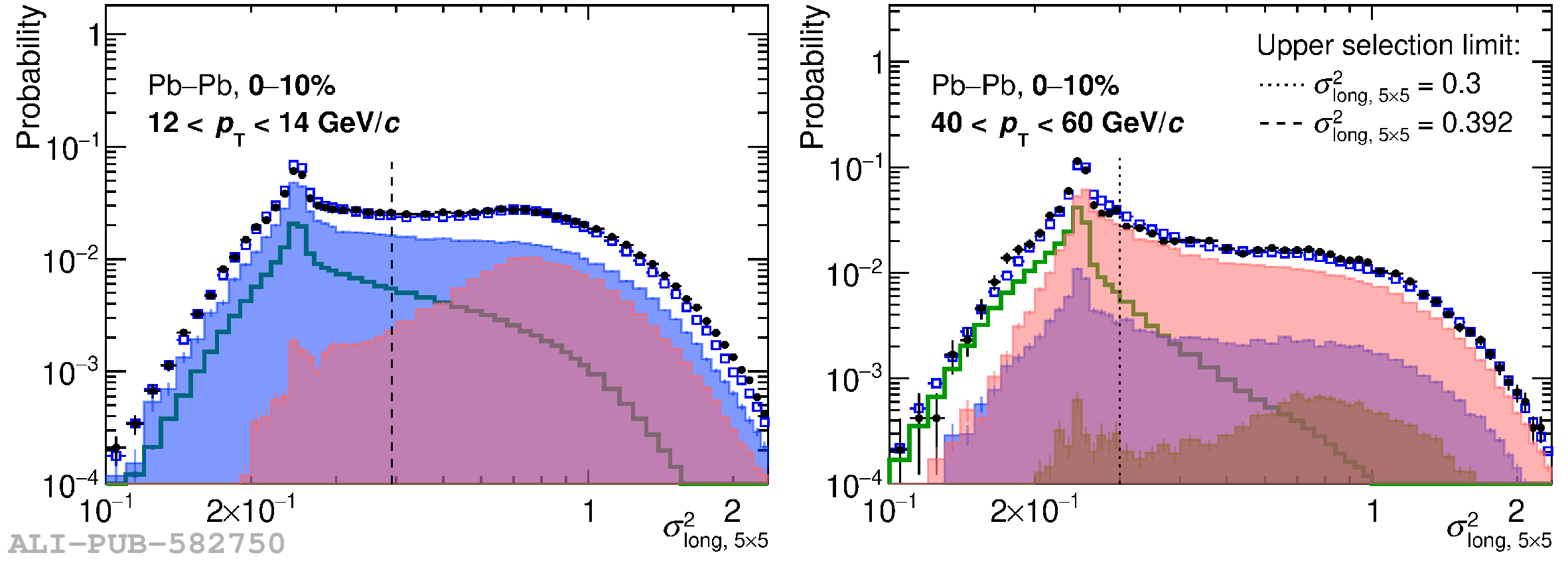
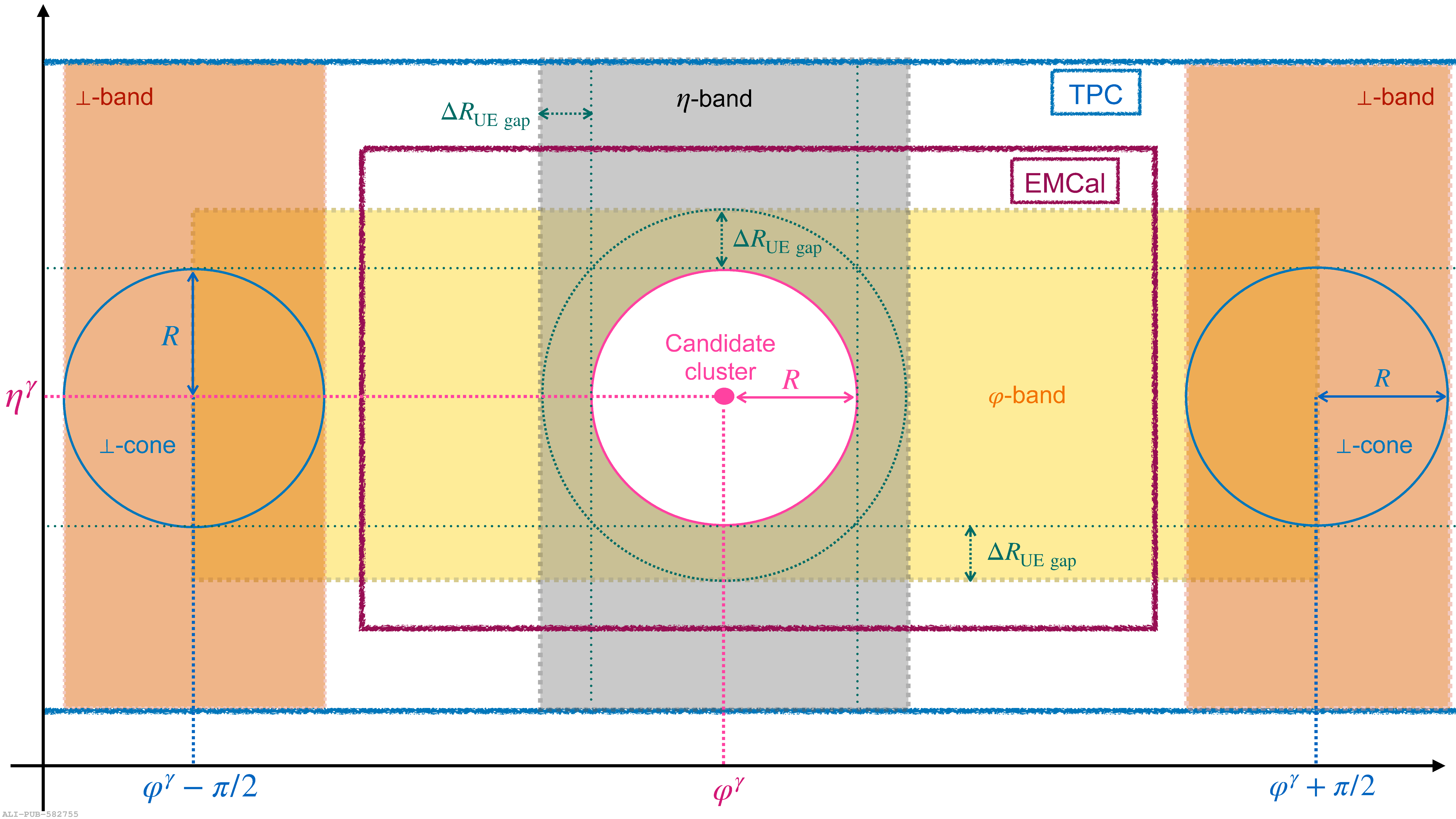
The ALICE Collaboration at the CERN LHC has measured the inclusive production cross section of isolated photons at midrapidity as a function of the photon transverse momentum ($p_{\rm T}^{\gamma}$), in Pb$-$Pb collisions in different centrality intervals, and in pp collisions, at centre-of-momentum energy per nucleon pair of $\sqrt{s_{\rm NN}}=5.02$ TeV. The photon transverse momentum range is between 10-14 and 40-140 GeV/$c$, depending on the collision system and on the Pb$-$Pb centrality class. The result extends to lower $p_{\rm T}^{\gamma}$ than previously published results by the ATLAS and CMS experiments at the same collision energy. The covered pseudorapidity range is $|\eta^{\gamma}| <~0.67$. The isolation selection is based on a charged particle isolation momentum threshold $p_{\rm T}^{\rm iso,~ch} = 1.5$ GeV/$c$ within a cone of radii $R=0.2$ and $0.4$. The nuclear modification factor is calculated and found to be consistent with unity in all centrality classes, and also consistent with the HG-PYTHIA model, which describes the event selection and geometry biases that affect the centrality determination in peripheral Pb$-$Pb collisions. The measurement is compared to next-to-leading order perturbative QCD calculations and to the measurements of isolated photons and Z$^0$ bosons from the CMS experiment, which are all found to be in agreement.
Eur. Phys. J. C (2025) 85:553
HEP Data
e-Print: arXiv:2409.12641 | PDF | inSPIRE
CERN-EP-2024-244
Figure group