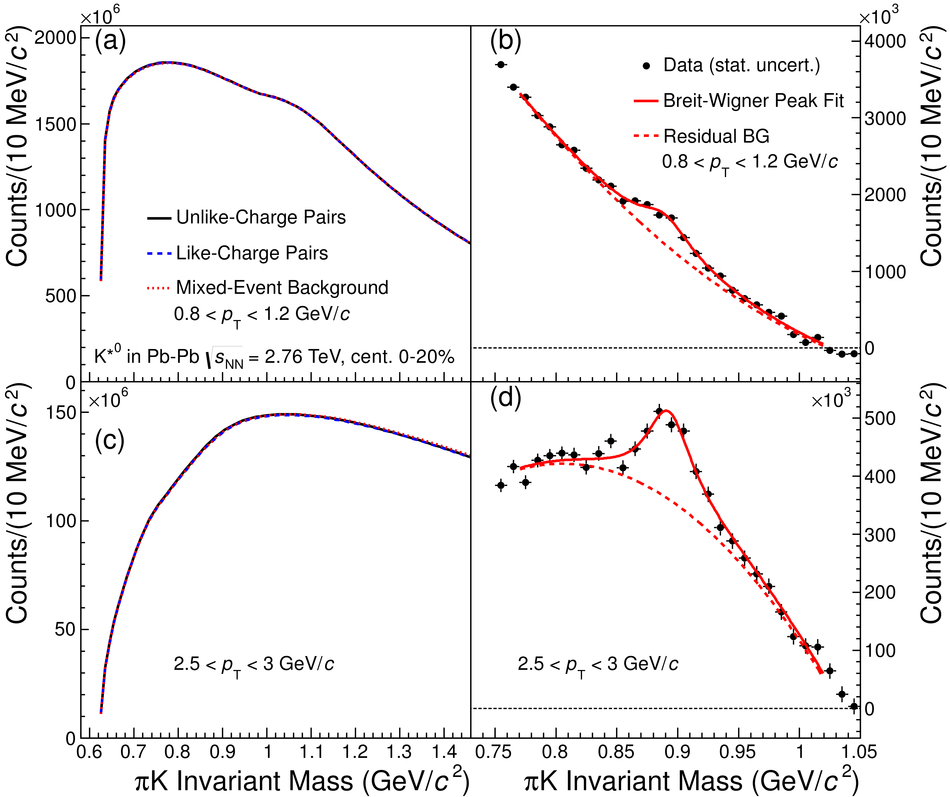
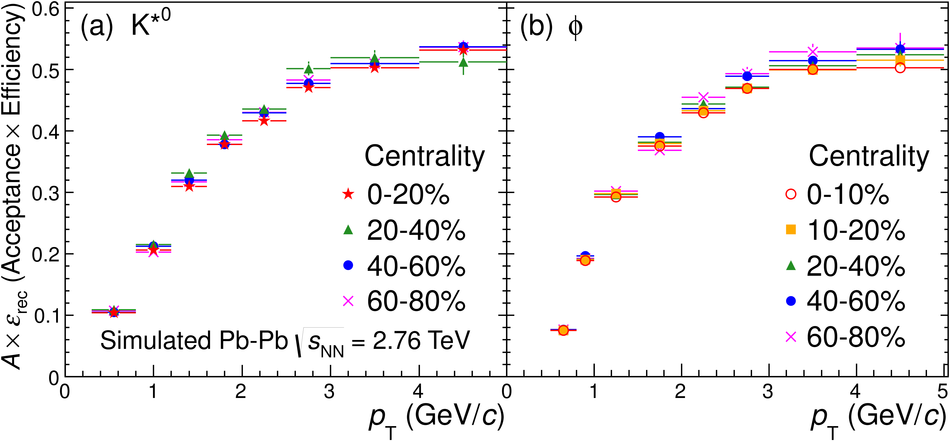
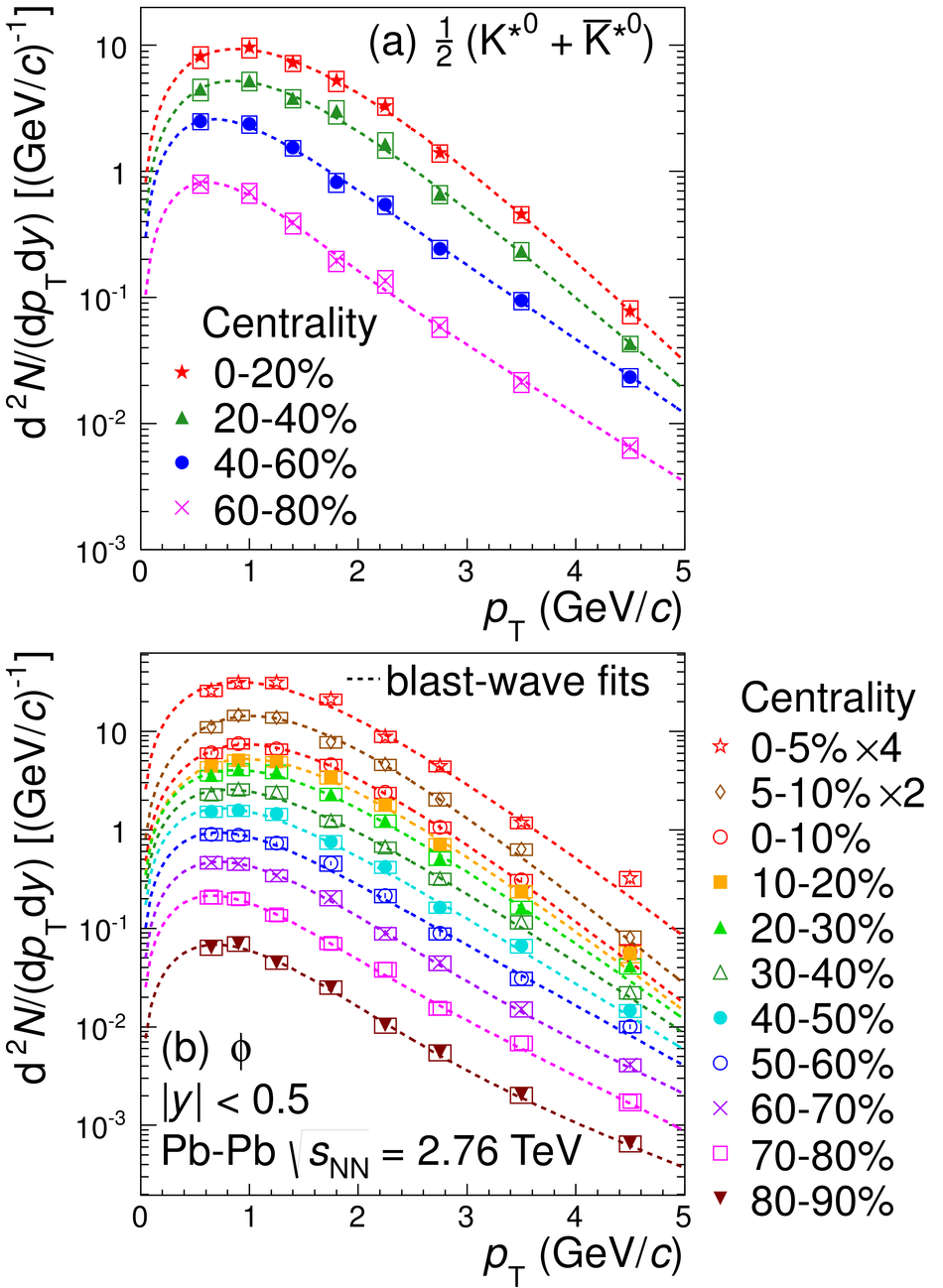
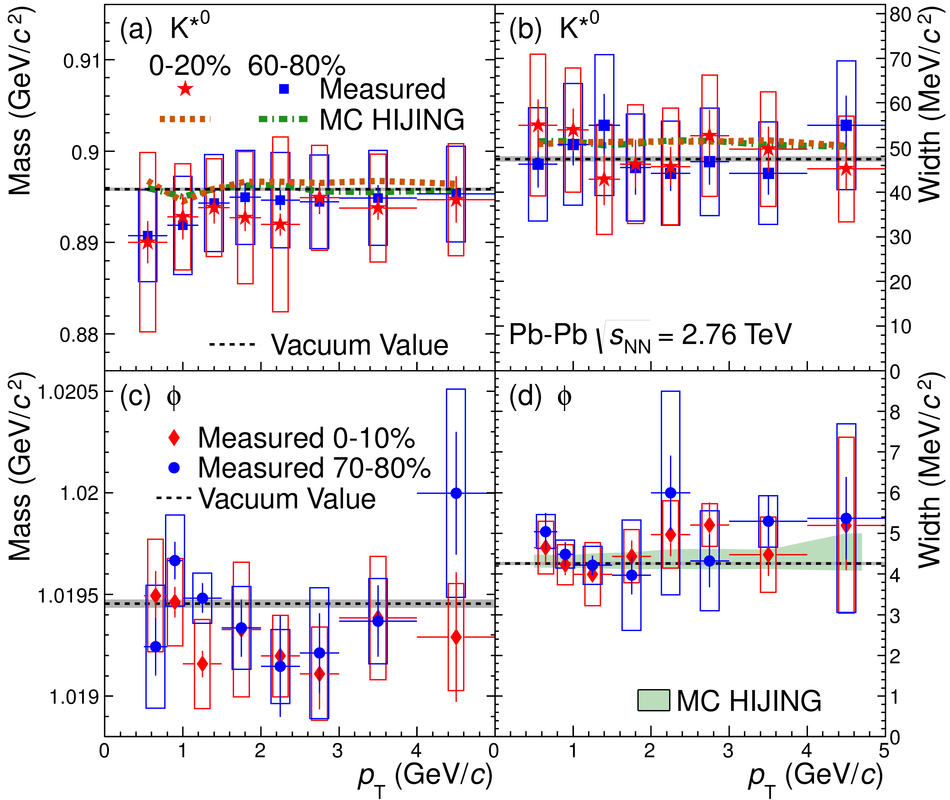
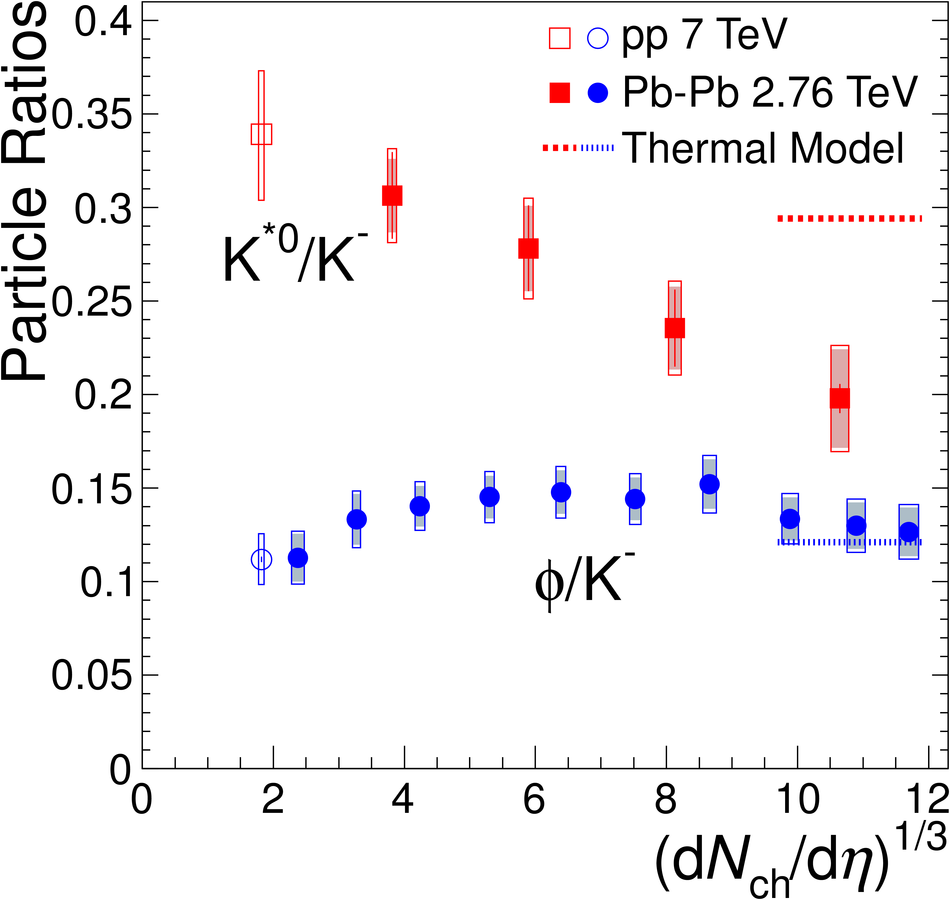
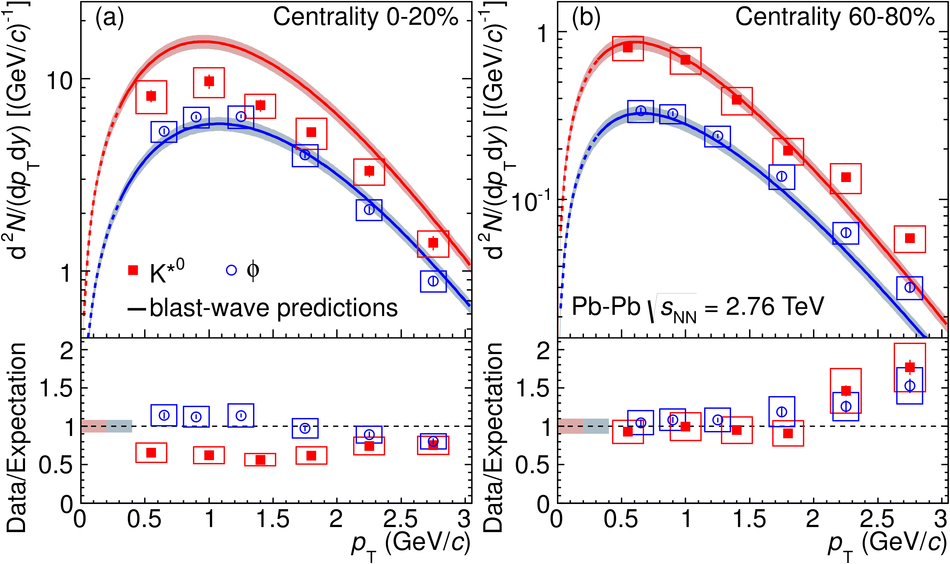
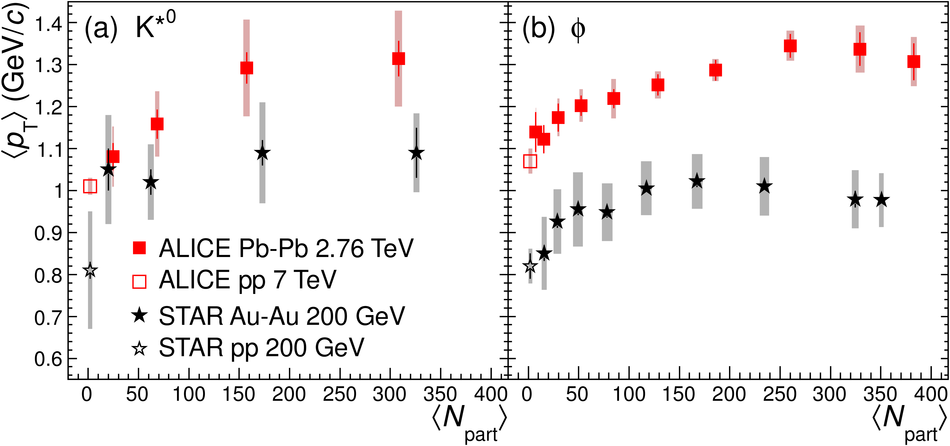
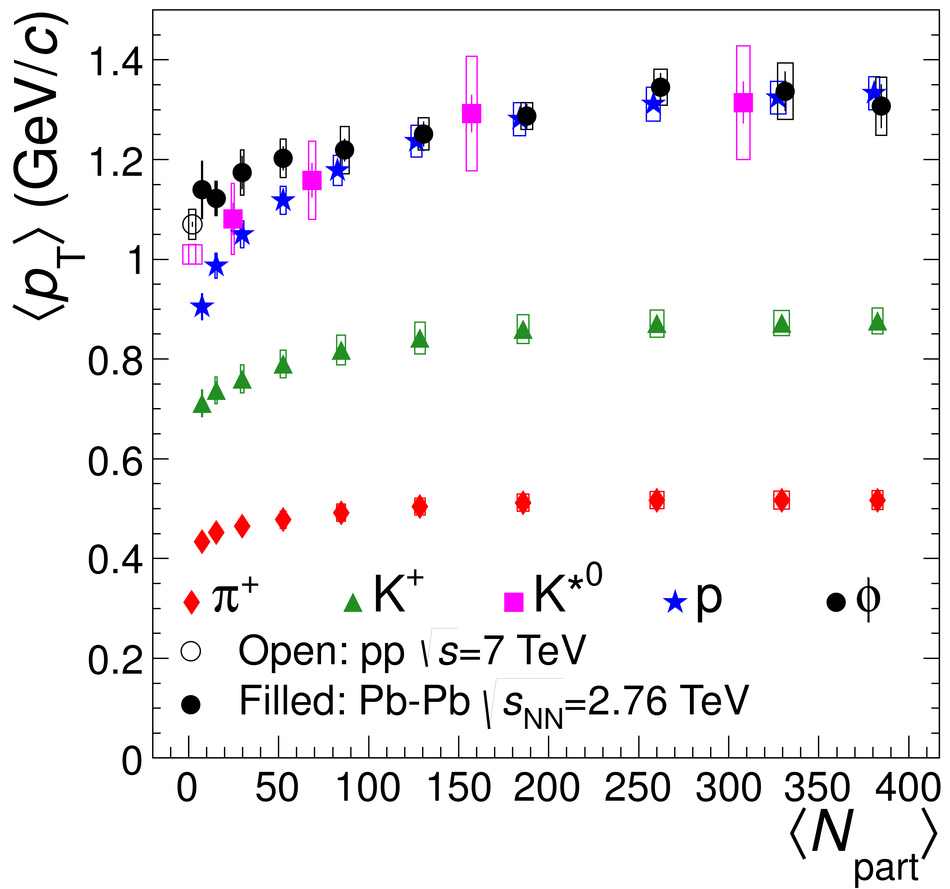
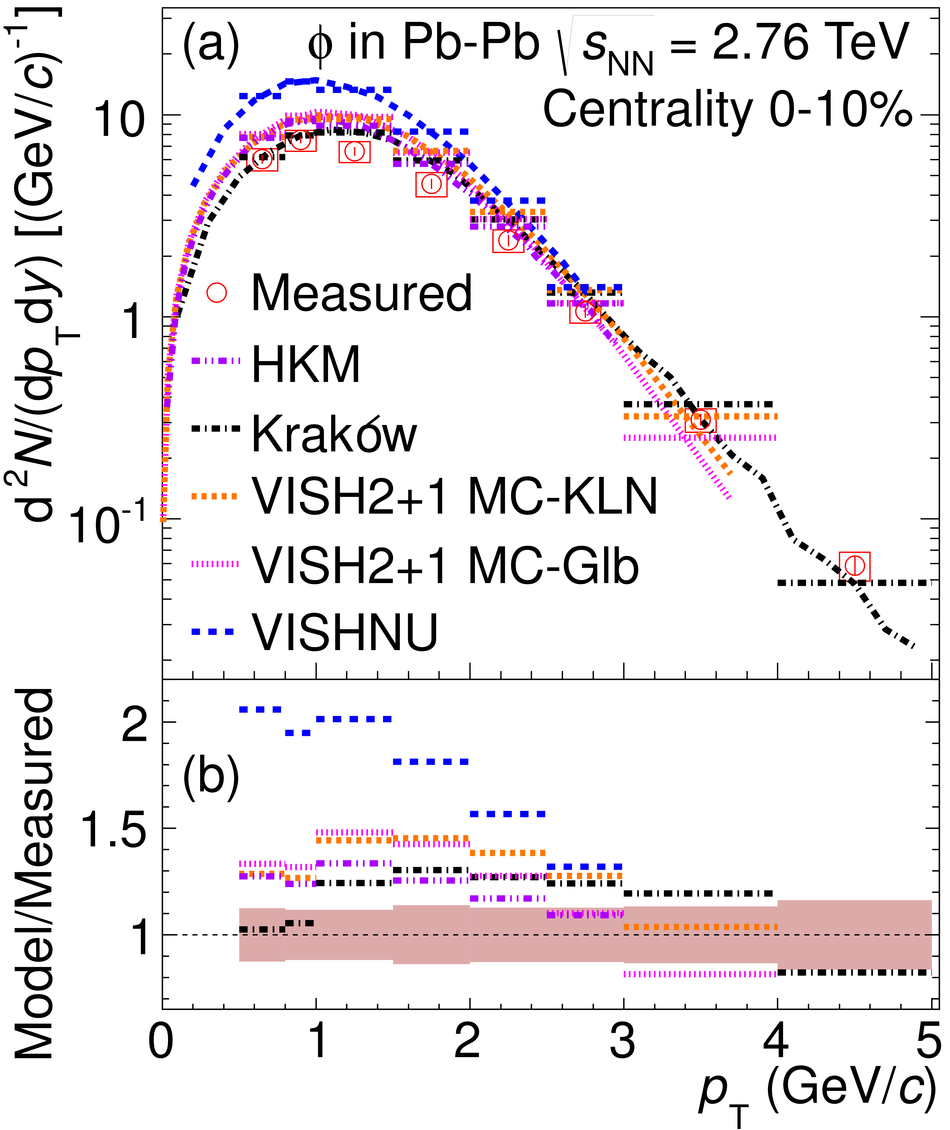
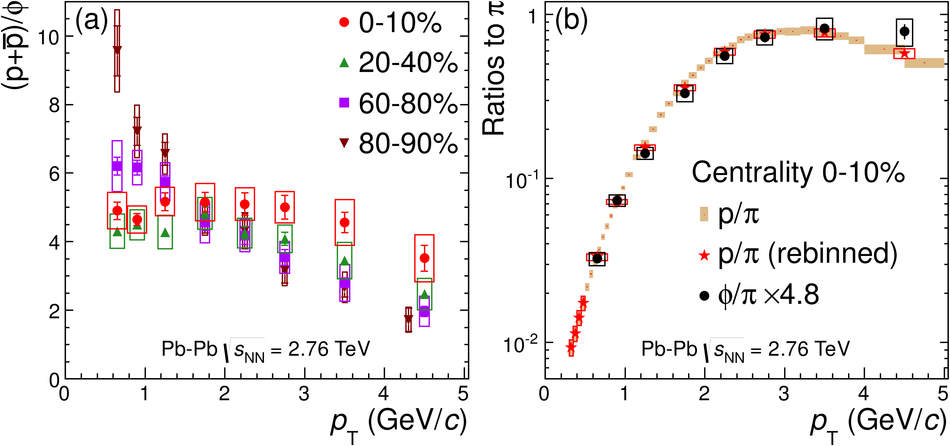
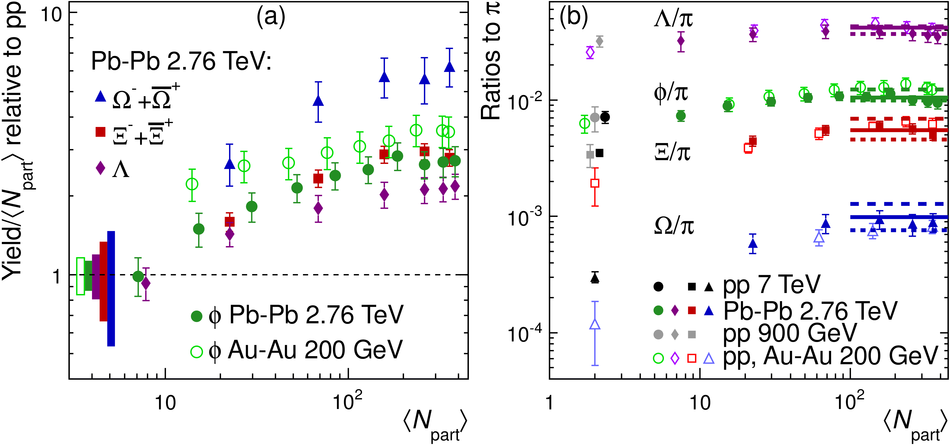
The yields of the K*(892)$^{0}$ and $\Phi$(1020) resonances are measured in Pb-Pb collisions at $\sqrt{s_{\rm NN}}$ = 2.76 TeV through their hadronic decays using the ALICE detector. The measurements are performed in multiple centrality intervals at mid-rapidity (|$y$|<0.5) in the transverse-momentum ranges 0.3 < $p_{\rm T}$ < 5 GeV/$c$ for the K*(892)$^{0}$ and 0.5 < $p_{\rm T}$ < 5 GeV/$c$ for the $\Phi$(1020). The yields of K*(892)$^{0}$ are suppressed in central Pb-Pb collisions with respect to pp and peripheral Pb-Pb collisions (perhaps due to rescattering of its decay products in the hadronic medium), while the longer lived $\Phi$(1020) meson is not suppressed. These particles are also used as probes to study the mechanisms of particle production. The shape of the $p_{\rm T}$ distribution of the $\Phi$(1020) meson, but not its yield, is reproduced fairly well by hydrodynamic models for central Pb-Pb collisions. In central Pb-Pb collisions at low and intermediate $p_{\rm T}$, the p/$\Phi$(1020) ratio is flat in $p_{\rm T}$, while the p/$\pi$ and $\Phi$(1020)/$\pi$ ratios show a pronounced increase and have similar shapes to each other. These results indicate that the shapes of the $p_{\rm T}$ distributions of these particles in central Pb-Pb collisions are determined predominantly by the particle masses and radial flow. Finally, $\Phi$(1020) production in Pb-Pb collisions is enhanced, with respect to the yield in pp collisions and the yield of charged pions, by an amount similar to the $\Lambda$ and $\Xi$.
Phys. Rev. C 91 (2015) 024609
HEP Data
e-Print: arXiv:1404.0495 | PDF | inSPIRE
CERN-PH-EP-2014-060