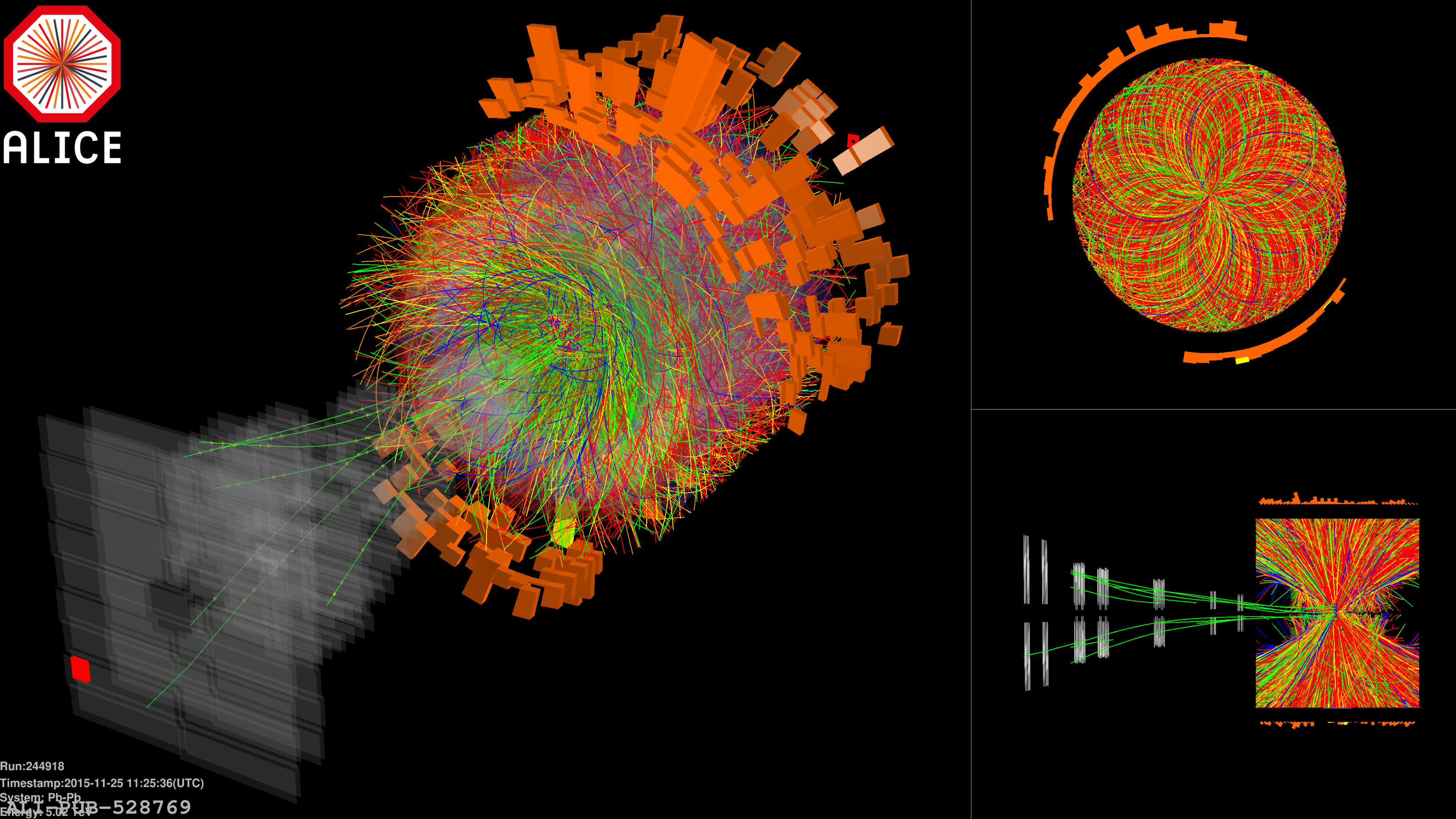
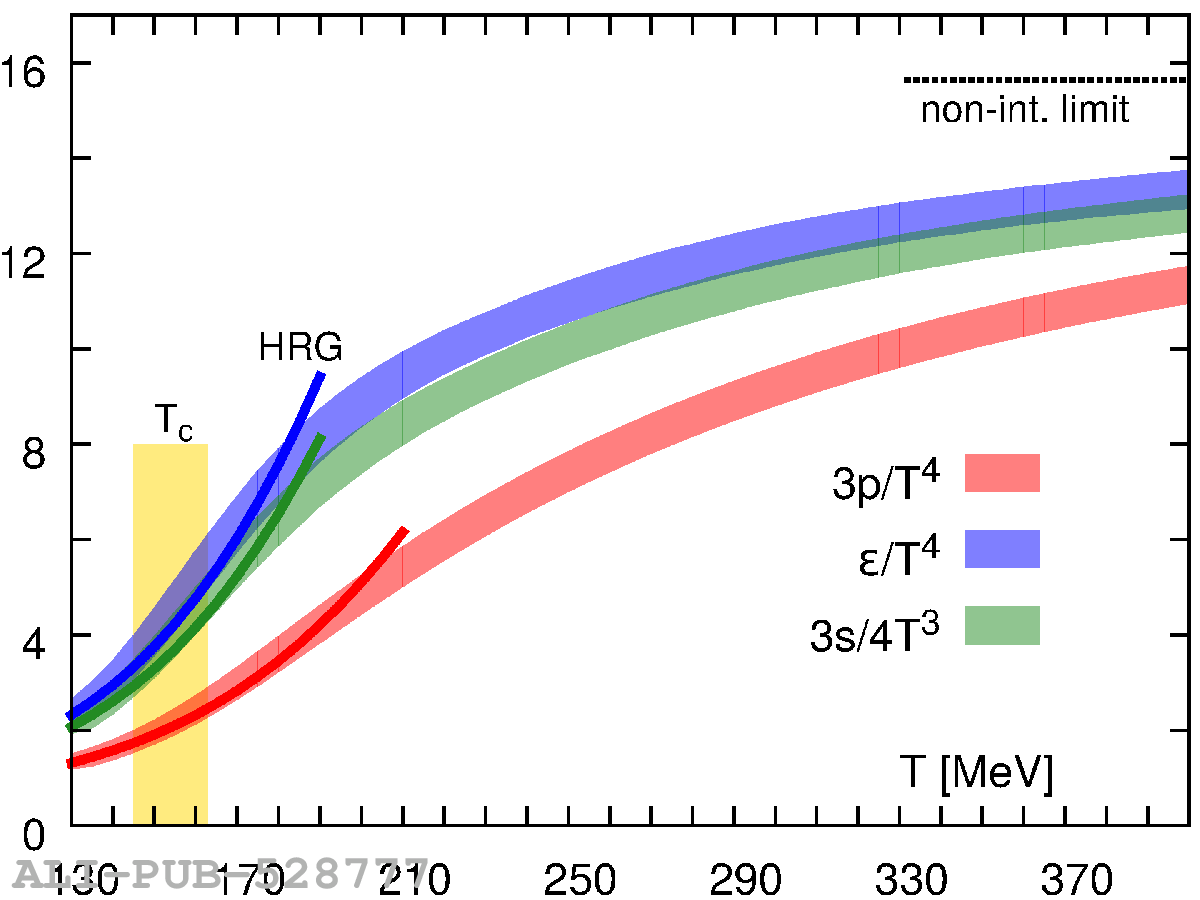
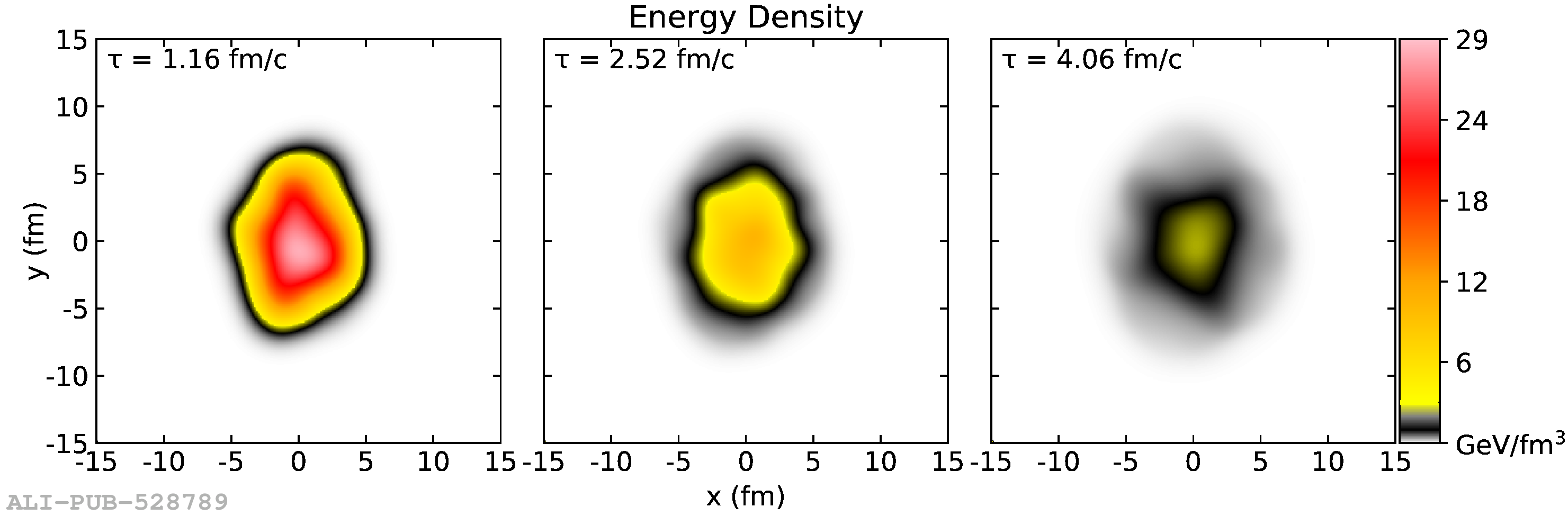
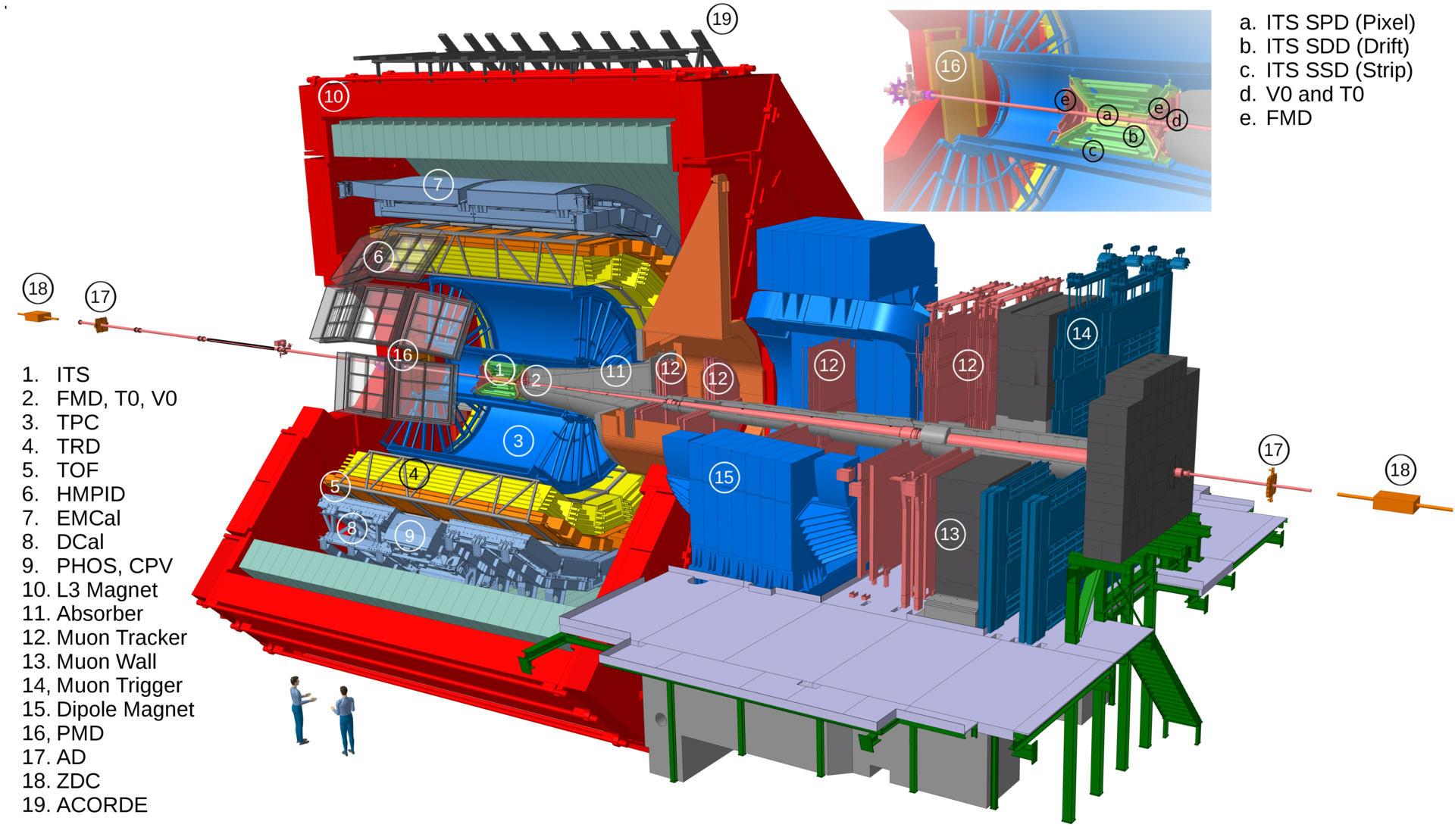
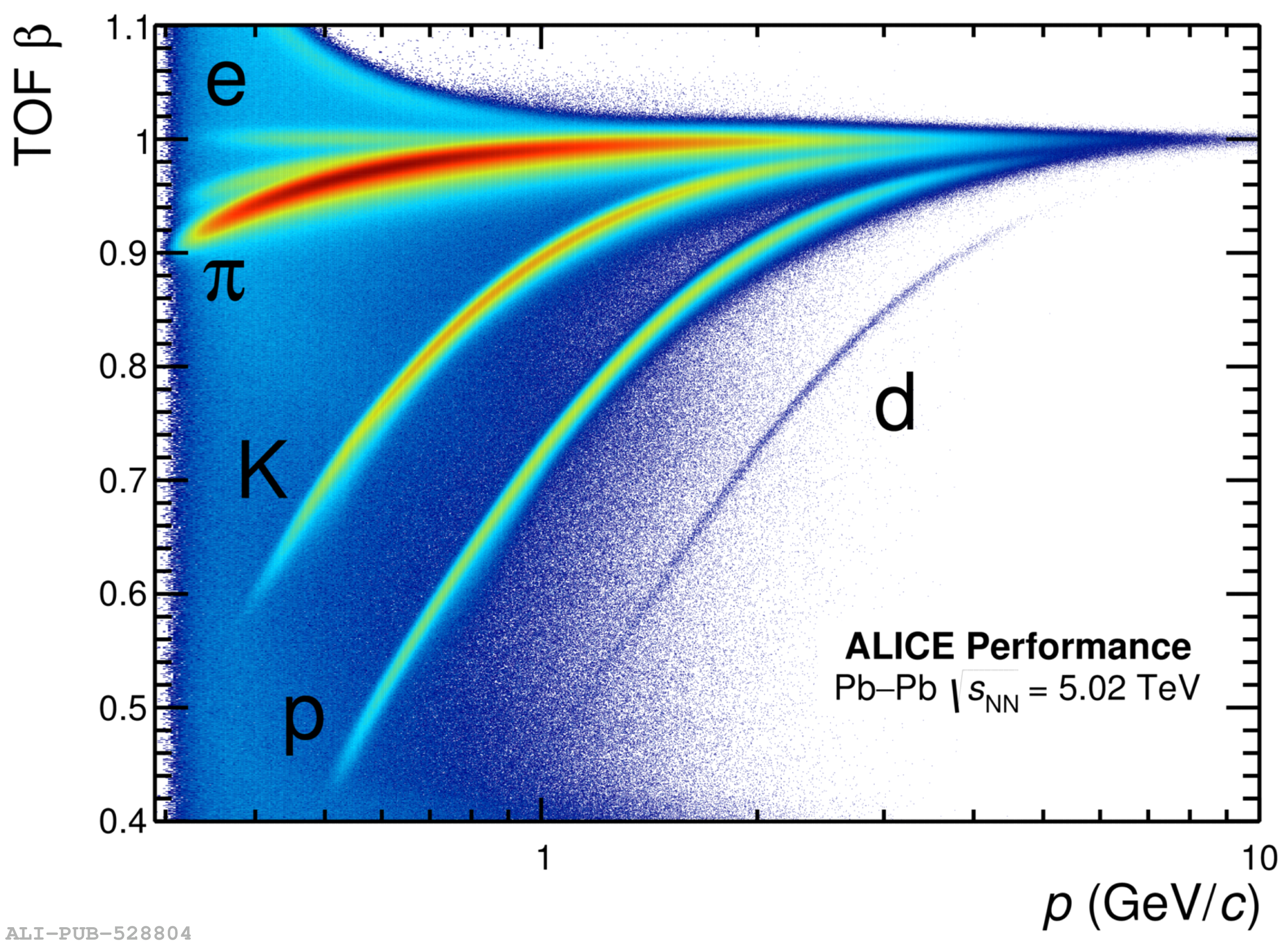
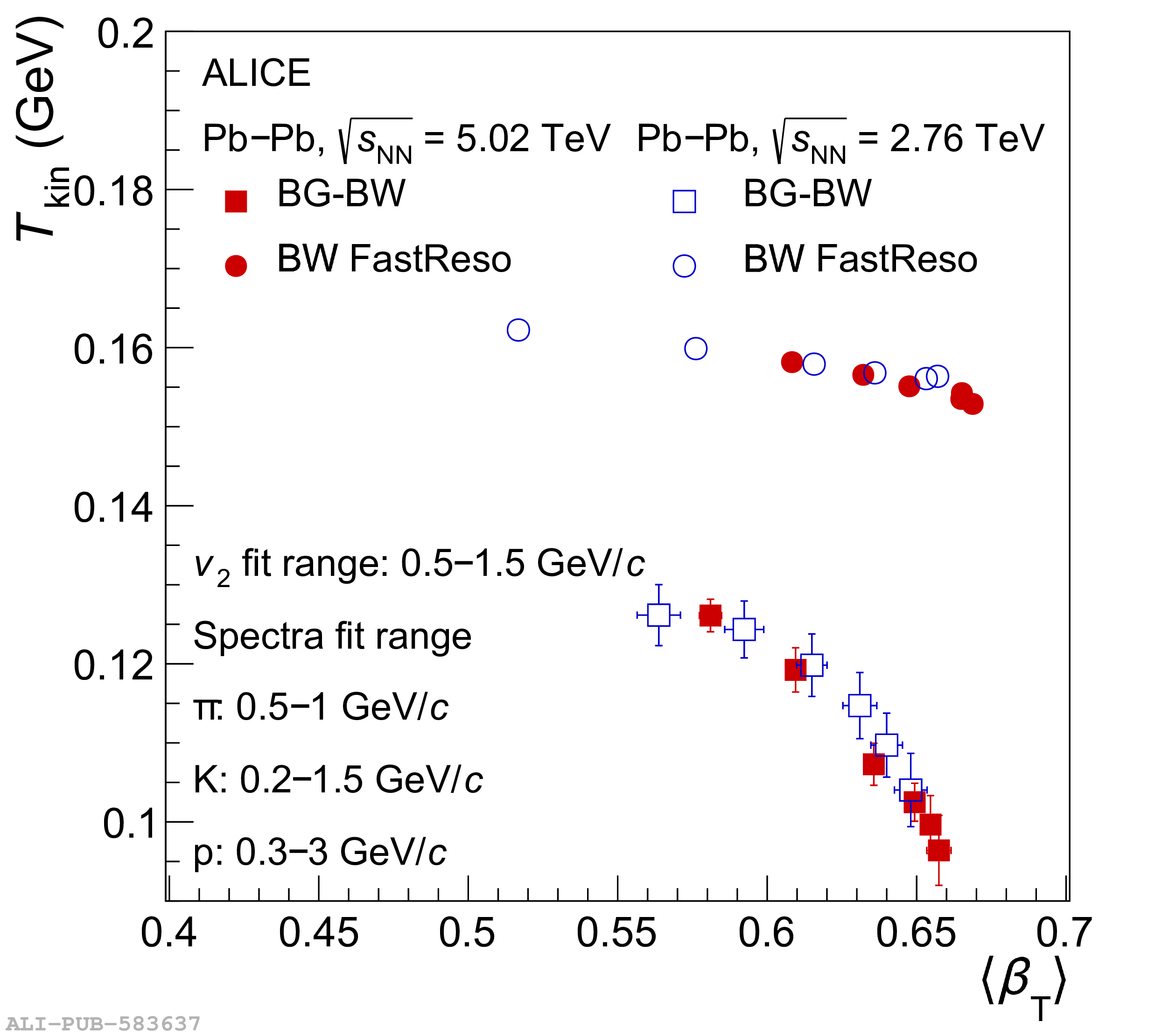
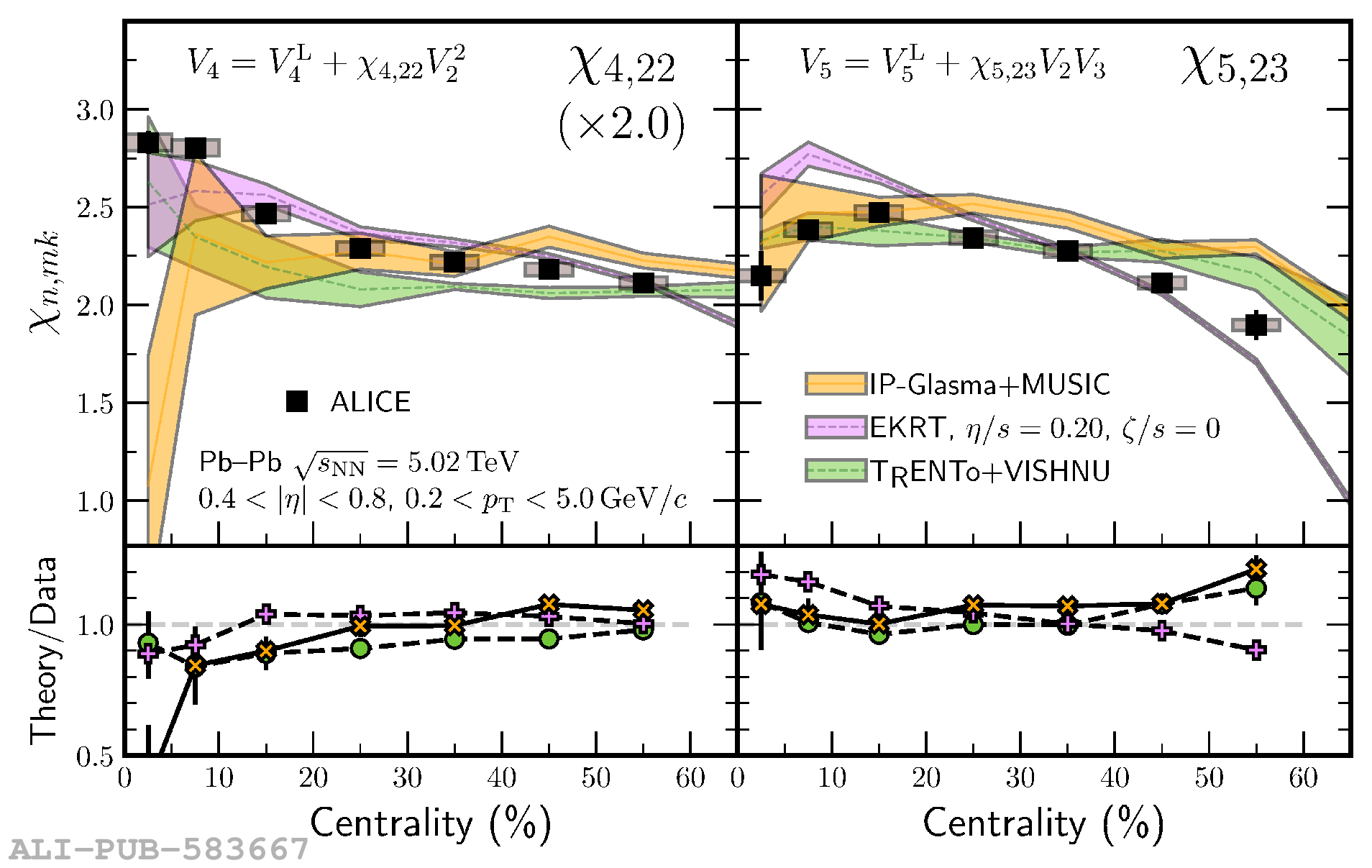
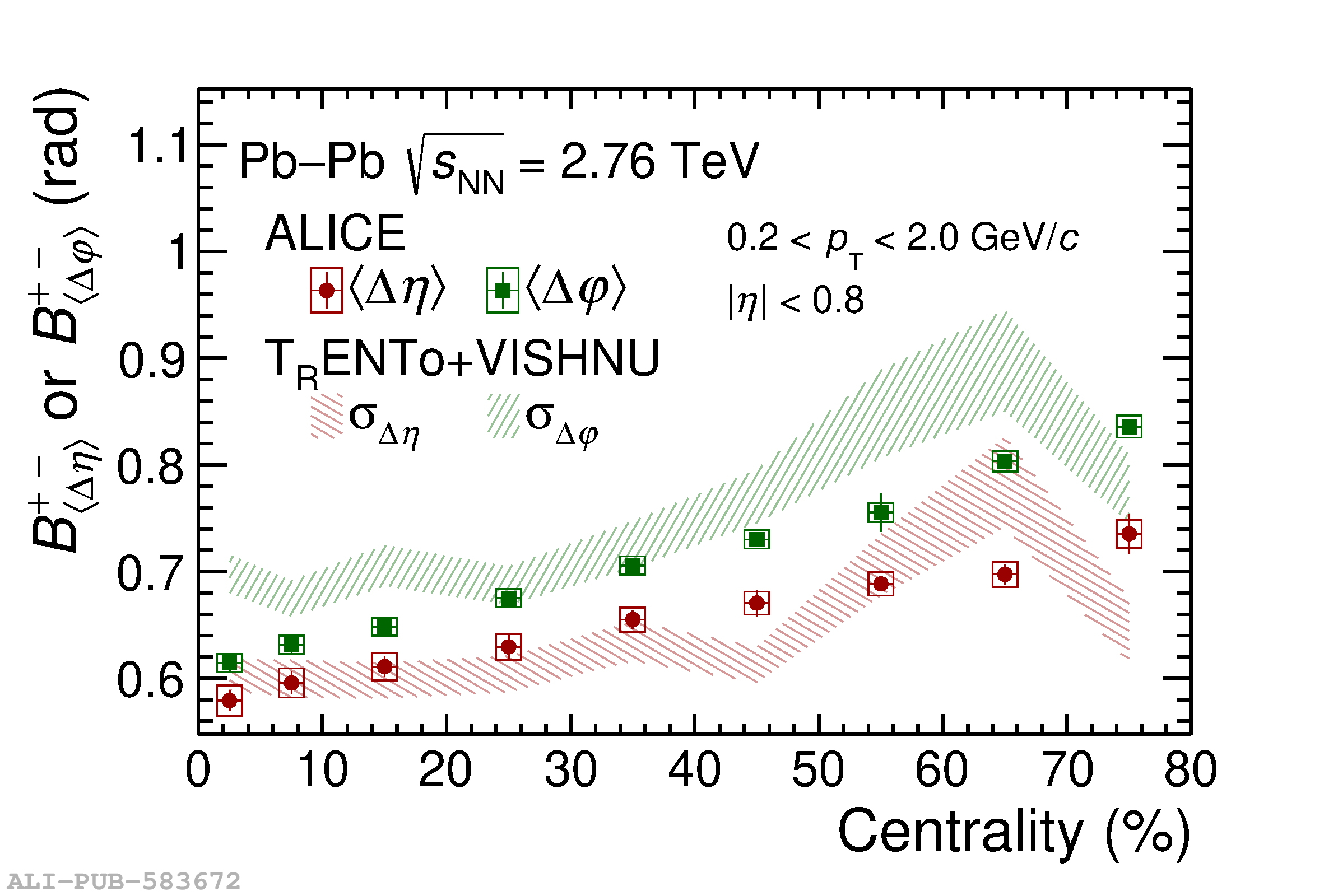
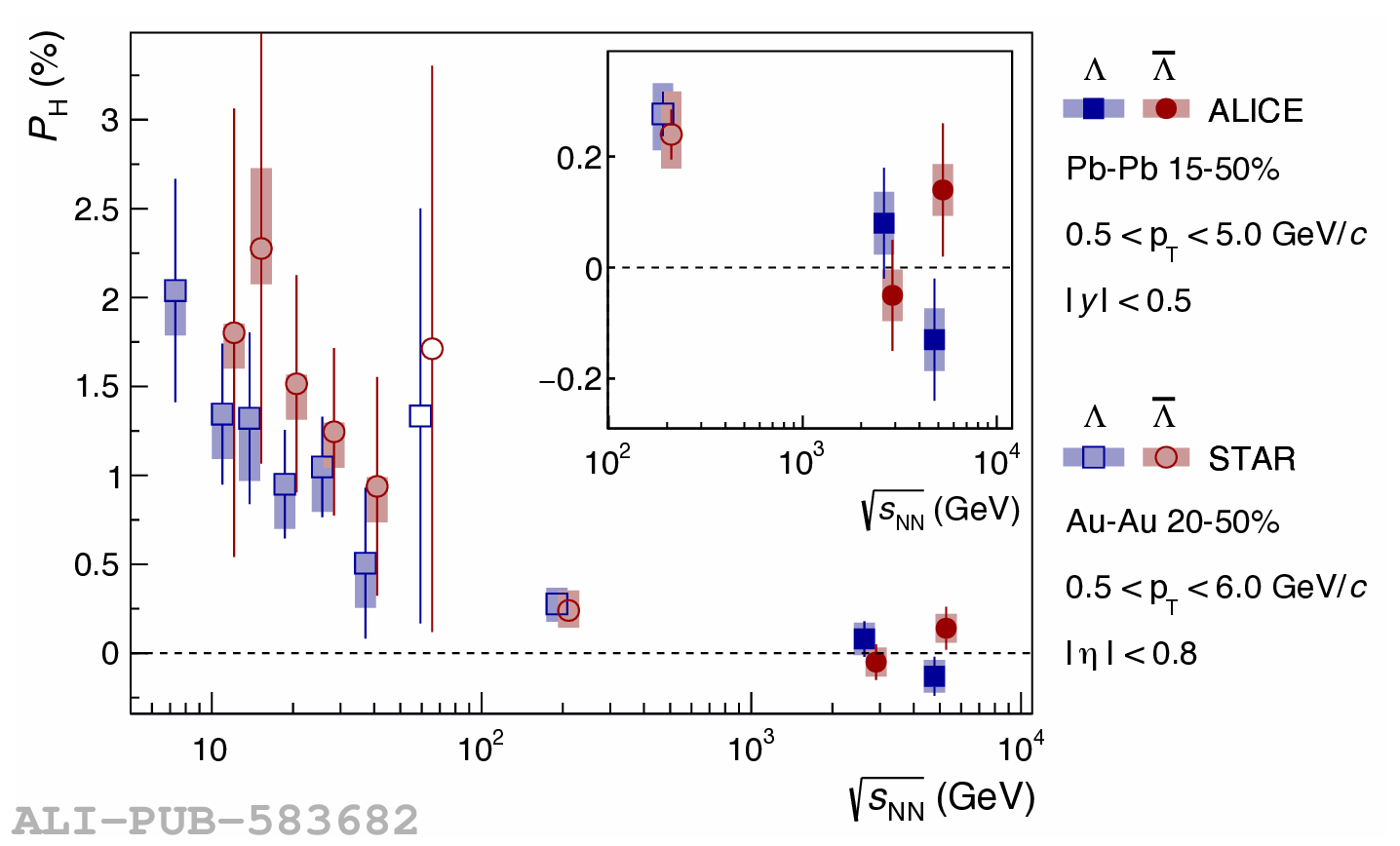
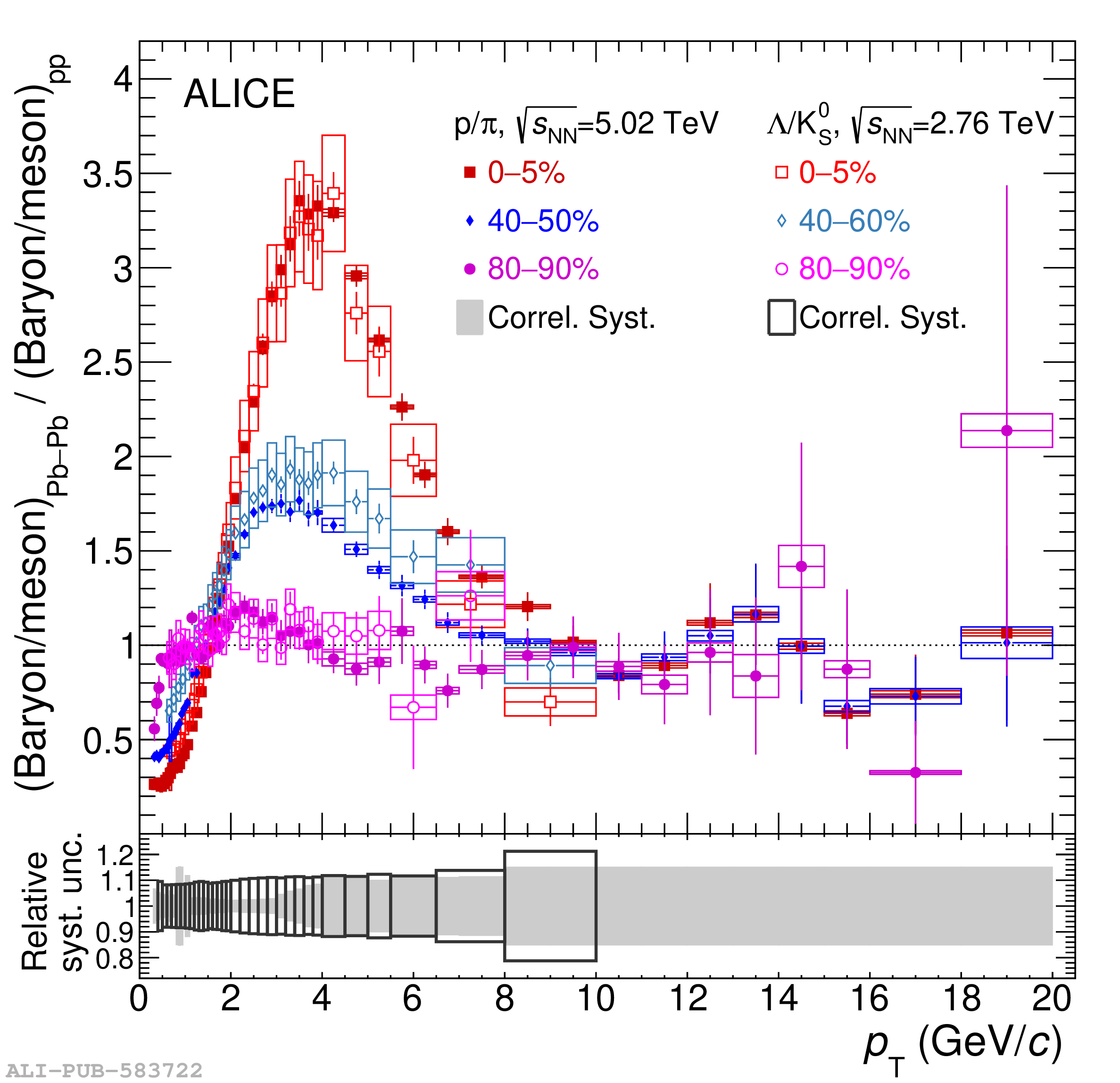
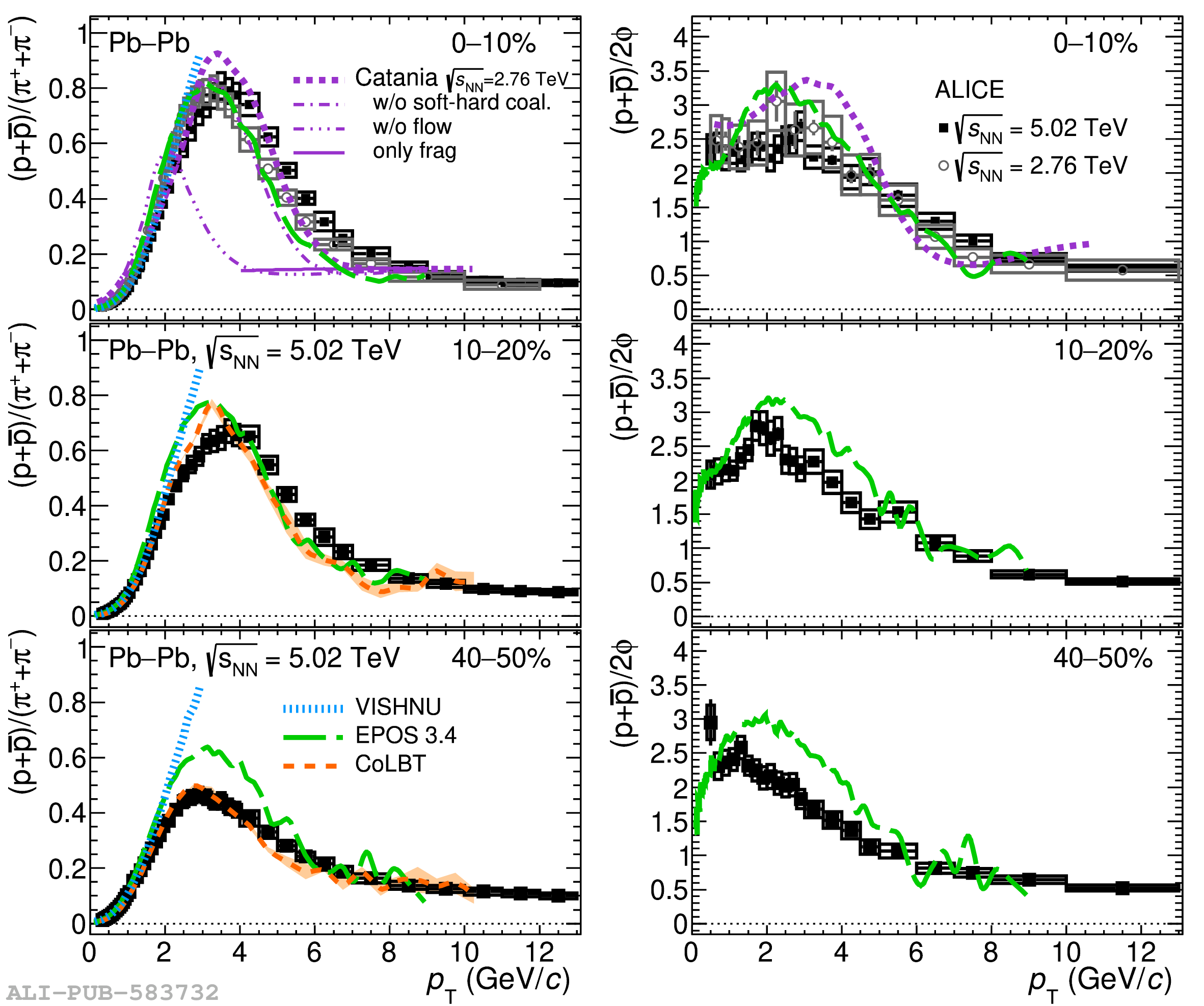
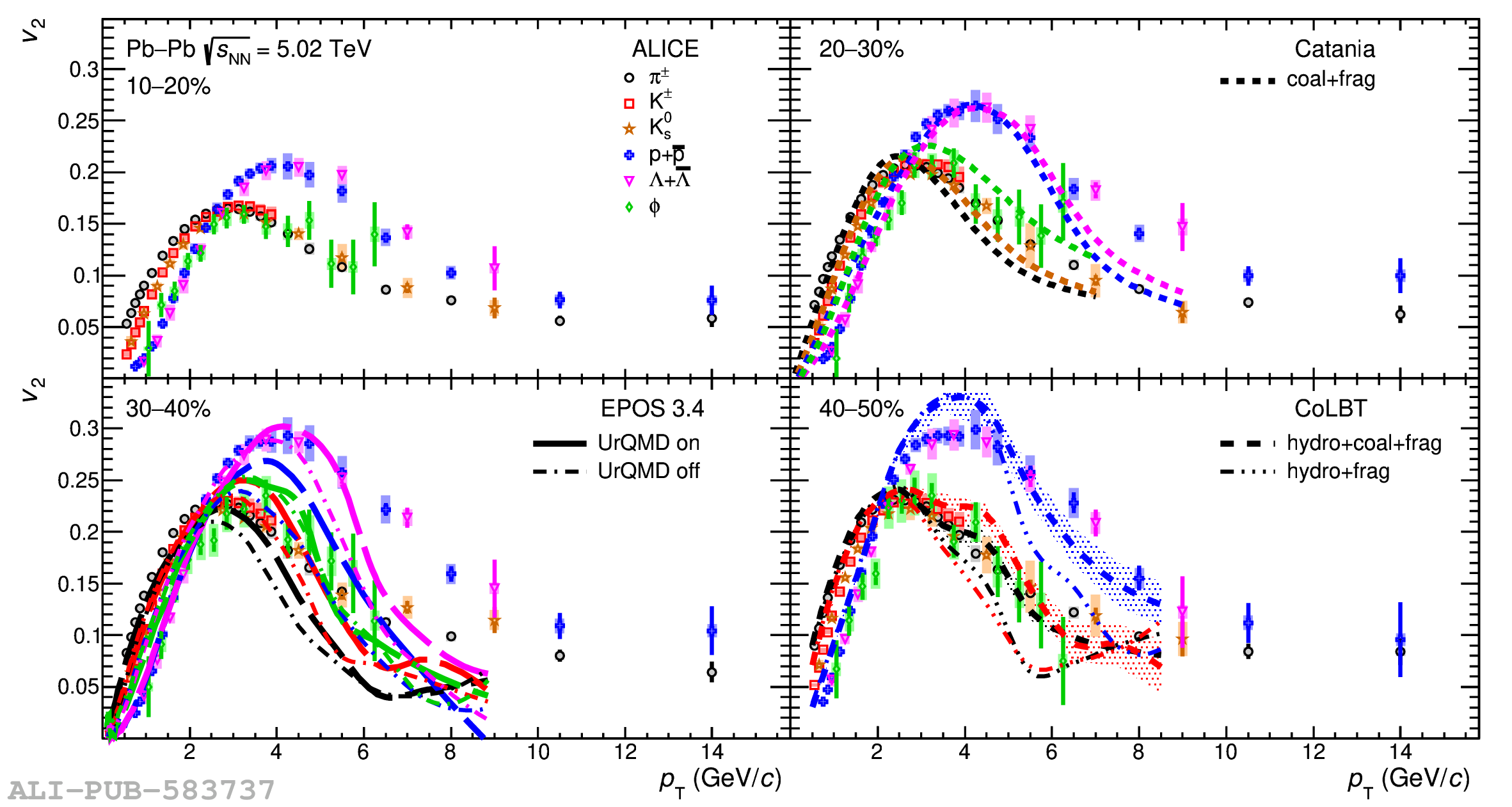
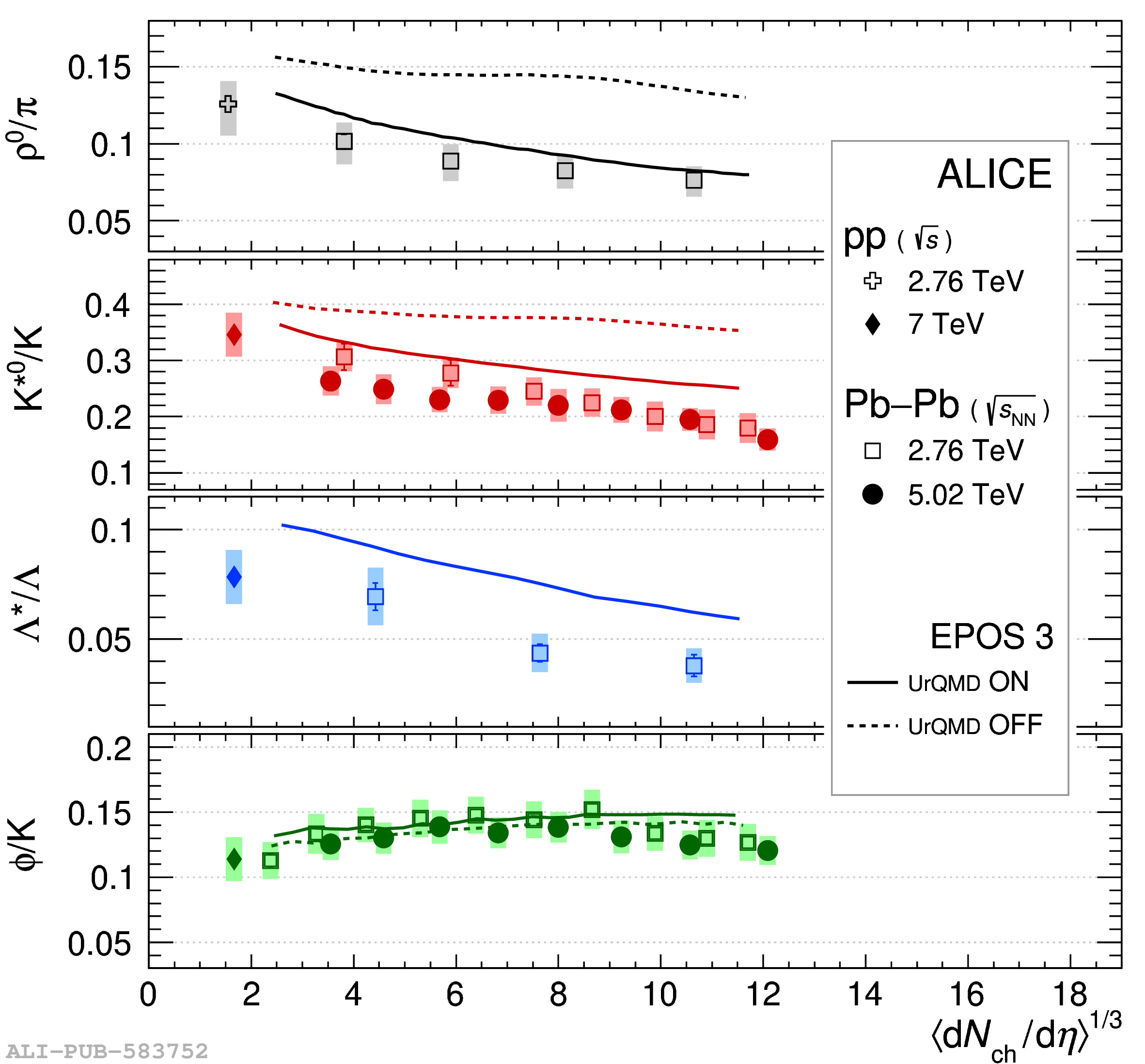
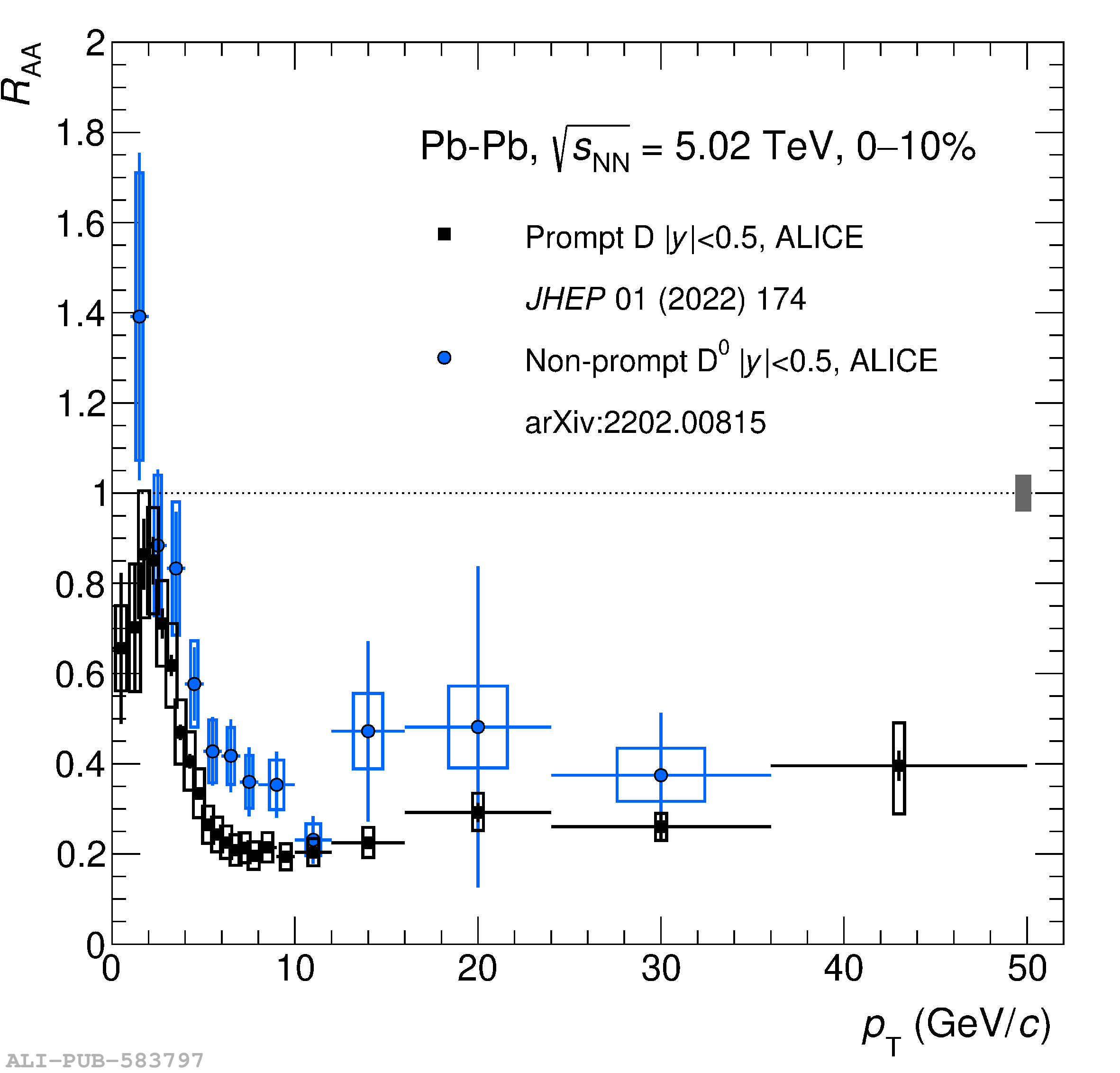
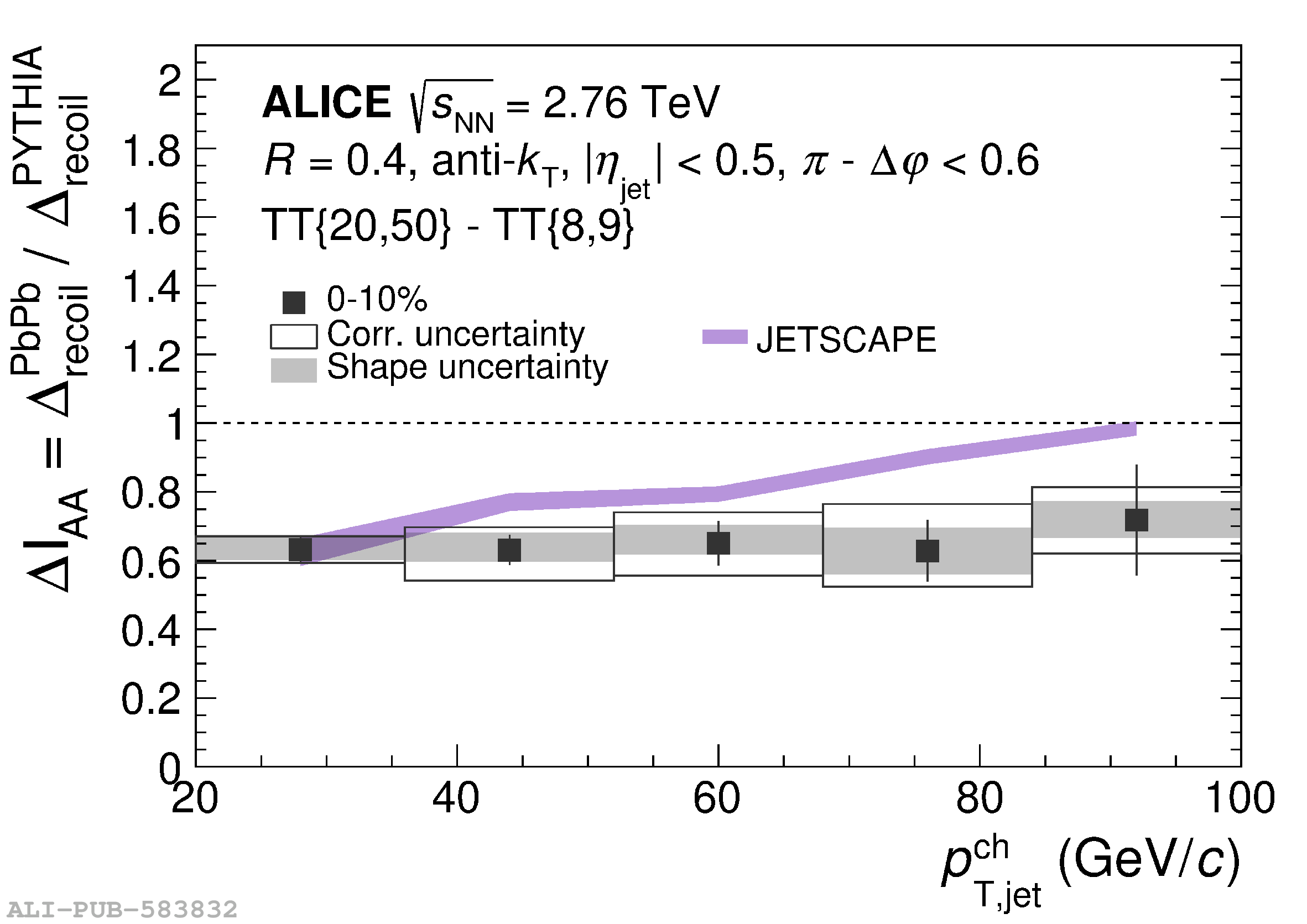
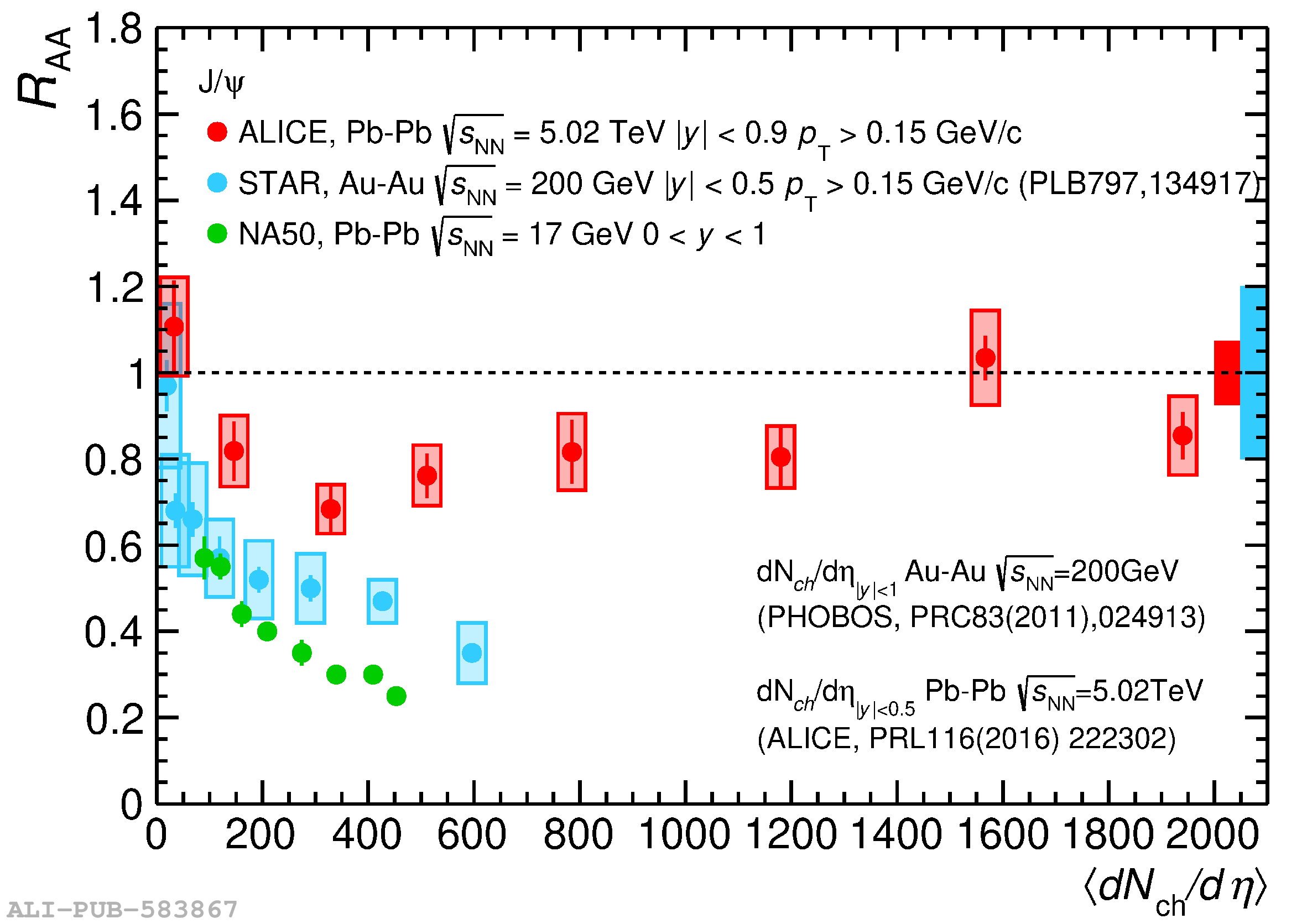
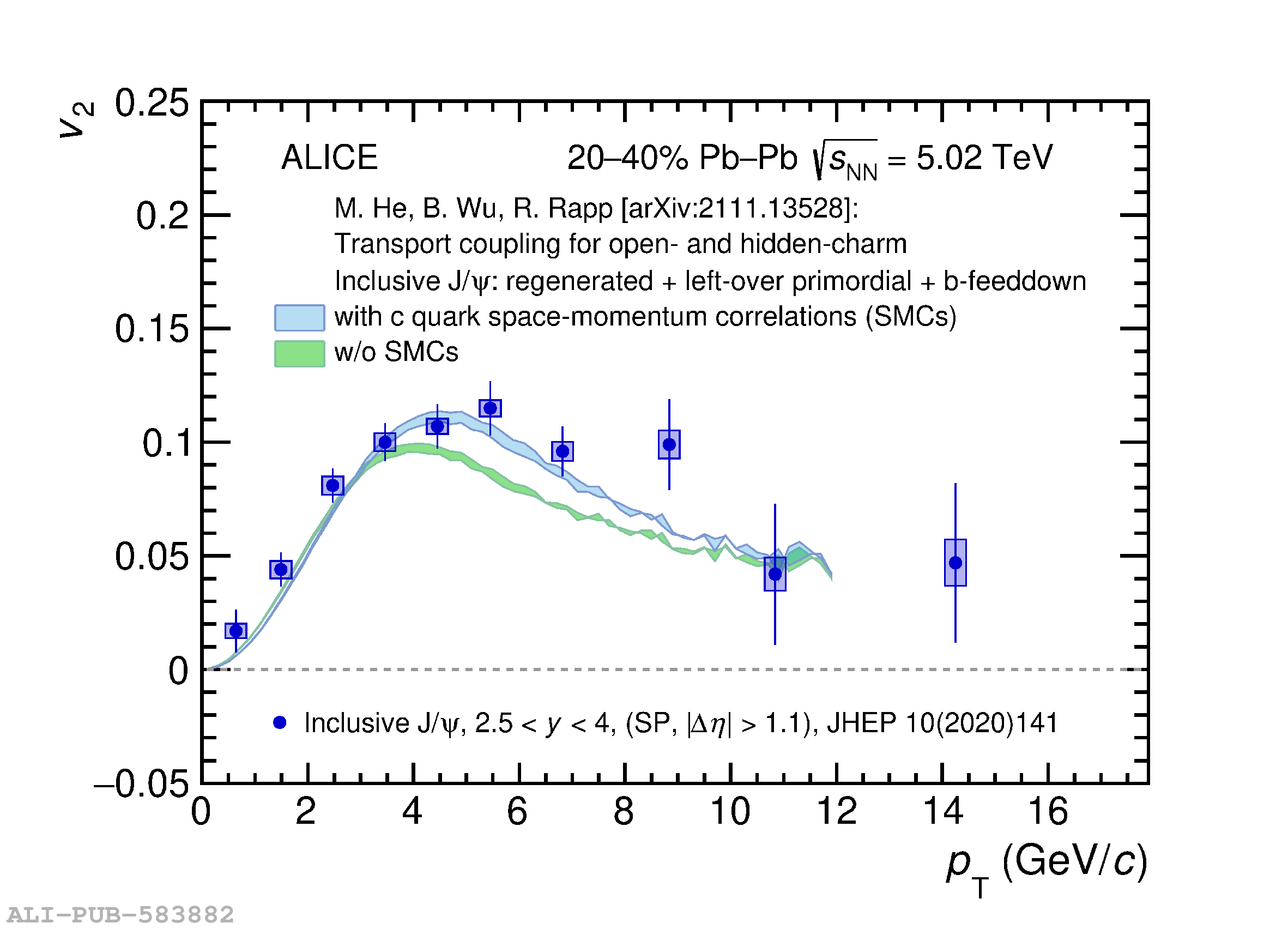
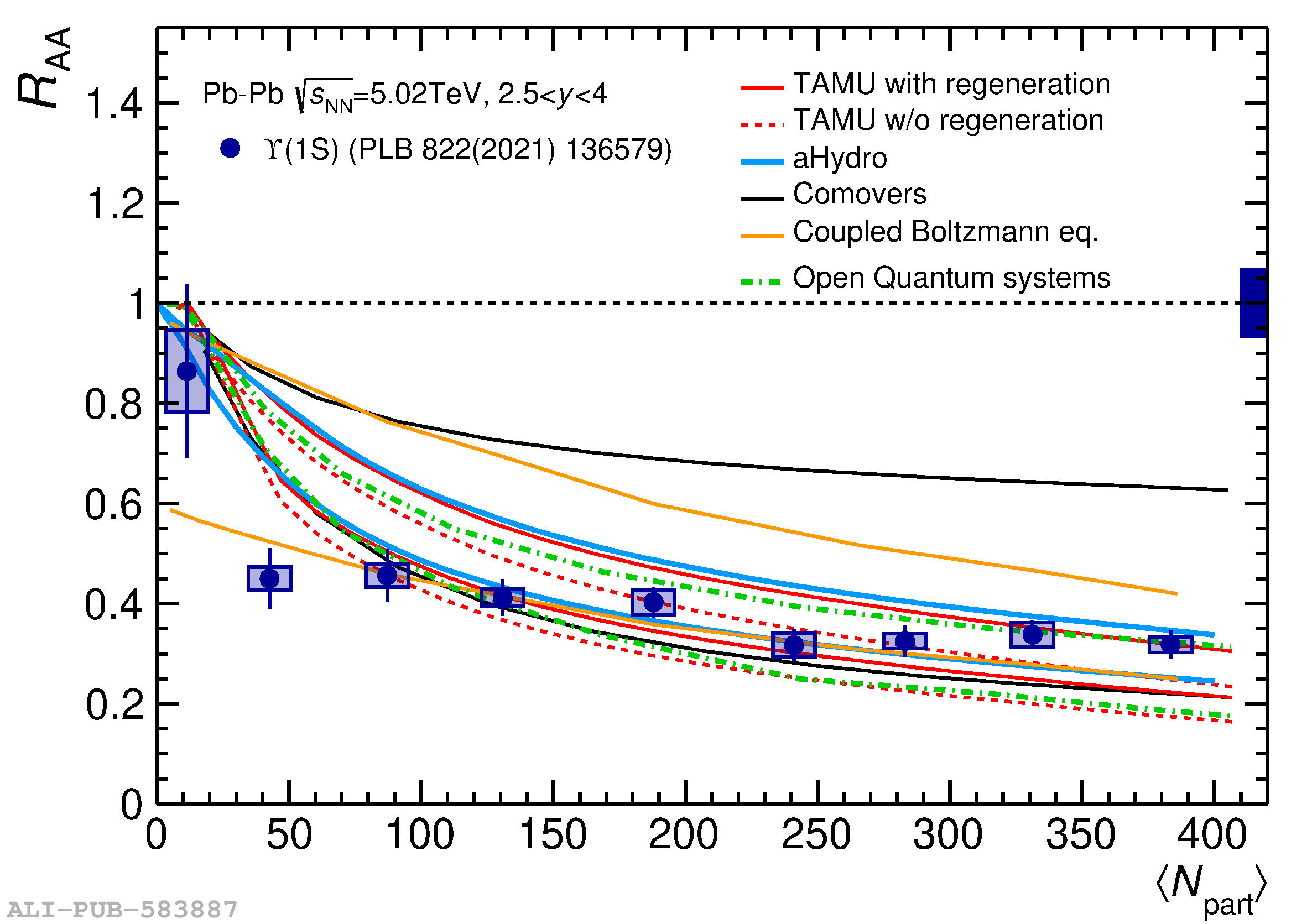
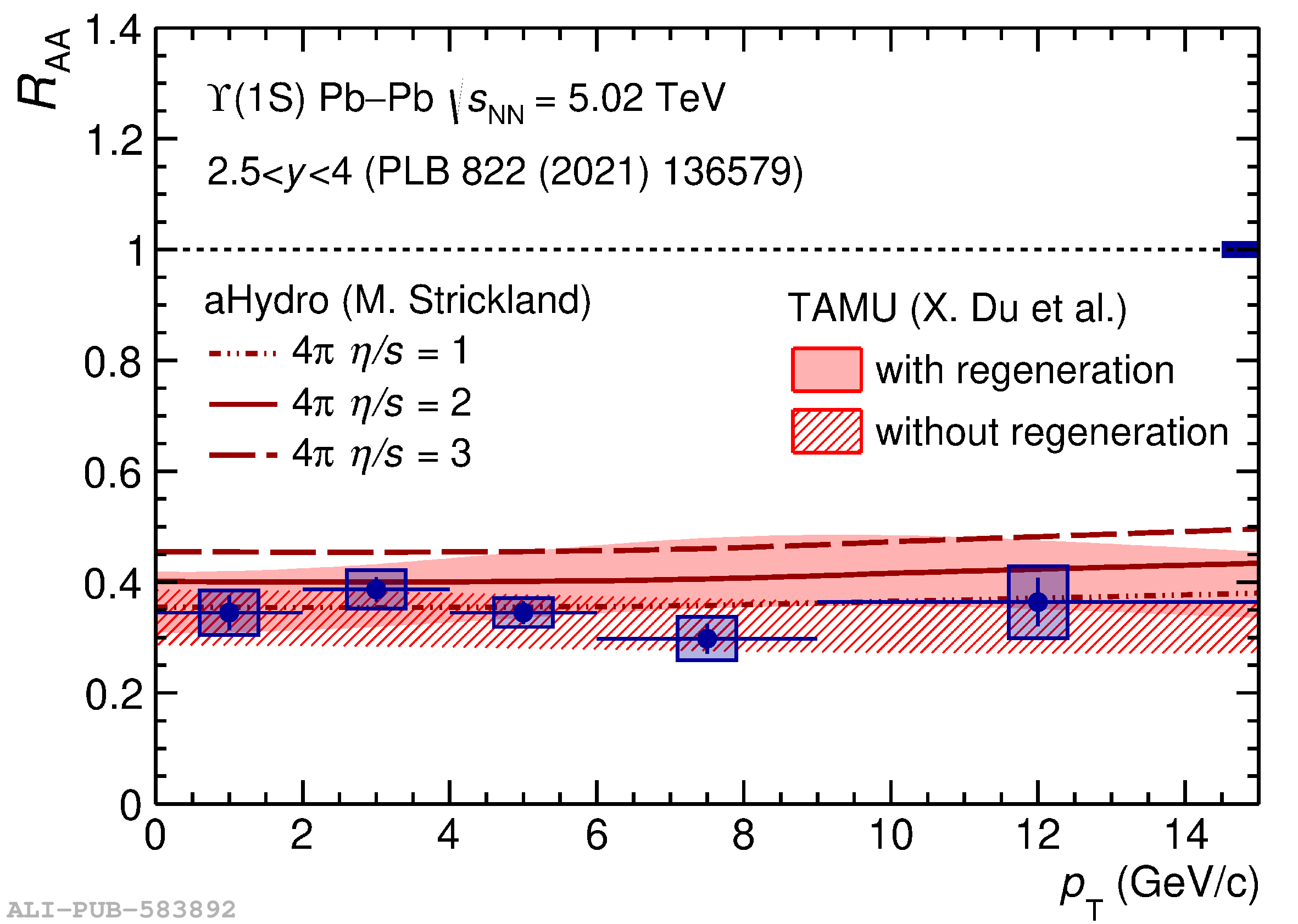
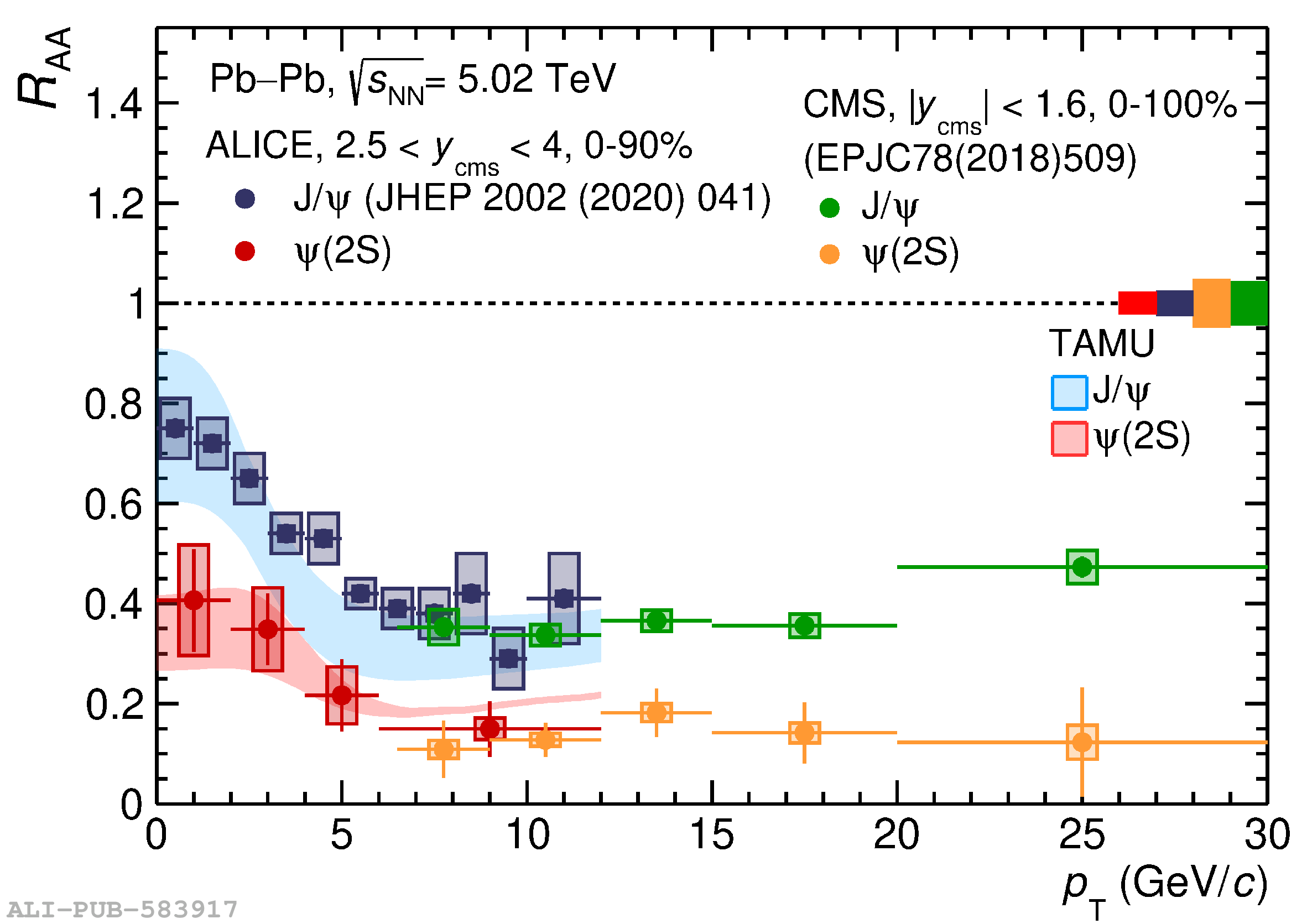
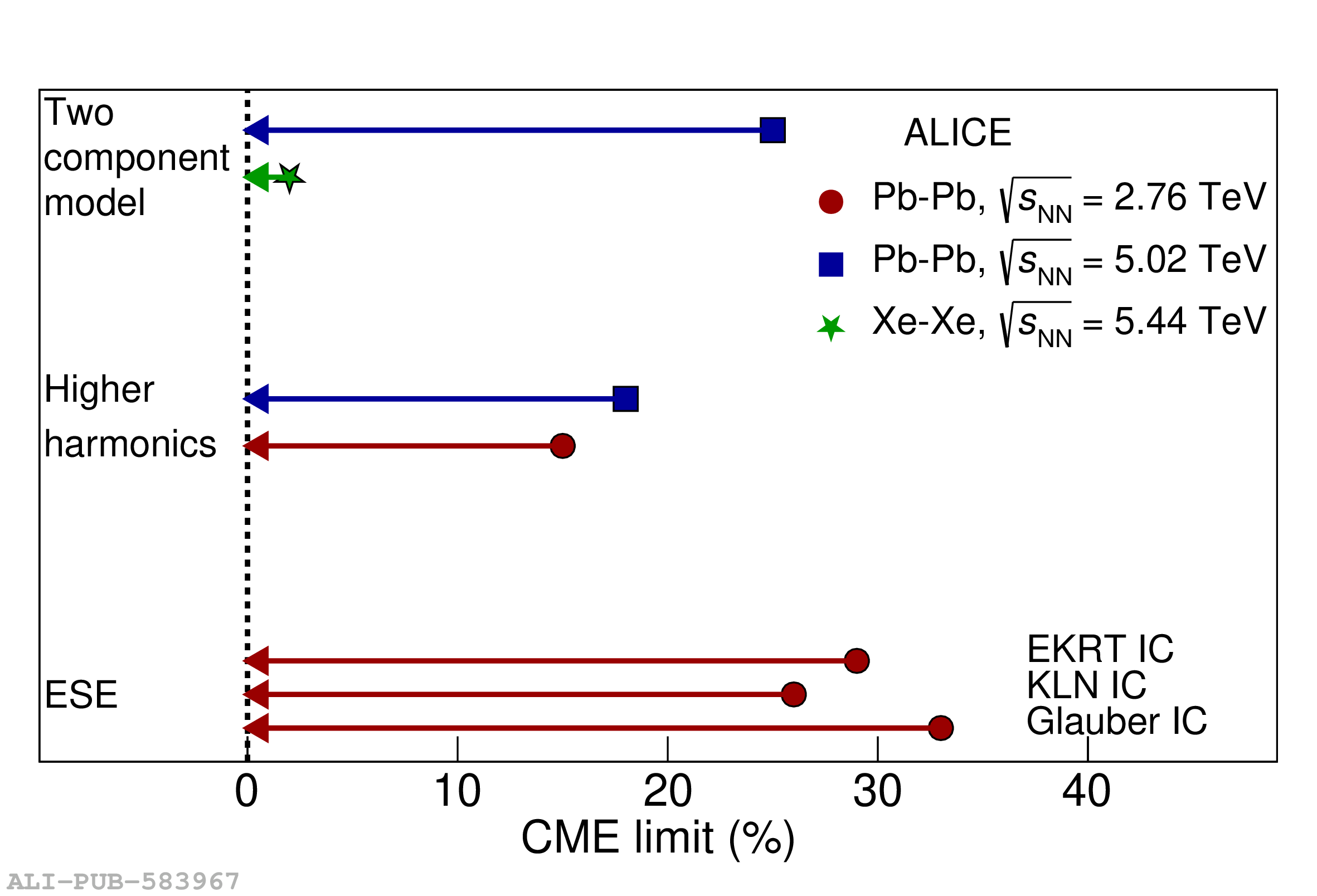
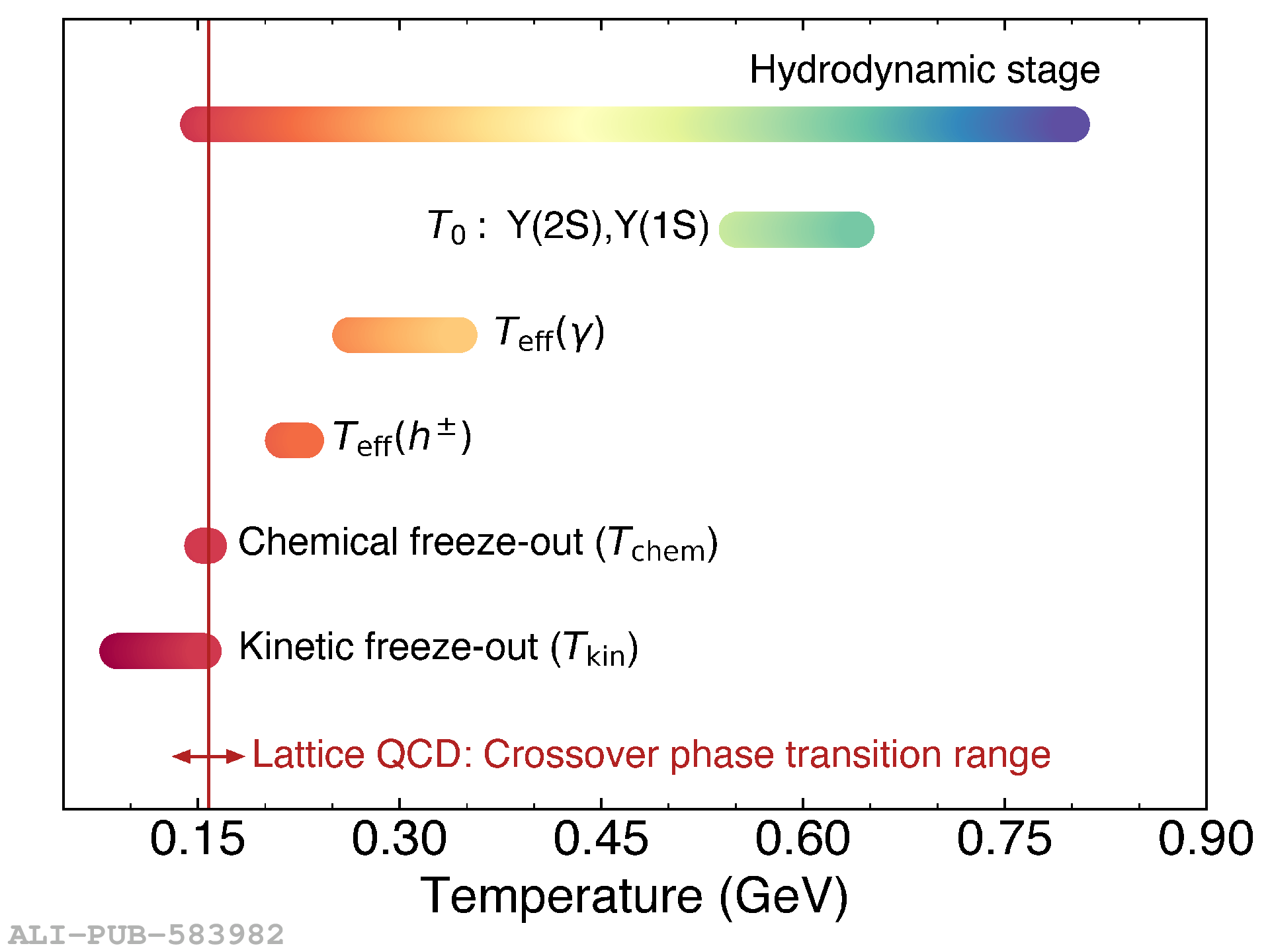
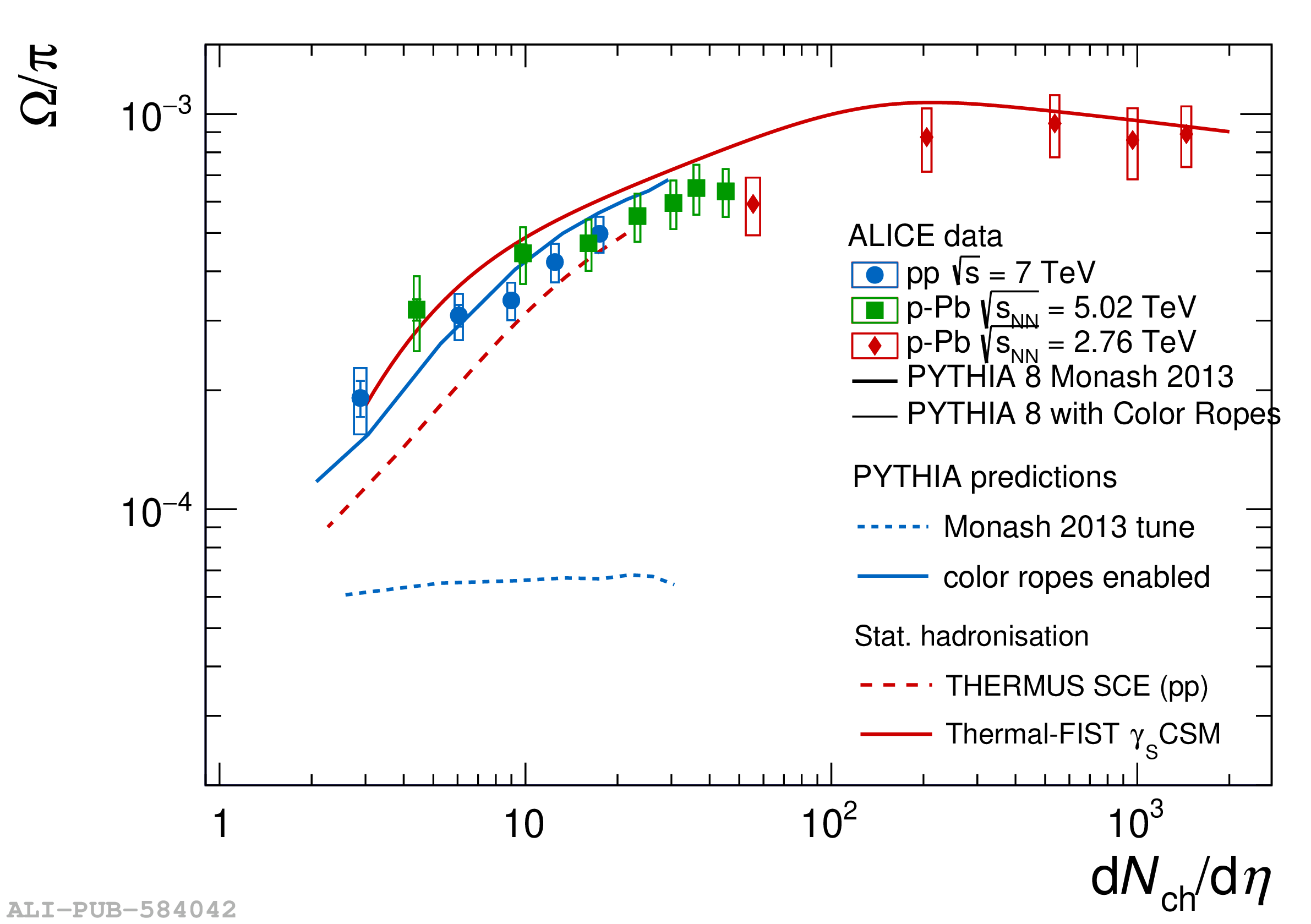
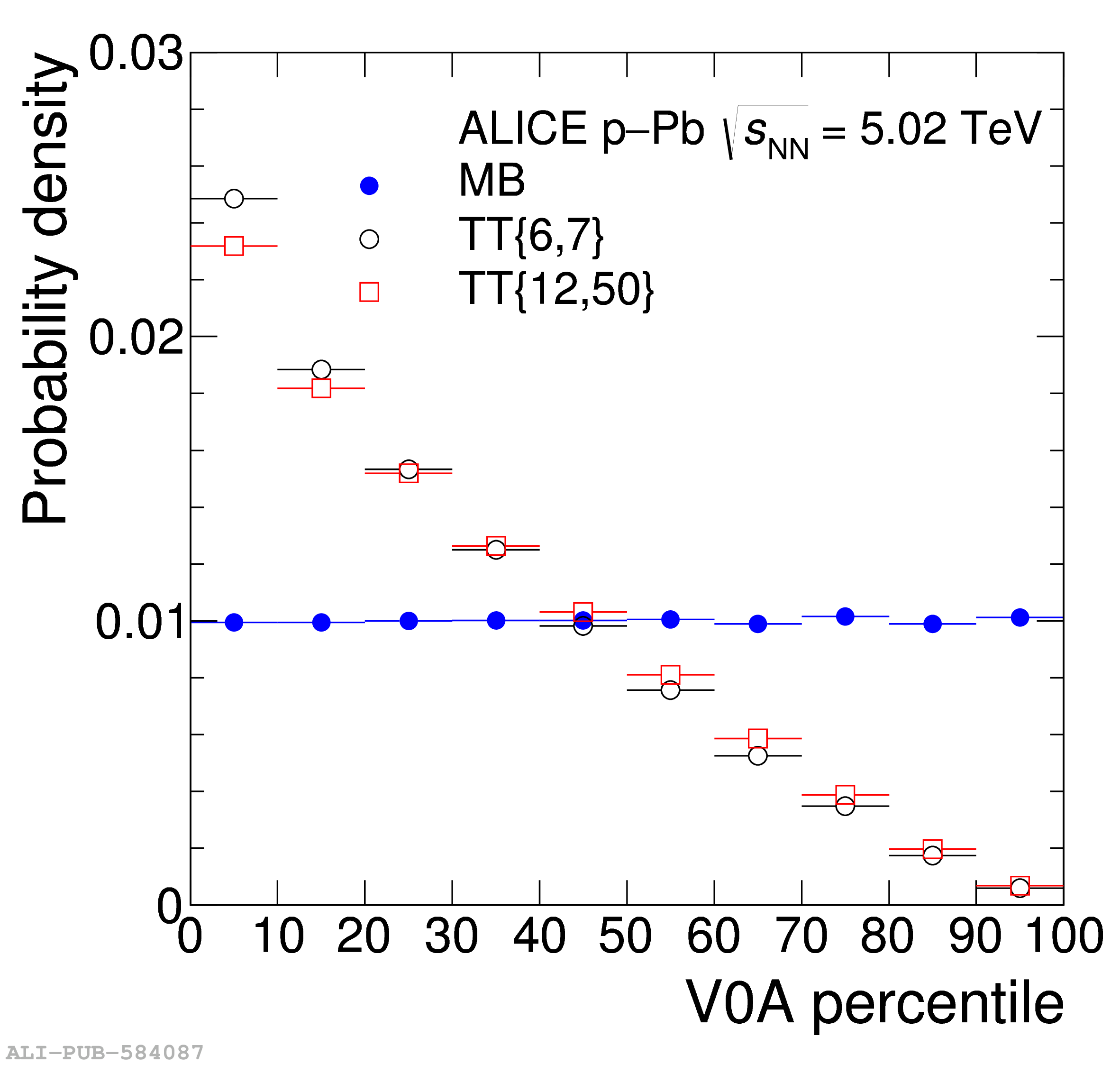
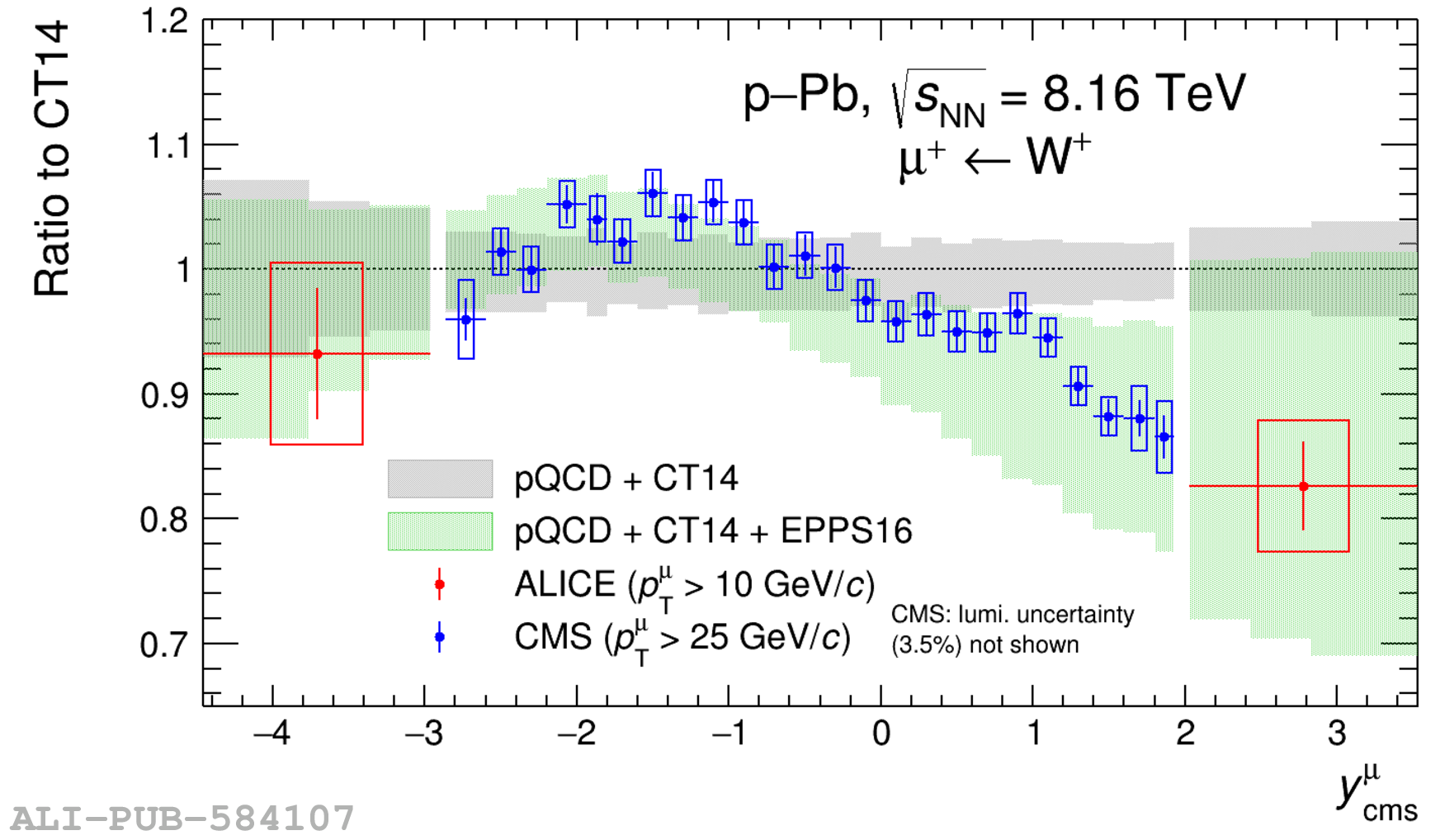
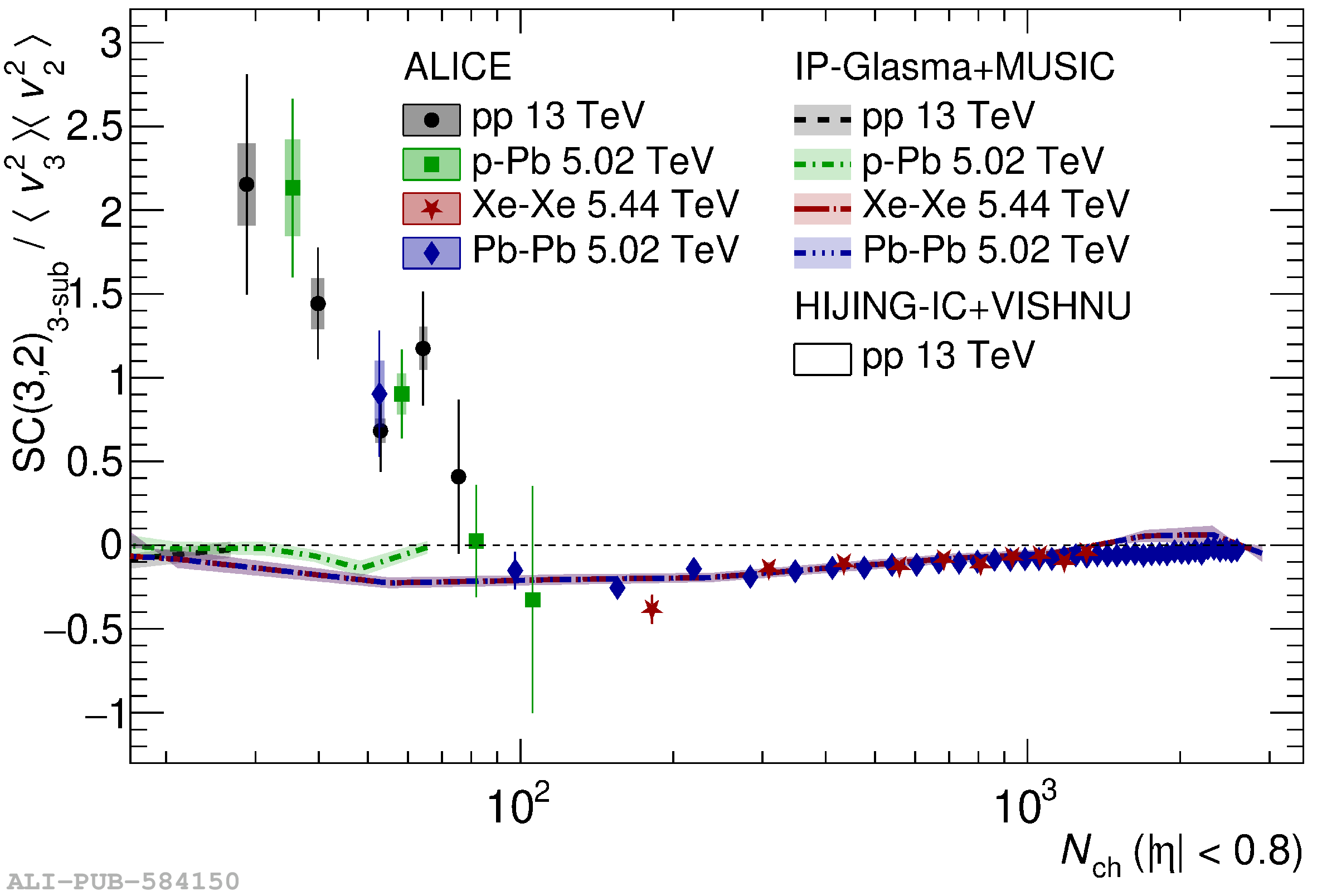
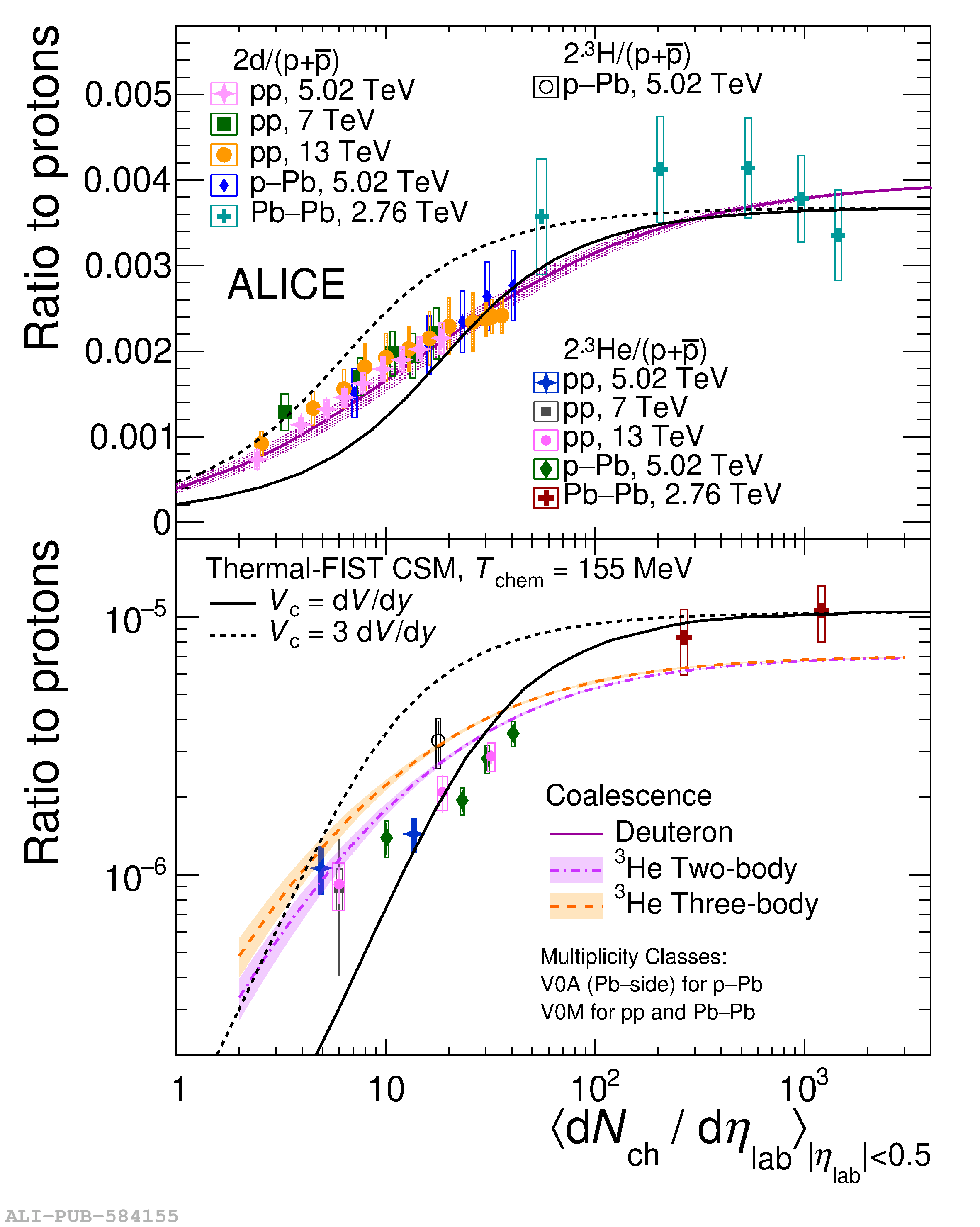
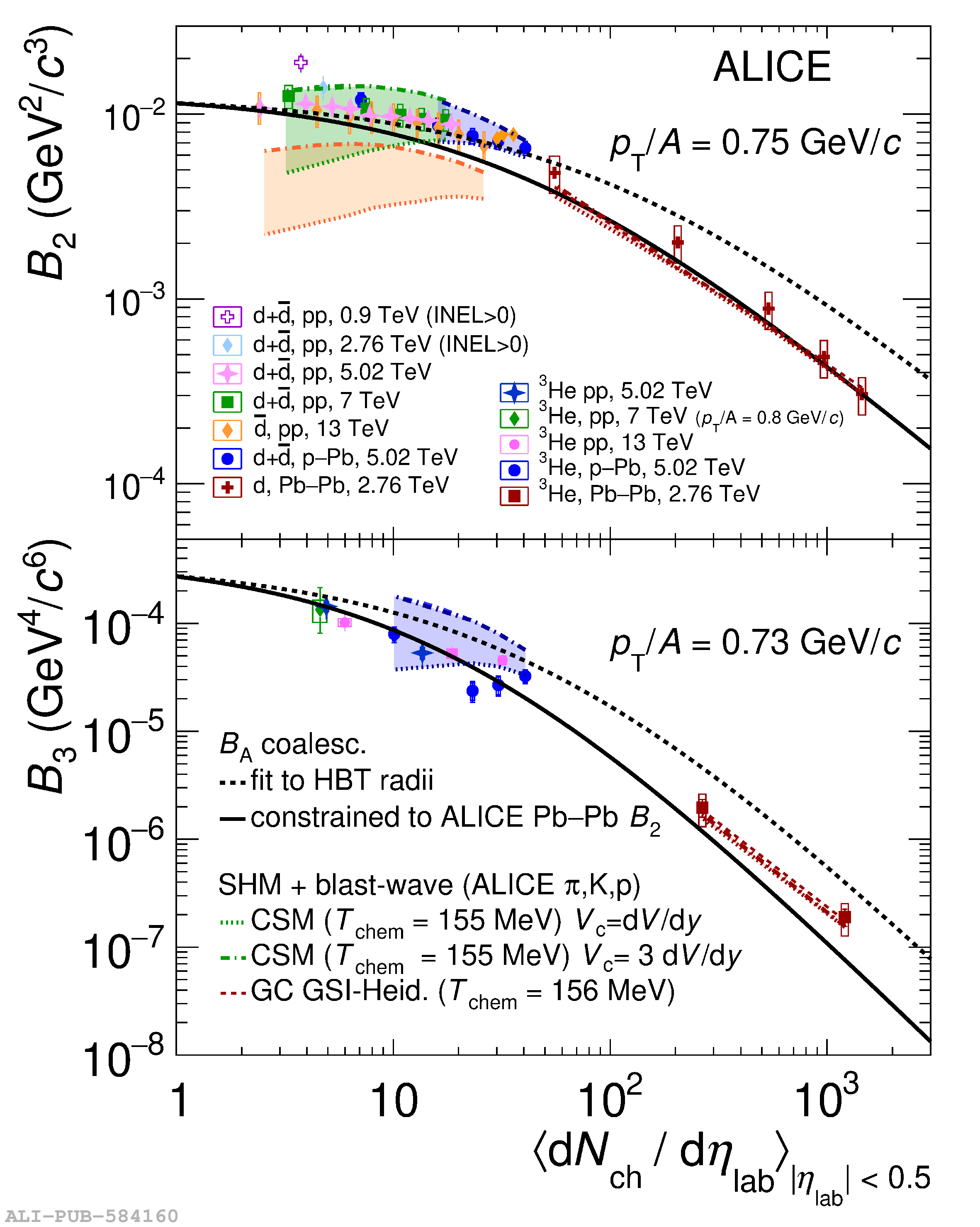
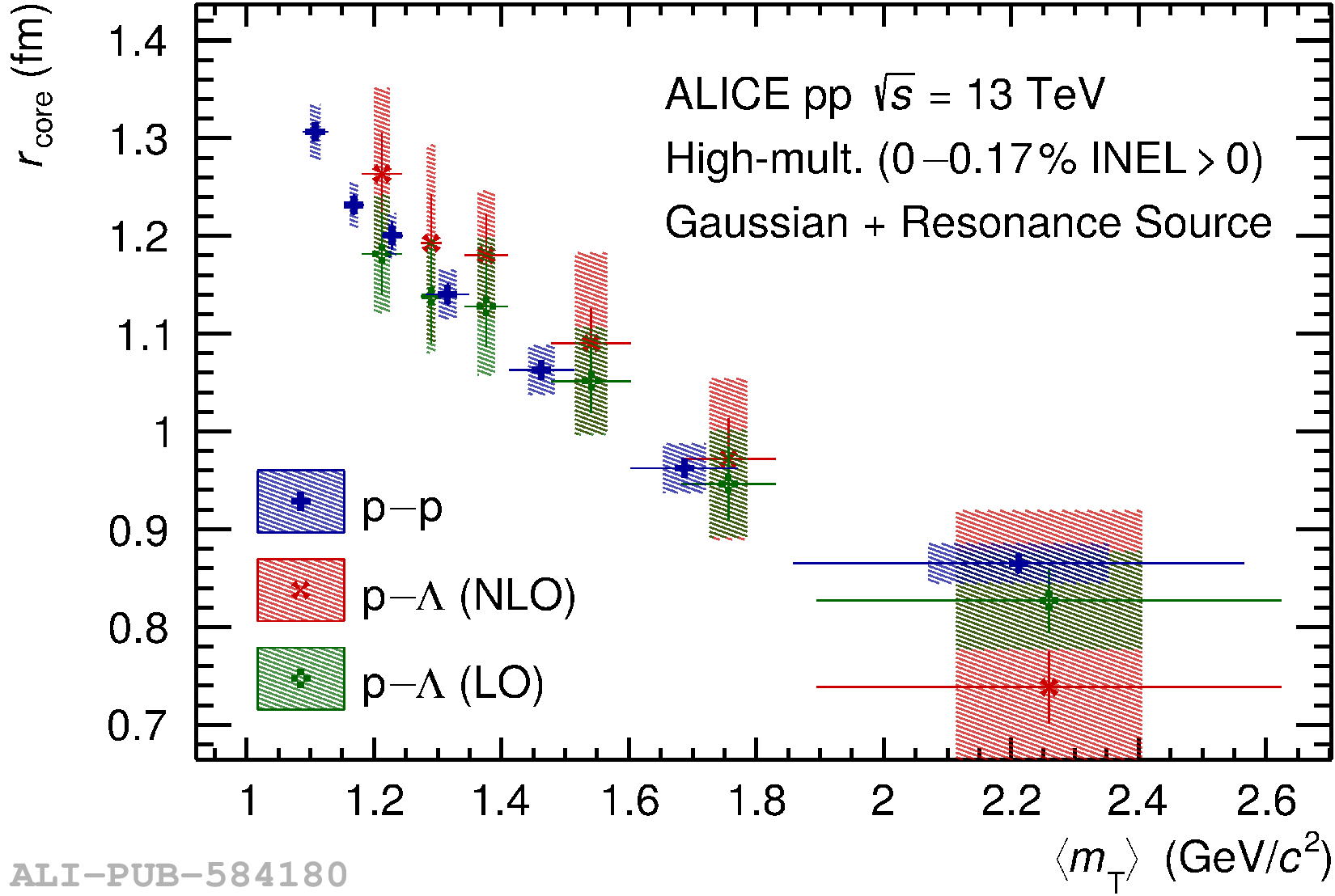
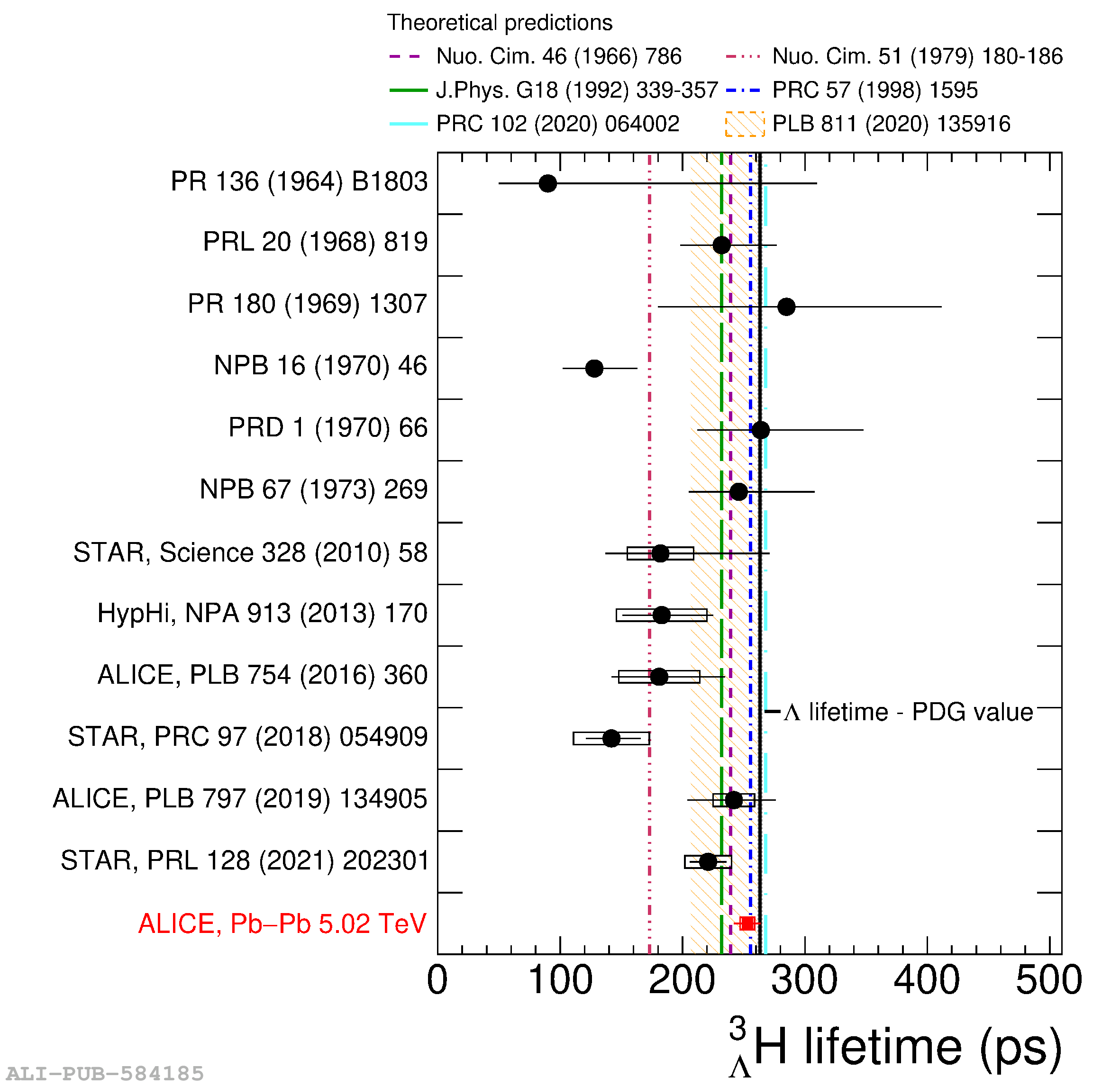
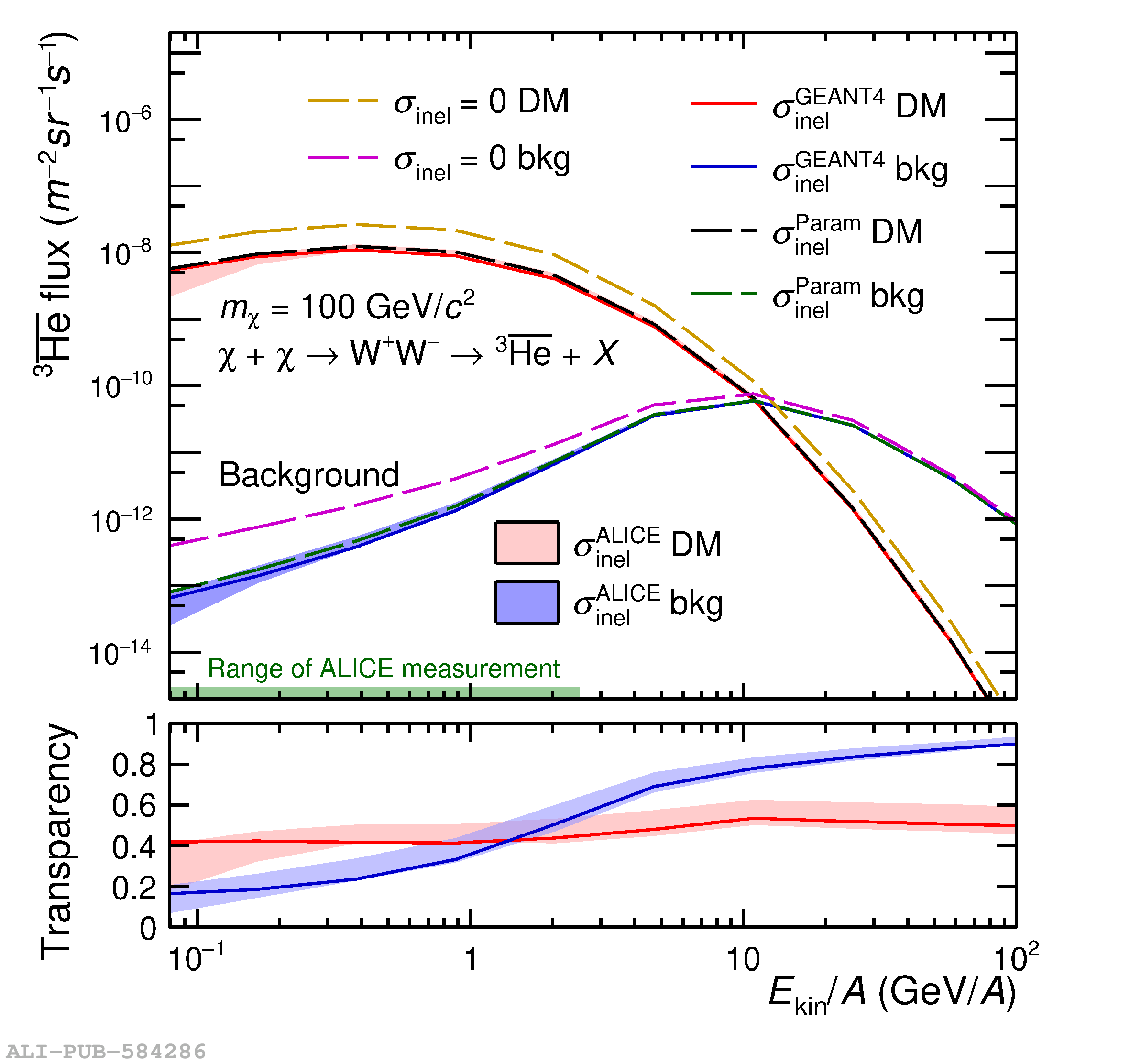
The ALICE experiment was proposed in 1993, to study strongly-interacting matter at extreme energy densities and temperatures. This proposal entailed a comprehensive investigation of nuclear collisions at the LHC. Its physics programme initially focused on the determination of the properties of the quark-gluon plasma (QGP), a deconfined state of quarks and gluons, created in such collisions. The ALICE physics programme has been extended to cover a broader ensemble of observables related to Quantum Chromodynamics (QCD), the theory of strong interactions. The experiment has studied Pb-Pb, Xe-Xe, p-Pb and pp collisions in the multi-TeV centre of mass energy range, during the Run 1-2 data-taking periods at the LHC (2009-2018). The aim of this review is to summarise the key ALICE physics results in this endeavor, and to discuss their implications on the current understanding of the macroscopic and microscopic properties of strongly-interacting matter at the highest temperatures reached in the laboratory. It will review the latest findings on the properties of the QGP created by heavy-ion collisions at LHC energies, and describe the surprising QGP-like effects in pp and p-Pb collisions. Measurements of few-body QCD interactions, and their impact in unraveling the structure of hadrons and hadronic interactions, will be discussed. ALICE results relevant for physics topics outside the realm of QCD will also be touched upon. Finally, prospects for future measurements with the ALICE detector in the context of its planned upgrades will also be briefly described.
Eur. Phys. J. C 84 (2024) 813
e-Print: arXiv:2211.04384 | PDF | inSPIRE
CERN-EP-2022-227
Figure group