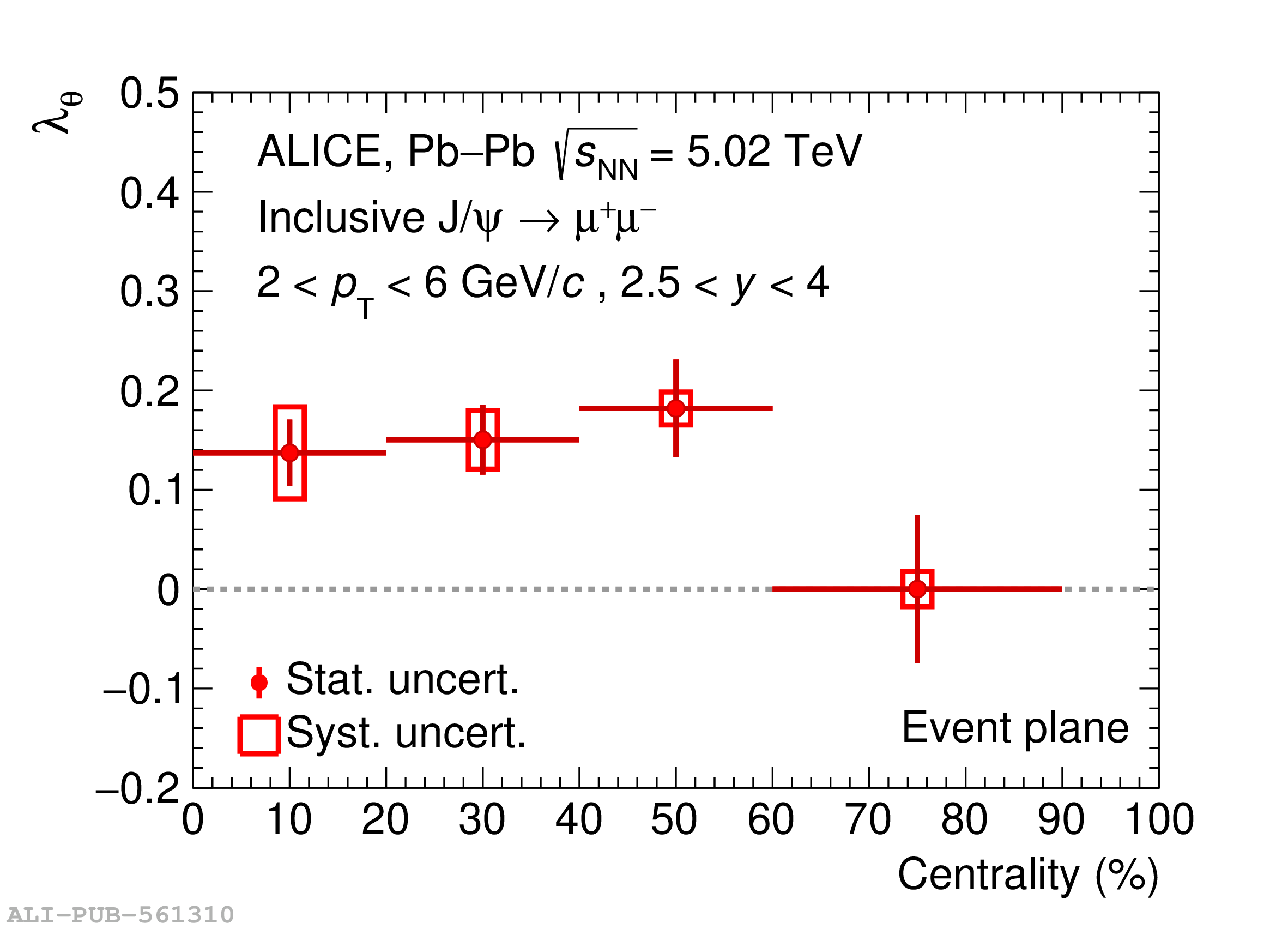
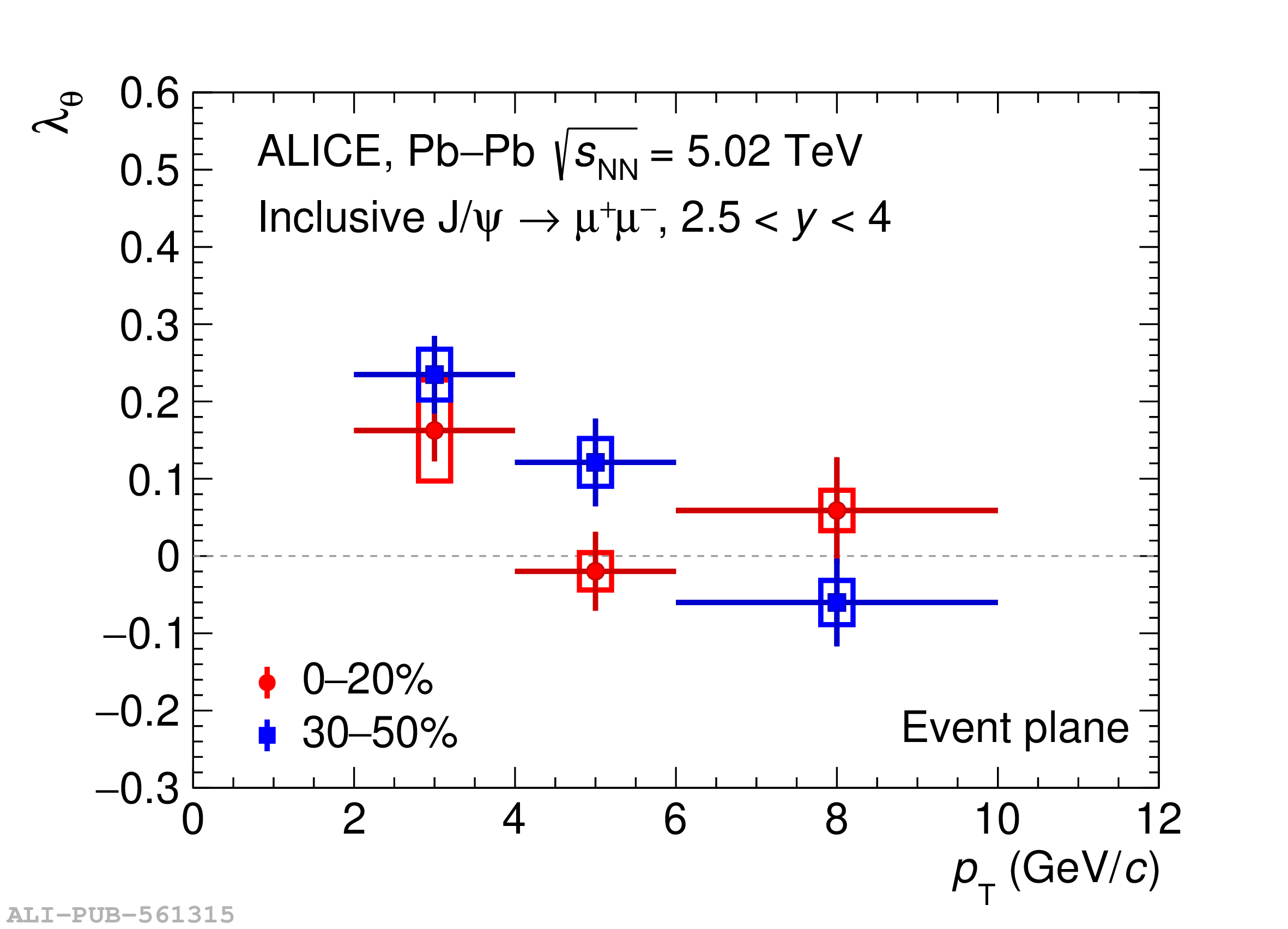
We study the polarization of inclusive J/$\psi$ produced in Pb$-$Pb collisions at $\sqrt{s_{\rm NN}}=5.02$ TeV at the LHC in the dimuon channel, via the measurement of the angular distribution of its decay products. We perform the study in the rapidity region $2.5<~y<~4$, for three transverse momentum intervals ($2<~p_{\rm T}<~4$, $4<~p_{\rm T}<~6$, $6<~p_{\rm T}<~10$ GeV/$c$) and as a function of the centrality of the collision for $2<~p_{\rm T}<~6$ GeV/c. For the first time, the polarization is measured with respect to the event plane of the collision, by considering the angle between the positive-charge decay muon in the J/$\psi$ rest frame and the axis perpendicular to the event-plane vector in the laboratory system. A small transverse polarization is measured, with a significance reaching 3.9$\sigma$ at low $p_{\rm T}$ and for intermediate centrality values. The polarization could be connected with the behaviour of the quark$-$gluon plasma, formed in Pb$-$Pb collisions, as a rotating fluid with large vorticity, as well as with the existence of a strong magnetic field in the early stage of its formation.
Phys. Rev. Lett. 131 (2023) 042303
HEP Data
e-Print: arXiv:2204.10171 | PDF | inSPIRE
CERN-EP-2022-066
Figure group