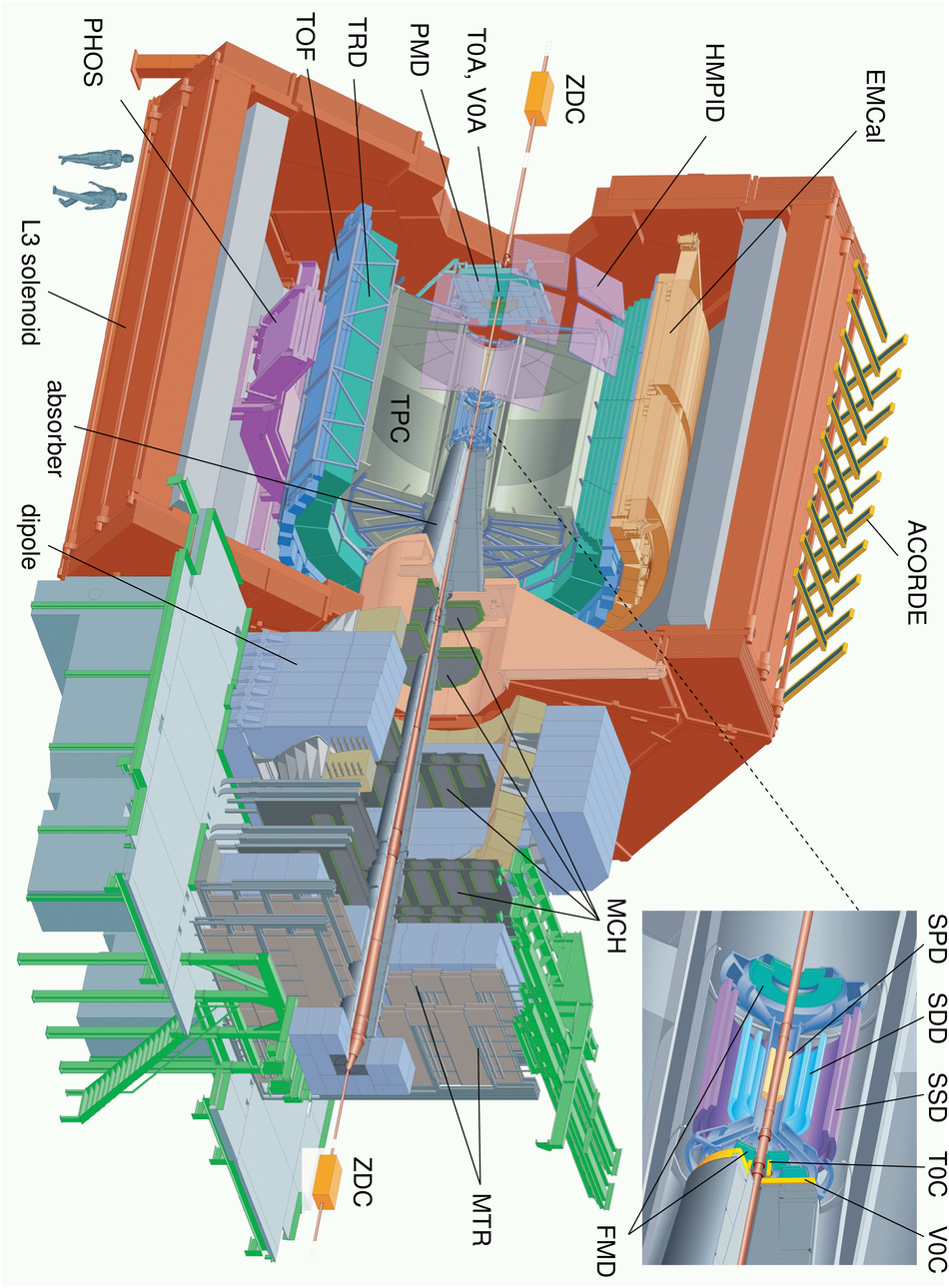
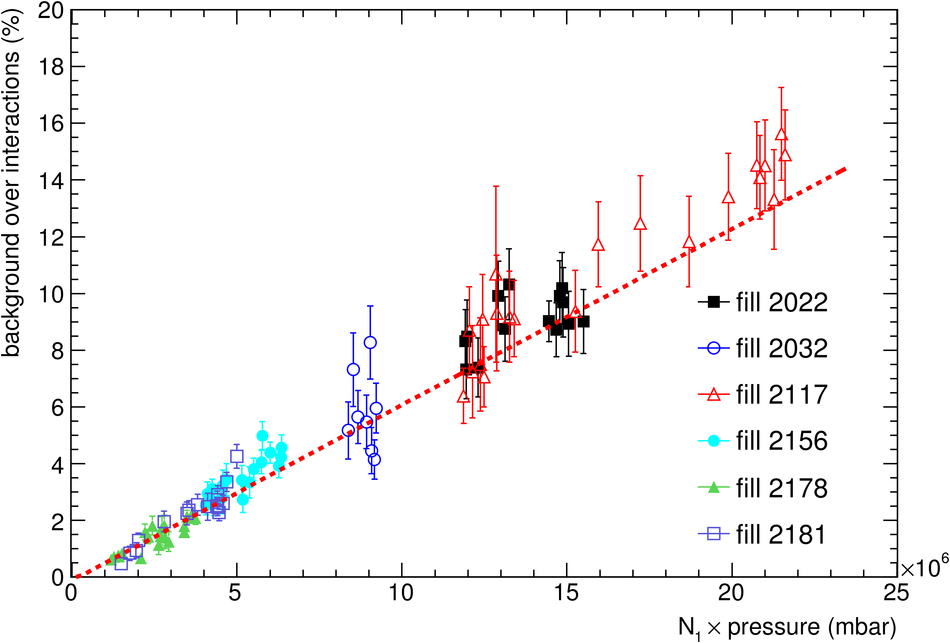
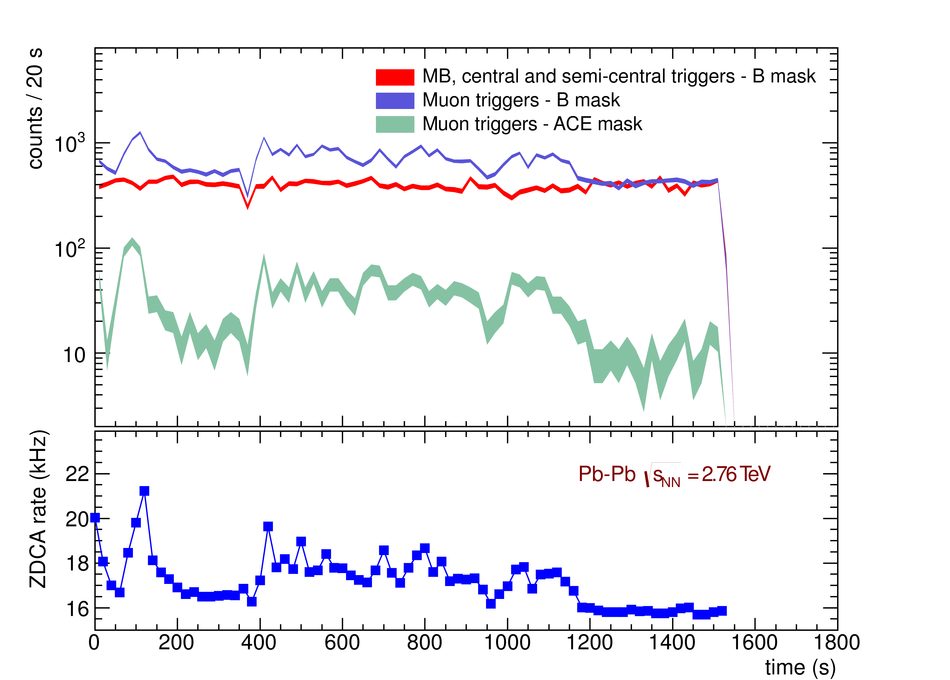
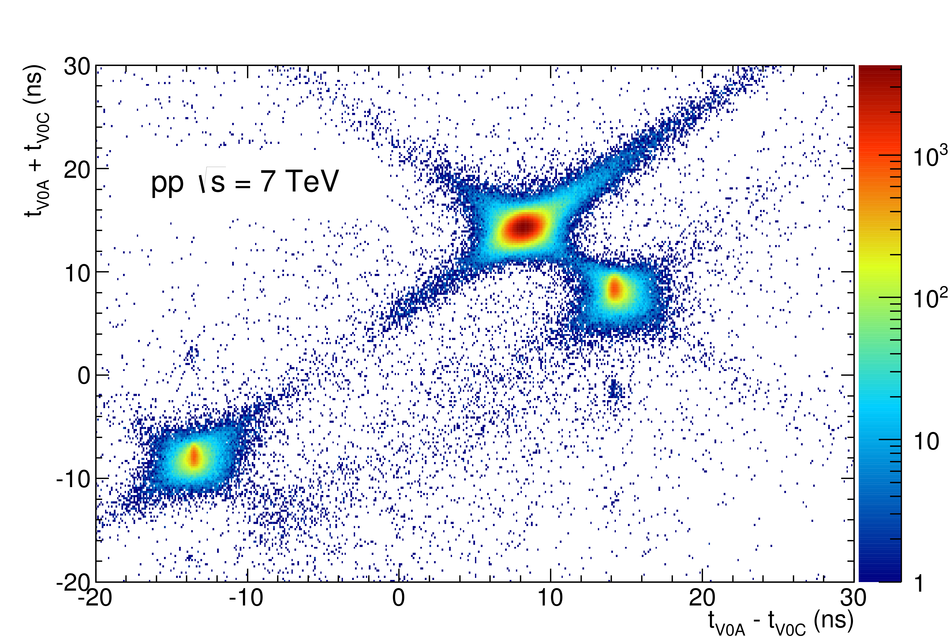
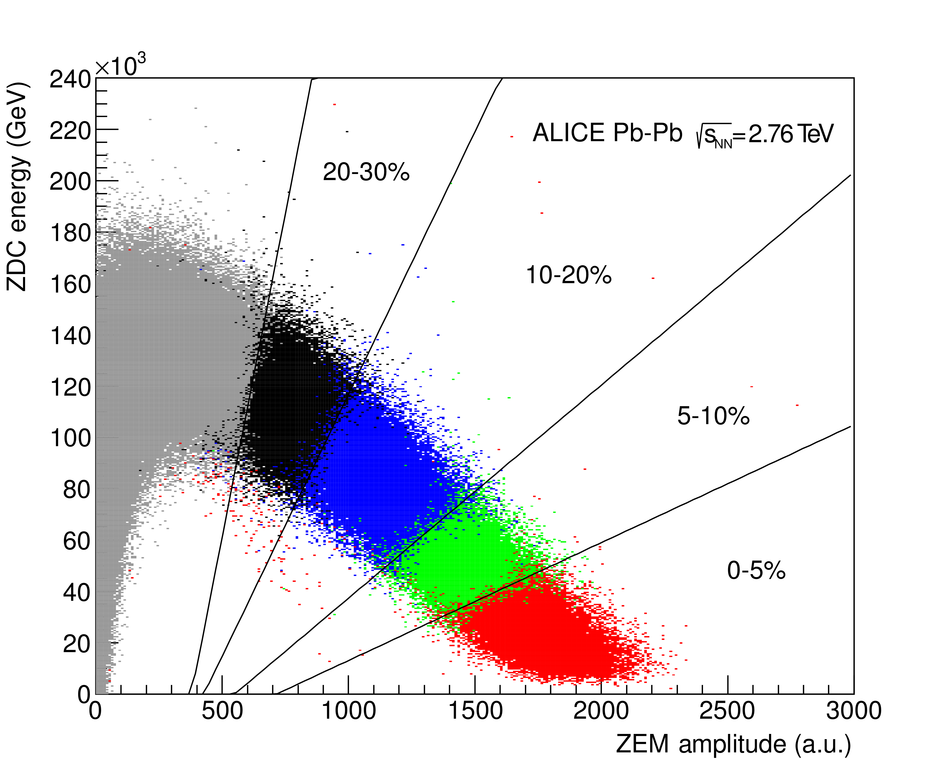
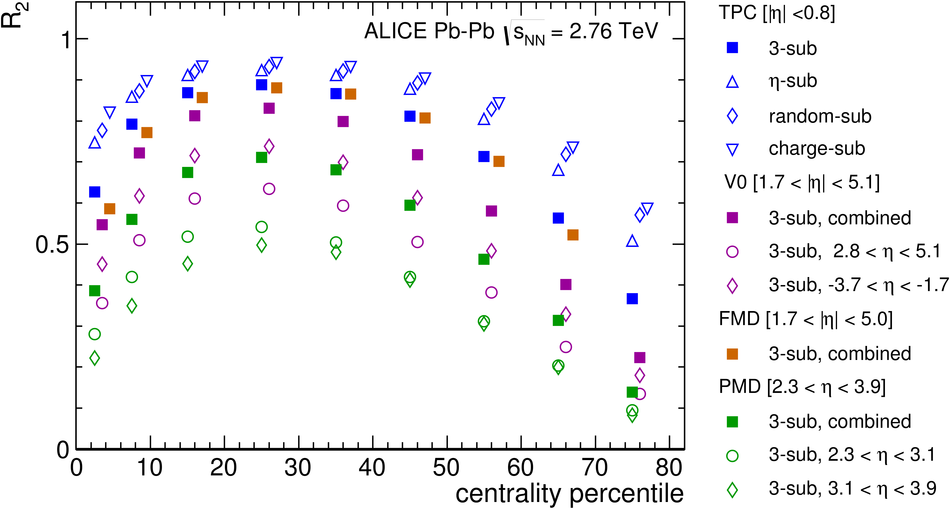
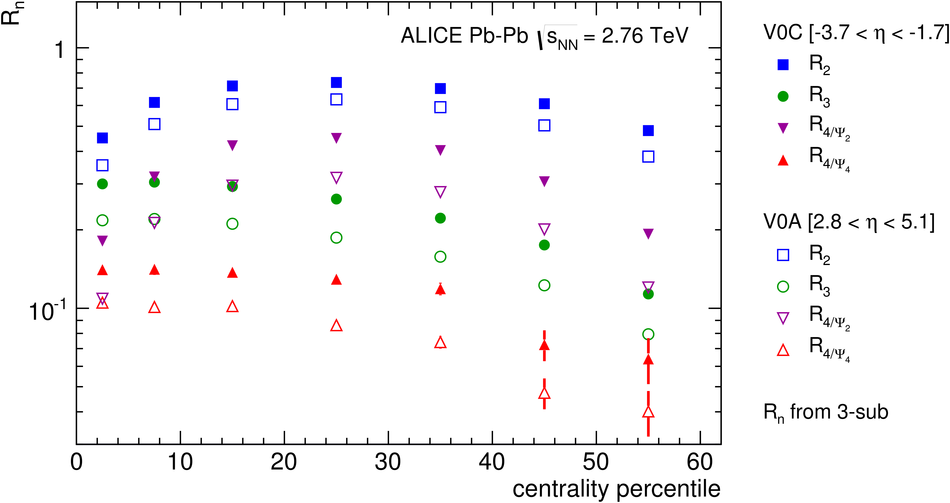
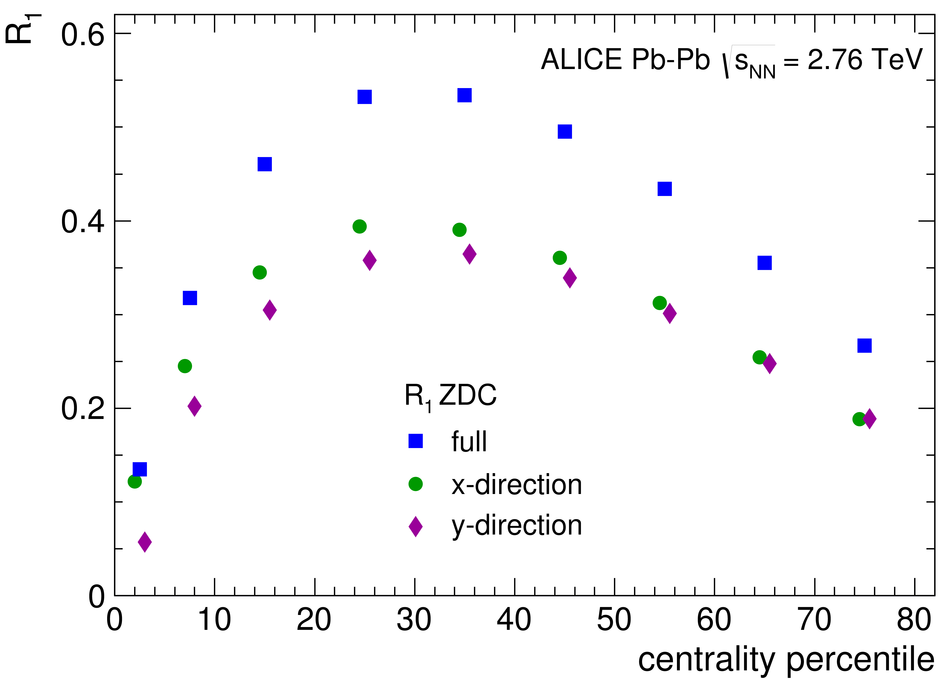
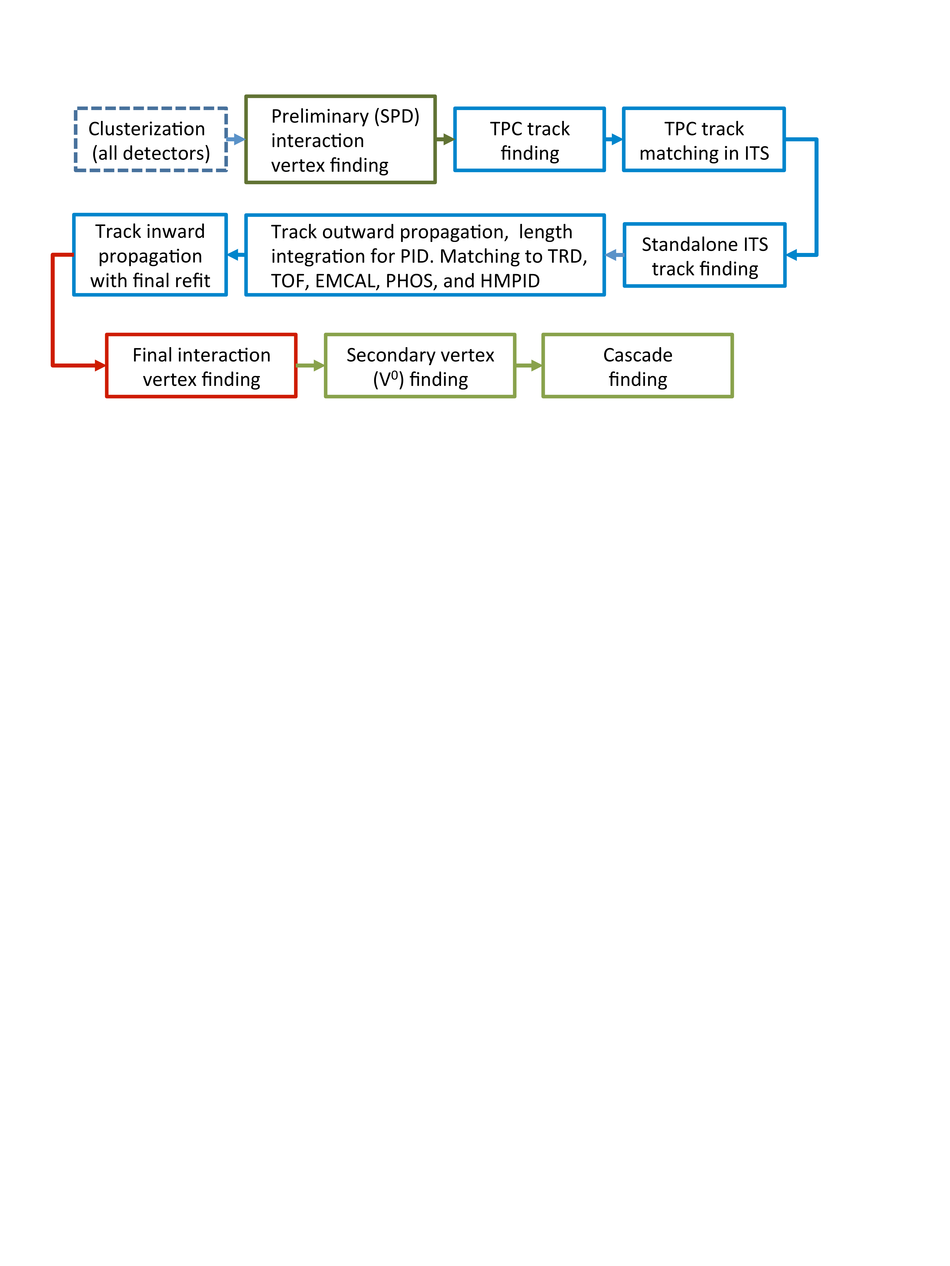
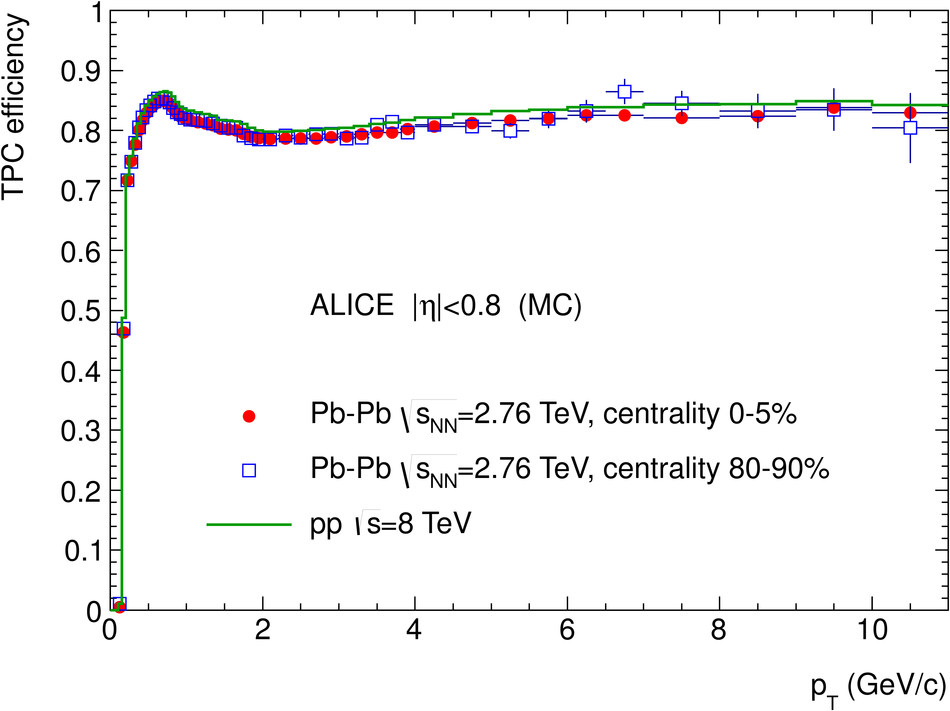
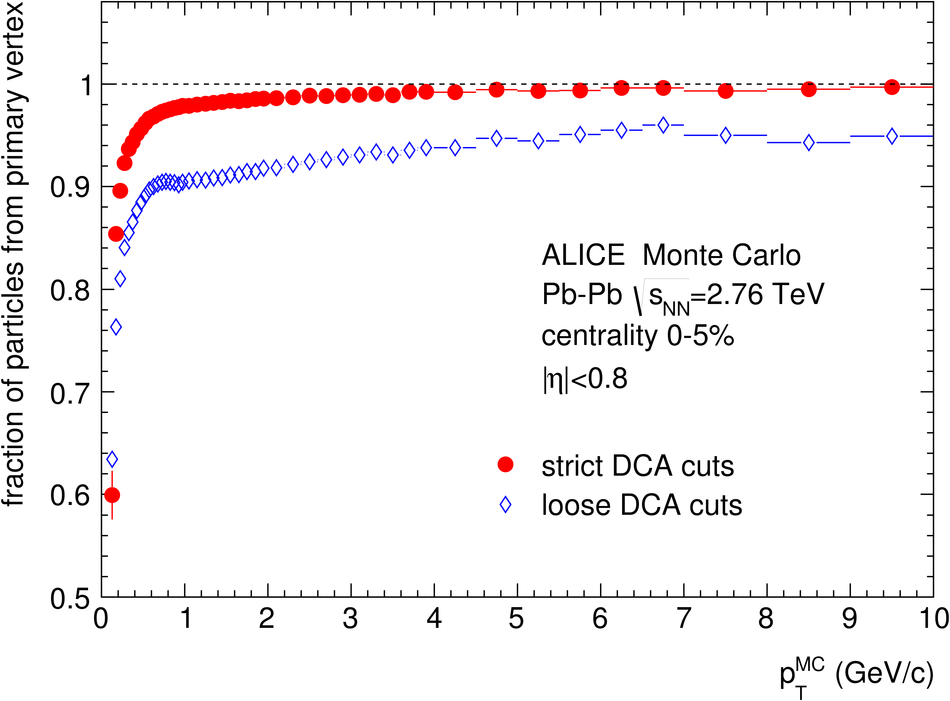
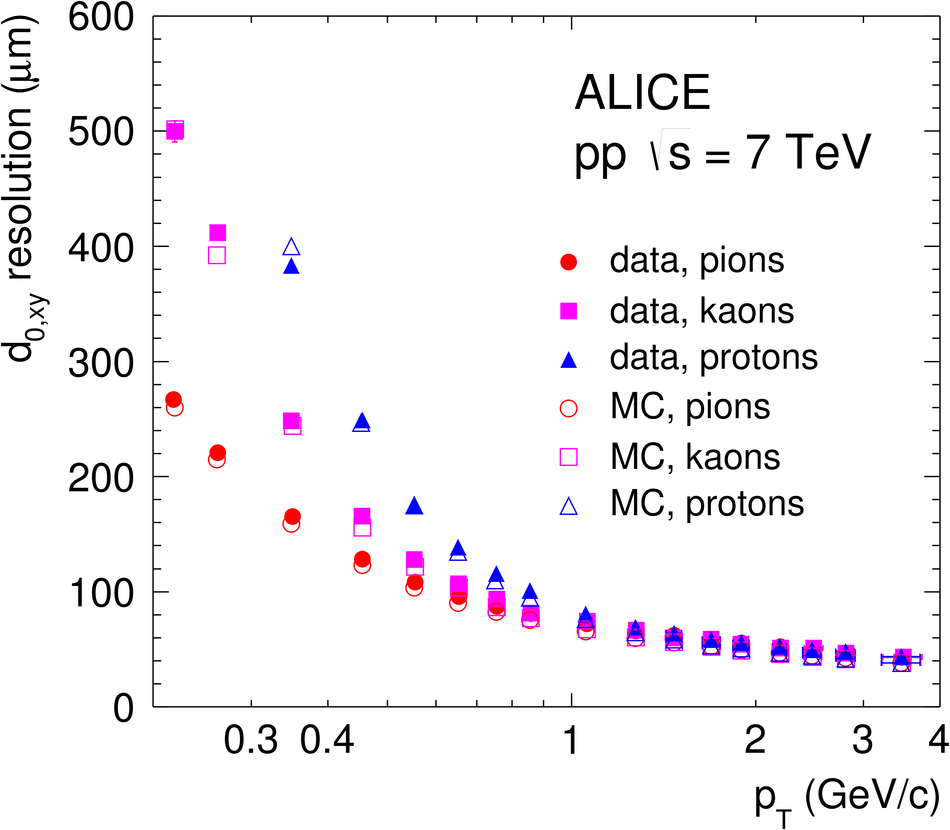
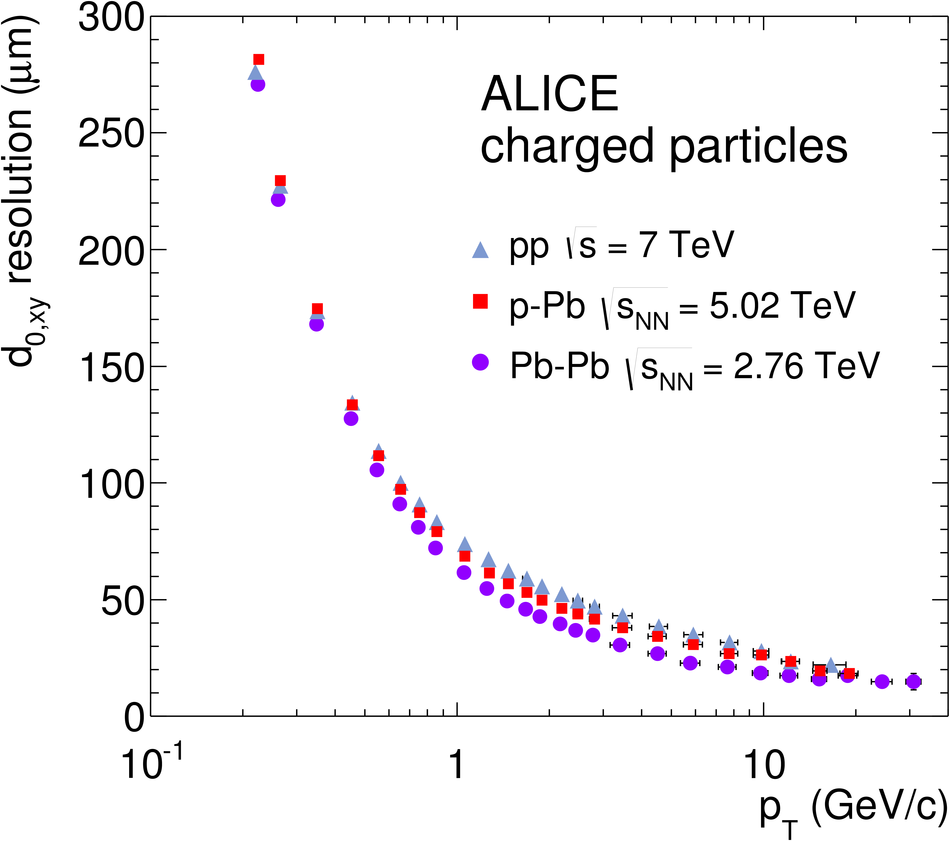
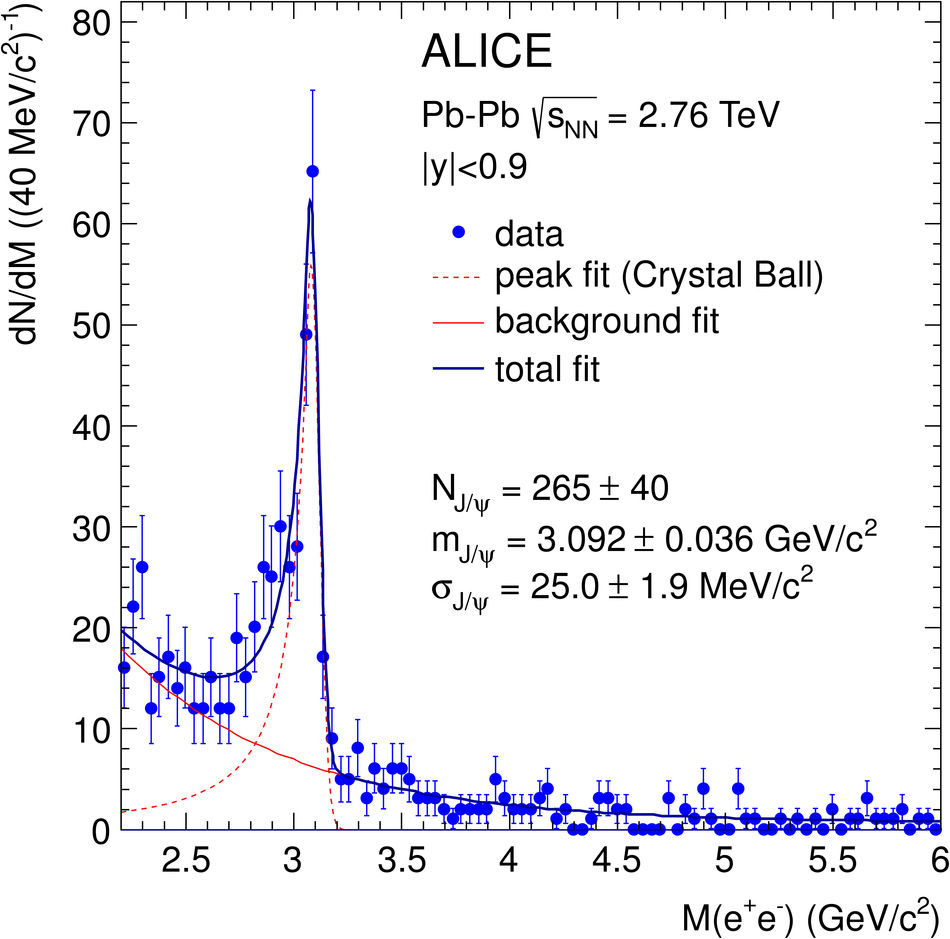
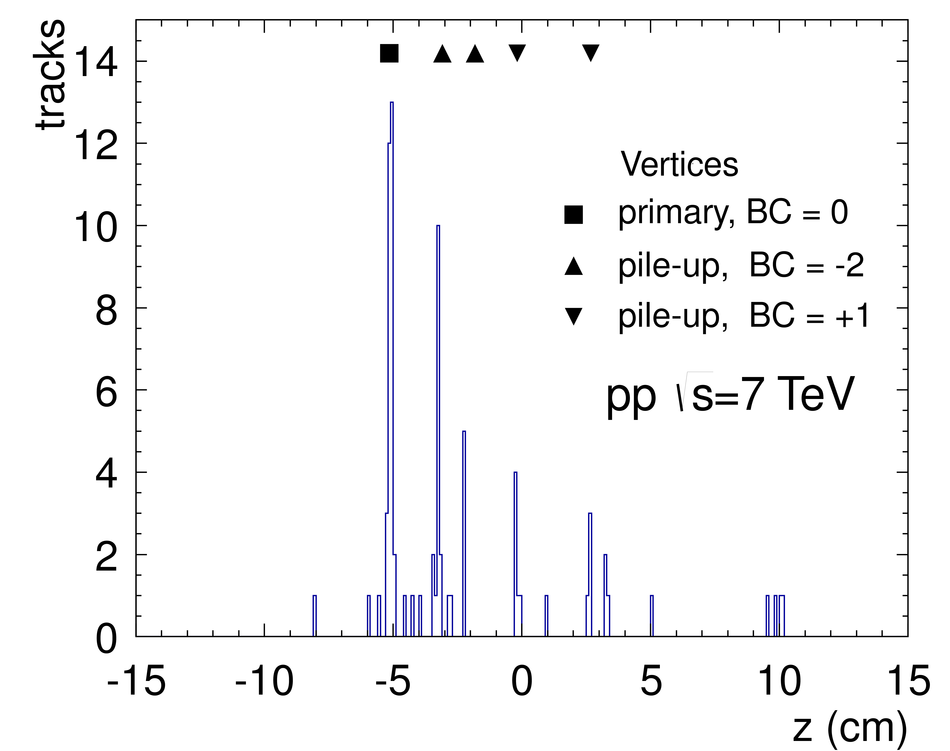
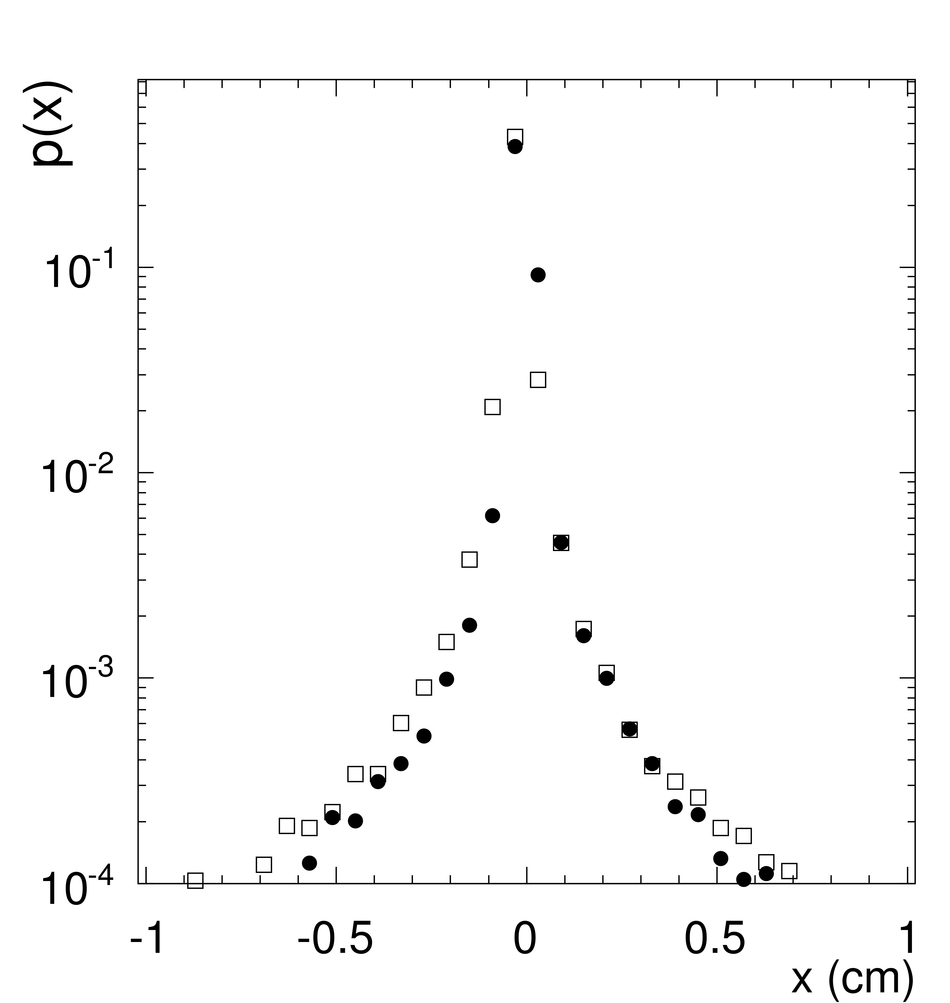
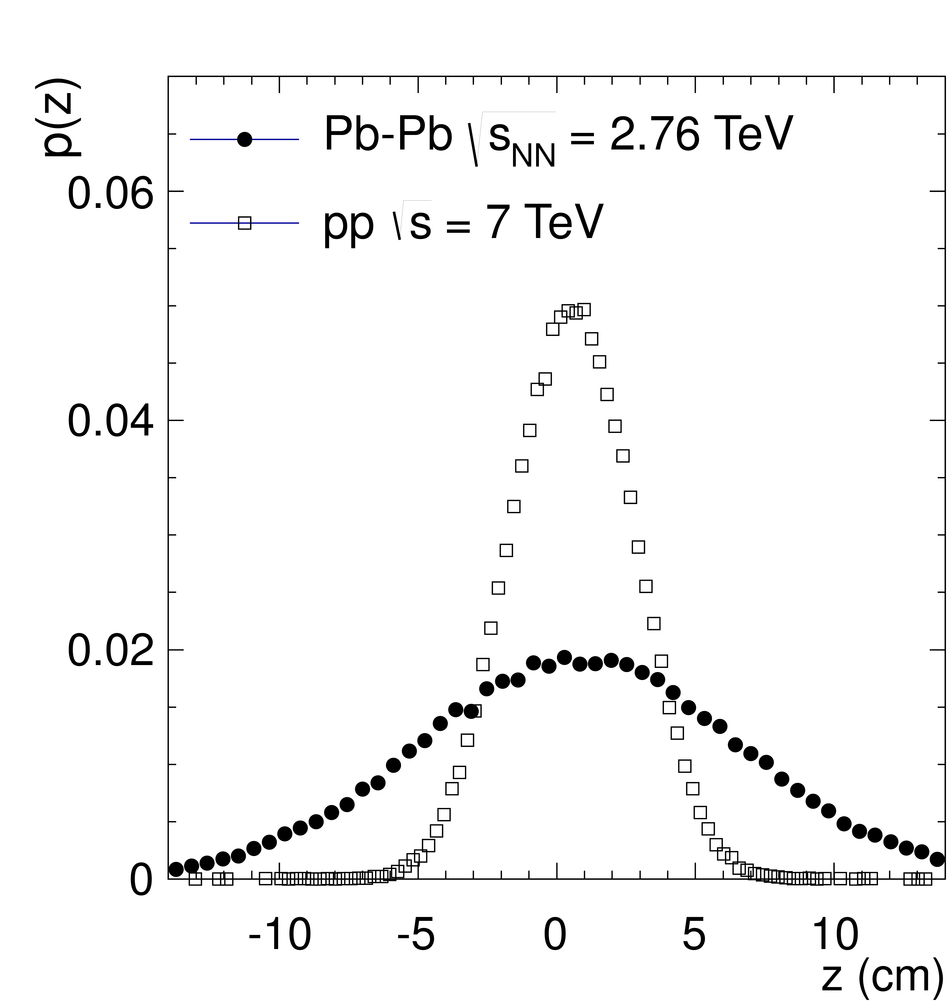
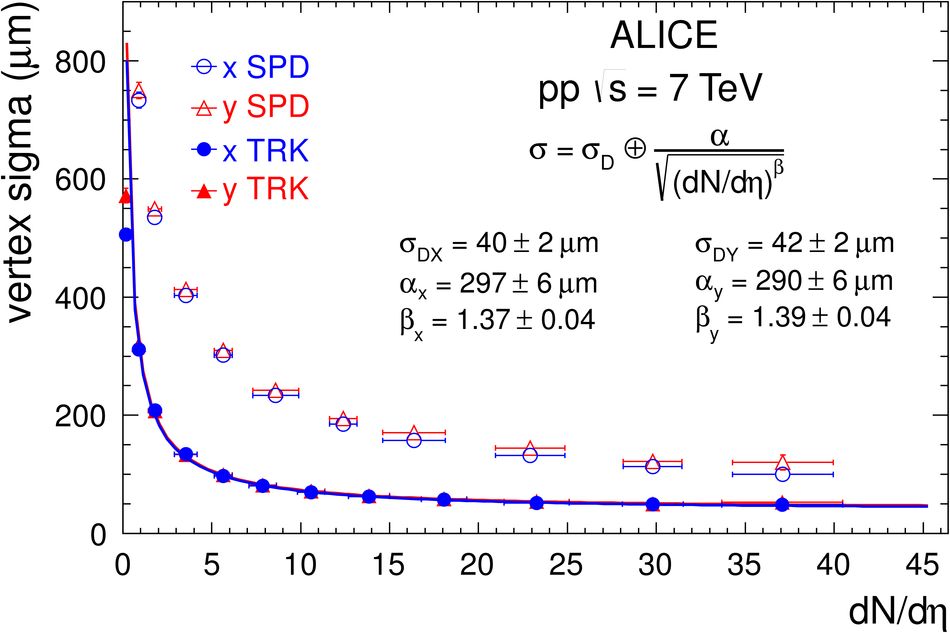
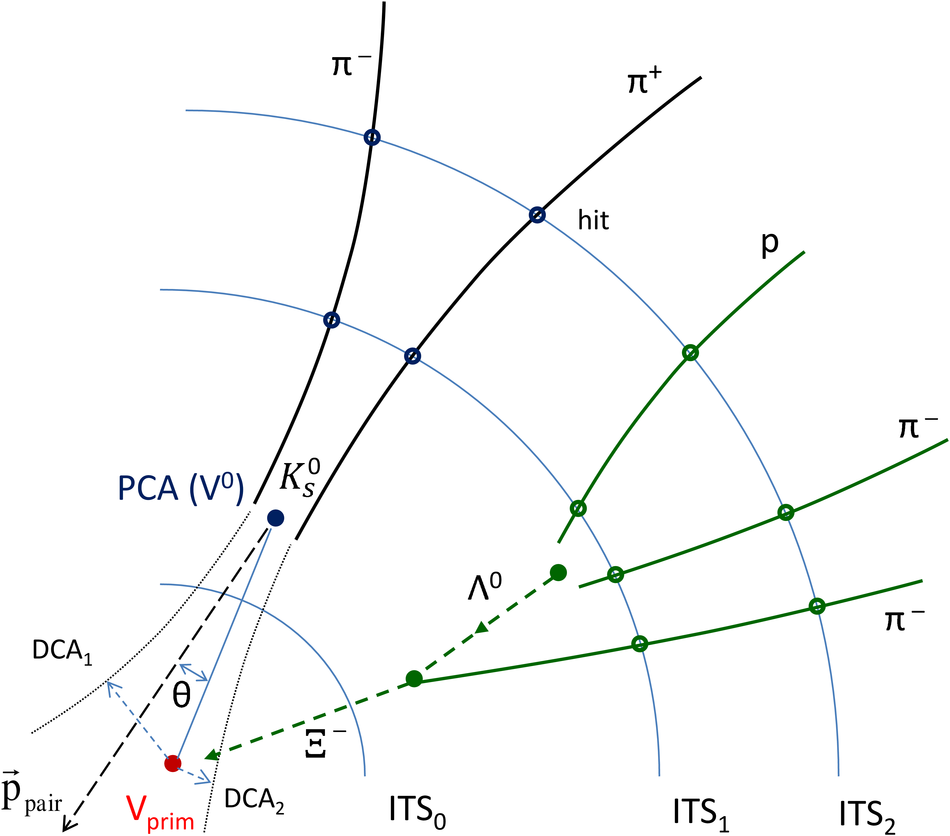
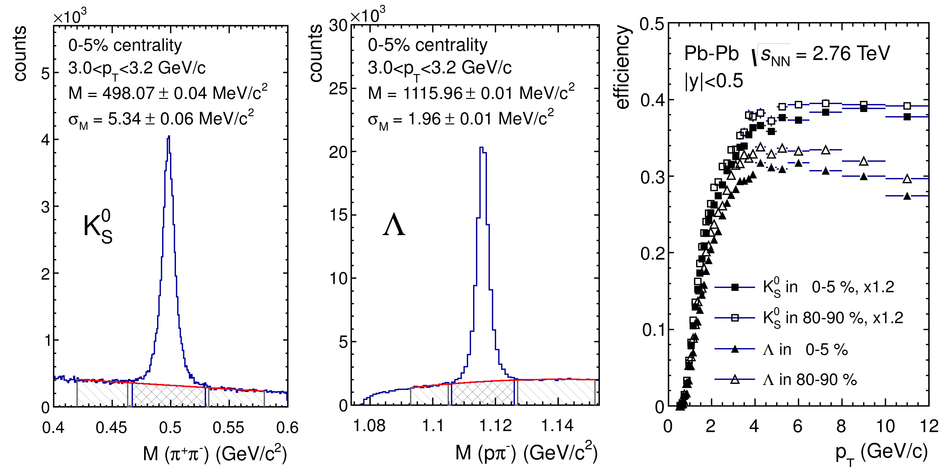
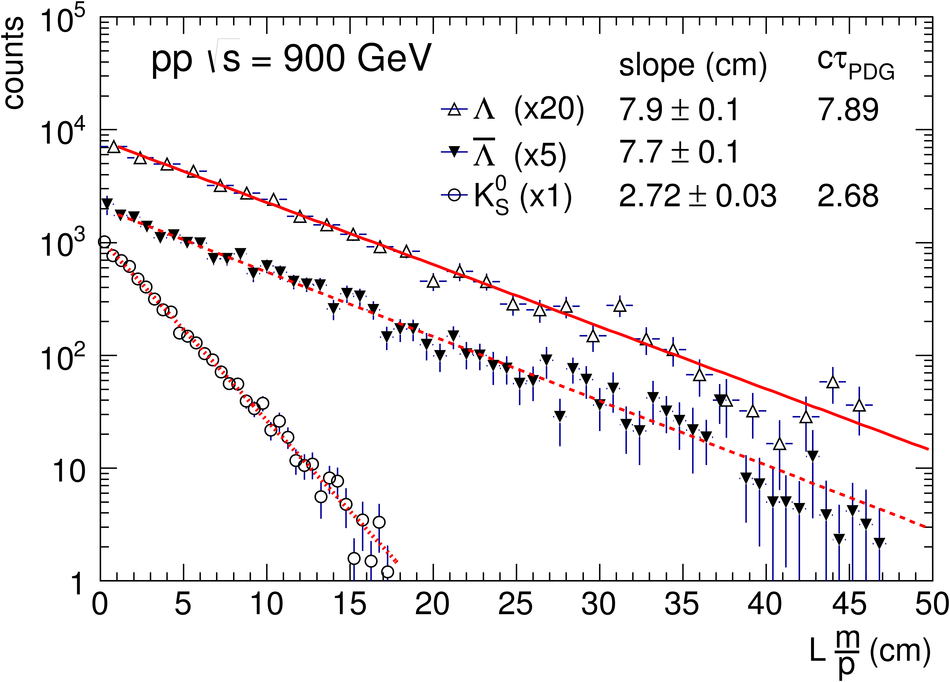
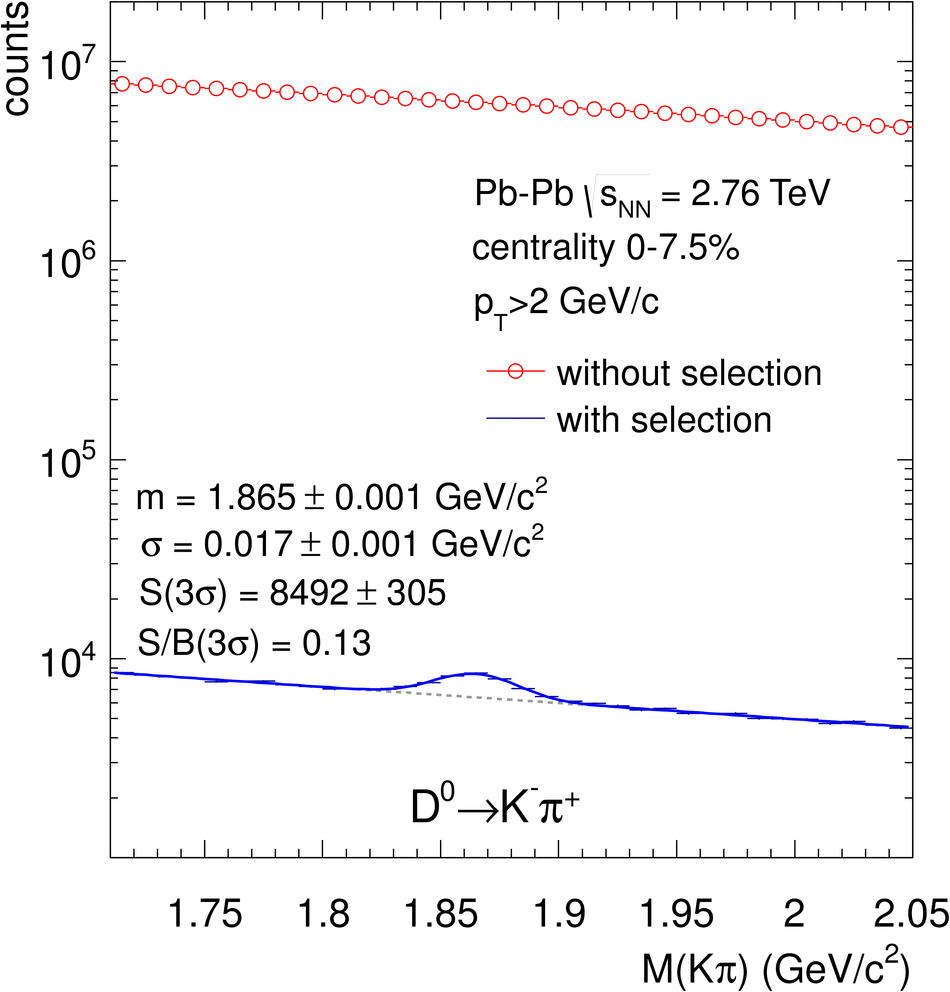
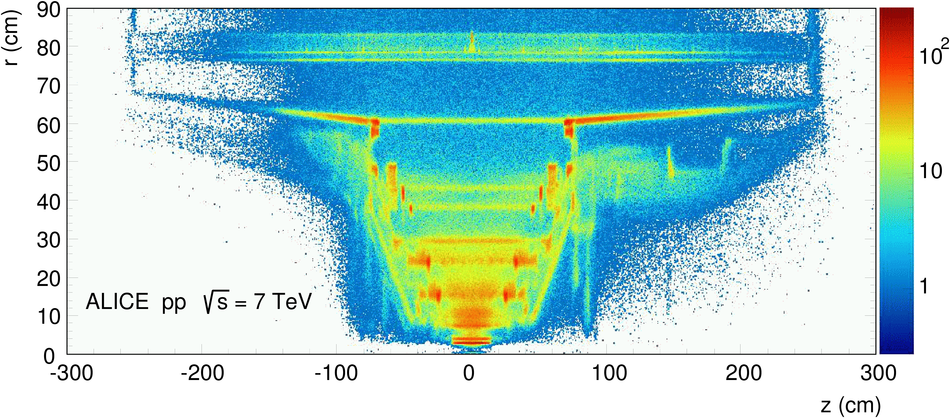
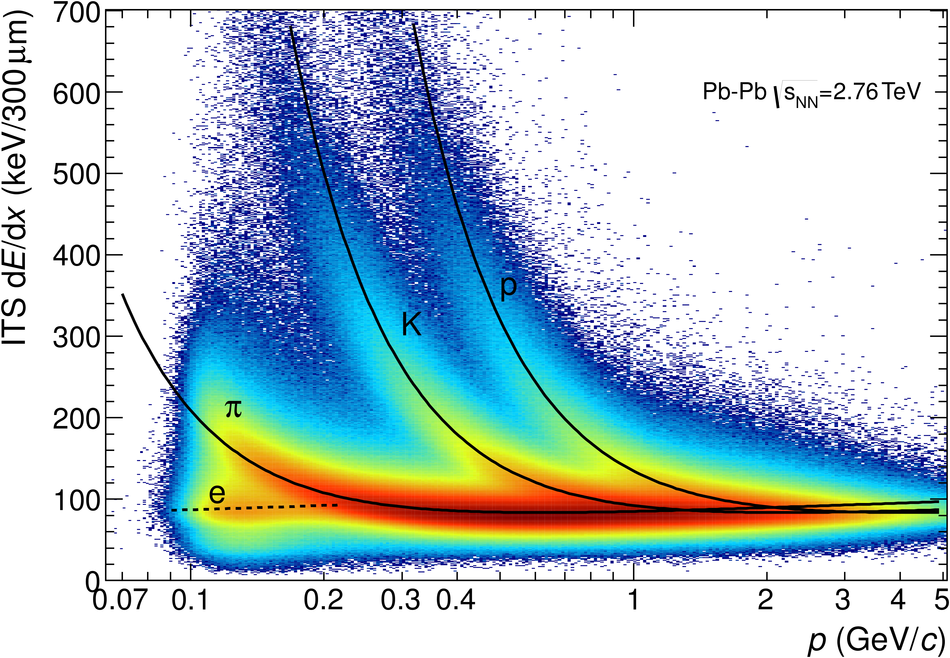
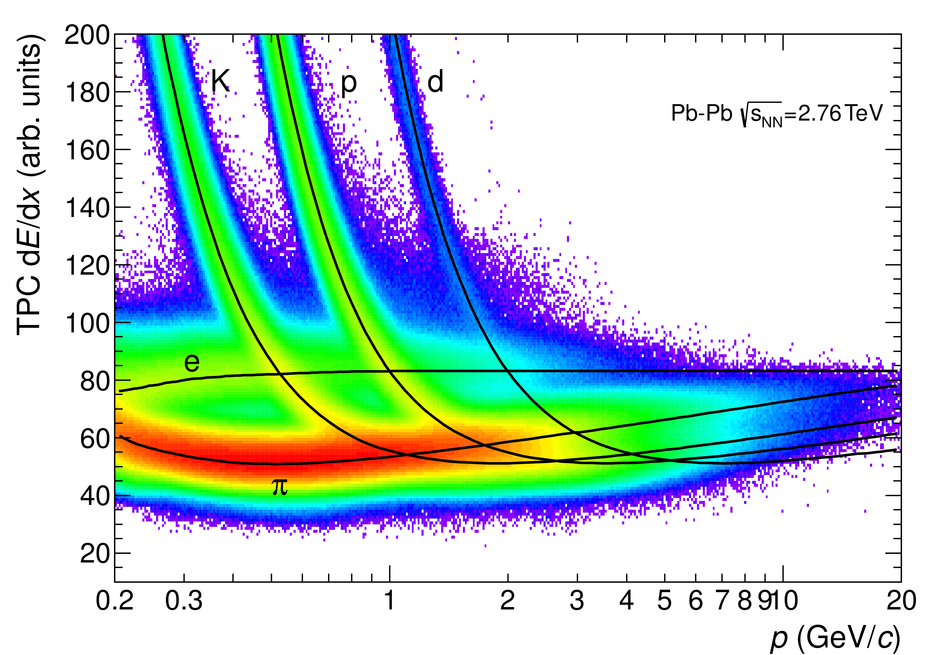
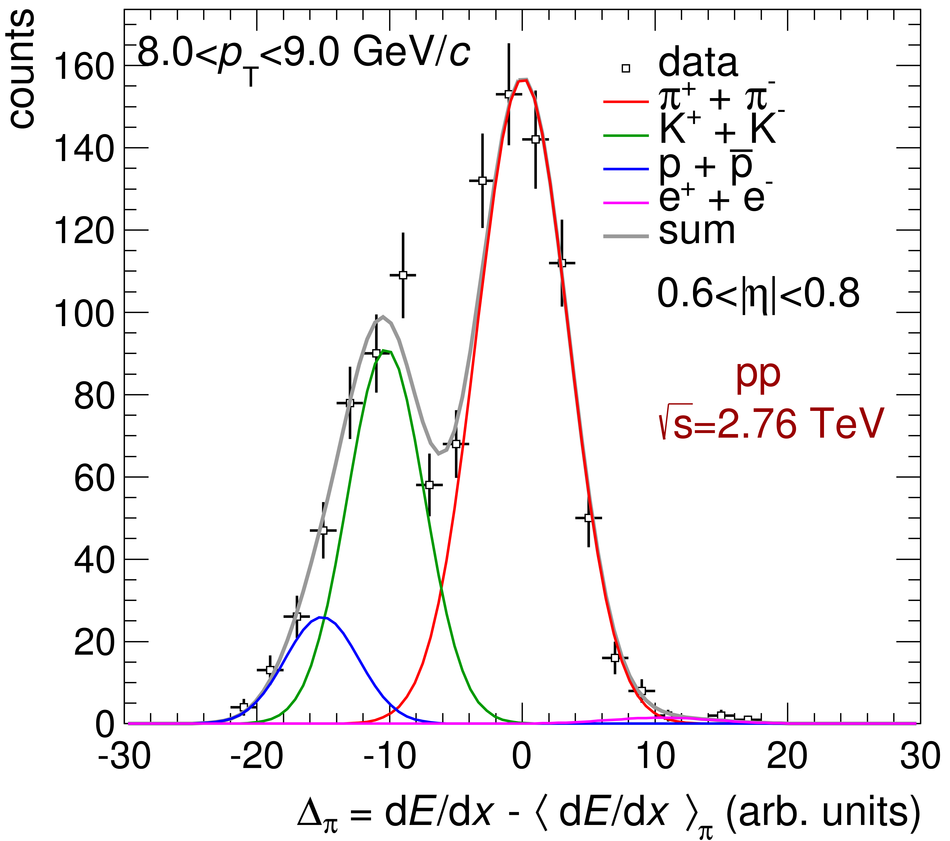
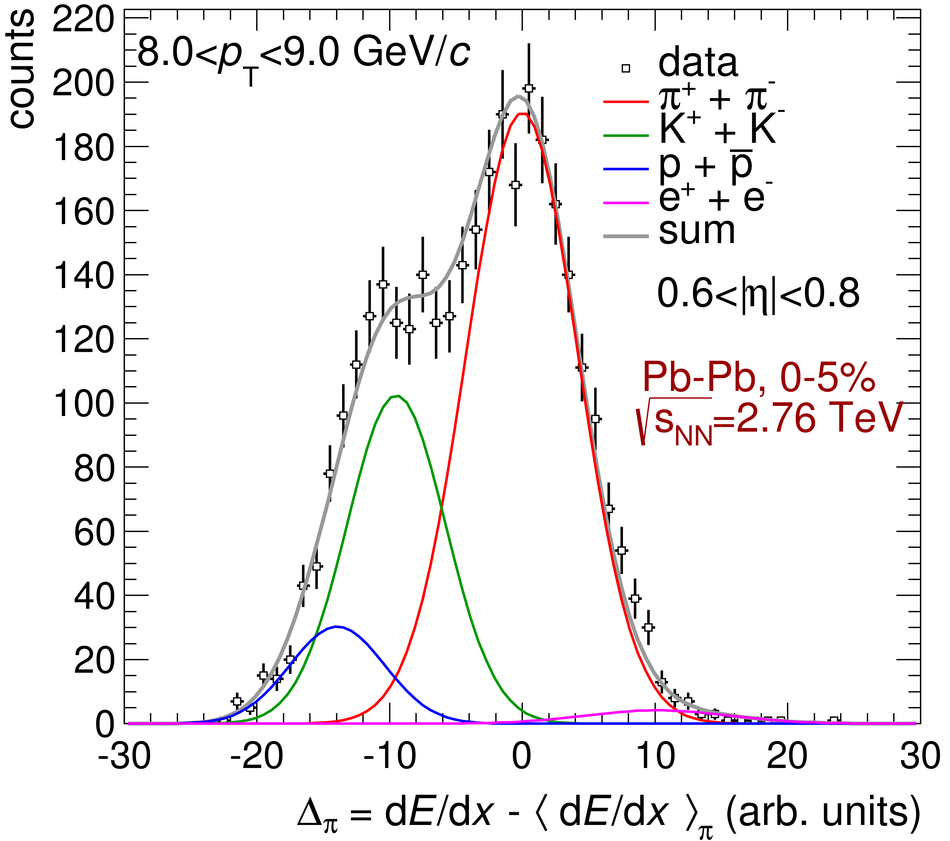
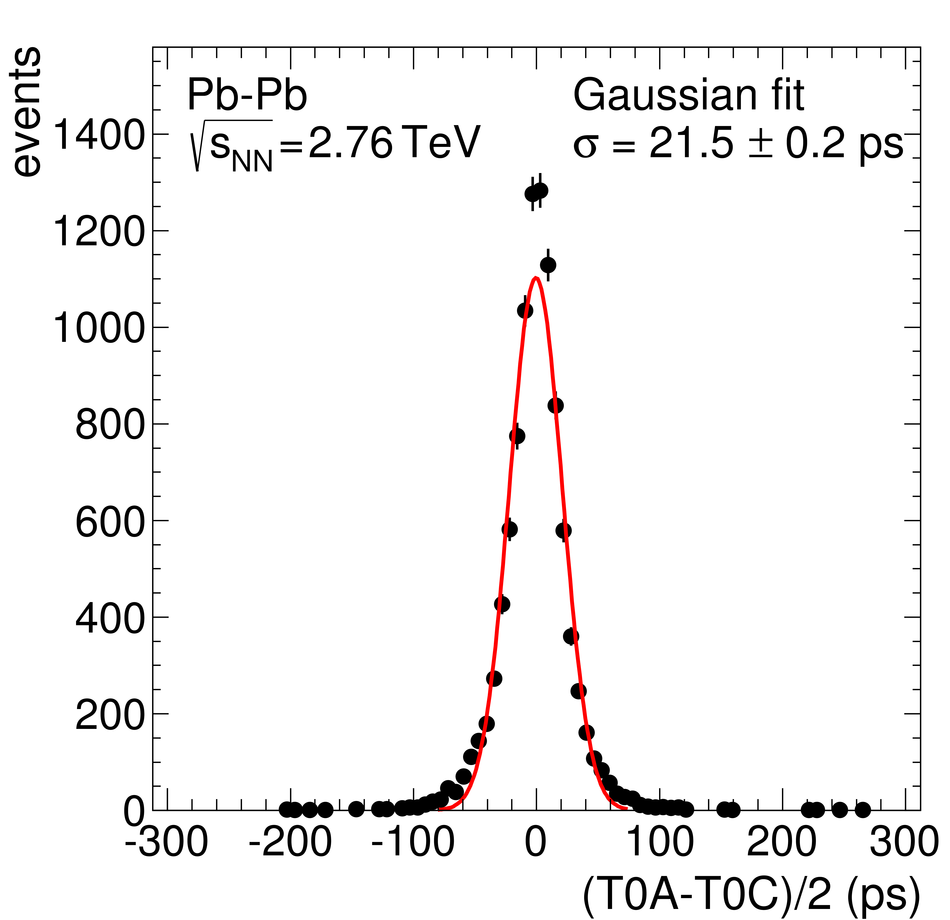
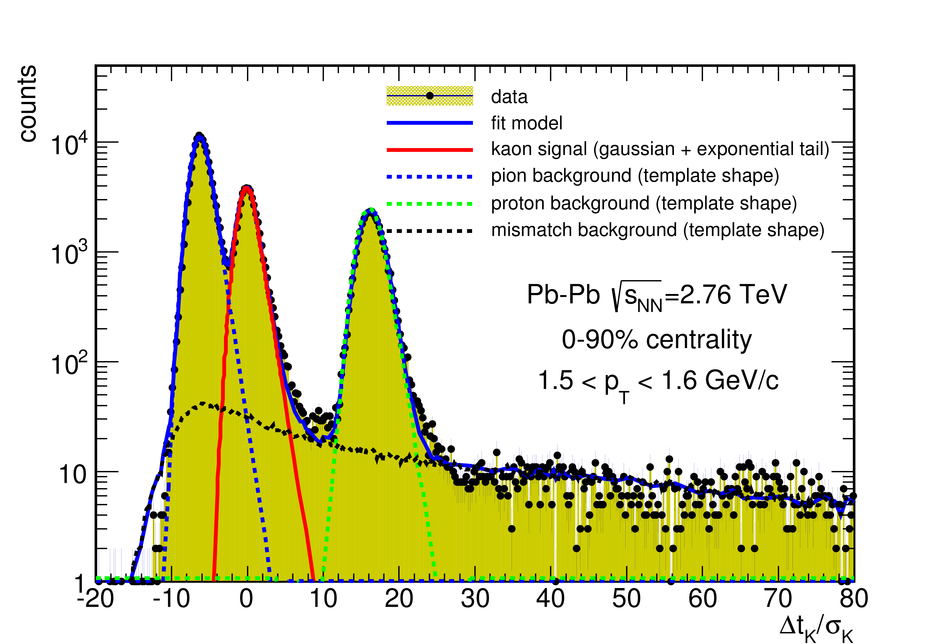
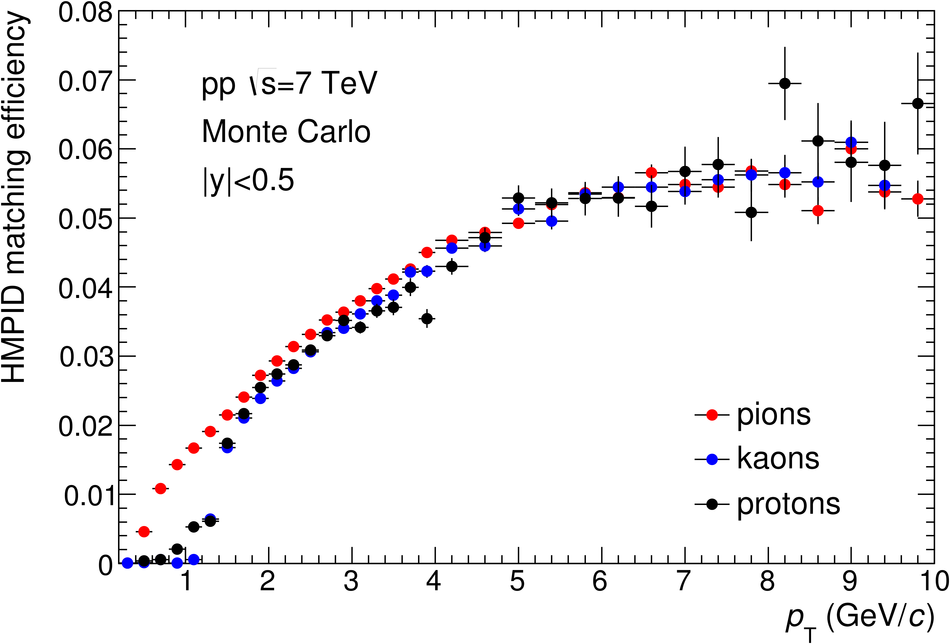
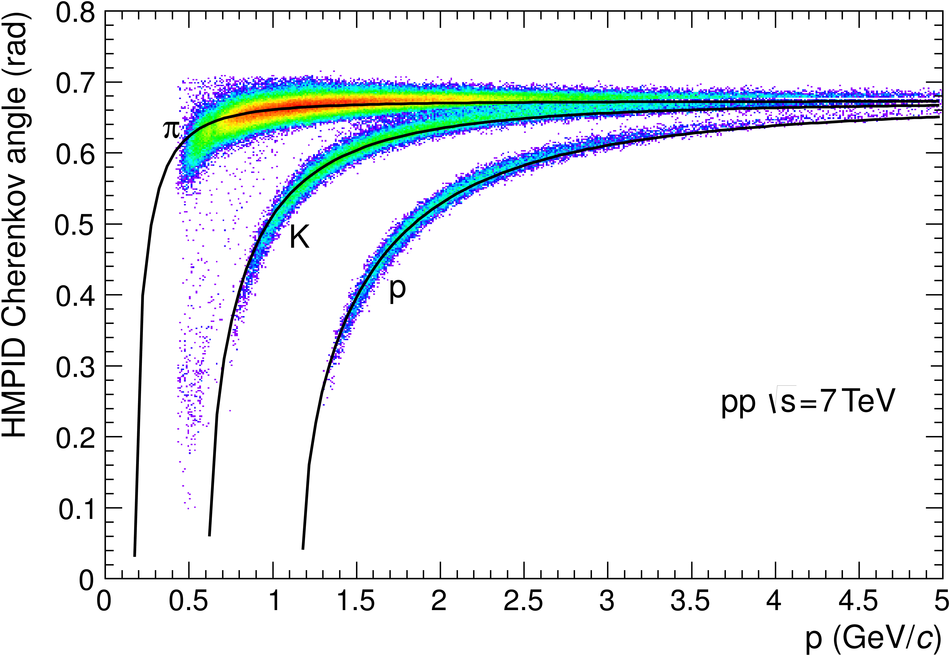
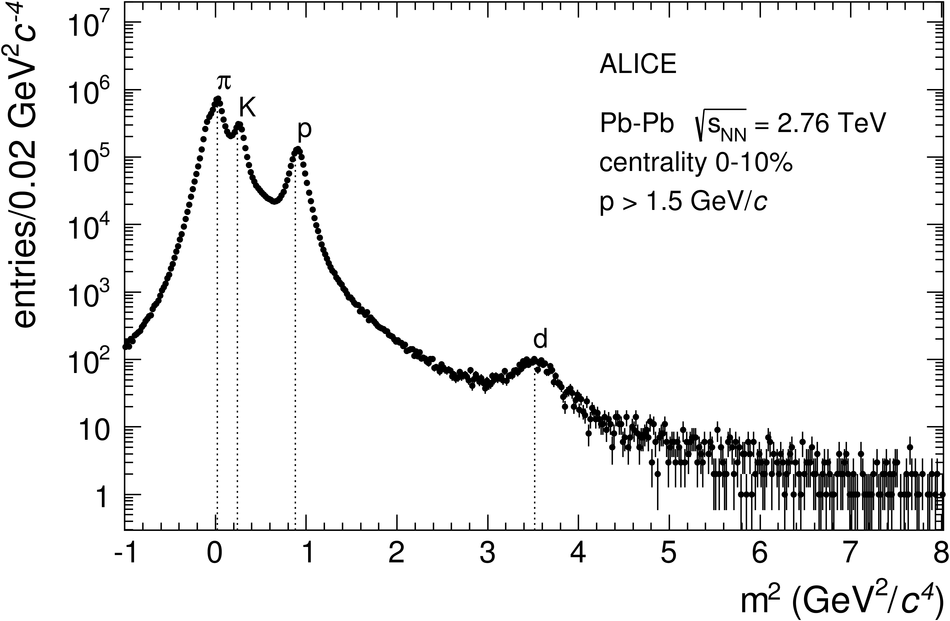
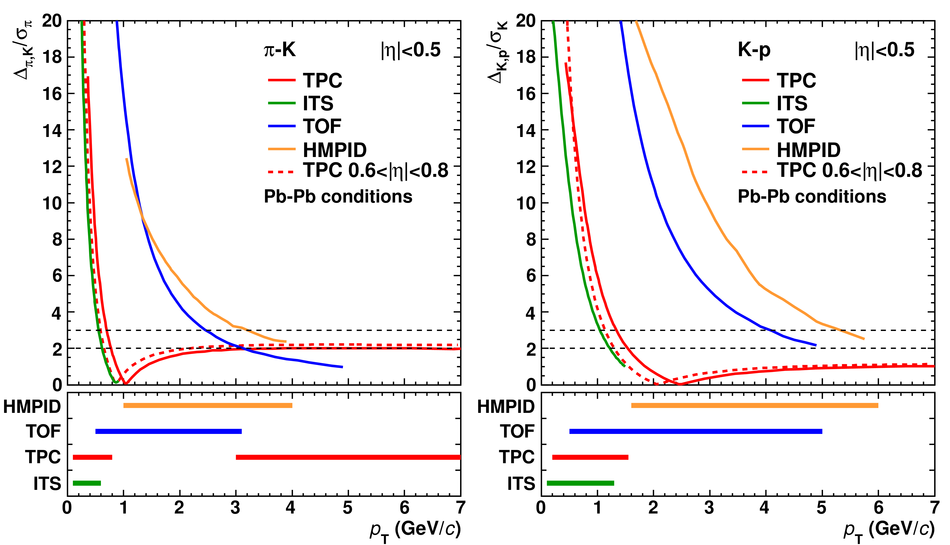
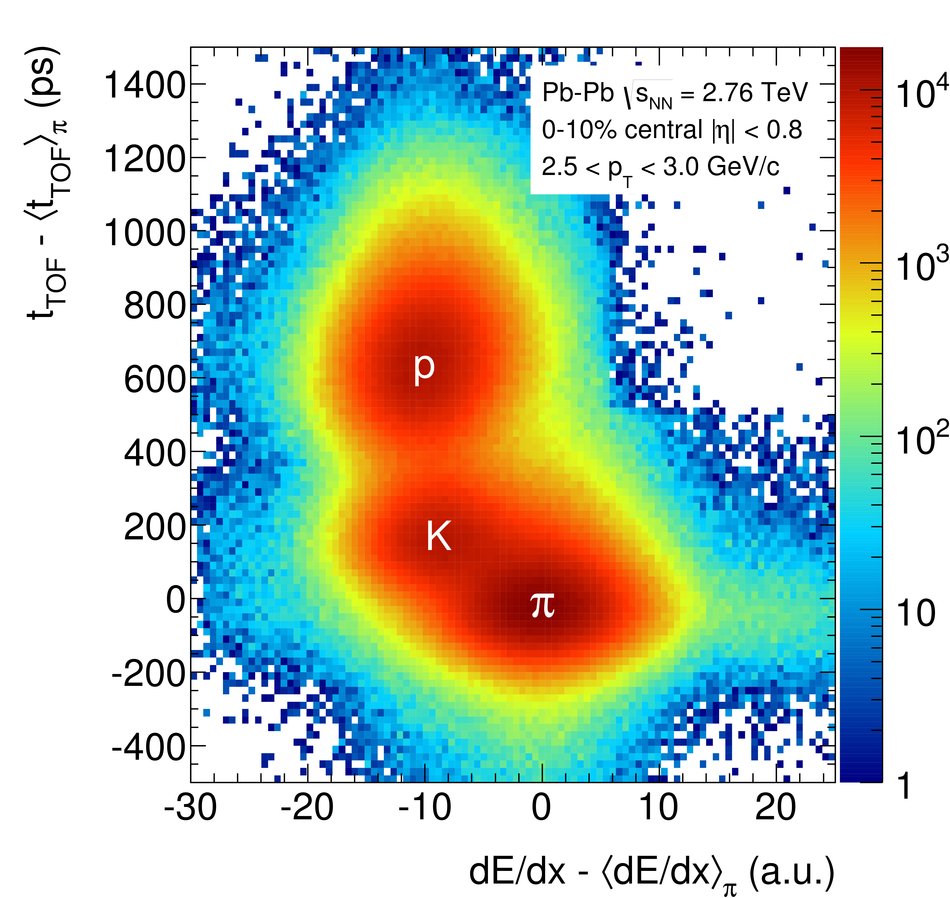
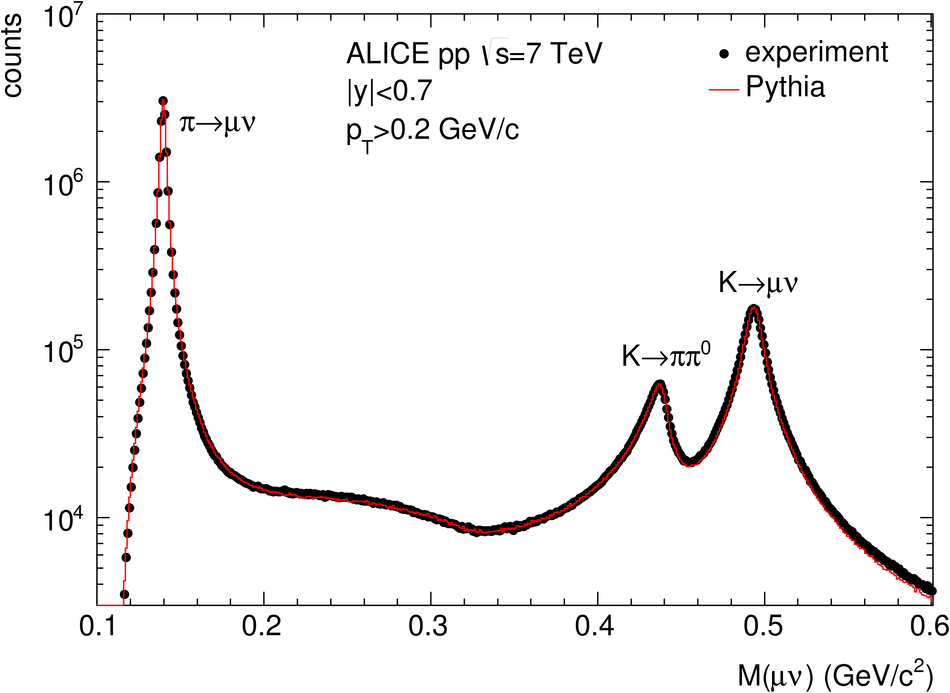
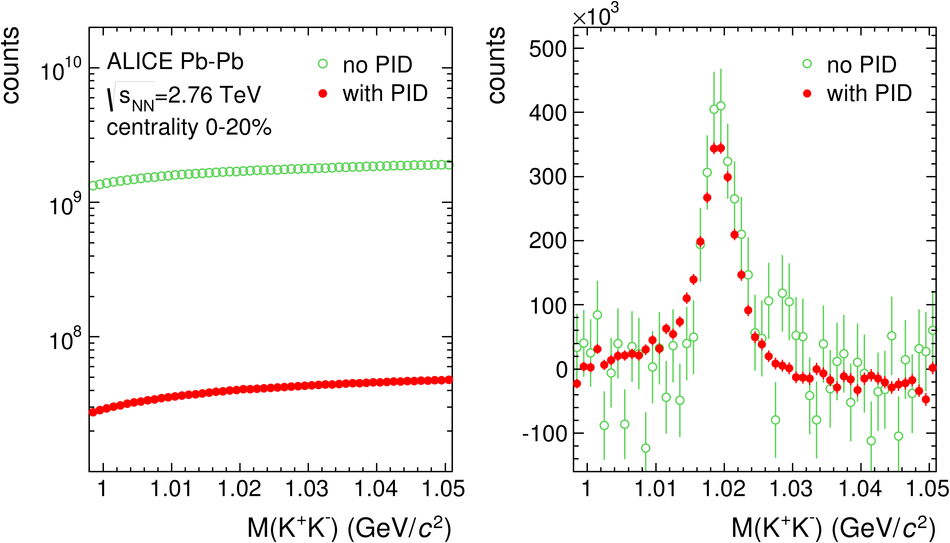
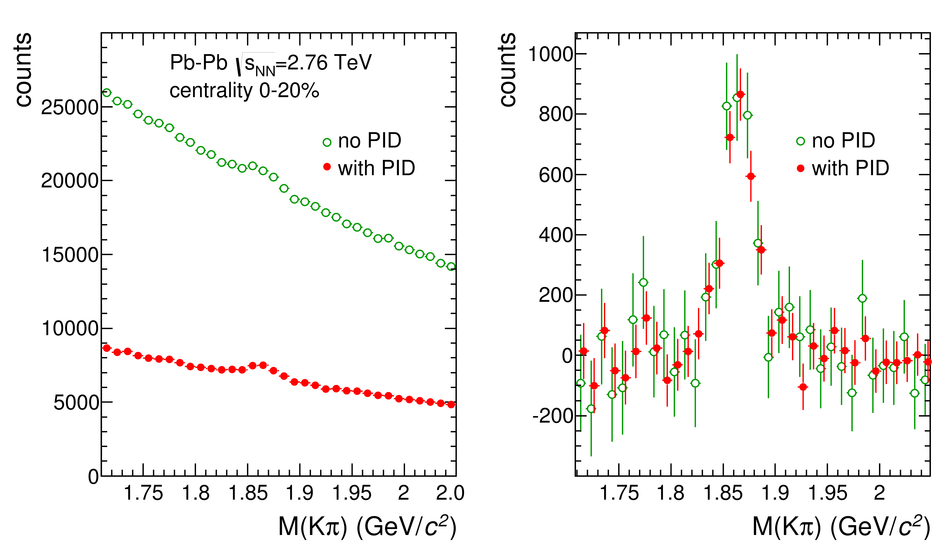
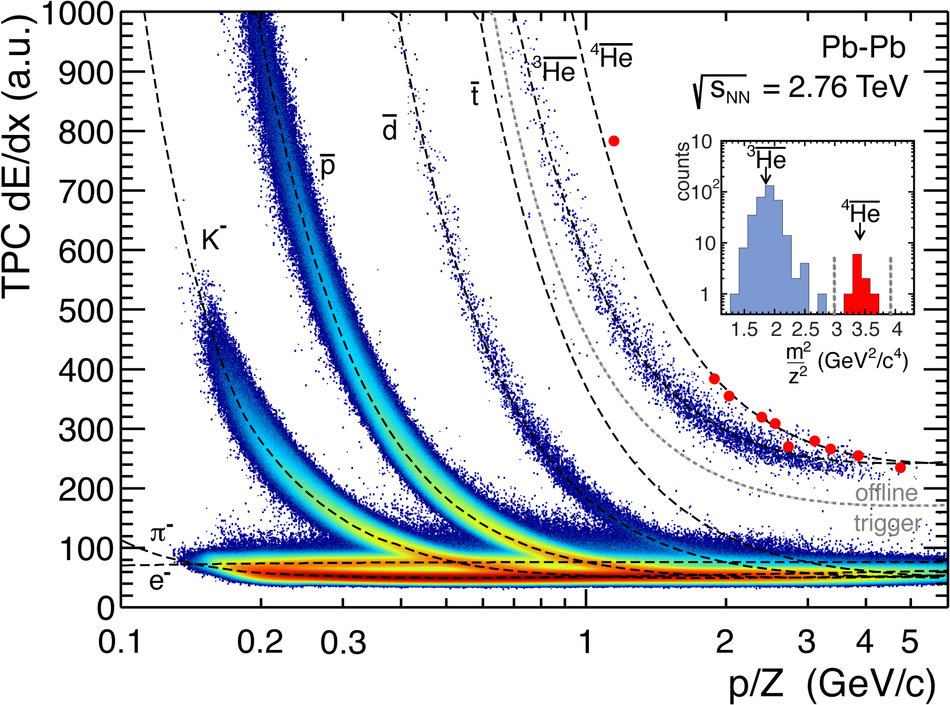
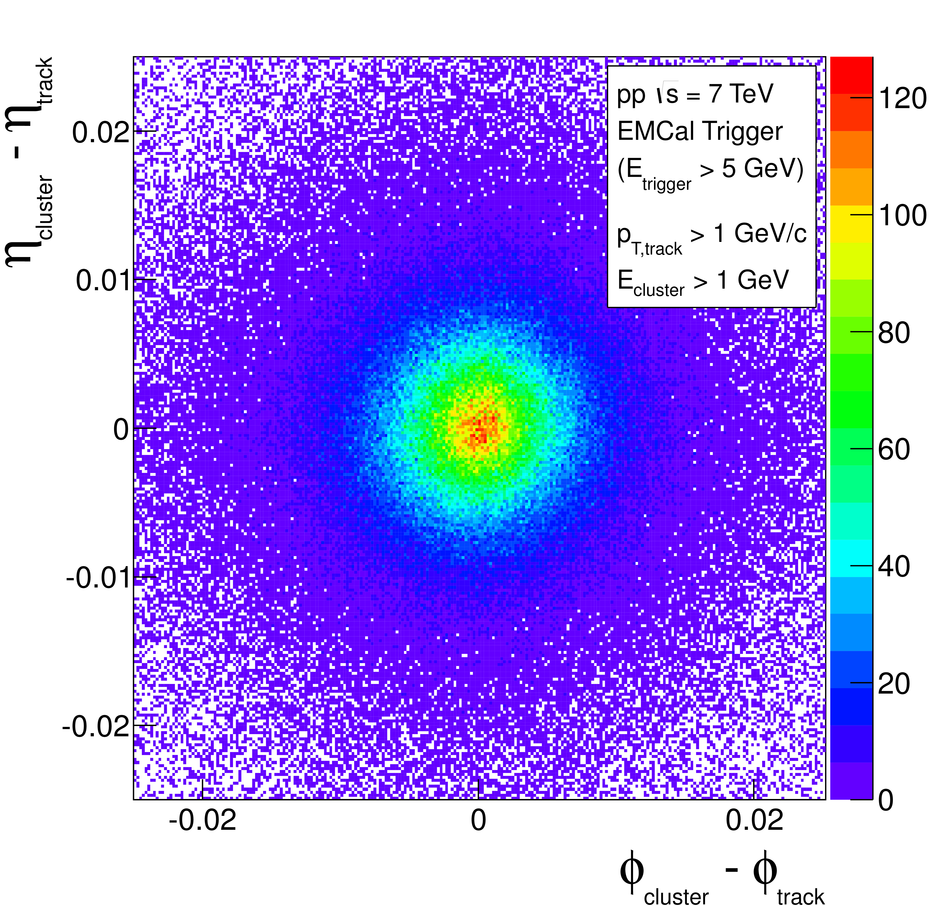
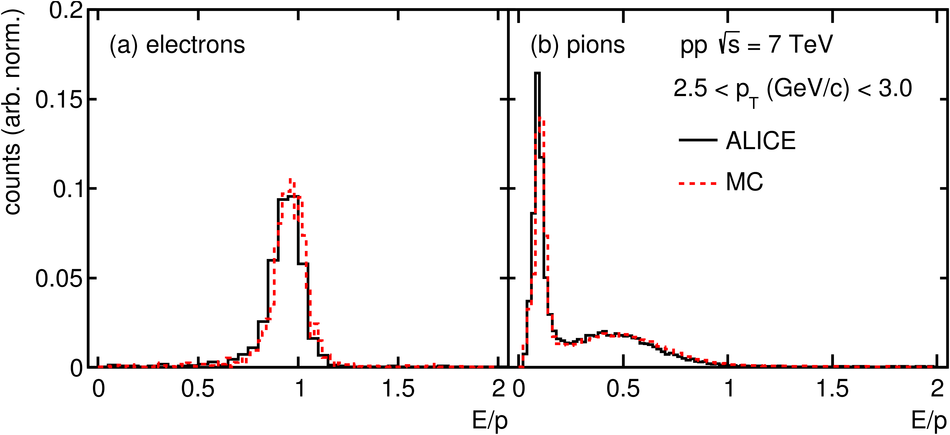
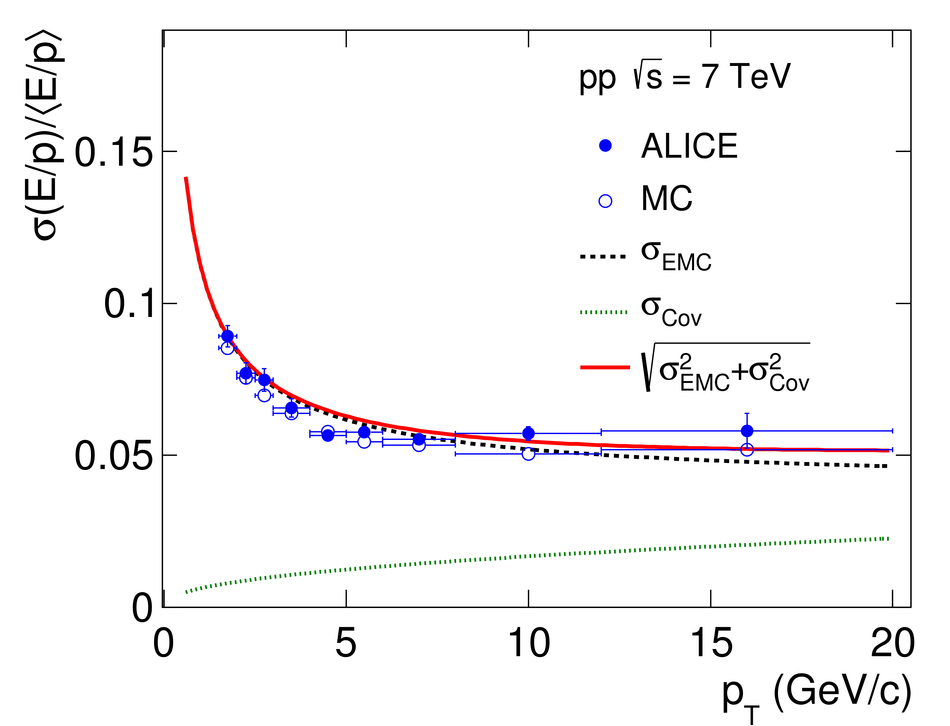
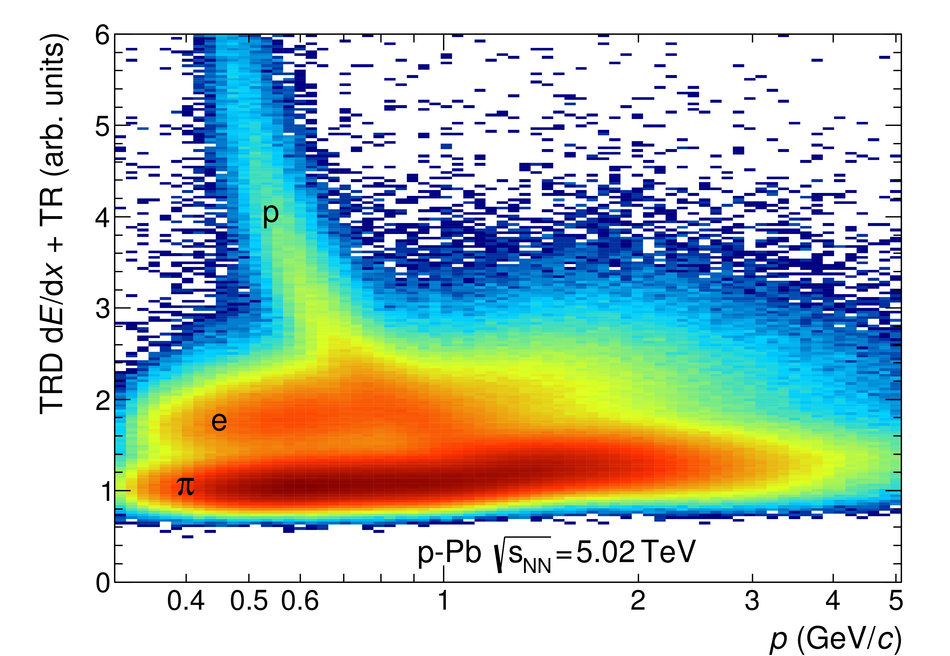
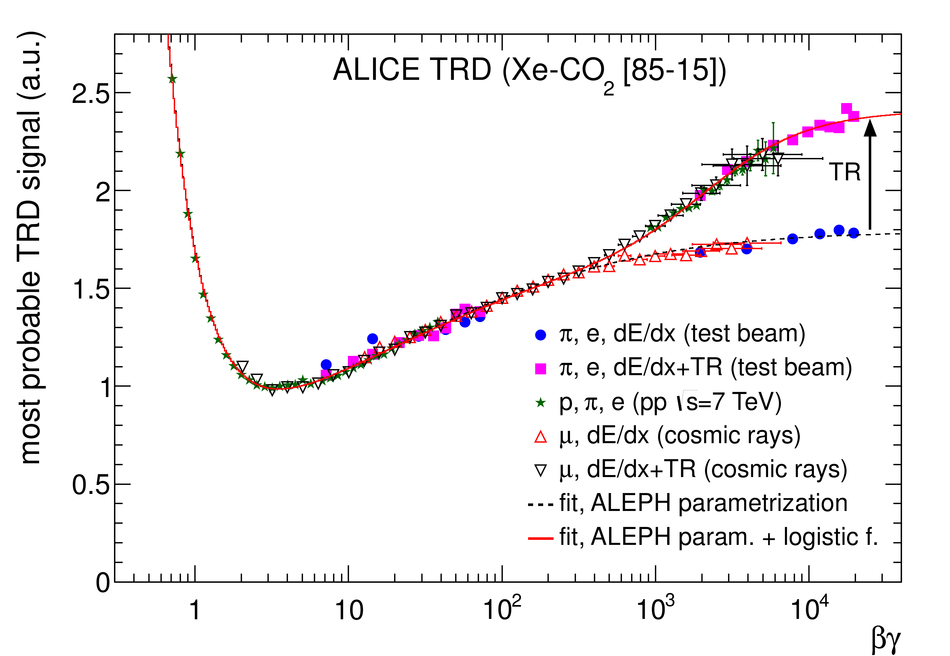
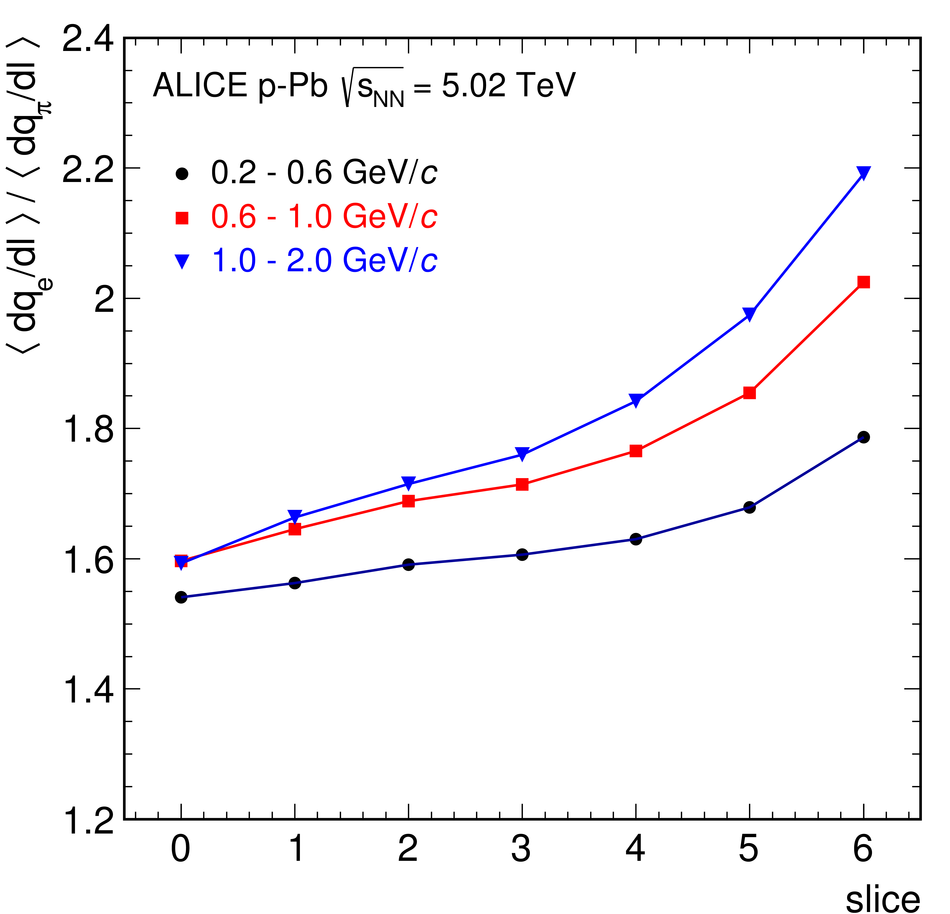
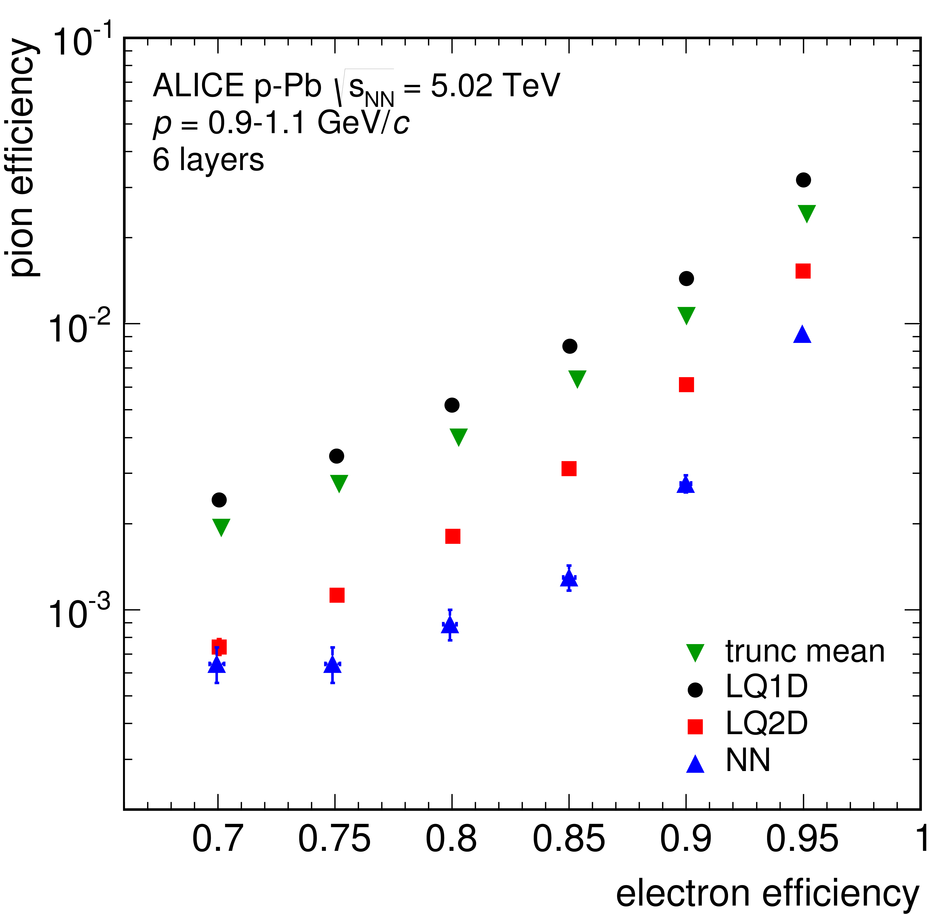
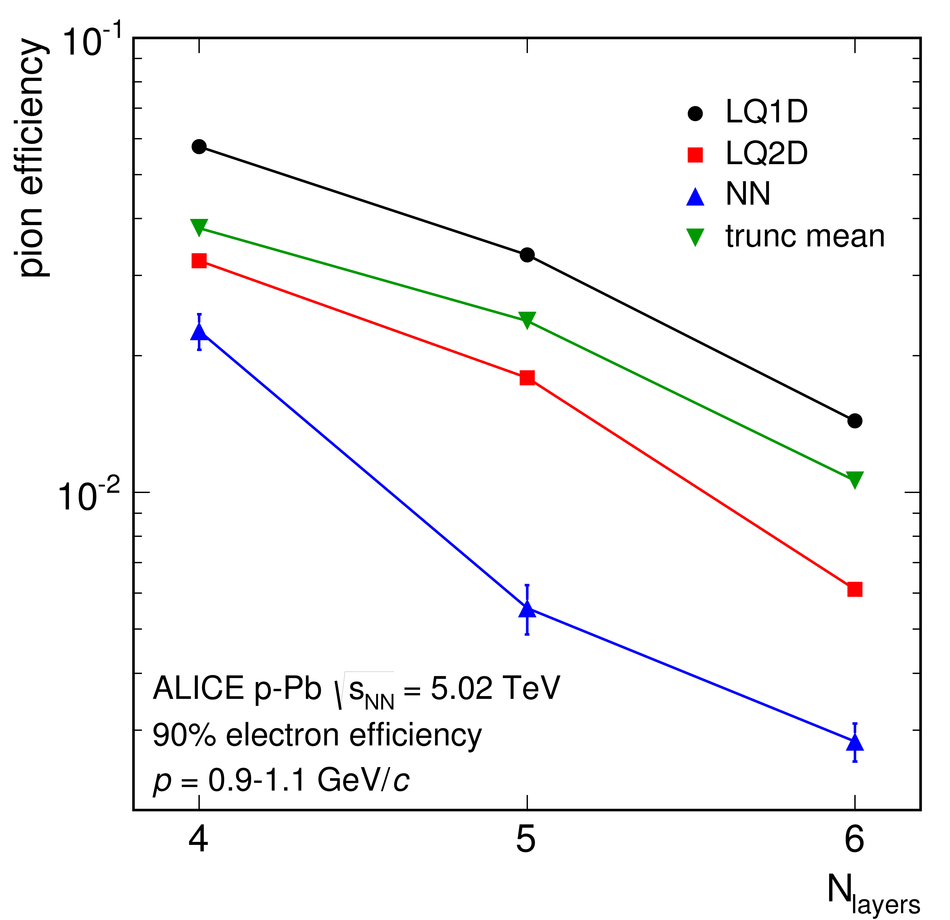
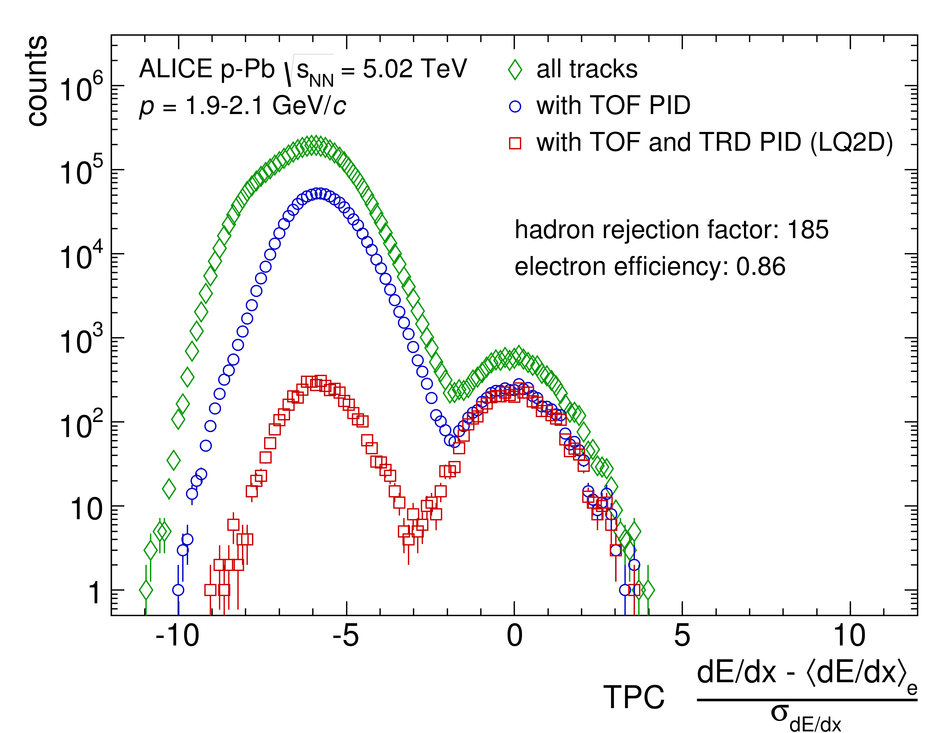
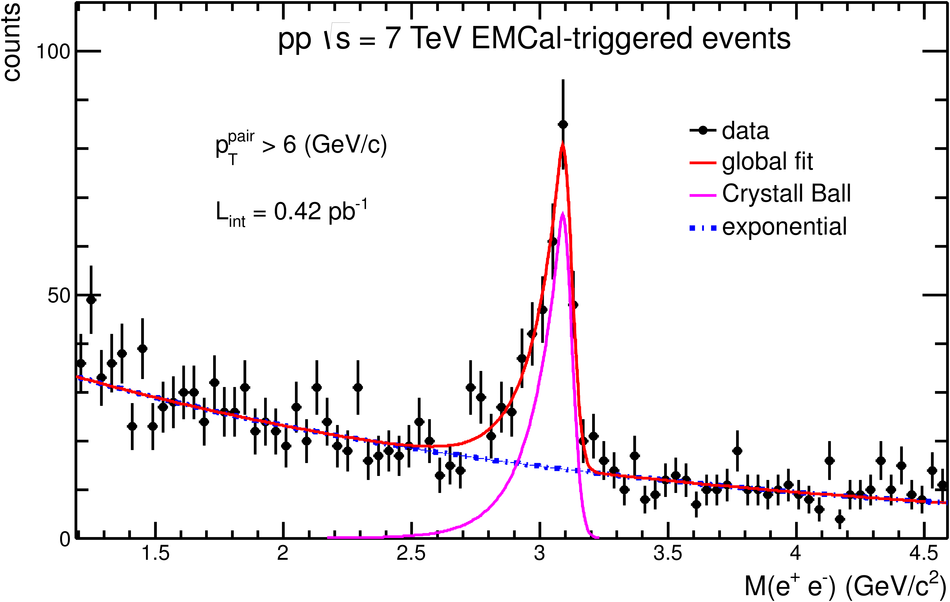
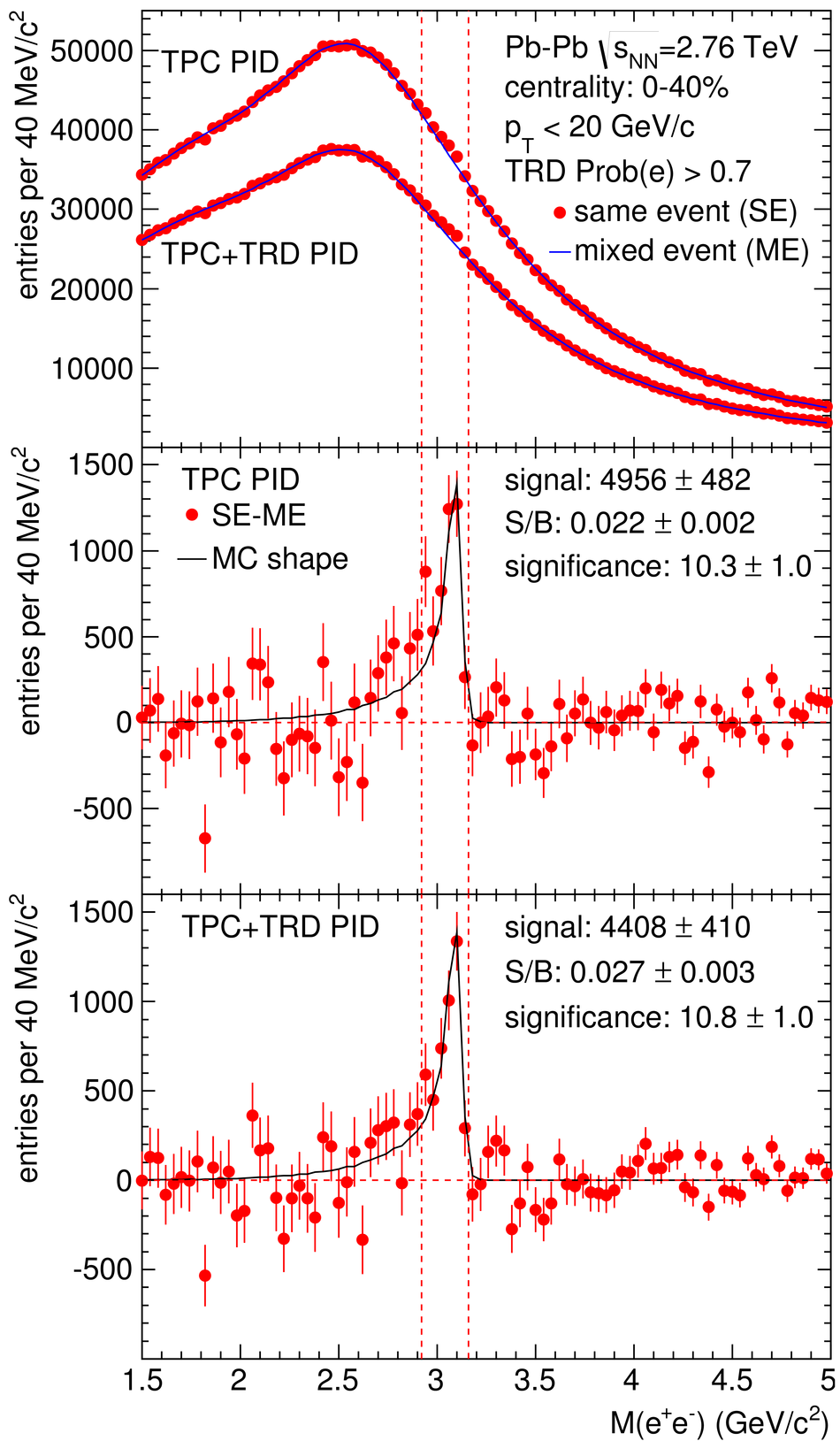
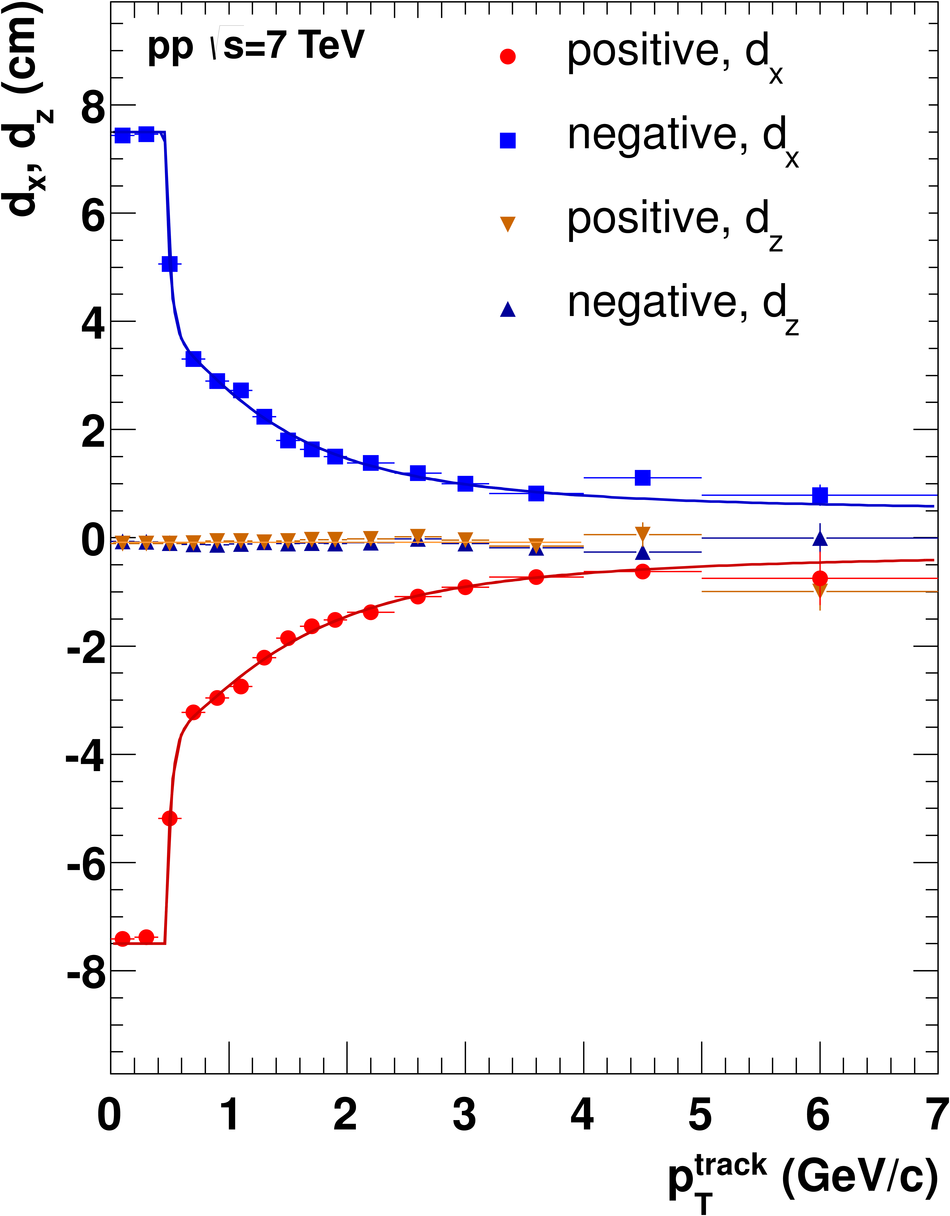
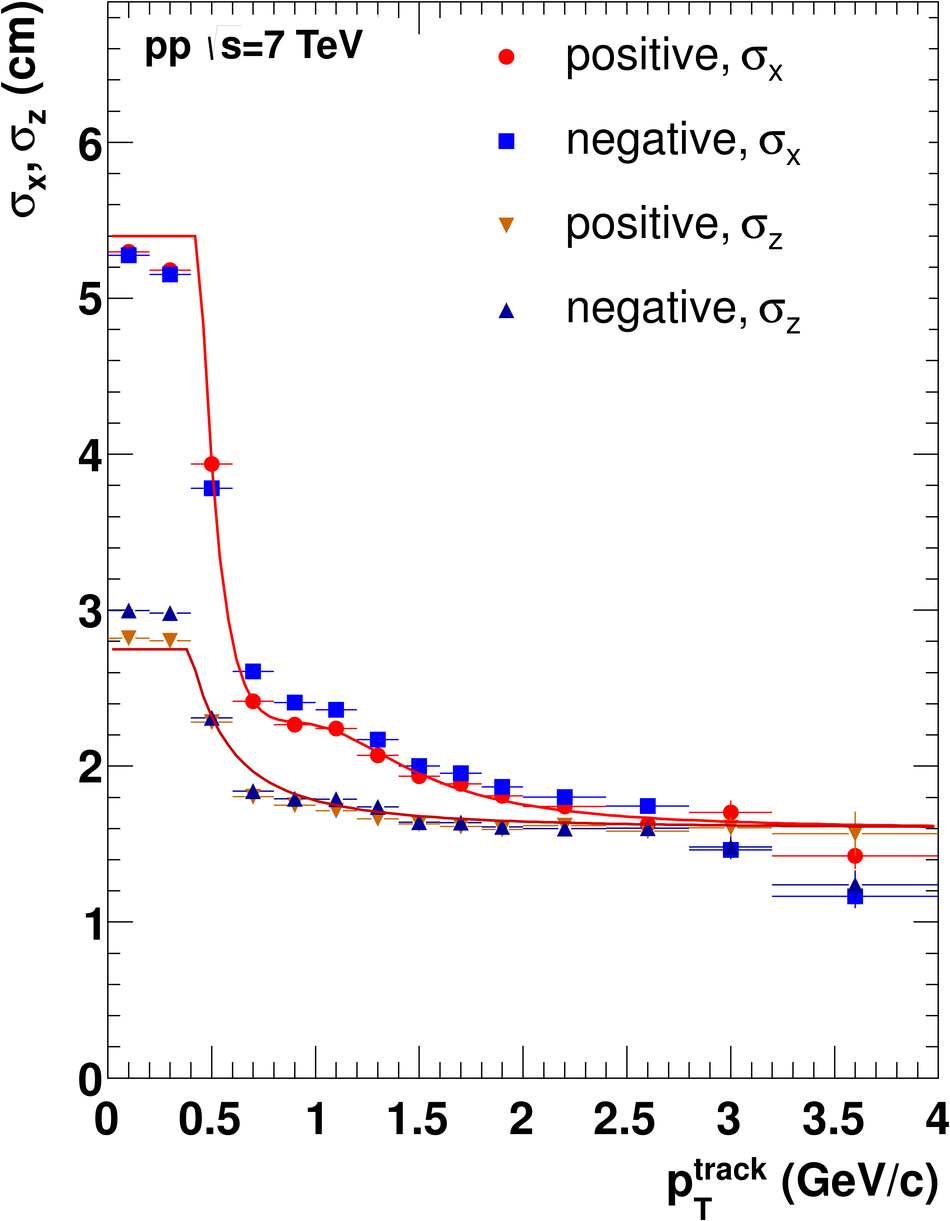
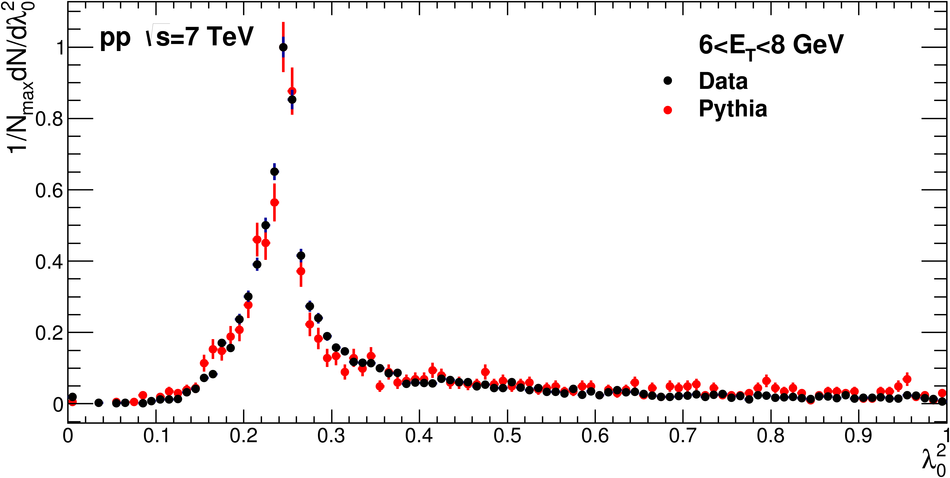
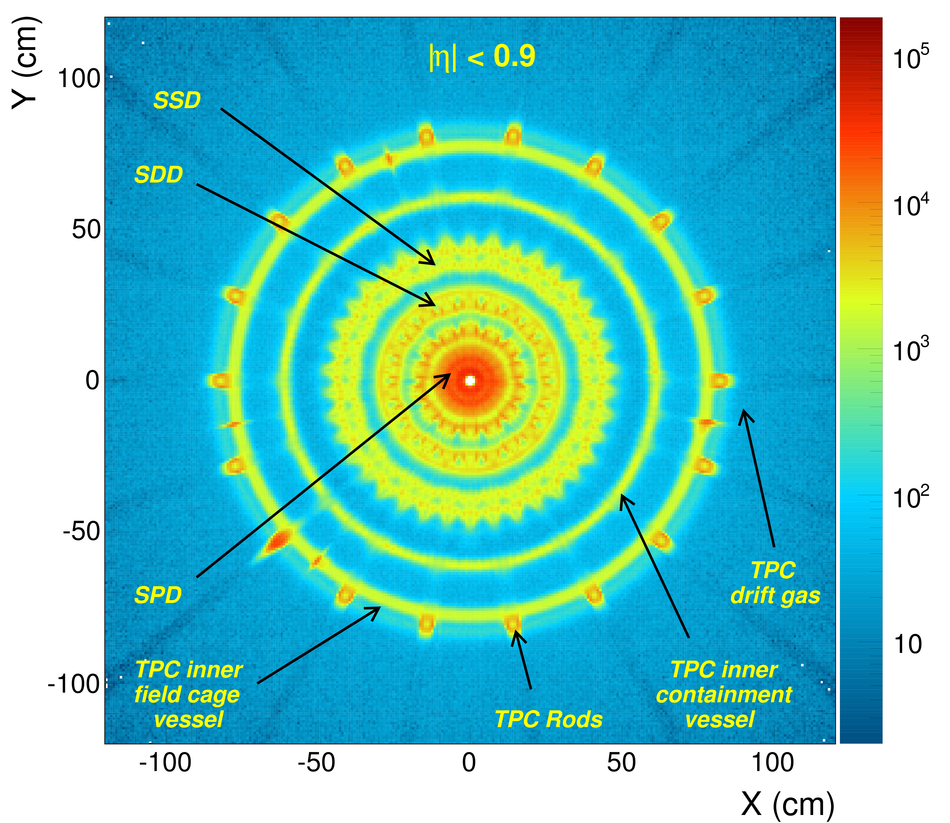
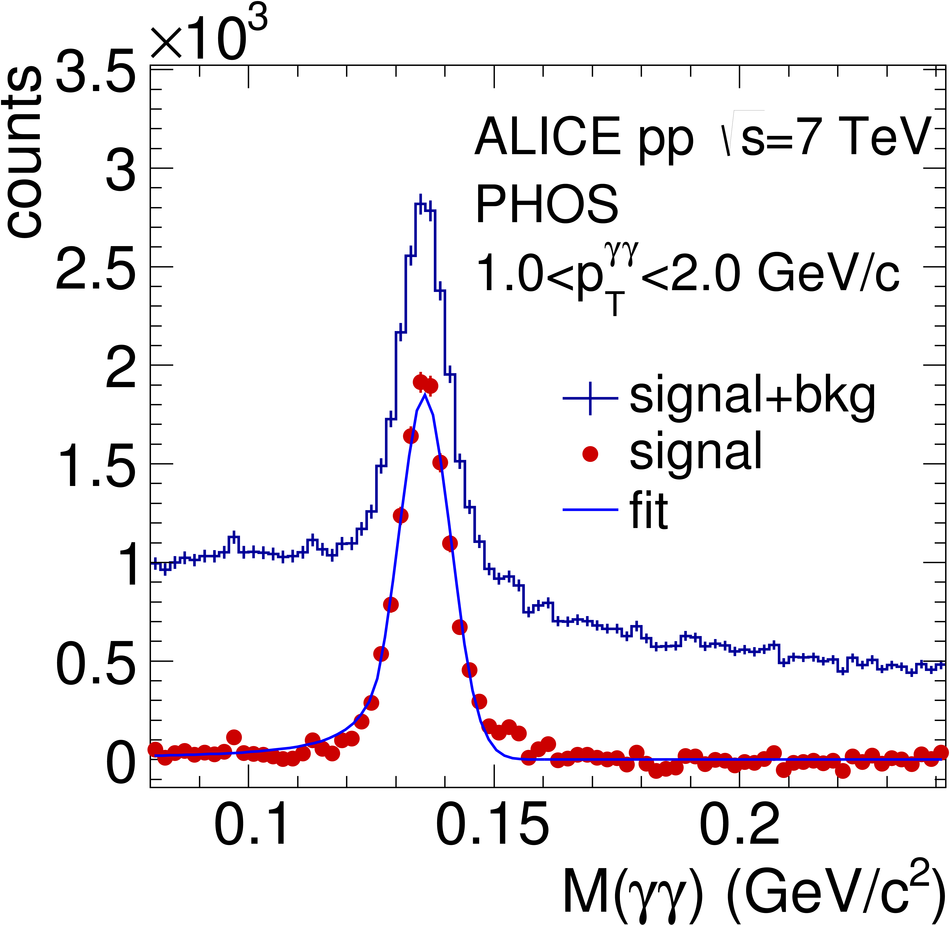
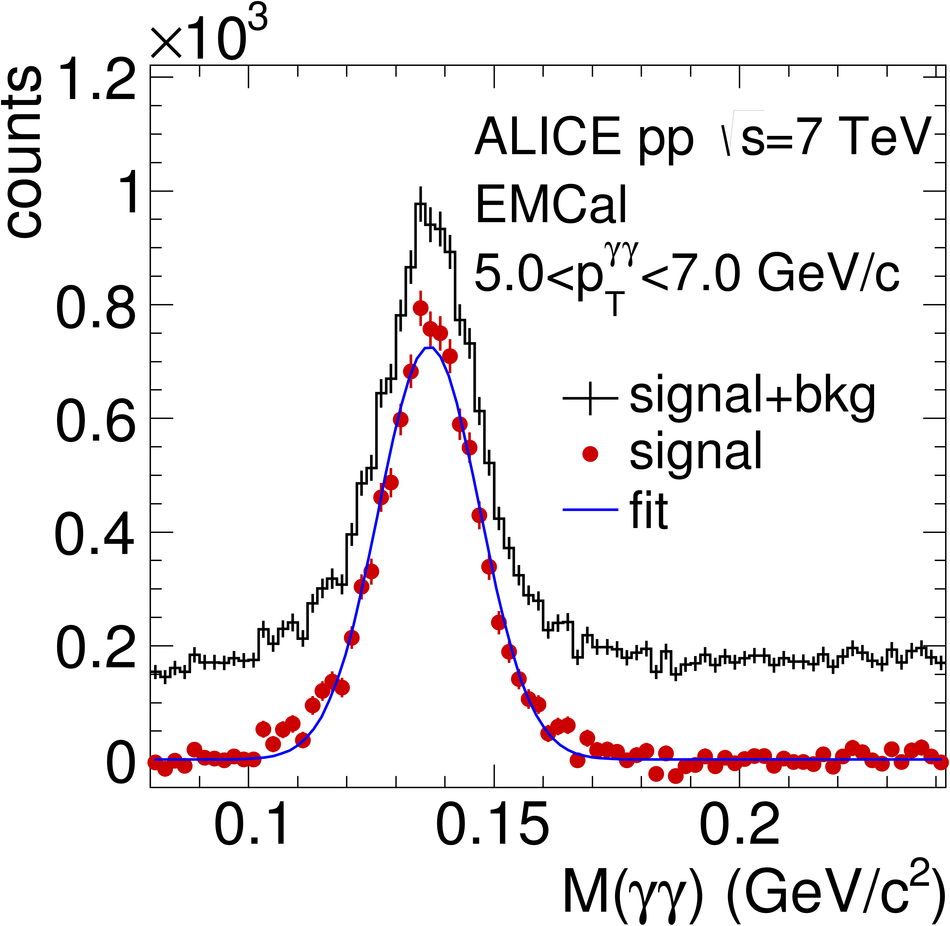
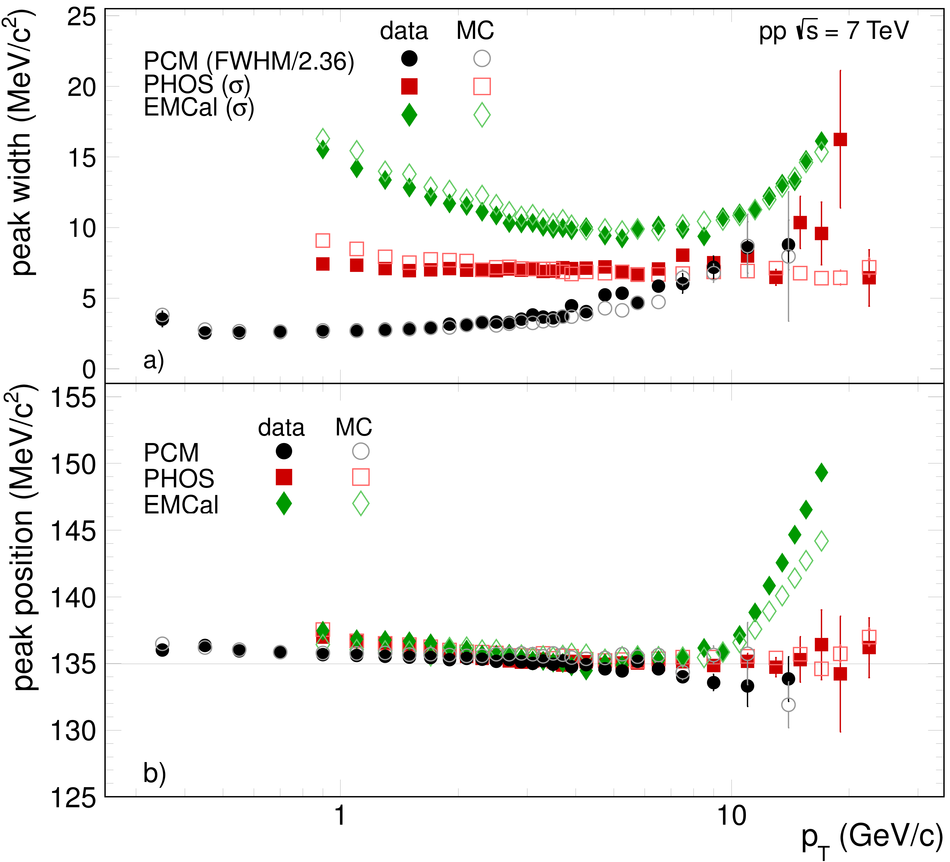
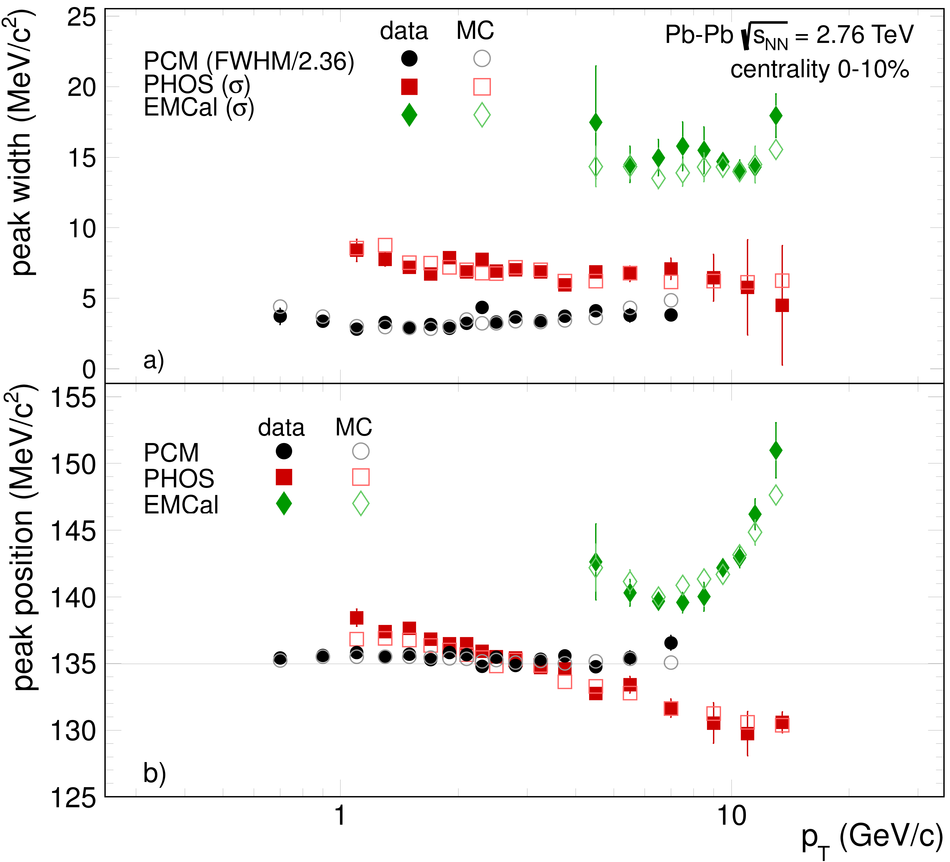
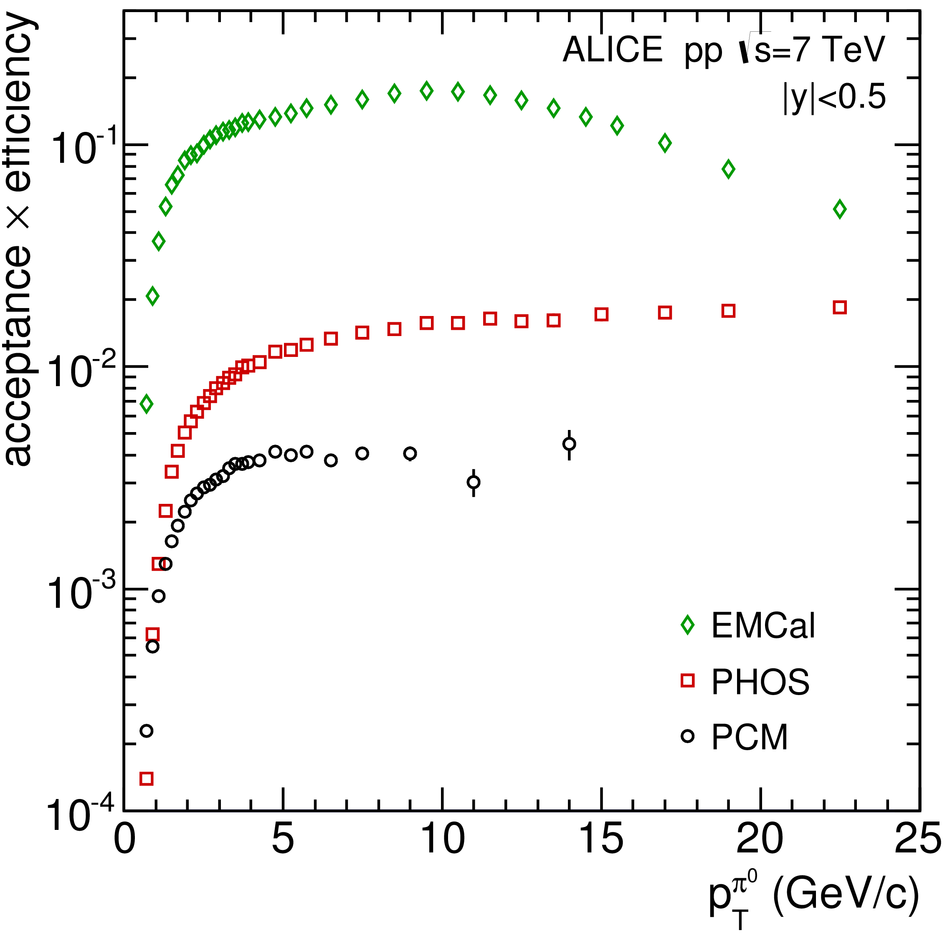
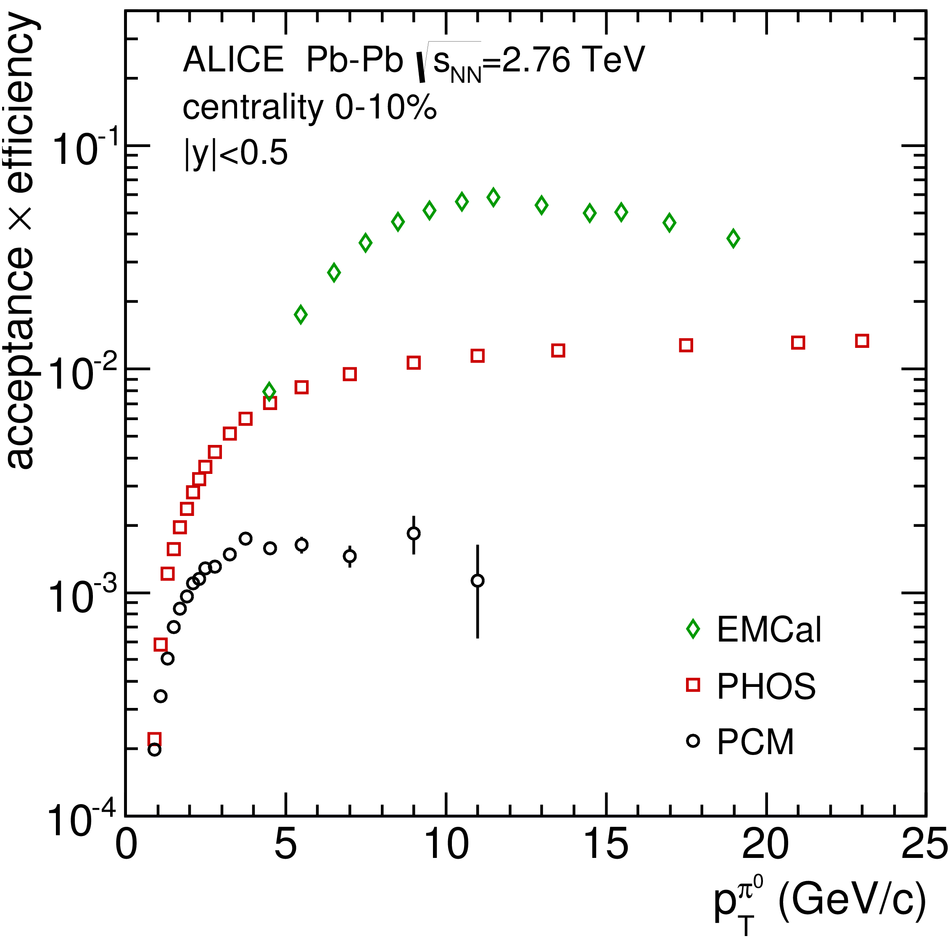
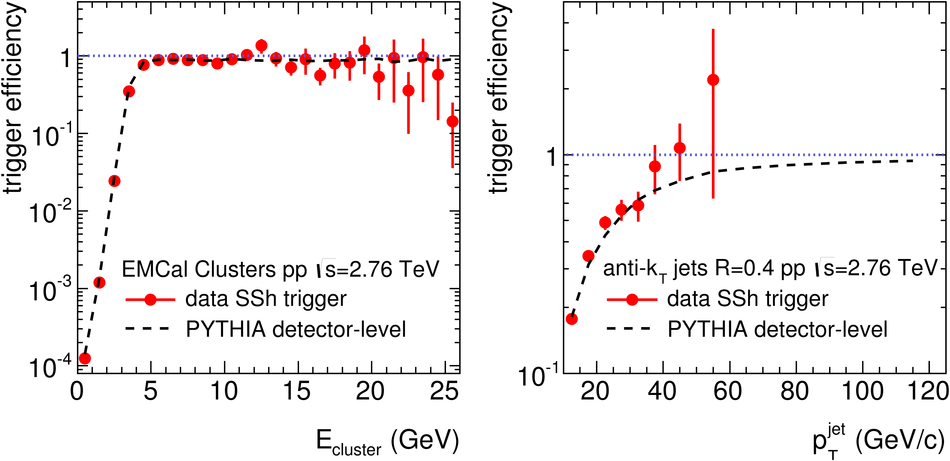
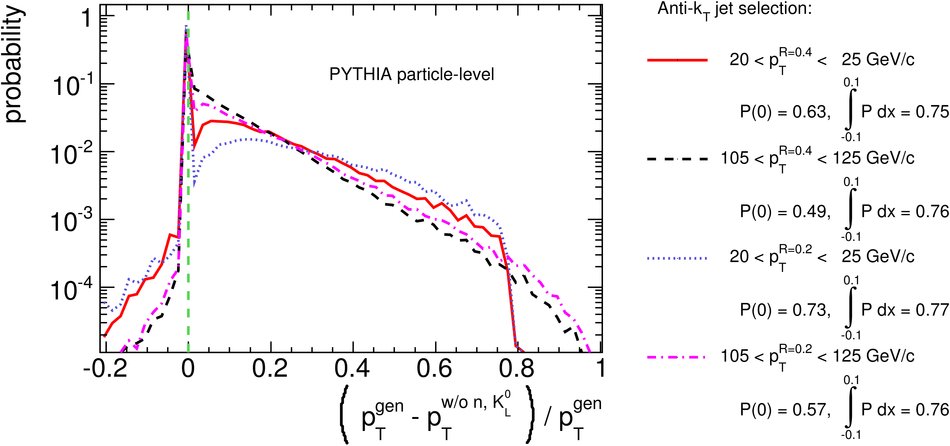
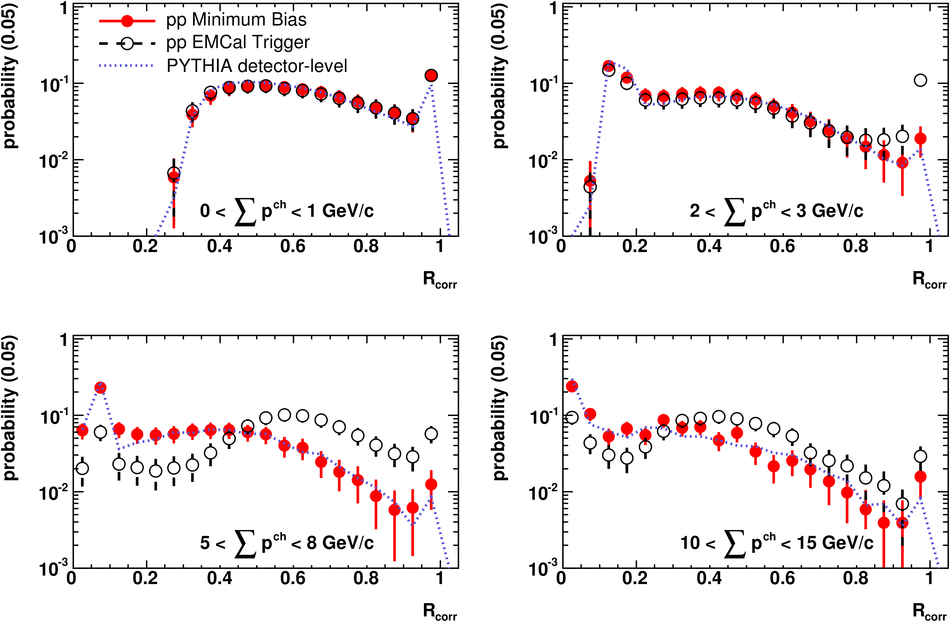
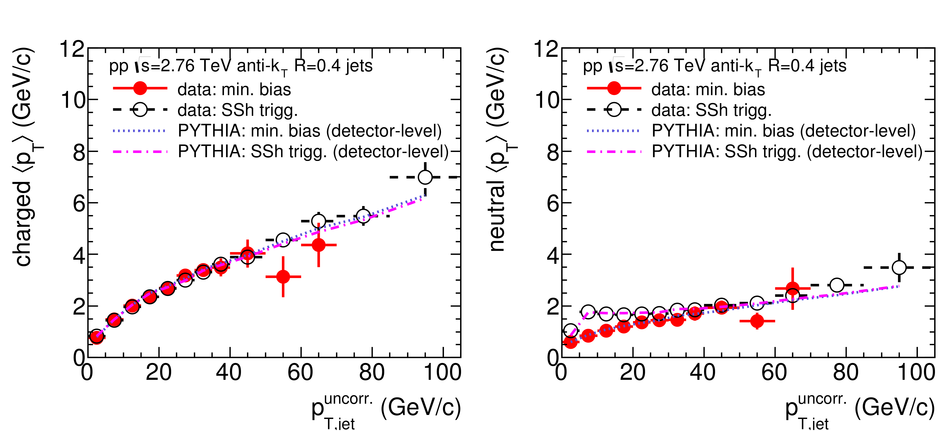
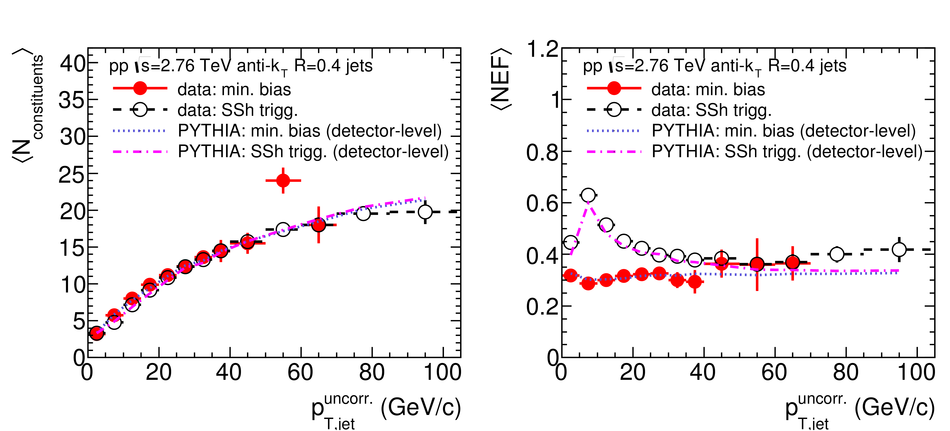
ALICE is the heavy-ion experiment at the CERN Large Hadron Collider. The experiment continuously took data during the first physics campaign of the machine from fall 2009 until early 2013, using proton and lead-ion beams. In this paper we describe the running environment and the data handling procedures, and discuss the performance of the ALICE detectors and analysis methods for various physics observables.
Int. J. Mod. Phys. A 29 (2014) 1430044
e-Print: arXiv:1402.4476 | PDF | inSPIRE
CERN-PH-EP-2014-031