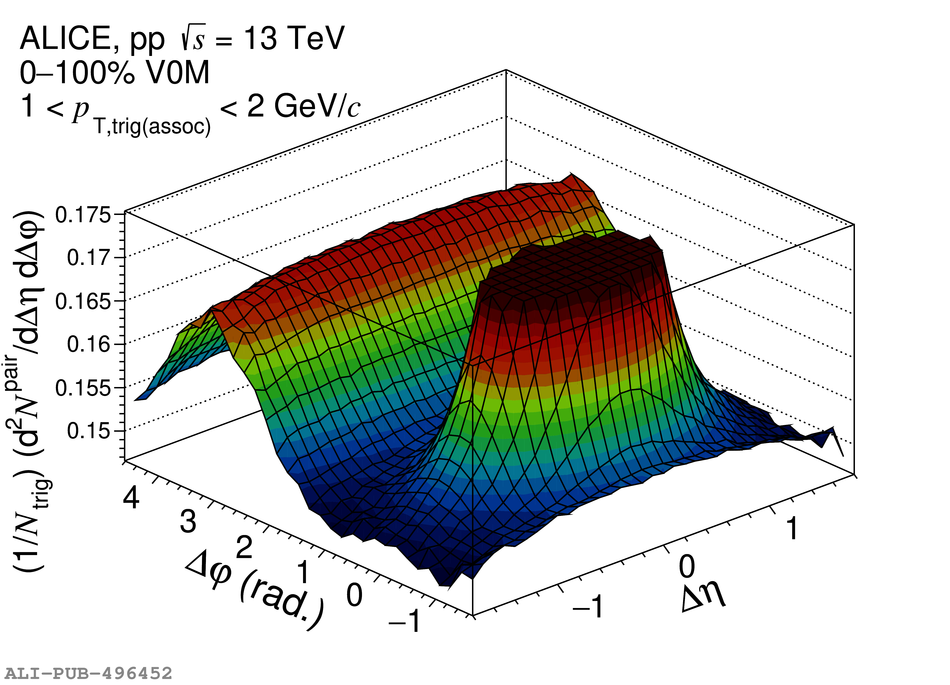
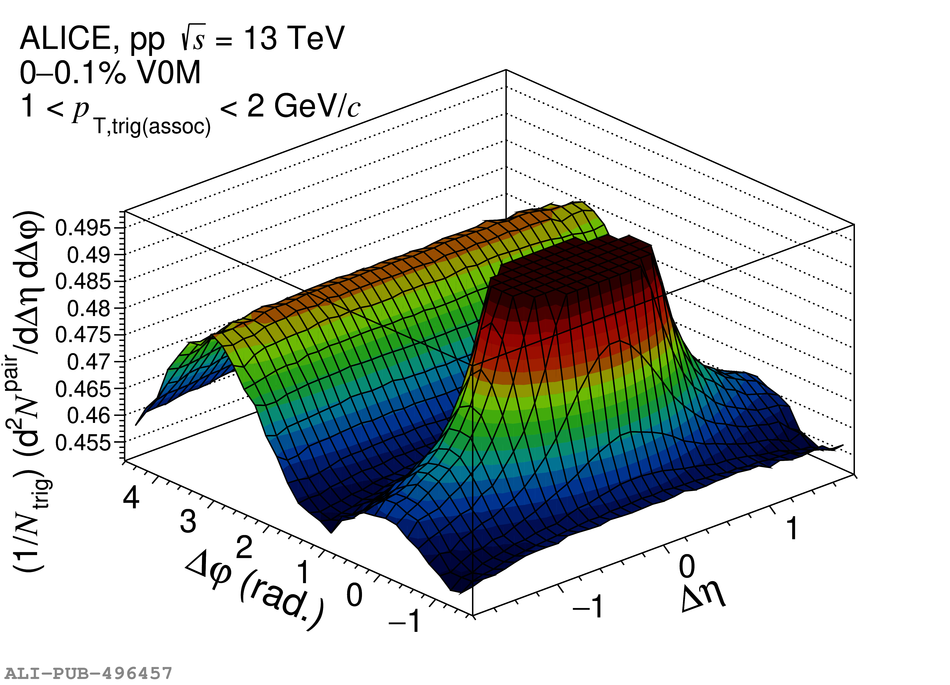
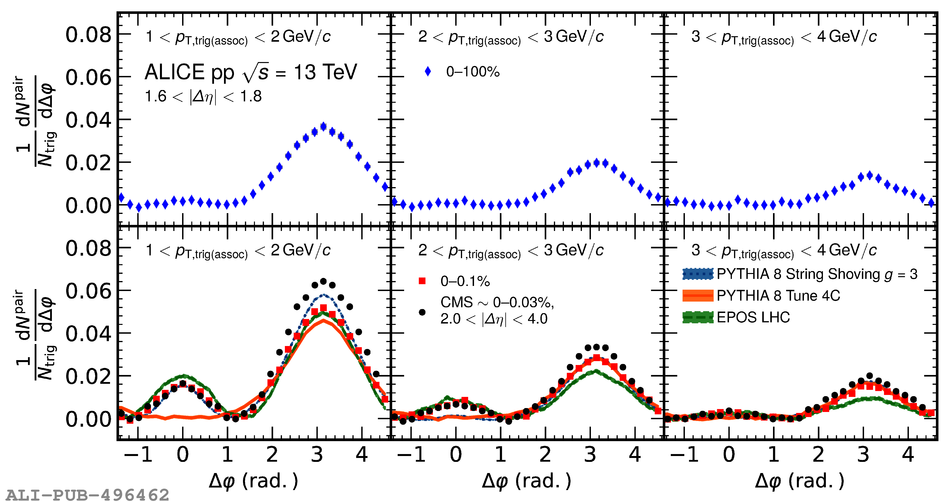
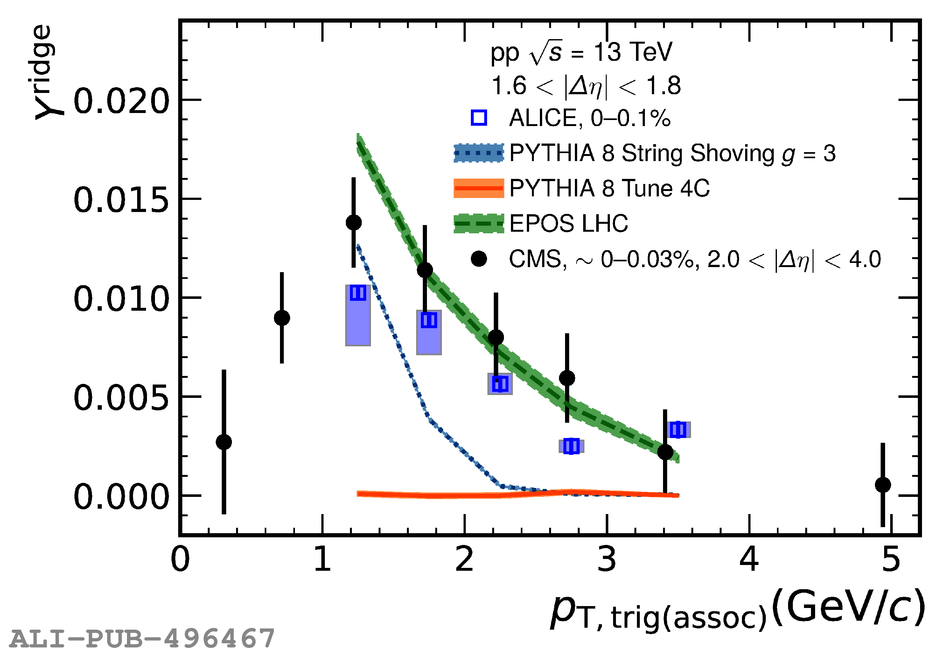
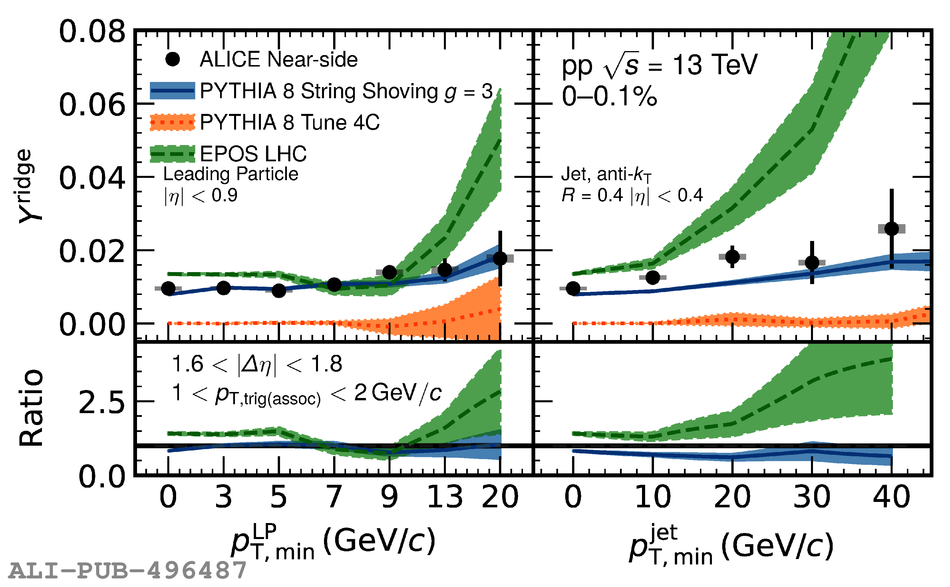
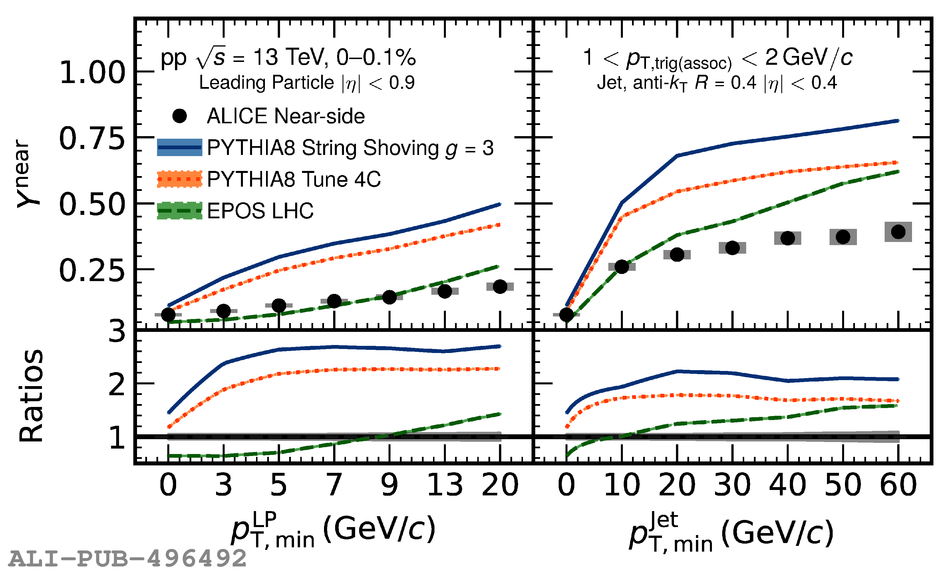
Two-particle angular correlations are measured in high-multiplicity proton-proton collisions at $\sqrt{s} =13$ TeV by the ALICE Collaboration. The yields of particle pairs at short-($\Delta\eta$ $\sim$ 0) and long-range ($1.6 <~ |\Delta\eta| <~ 1.8$) in pseudorapidity are extracted on the near-side ($\Delta\varphi$ $\sim$ 0). They are reported as a function of transverse momentum ($p_{\mathrm T}$) in the range $1 <~p_{\mathrm T}<~ 4$ GeV/$c$. Furthermore, the event-scale dependence is studied for the first time by requiring the presence of high-$p_{\rm T}$ leading particles and jets for varying $p_{\rm T}$ thresholds. The results demonstrate that the long-range "ridge" yield, possibly related to the collective behavior of the system, is present in events with high-$p_{\mathrm T}$ processes. The magnitudes of the short- and long-range yields are found to grow with the event scale. The results are compared to EPOS LHC and PYTHIA 8 calculations, with and without string-shoving interactions. It is found that while both models describe the qualitative trends in the data, calculations from EPOS LHC show a better quantitative agreement, in particular for the $p_{\rm T}$ and event-scale dependencies.
JHEP 05 (2021) 290
HEP Data
e-Print: arXiv:2101.03110 | PDF | inSPIRE
CERN-EP-2021-006
Figure group