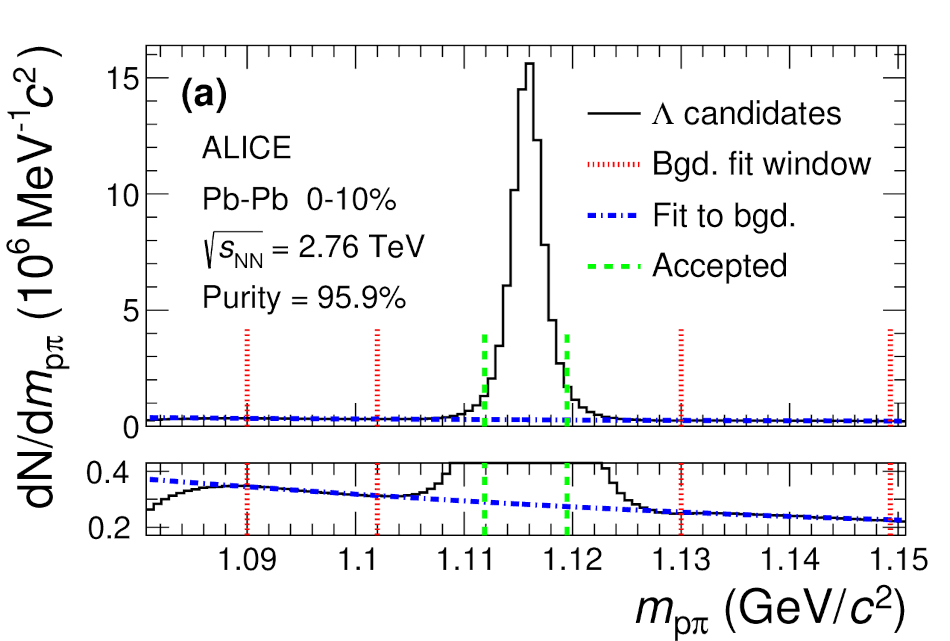
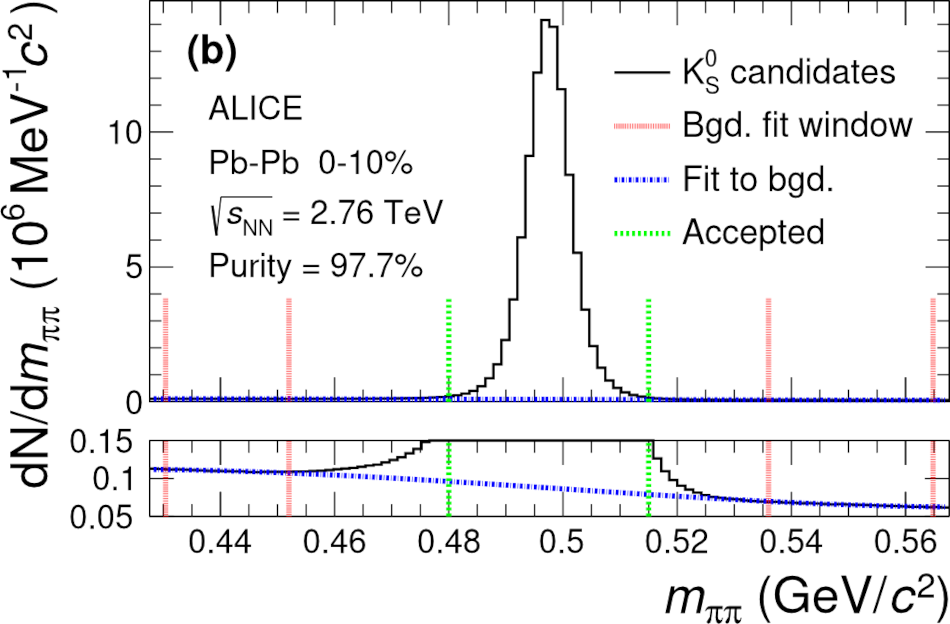
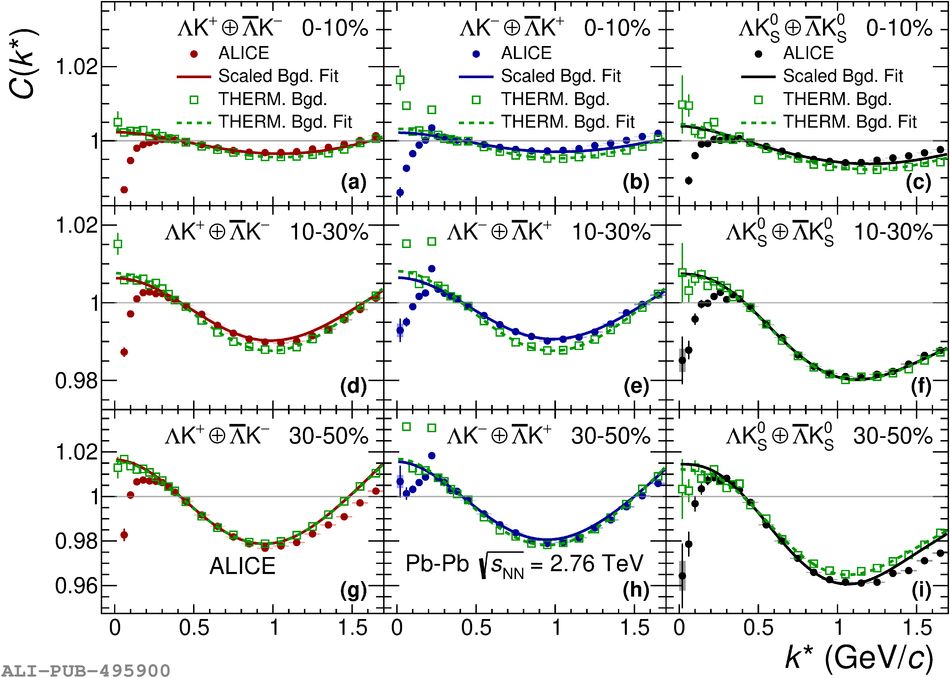
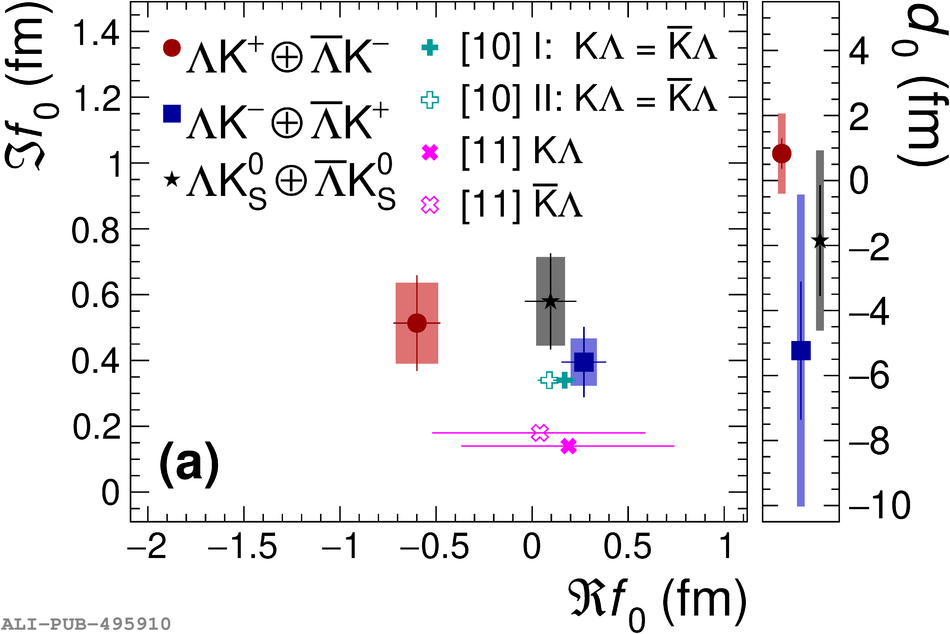
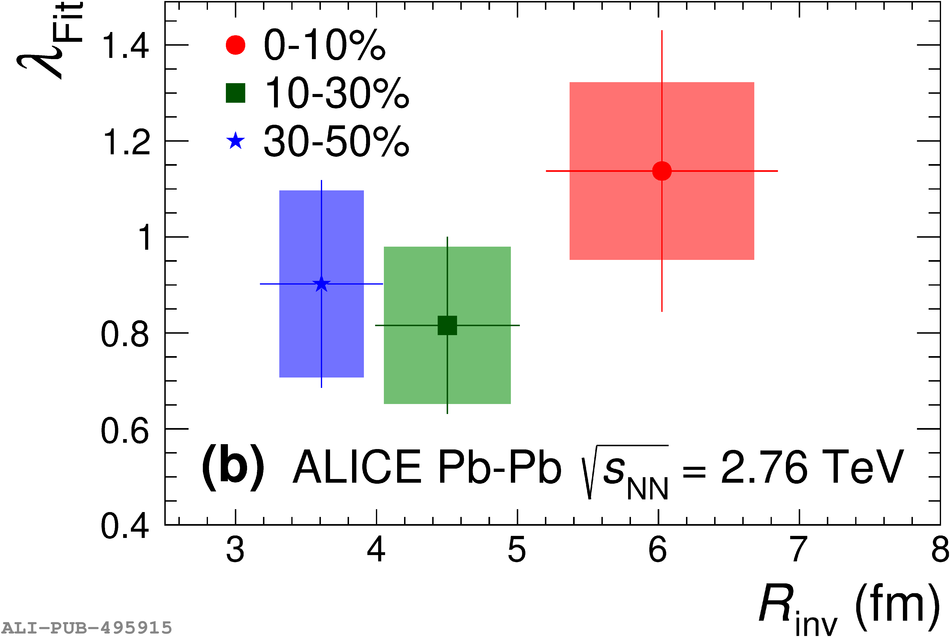
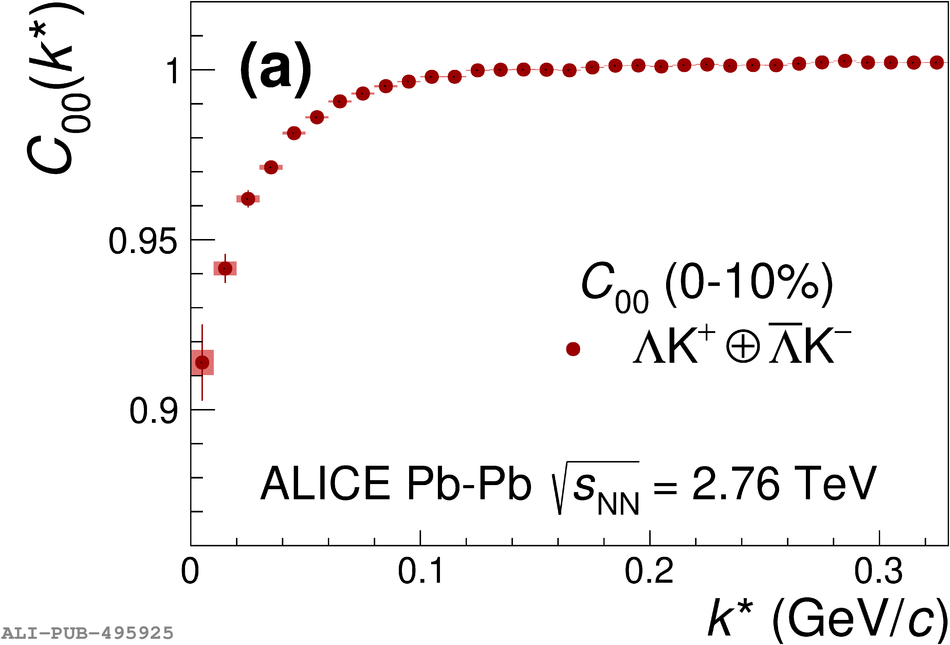
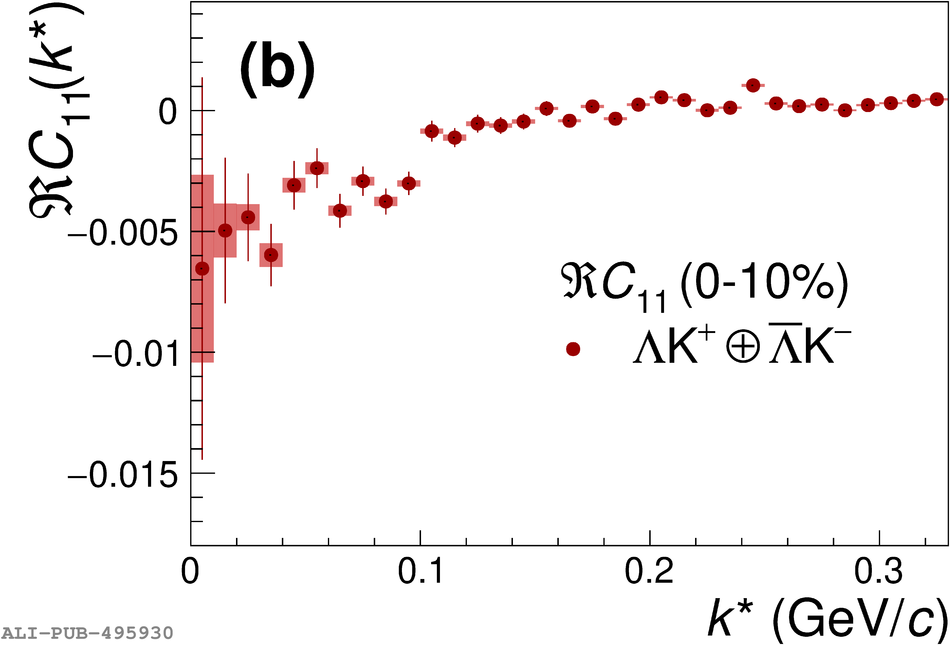
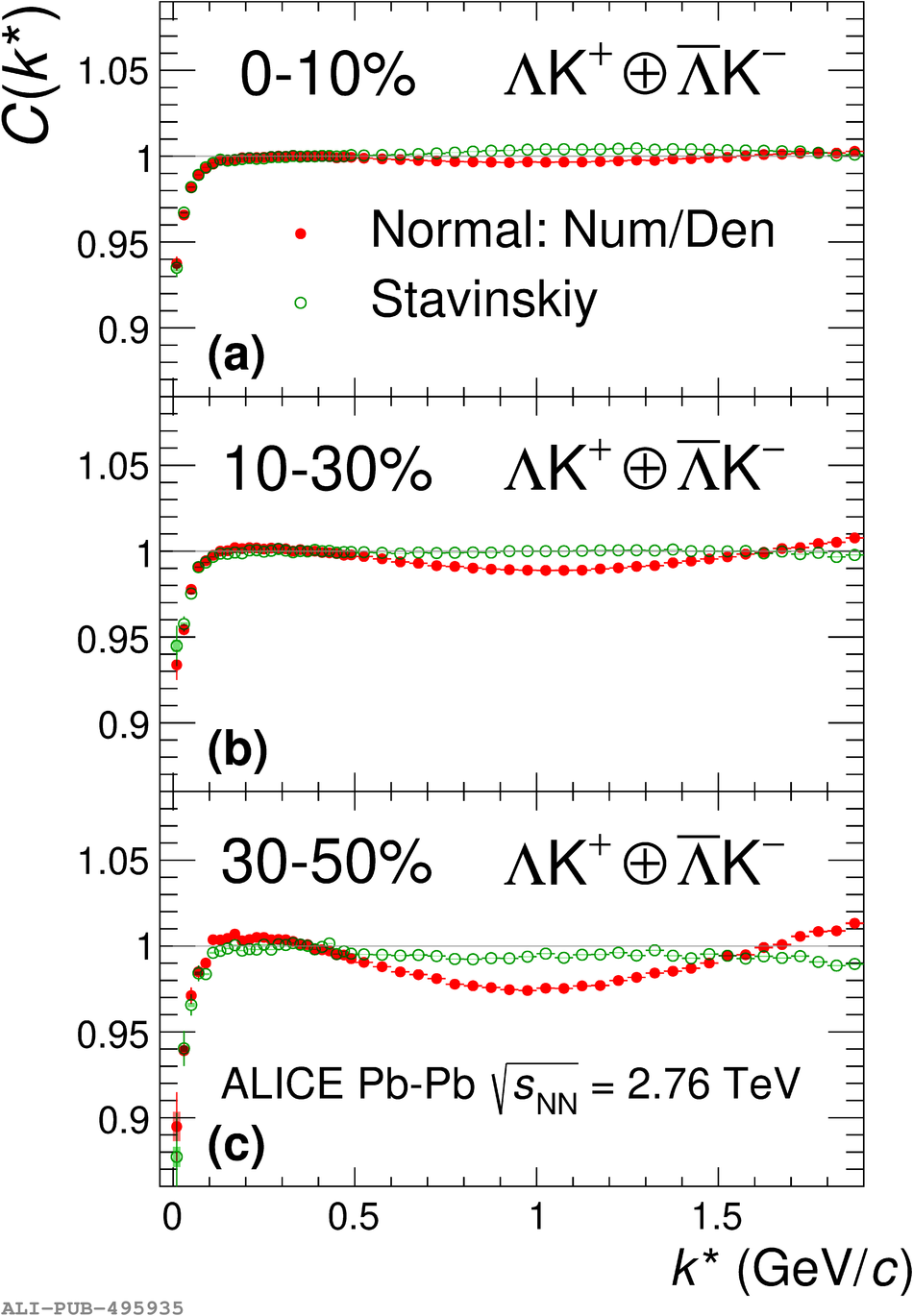
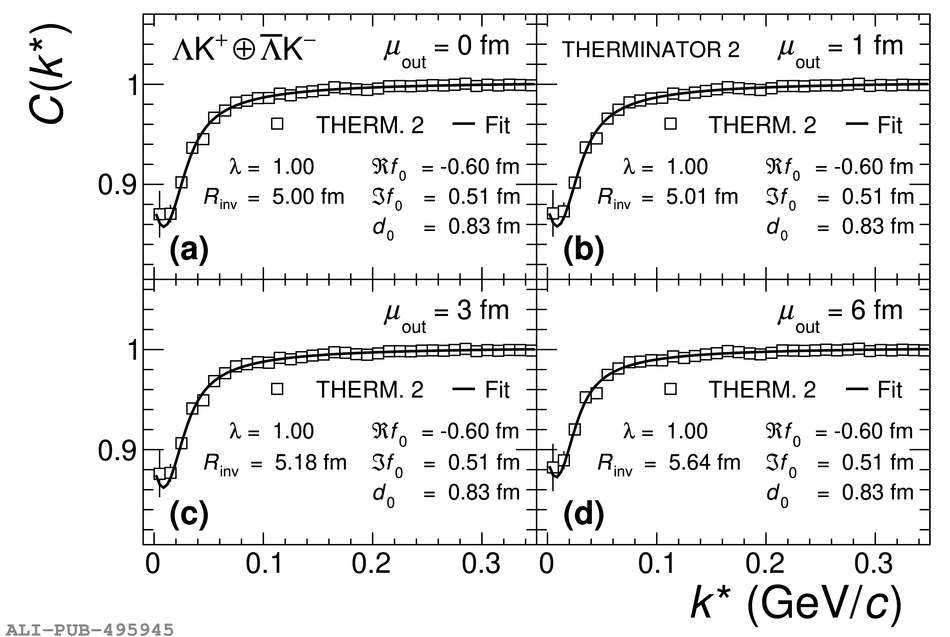
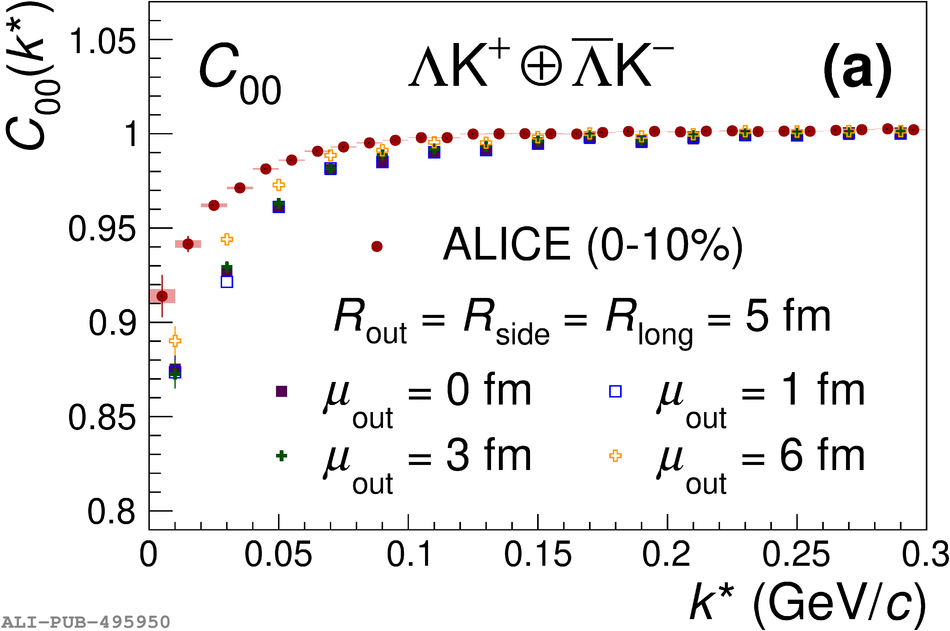
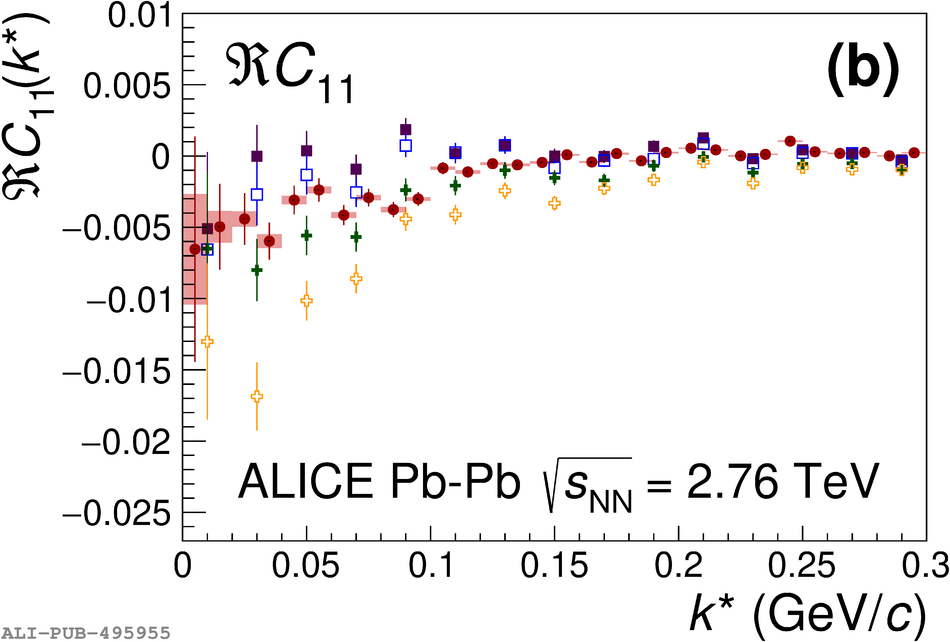
The first measurements of the scattering parameters of $\Lambda$K pairs in all three charge combinations ($\Lambda$K$^{+}$, $\Lambda$K$^{-}$, and $\Lambda\mathrm{K^{0}_{S}}$) are presented. The results are achieved through a femtoscopic analysis of $\Lambda$K correlations in Pb-Pb collisions at $\sqrt{s_{\mathrm{NN}}}$ = 2.76 TeV recorded by ALICE at the LHC. The femtoscopic correlations result from strong final-state interactions, and are fit with a parametrization allowing for both the characterization of the pair emission source and the measurement of the scattering parameters for the particle pairs. Extensive studies with the THERMINATOR 2 event generator provide a good description of the non-femtoscopic background, which results mainly from collective effects, with unprecedented precision. Furthermore, together with HIJING simulations, this model is used to account for contributions from residual correlations induced by feed-down from particle decays. The extracted scattering parameters indicate that the strong force is repulsive in the $\Lambda\rm{K}^{+}$ interaction and attractive in the $\Lambda\rm{K}^{-}$ interaction. The data hint that the and $\Lambda\rm{K}^{0}_{S}$ interaction is attractive, however the uncertainty of the result does not permit such a decisive conclusion. The results suggest an effect arising either from different quark-antiquark interactions between the pairs ($\rm s\overline{s}$ in $\Lambda$K$^{+}$ and $\rm u\overline{u}$ in $\Lambda$K$^{-}$) or from different net strangeness for each system (S = 0 for $\Lambda$K$^{+}$, and S = $-2$ for $\Lambda$K$^{-}$). Finally, the $\Lambda$K systems exhibit source radii larger than expected from extrapolation from identical particle femtoscopic studies. This effect is interpreted as resulting from the separation in space-time of the single-particle $\Lambda$ and K source distributions.
Phys. Rev. C 103 (2021) 055201
HEP Data
e-Print: arXiv:2005.11124 | PDF | inSPIRE
CERN-EP-2020-080