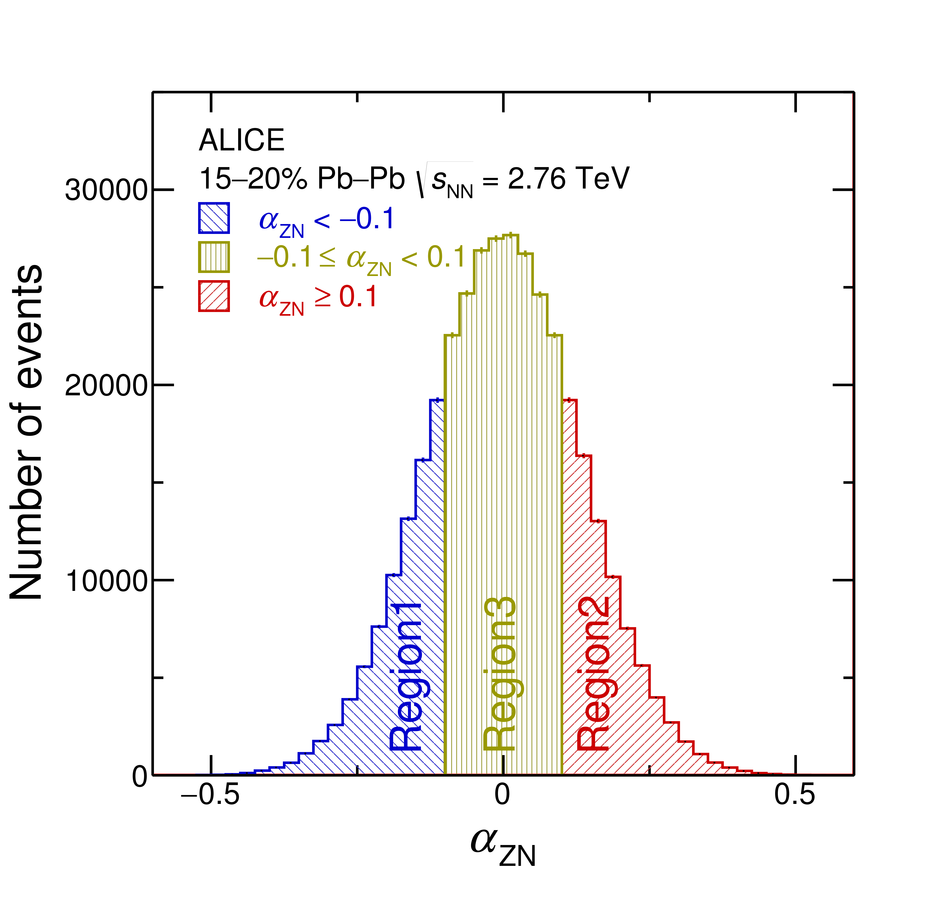
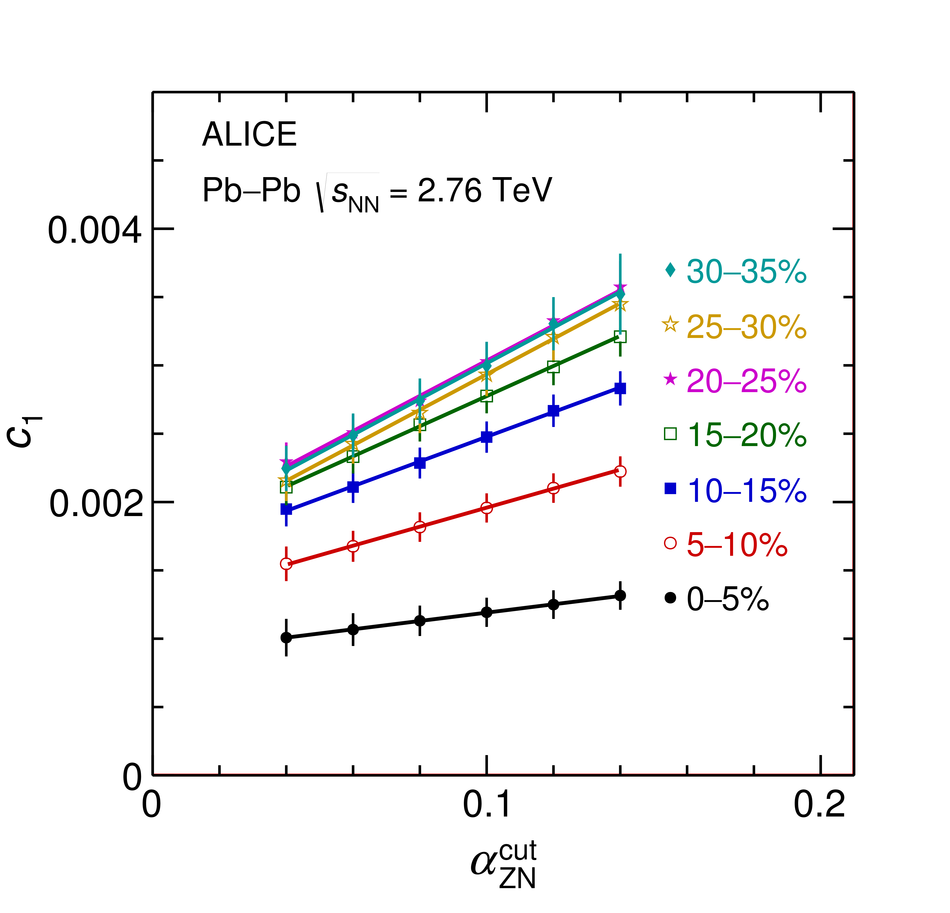
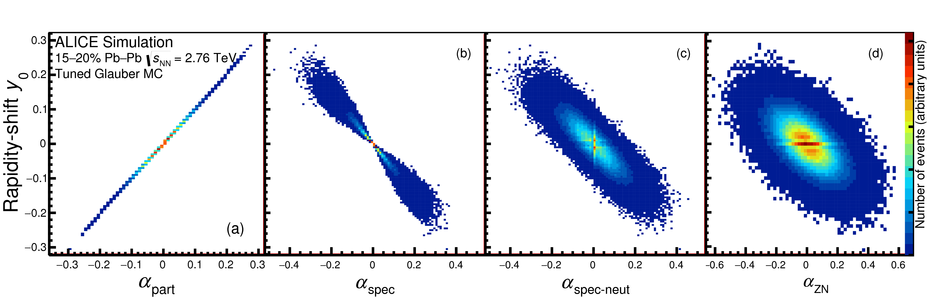
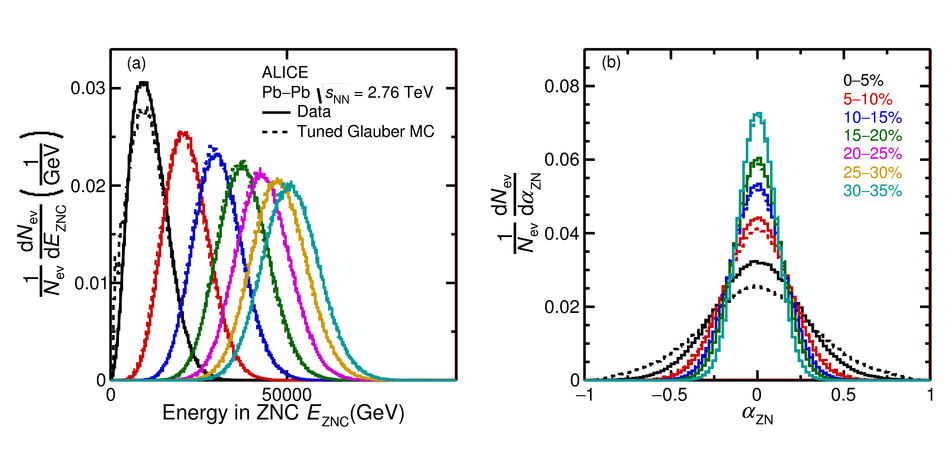
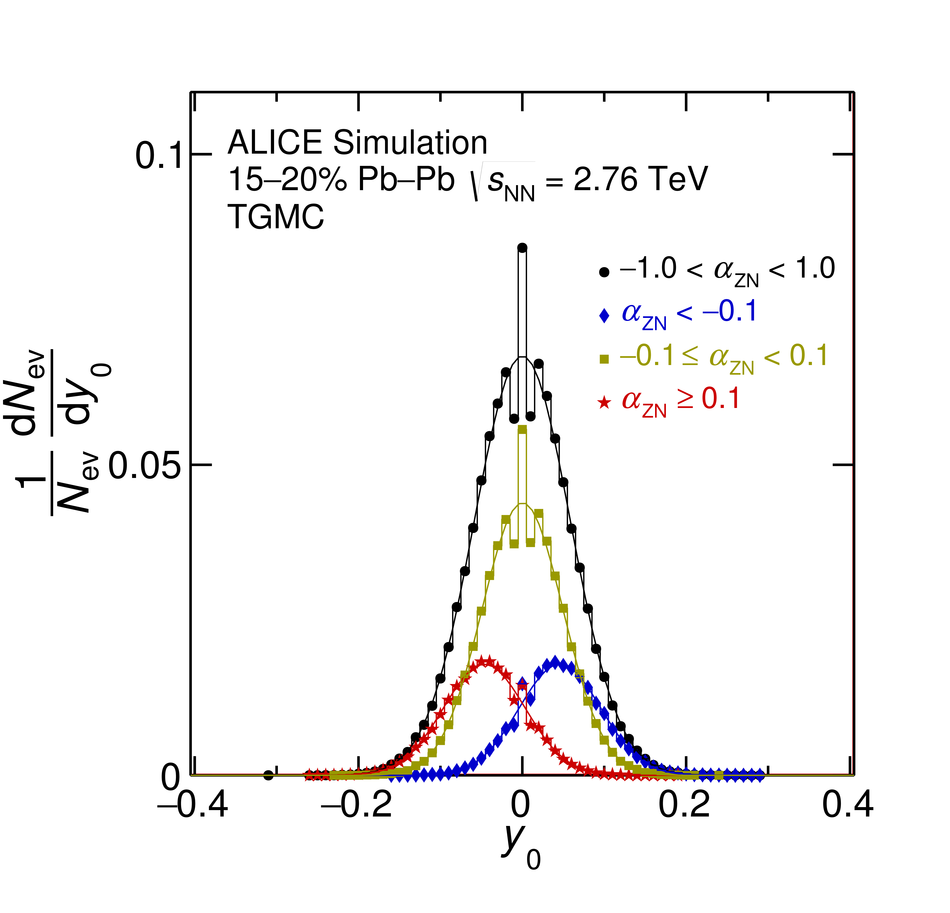
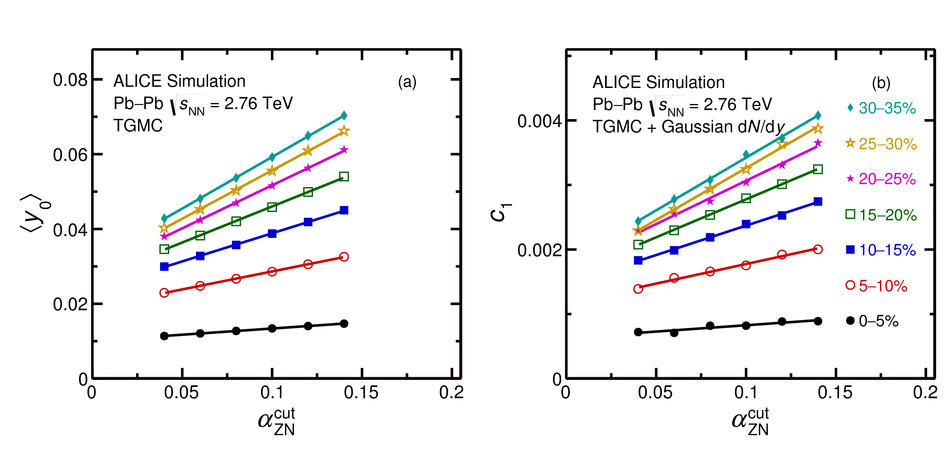
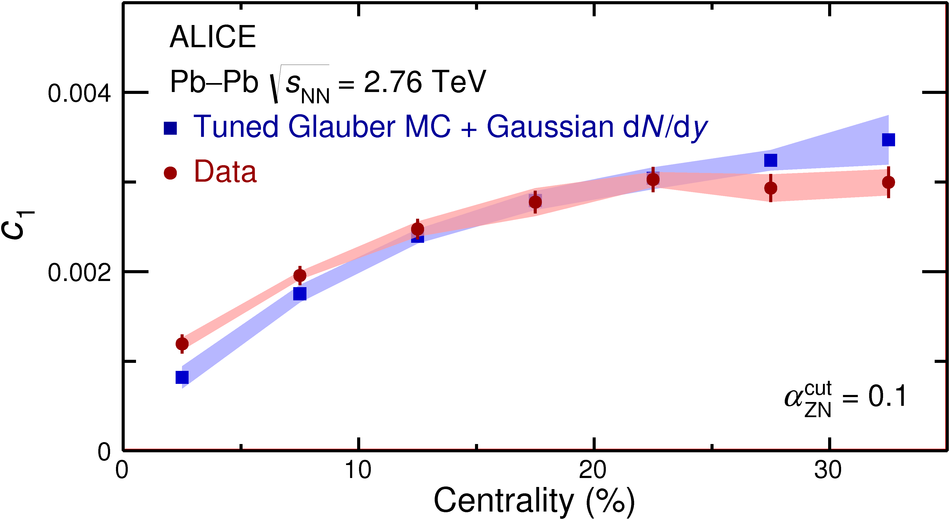
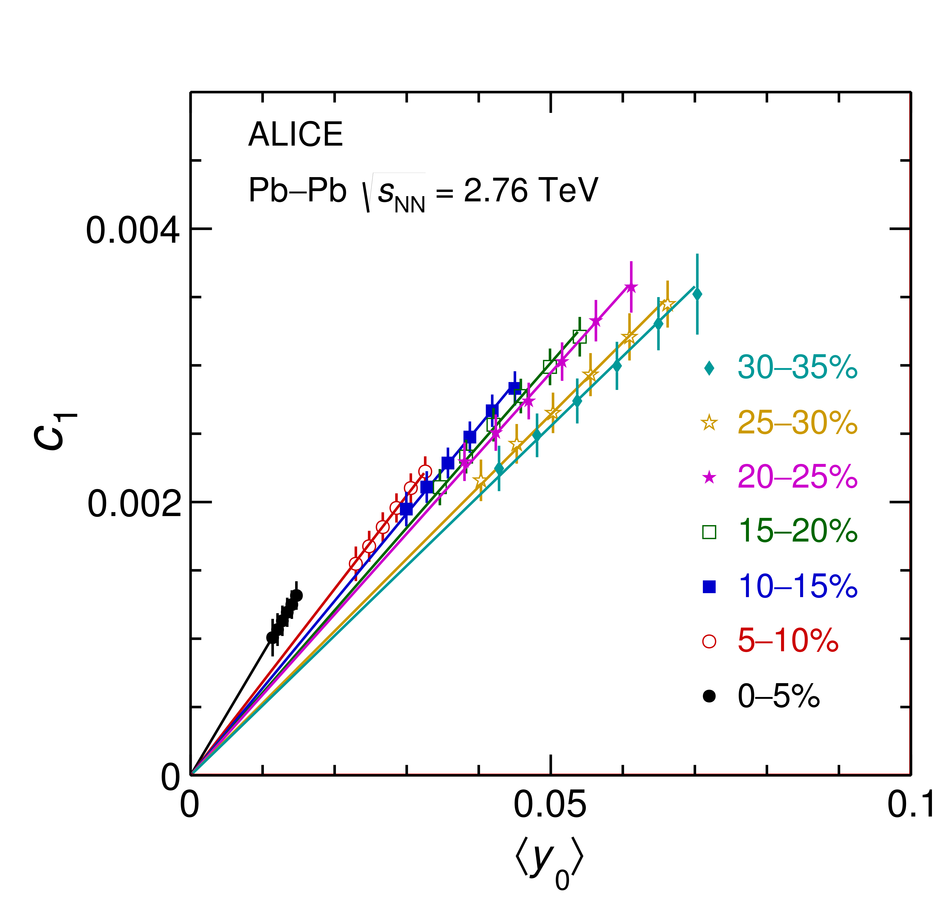
First results on the longitudinal asymmetry and its effect on the pseudorapidity distributions in Pb-Pb collisions at $\sqrt{s_{\mathrm{NN}}}$ = 2.76 TeV at the Large Hadron Collider are obtained with the ALICE detector. The longitudinal asymmetry arises because of an unequal number of participating nucleons from the two colliding nuclei, and is estimated for each event by measuring the energy in the forward neutron-Zero-Degree-Calorimeters (ZNs). The effect of the longitudinal asymmetry is measured on the pseudorapidity distributions of charged particles in the regions $|\eta| <~ 0.9$, $2.8 <~ \eta <~ 5.1$ and $-3.7 <~ \eta <~ -1.7 $ by taking the ratio of the pseudorapidity distributions from events corresponding to different regions of asymmetry. The coefficients of a polynomial fit to the ratio characterise the effect of the asymmetry. A Monte Carlo simulation using a Glauber model for the colliding nuclei is tuned to reproduce the spectrum in the ZNs and provides a relation between the measurable longitudinal asymmetry and the shift in the rapidity ($y_{\mathrm{0}}$) of the participant zone formed by the unequal number of participating nucleons. The dependence of the coefficient of the linear term in the polynomial expansion, $c_{\rm 1}$, on the mean value of $y_{\mathrm{0}}$ is investigated.
Phys. Lett. B 781 (2018) 20-32
e-Print: arXiv:1710.07975 | PDF | inSPIRE
CERN-EP-2017-277