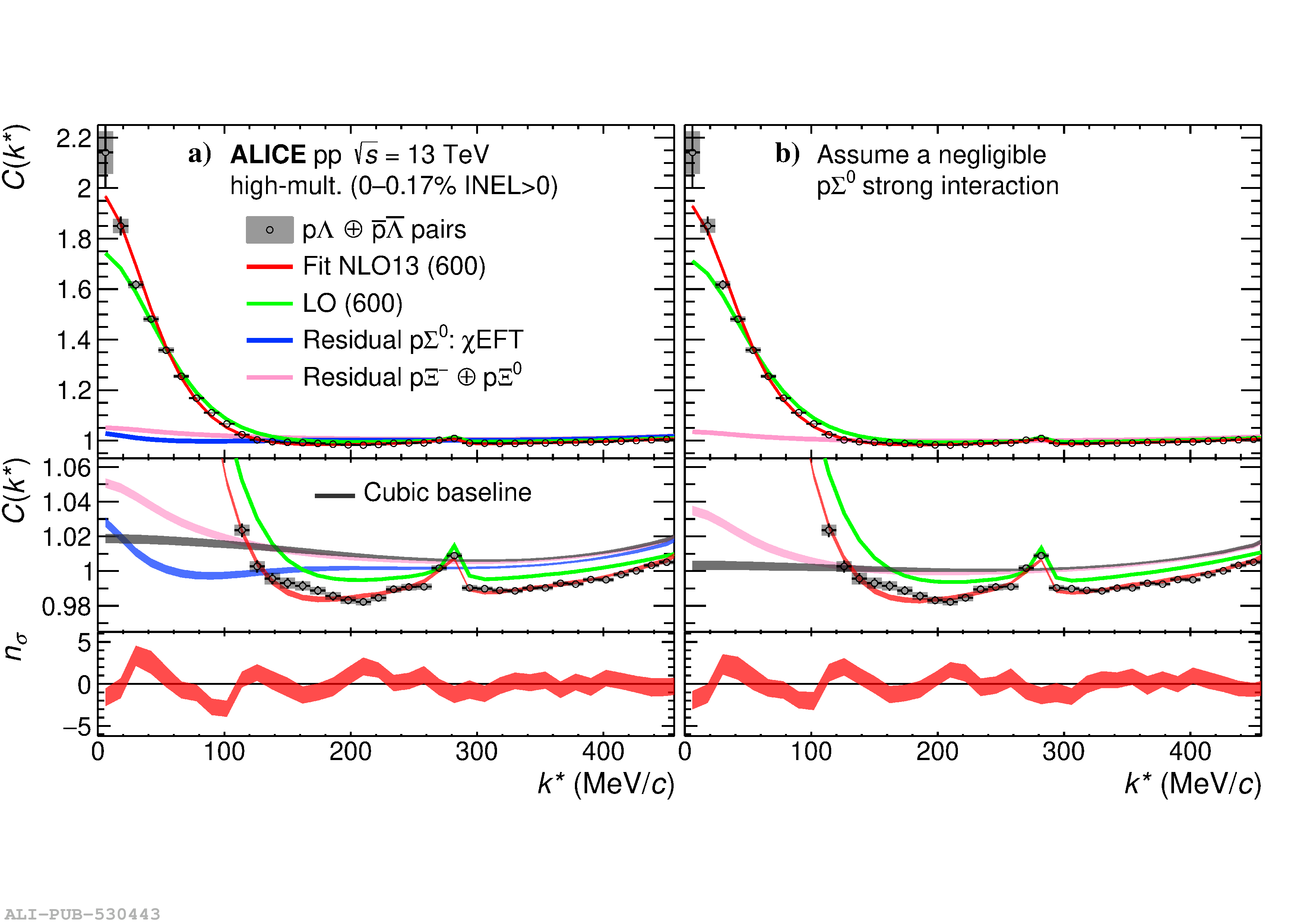
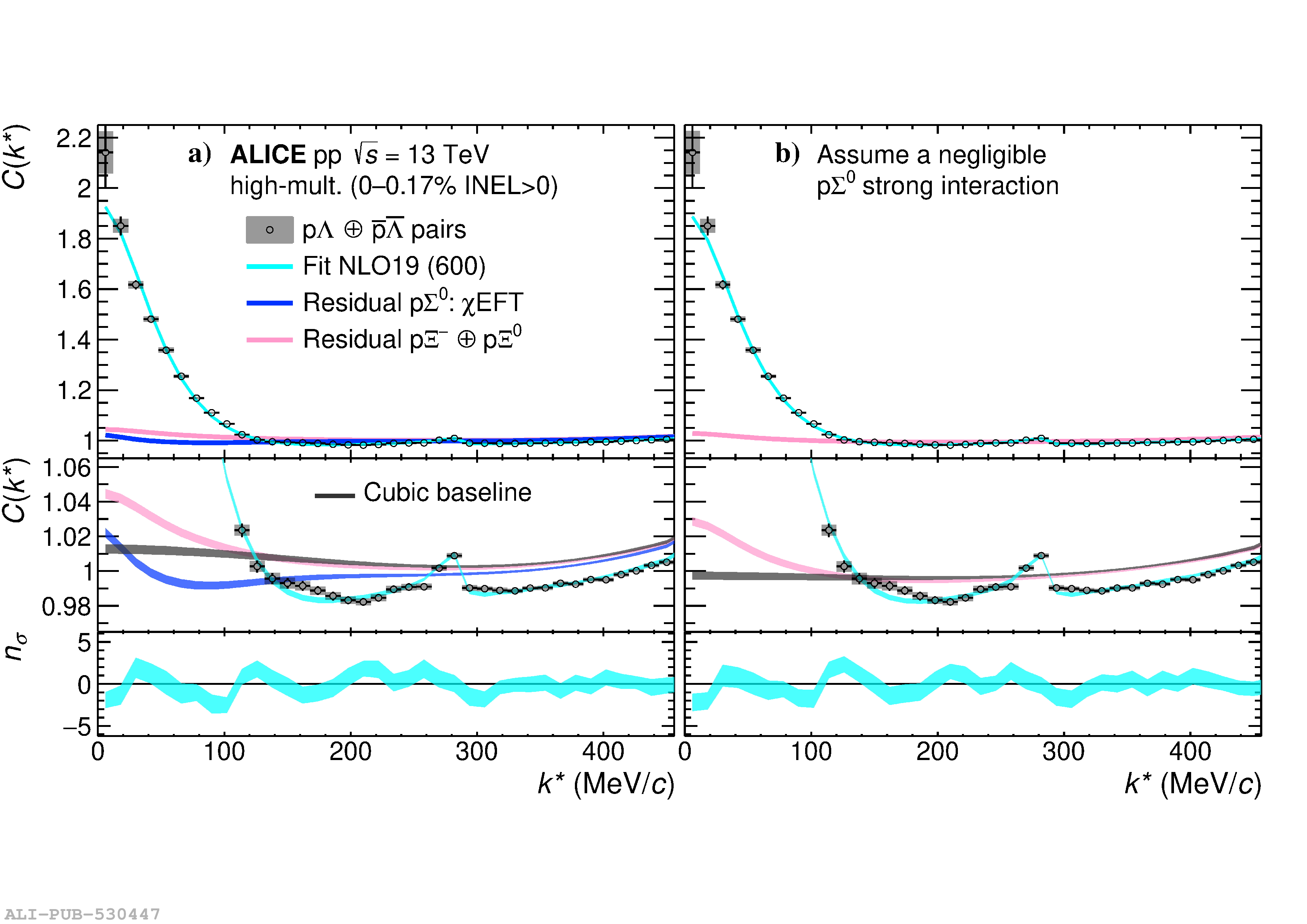
The interaction of $\Lambda$ and $\Sigma$ hyperons (Y) with nucleons (N) is strongly influenced by the coupled-channel dynamics. Due to the small mass difference of the $\rm N \Lambda$ and $\rm N \Sigma$ systems, the sizeable coupling strength of the $\rm N \Sigma\leftrightarrow N \Lambda$ processes constitutes a crucial element in the determination of the N$\Lambda$ interaction. In this letter we present the most precise measurements on the interaction of p$\Lambda$ pairs, from zero relative momentum up to the opening of the $\rm N \Sigma$ channel. The correlation function in the relative momentum space for $\mathrm{p}\Lambda\oplus\overline{\mathrm{p}}\overline{\Lambda}$ pairs measured in high-multiplicity triggered pp collisions at $\sqrt{s}~=~13$ TeV at the LHC is reported. The opening of the inelastic N$\Sigma$ channels is visible in the extracted correlation function as a cusp-like structure occurring at relative momentum $k^{*}$ = 289 MeV/$c$. This represents the first direct experimental observation of the $\rm N \Sigma\rightarrow N \Lambda$ coupled channel in the p$\Lambda$ system. The correlation function is compared with recent chiral effective field theory calculations, based on different strengths of the $\rm N \Sigma\leftrightarrow N \Lambda$ transition potential. A weaker coupling, as possibly supported by the present measurement, would require a more repulsive three-body NN$\Lambda$ interaction for a proper description of the $\Lambda$ in-medium properties, which has implications on the nuclear equation of state and for the presence of hyperons inside neutron stars.