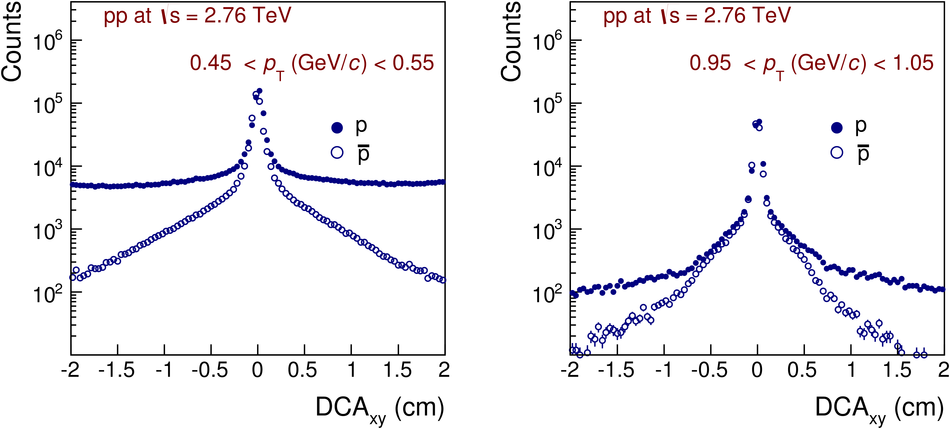
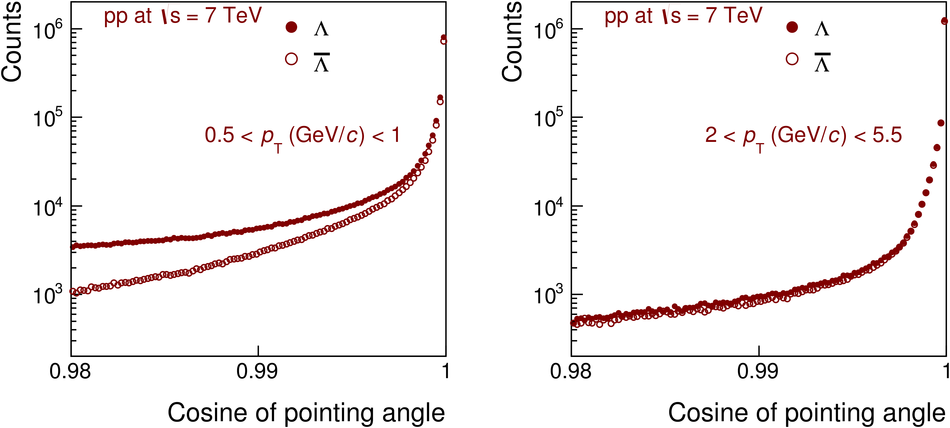
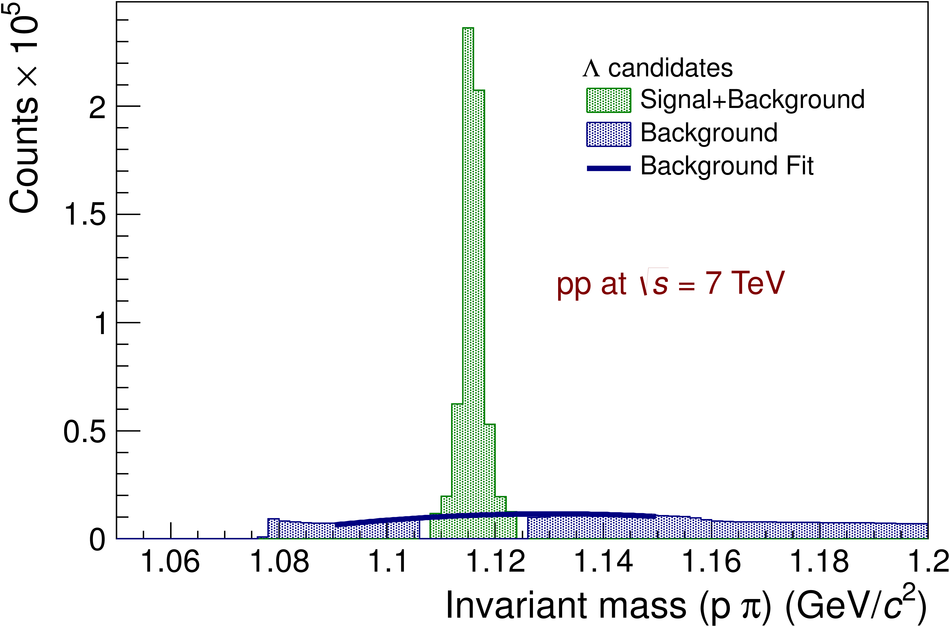
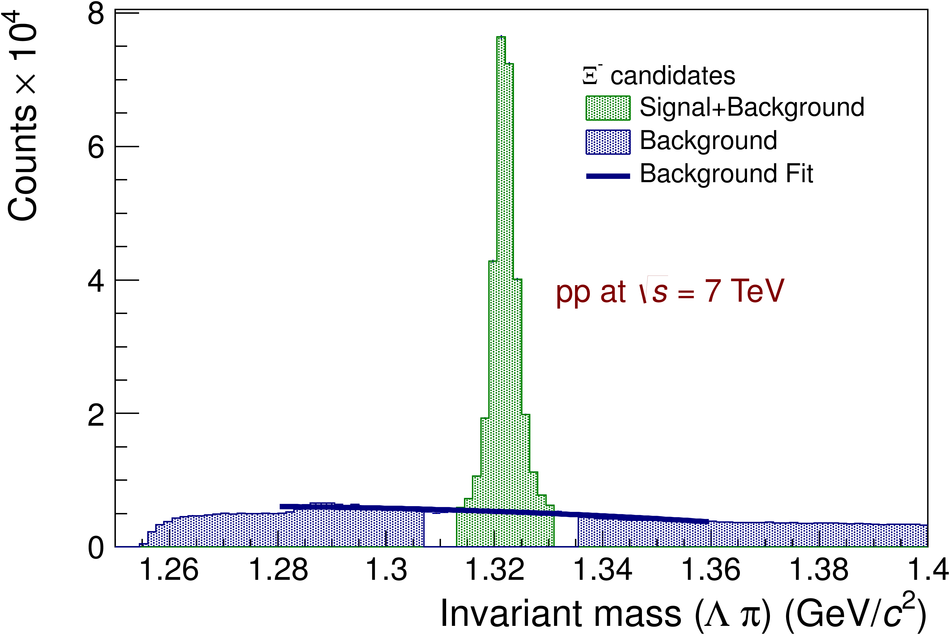
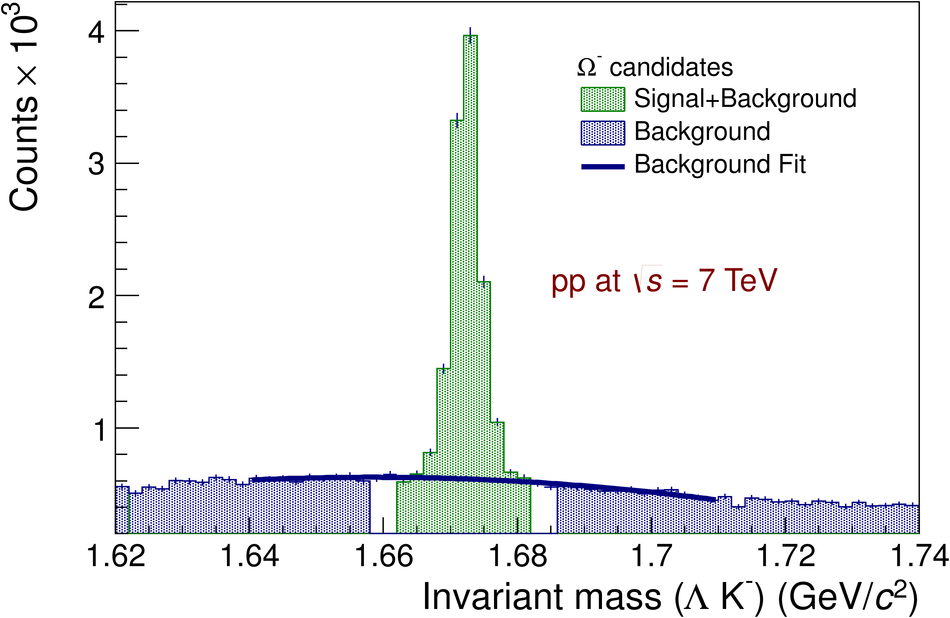
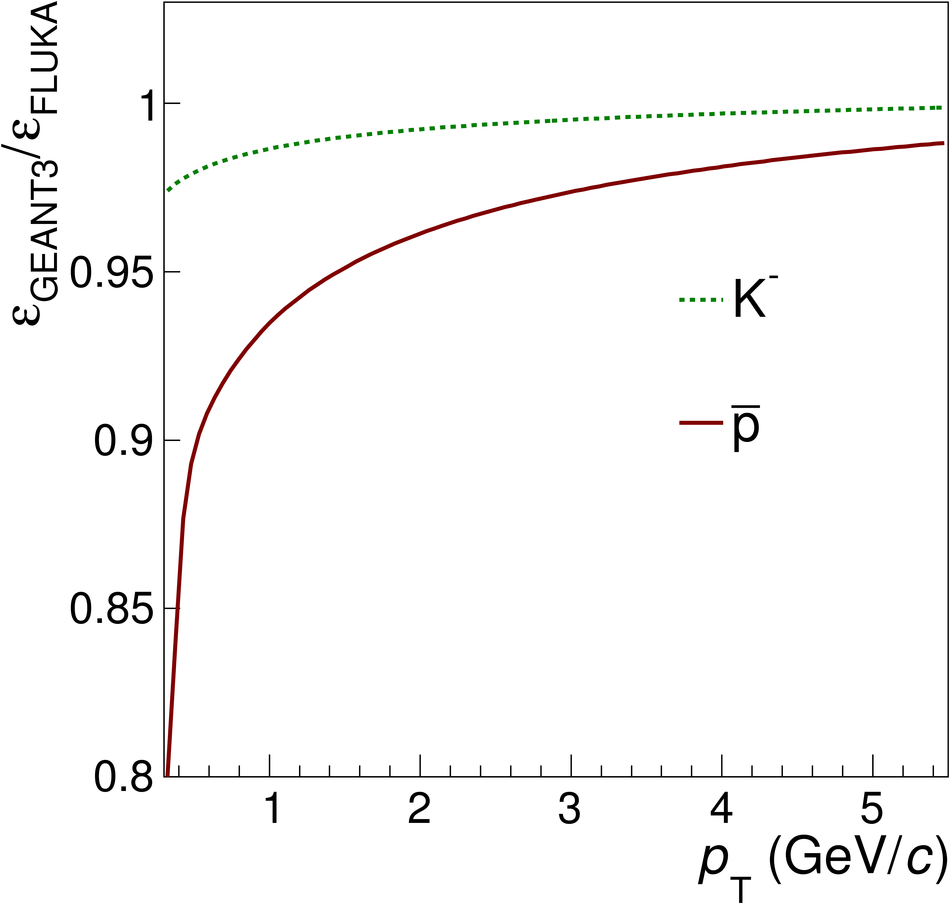
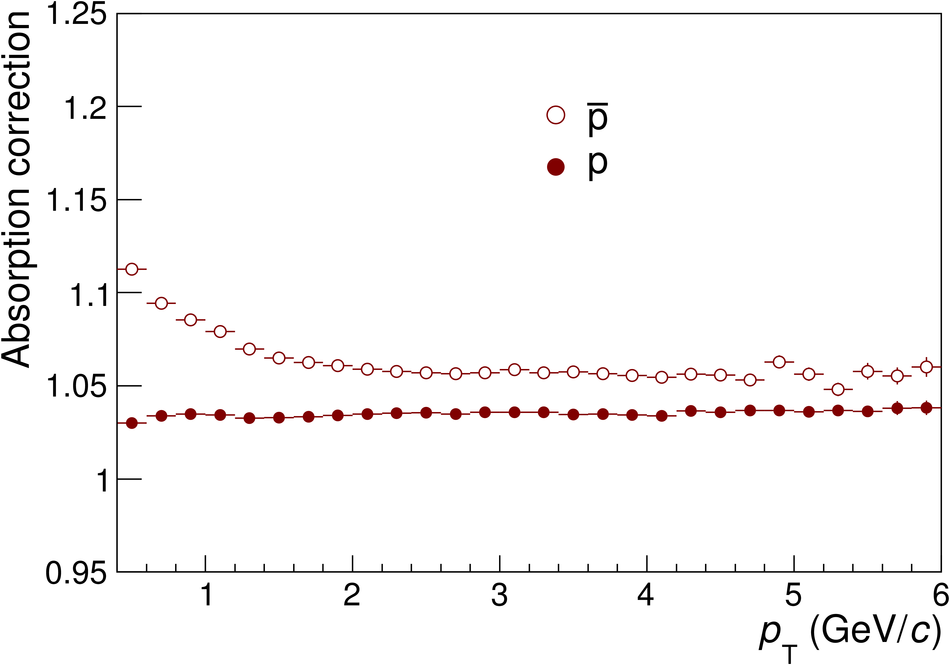
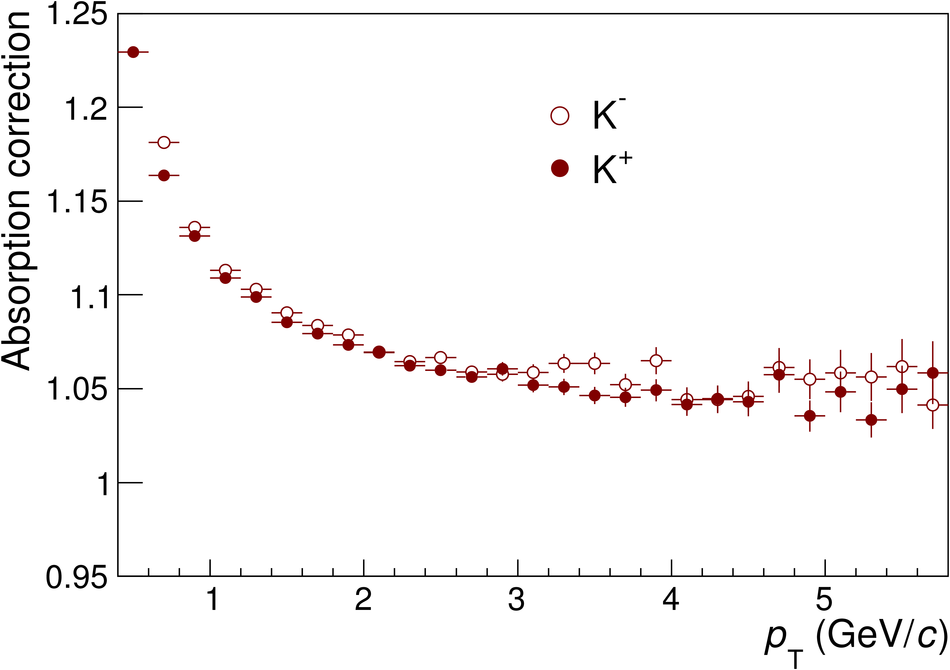
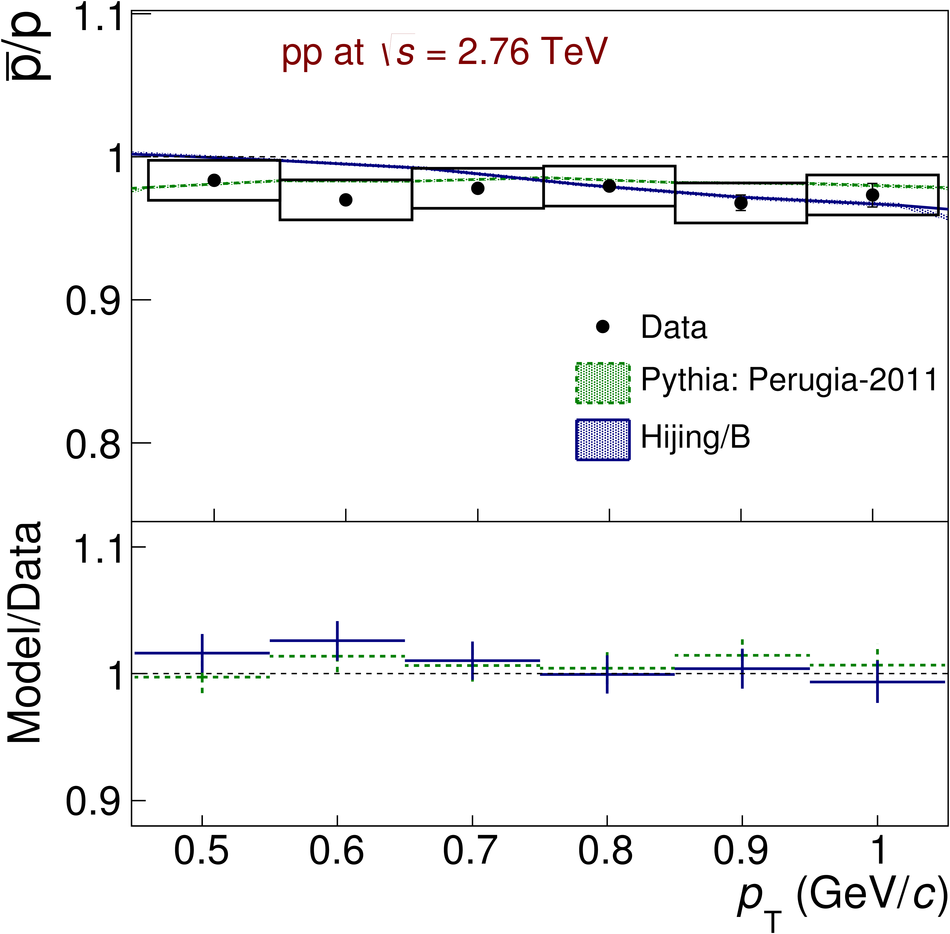
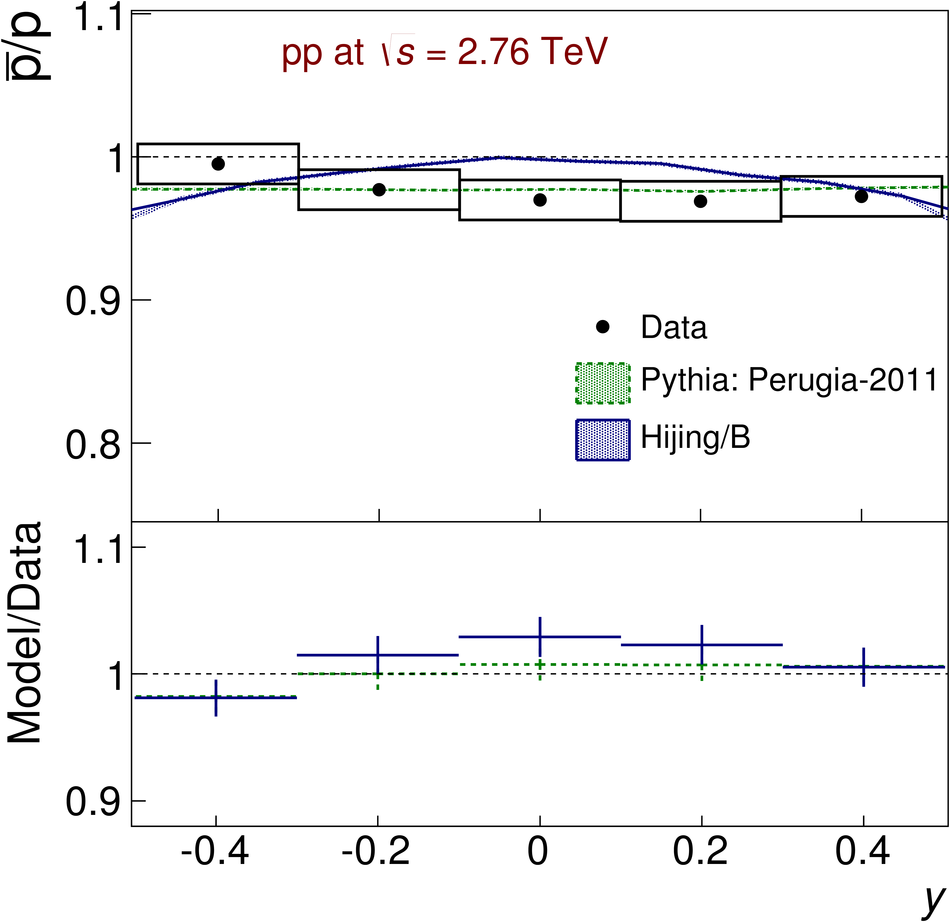
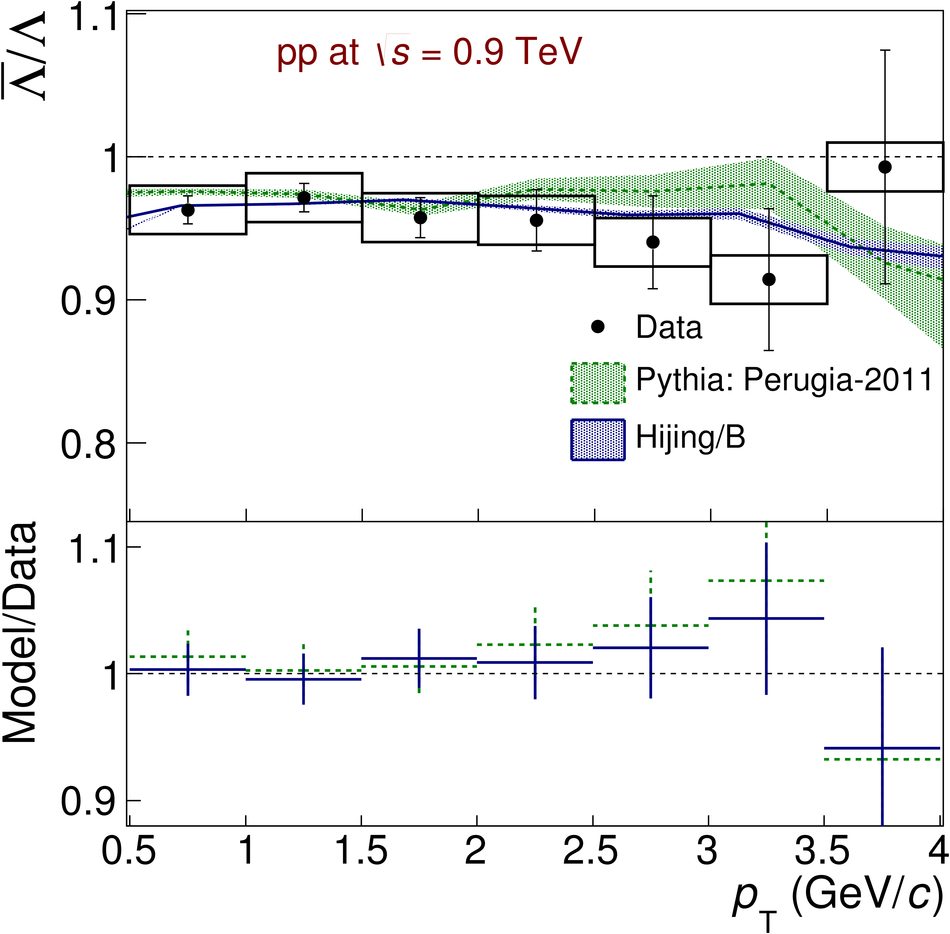
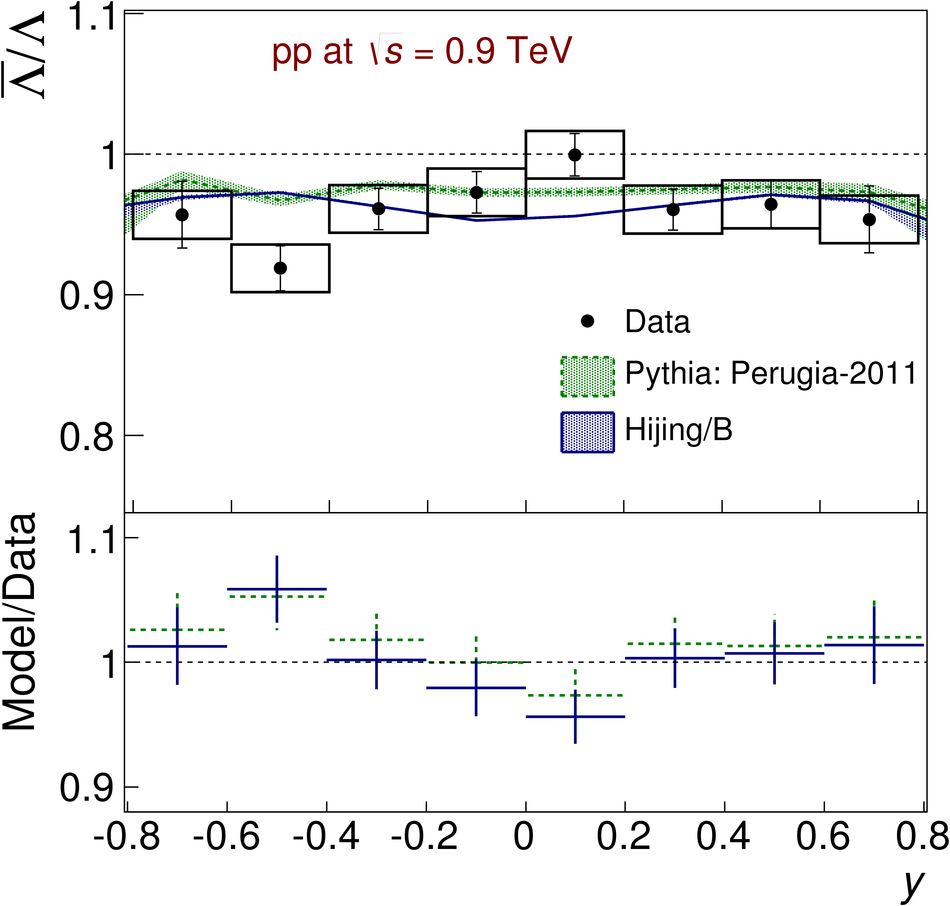
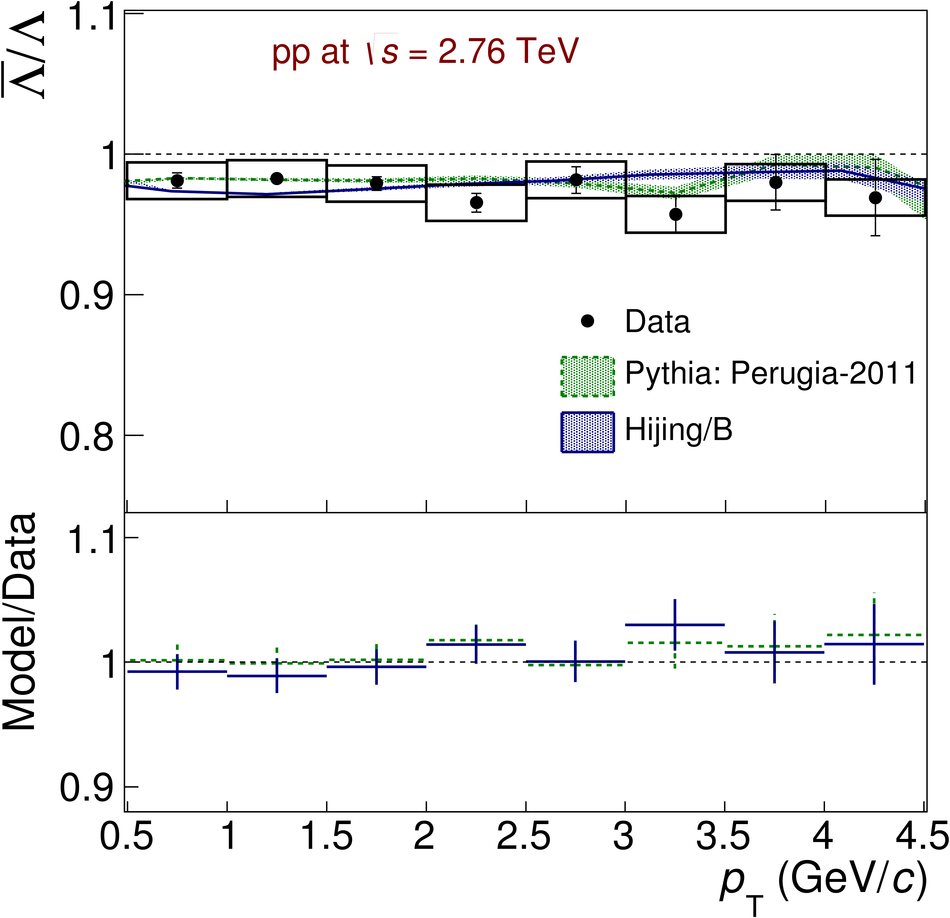
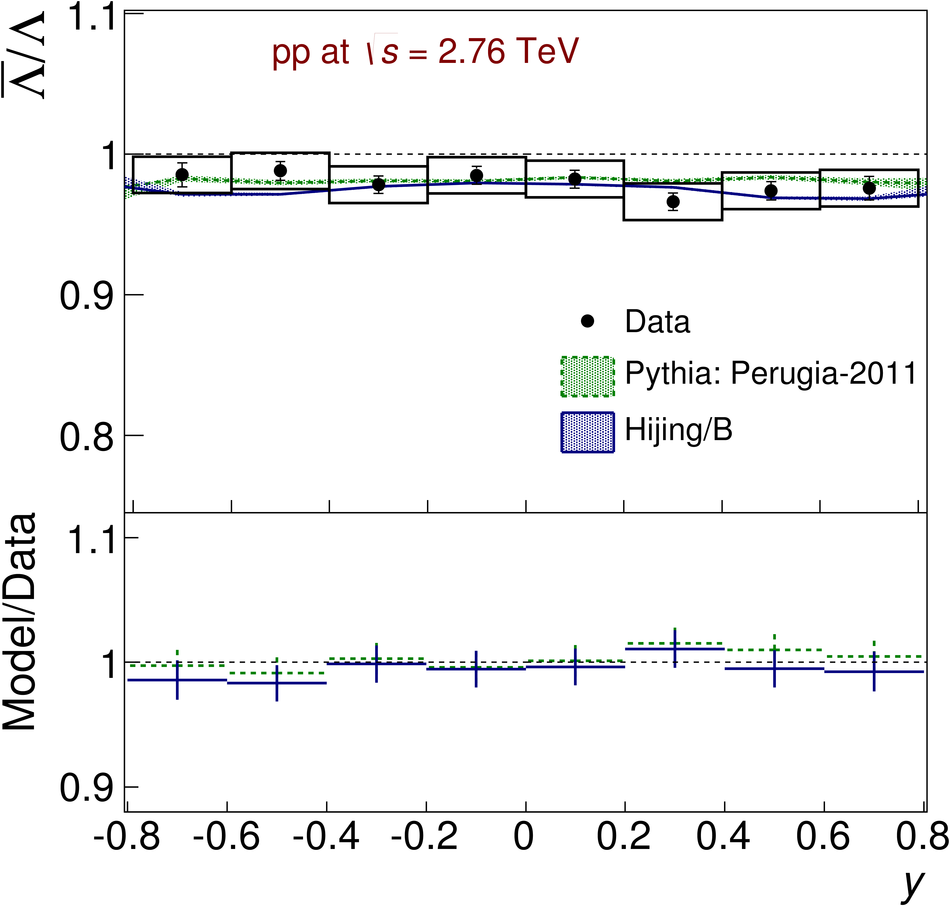
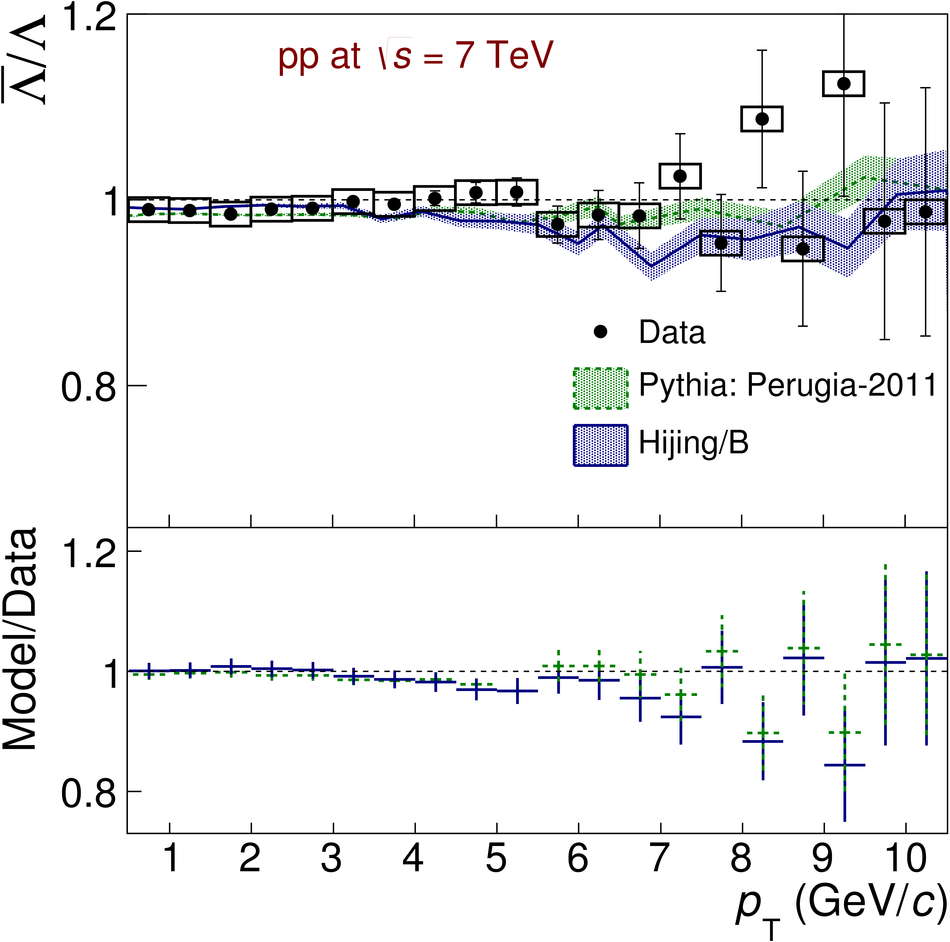
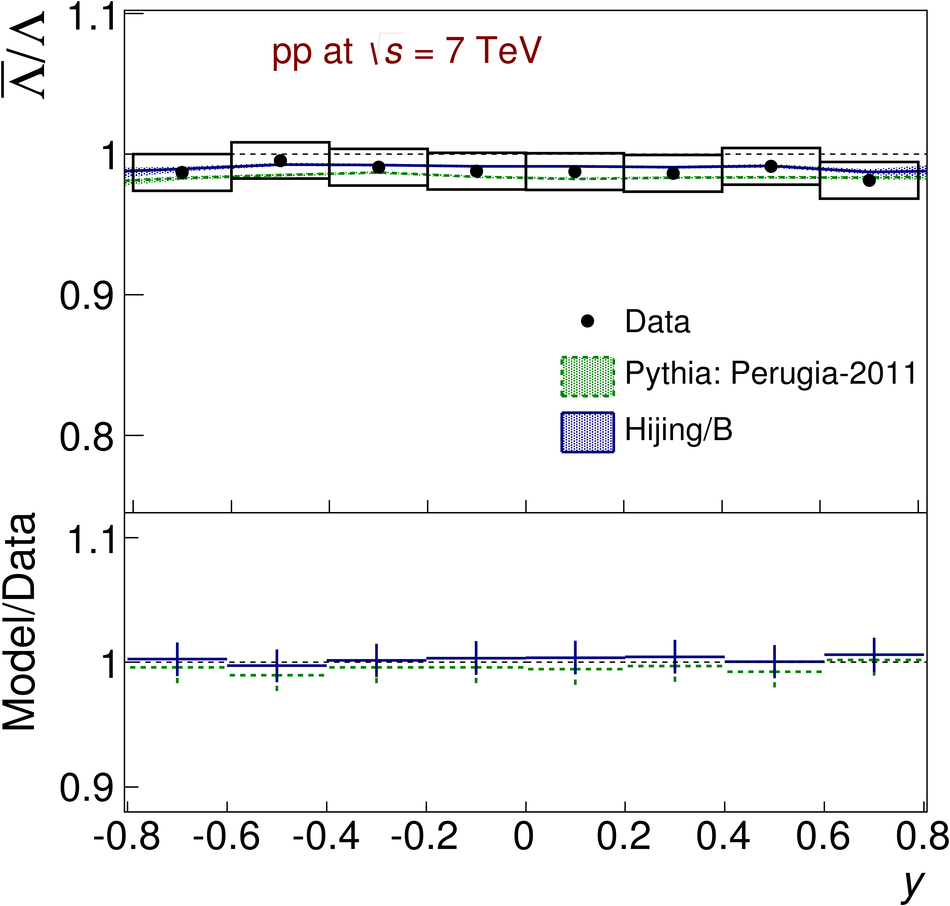
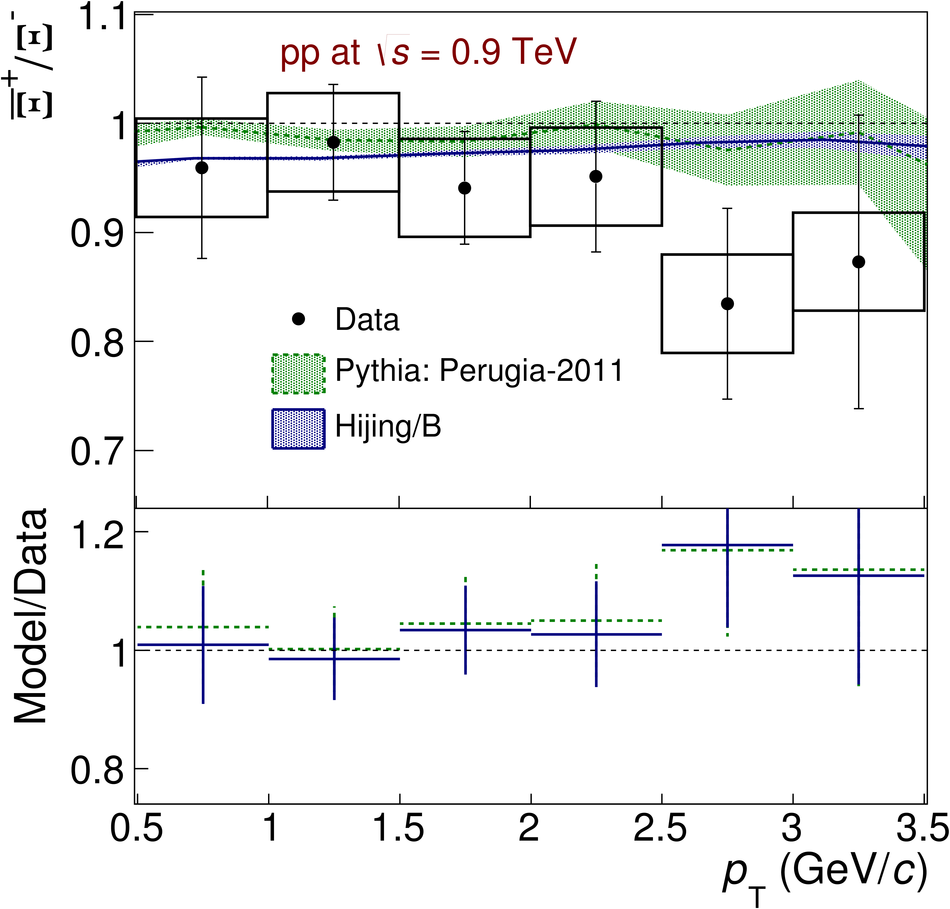
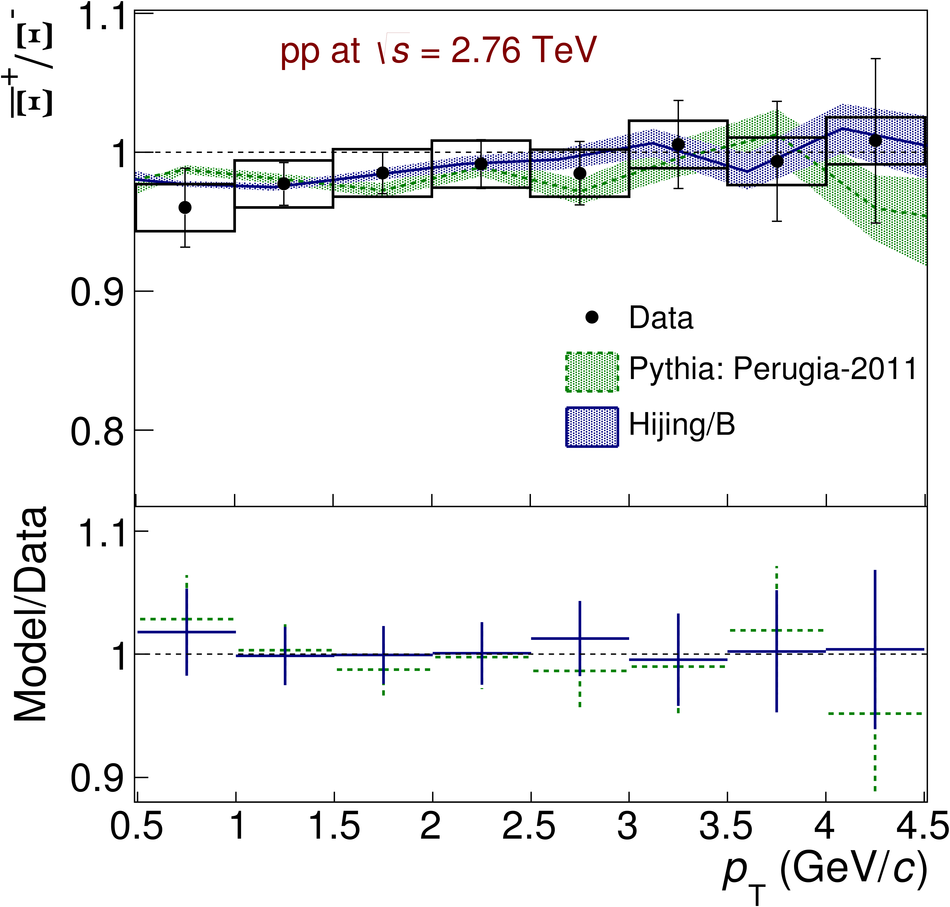
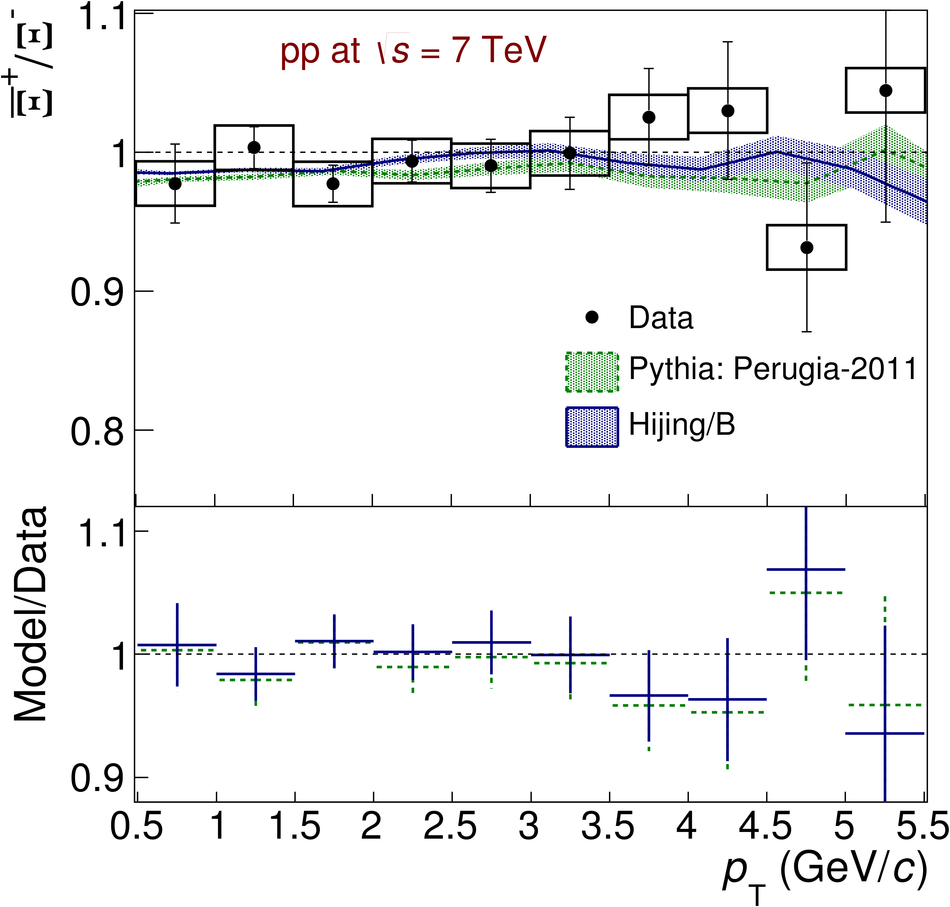
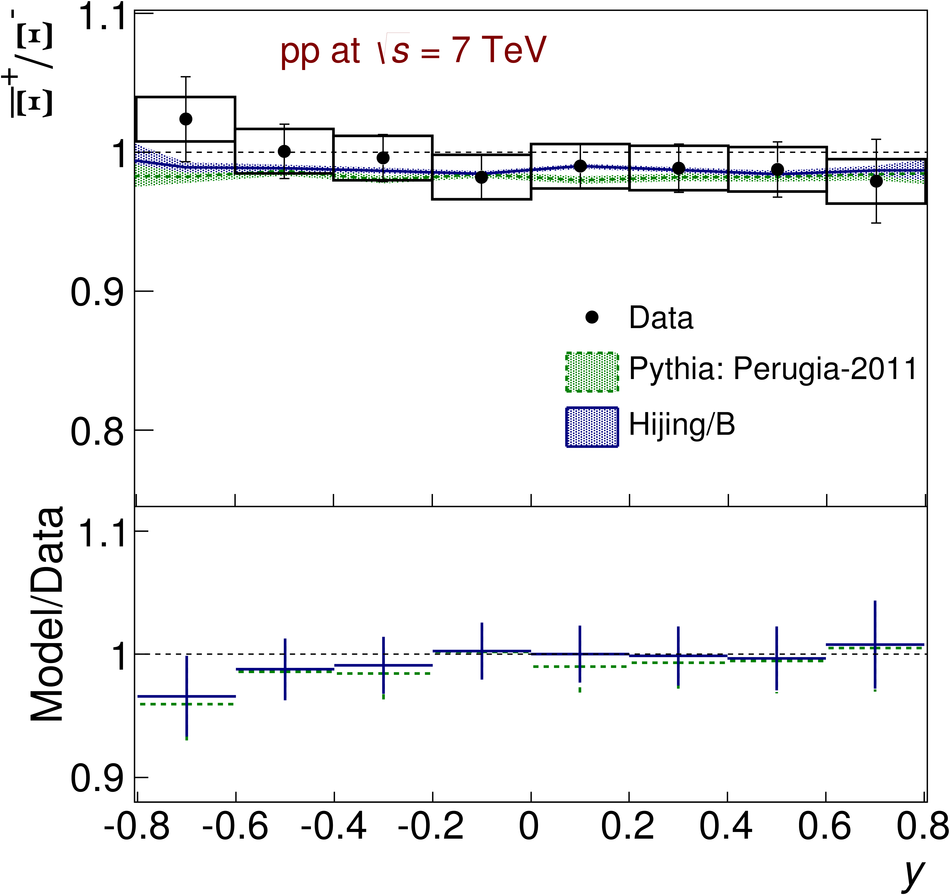
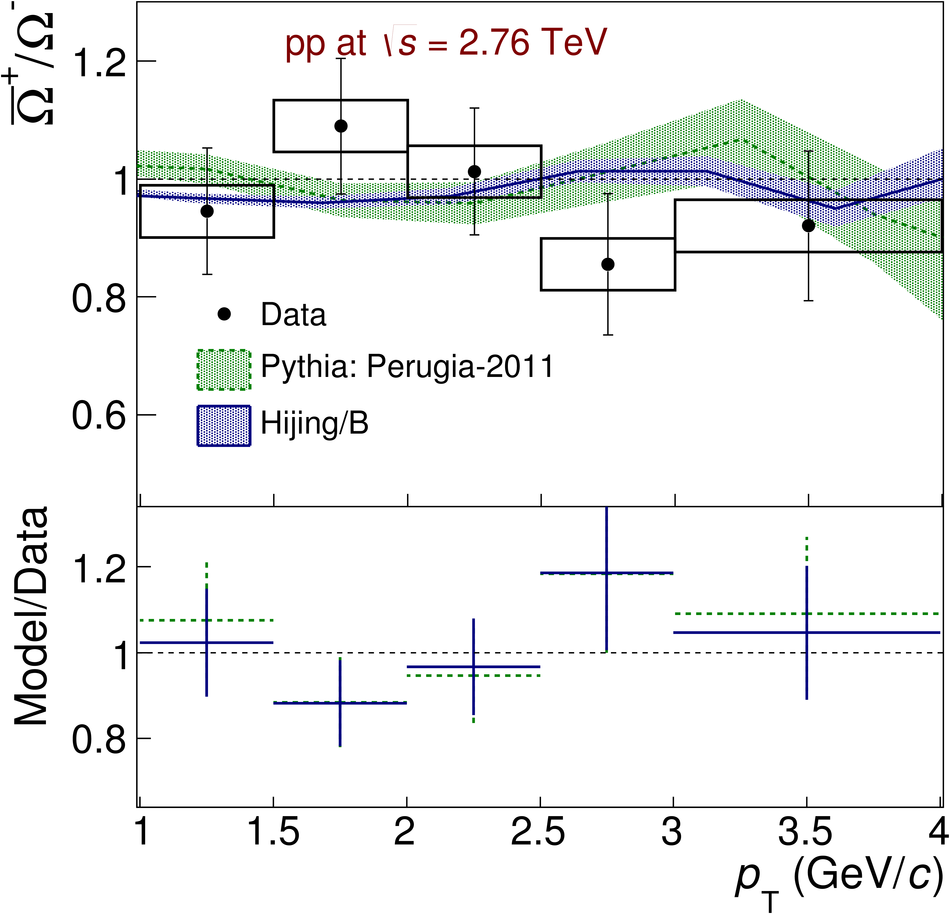
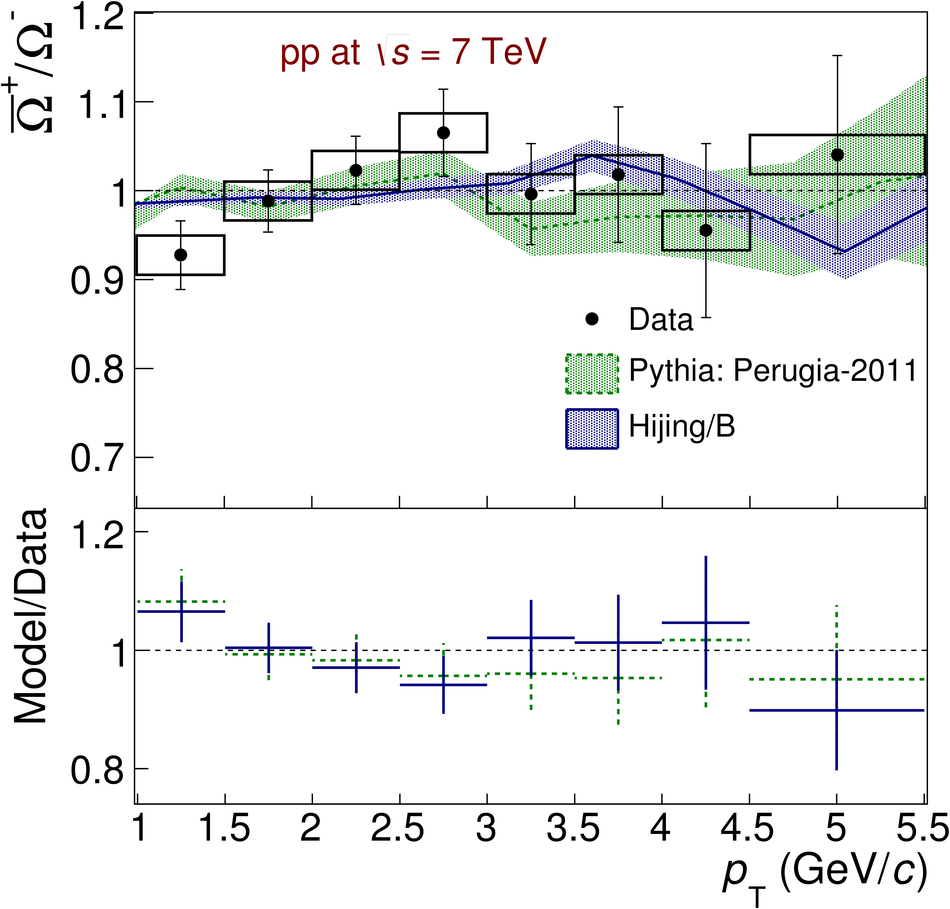
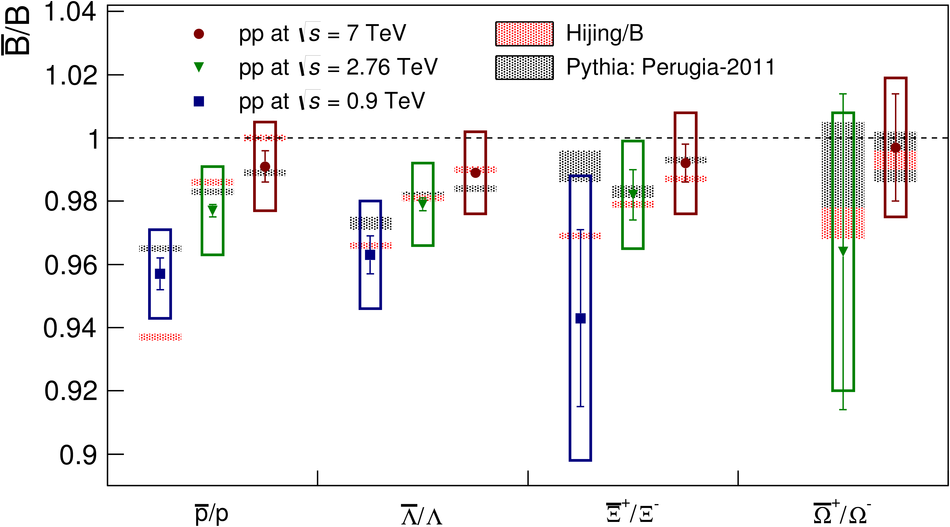
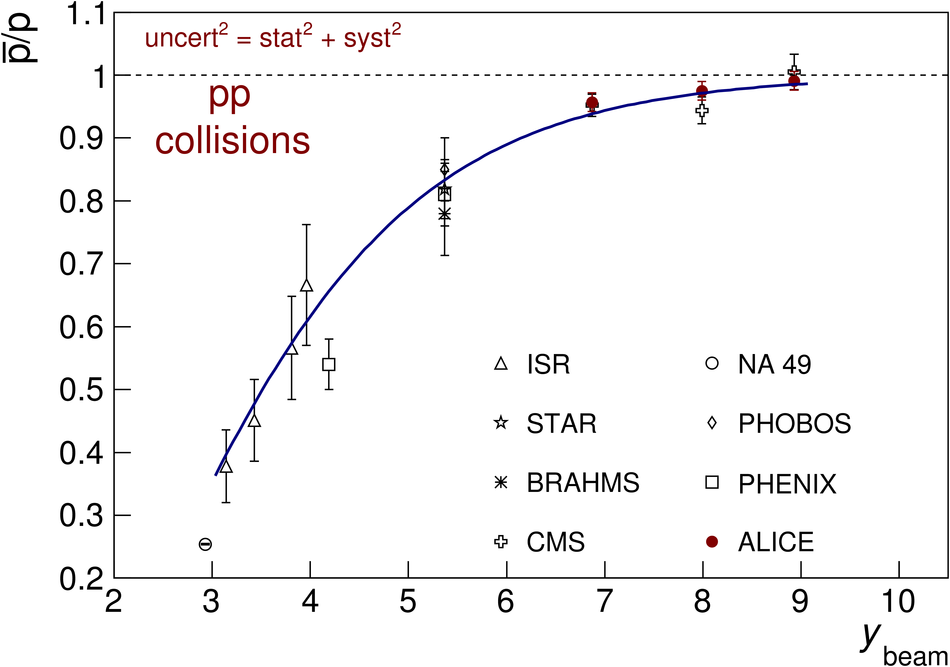
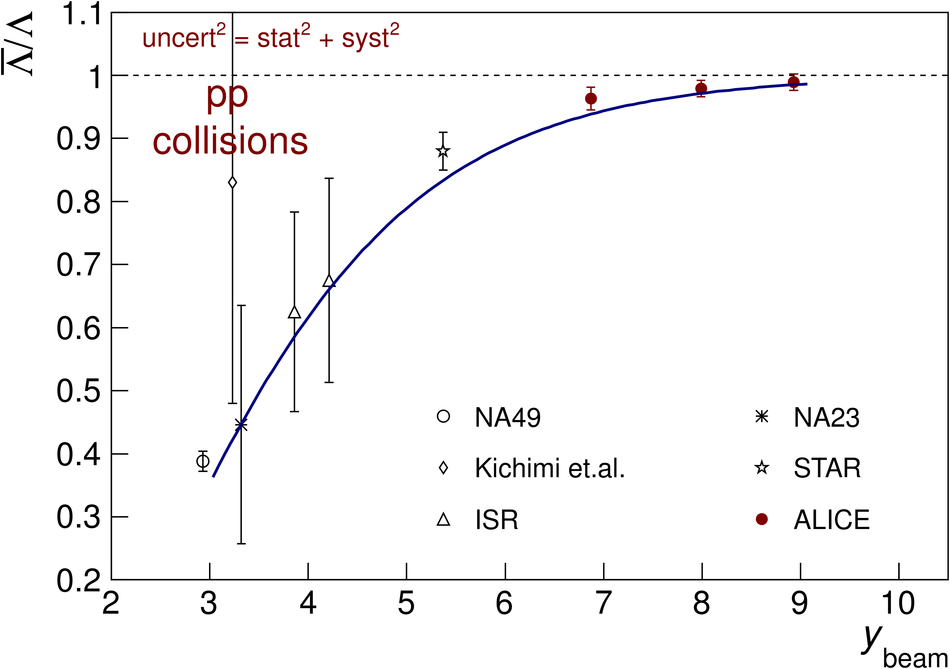
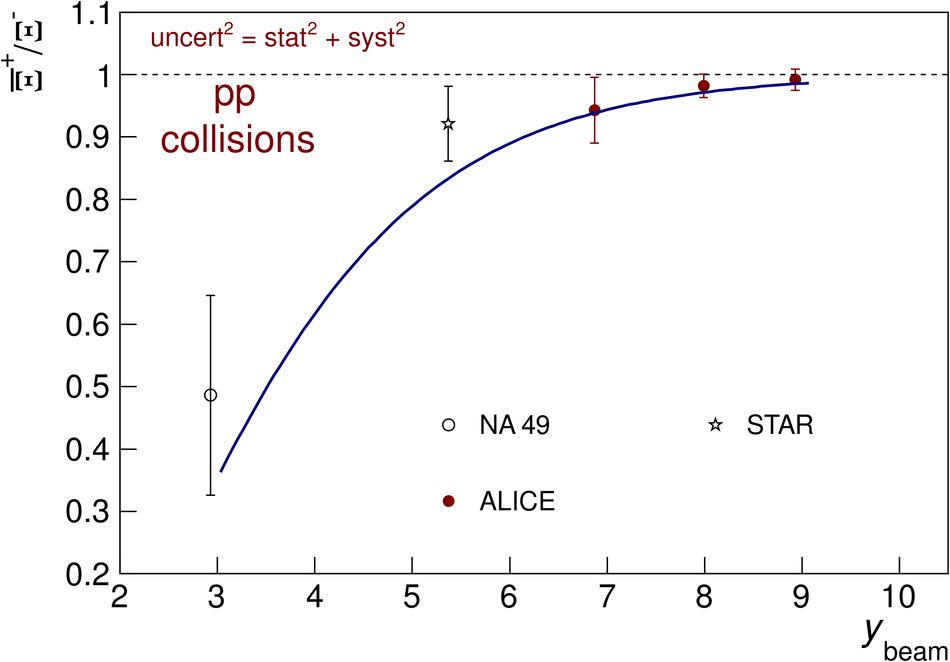
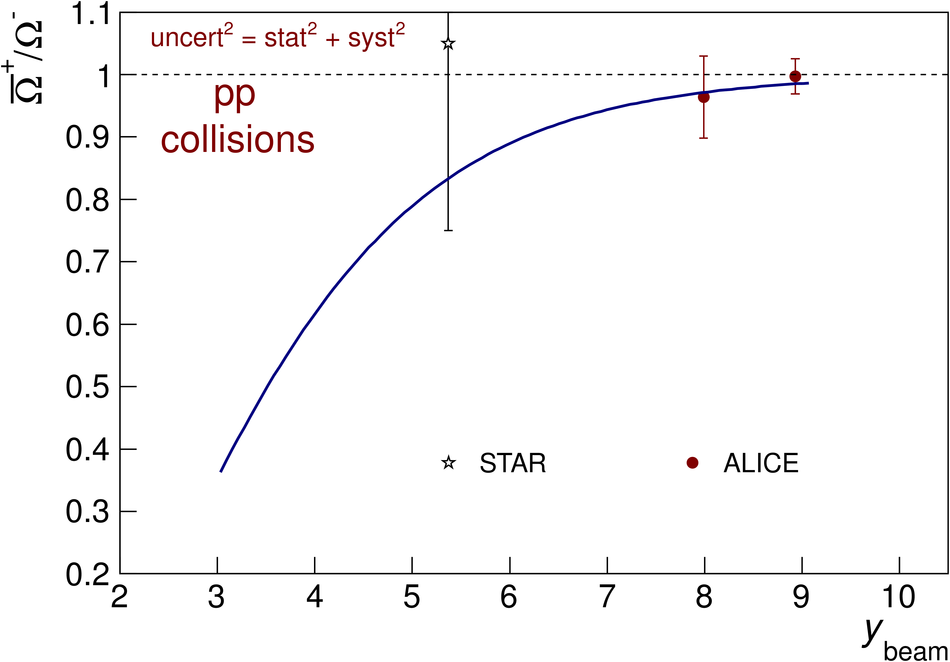
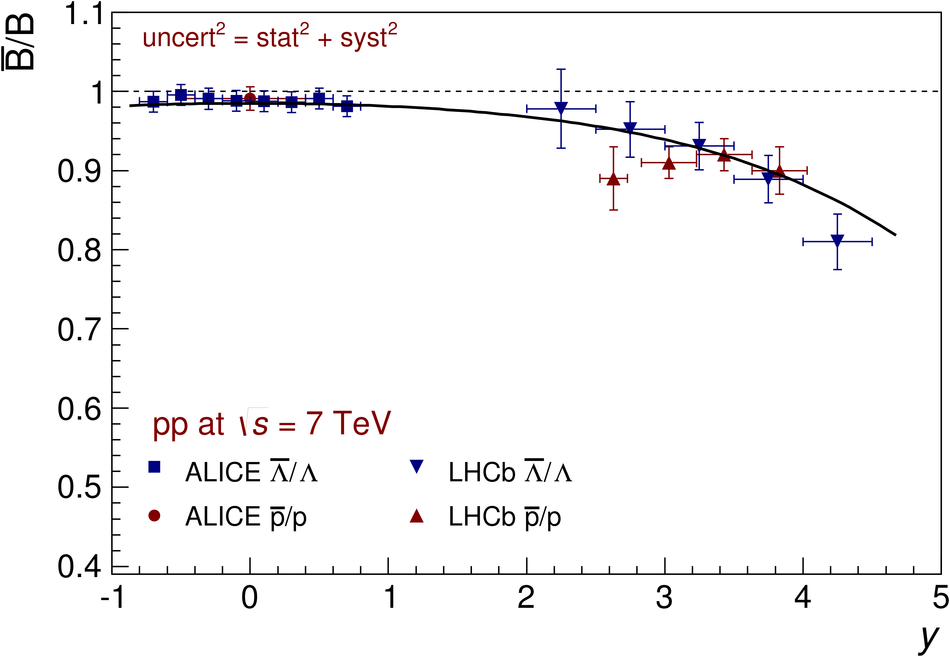
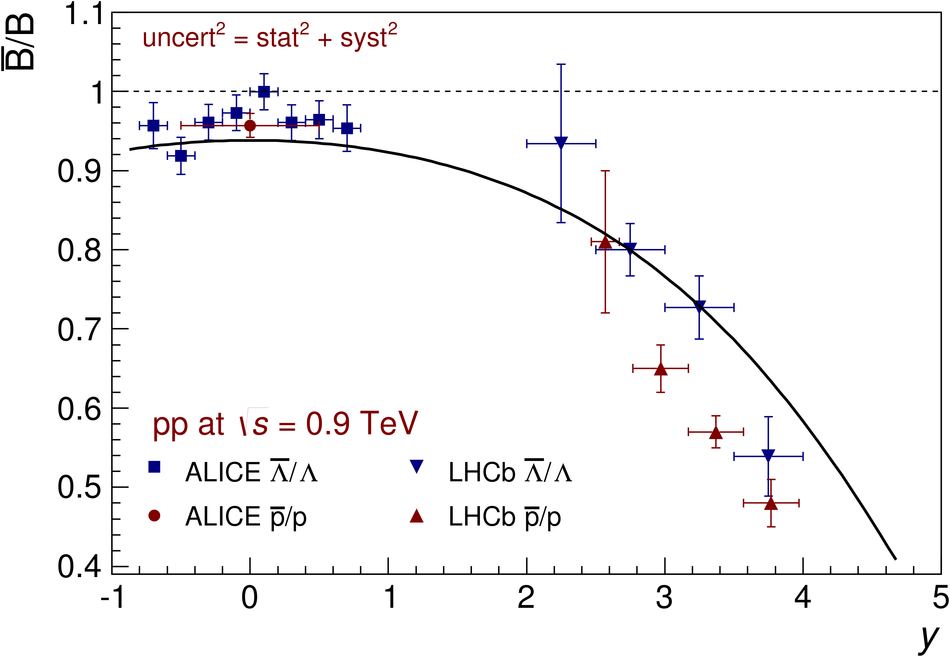
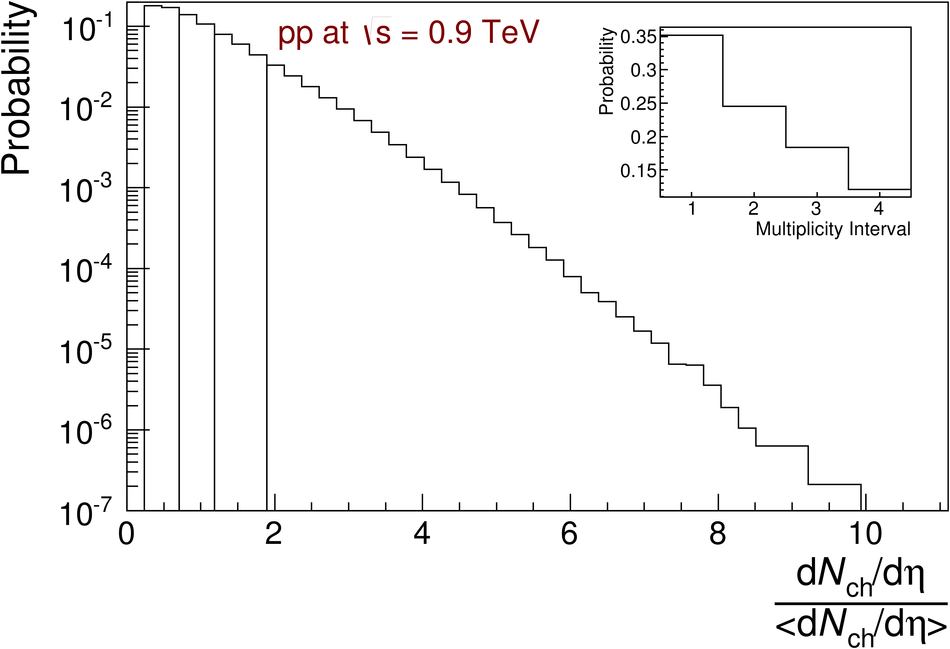
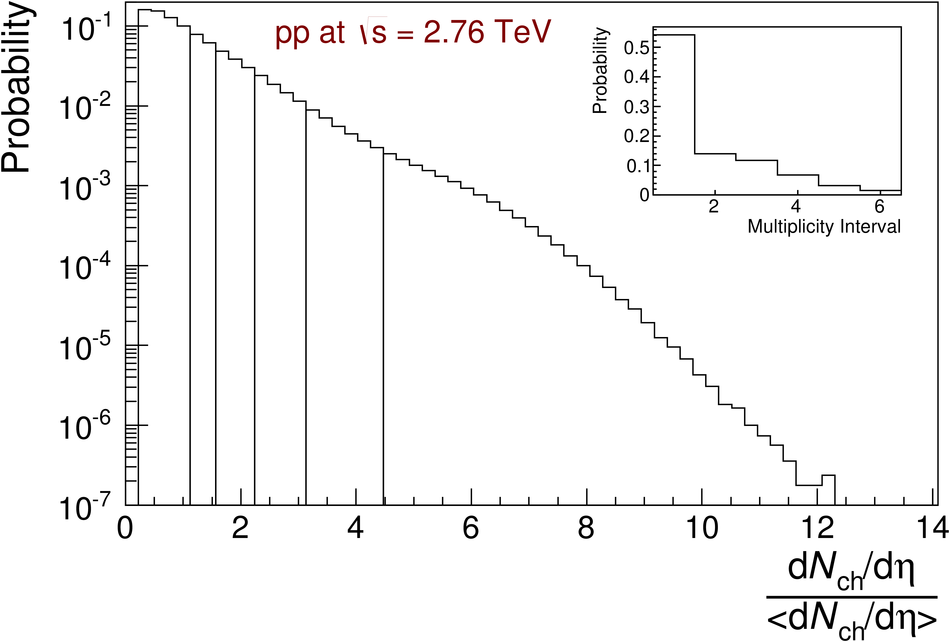
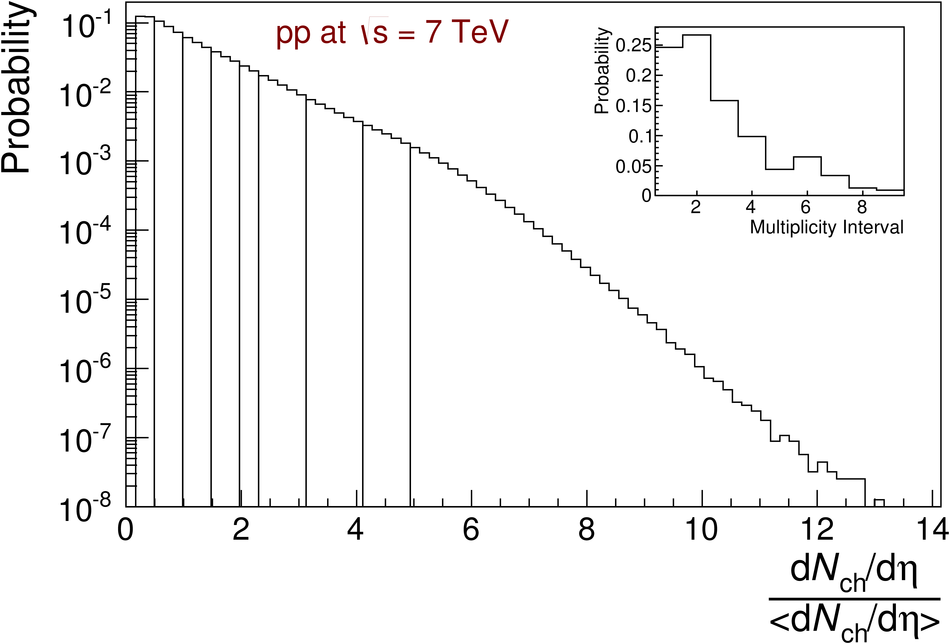
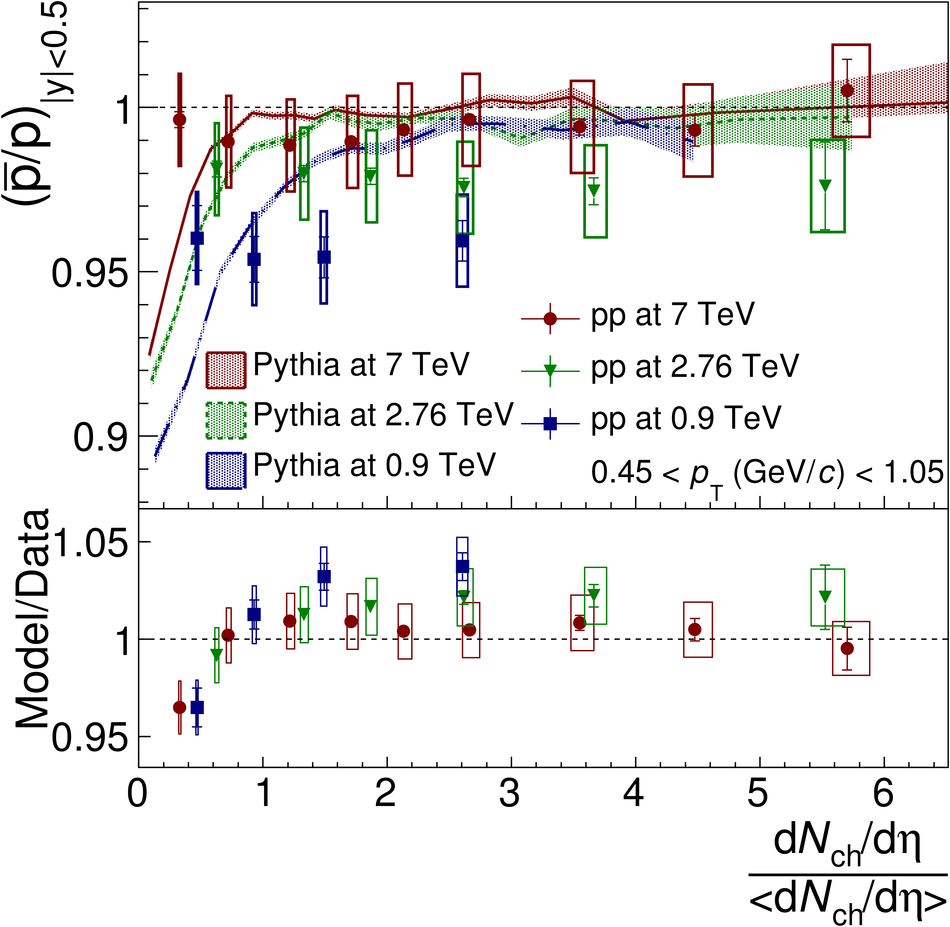
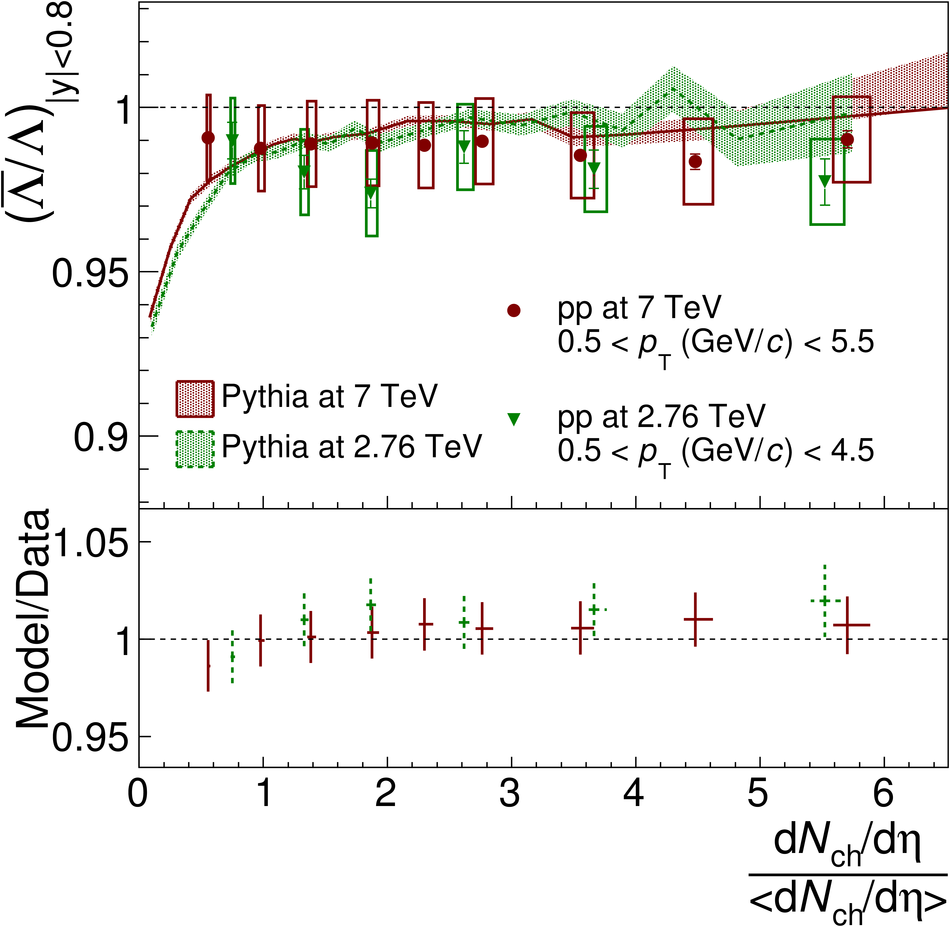
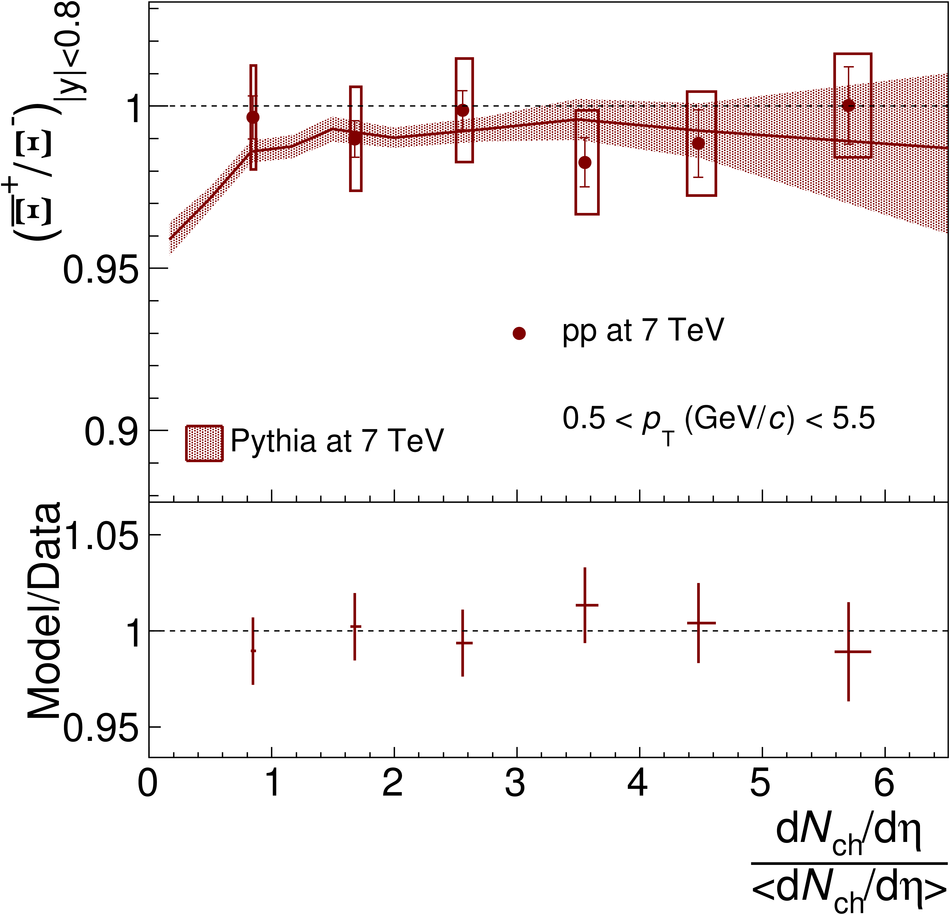
The ratios of yields of anti-baryons to baryons probes the mechanisms of baryon-number transport. Results for $\bar{\rm p}/{\rm p}$, $\bar{\rm \Lambda}/{\rm \Lambda}$, $\rm\bar{\Xi}$$^{+}/{\rm \Xi}^{-}$ and $\rm\bar{\Omega}$$^{+}/{\rm \Omega}^{-}$ in pp collisions at $\sqrt{s} = 0.9$, 2.76 and 7 TeV, measured with the ALICE detector at the LHC, are reported. Within the experimental uncertainties and ranges covered by our measurement, these ratios are independent of rapidity, transverse momentum and multiplicity for all measured energies. The results are compared to expectations from event generators, such as PYTHIA and HIJING-B, that are used to model the particle production in pp collisions. The energy dependence of $\bar{\rm p}/{\rm p}$, $\bar{\rm \Lambda}/{\rm \Lambda}$, $\rm\bar{\Xi}$$^{+}/{\rm \Xi^{-}}$ and $\rm\bar{\Omega}$$^{+}/{\rm \Omega^{-}}$, reaching values compatible with unity for $\sqrt{s} = 7$ TeV, complement the earlier $\bar{\rm p}/{\rm p}$ measurement of ALICE. These dependencies can be described by exchanges with the Regge-trajectory intercept of $\alpha_{\rm {J}} \approx 0.5$, which are suppressed with increasing rapidity interval ${\rm \Delta} y$. Any significant contribution of an exchange not suppressed at large ${\rm \Delta} y$ (reached at LHC energies) is disfavoured.
Eur. Phys. J. C 73 (2013) 2496
HEP Data
e-Print: arXiv:1305.1562 | PDF | inSPIRE