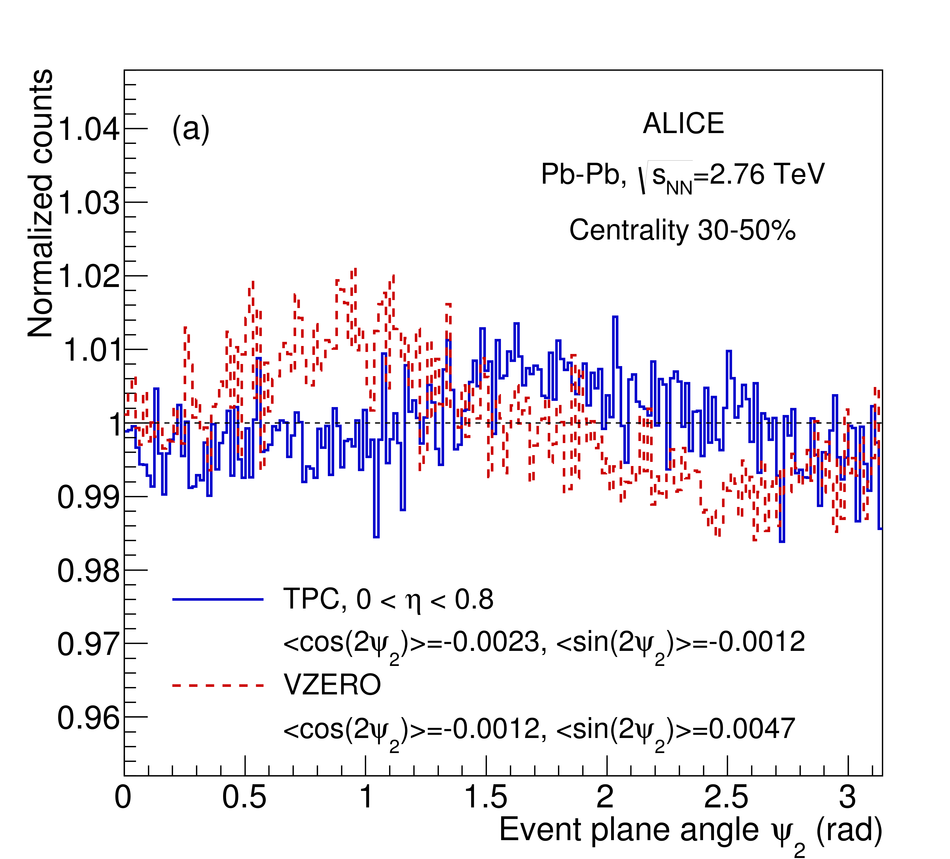
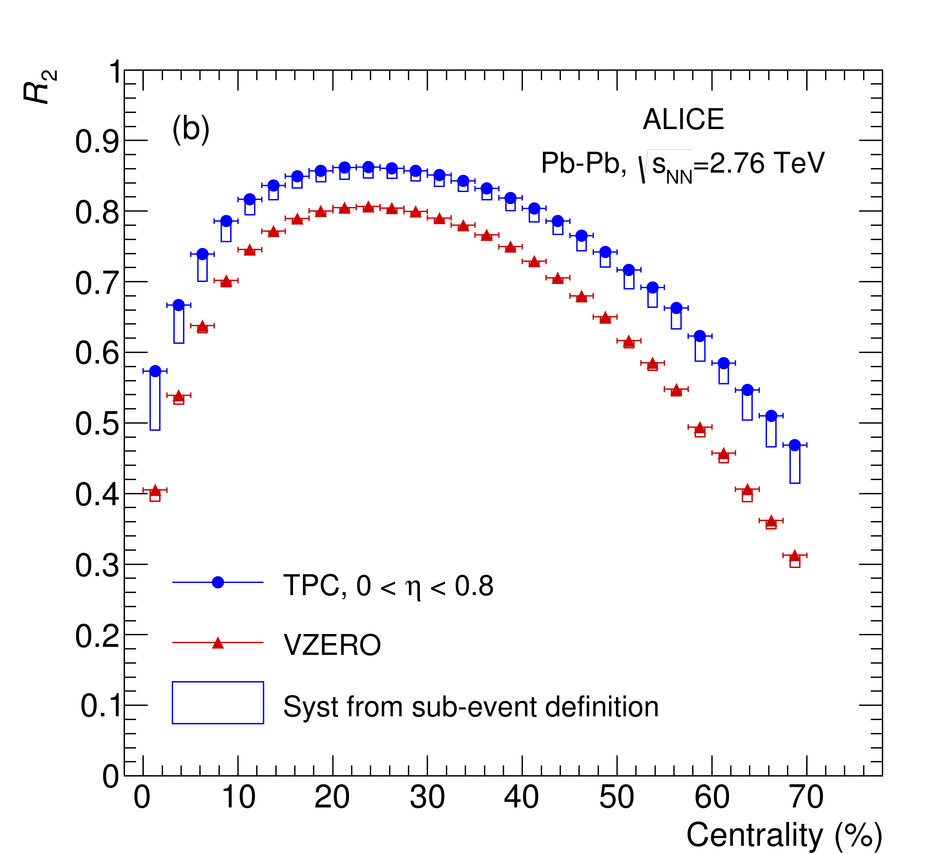
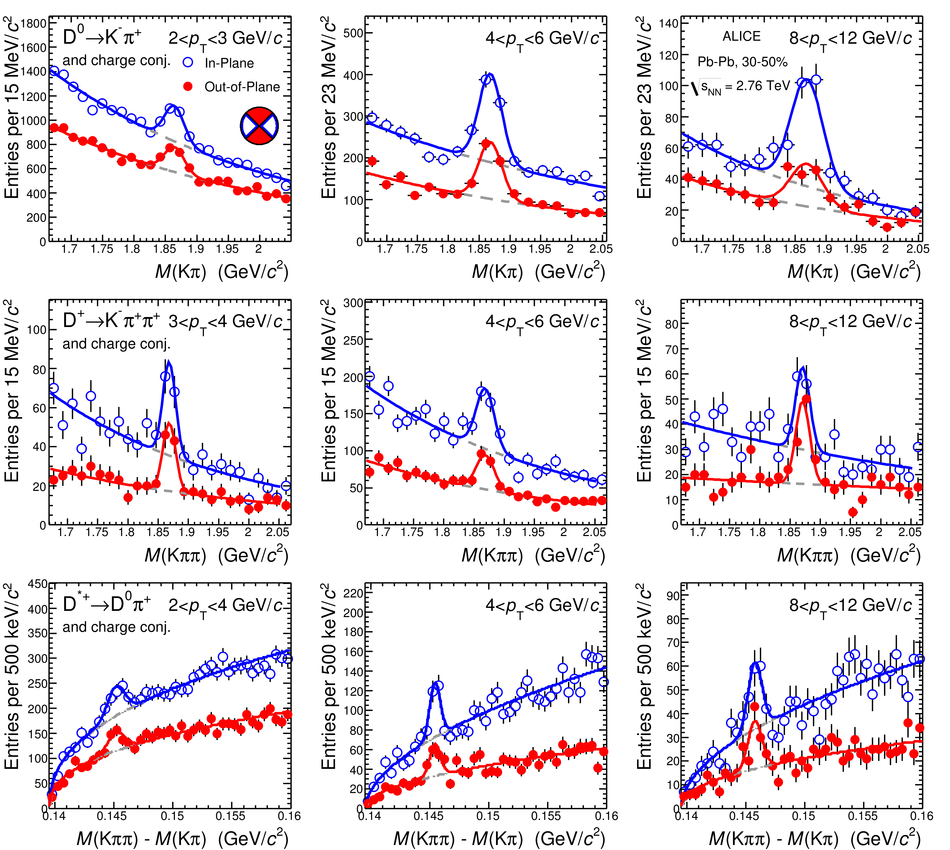
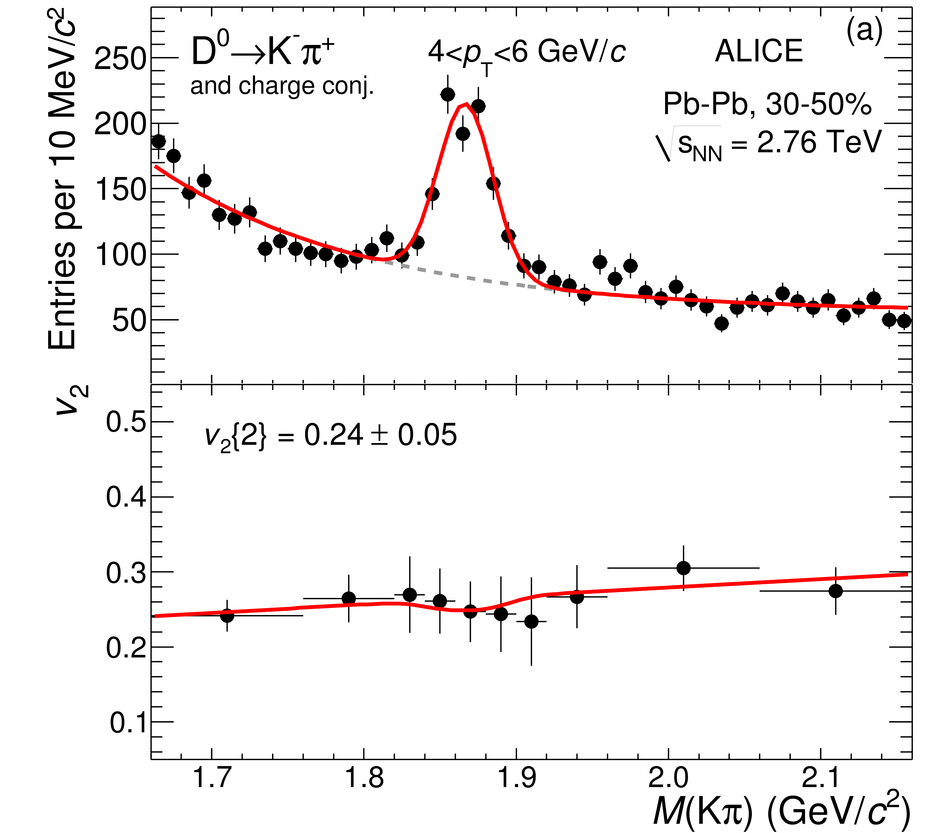
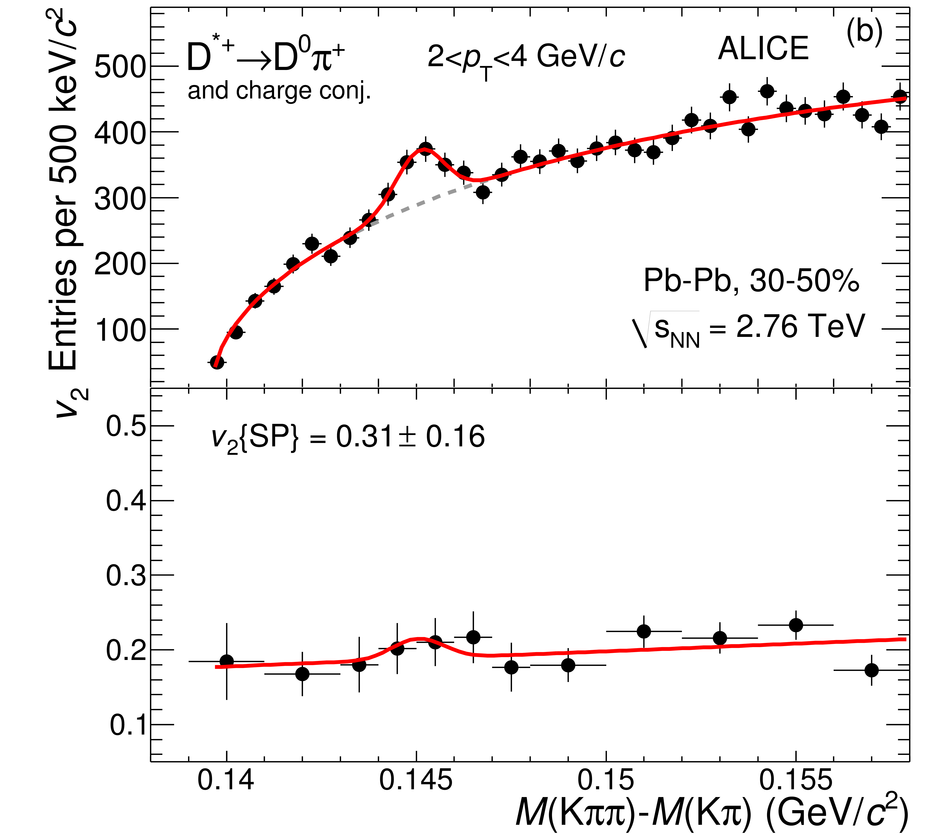
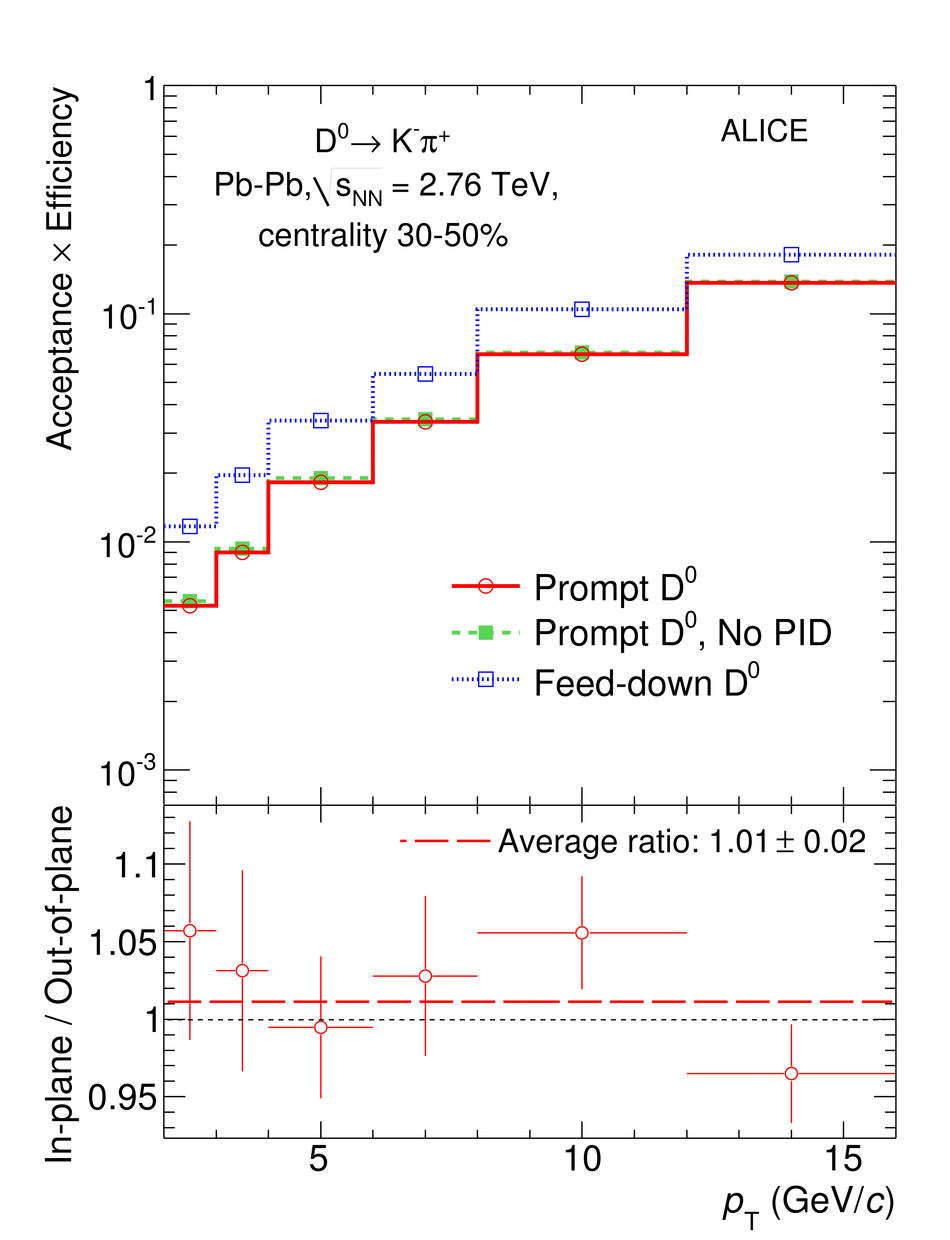
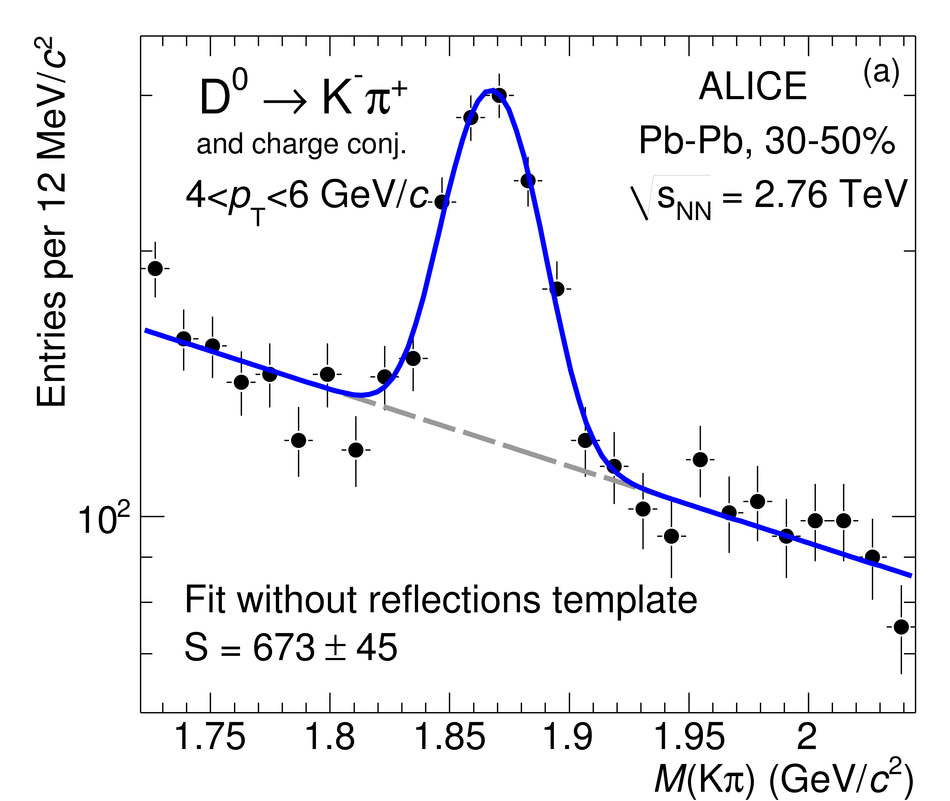
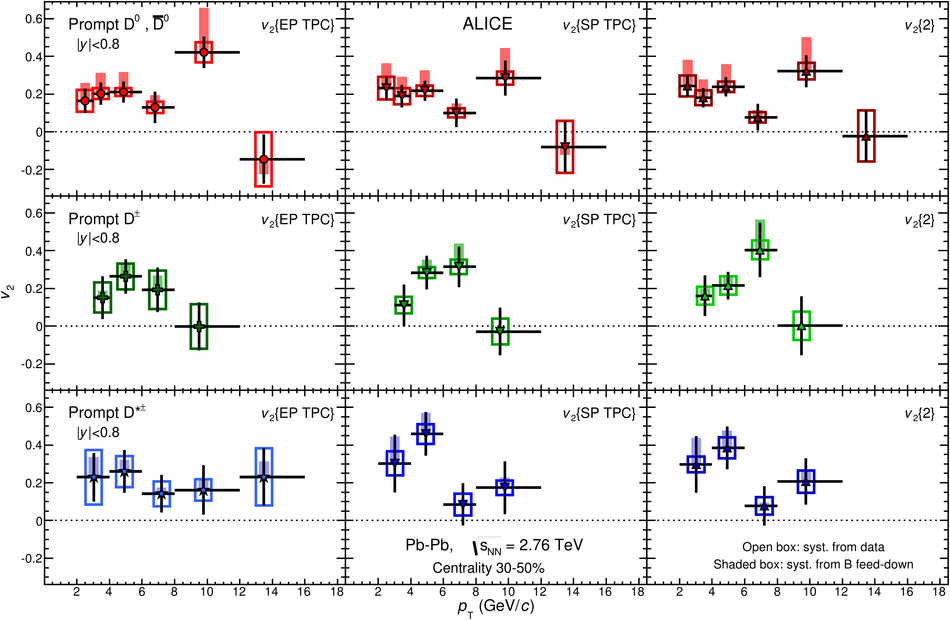
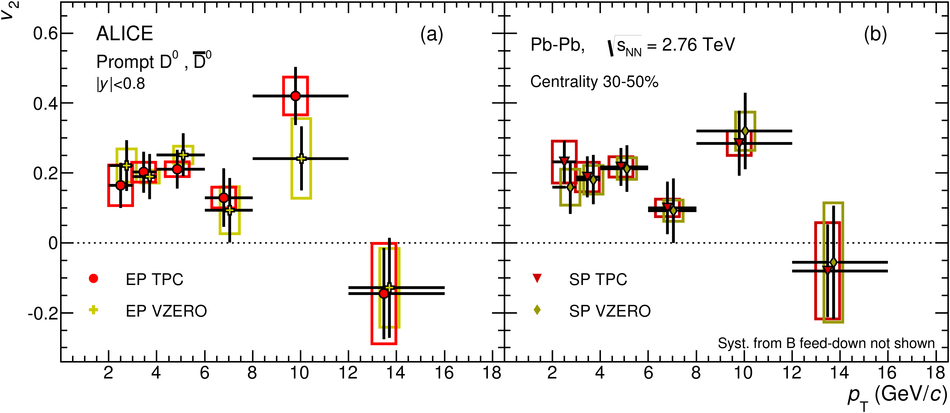
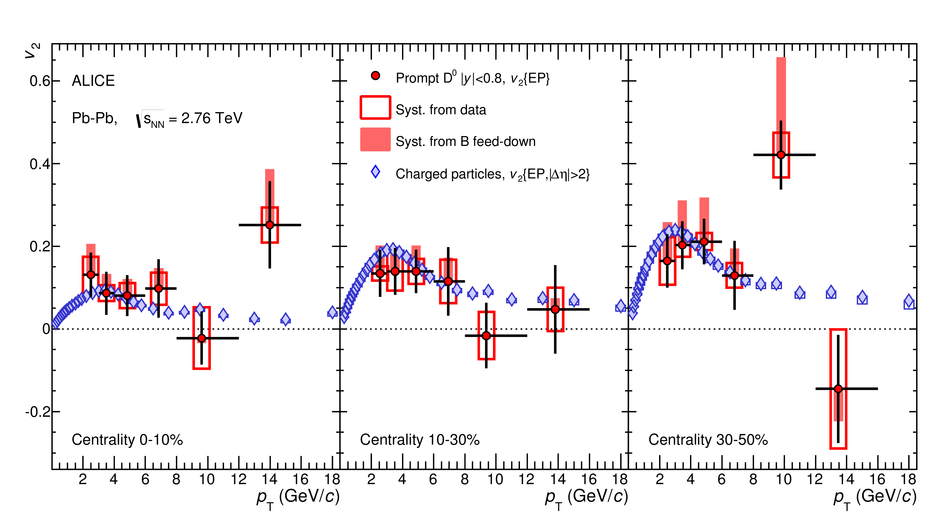
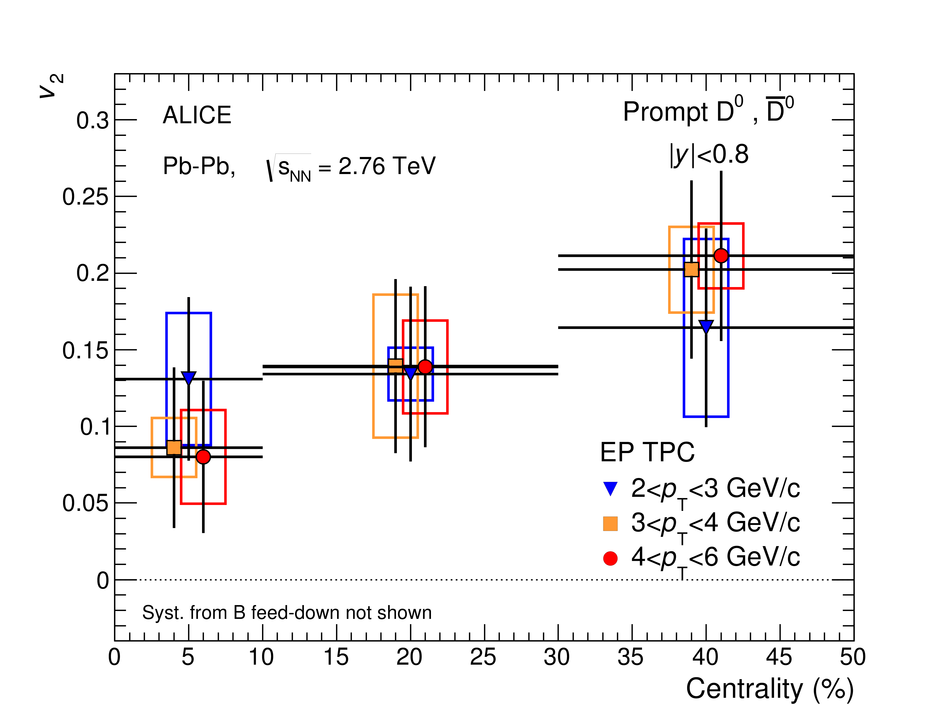
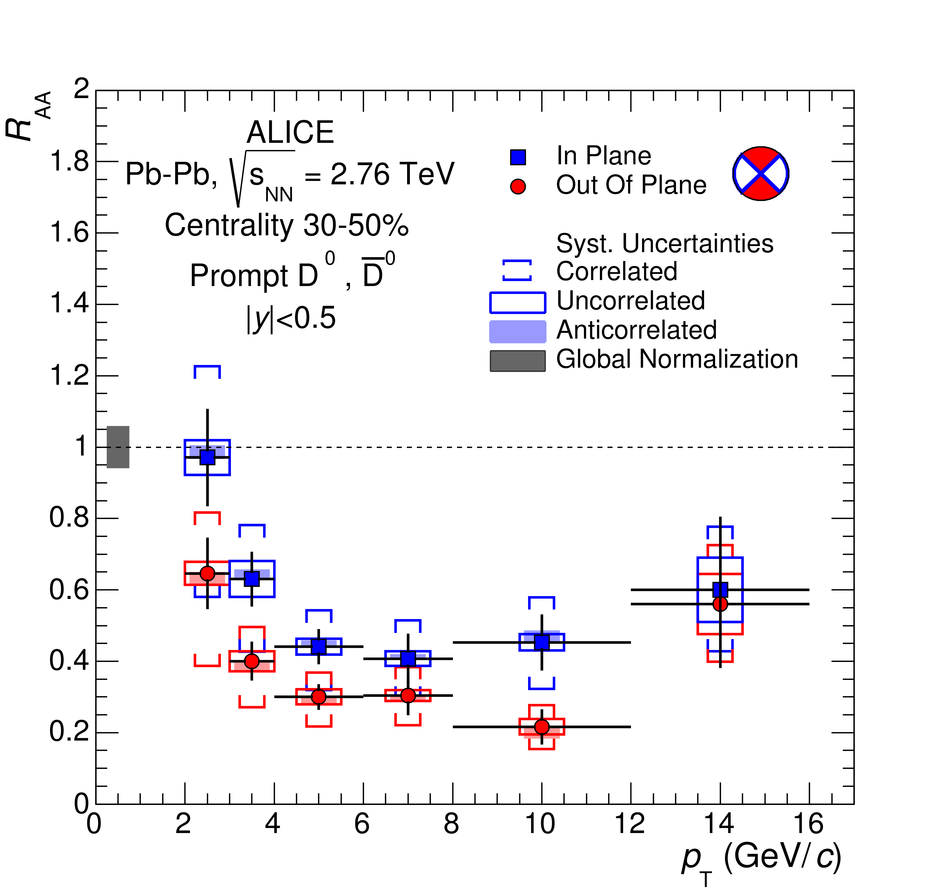
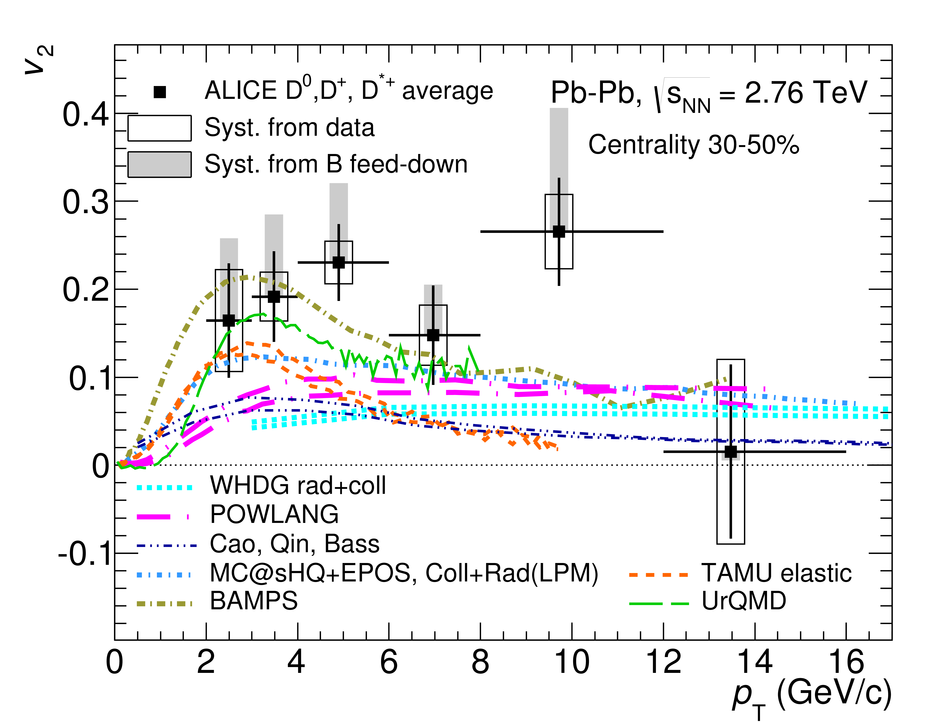
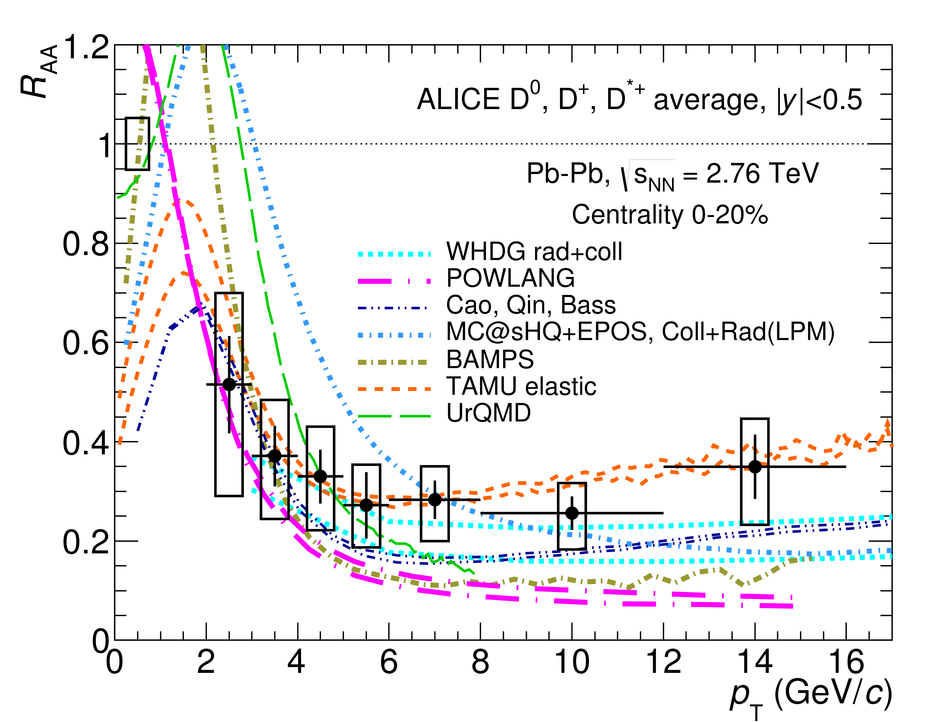
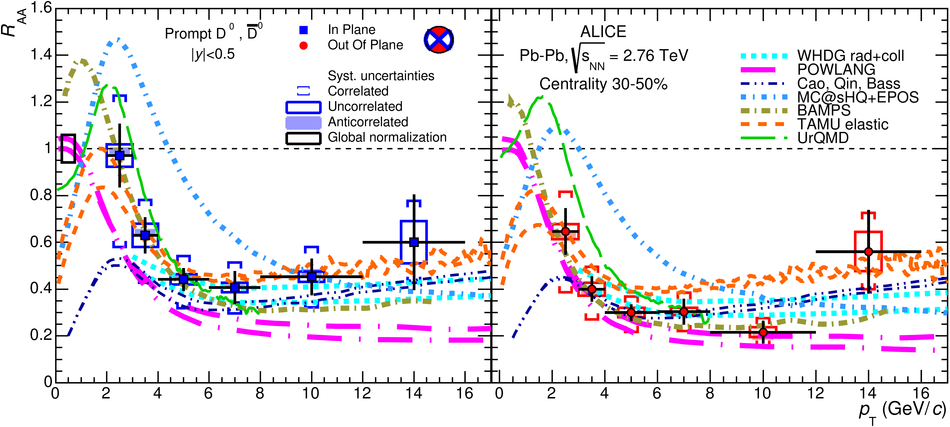
The production of the prompt charmed mesons $D^0$, $D^+$ and $D^{*+}$ relative to the reaction plane was measured in Pb-Pb collisions at a centre-of-mass energy per nucleon-nucleon collision of $\sqrt{s_{\rm NN}} = 2.76$ TeV with the ALICE detector at the LHC. D mesons were reconstructed via their hadronic decays at central rapidity in the transverse momentum ($p_{\rm T}$) interval of 2-16 GeV/$c$. The azimuthal anisotropy is quantified in terms of the second coefficient $v_2$ in a Fourier expansion of the D meson azimuthal distribution, and in terms of the nuclear modification factor $R_{\rm AA}$, measured in the direction of the reaction plane and orthogonal to it. The $v_2$ coefficient was measured with three different methods and in three centrality classes in the interval 0-50%. A positive $v_2$ is observed in mid-central collisions (30-50% centrality class), with an mean value of $0.204_{-0.036}^{+0.099}$ (tot.unc.) in the interval $2 < p_{\rm T} < 6$ GeV/$c$, which decreases towards more central collisions (10-30% and 0-10% classes). The positive $v_2$ is also reflected in the nuclear modification factor, which shows a stronger suppression in the direction orthogonal to the reaction plane for mid-central collisions. The measurements are compared to theoretical calculations of charm quark transport and energy loss in high-density strongly-interacting matter at high temperature. The models that include substantial elastic interactions with an expanding medium provide a good description of the observed anisotropy. However, they are challenged to simultaneously describe the strong suppression of high-$p_{\rm T}$ yield of D mesons in central collisions and their azimuthal anisotropy in non-central collisions.
Phys. Rev. C 90 (2014) 034904
HEP Data
e-Print: arXiv:1405.2001 | PDF | inSPIRE
CERN-PH-EP-2014-083
Figure 1
(a) Distribution of event plane angle $\psi_2$, estimated from TPC tracks with $0< \eta< 0.8$ (solid line) or with the VZERO detector signals (dashed line) in the centrality range 30--50\%. The distributions are normalized by their integral. (b) Event plane resolution correction factor $R_2$ as a function of centrality for the TPC and VZERO detectors. The boxes represent the systematic uncertainties estimated from the variation of $R_2$ when changing the sub-events used for its determination. |  |
Figure 2
Distributions of the invariant mass for $\Dzero$ (upper panels) and $\Dplus$ (central panels) candidates and of the mass difference for $\Dstar$ candidates (lower panels) in the two $\Delta\varphi$ intervals used in the event plane method, for Pb-Pb collisions in the 30-50% centrality class. The rapidity interval is $|y|< y_{\rm fid}$ (see text for details). For each meson species three $\pt$ intervals are shown, along with the fits used to extract the signal yield. The definition of the two $\Delta\varphi$ intervals is sketched in the top-left panel. |  |
Figure 3
Examples of $v_2$ extraction with two-particle correlation methods in a selected $\pt$ interval for Pb-Pb collisions in the 30-50% centrality range: the two-particle cumulants method for $\rm D^0$ (a) and the scalar product method for $\rm D^{*+}$ (b). The lower panels report the D meson $v_2$ values obtained with the simultaneous fit procedure, as described in the text. The rapidity interval is $|y|< y_{\rm fid}$ (see Section text for details). |  |
Figure 4
Product of acceptance and efficiency for $\Dzero$ mesons in Pb-Pb collisions for 30-50% centrality class (upper panel). The rapidity interval is $|y|< y_{\rm fid}$ (see text for details). The values for prompt (solid lines) and feed-down (dotted lines) $\Dzero$ mesons are shown. Also displayed, for comparison, are the values for prompt $\Dzero$ mesons without PID selection (dashed lines). The lower panel shows the ratio of the efficiencies for prompt $\Dzero$ mesons in the in-plane and out-of-plane regions used for the analysis. This ratio was estimated using simulation samples with a difference in particle multiplicity similar to that observed in data for the two azimuthal regions. |  |
Figure 5
Invariant mass distribution of $\rm D^0$ candidates with $4< \pt< 6$ GeV/$c$ in the centrality class 30-50%:
(a) fit without template for reflections and
(b) with template for reflections (dotted line).
The raw yield obtained as integral of the signal Gaussian function is reported. |  |
Figure 6
$v_2$ as a function of $\pt$ in the 30-50% centrality class, for $\rm D^0$, $\rm D^+$ and $\rm D^{*+}$ mesons (rows) with the event plane, scalar product and two-particle cumulant methods (columns). For the first method, the event plane was estimated with TPC tracks in $0< \eta< 0.8$; for the other methods, TPC tracks in $-0.8< \eta< 0.8$ were used as RFP. The symbols are positioned at the average $\pt$ measured within each interval. |  |
Figure 7
$\rm D^0$ meson $v_2$ as a function of $\pt$ in the 30-50% centrality class, with the reference particles from the TPC or from the VZERO detectors ($-3.7< \eta< -1.7$ and $2.8< \eta< 5.1$).
(a) Event plane method.
(b) Scalar product method.
For visibility, the symbols for the VZERO case are slightly displaced horizontally. |  |
Figure 10
Nuclear modification factor $\RAA$ of $\Dzero$ mesons in the 30-50% centrality class in two $90^\circ$-wide azimuthal intervals centred on the in-plane and on the out-of-plane directions. The correlated, uncorrelated, and anti-correlated contributions to the systematic uncertainty are shown separately. |  |
Figure 11
Model comparisons for average D meson $v_2$ in the 30-50% centrality class (top), average D meson $\RAA$ in the 0-20% centrality class (middle), $\Dzero$ $\RAA$ in-plane and out-of-plane in the 30-50% centrality class (bottom). The seven model calculations are described in the text: WHDG rad+coll, POWLANG, Cao, Qin, Bass, MC@sHQ+EPOS, Coll+Rad(LPM), BAMPS, TAMU elastic, UrQMD. The models WHDG rad+coll, POWLANG, TAMU elastic and UrQMD are shown by two lines that represent their uncertainty. |  |
