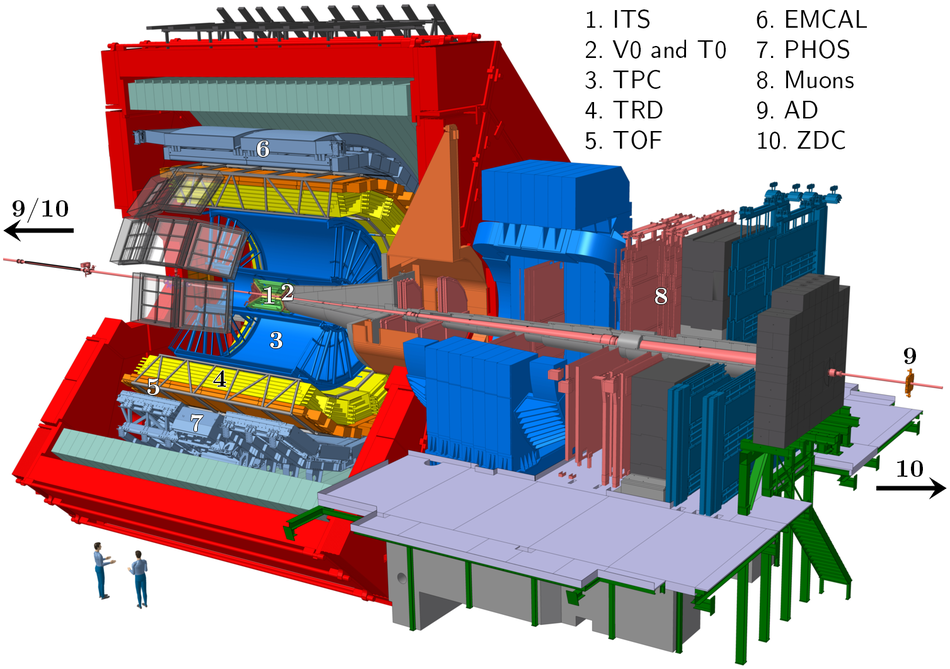
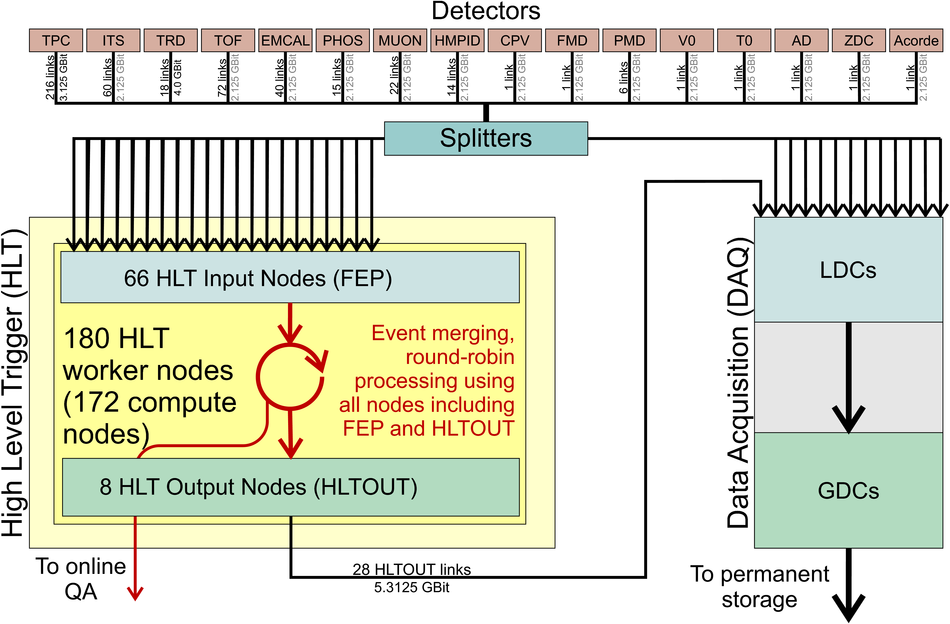
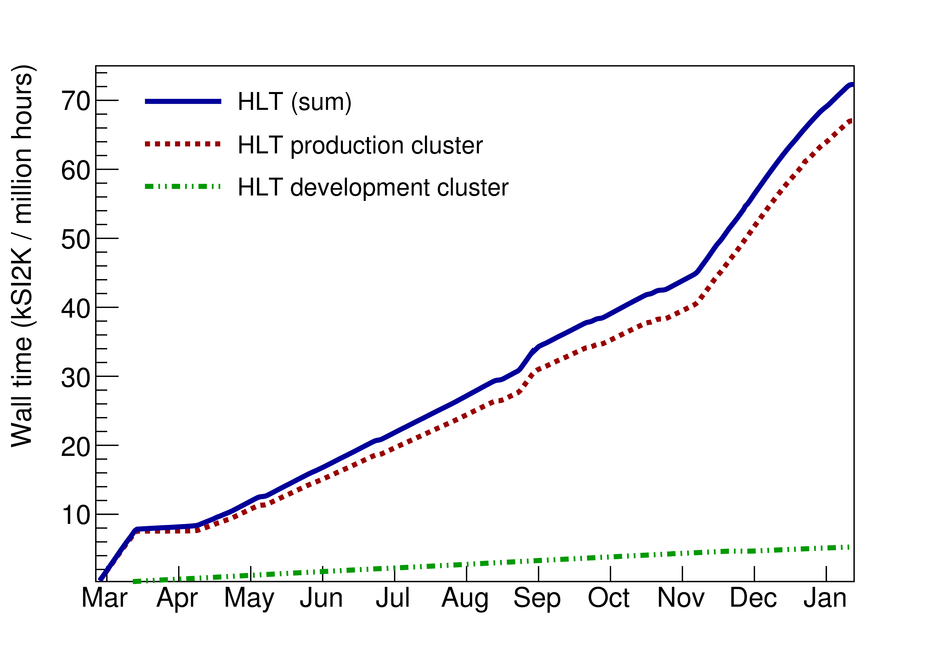
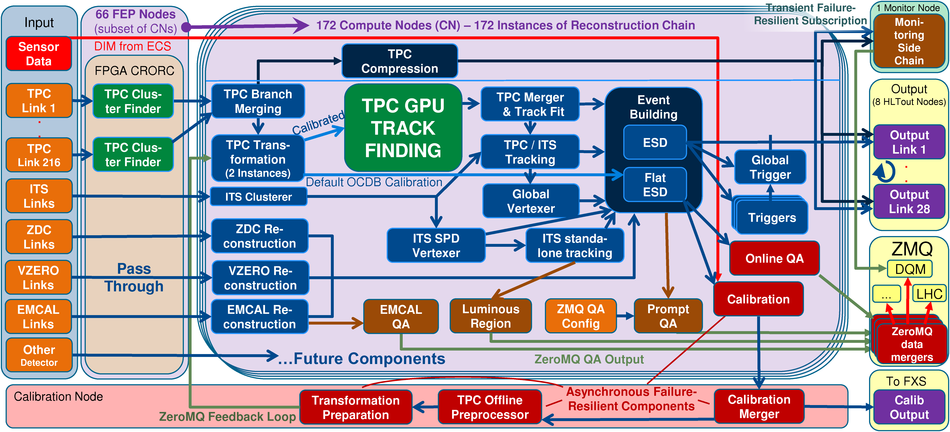
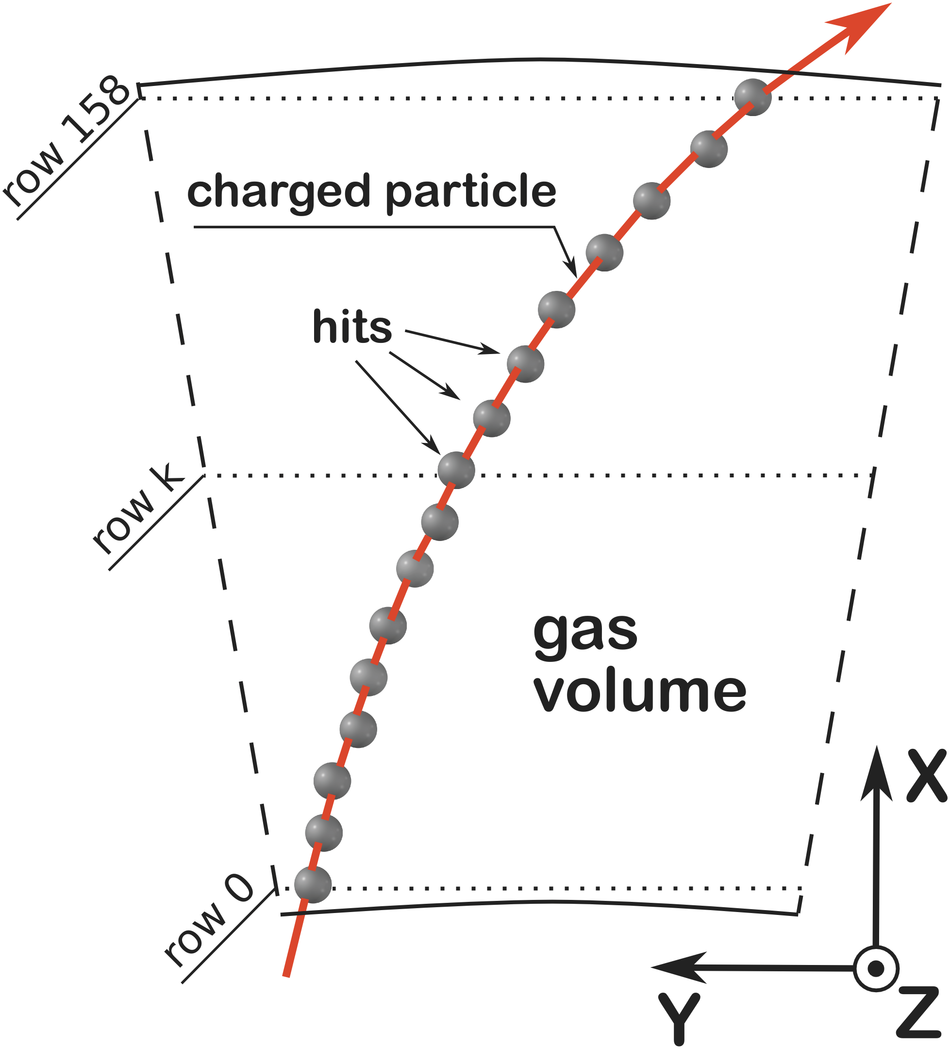
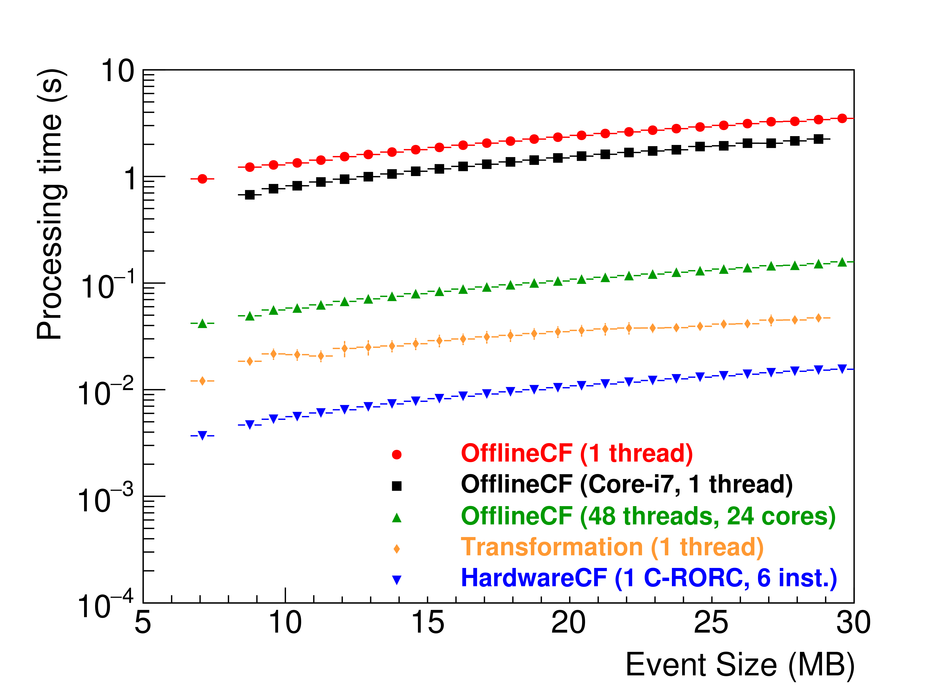
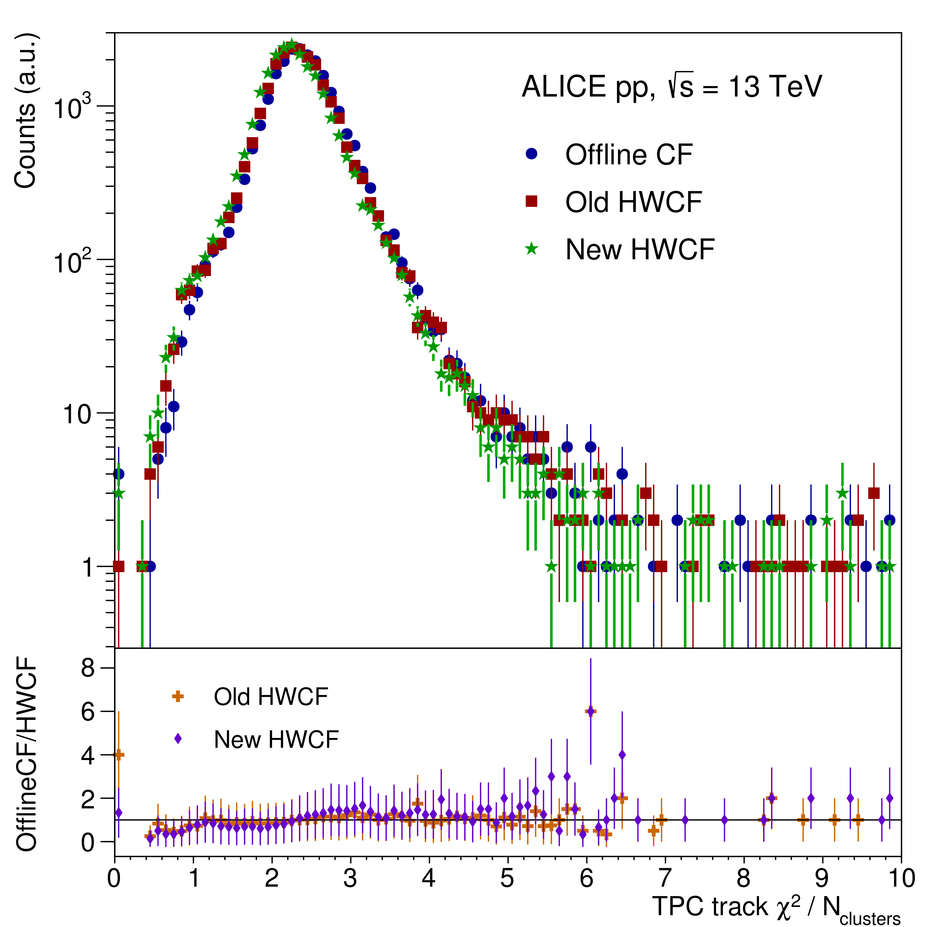
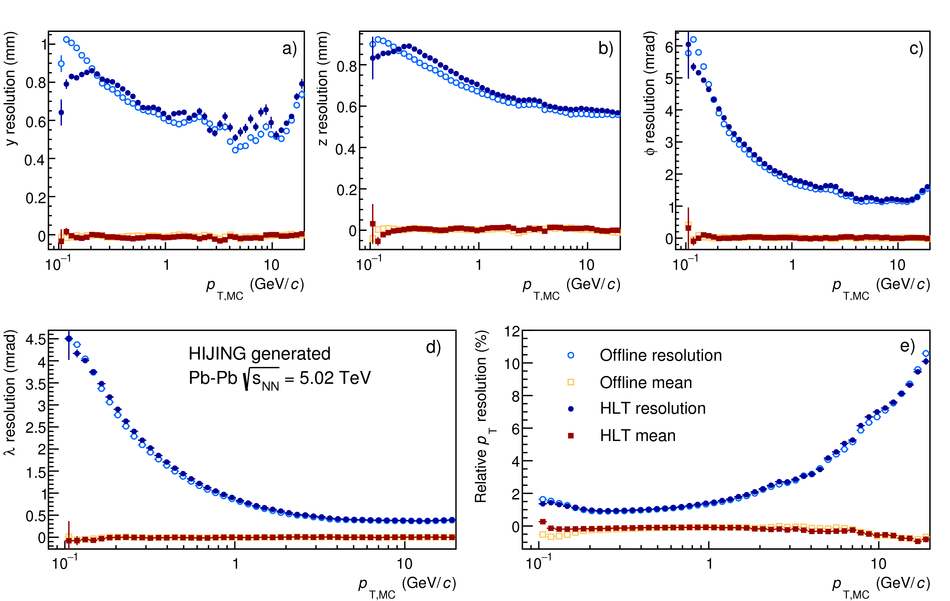
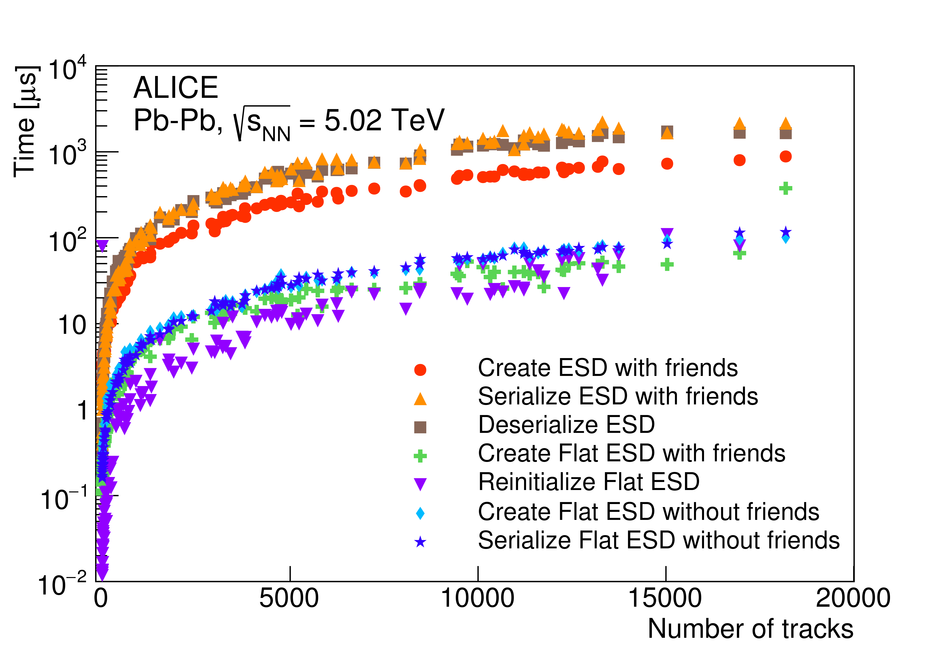
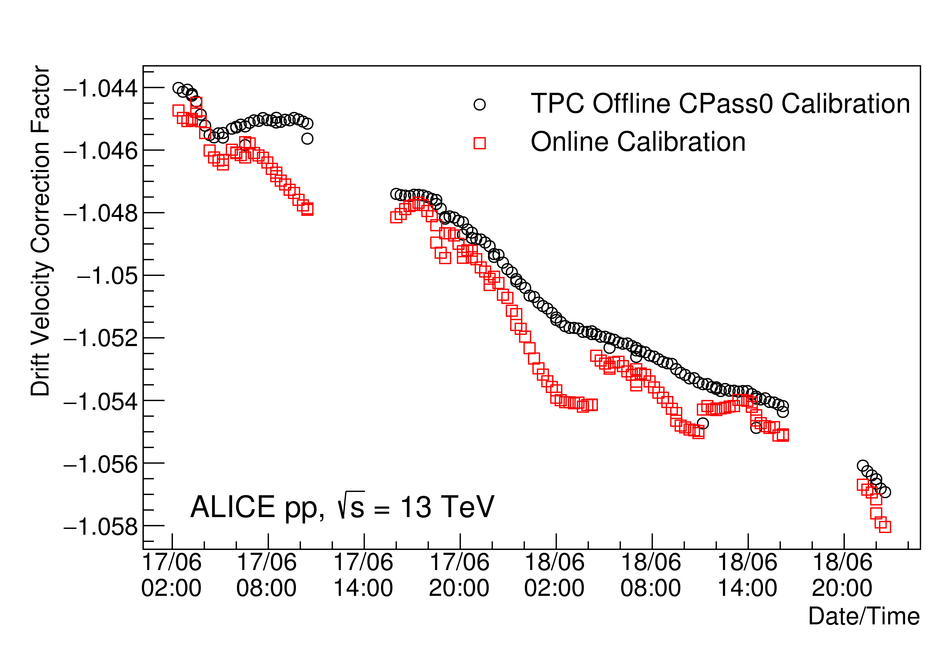
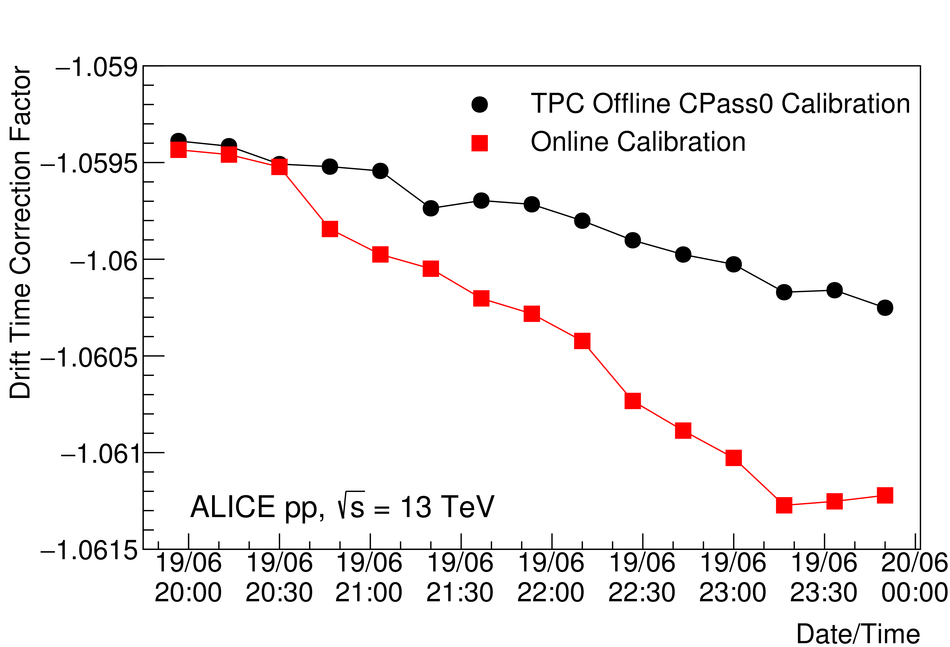
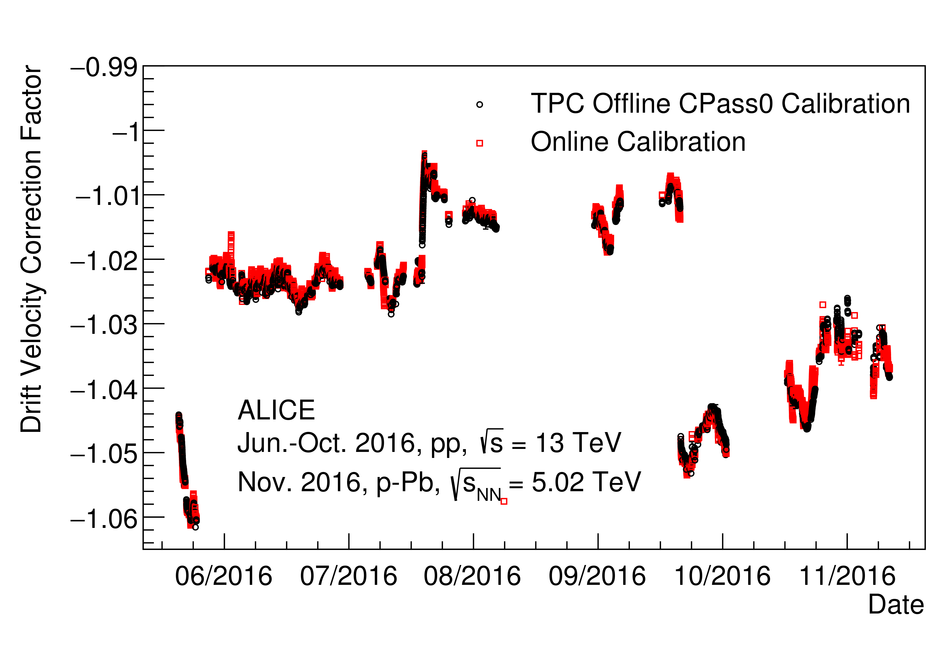
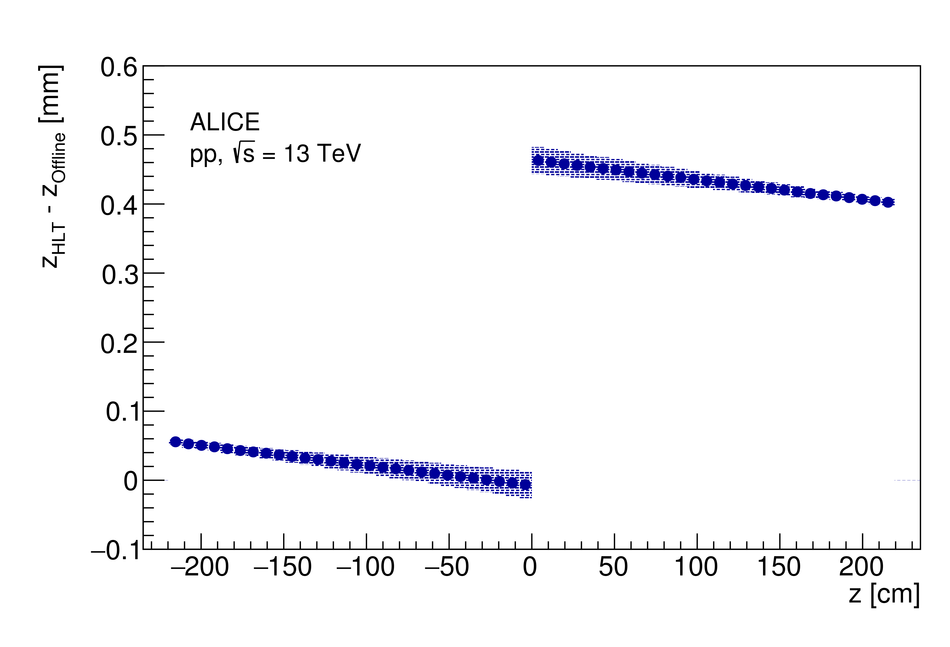
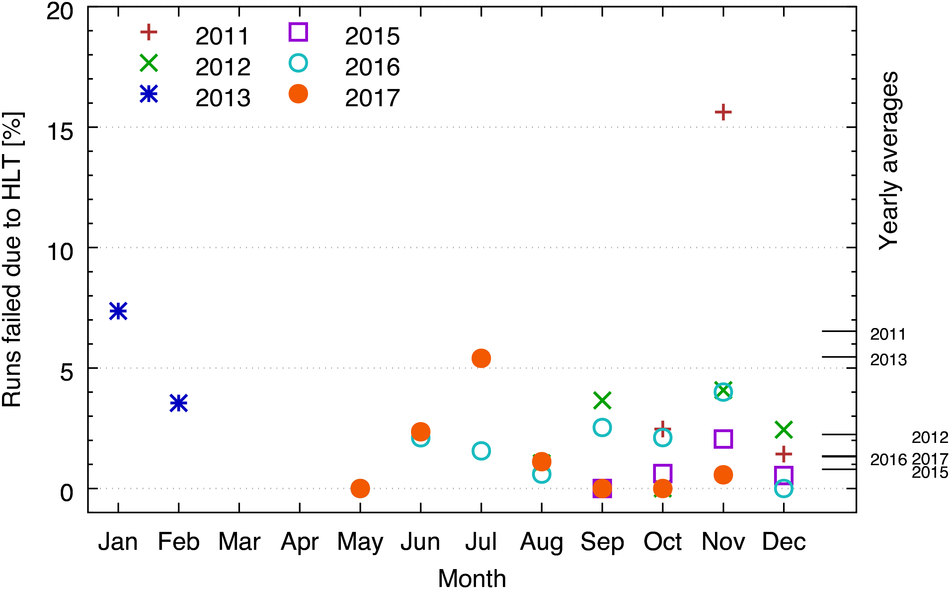
At the Large Hadron Collider at CERN in Geneva, Switzerland, atomic nuclei are collided at ultra-relativistic energies. Many final-state particles are produced in each collision and their properties are measured by the ALICE detector. The detector signals induced by the produced particles are digitized leading to data rates that are in excess of 48 GB/$s$. The ALICE High Level Trigger (HLT) system pioneered the use of FPGA- and GPU-based algorithms to reconstruct charged-particle trajectories and reduce the data size in real time. The results of the reconstruction of the collision events, available online, are used for high level data quality and detector-performance monitoring and real-time time-dependent detector calibration. The online data compression techniques developed and used in the ALICE HLT have more than quadrupled the amount of data that can be stored for offline event processing.
Comput. Phys. Commun. 242 (2019) 25-48
e-Print: arXiv:1812.08036 | PDF | inSPIRE
CERN-EP-2018-337