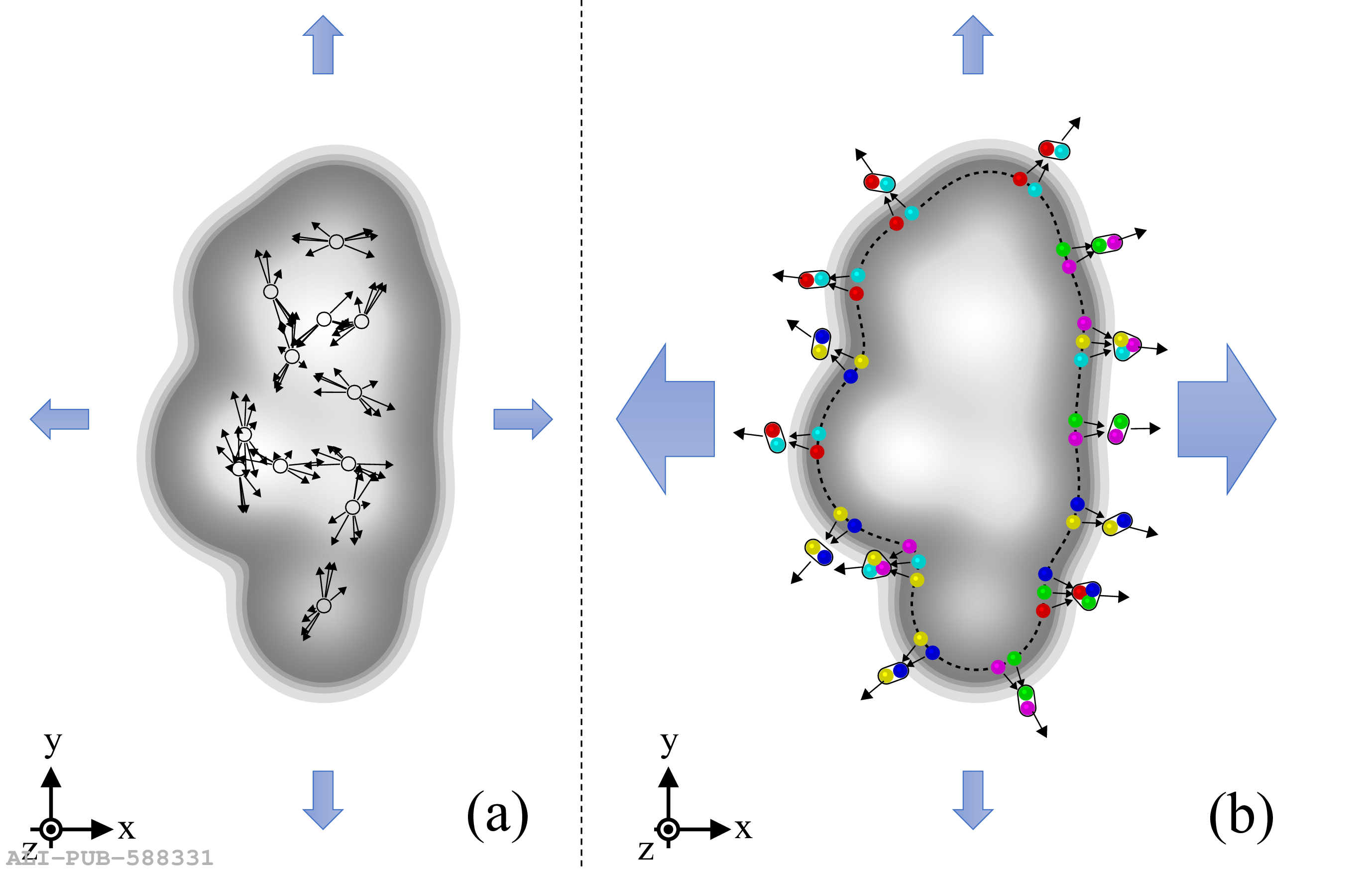
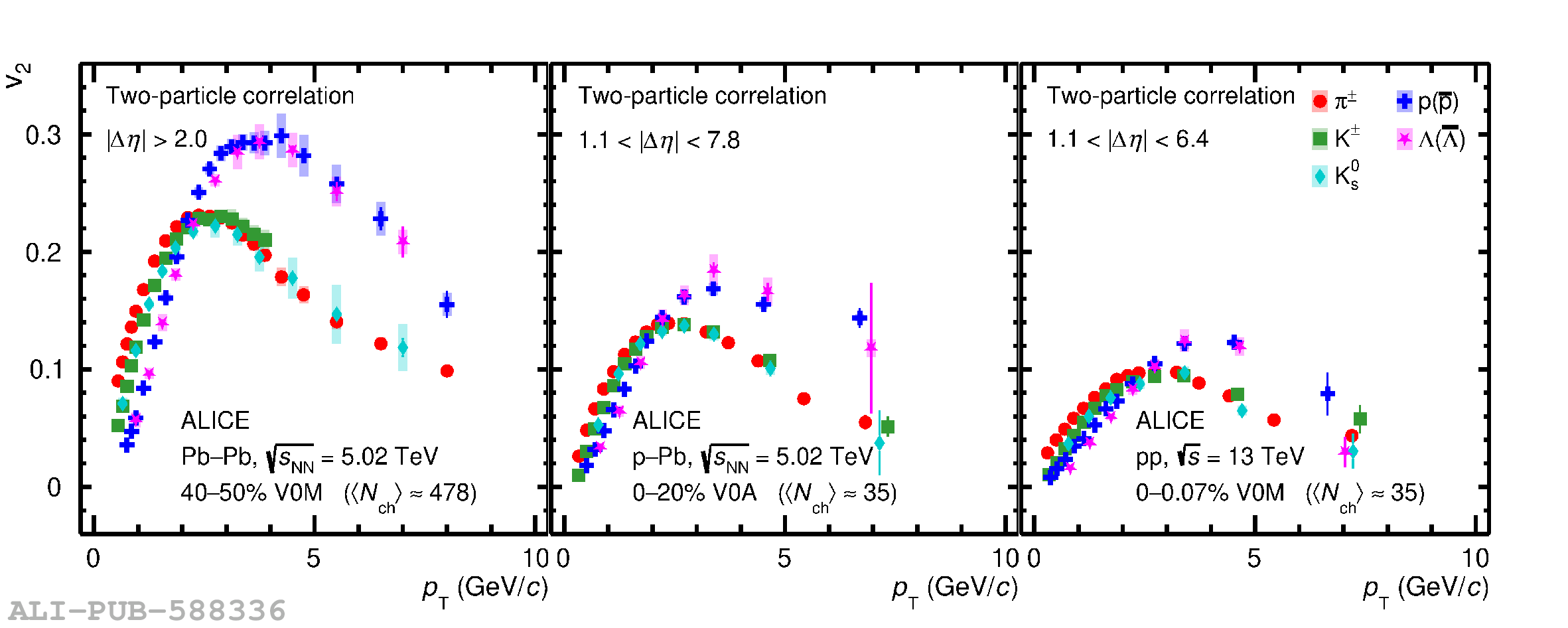
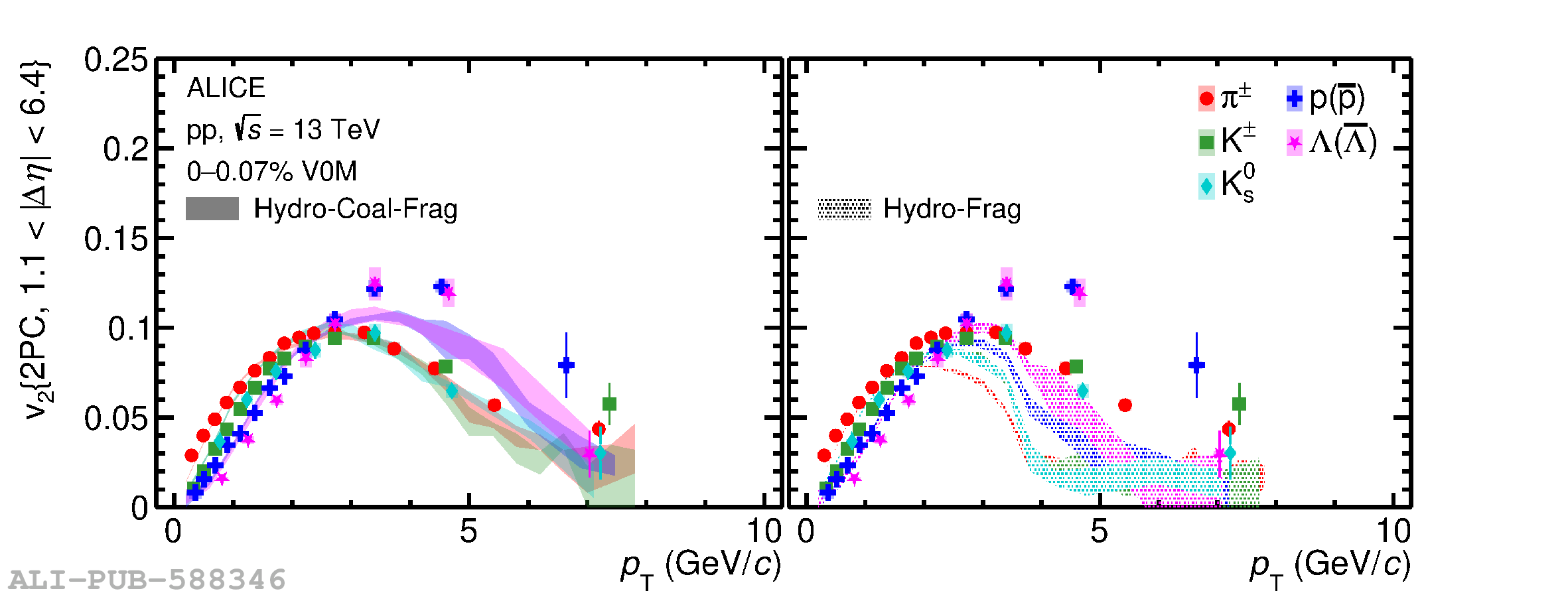
Quantum Chromodynamics predicts a phase transition from ordinary hadronic matter to the quark-gluon plasma (QGP) at high temperatures and energy densities, where quarks and gluons (partons) are not confined within hadrons. The QGP is generated in ultrarelativistic heavy-ion collisions. Anisotropic flow coefficients, quantifying the anisotropic azimuthal expansion of the produced matter, provide a unique tool to unravel QGP properties. Flow measurements in high-energy heavy-ion collisions show a distinctive grouping of anisotropic flow for baryons and mesons at intermediate transverse momentum, a feature associated with flow being imparted at the quark level, confirming the existence of the QGP. The observation of QGP-like features in relativistic proton-proton and proton-ion collisions has sparked debate about possible QGP formation in smaller collision systems, which remains unresolved. In this article, we demonstrate for the first time the distinctive grouping of anisotropic flow for baryons and mesons in high-multiplicity proton-lead and proton-proton collisions at the Large Hadron Collider (LHC). These results are described by a model that includes hydrodynamic flow followed by hadron formation via quark coalescence, replicating features observed in heavy-ion collisions. This observation is consistent with the formation of a partonic flowing system in proton-proton and proton-lead collisions at the LHC.
Submitted to: OTHERS
e-Print: arXiv:2411.09323 | PDF | inSPIRE
CERN-EP-2024-299
Figure group
Figure 1
A schematic representation of the overlap region in a collision is shown in gray, along with overall particle emission patterns in the transverse (x-y) plane, represented by large arrows. a) Non-flow sources: These are independent emissions, such as those from resonance decays or jets, where jets are collimated streams of hadrons created when a high-energy quark or gluon fragments after a collision. These effects lead to few-particle correlations but are not related to collective behavior in the system and have been subtracted from the final anisotropic flow measurements (see methods subsection \ref{SubSec:corr_template} for details). b) Anisotropic flow: This illustrates the development of anisotropic flow in a partonic system, propagated to the level of hadrons via the quark coalescence process, which describes the experimental measurements in the intermediate \pt range ($\sim$3--8 GeV/c). In this process, two or three flowing partons coalesce to form mesons or baryons, which then interact with each other. The large arrows represent the overall anisotropy of particle emission in the transverse plane, with stronger expansion along the short (x) axis. |  |
Figure 2
Left: \pt-differential $v_2$ measured with the two-particle correlation method for mesons (\pipm{}, \kapm{}, \kzero{}) and baryons (p+\pbar{}, \lmb{}+\almb{}) in semicentral Pb--Pb collisions at $\sqrt{s_{\mathrm{NN}}} = 5.02$ TeV. Middle: \pt-differential $v_2$ measured with the two-particle correlation method for mesons (\pipm{}, \kapm{}, \kzero{}) and baryons (p+\pbar{}, \lmb{}+\almb{}) in high-multiplicity p--Pb collisions at $\sqrt{s_{\mathrm{NN}}} = 5.02$ TeV. Right: Same for pp collisions at $\sqrt{s} = 13$ TeV. $\langle N_{\rm ch} \rangle$ is the average number of reconstructed, efficiency-corrected charged particles with $0.2 p_{\rm T} 3.0$ GeV/$c$ at midrapidity ($|\eta| 0.8$). |  |
Figure 3
\pt-differential $v_2$ measured with two-particle correlation for mesons (\pipm{}, \kapm{}, \kzero{}) and baryons (p+\pbar{}, \lmb{}+\almb{}) in high-multiplicity p--Pb collisions at $\sqrt{s_{\mathrm{NN}}} = 5.02$ TeV. Comparisons with the calculations from the Hydro-Coal-Frag model (left) and the Hydro-Frag model (right) are also presented . Only statistical uncertainties are shown for the calculations. |  |
Figure 4
\pt-differential $v_2$ measured with two-particle correlation for mesons (\pipm{}, \kapm{}, \kzero{}) and baryons (p+\pbar{}, \lmb{}+\almb{}) in high-multiplicity pp collisions at $\sqrt{s} = 13$ TeV. Comparisons with the calculations from the Hydro-Coal-Frag model (left) and the Hydro-Frag model (right) are also presented . Only statistical uncertainties are shown for the calculations. |  |