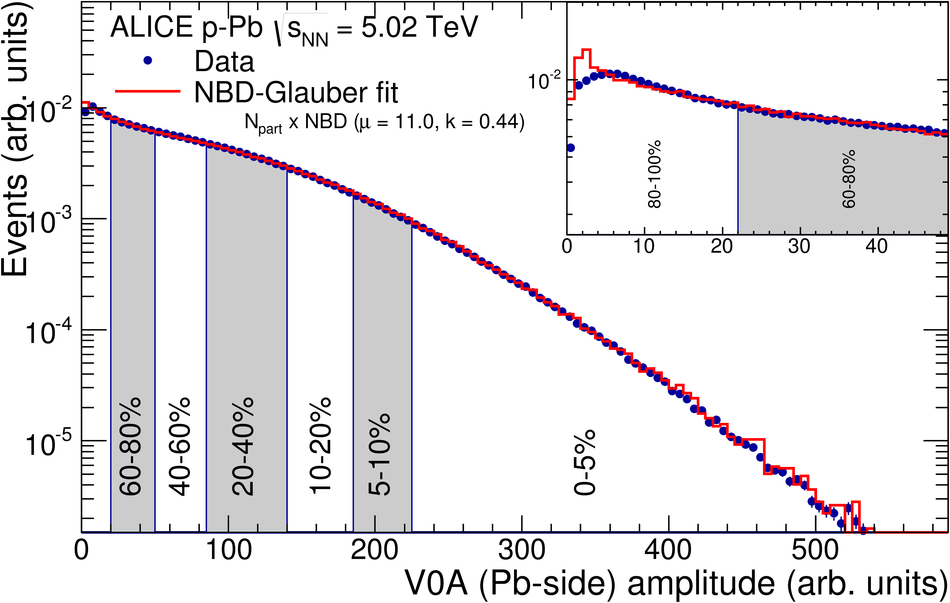
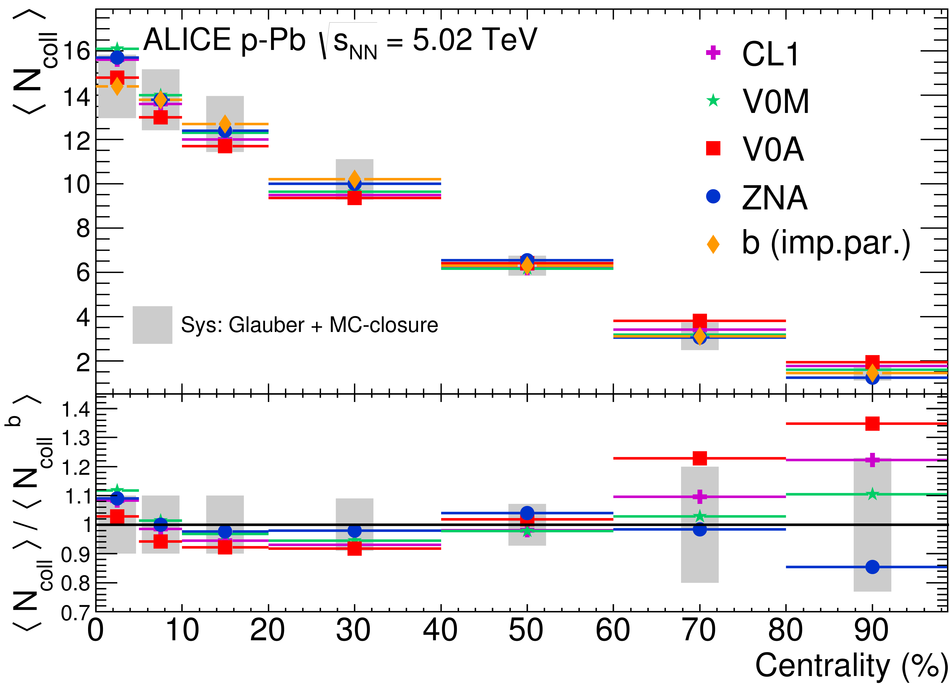
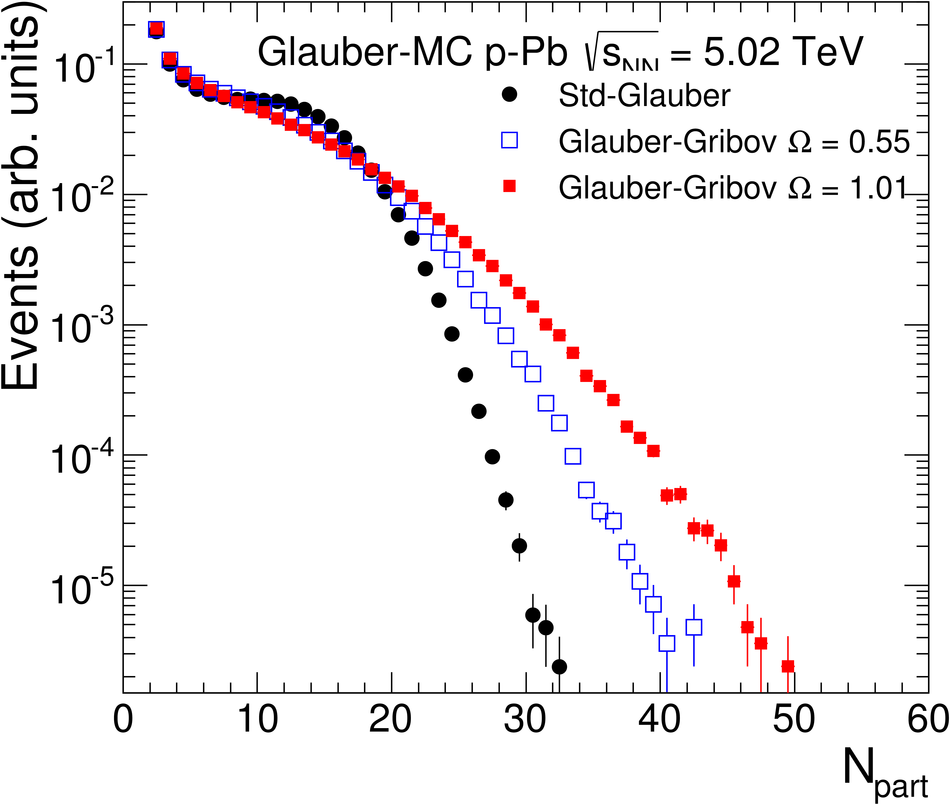
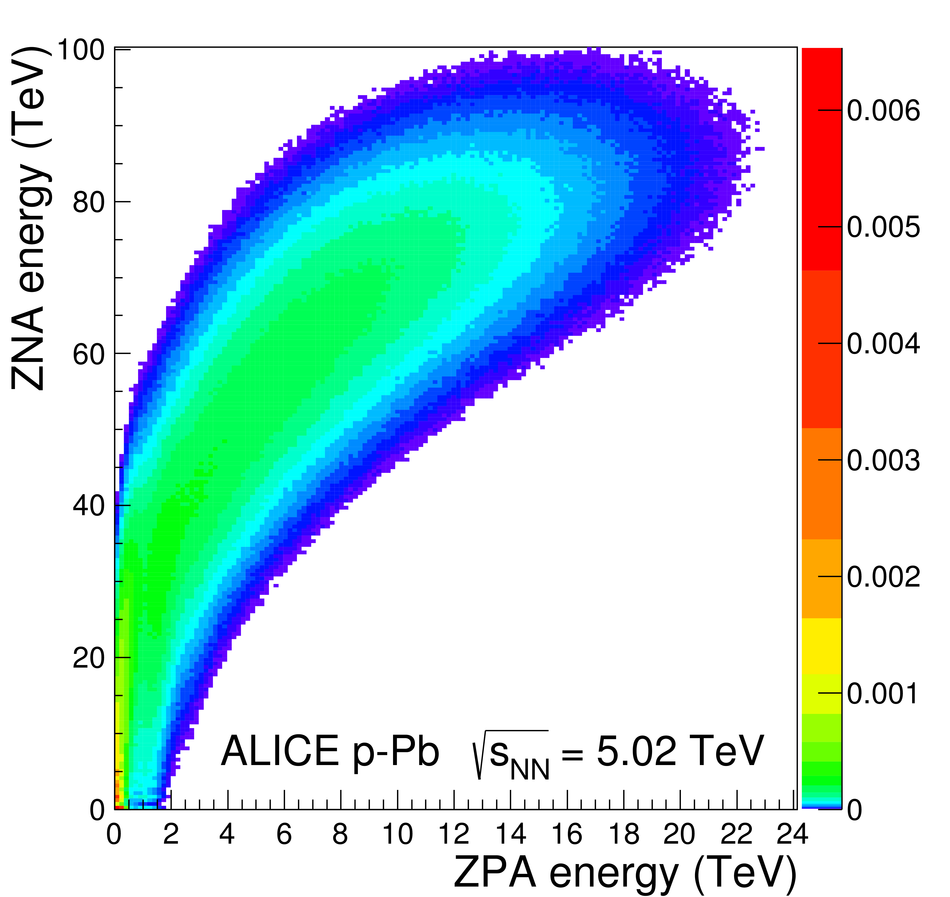
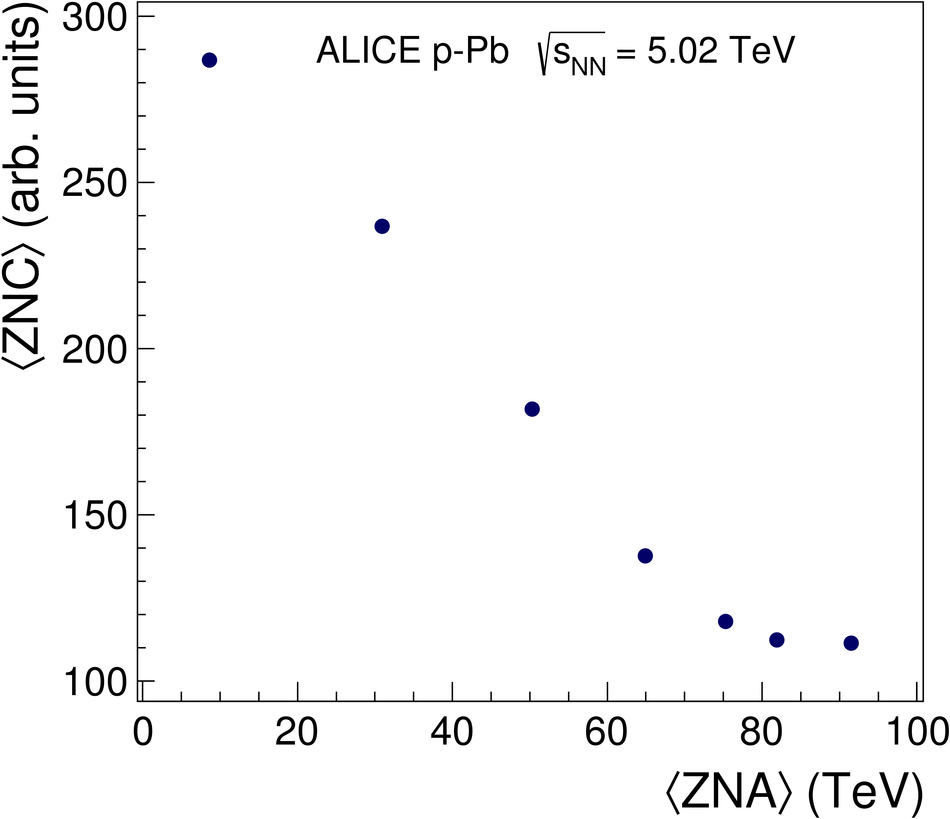
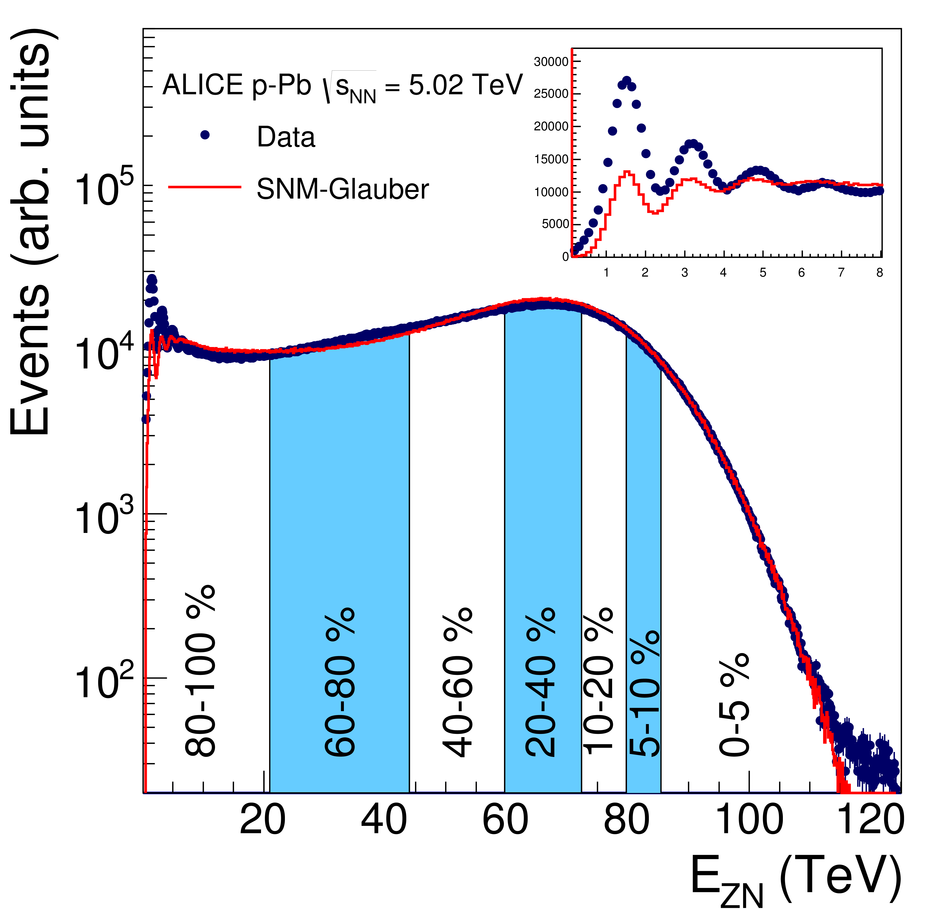
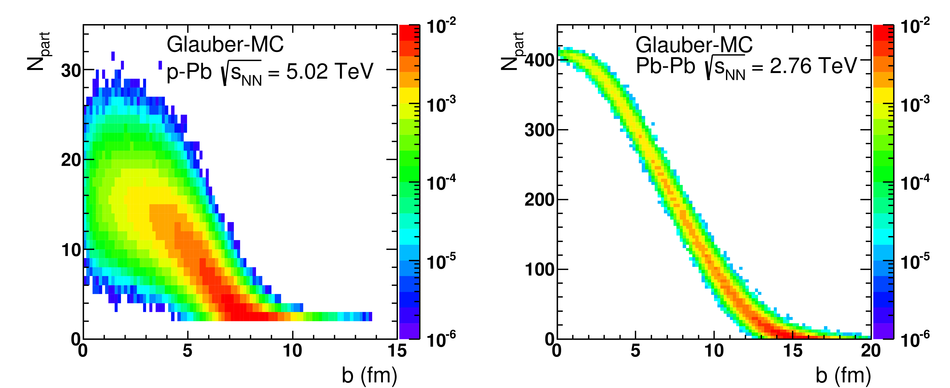
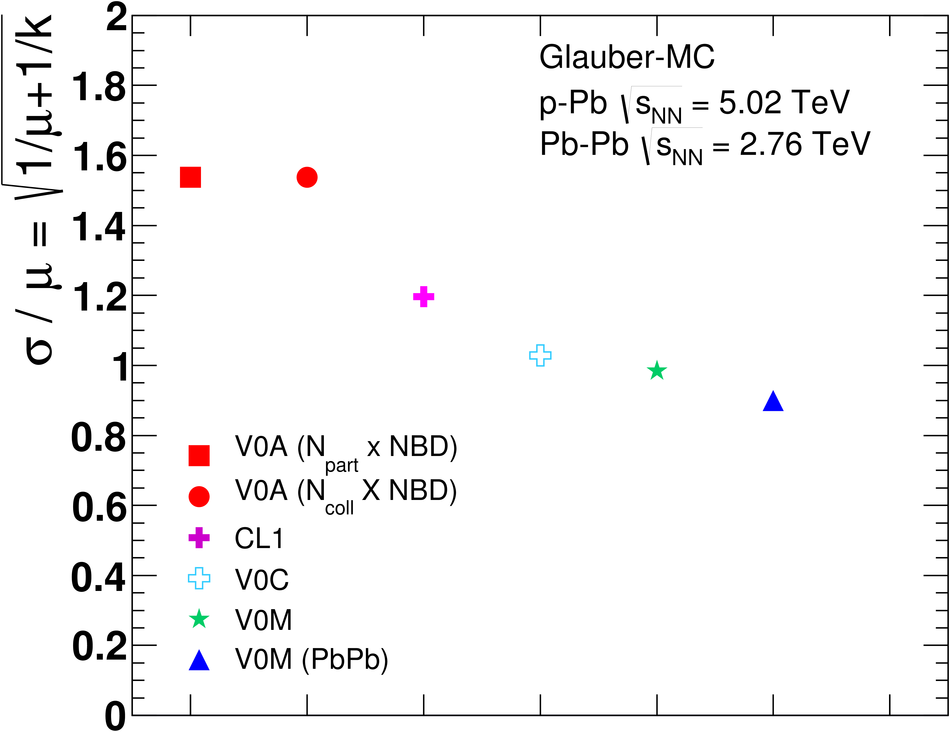
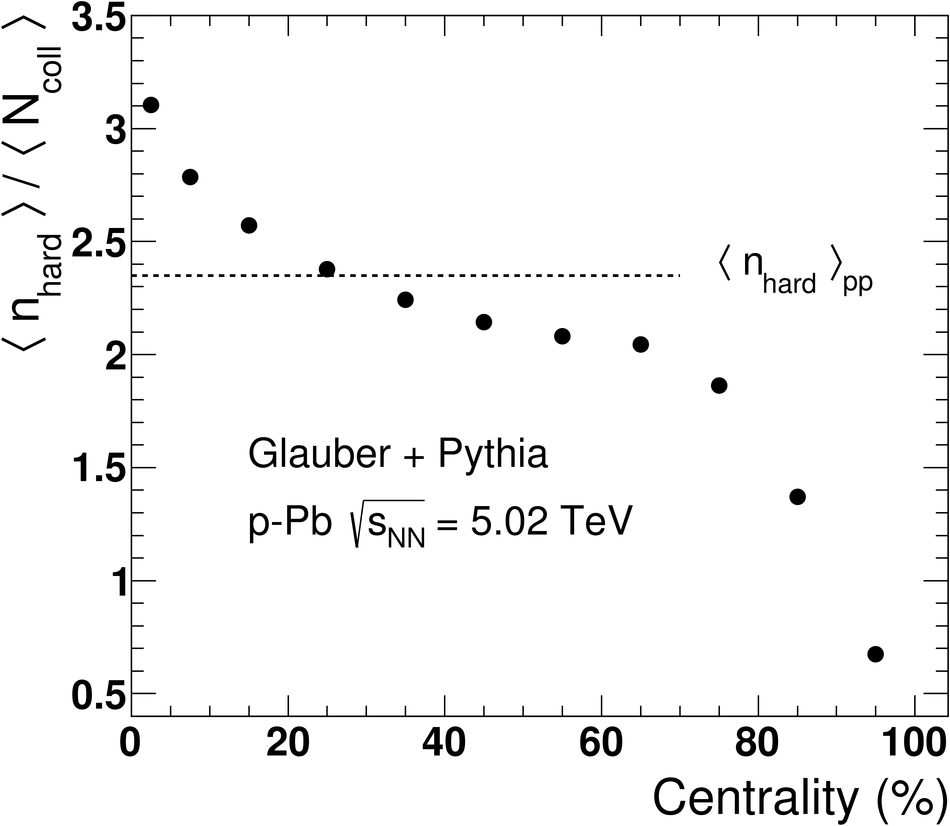
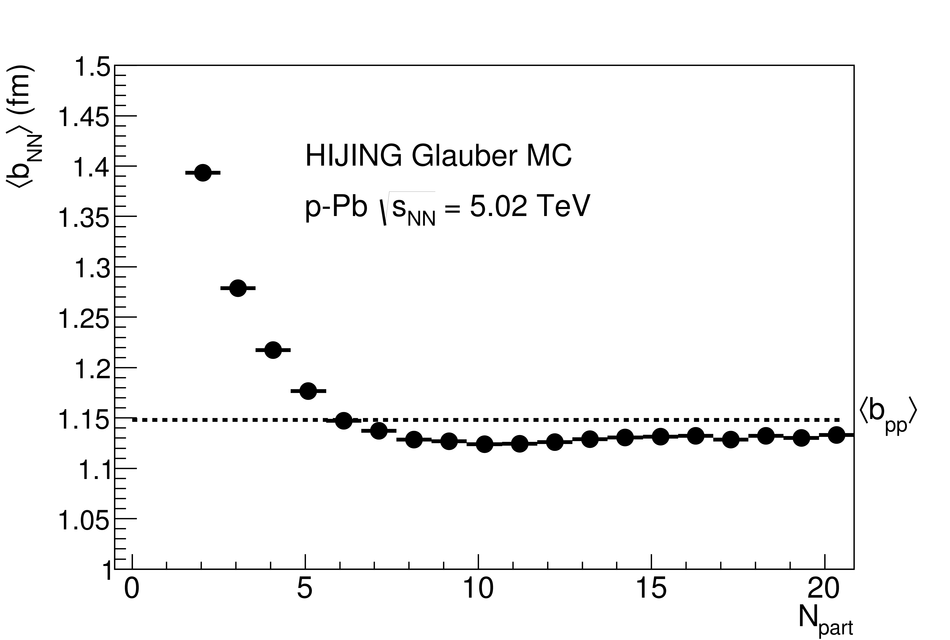
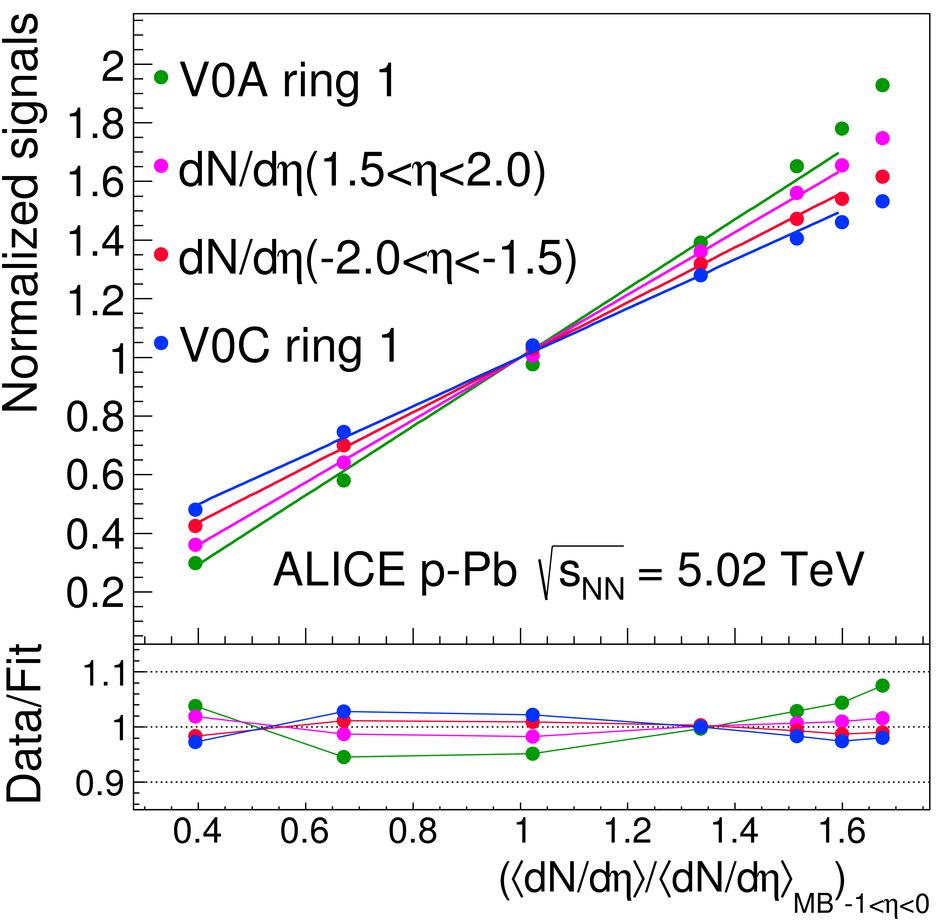
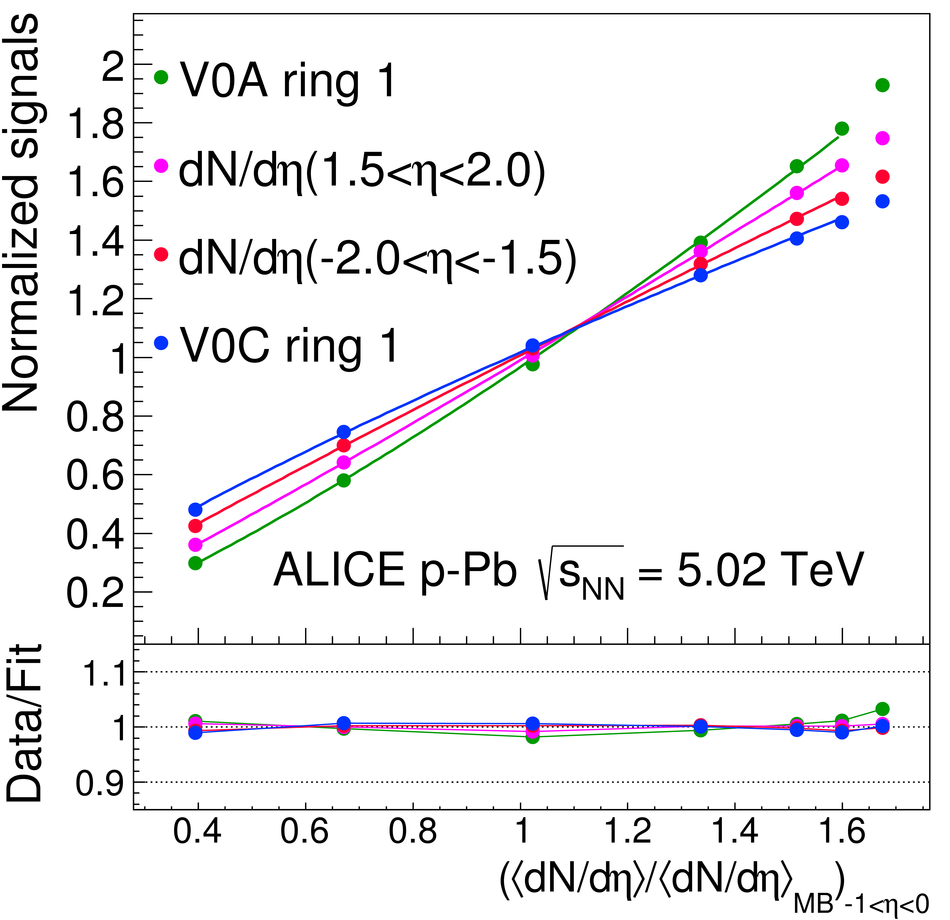
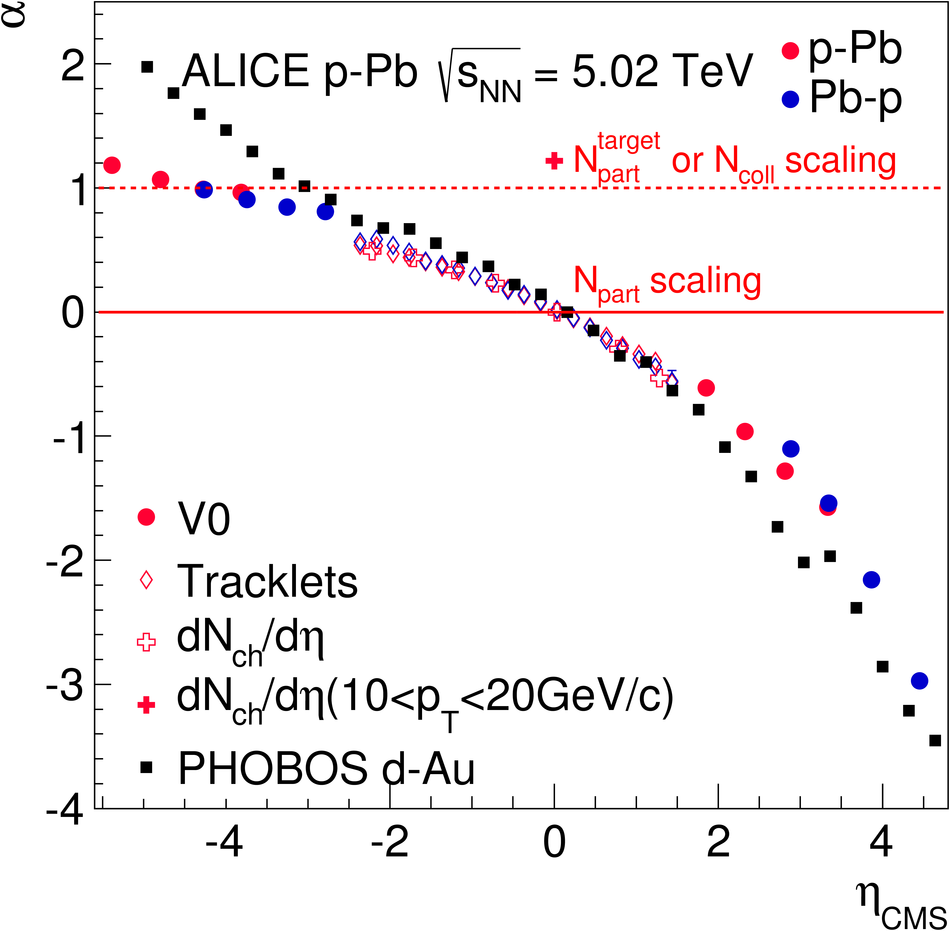
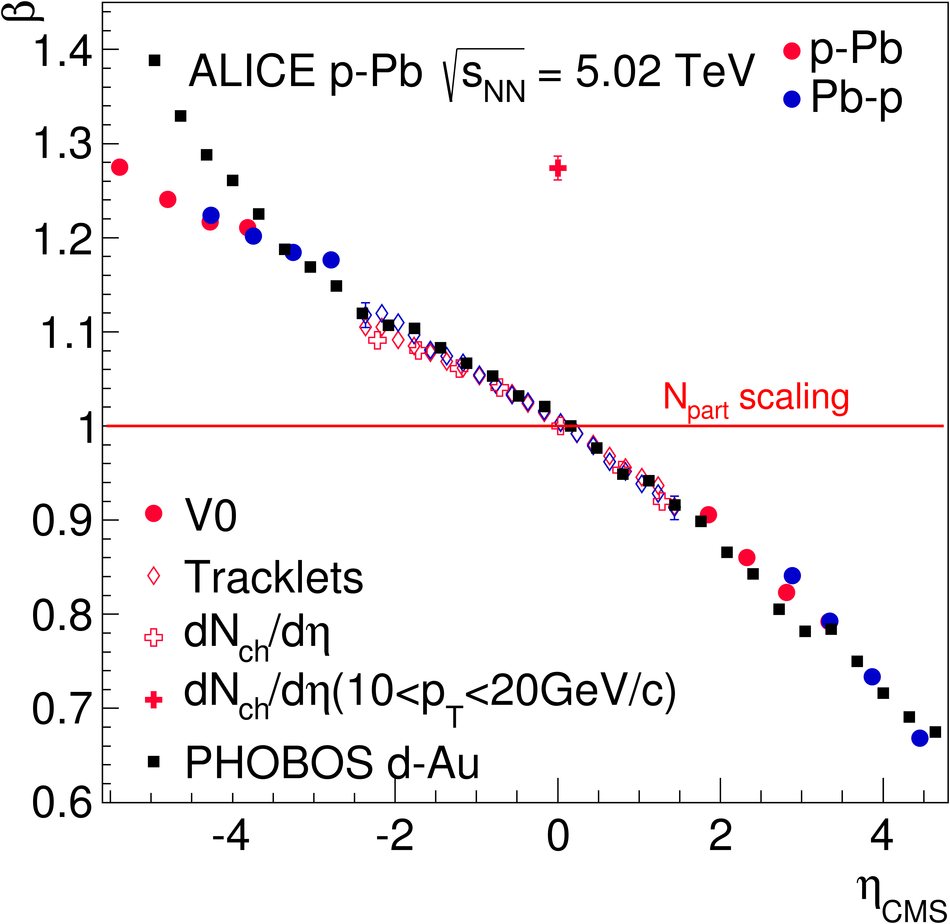
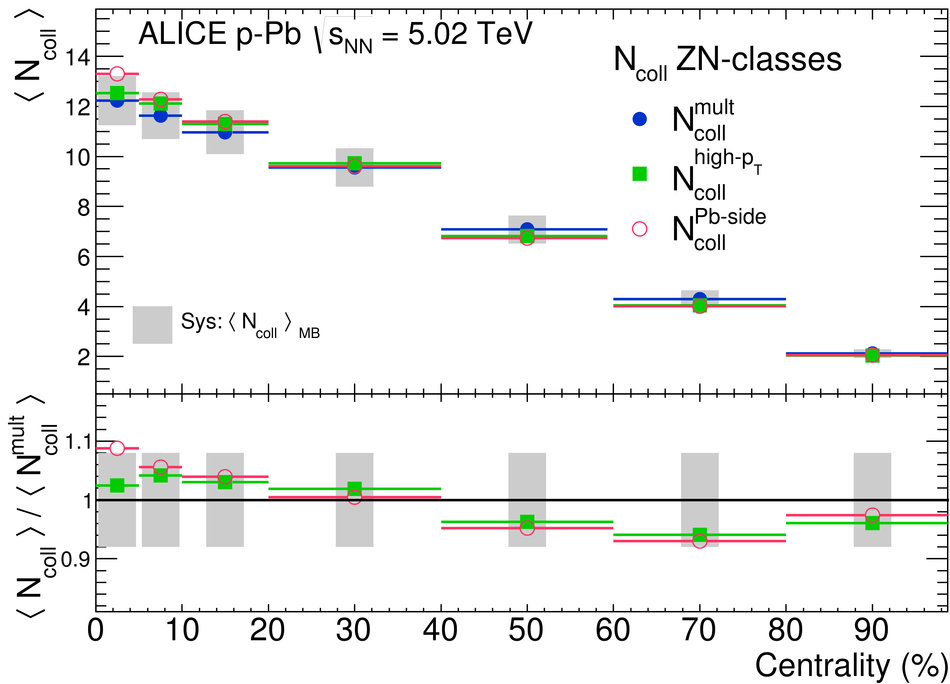
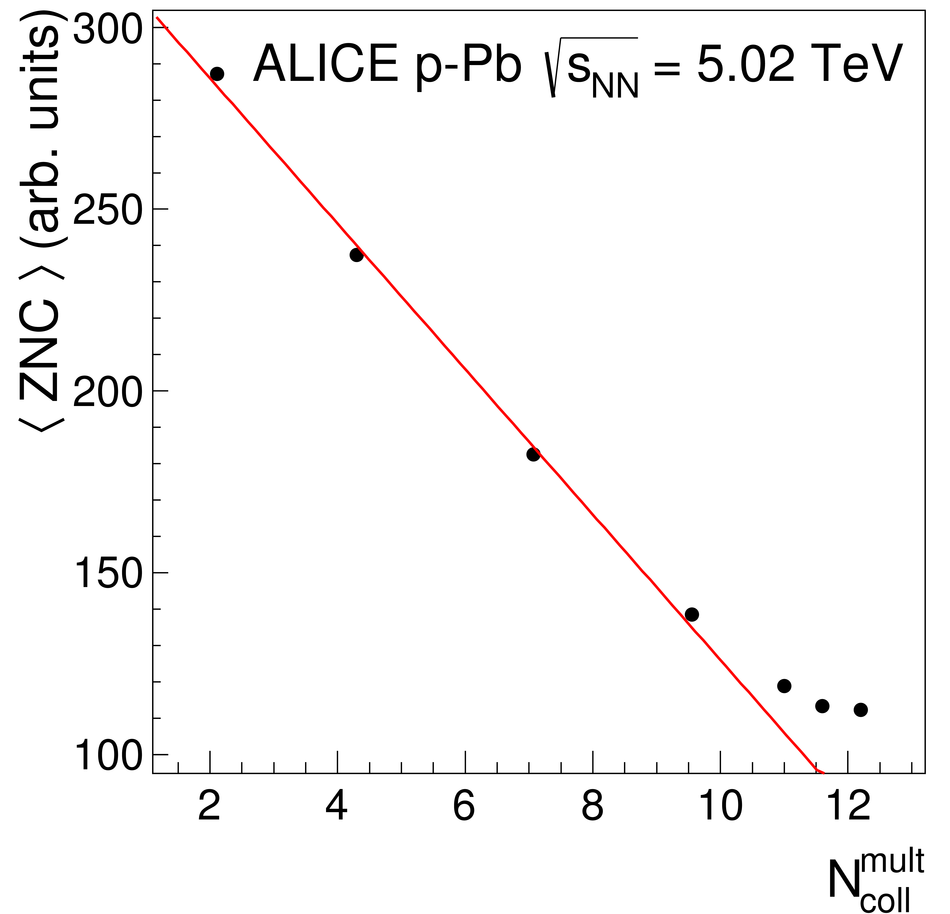
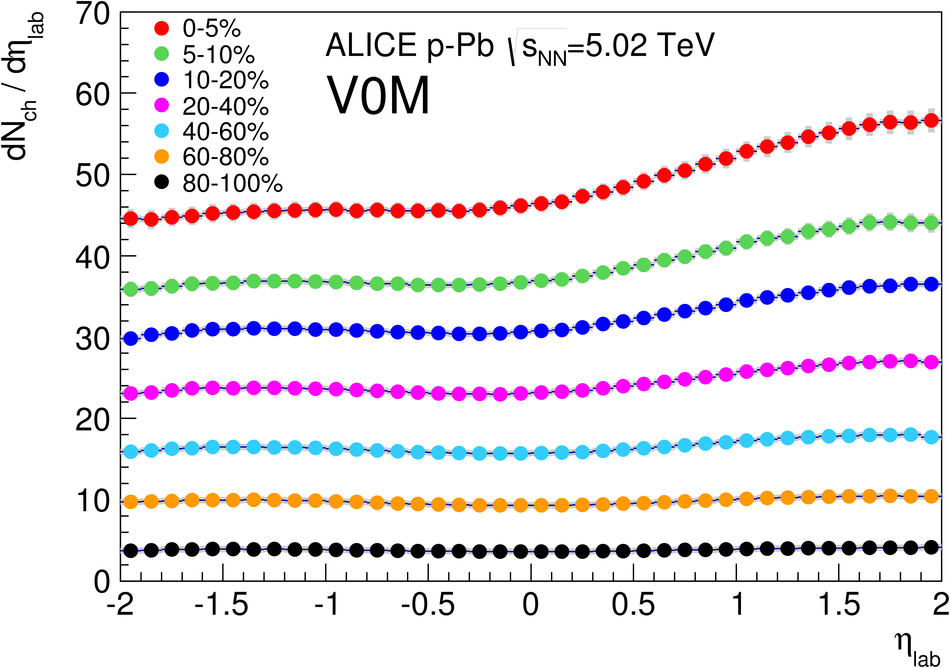
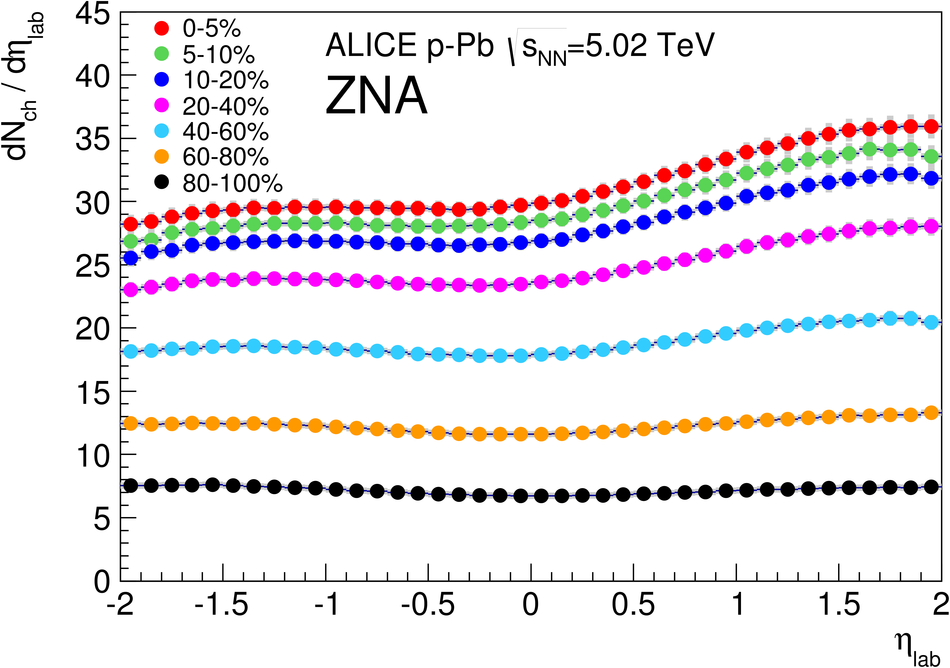
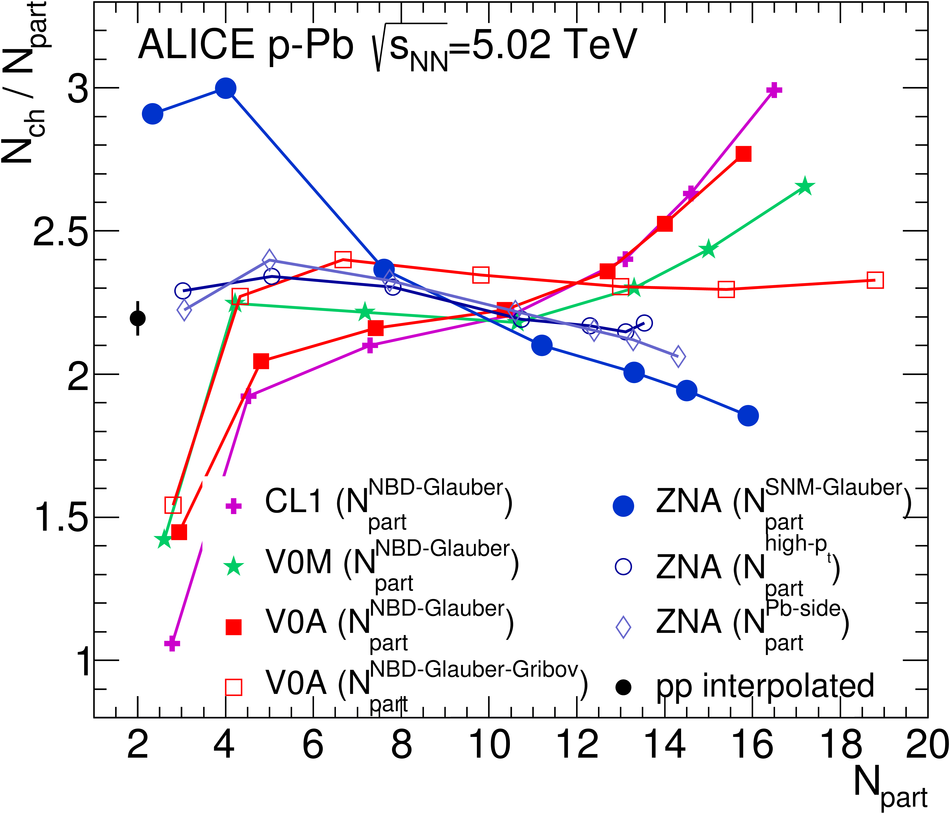
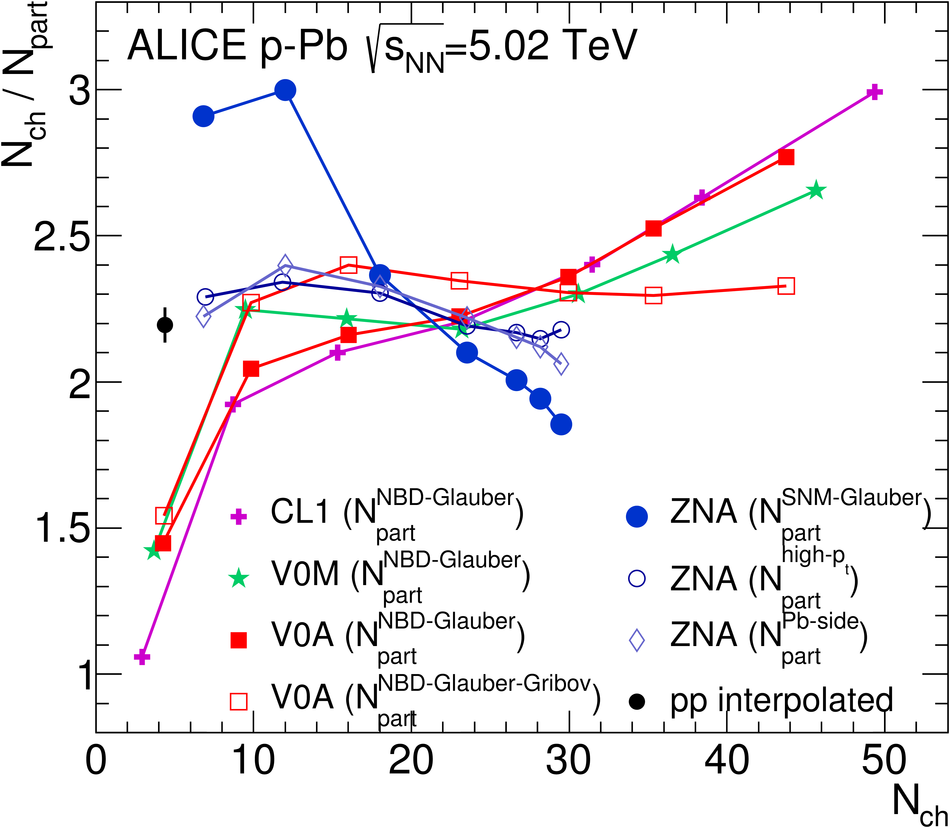
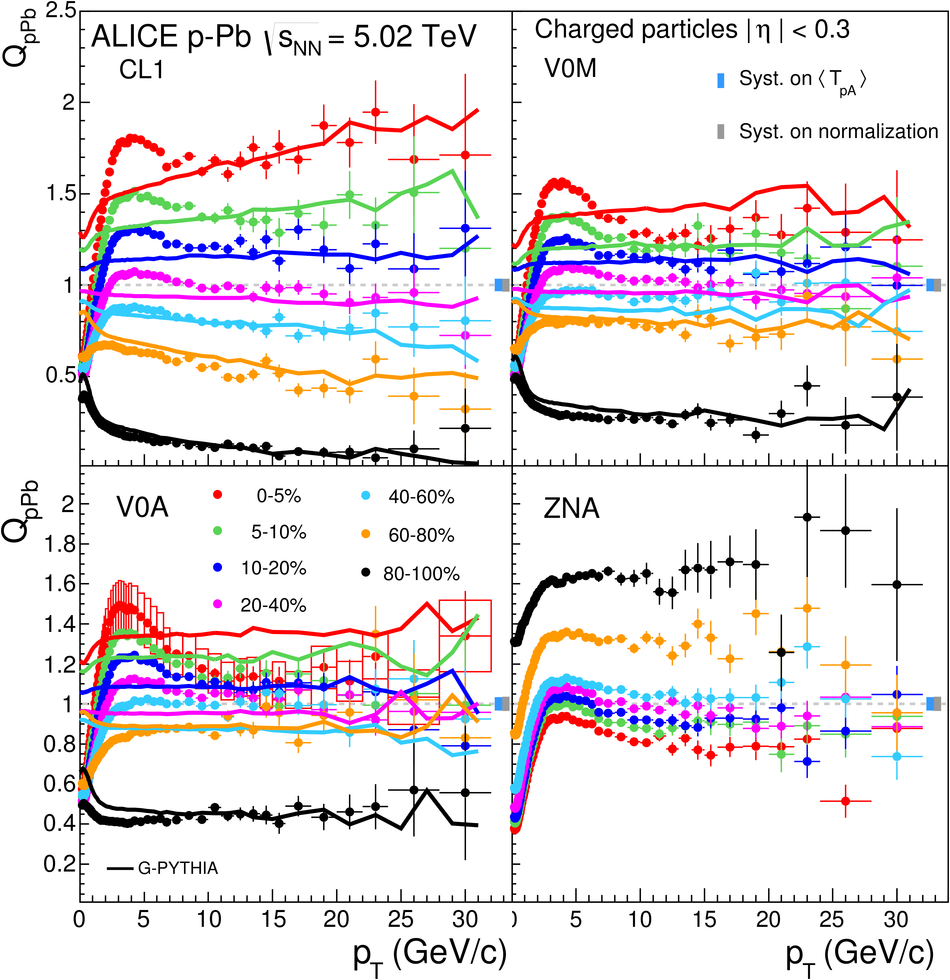
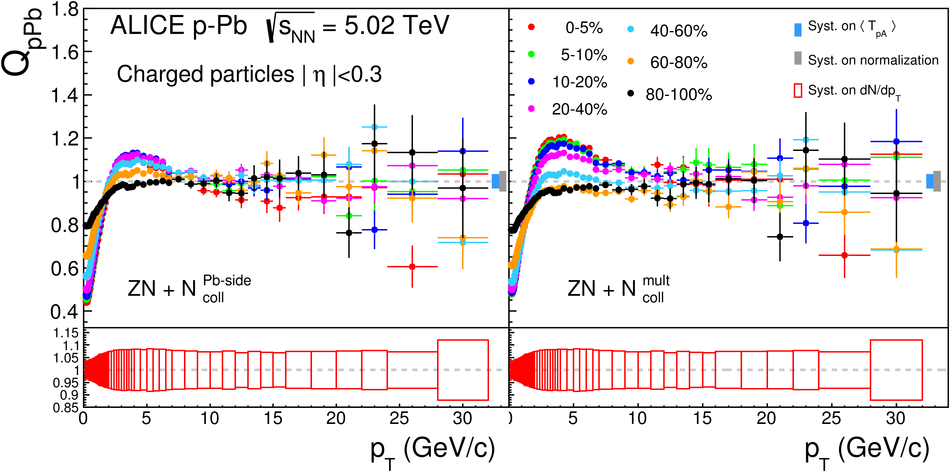
We report measurements of the primary charged particle pseudorapidity density and transverse momentum distributions in p-Pb collisions at $\sqrt{s_{\rm NN}}$ = 5.02 TeV, and investigate their correlation with experimental observables sensitive to the centrality of the collision. Centrality classes are defined using different event activity estimators, i.e. charged particle multiplicities measured in three disjunct pseudorapidity regions as well as the energy measured at beam rapidity (zero-degree). The procedures to determine the centrality, quantified by the number of participants ($N_{\rm part}$), or the number of nucleon-nucleon binary collisions ($N_{\rm coll}$), are described. We show that, in contrast to Pb-Pb collisions, in p-Pb collisions large multiplicity fluctuations together with the small range of participants available, generate a dynamical bias in centrality classes based on particle multiplicity. We propose to use the zero-degree energy, which we expect not to introduce a dynamical bias, as an alternative event-centrality estimator. Based on zero-degree energy centrality classes, the $N_{\rm part}$ dependence of particle production is studied. Under the assumption that the multiplicity measured in the Pb-going rapidity region scales with the number of Pb-participants, an approximate independence of the multiplicity per participating nucleon measured at mid-rapitity of the number of participating nucleons is observed. Furthermore, at high-$p_{\rm T}$ the p-Pb spectra are found to be consistent with the pp spectra scaled by $N_{\rm coll}$ for all centrality classes. Our results represent valuable input for the study of the event activity dependence of hard probes in p-Pb collision and, hence, help to establish baselines for the interpretation of the Pb-Pb data.
Phys. Rev. C 91 (2015) 064905
HEP Data
e-Print: arXiv:1412.6828 | PDF | inSPIRE
CERN-PH-EP-2014-281