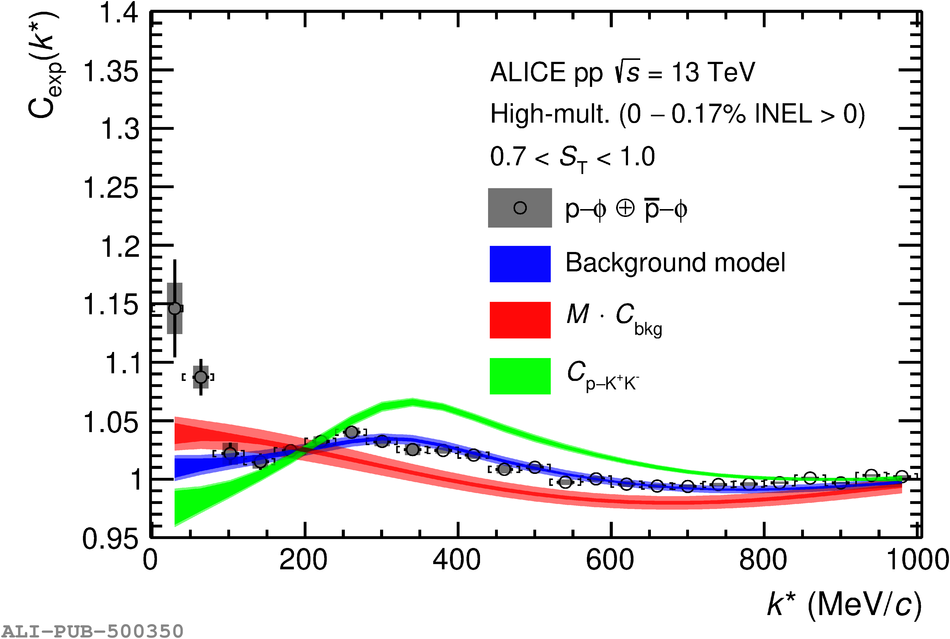
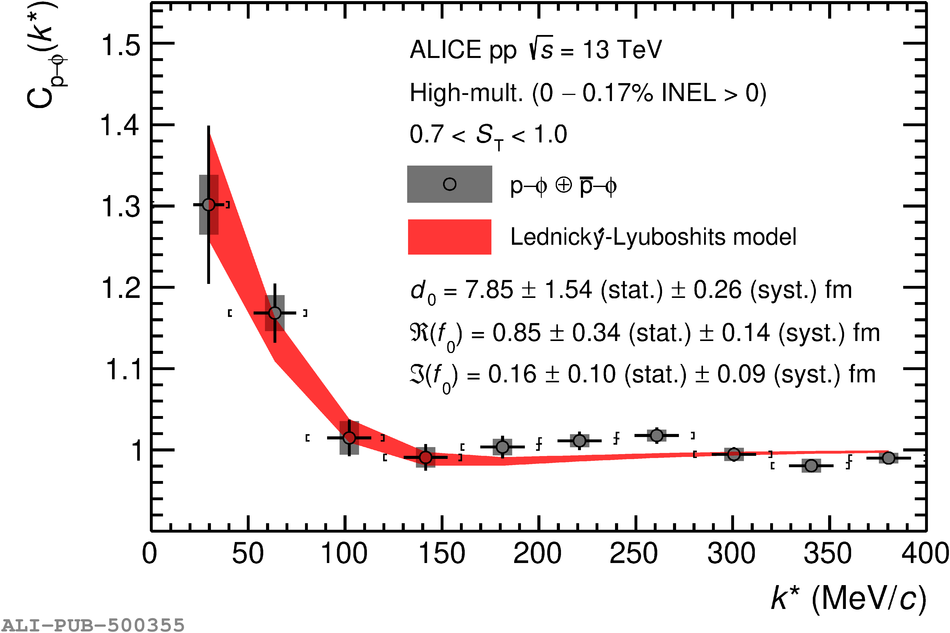
This Letter presents the first experimental evidence of the attractive strong interaction between a proton and a $\phi$ meson. The result is obtained from two-particle correlations of combined p-$\phi \oplus \overline{\rm {p}}$-$\phi$ pairs measured in high-multiplicity pp collisions at $\sqrt{s}~=~13$ TeV by the ALICE collaboration. The spin-averaged scattering length and effective range of the p-$\phi$ interaction are extracted from the fully corrected correlation function employing the Lednick\'y-Lyuboshits approach. In particular, the imaginary part of the scattering length vanishes within uncertainties, indicating that inelastic processes do not play a prominent role for the p-$\phi$ interaction. These data demonstrate that the interaction is dominated by elastic p-$\phi$ scattering. Furthermore, an analysis employing phenomenological Gaussian- and Yukawa-type potentials is conducted. Under the assumption of the latter, the N-$\phi$ coupling constant is found to be $g_{\rm{N}-\phi} = 0.14\pm 0.03\,(\mathrm{stat.})\pm 0.02\,(\mathrm{syst.})$. This work provides valuable experimental input to accomplish a self-consistent description of the N-$\phi$ interaction, which is particularly relevant for the more fundamental studies on partial restoration of chiral symmetry in nuclear medium.
PRL 127 (2021) 172301
HEP Data
e-Print: arXiv:2105.05578 | PDF | inSPIRE
CERN-EP-2021-081
Figure group