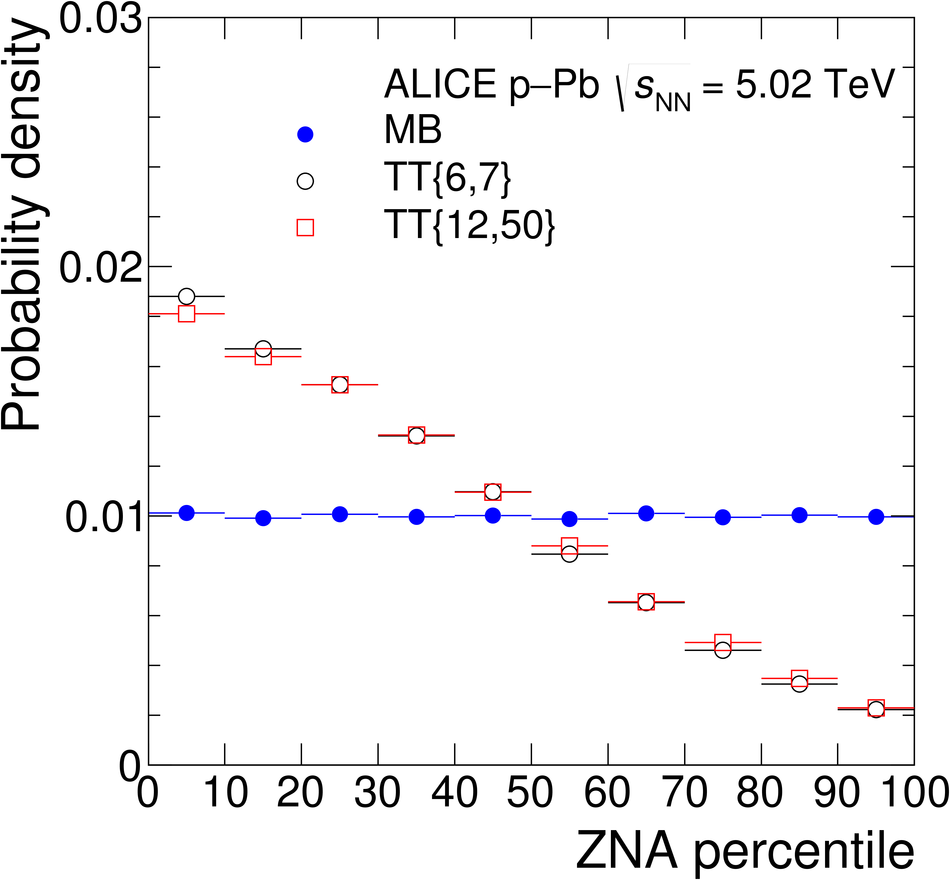
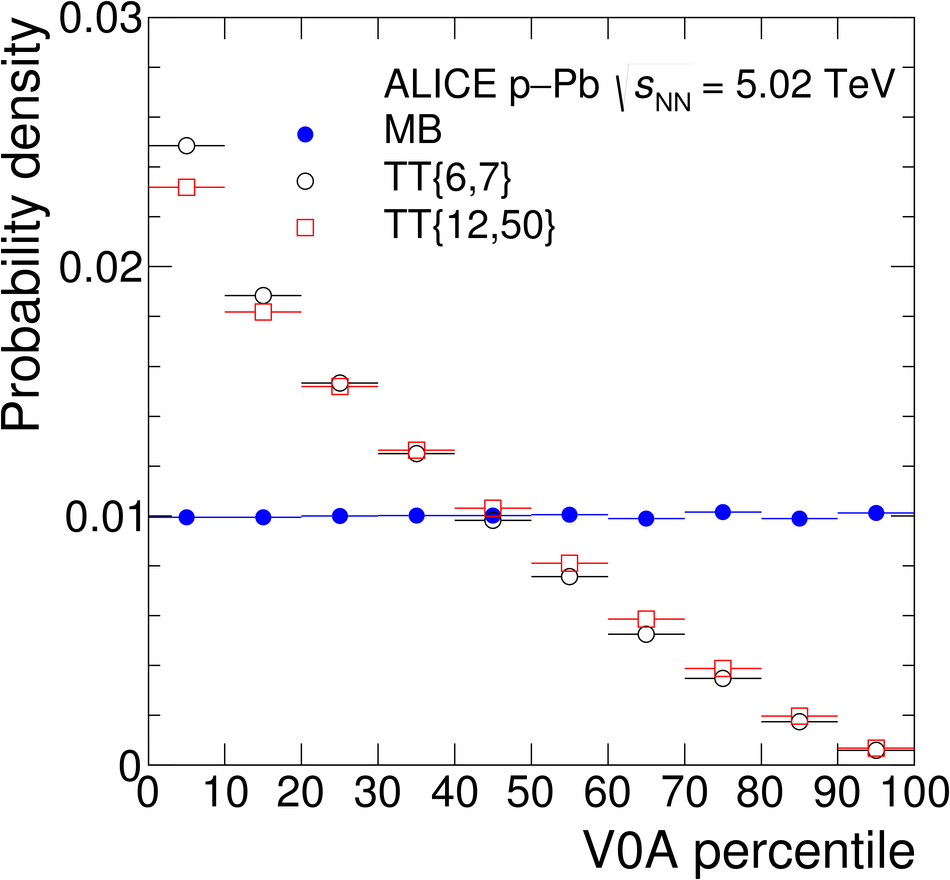
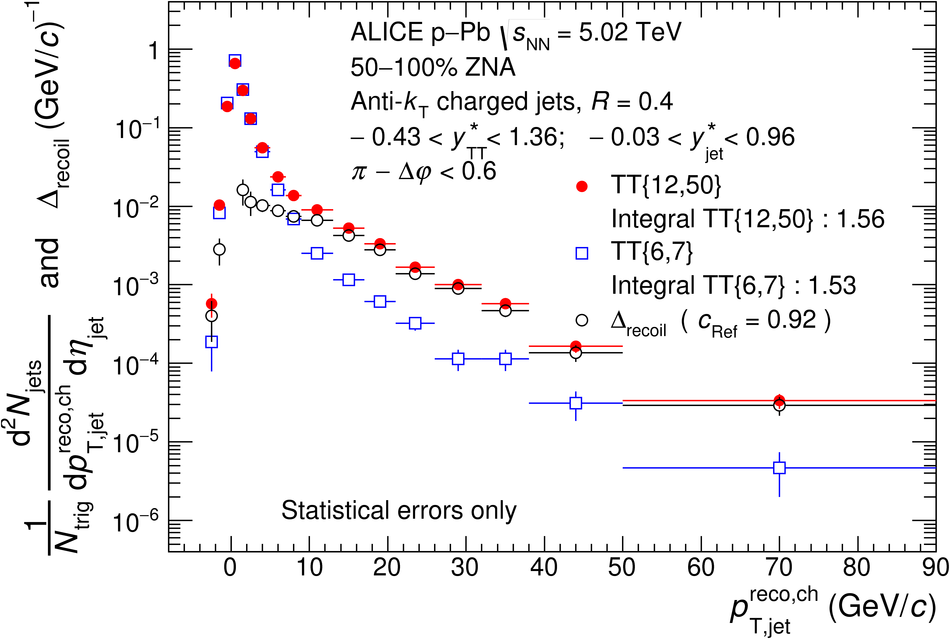
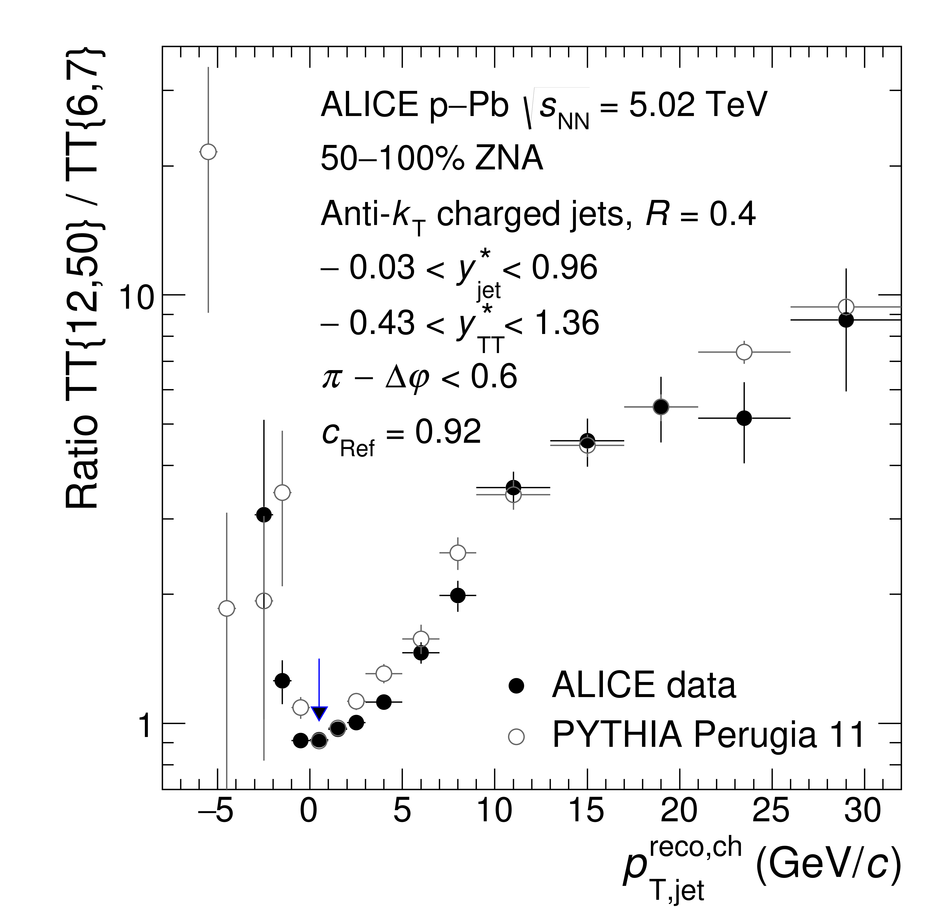
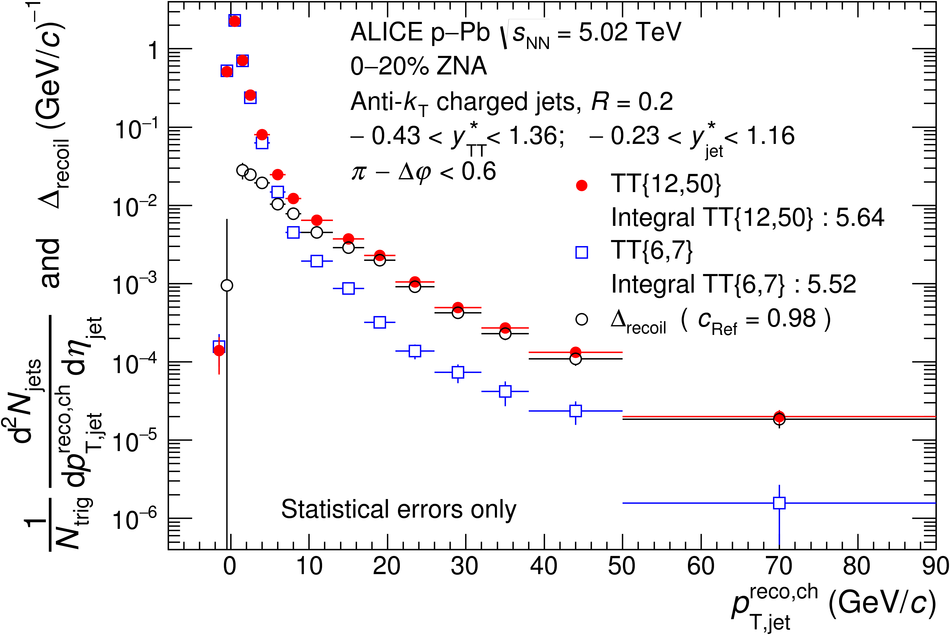
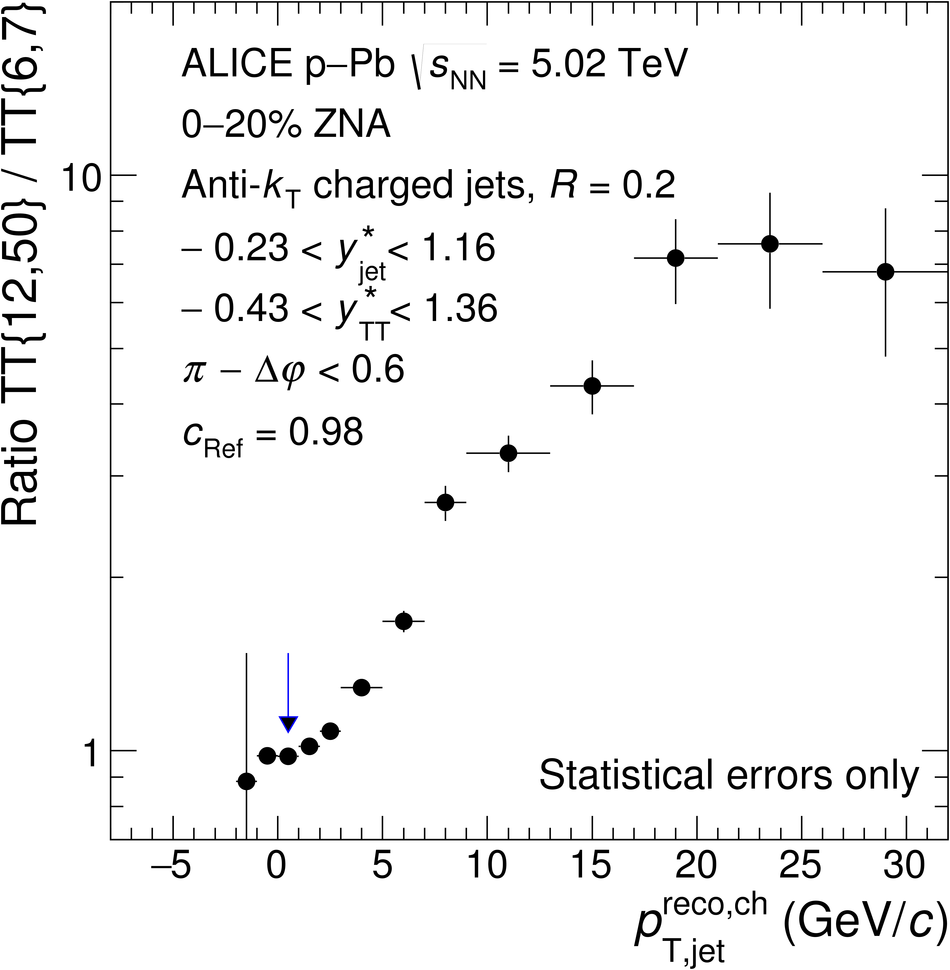
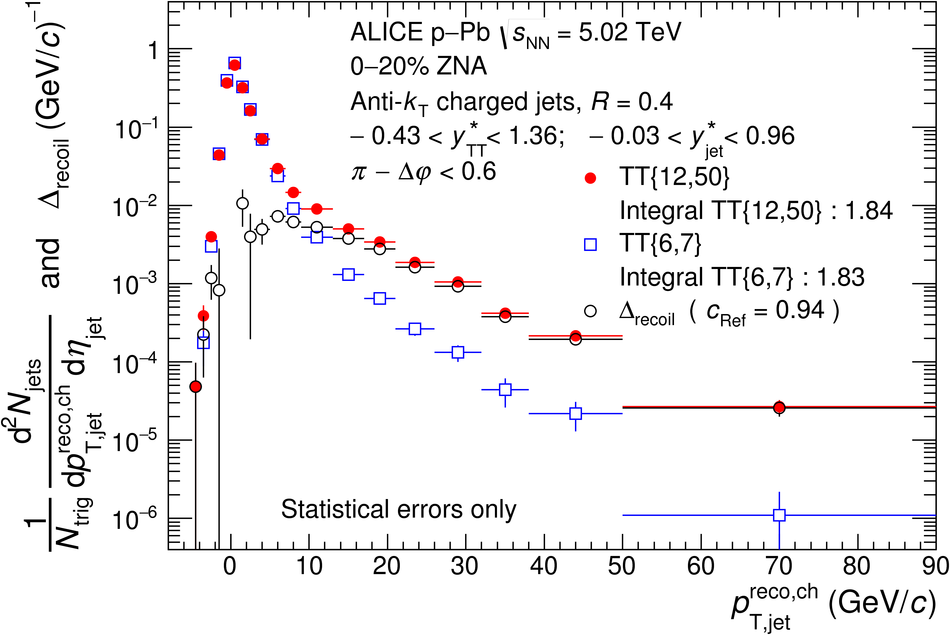
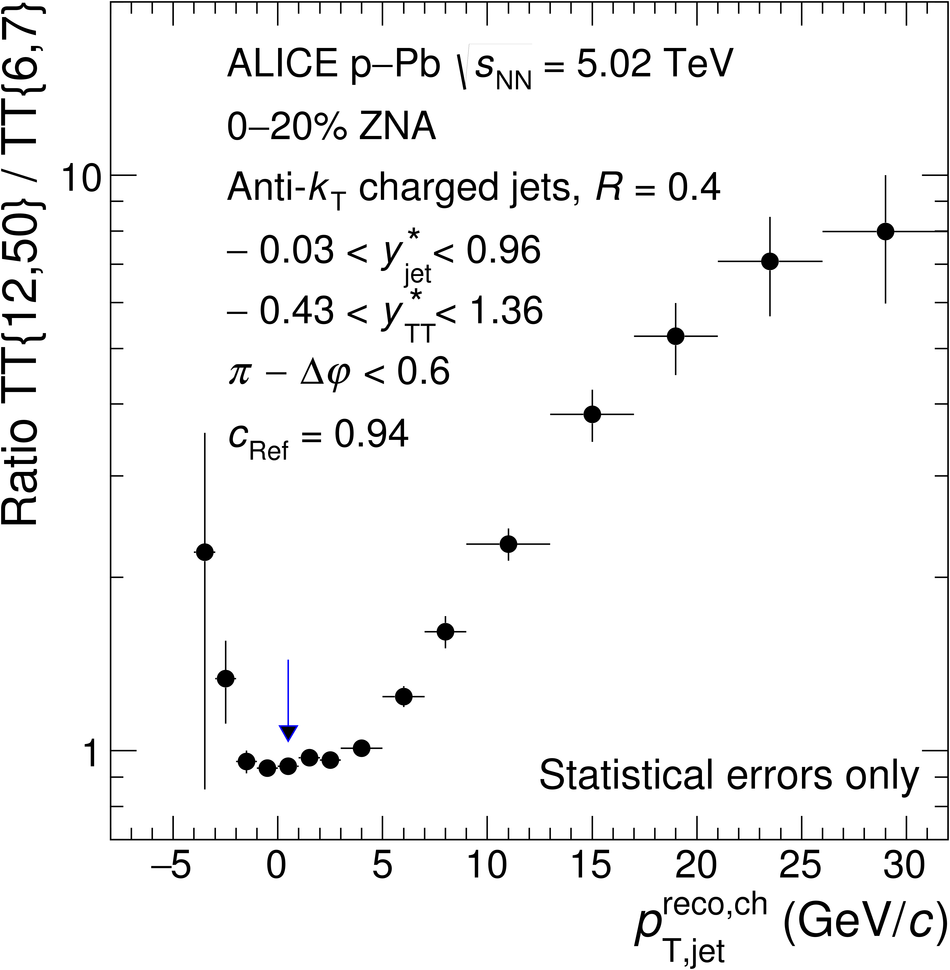
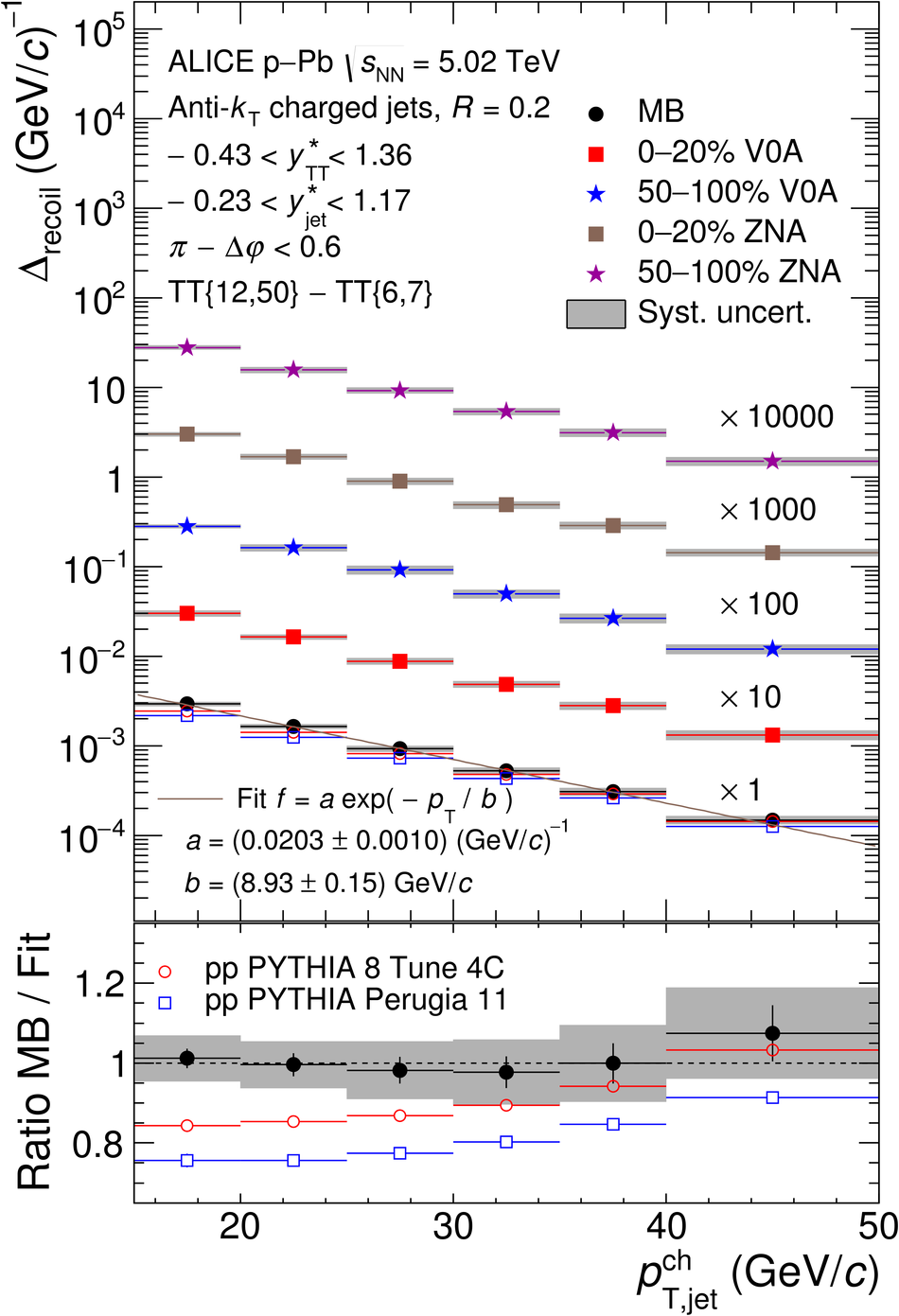
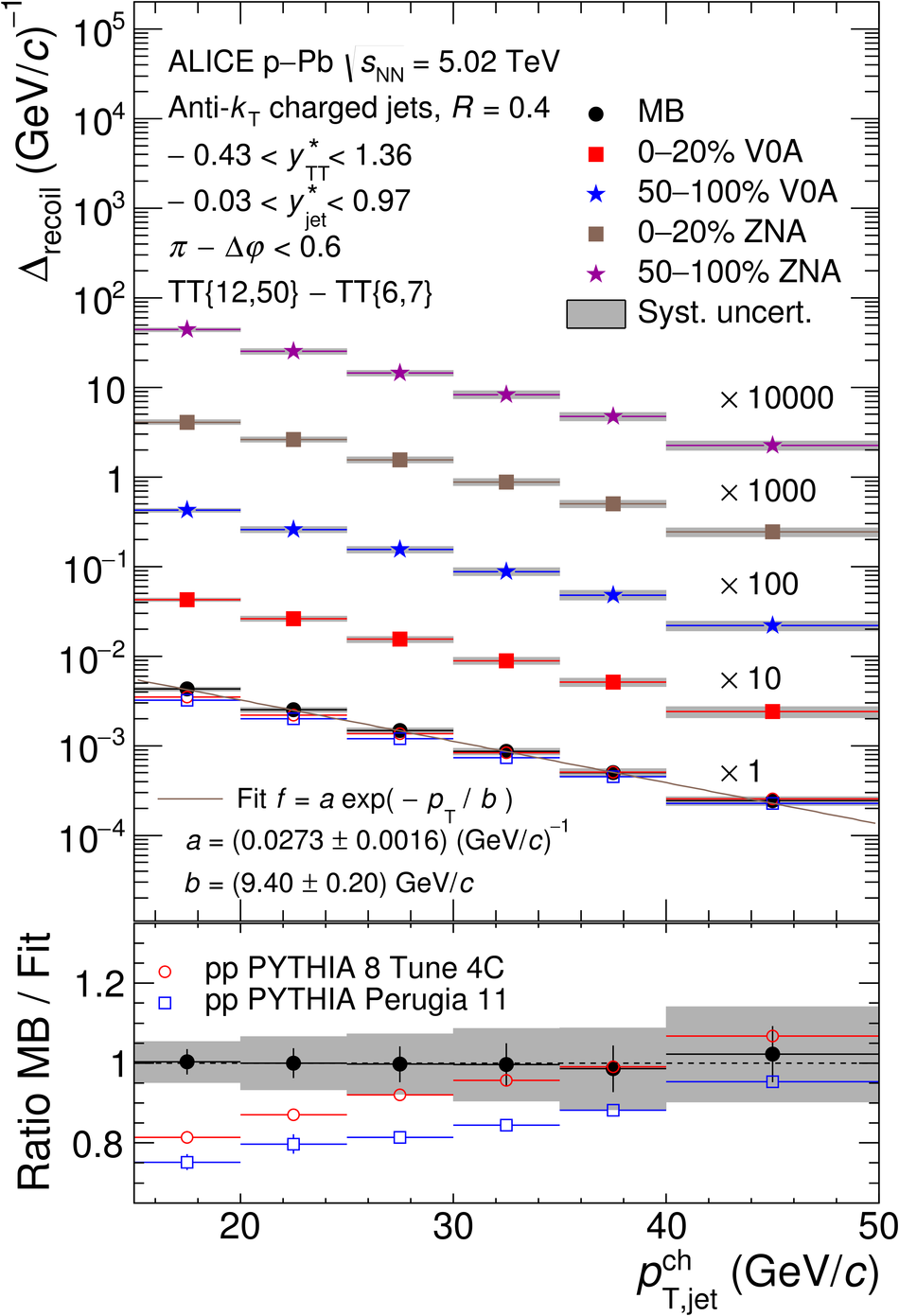
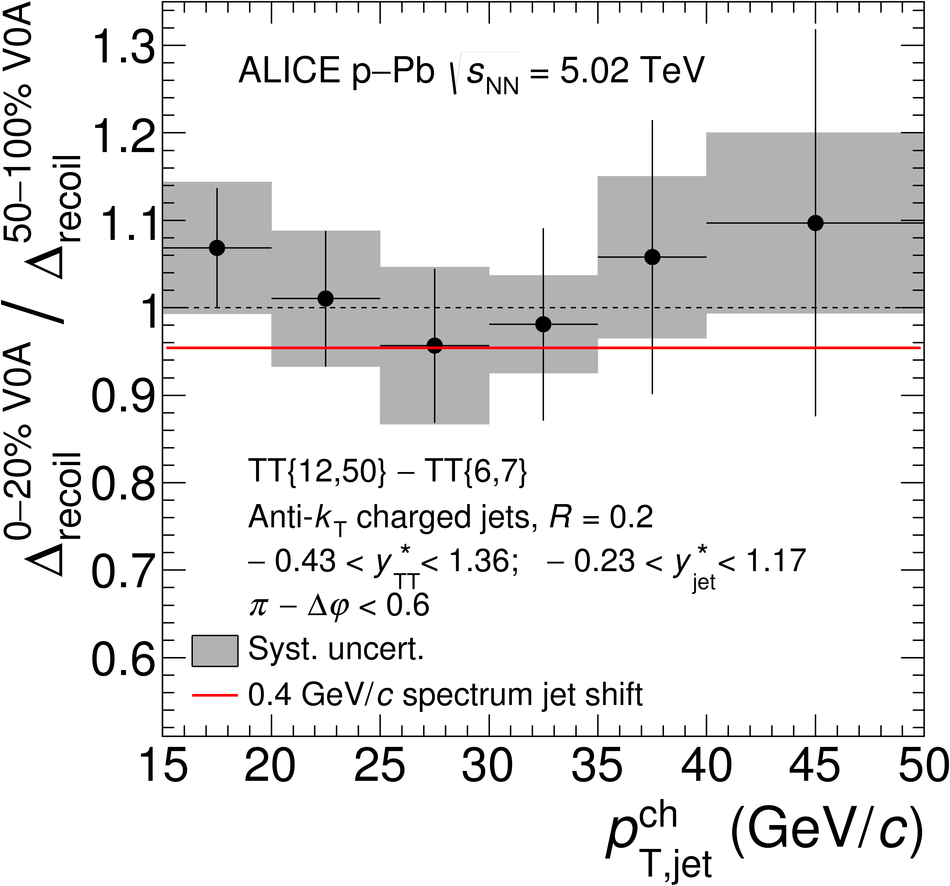
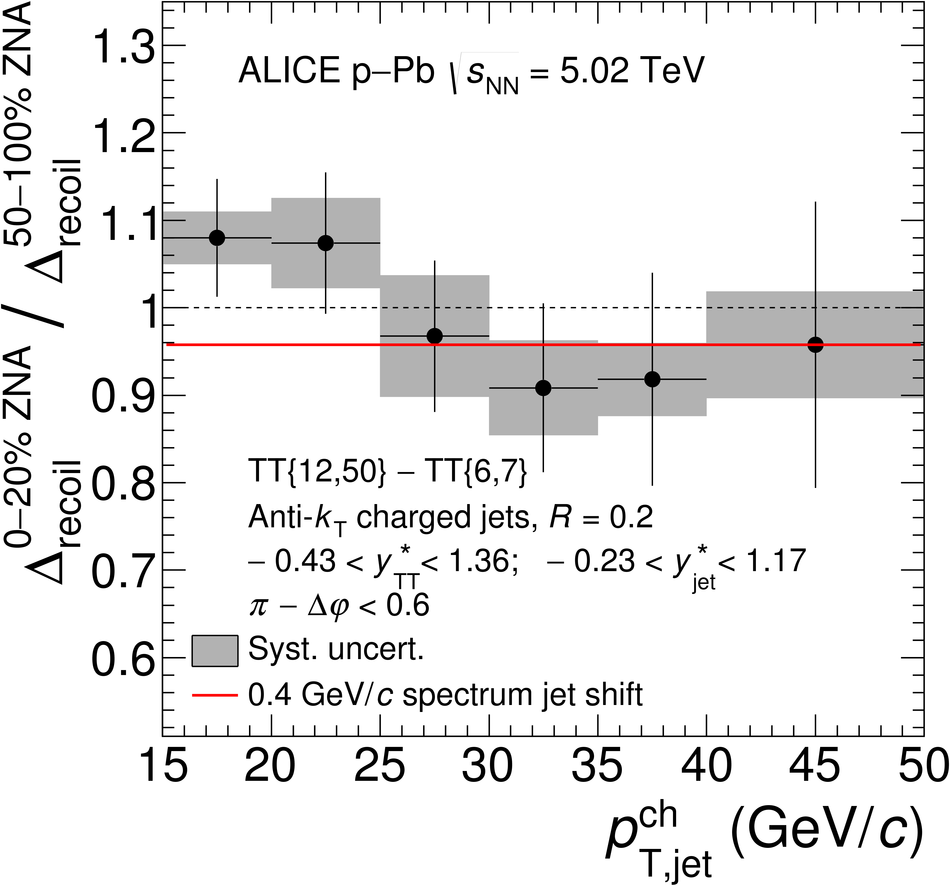
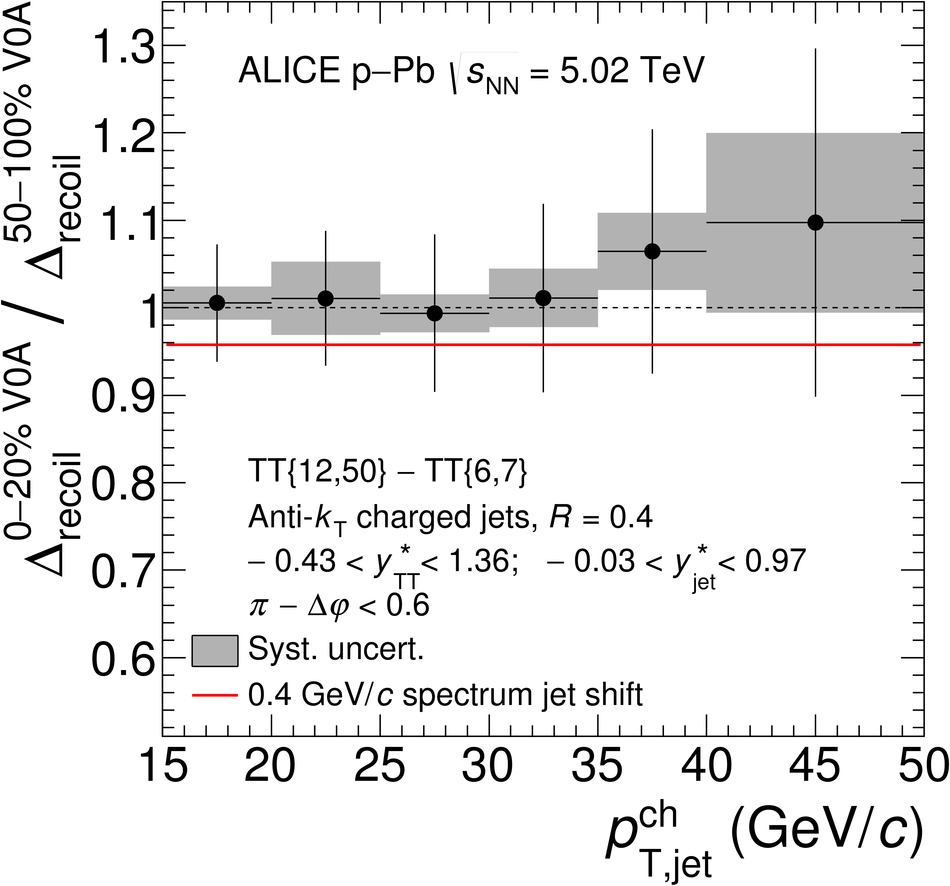
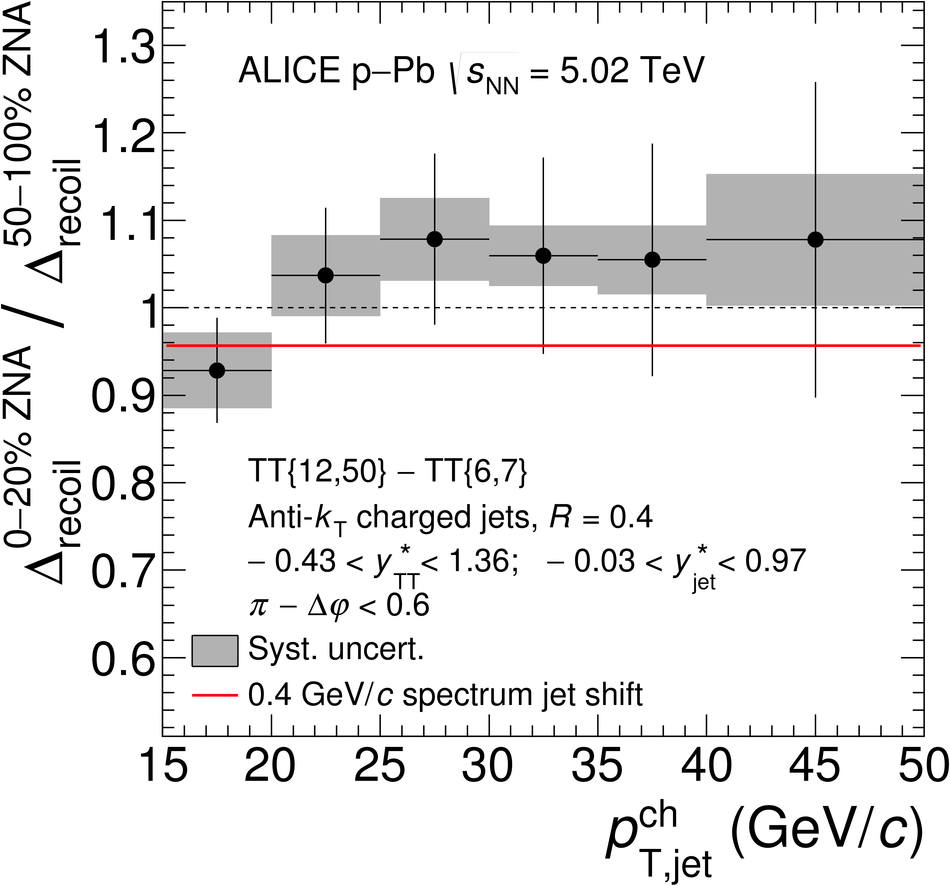
The ALICE Collaboration reports the measurement of semi-inclusive distributions of charged-particle jets recoiling from a high-transverse momentum trigger hadron in p-Pb collisions at $\sqrt{s_{\rm NN}} =5.02$ TeV. Jets are reconstructed from charged-particle tracks using the anti-$k_{\rm T}$ algorithm with resolution parameter $R=0.2$ and $0.4$. A data-driven statistical approach is used to correct the uncorrelated background jet yield. Recoil jet distributions are reported for jet transverse momentum $15<~p_{\rm T,jet}^{\rm ch} <~50$ GeV/$c$ and are compared in various intervals of p-Pb event activity, based on charged-particle multiplicity and zero-degree neutral energy in the forward (Pb-going) direction. The semi-inclusive observable is self-normalized and such comparisons do not require the interpretation of p-Pb event activity in terms of collision geometry, in contrast to inclusive jet observables. These measurements provide new constraints on the magnitude of jet quenching in small systems at the LHC. In p-Pb collisions with high event activity, the average medium-induced out-of-cone energy transport for jets with $R=0.4$ and $15<~p_{\rm T,jet}^{\rm ch}<~50$ GeV/$c$ is measured to be less than 0.4 GeV/$c$ at 90% confidence, which is over an order of magnitude smaller than a similar measurement for central Pb-Pb collisions at $\sqrt{s_{\rm NN}}=2.76$ TeV. Comparison is made to theoretical calculations of jet quenching in small systems, and to inclusive jet measurements in p-Pb collisions selected by event activity at the LHC and in d-Au collisions at RHIC.
Phys. Lett. B 783 (2018) 95-113
HEP Data
e-Print: arXiv:1712.05603 | PDF | inSPIRE
CERN-EP-2017-324