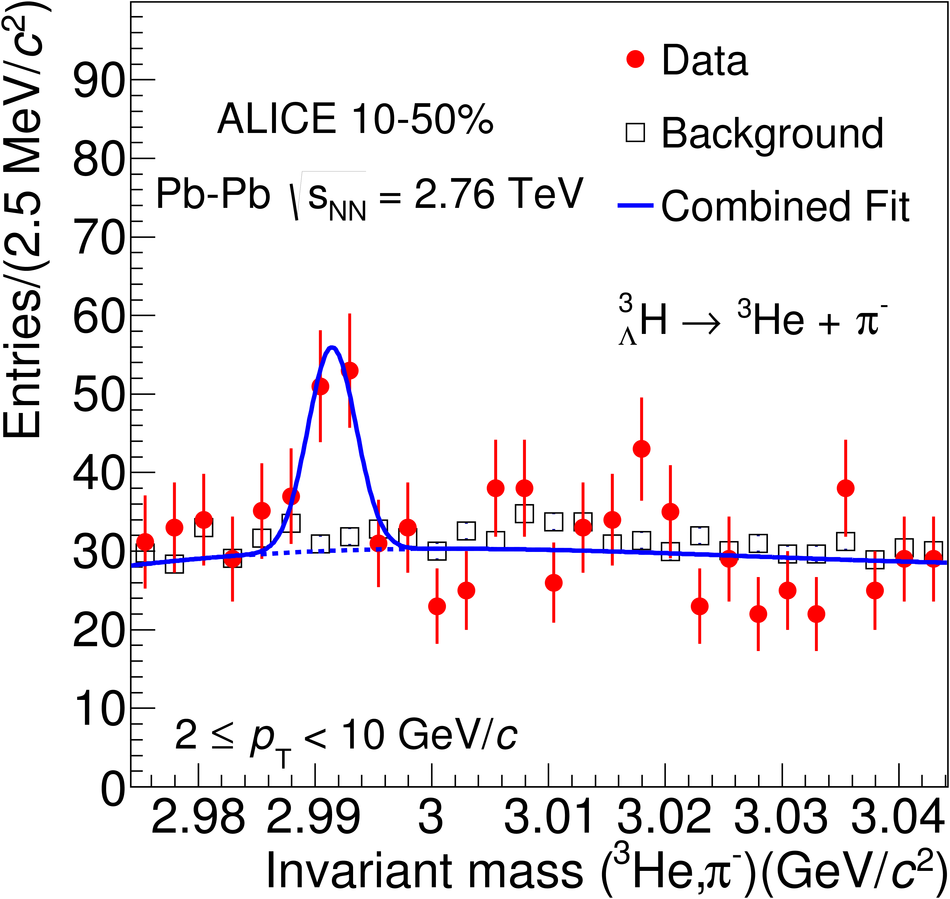
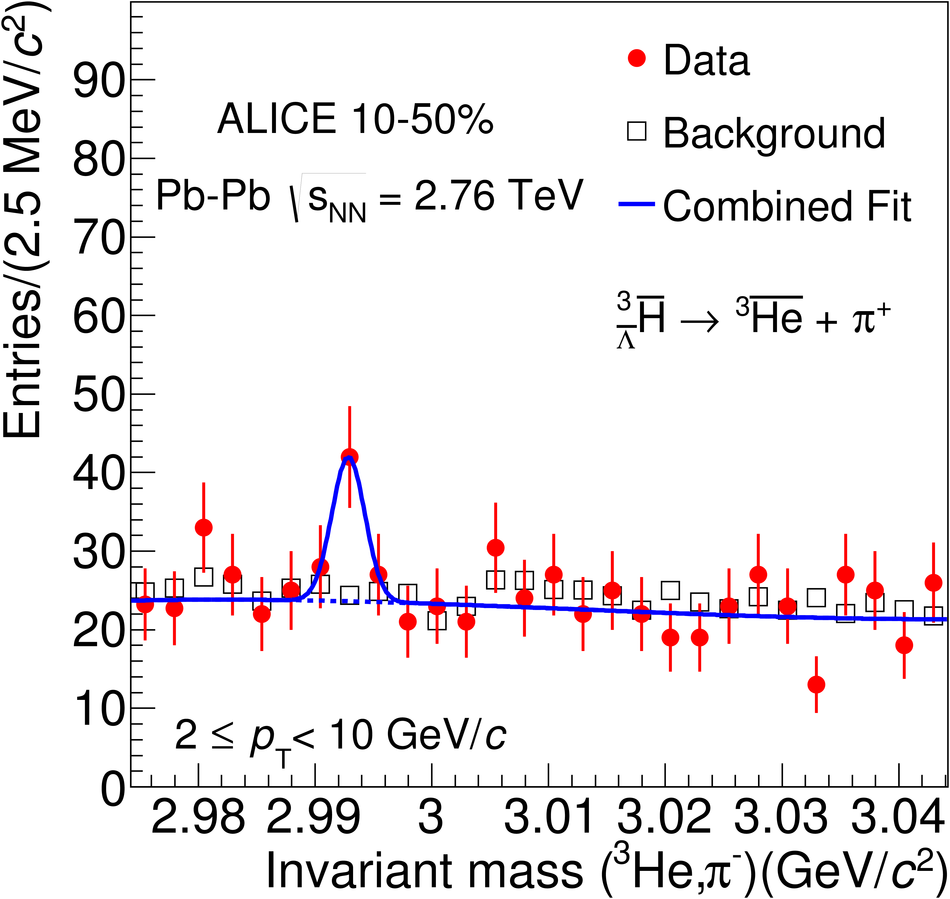
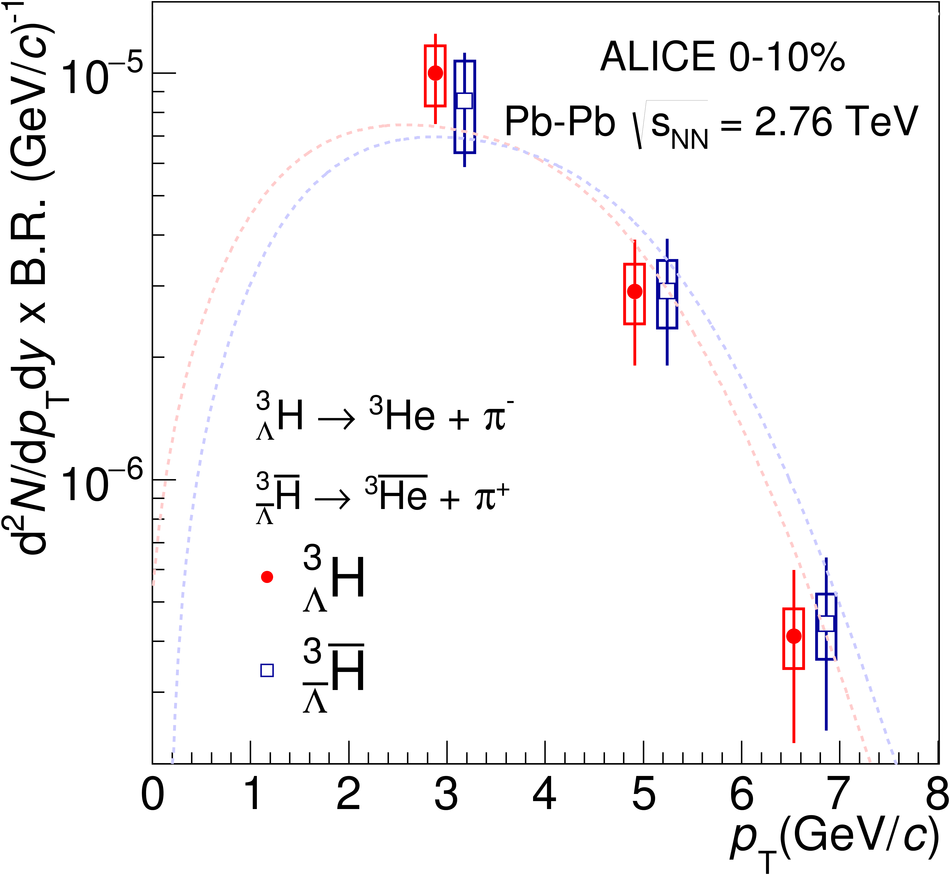
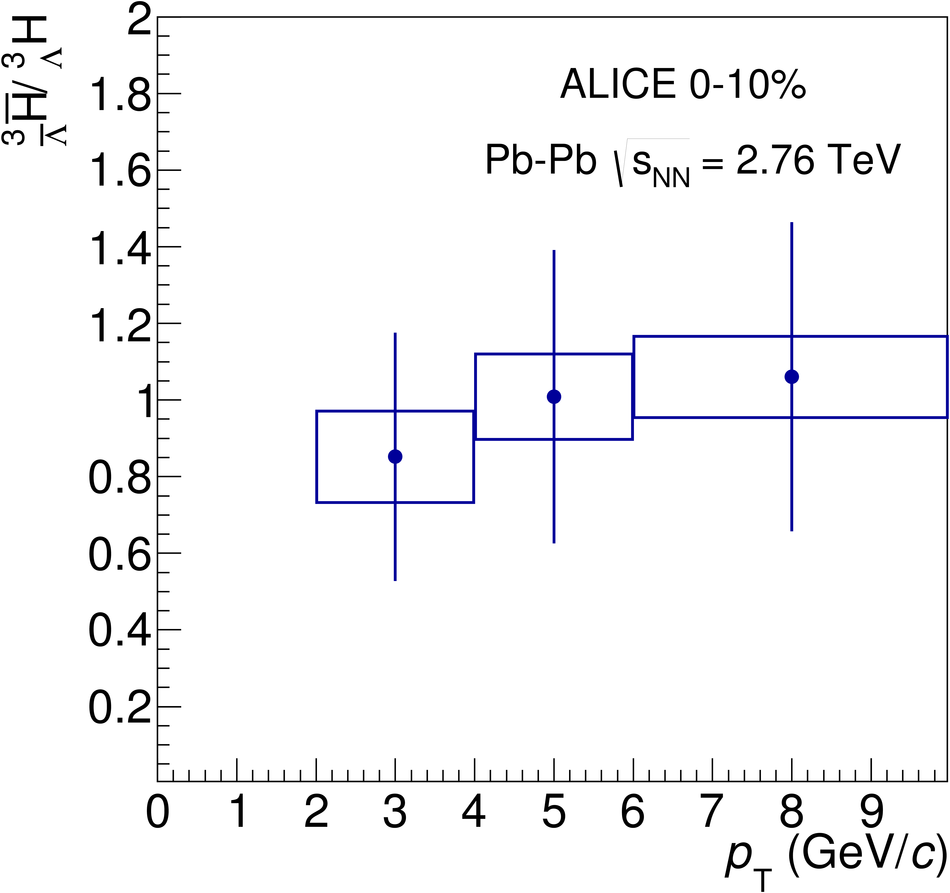
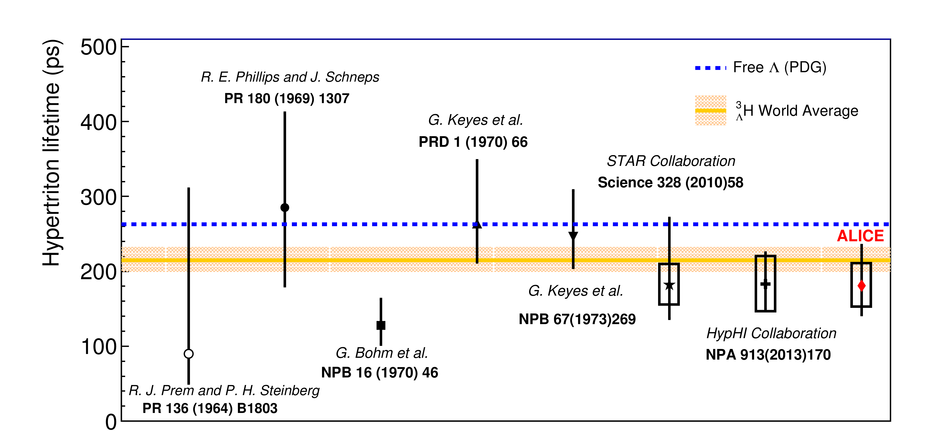
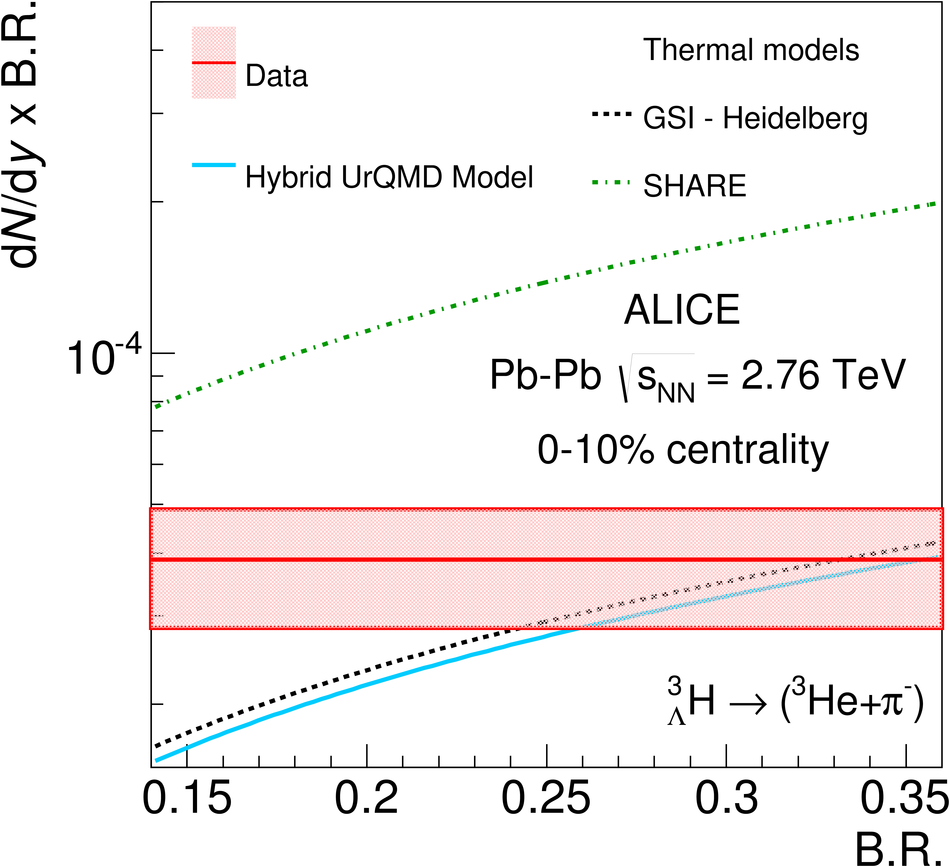
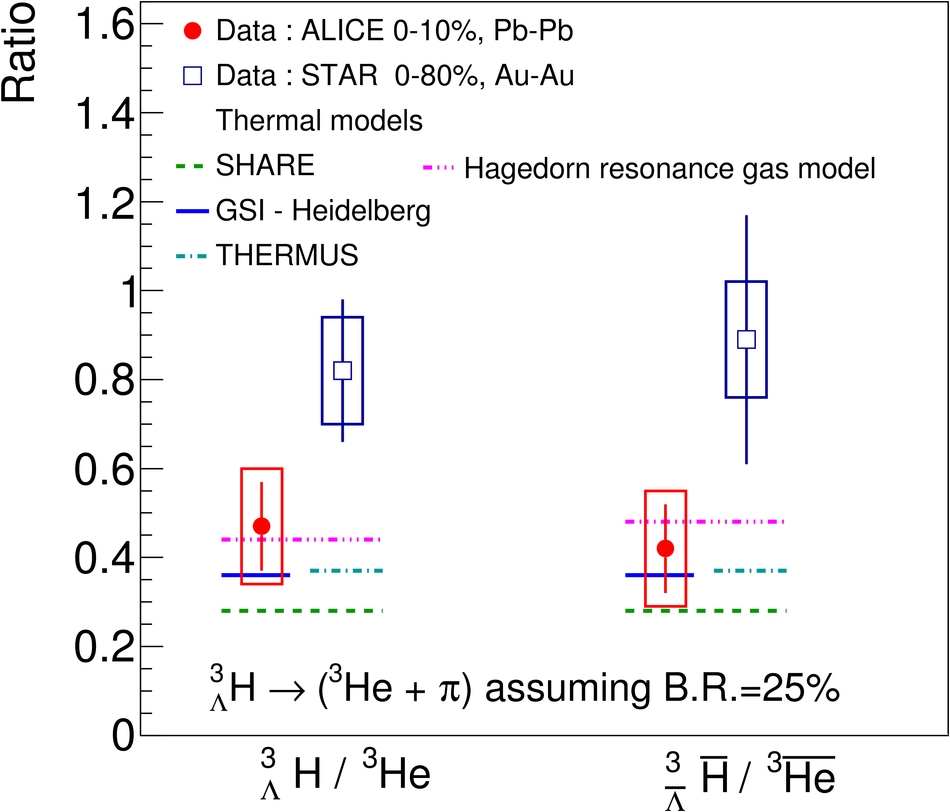
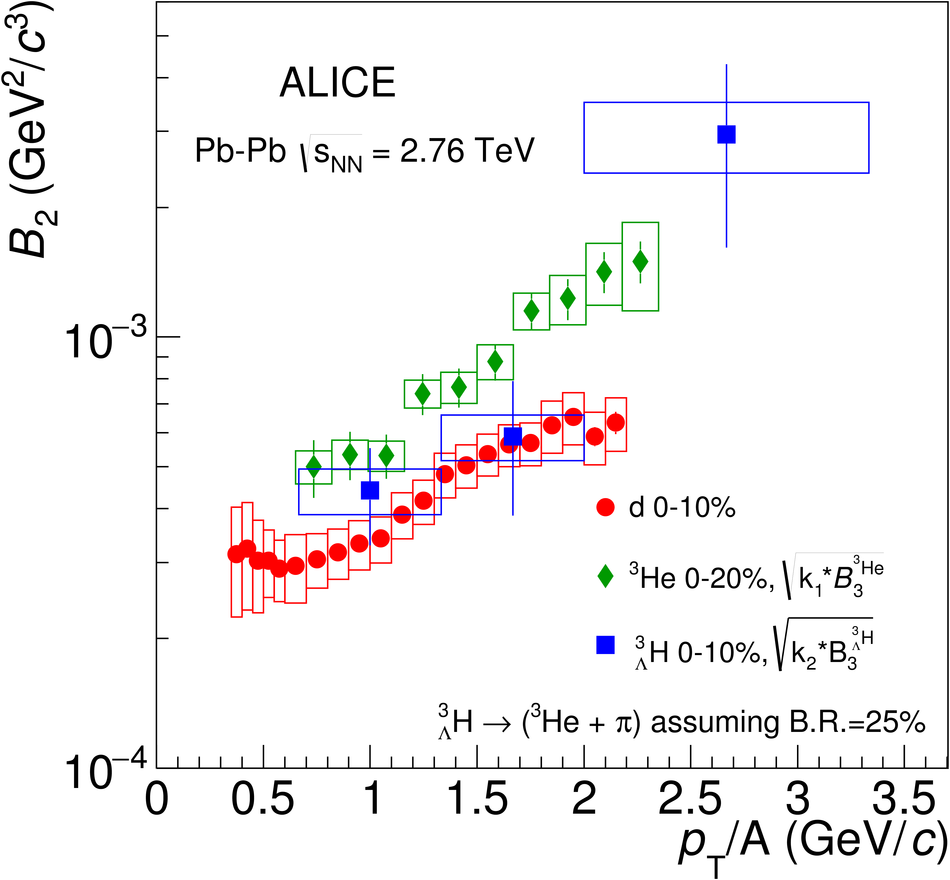
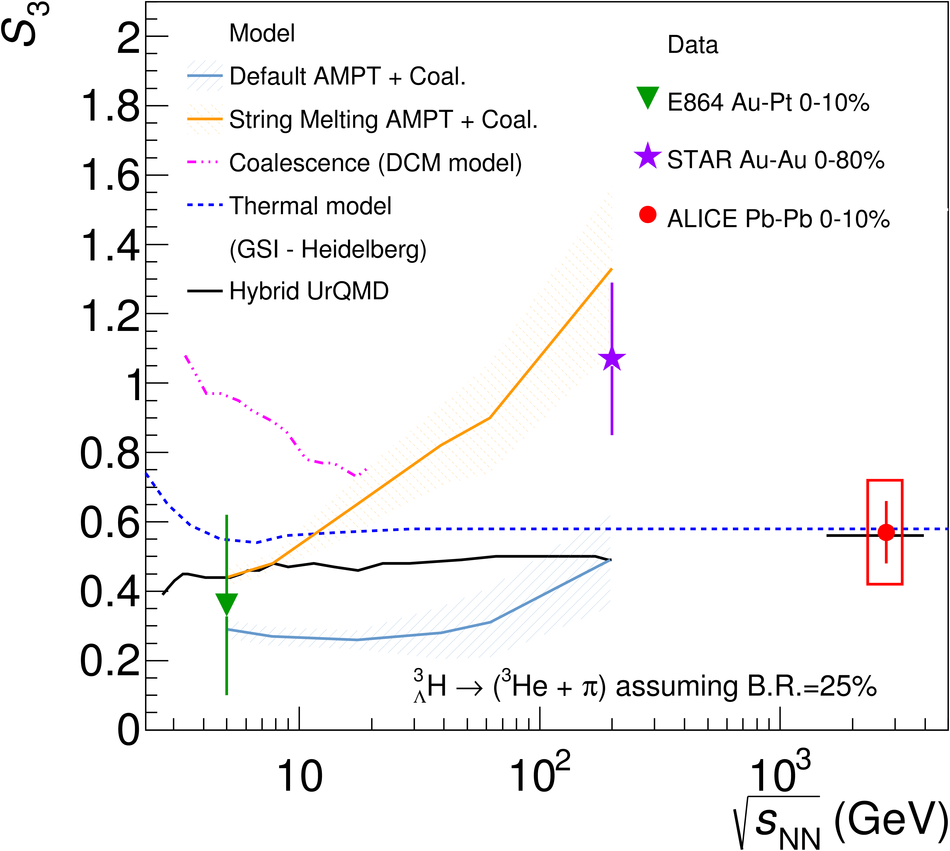
The production of the hypertriton nuclei $^{3}_{\Lambda}\mathrm H$ and $^{3}_{\bar{\Lambda}} \overline{\mathrm H}$ has been measured for the first time in Pb-Pb collisions at $\sqrt{s_{\rm NN}}$ = 2.76 TeV with the ALICE experiment at LHC energies. The total yield, d$N$/d$y$ $\times \mathrm{B.R.}_{\left( ^{3}_{\Lambda}\mathrm H \rightarrow ^{3}\mathrm{He},\pi^{-} \right)} = \left( 3.86 \pm 0.77 (\mathrm{stat.}) \pm 0.68 (\mathrm{syst.})\right) \times 10^{-5}$ in the 0-10% most central collisions, is consistent with the predictions from a statistical thermal model using the same temperature as for the light hadrons. The coalescence parameter $B_3$ shows a dependence on the transverse momentum, similar to the $B_2$ of deuterons and the $B_3$ of $^{3}\mathrm{He}$ nuclei. The ratio of yields $S_3$ = $^{3}_{\Lambda}\mathrm H$/($^{3}\mathrm{He}$ $\times \Lambda/\mathrm{p}$) was measured to be $S_3$ = 0.60 $\pm$ 0.13 (stat.) $\pm$ 0.21 (syst.) in 0-10% centrality events; this value is compared to different theoretical models. The measured $S_3$ is fully compatible with thermal model predictions. The measured $^{3}_{\Lambda}\mathrm H$ lifetime, $ \tau = 181^{+54}_{-39} (\mathrm{stat.}) \pm 33 (\mathrm{syst.})\ \mathrm{ps}$ is compatible within 1$\sigma$ with the world average value.
Phys. Lett. B 754 (2016) 360-372
HEP Data
e-Print: arXiv:1506.08453 | PDF | inSPIRE
CERN-PH-EP-2015-105
Figure 1
Invariant mass of ($^{3}\rm{He}$,$\pi^-$) (left) and ($^{3}\overline{\rm{He}}$,$\pi^+$) (right) for events with 10-50% centrality in the pair 2 $\leq \pt $< 10 Gev/$c$ interval. The data points are shown as filled circles, while the squares represent the background distributionas described in the text. The curve represents thefunction used to perform the fit and used to evaluate the background and the raw signal. The significance in $\pm$3$\sigma$ around the peak is 3.5 and 3.0 for the invariant massdistribution of ($^{3}\rm{He}$,$\pi^-$) and ($^{3}\overline{\rm{He}}$,$\pi^+$), respectively. |  |
Figure 2
Left: Transverse momentum spectra multiplied by the B.R. of the $^{3}_{\Lambda}\rm{H} \rightarrow ^{3}\rm{He} + \pi^-$ decay for $^{3}_{\Lambda}\rm{H}$ (filled circles) and $^{3}_{\bar{\Lambda}}\overline{\rm{H}}$ (squares) for the most central (0-10%) Pb-Pb collisions at $\sqrt{s}$ = 2.76 TeV for $|y| < $ 0.5. Symbols are displaced for better visibility. The dashed lines are the Blast-Wave curves used to extract the particle yields integrated over the full $\pt$ range. In order to take into account the large binning used in the analysis and the limited number of bins, the center of each bin was evaluated weighting the actual bin center with the Blast-Wave function Right: $^{3}_{\bar{\Lambda}}\overline{\rm{H}}$ to $^{3}_{\Lambda}\rm{H}$ ratio as a function of $\pt$. In both panels statistical uncertainties are represented by bars and systematic uncertainties are represented by open boxes. |  |
Figure 4
$^{3}_{\Lambda}\rm{H}$ lifetime ($\tau$) measured by in this analysis (red diamond) compared with published results. The band represents the world average of $^{3}_{\Lambda}\rm{H}$ lifetime measurements $\left(\tau = 215^{+18}_{-16}\right)$ ps, while the dashed line represent the lifetime of $\Lambda$ as reported by the Particle Data Group . |  |
Figure 5
$\pt$-integrated $^{3}_{\Lambda}\rm{H}$ yield times branching ratio as a function of branchingratio (d$N/$d$y \times$ B.R. vs B.R.) The horizontal line is the measured value and the band represents statistical and systematic uncertainties added in quadrature. Lines are different theoretical expectations as explained in the text. |  |
Figure 6
The ratios $^{3}_{\Lambda}\rm{H}$/$^{3}\rm{He}$ and $^{3}_{\bar{\Lambda}}\overline{\rm{H}}$/$^{3}\overline{\rm{He}}$ determined by the present analysis (filled circles) for matter and anti-matter compared with STAR results(squares) and theoretical predictions (lines) as described in the legend. |  |
Figure 7
Left: $B_2$ as a function of $\pt$ /A for d (filled circles) ,$^3$He (empty circles) , and $^{3}_{\Lambda}\rm{H}$ (filled squares). The $B_2^{(\mathrm{d},^{3}_{\Lambda}\mathrm{H})}$ and $B_2^{(\mathrm{d}, ^{3}\mathrm{He})}$ were evaluated as explained in the text. k$_1 = \frac{m_\mathrm{d}^2}{m_{^{3}\mathrm{He}}m_{\mathrm{p}}}$,and k$_2 = \frac{m_\mathrm{d}^2 m_{\Lambda}}{m_{\mathrm{p}}^2 m_{^{3}_{\Lambda}\mathrm H}}$ Right: $S_{3}$ ratio measured in this analysis compared with previous experimental results (E864 and STAR (triangle and star, respectively)) and different theoretical models as indicated in the legend. |  |
