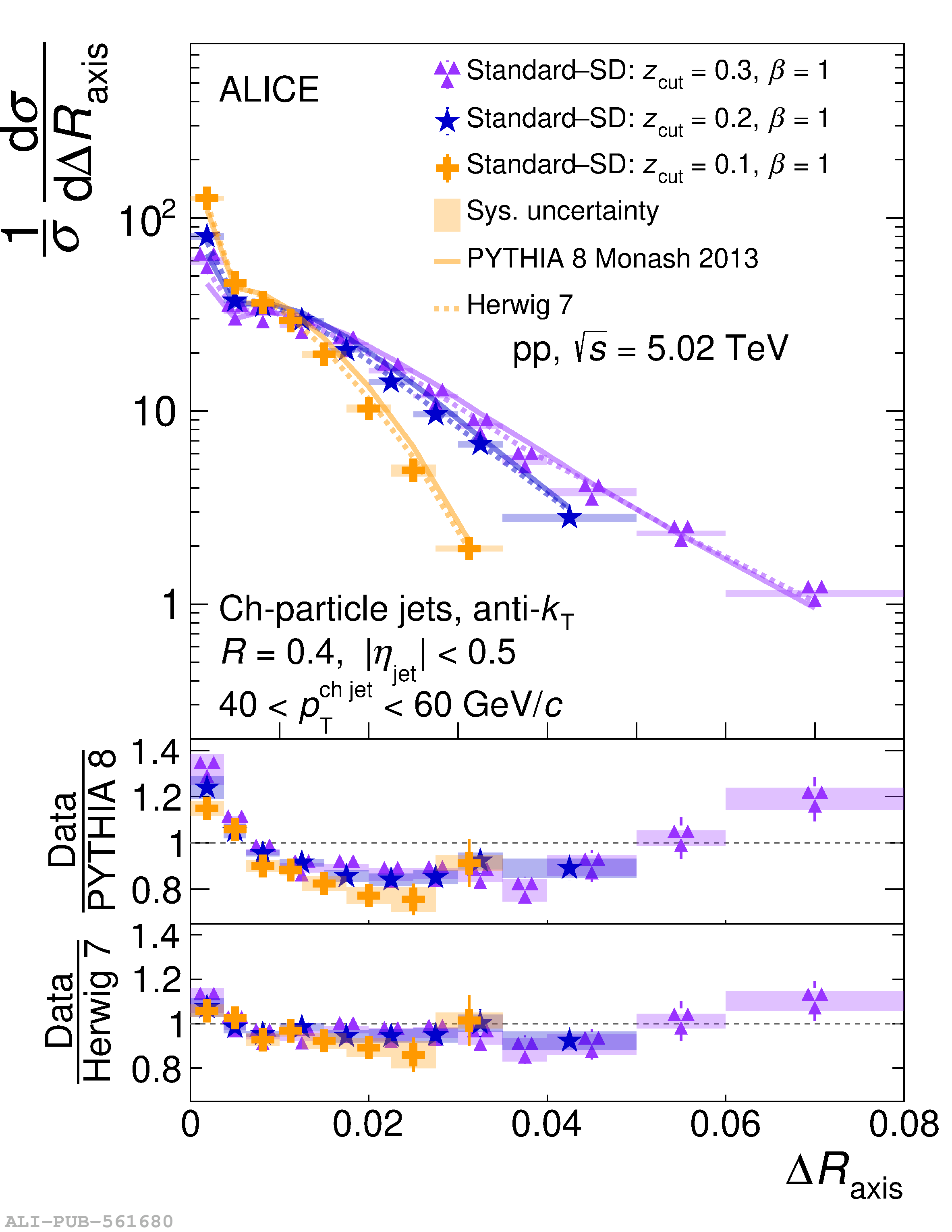
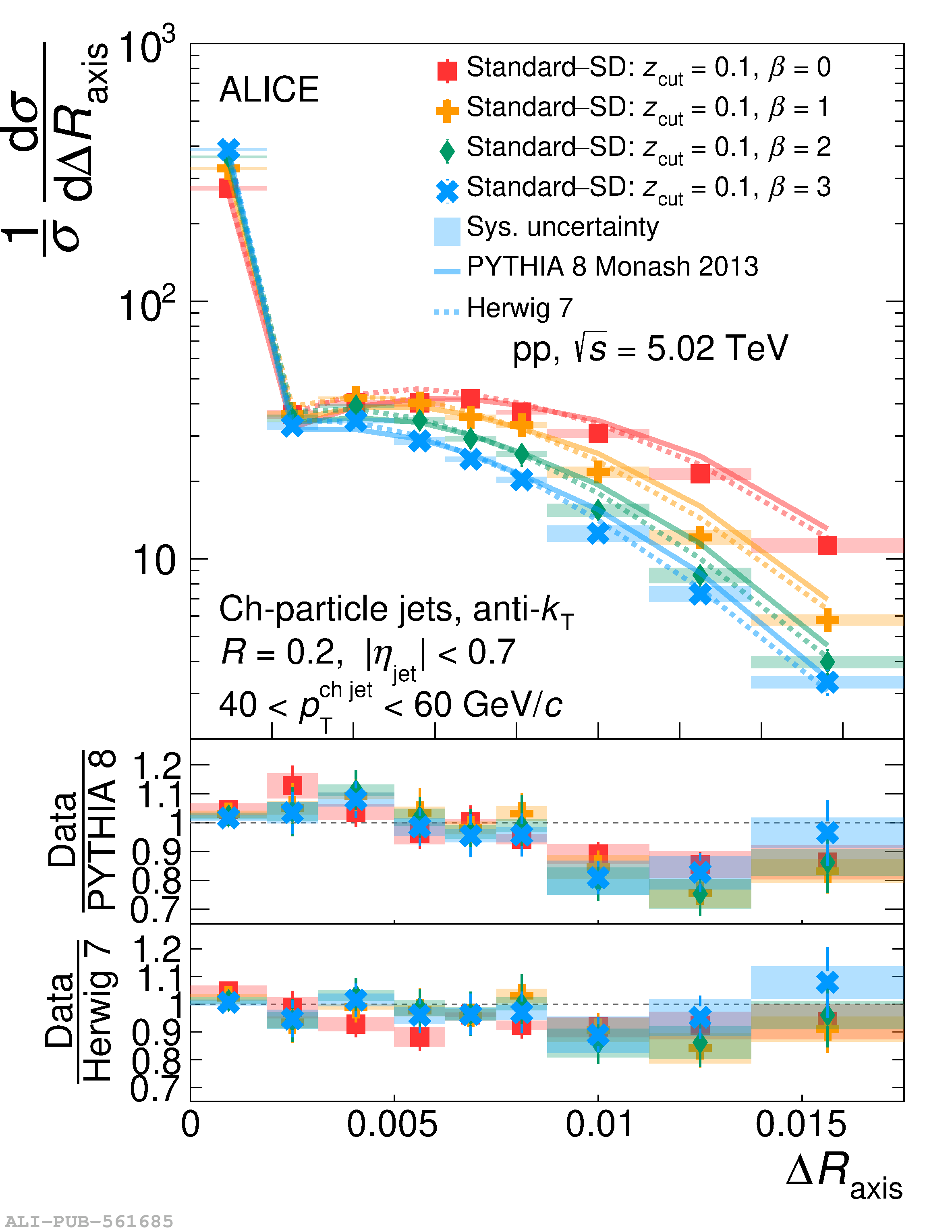
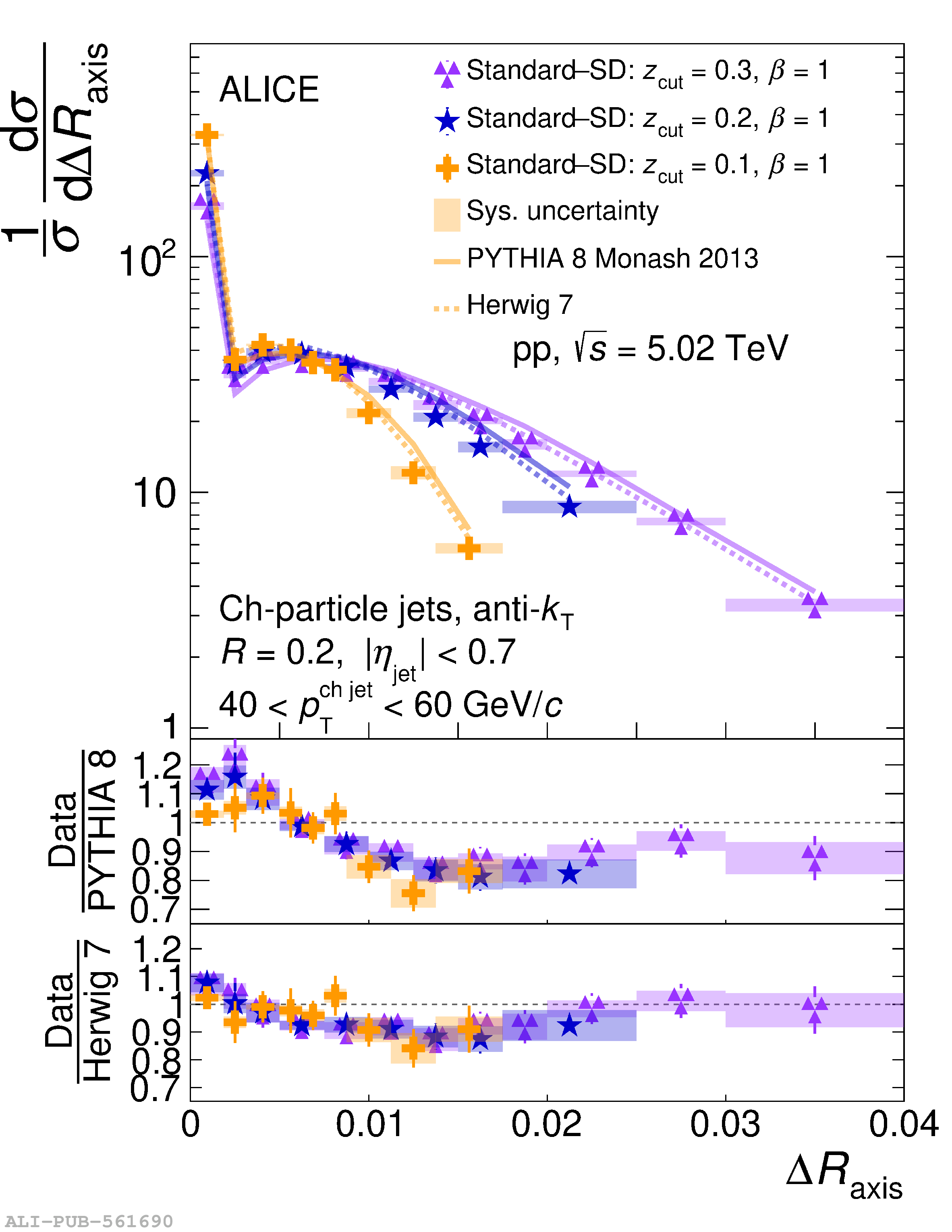
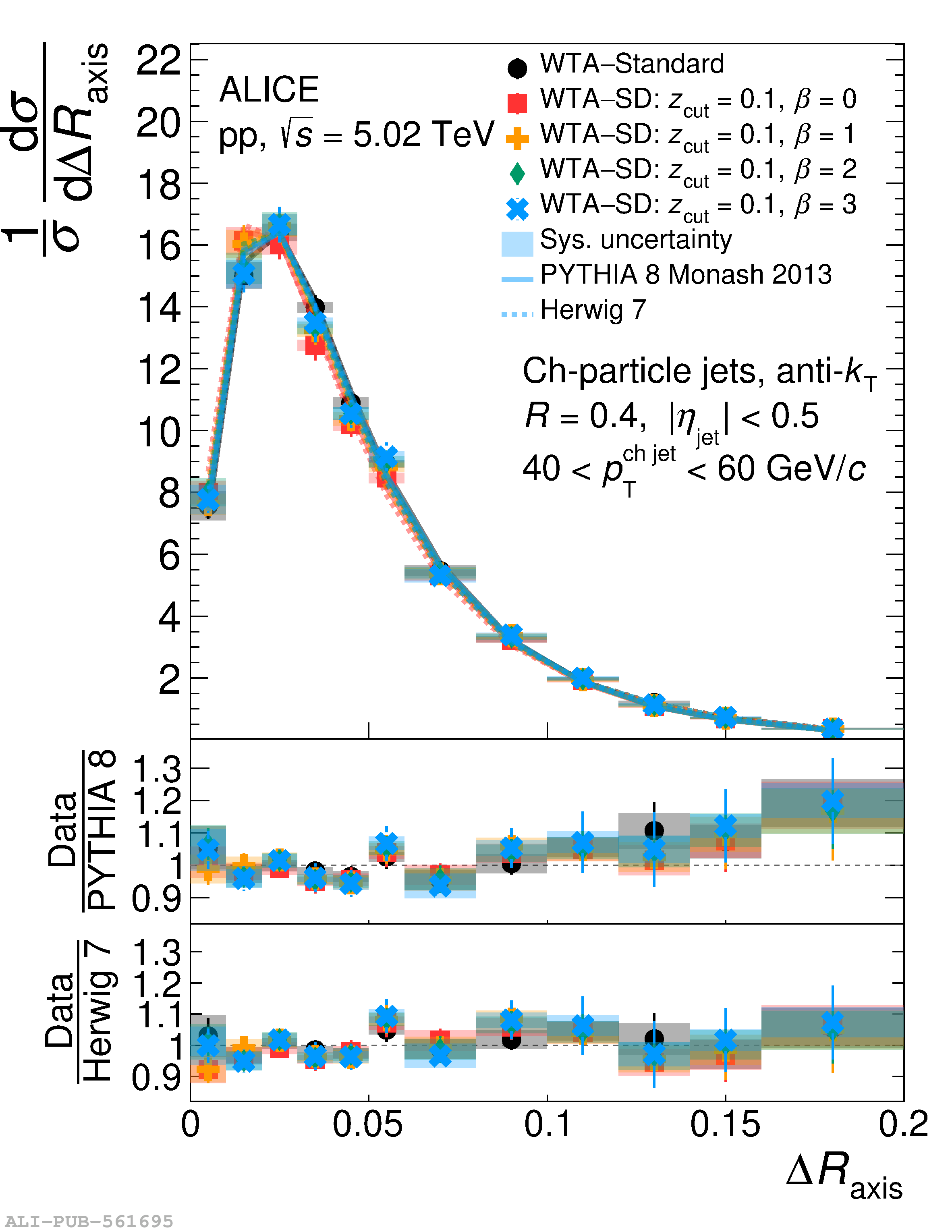
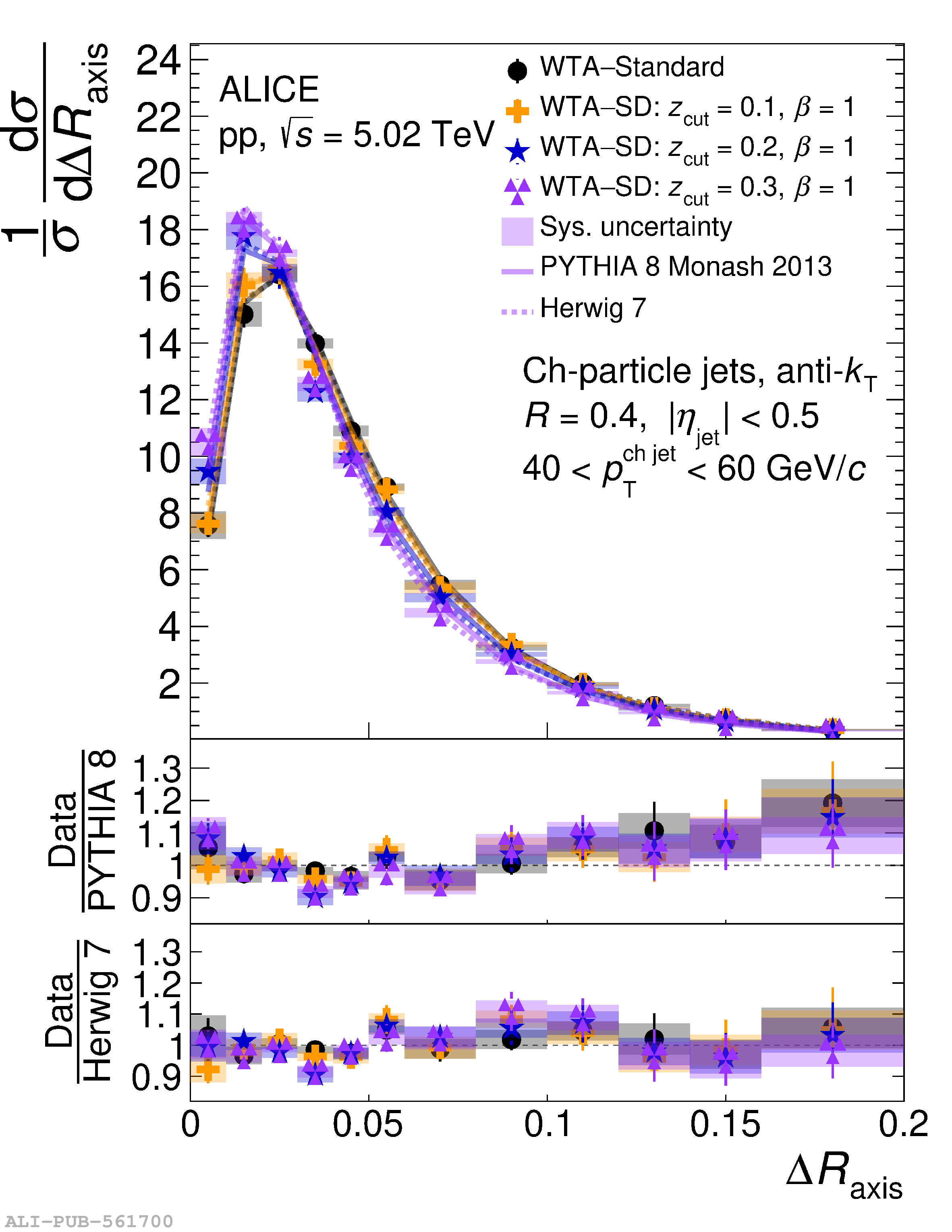
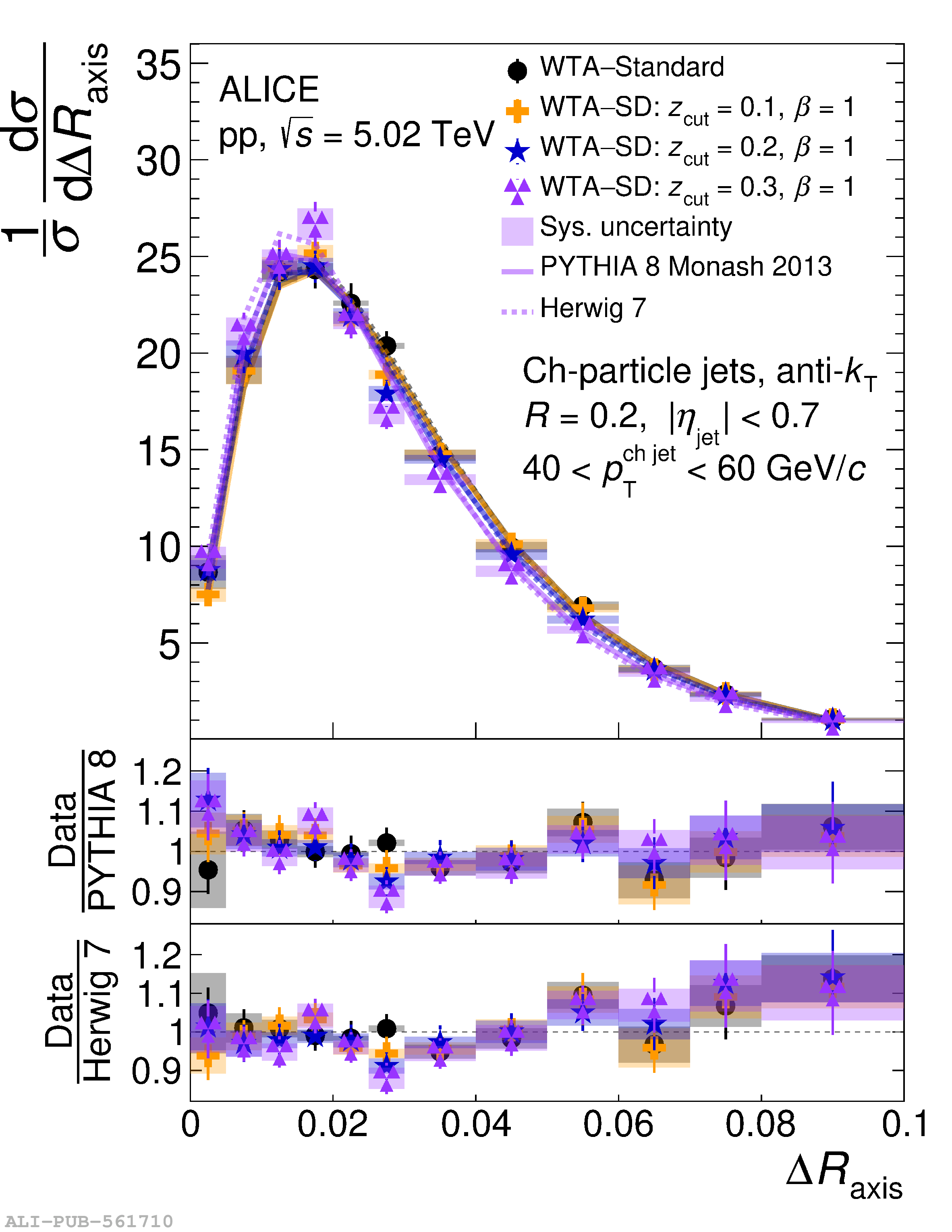
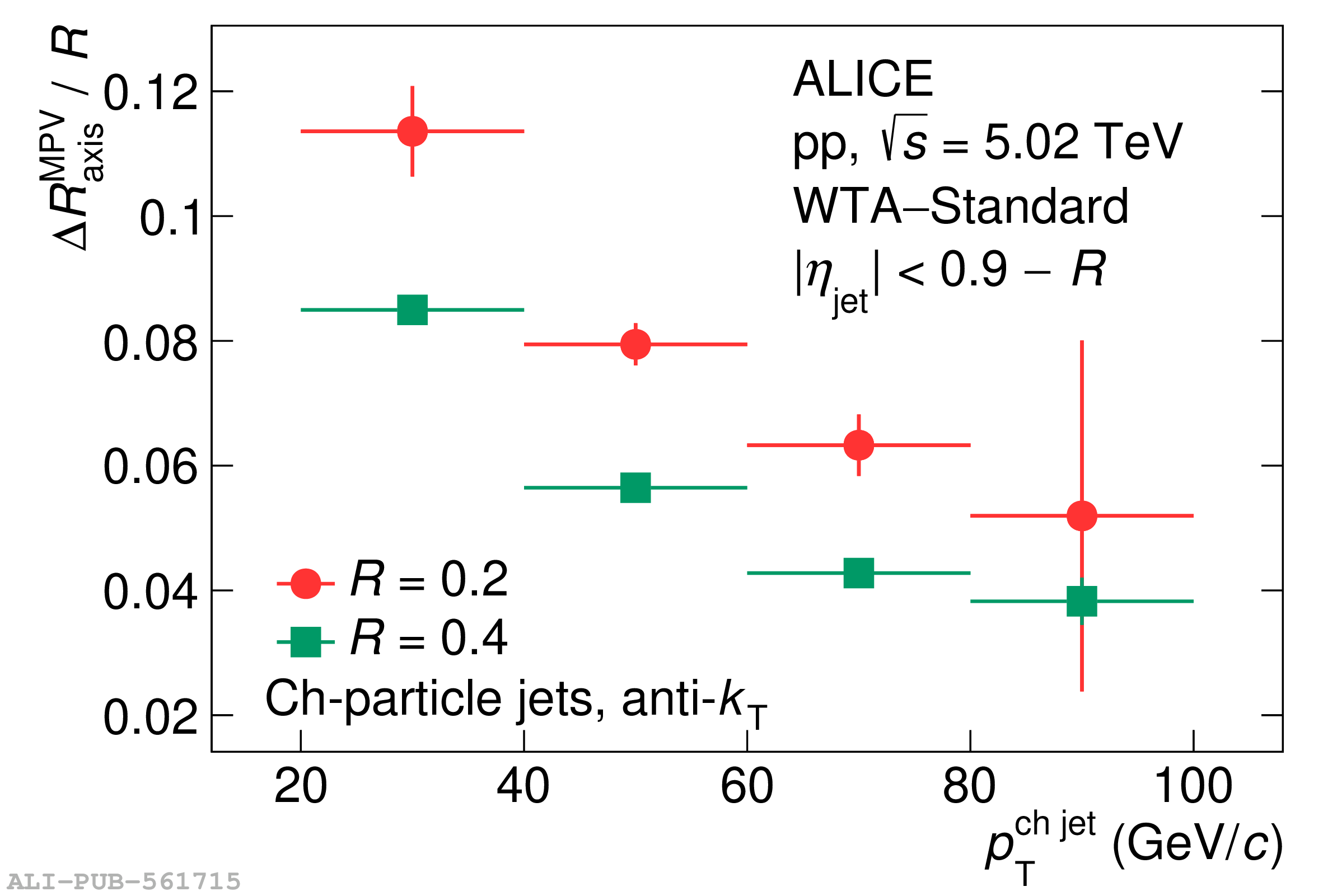
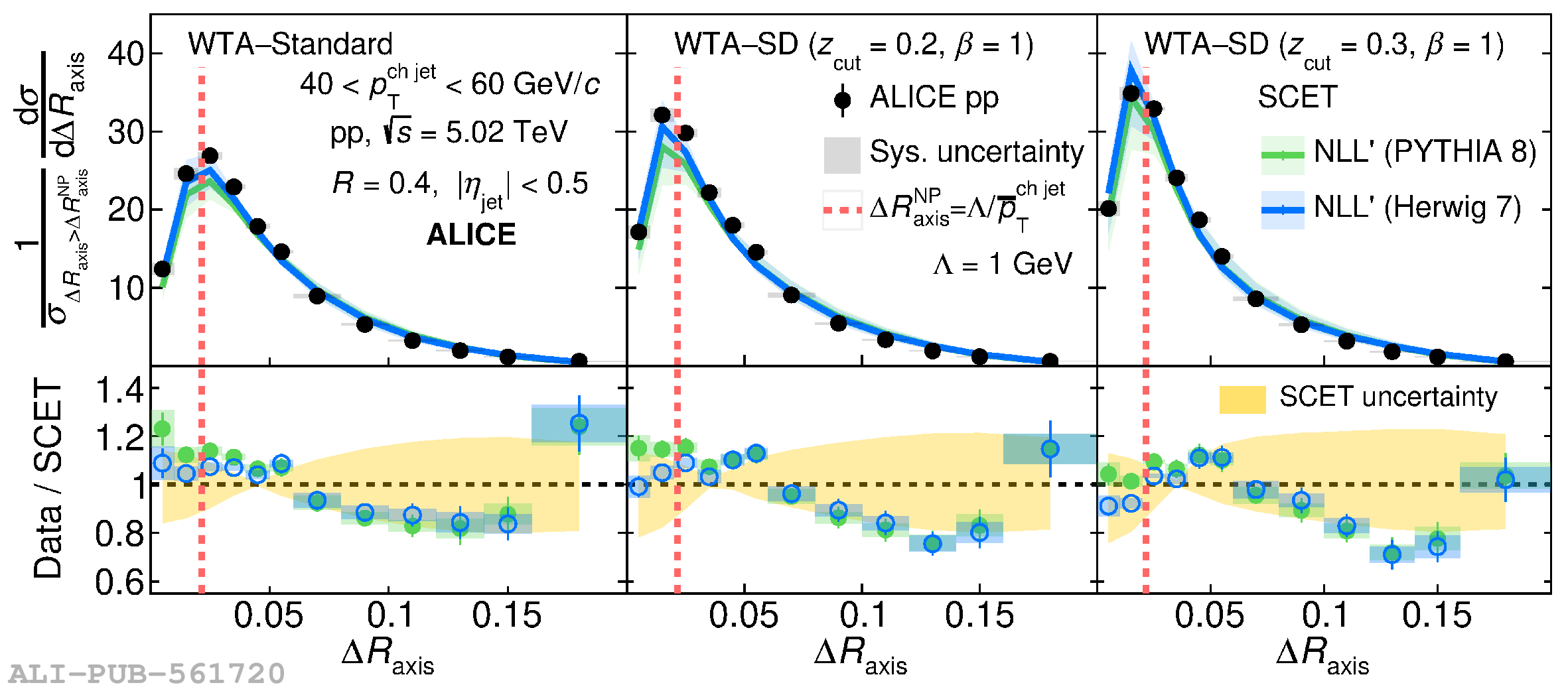
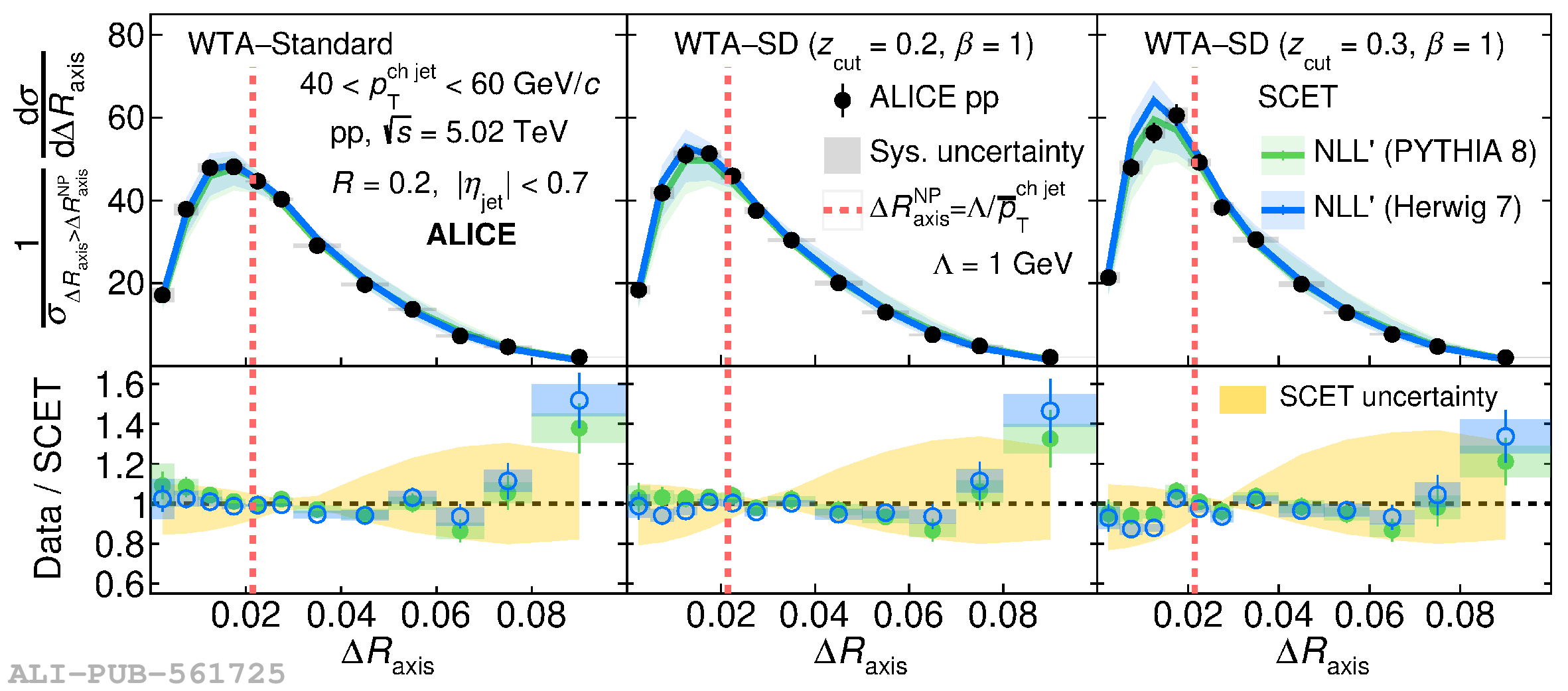
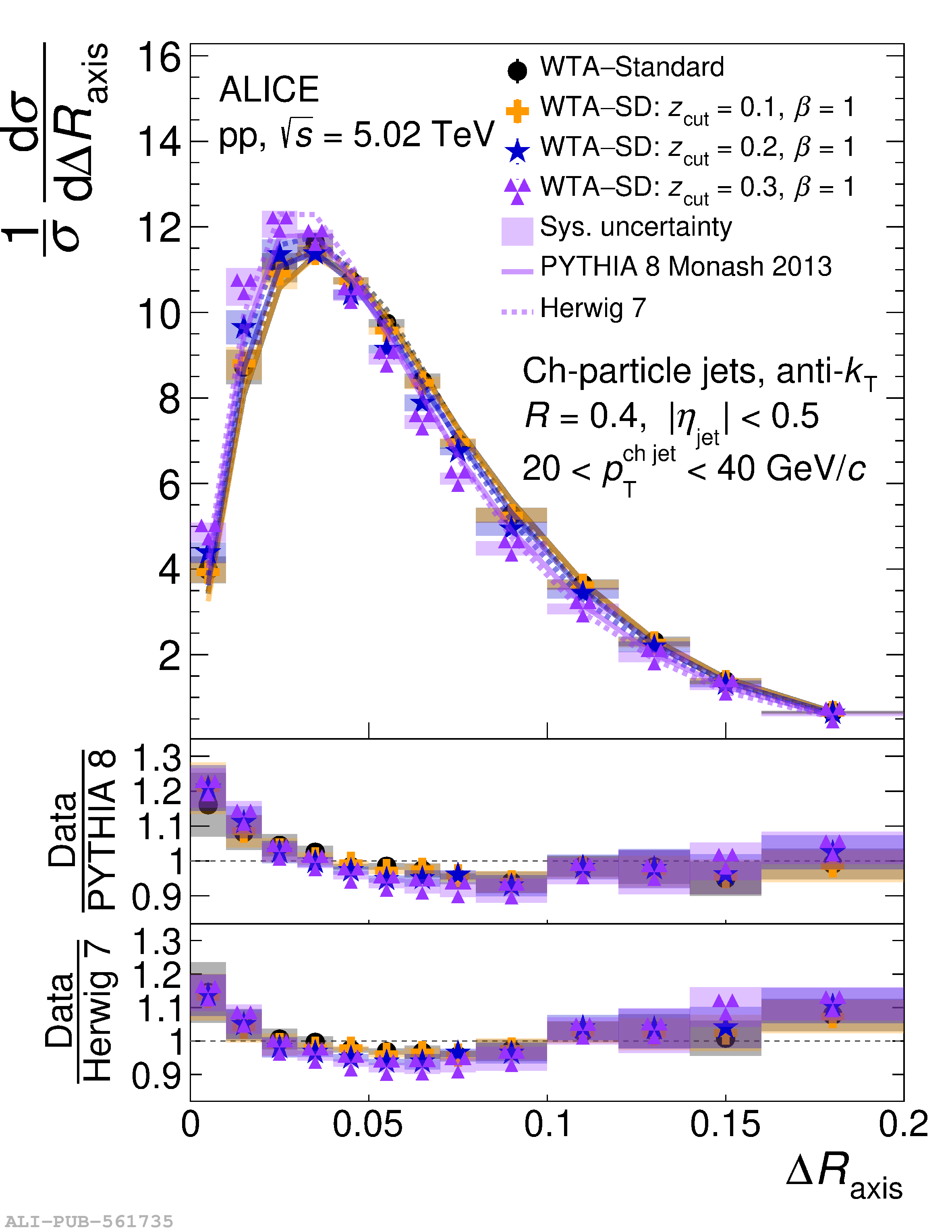
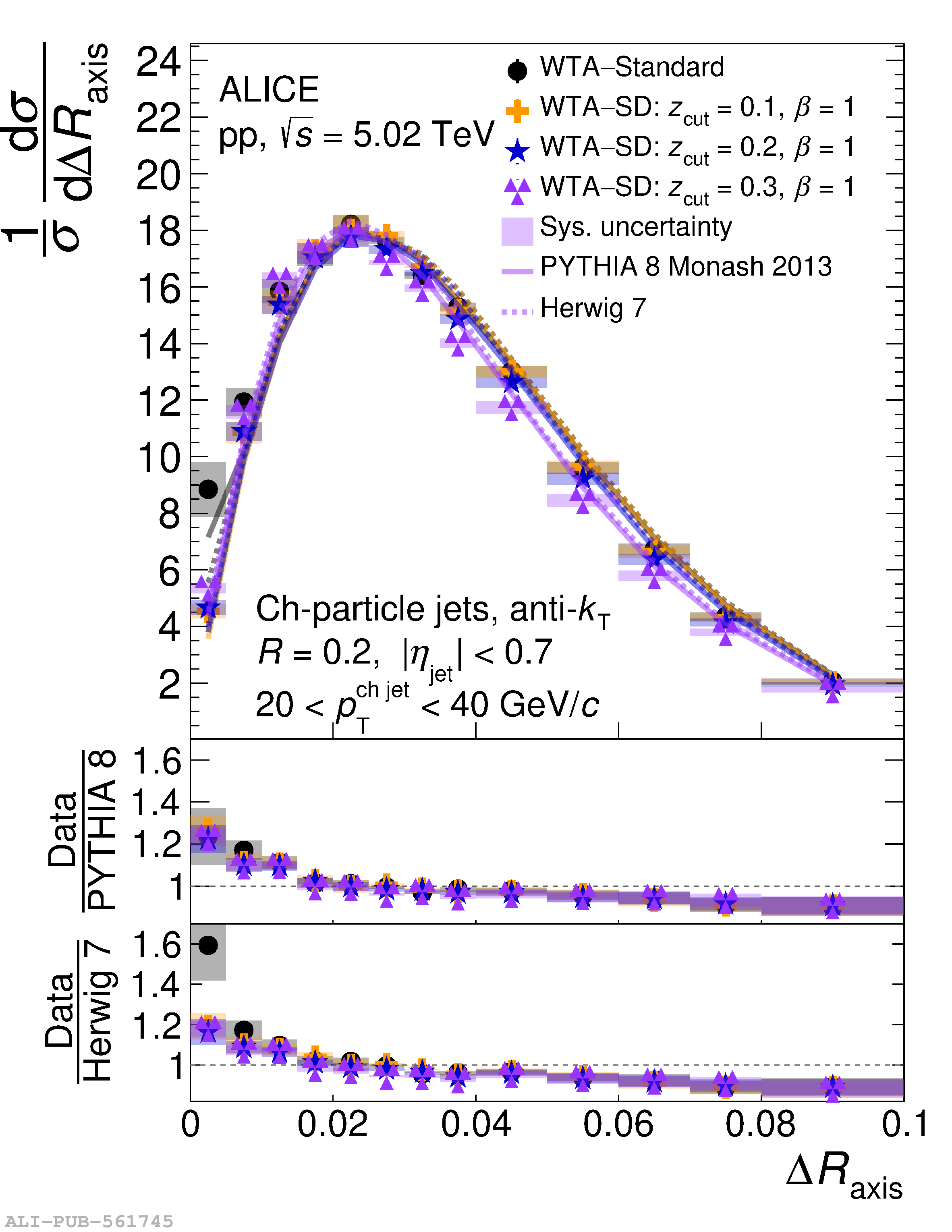
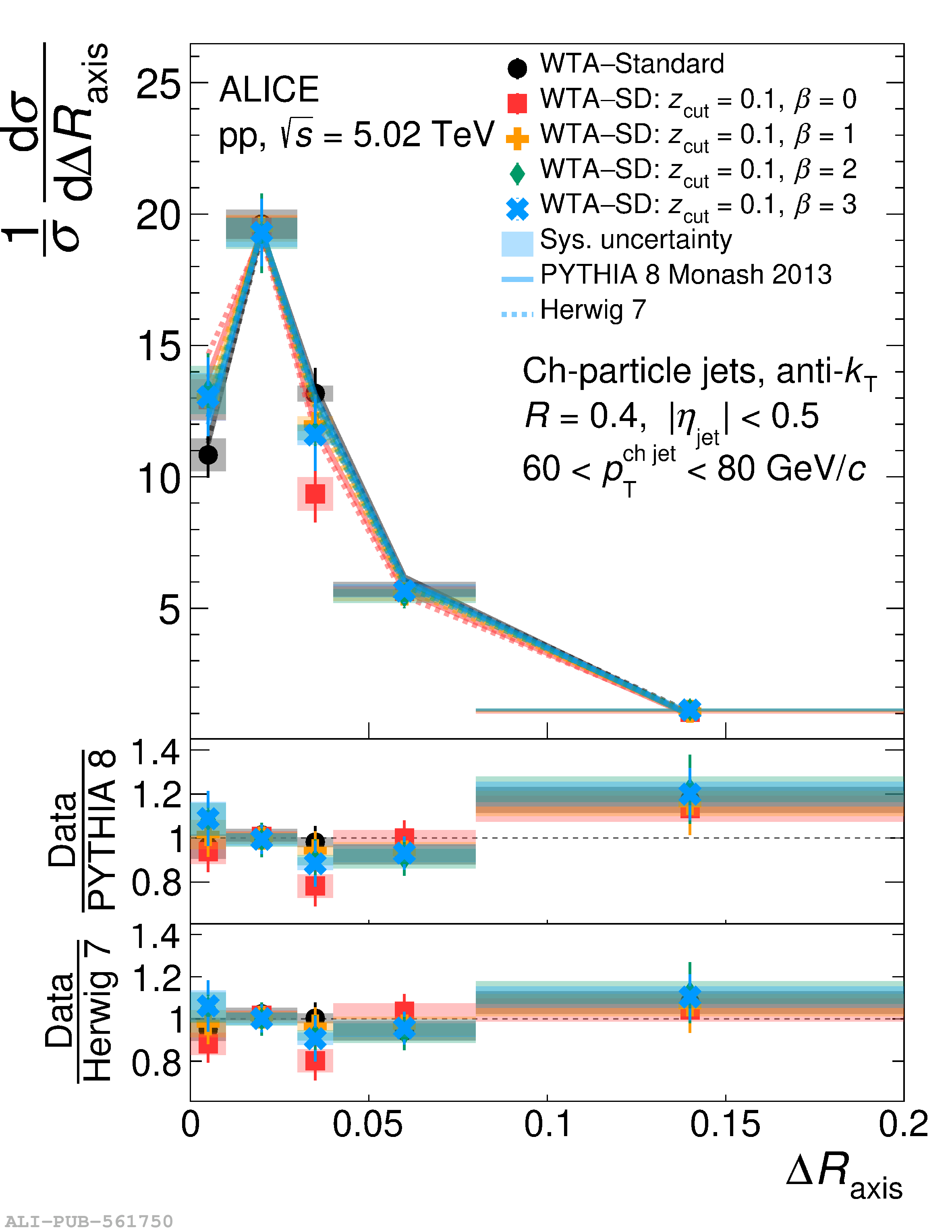
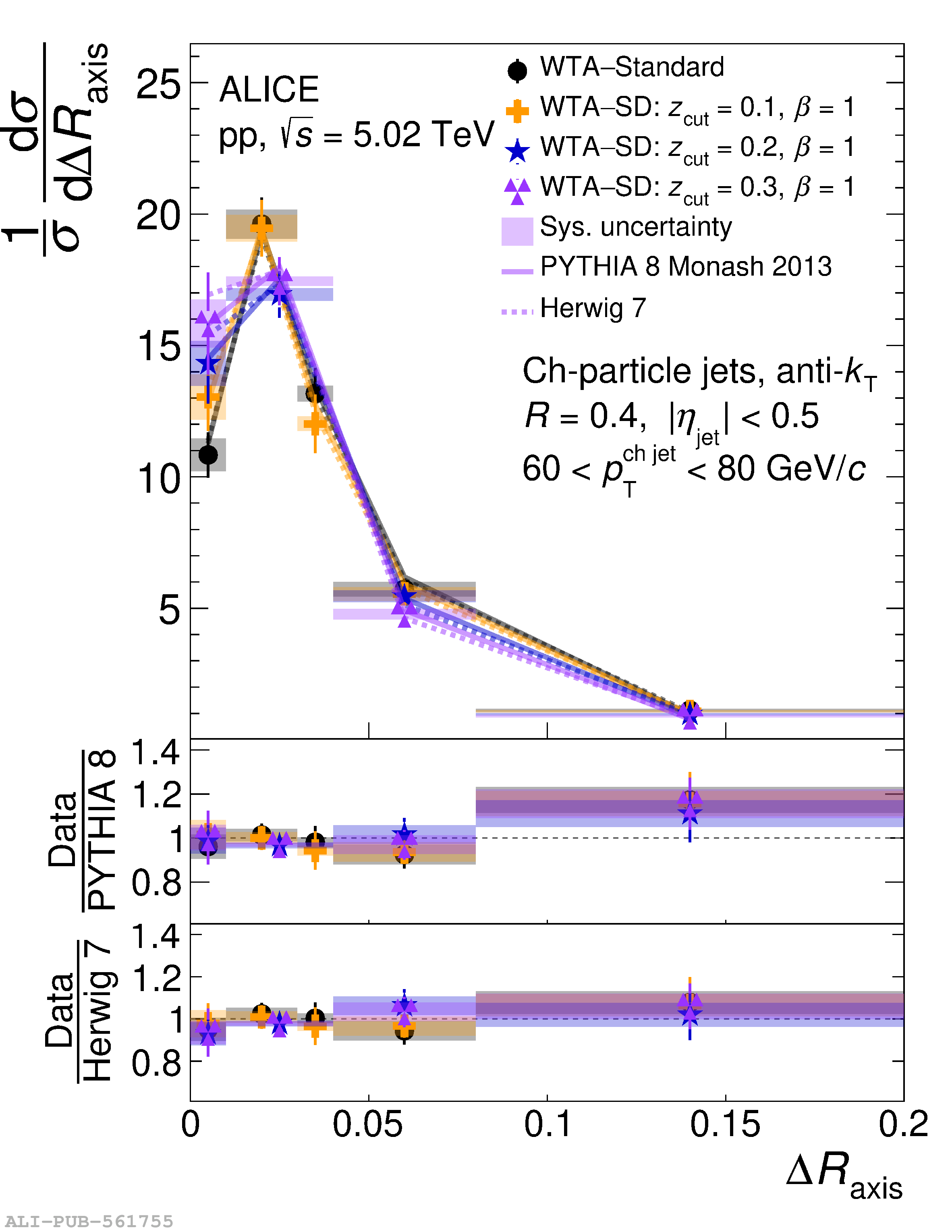
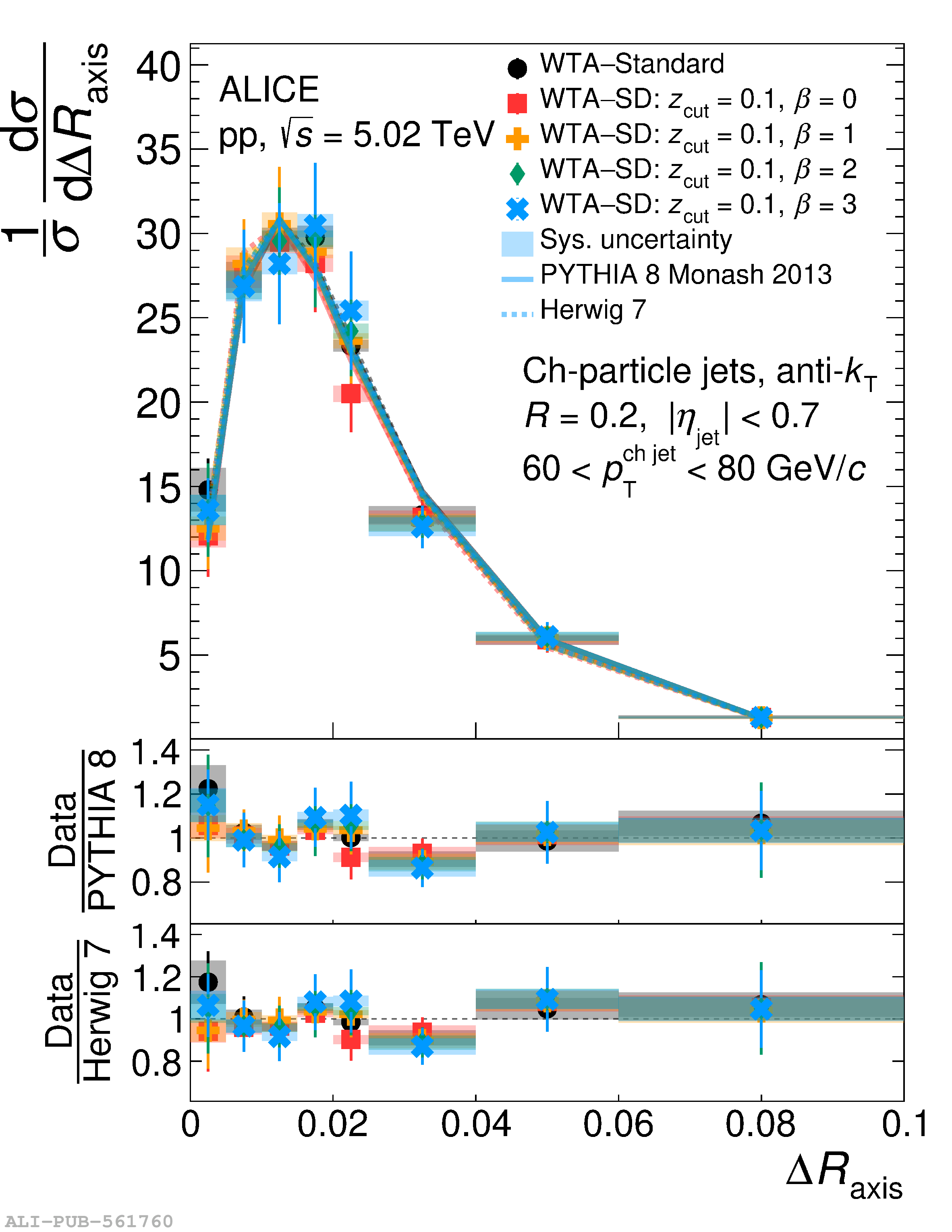
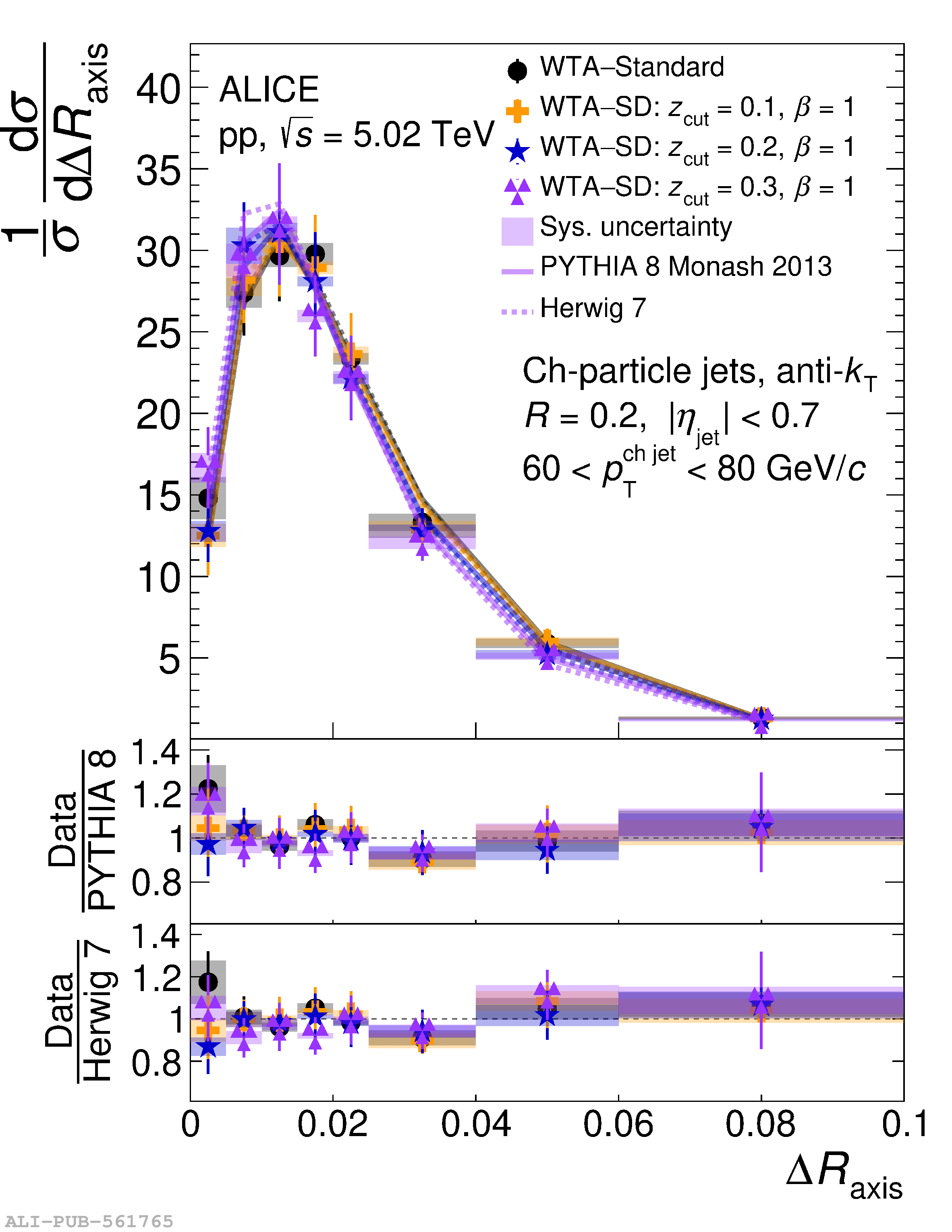
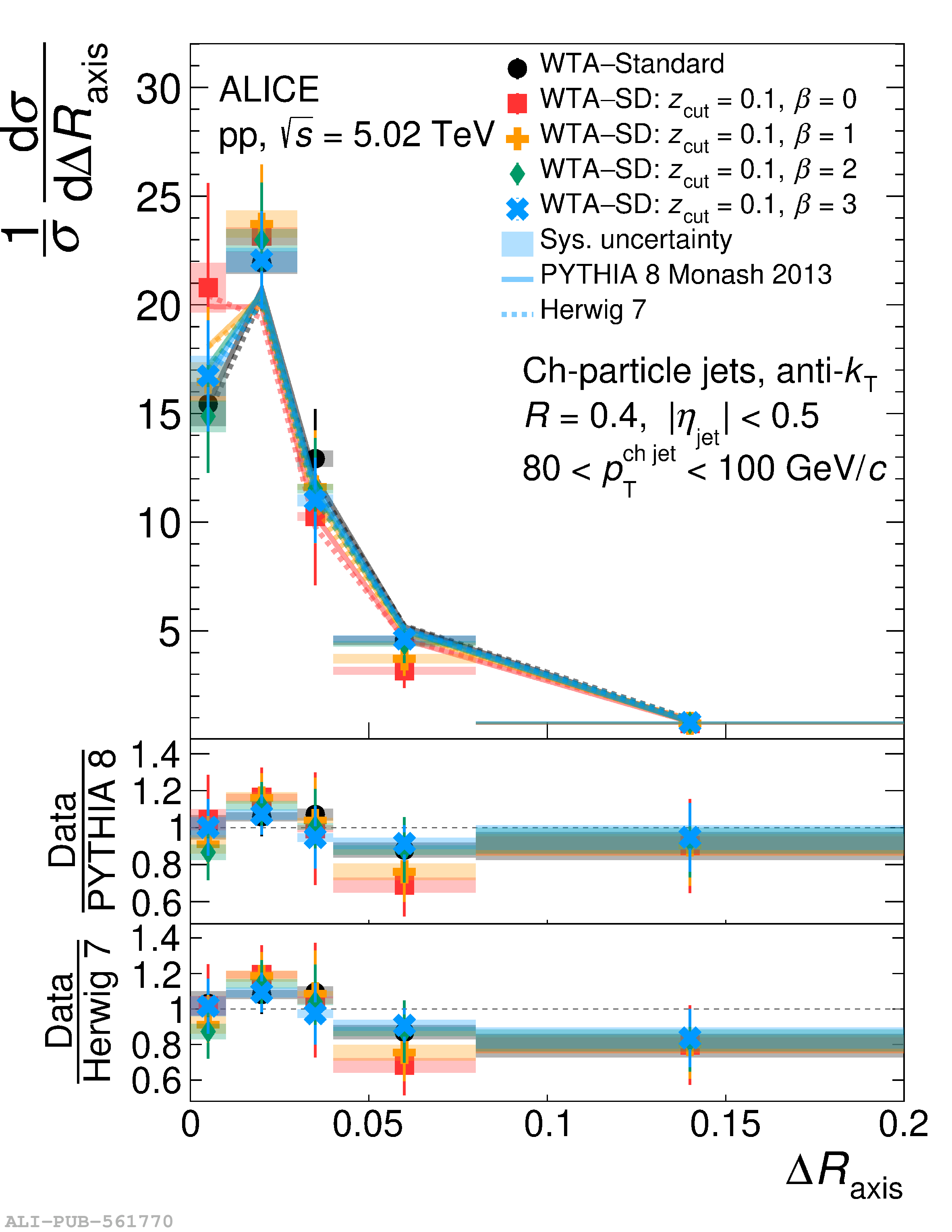
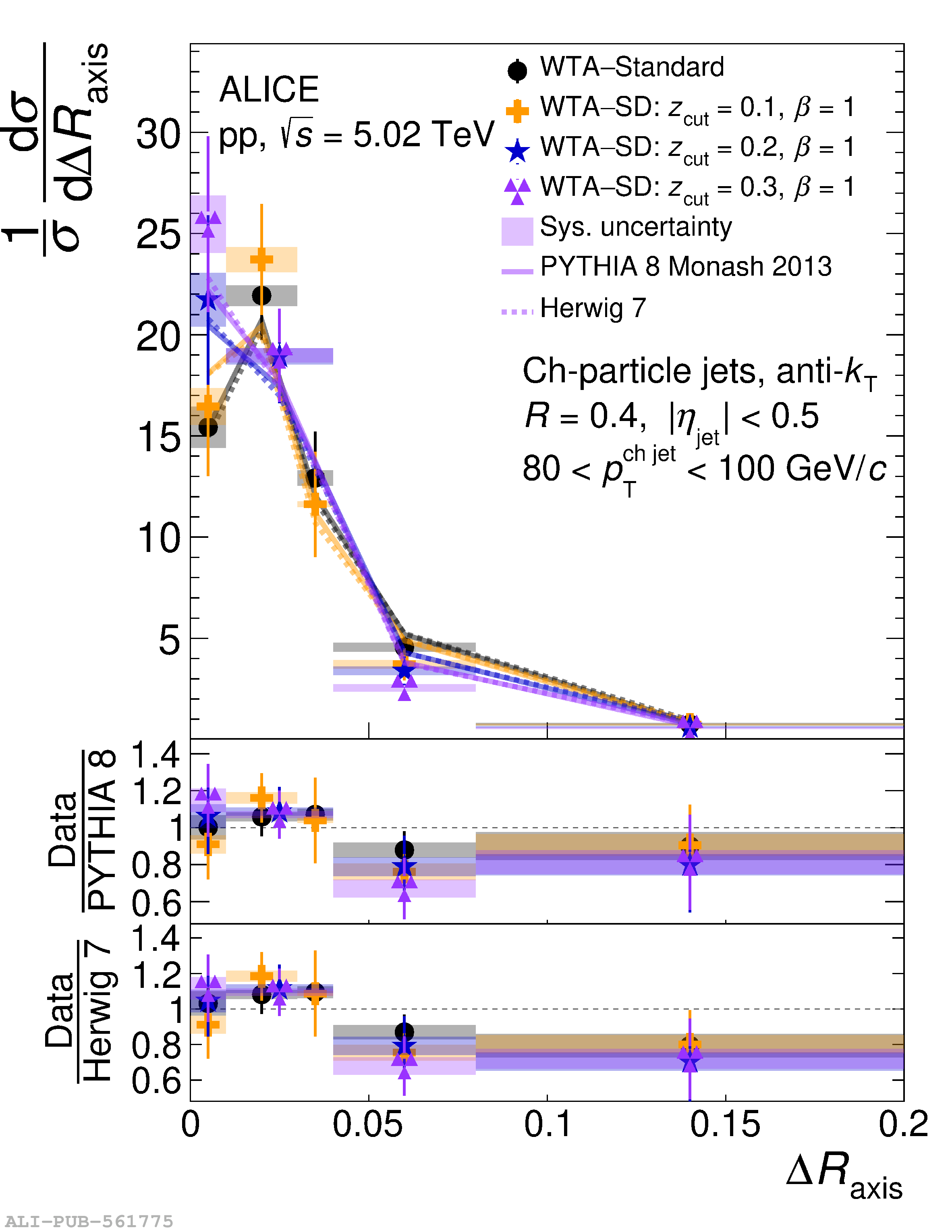
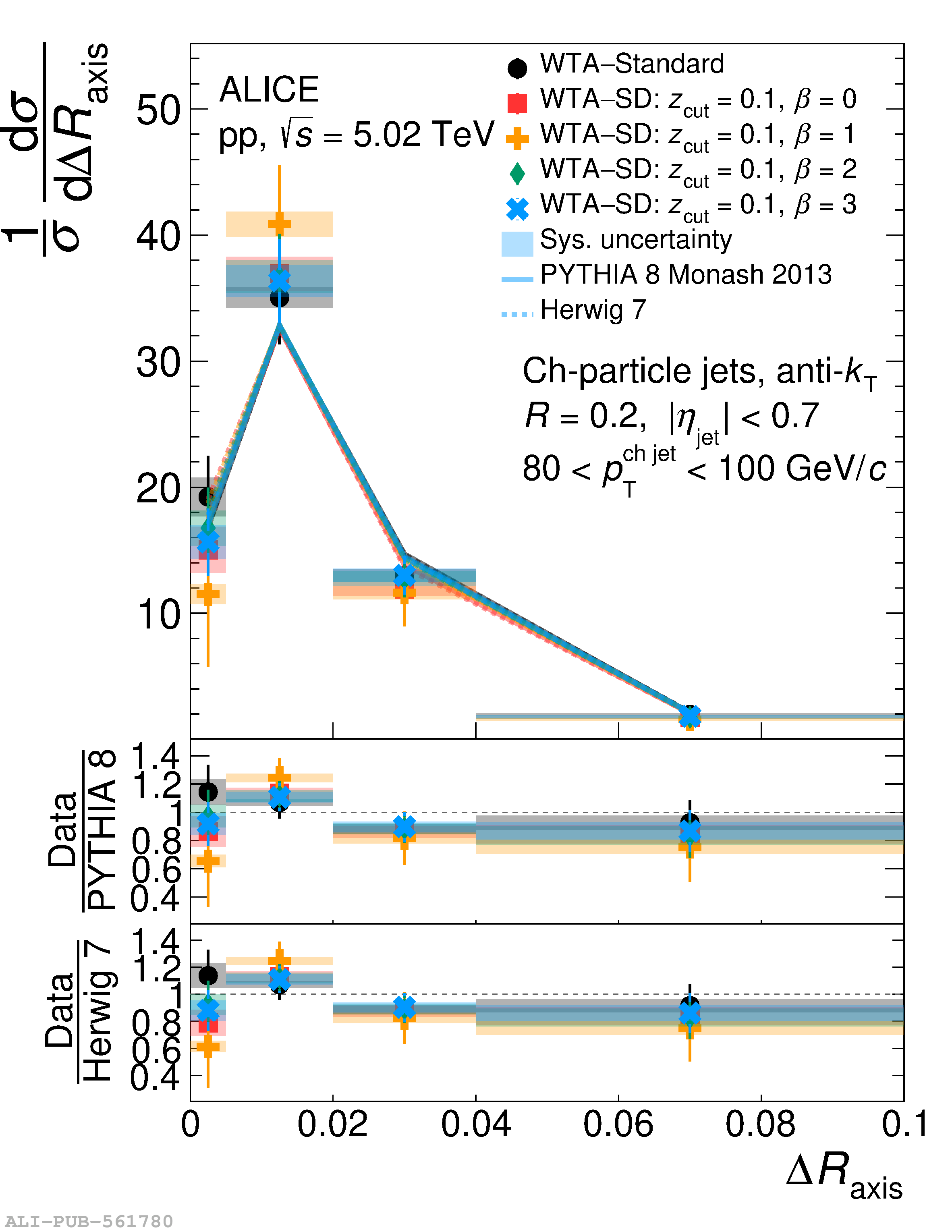
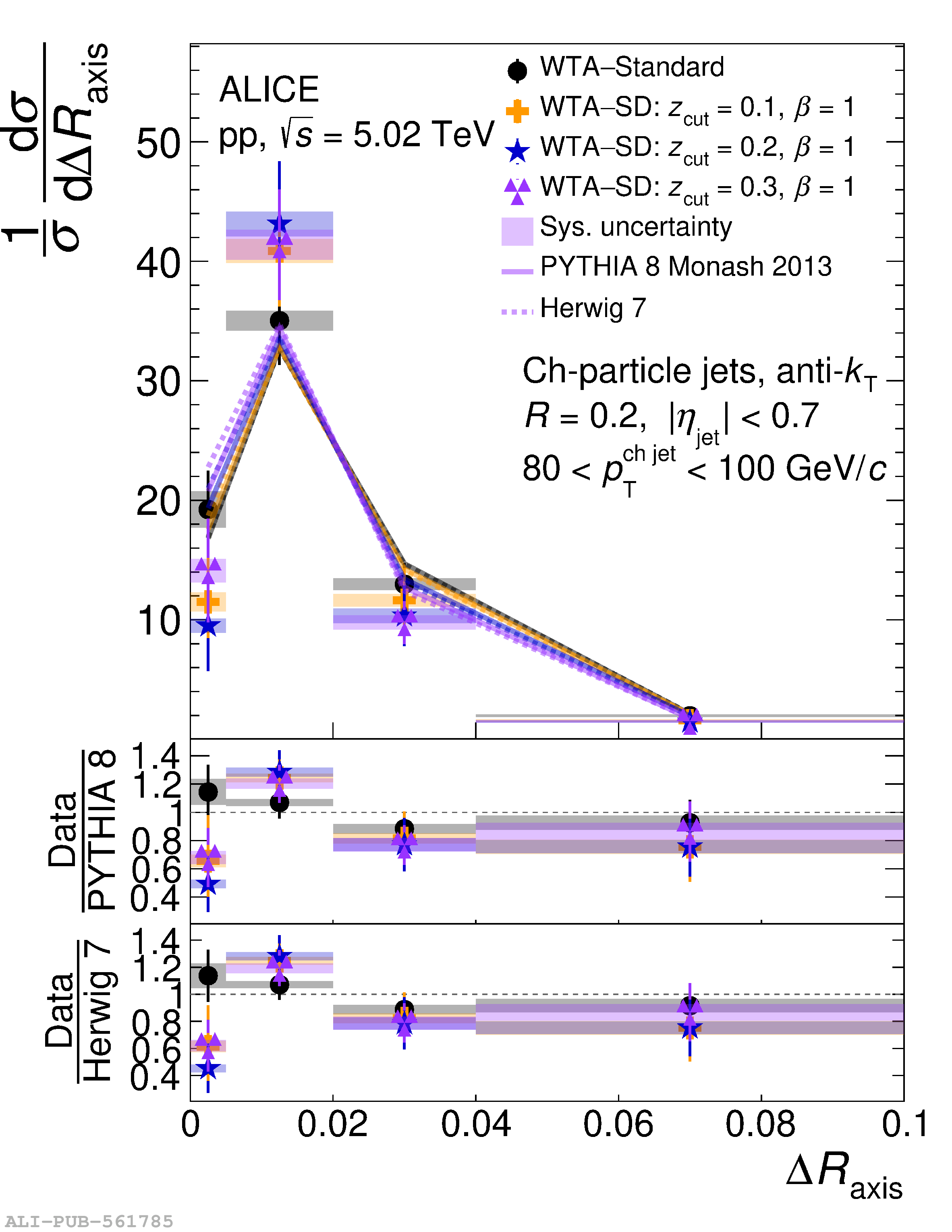
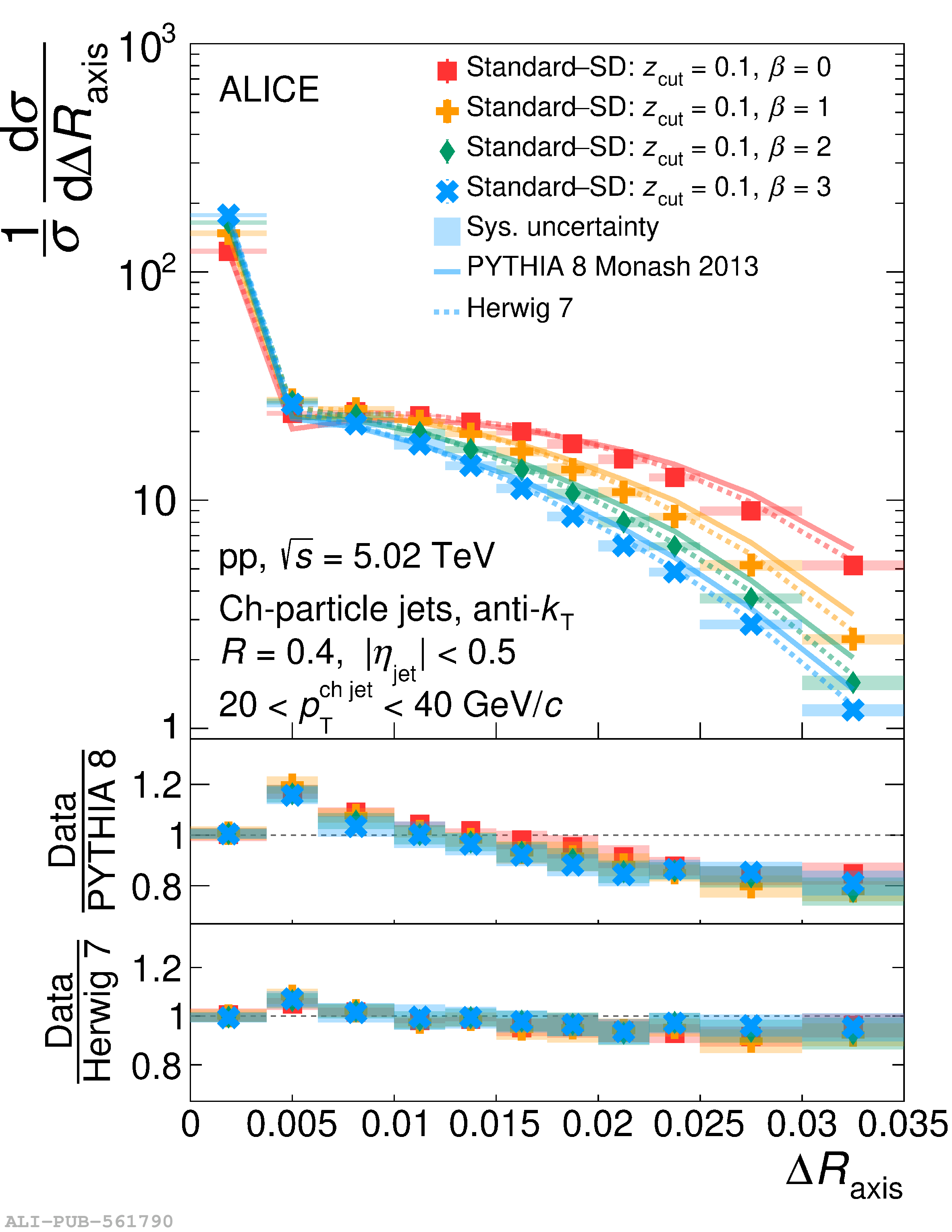
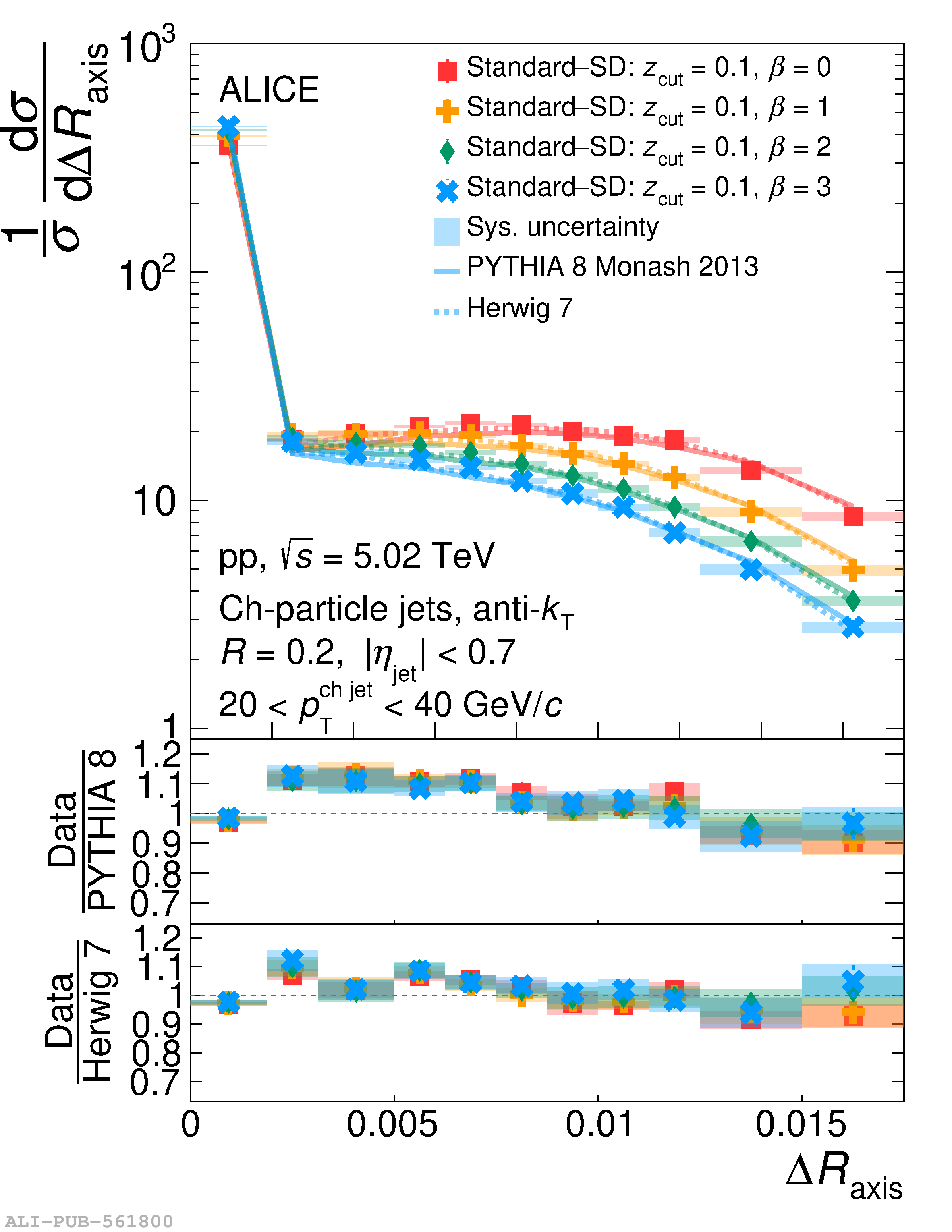
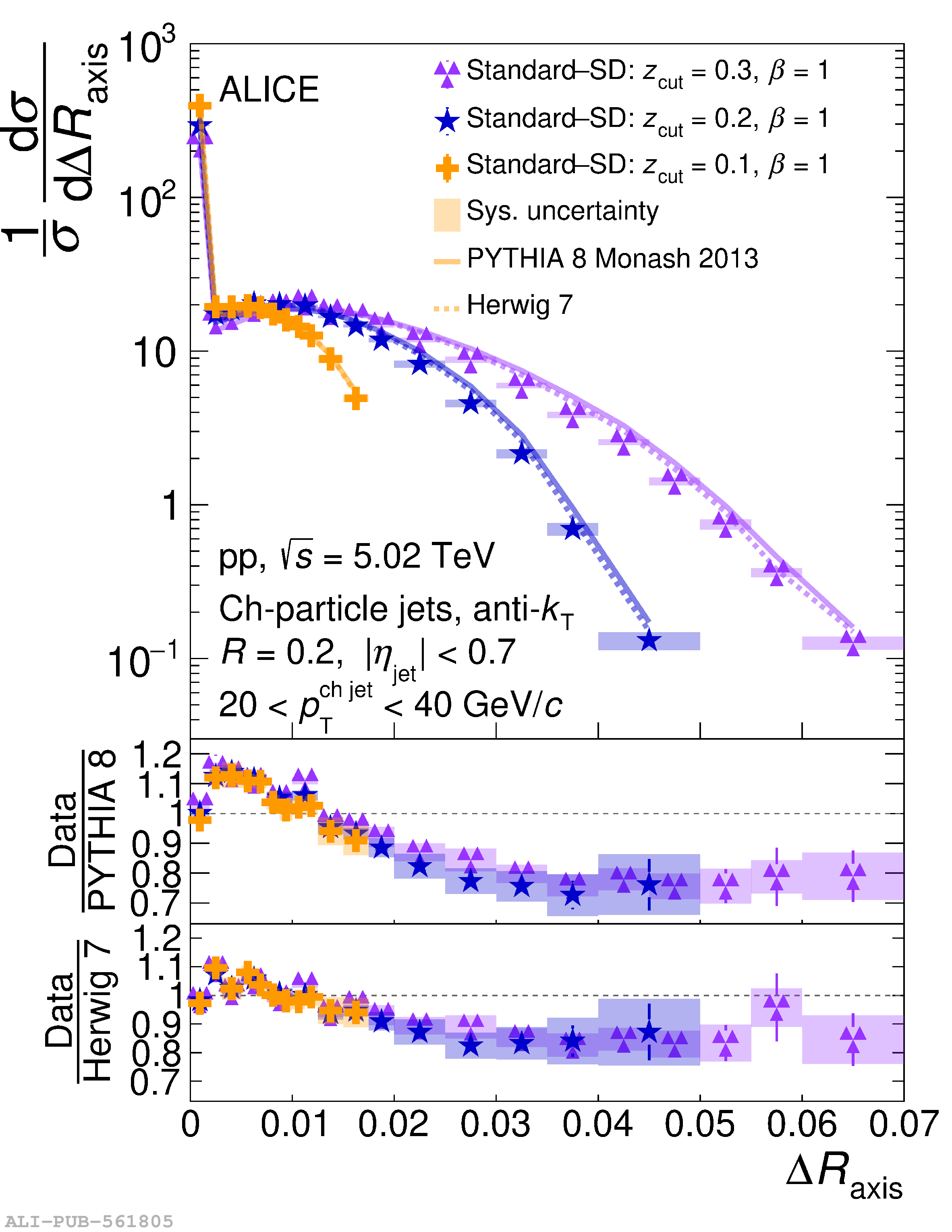
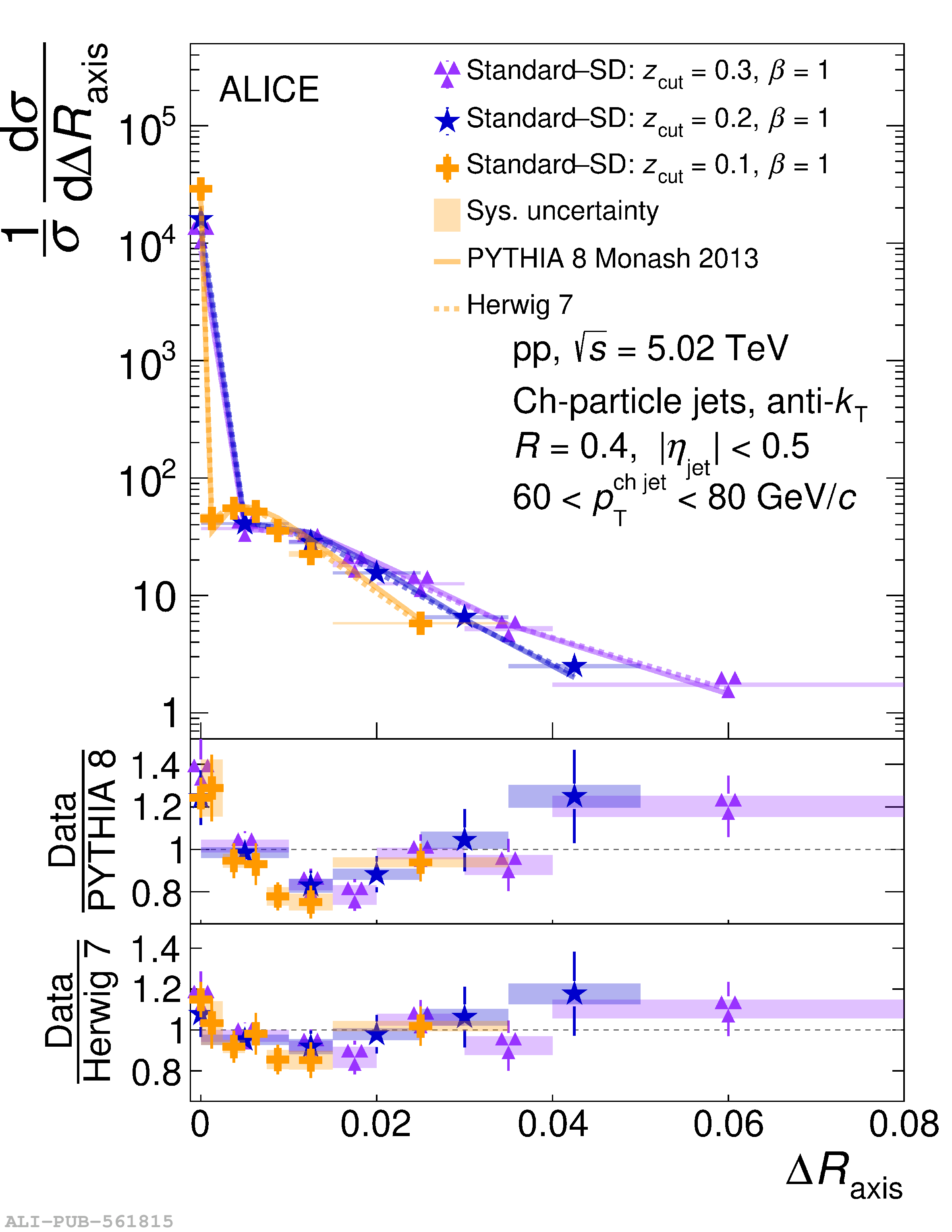
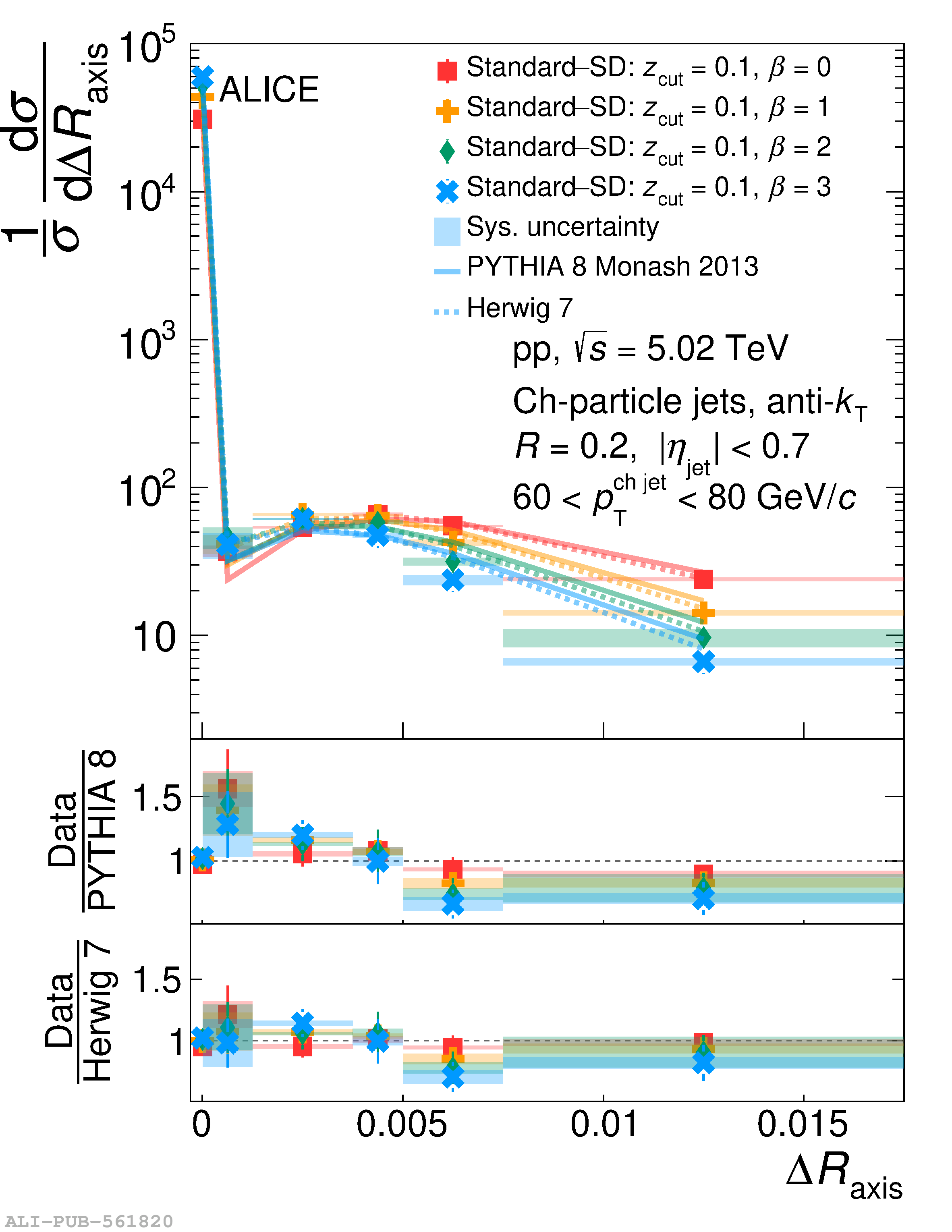
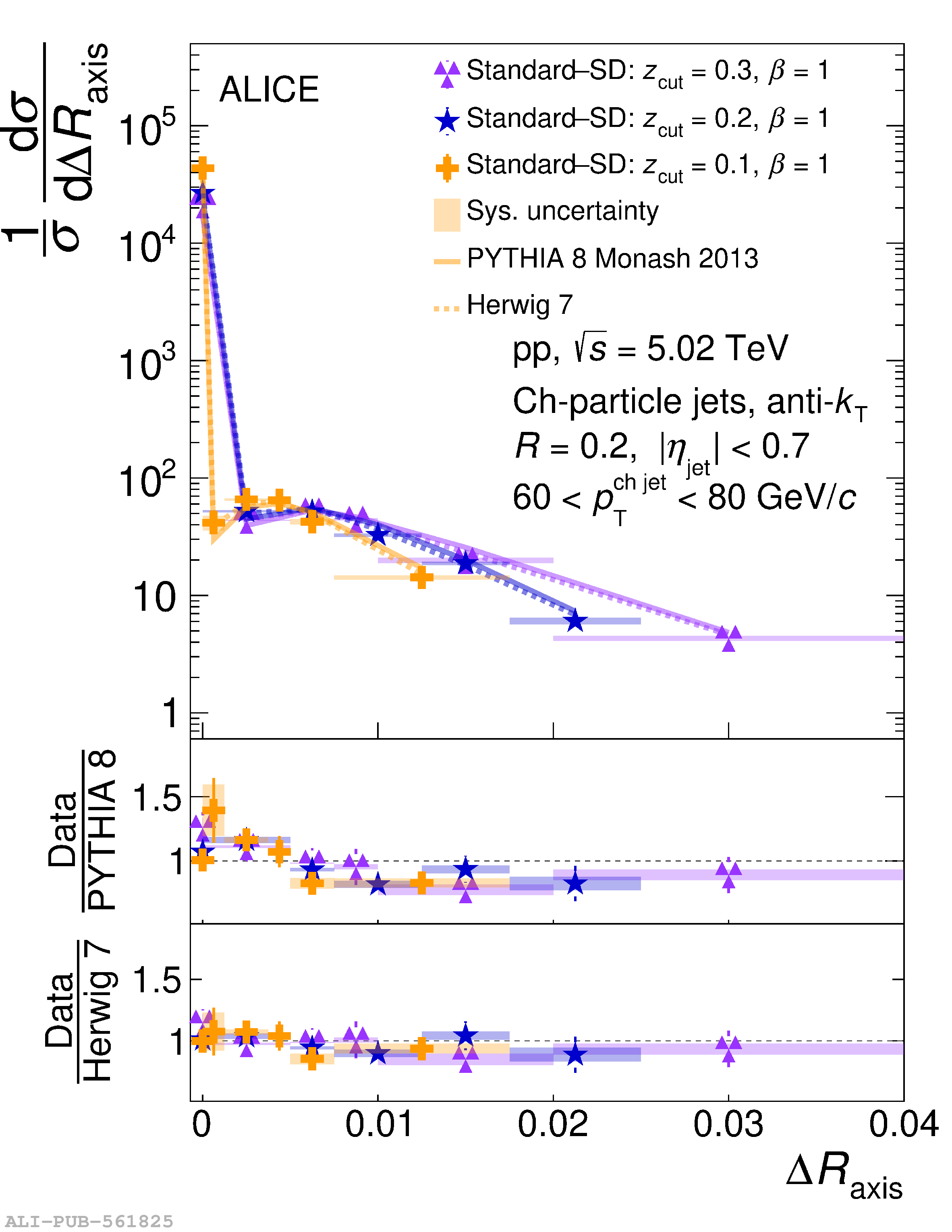
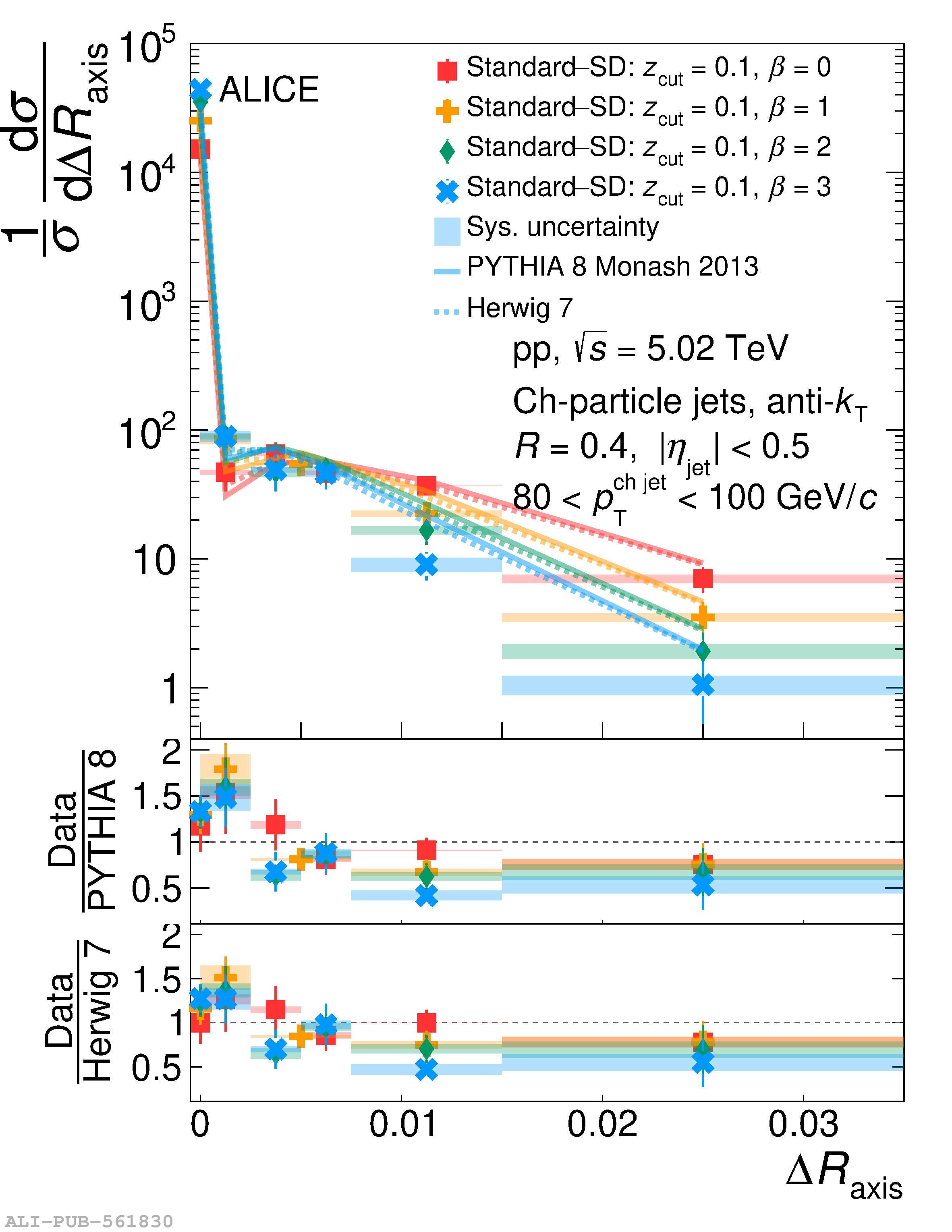
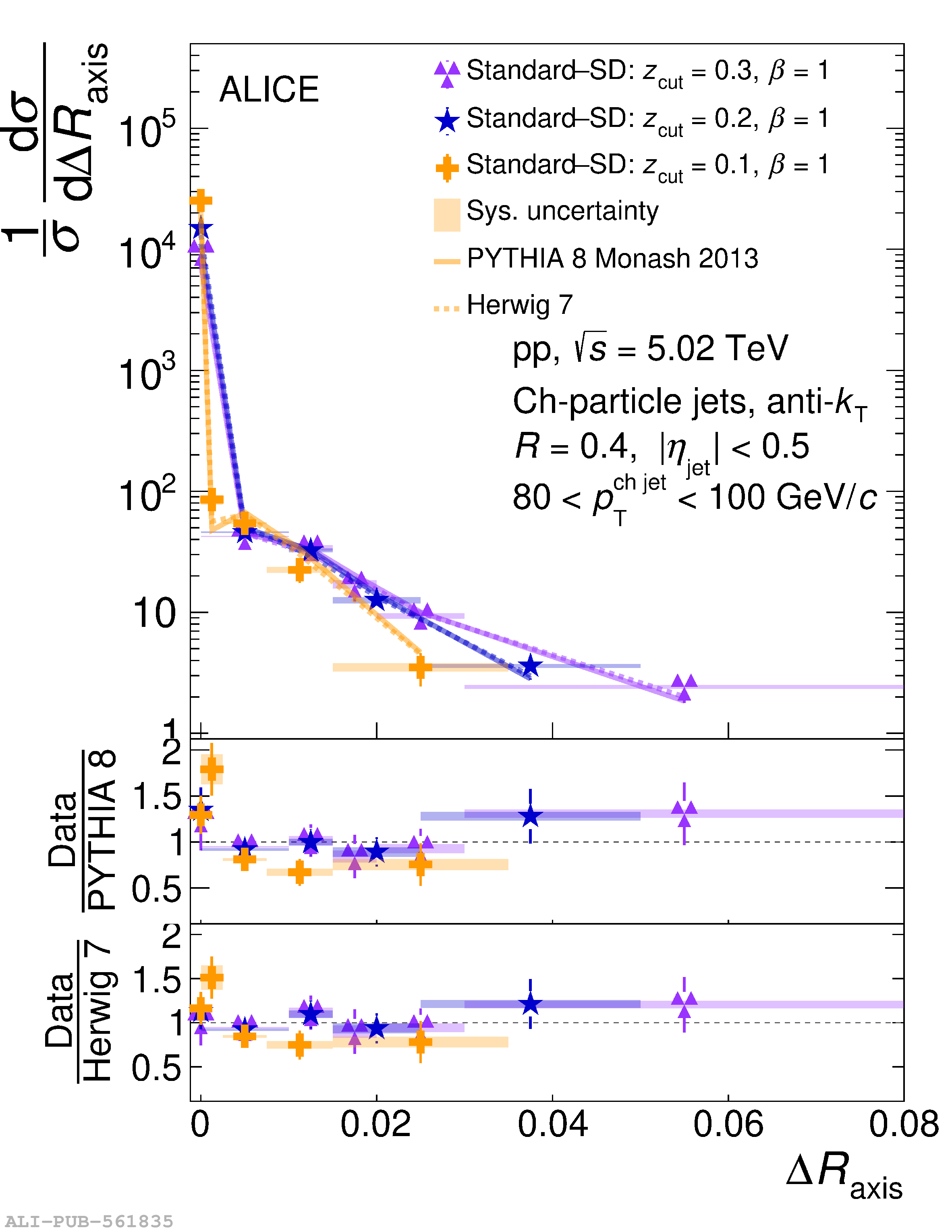
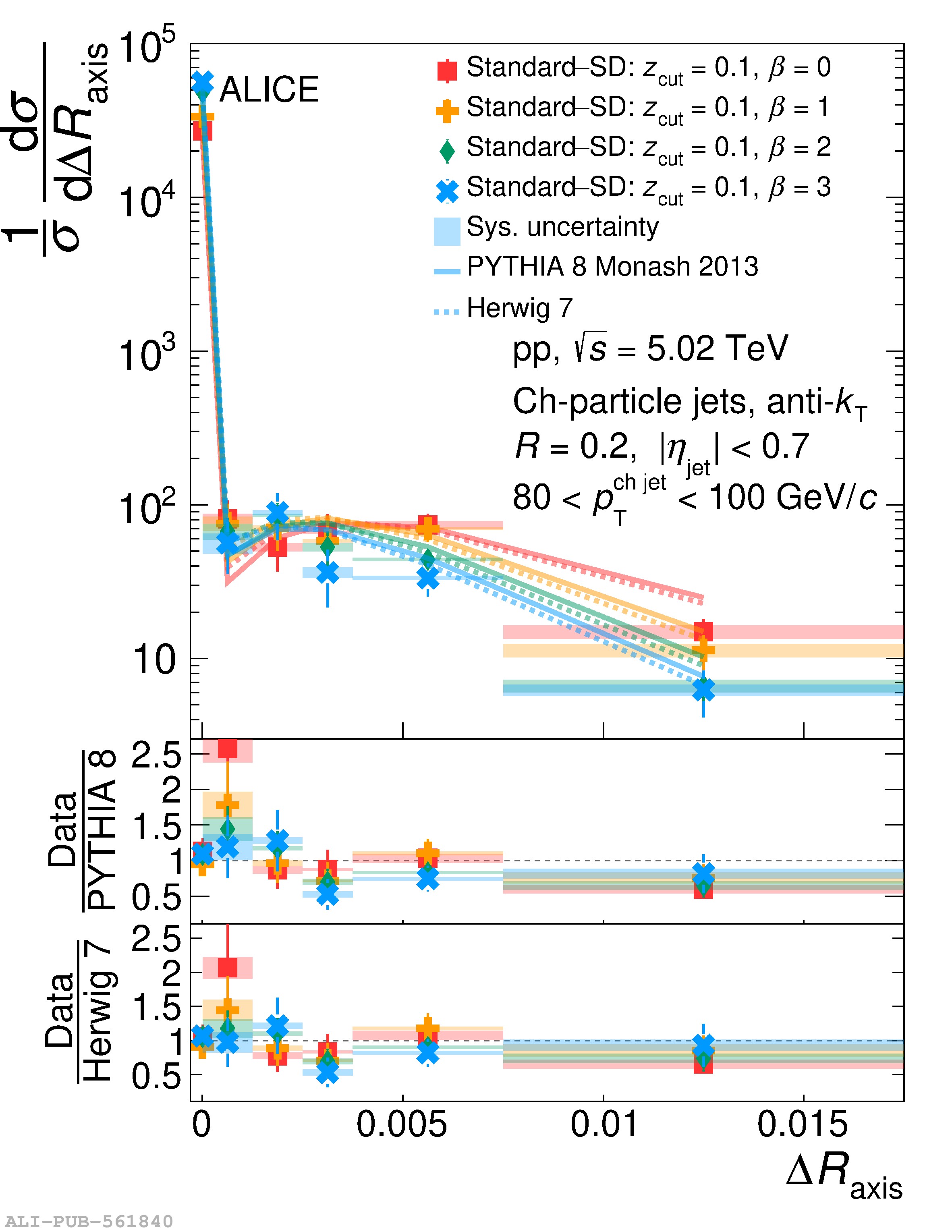
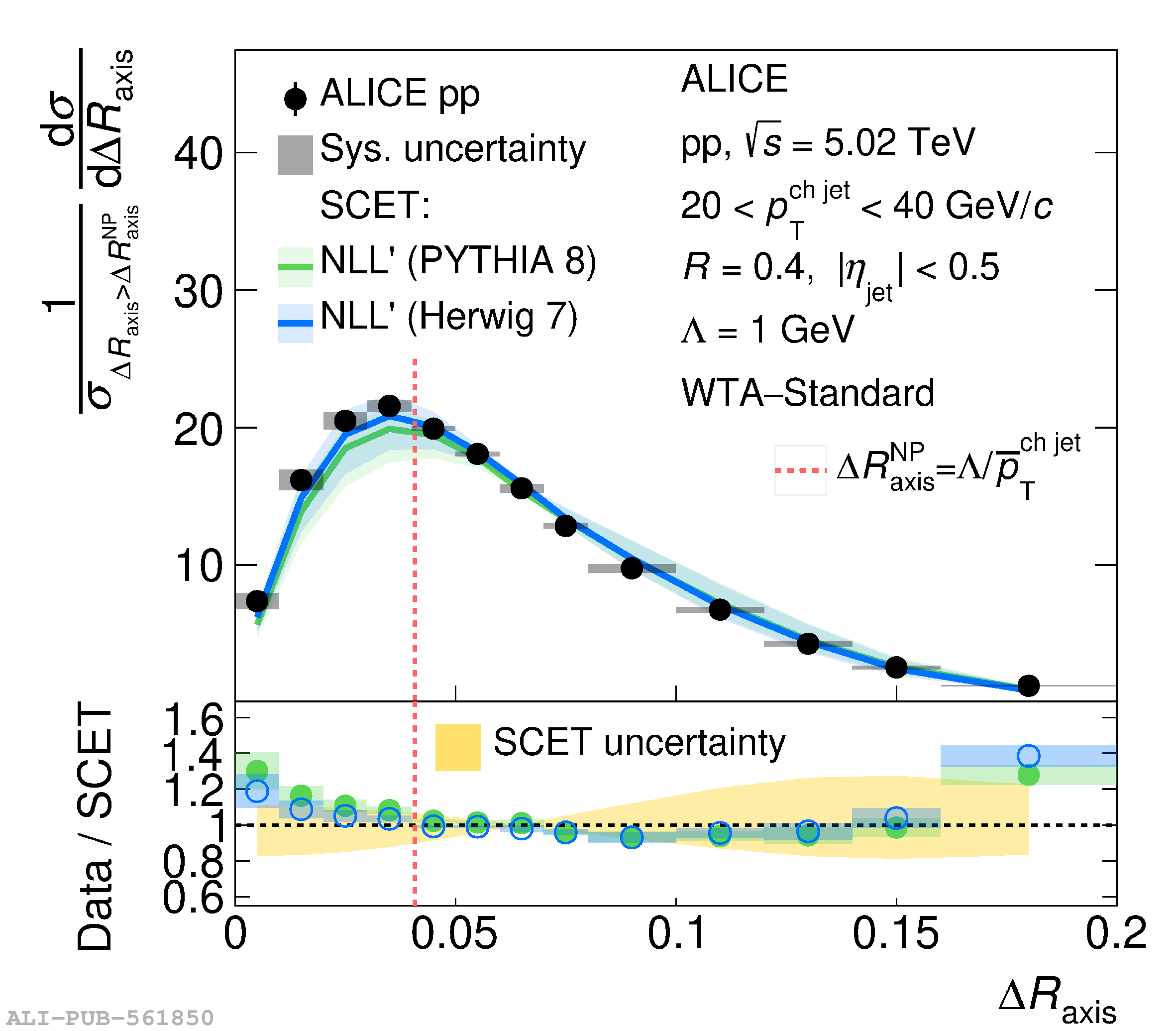
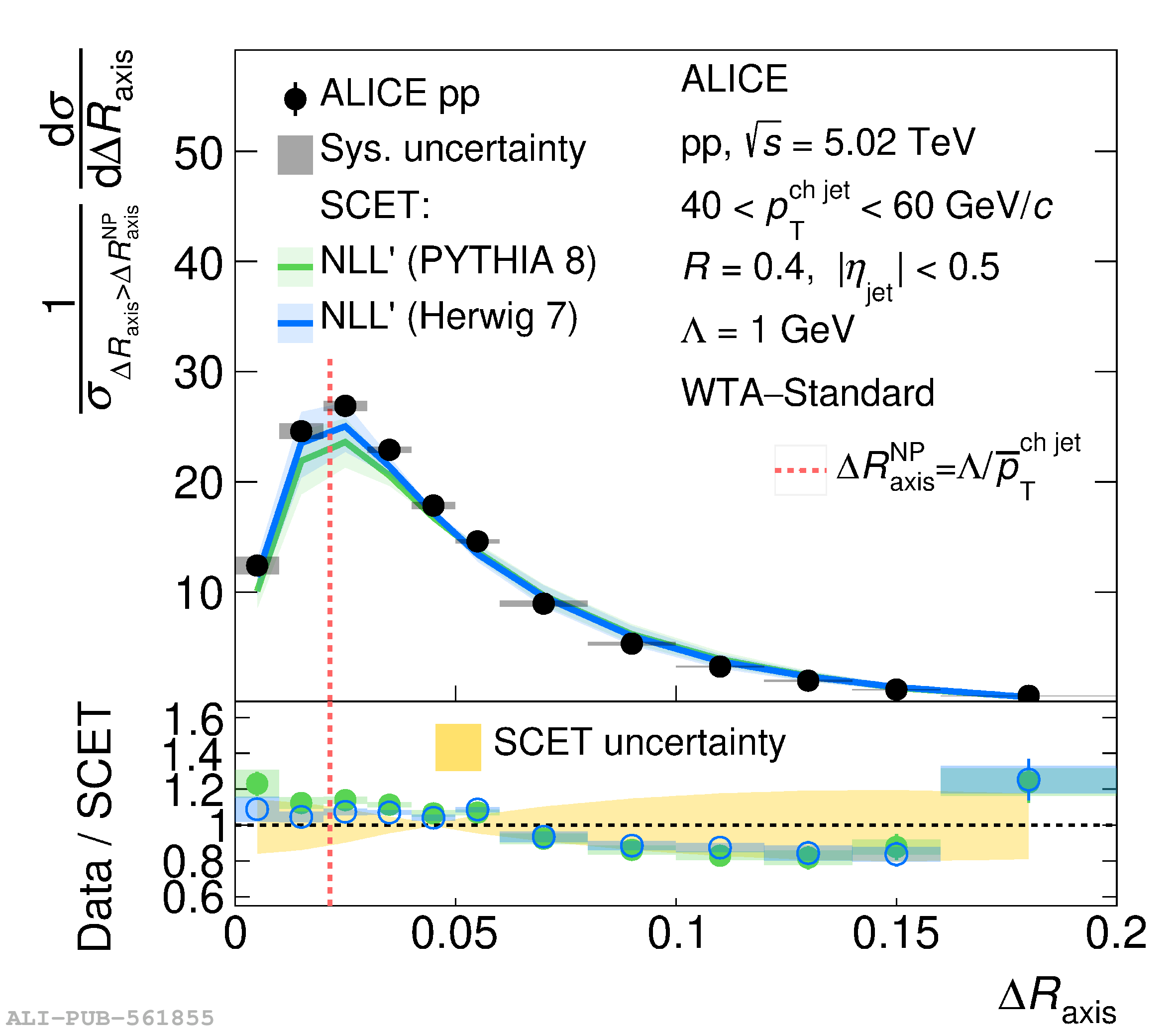
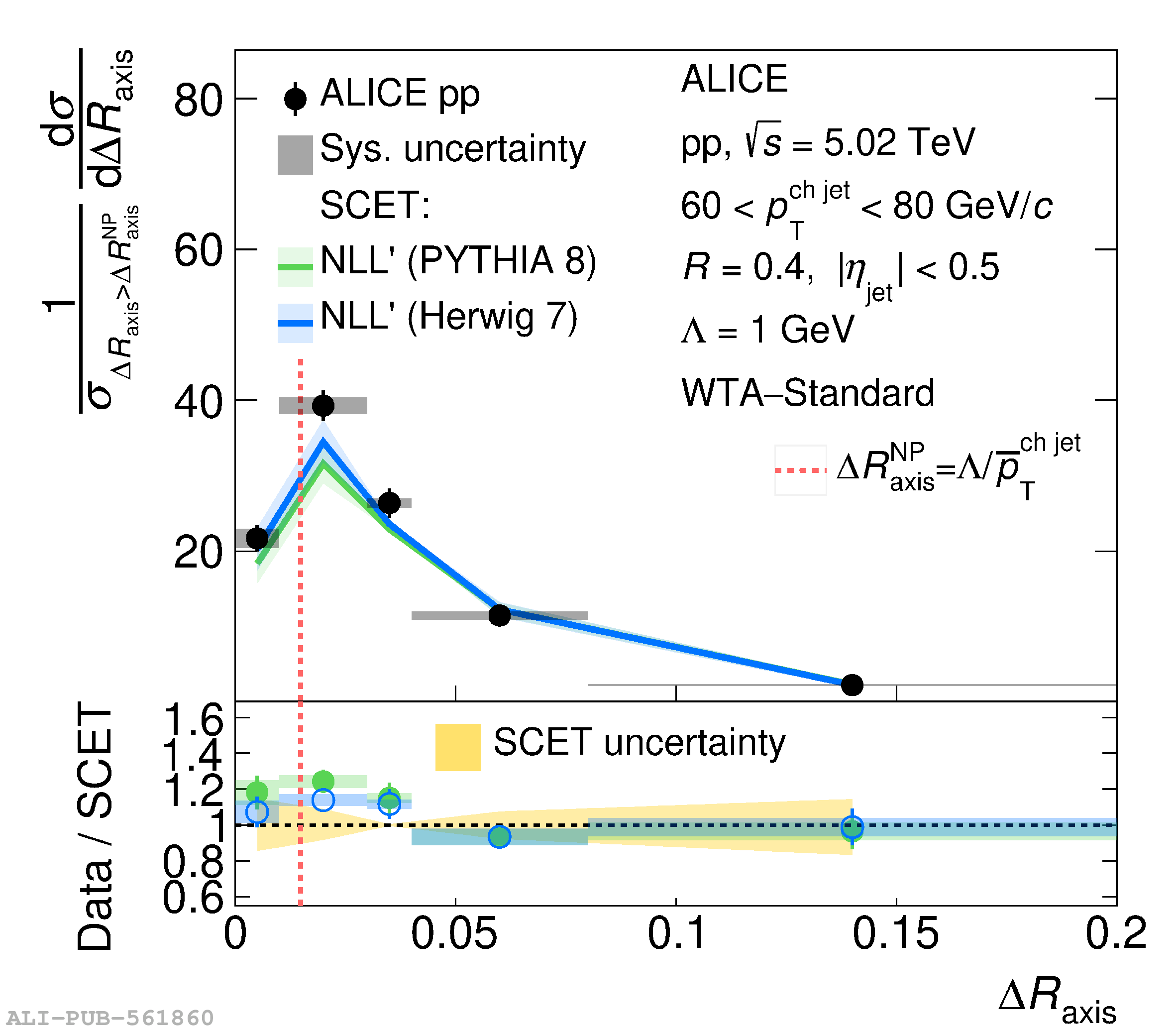
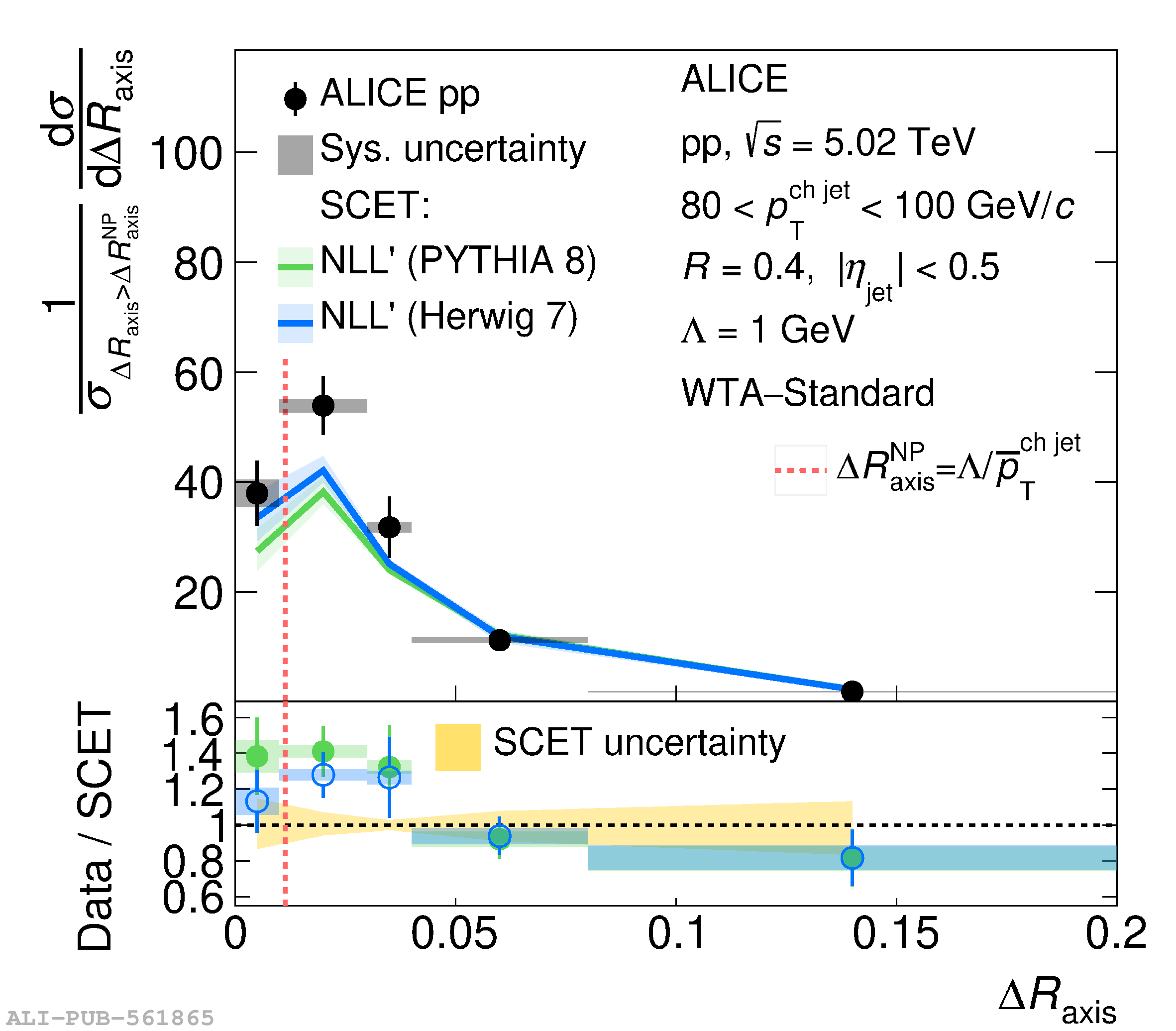
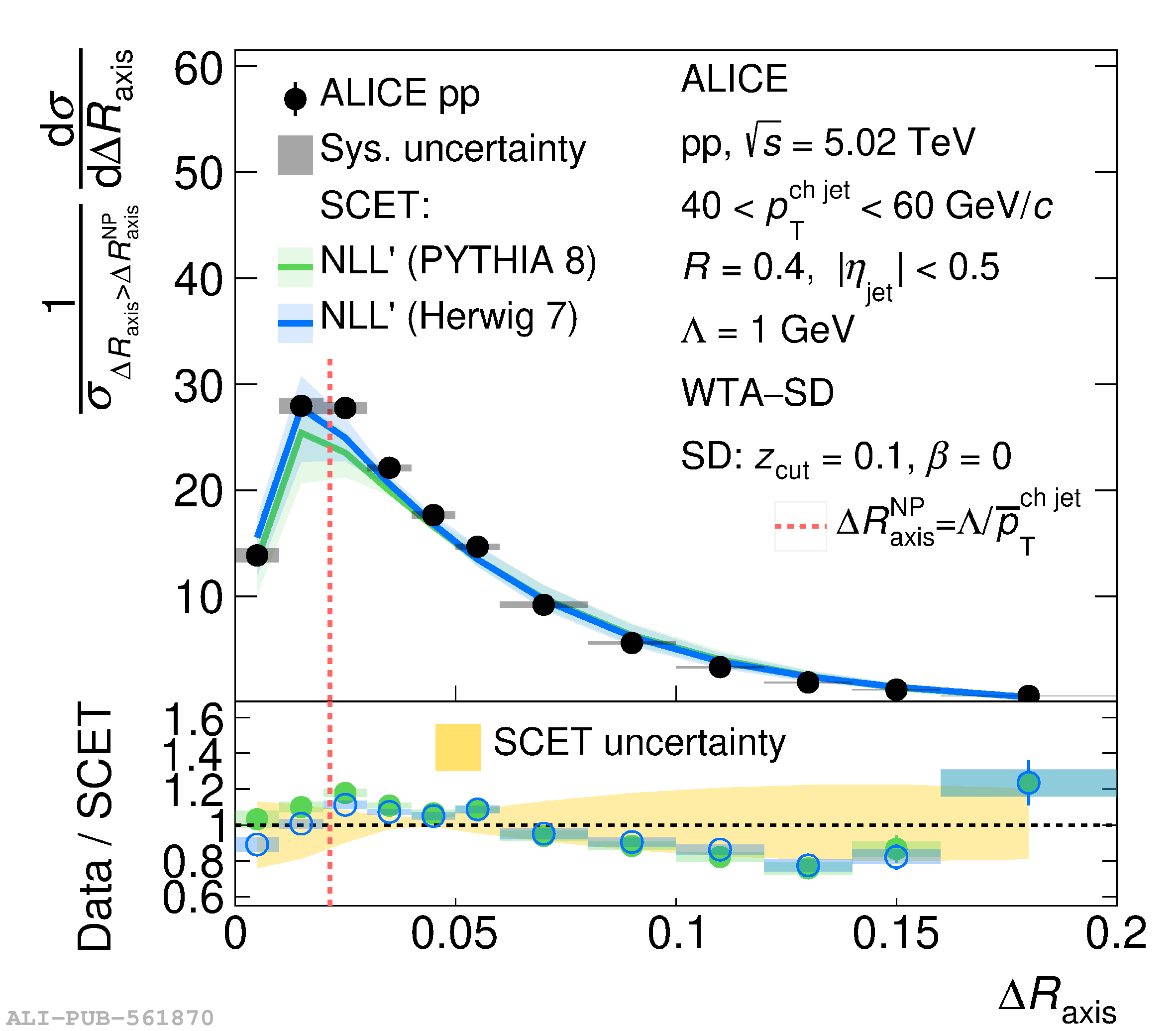
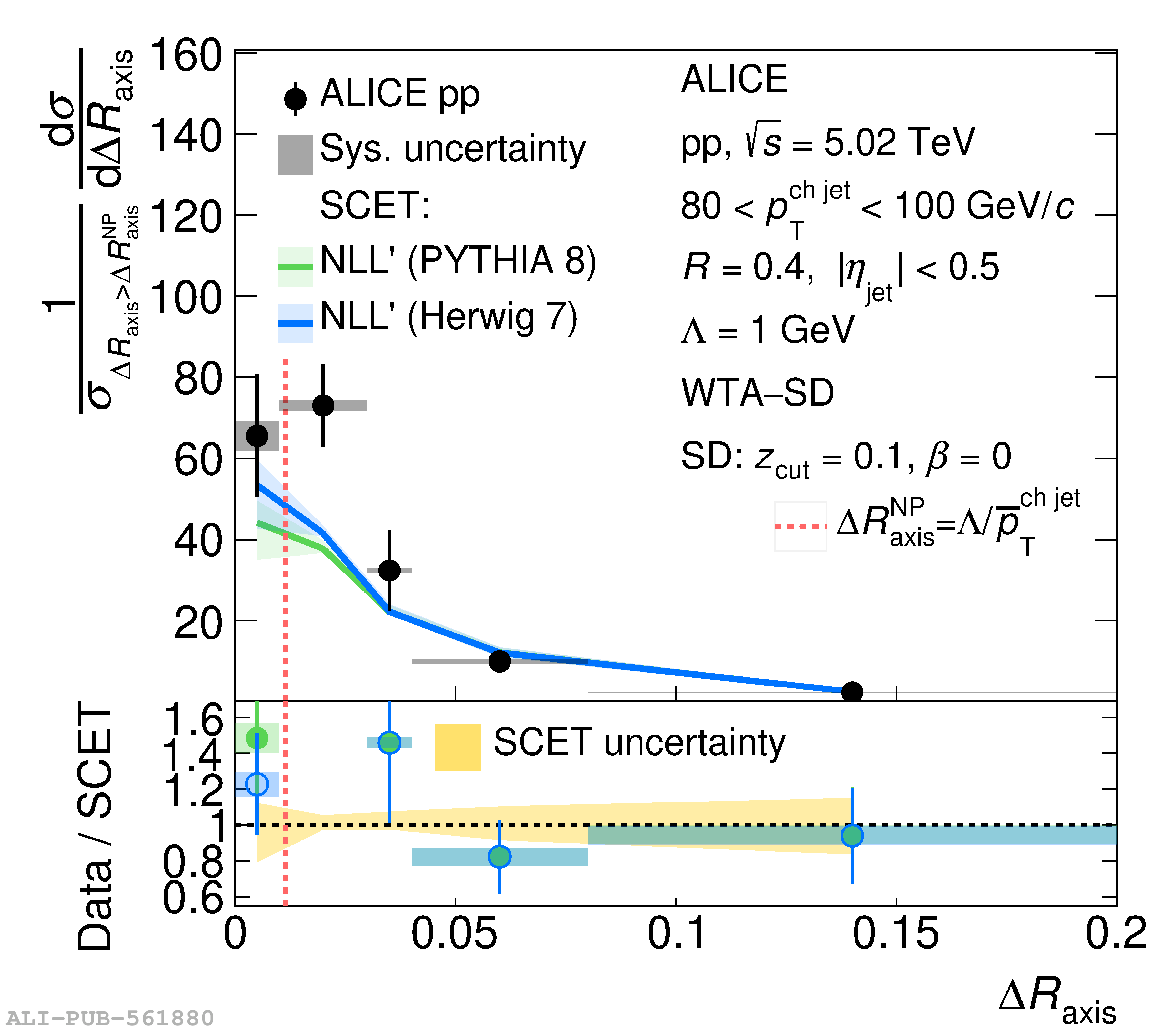
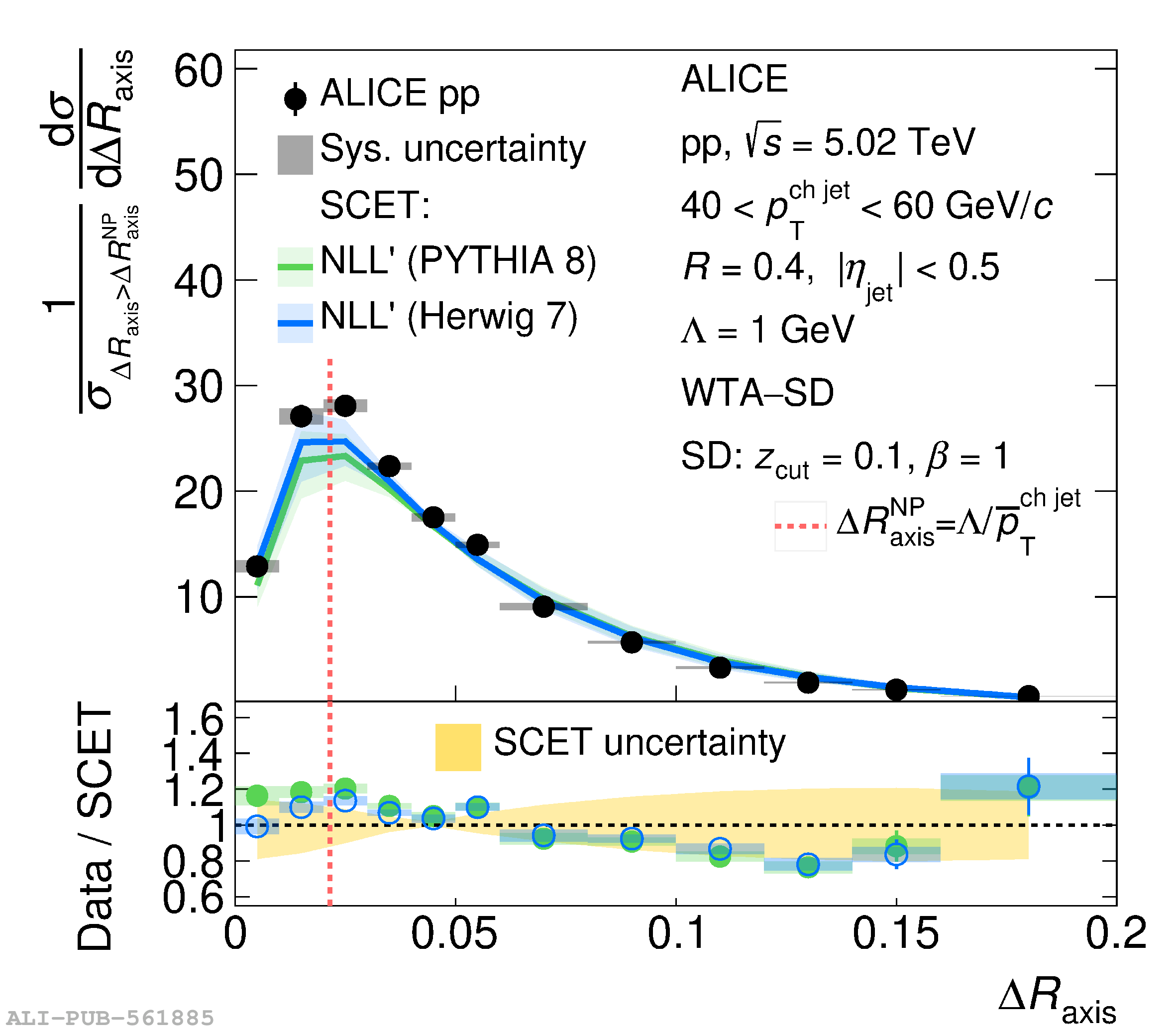
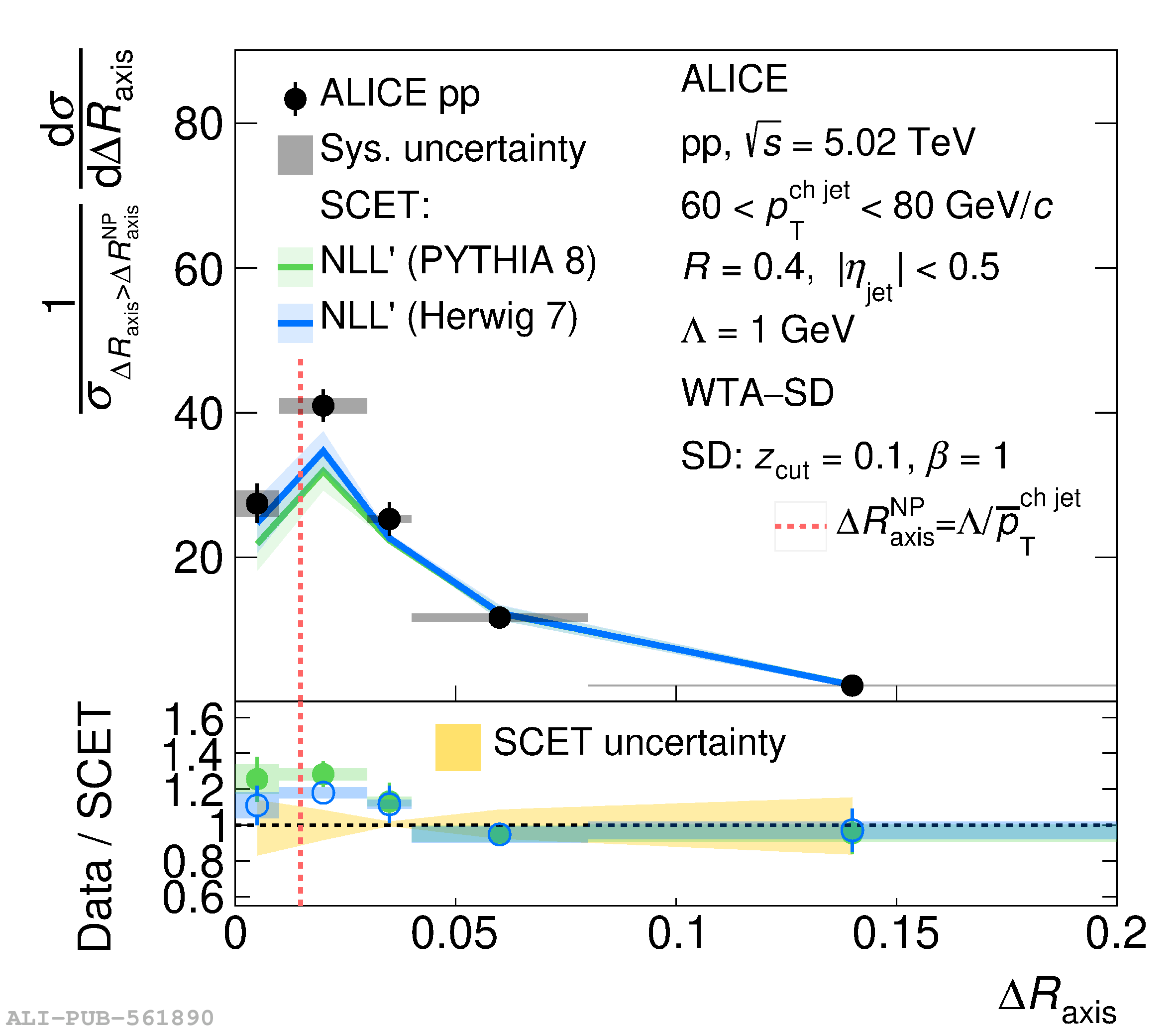
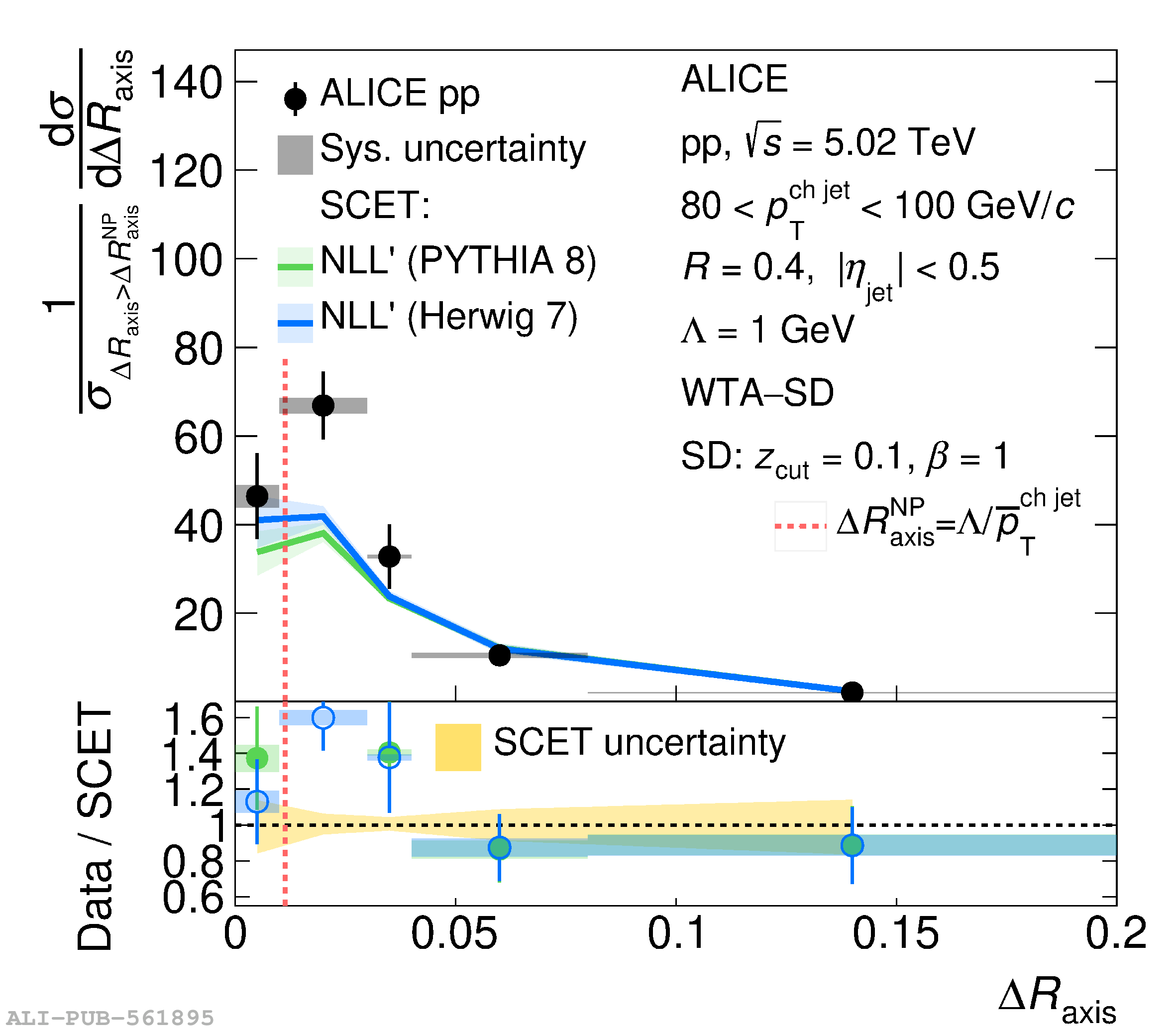
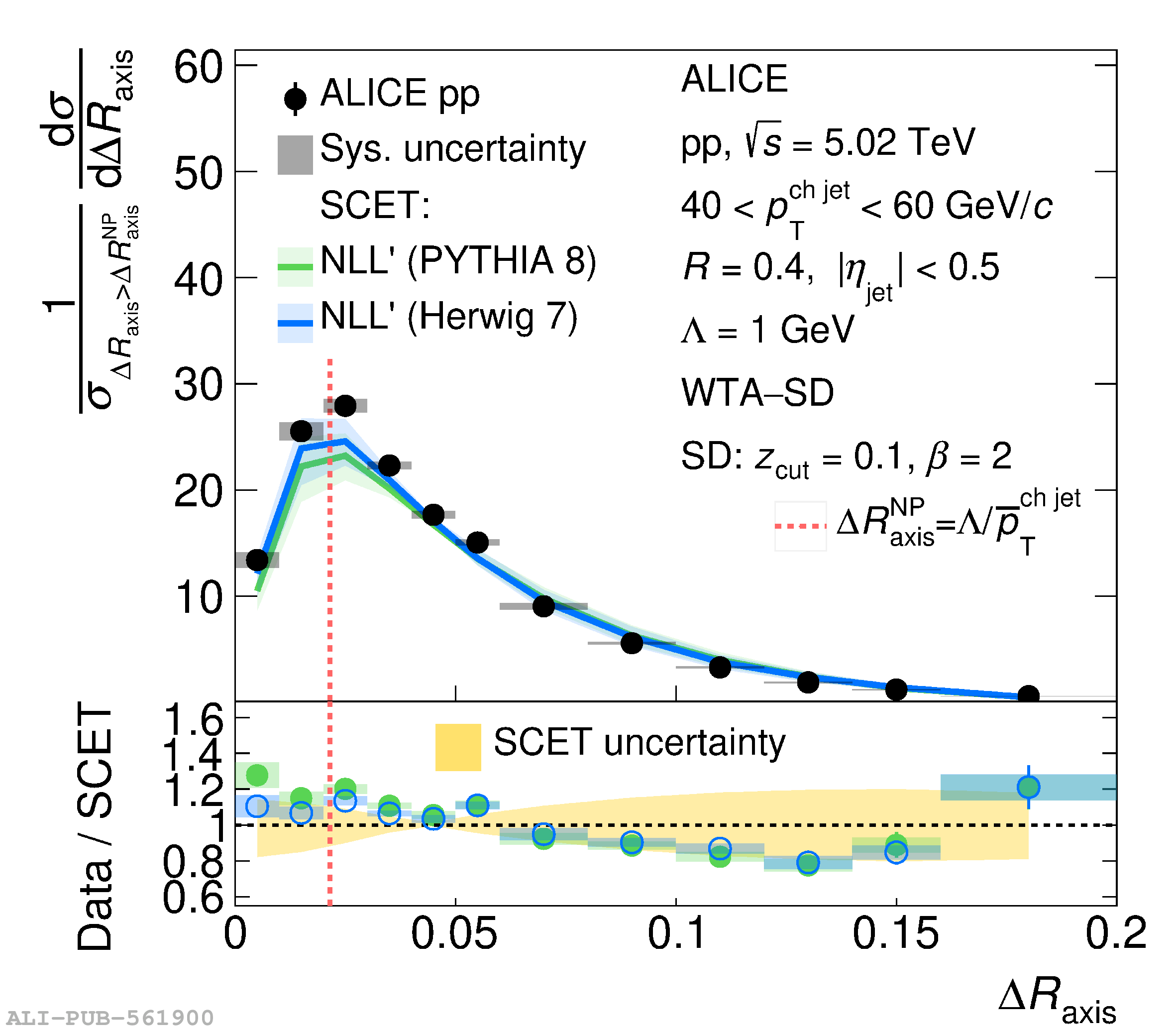
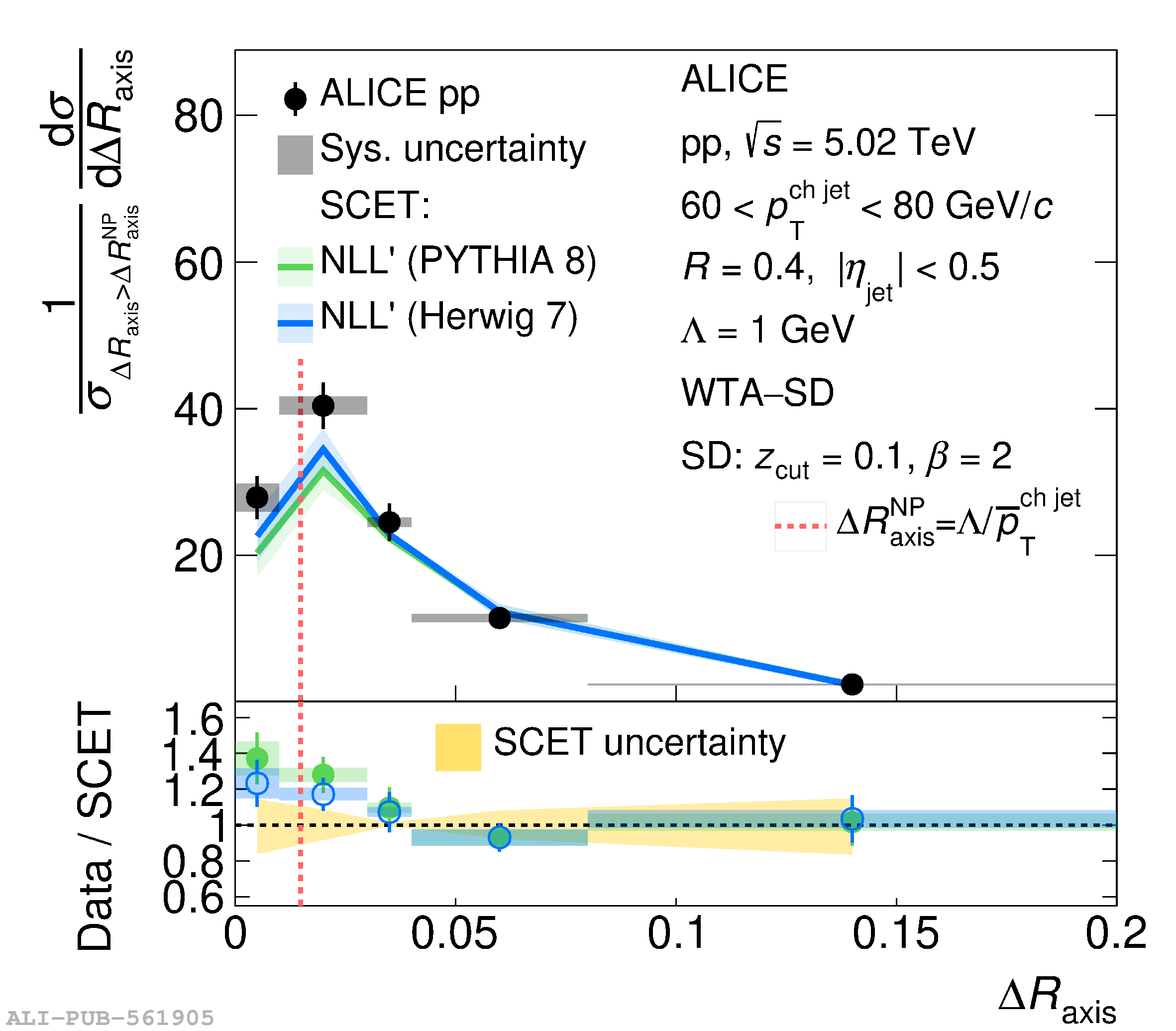
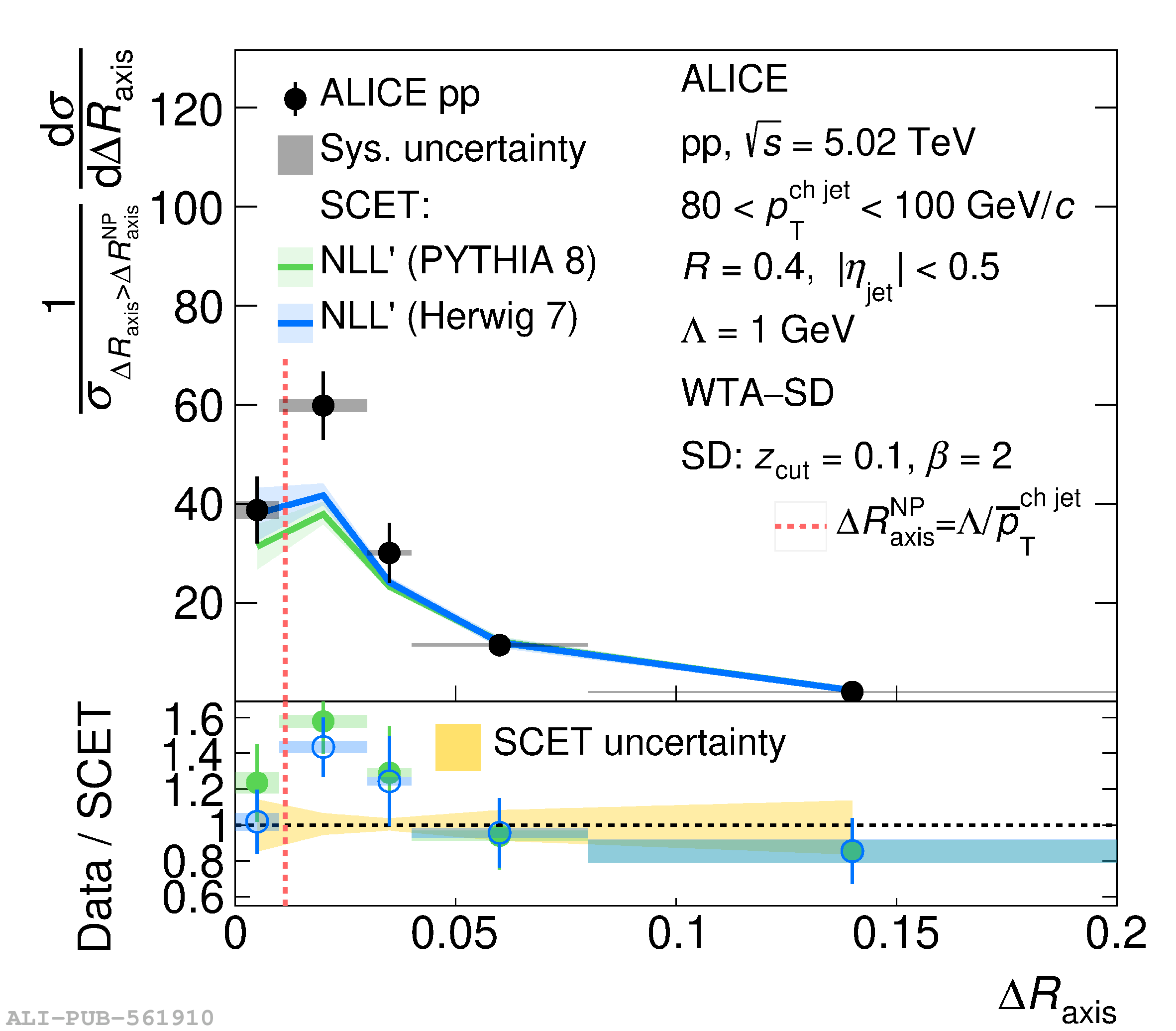
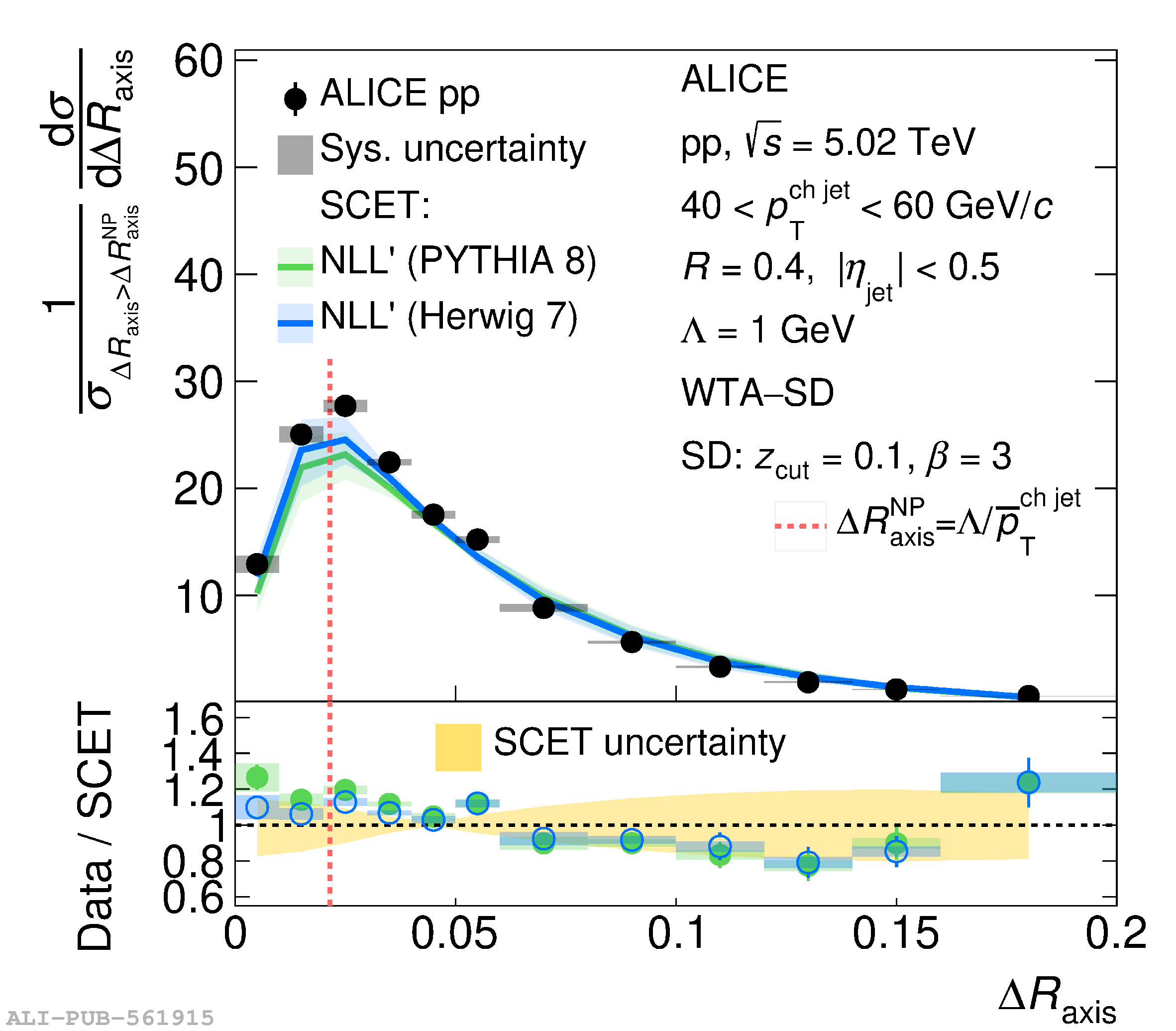
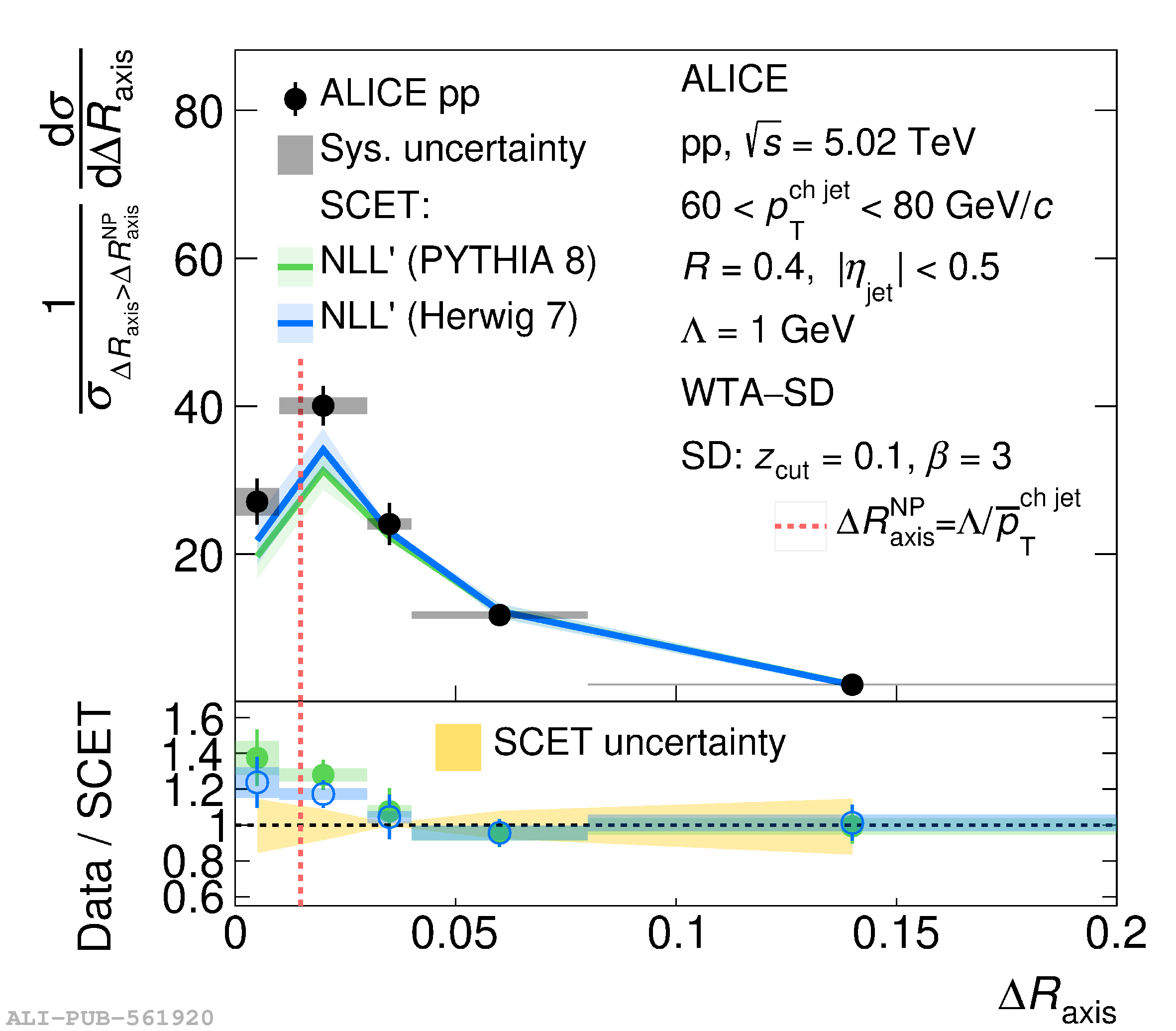
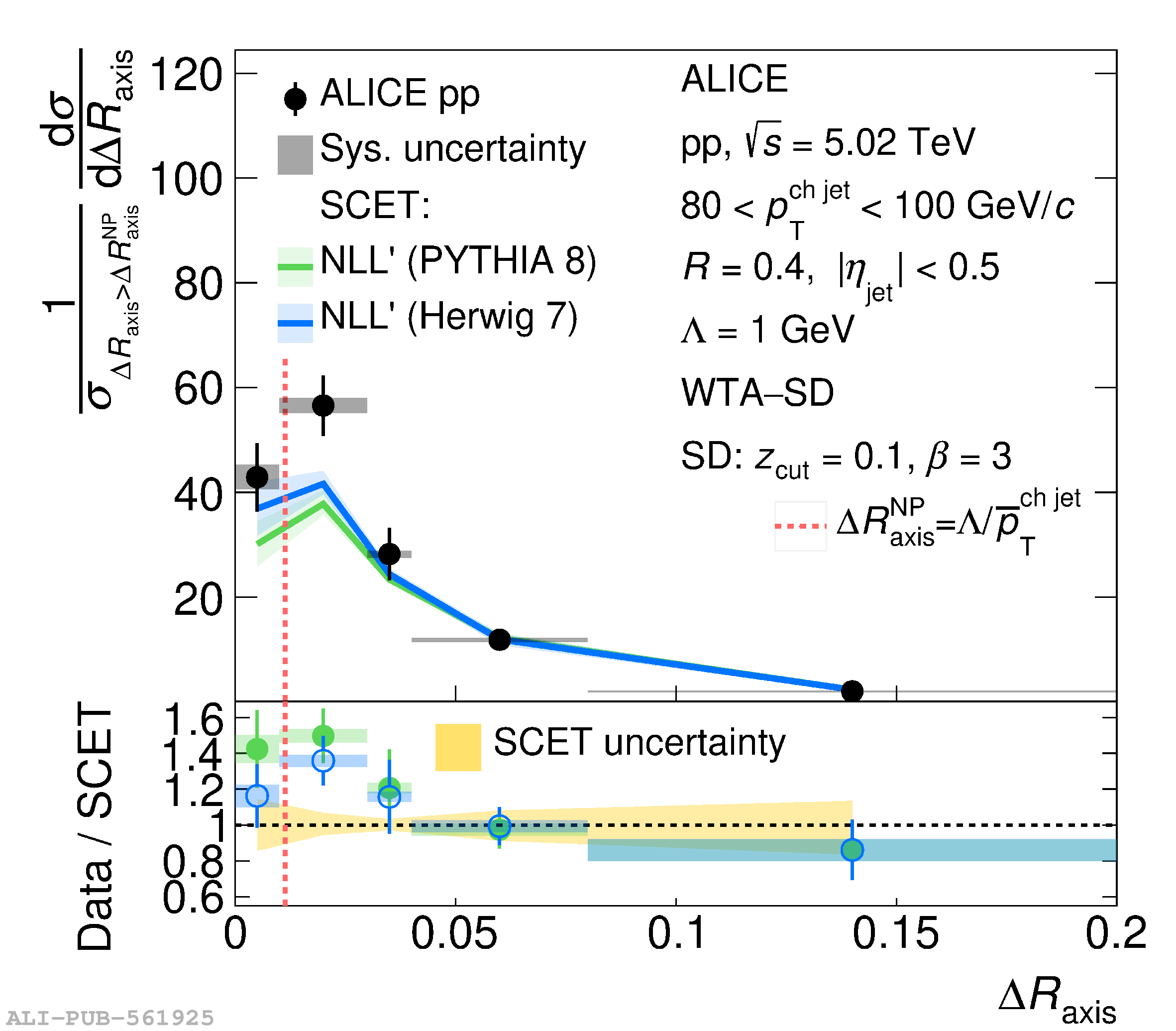
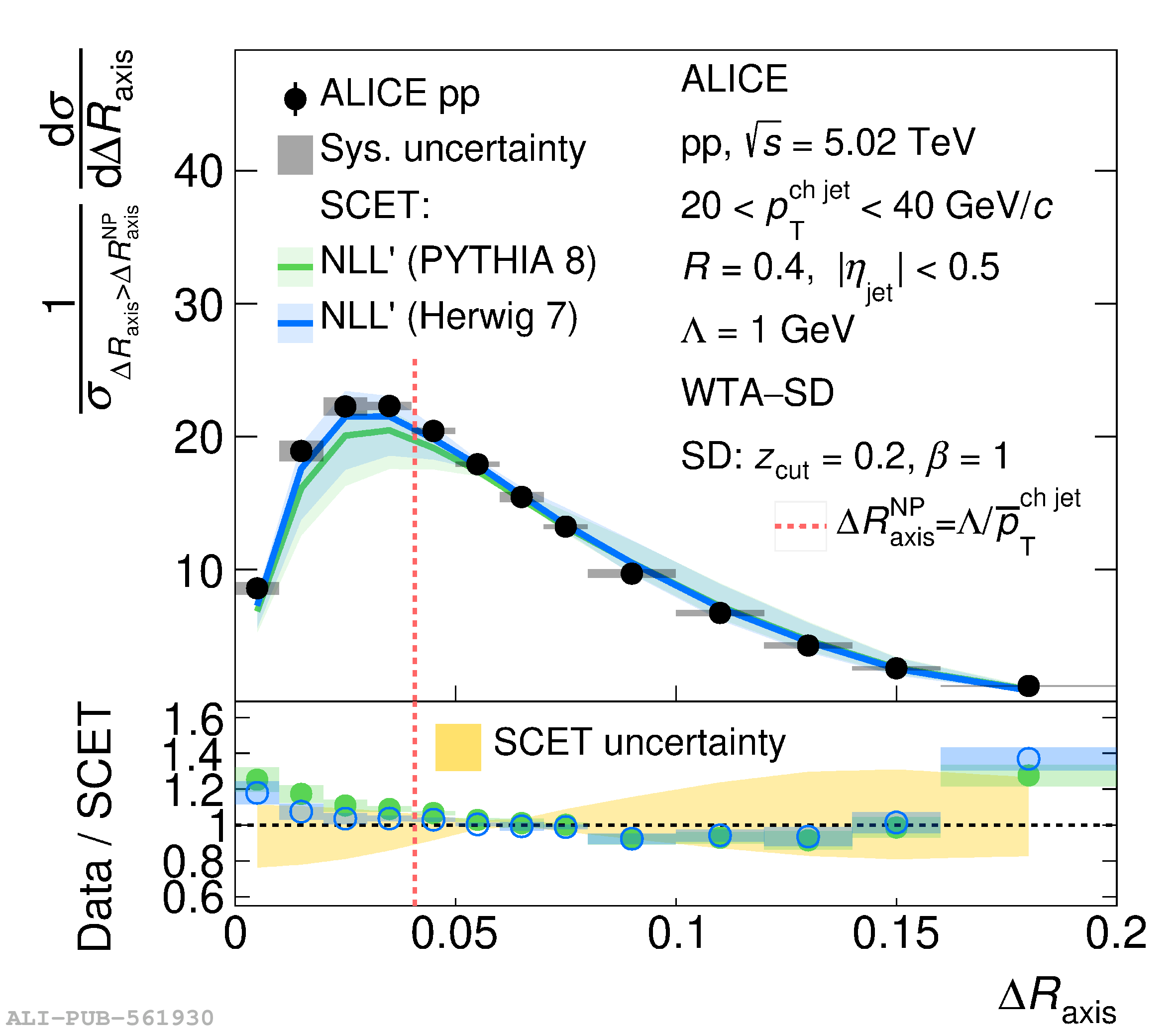
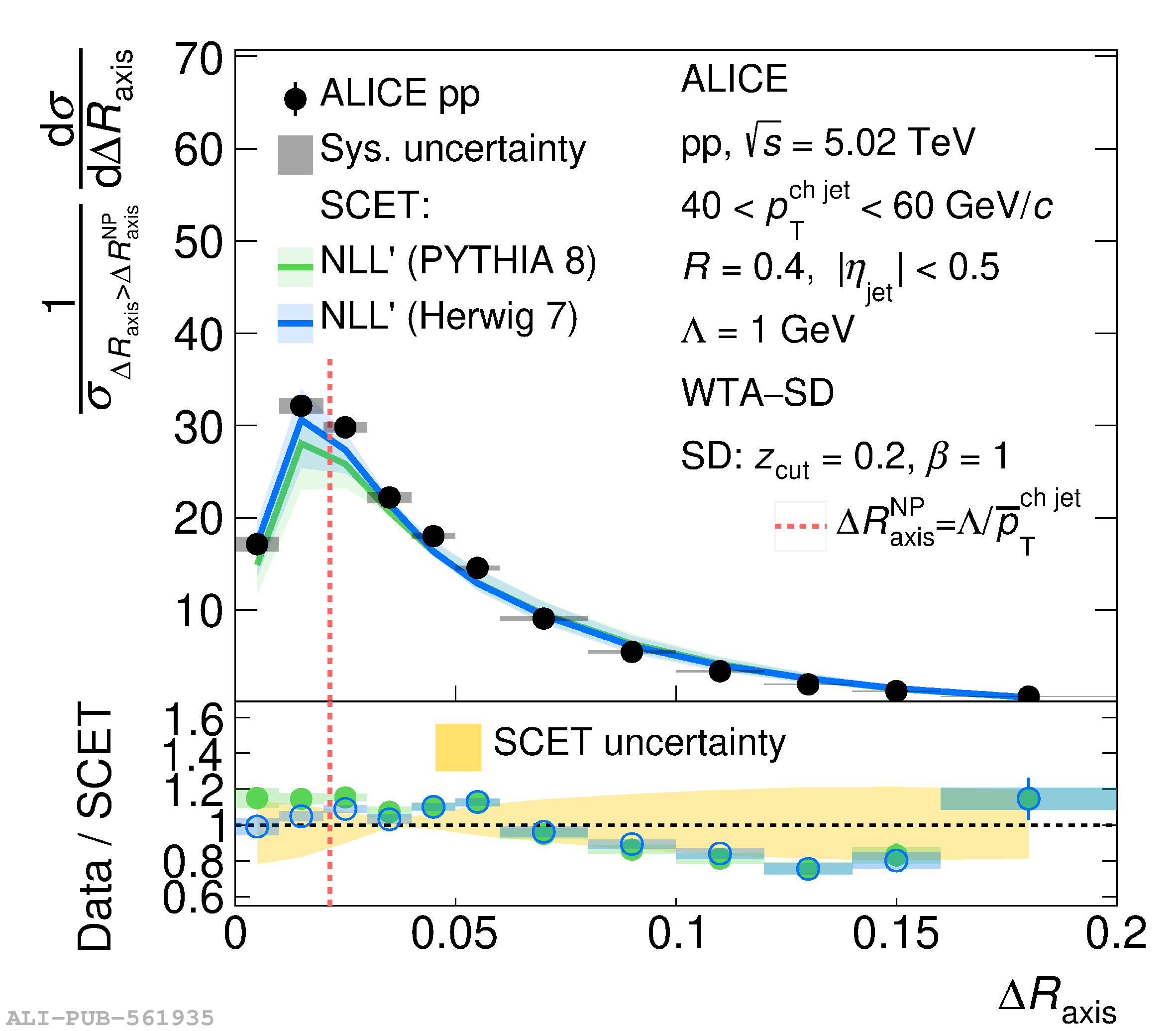
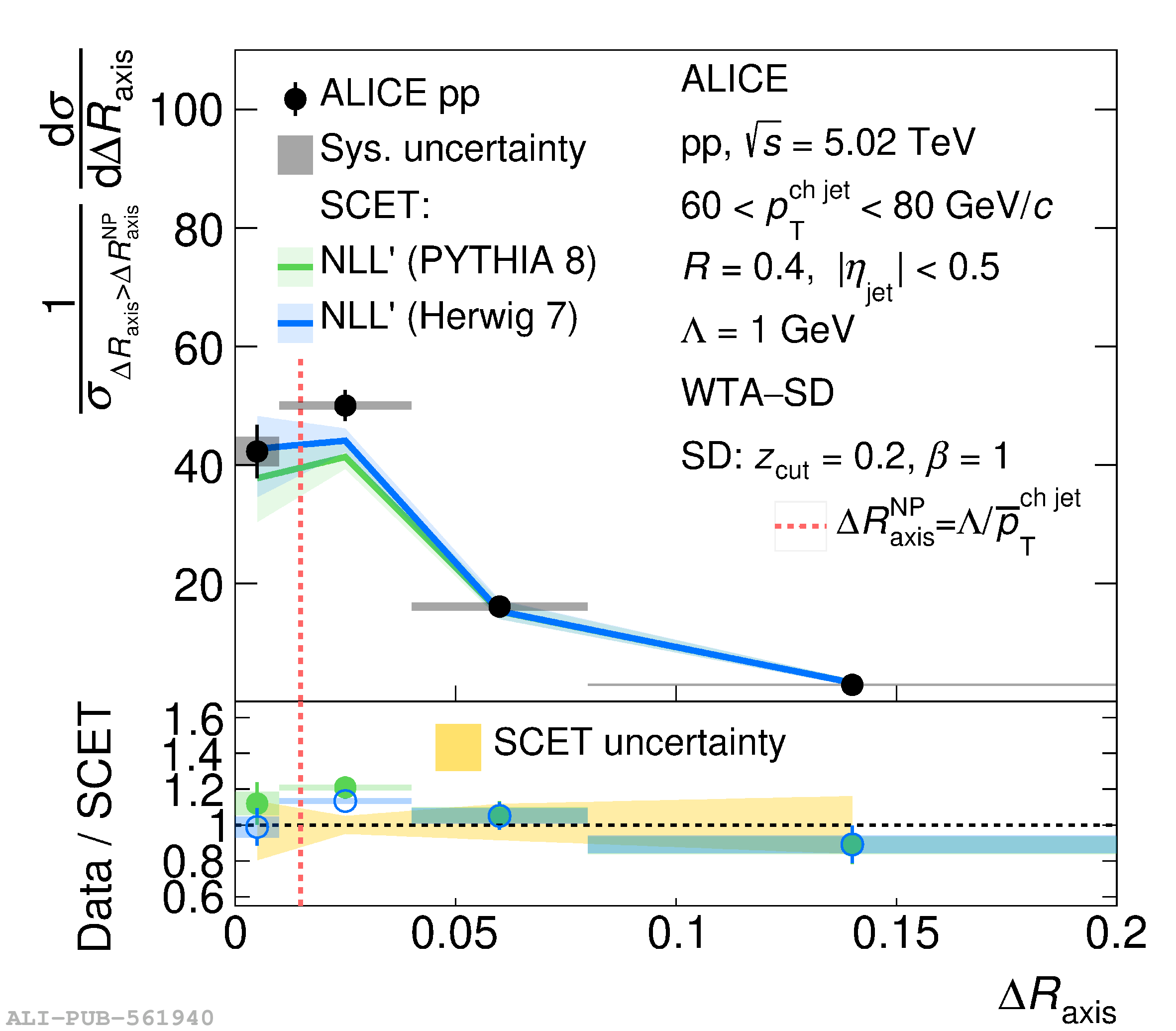
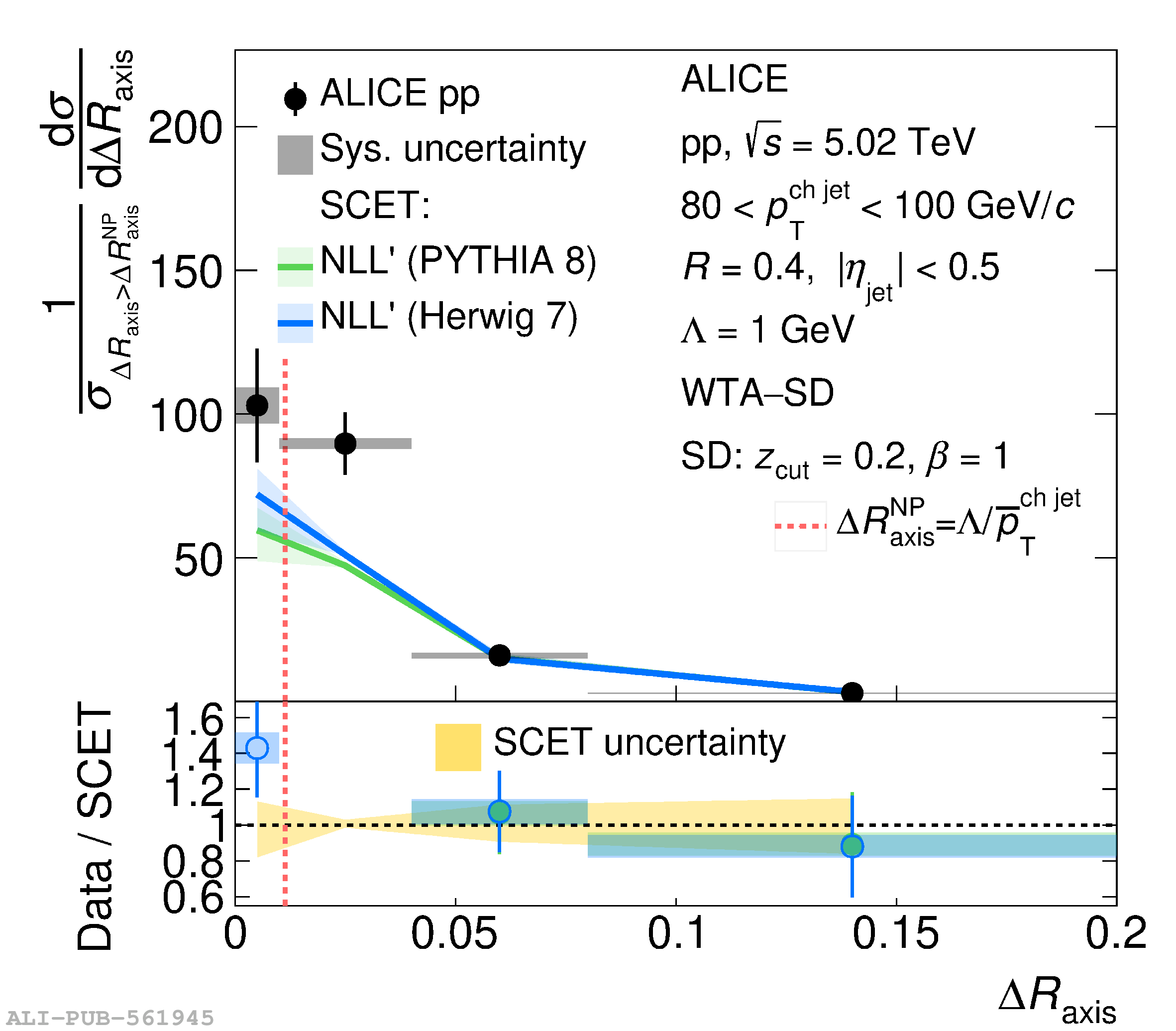
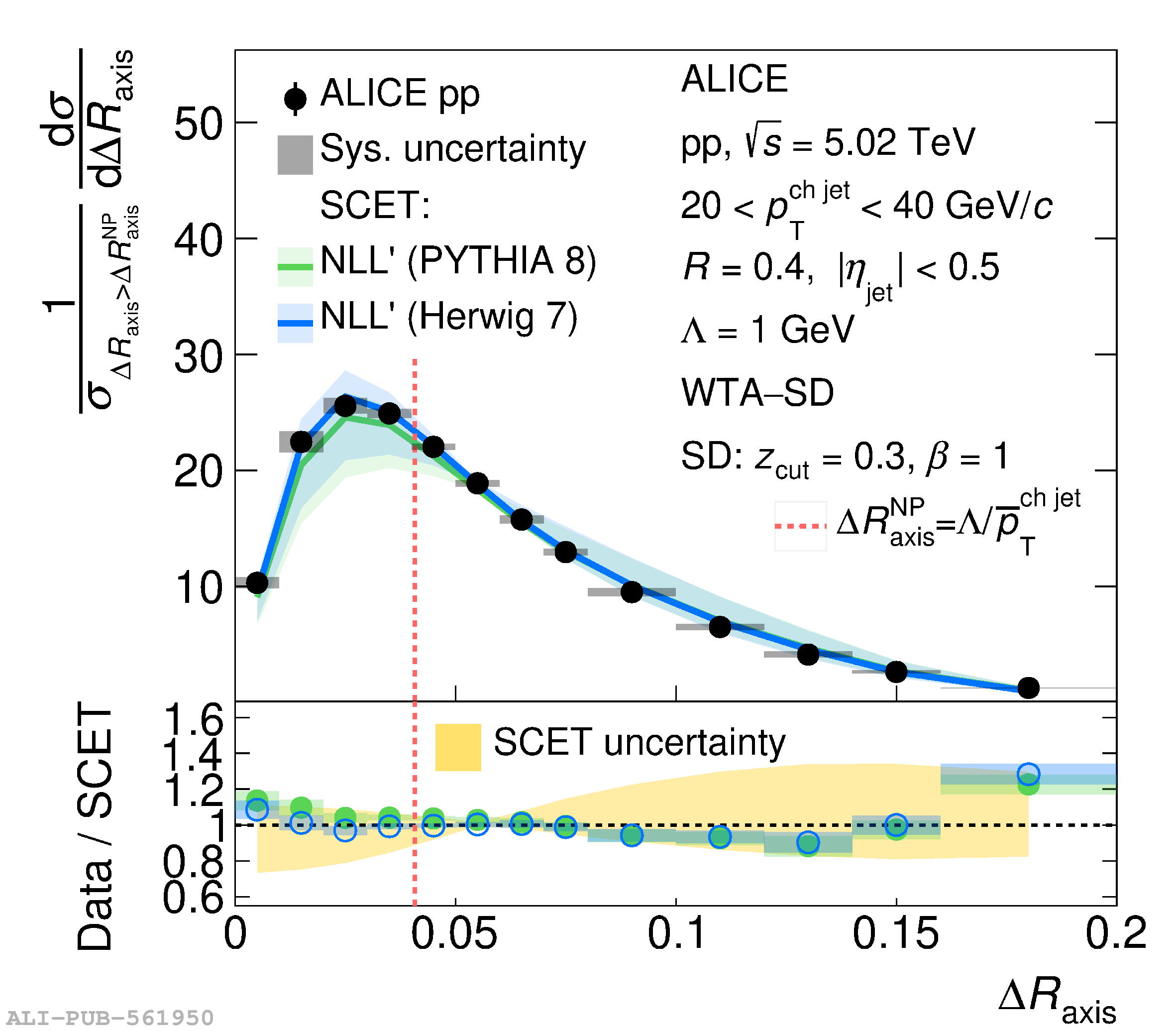
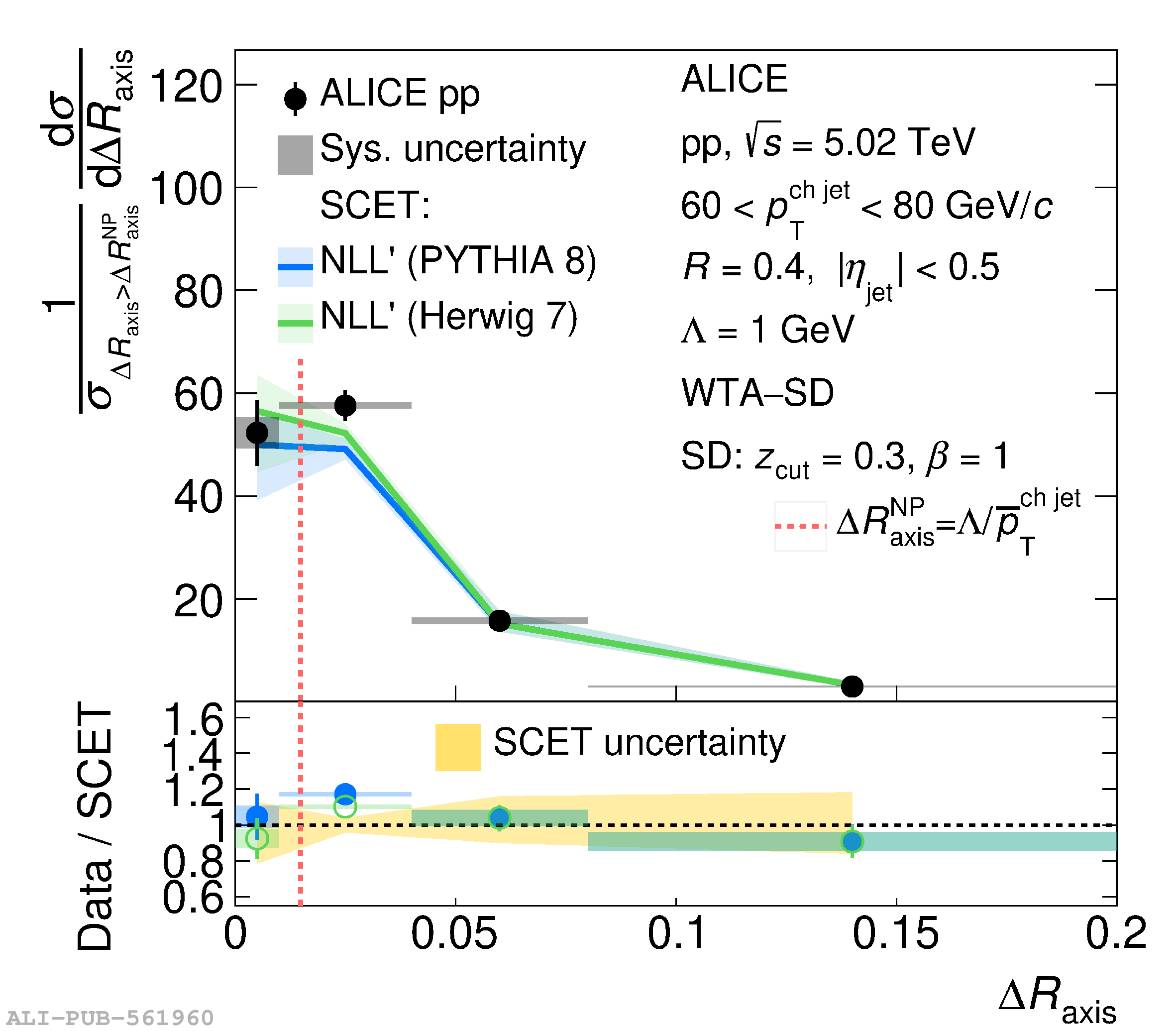
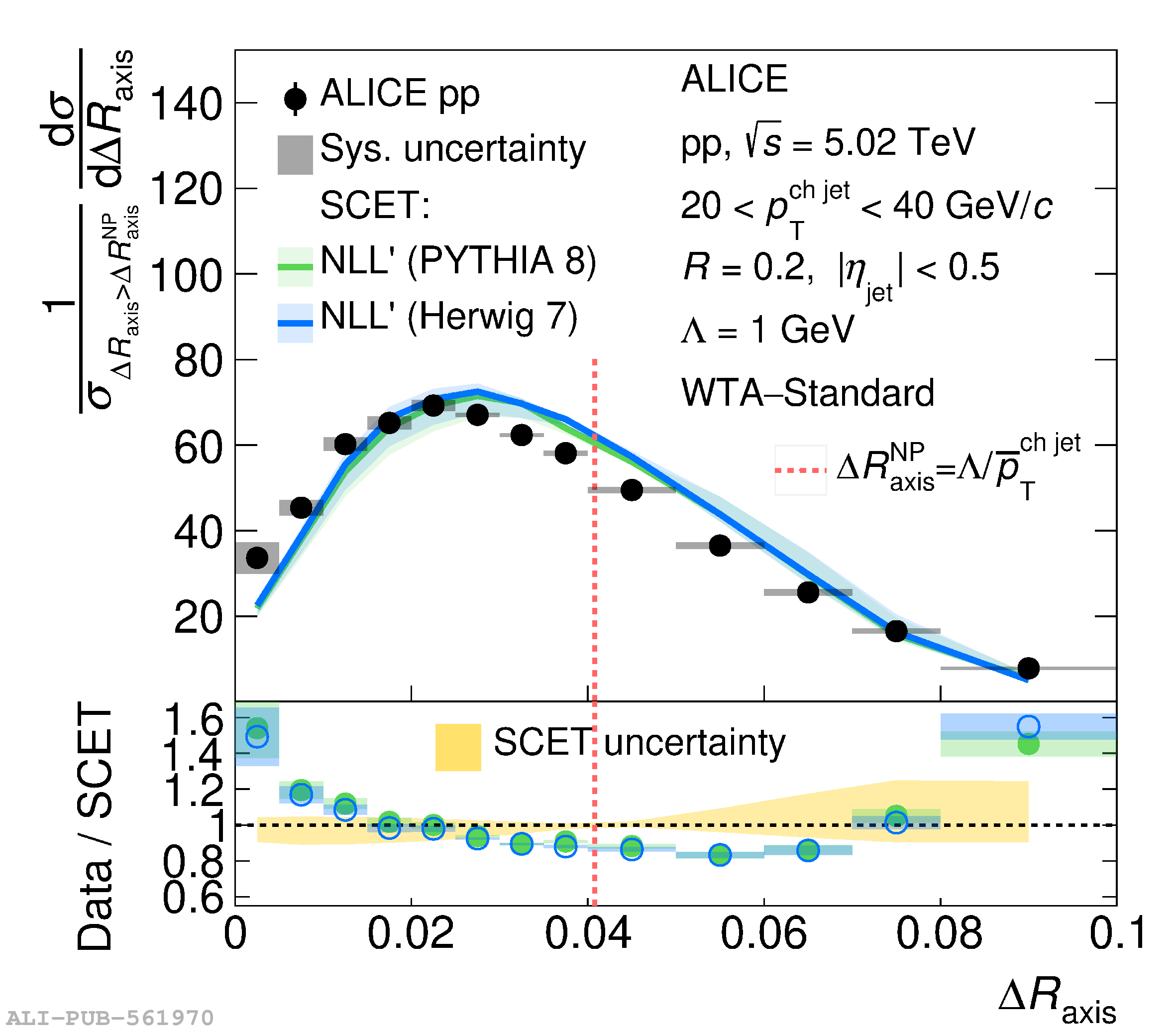
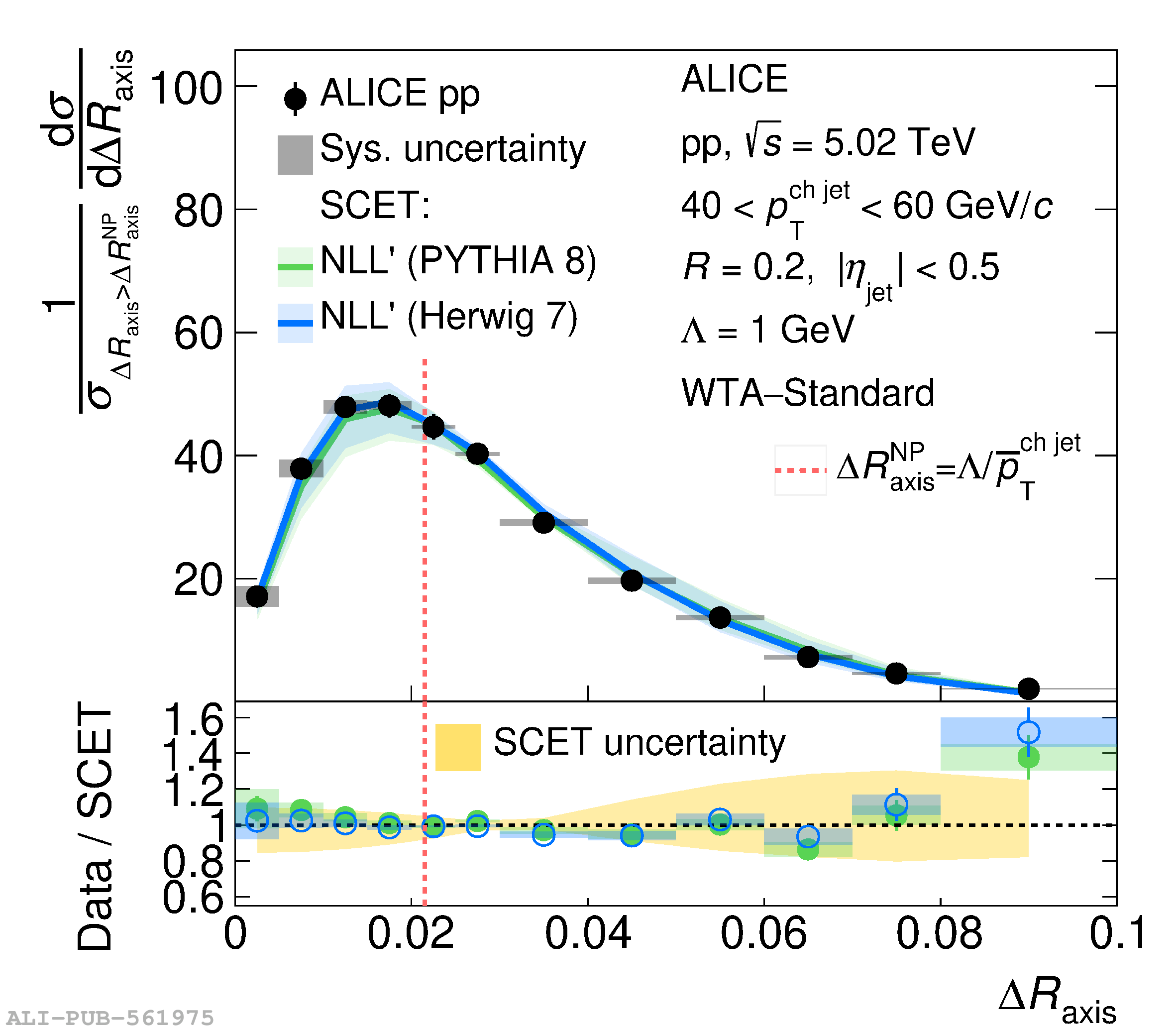
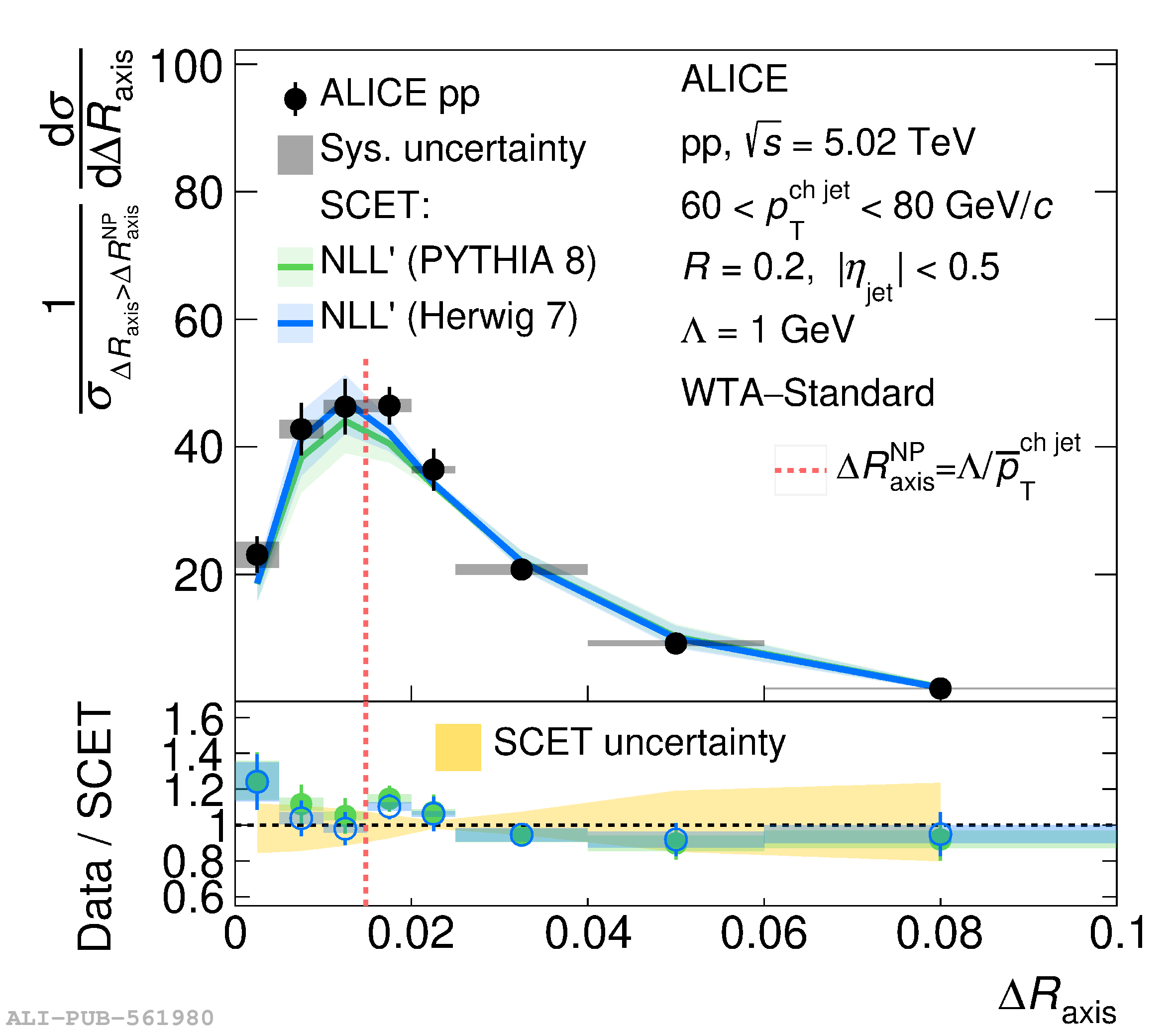
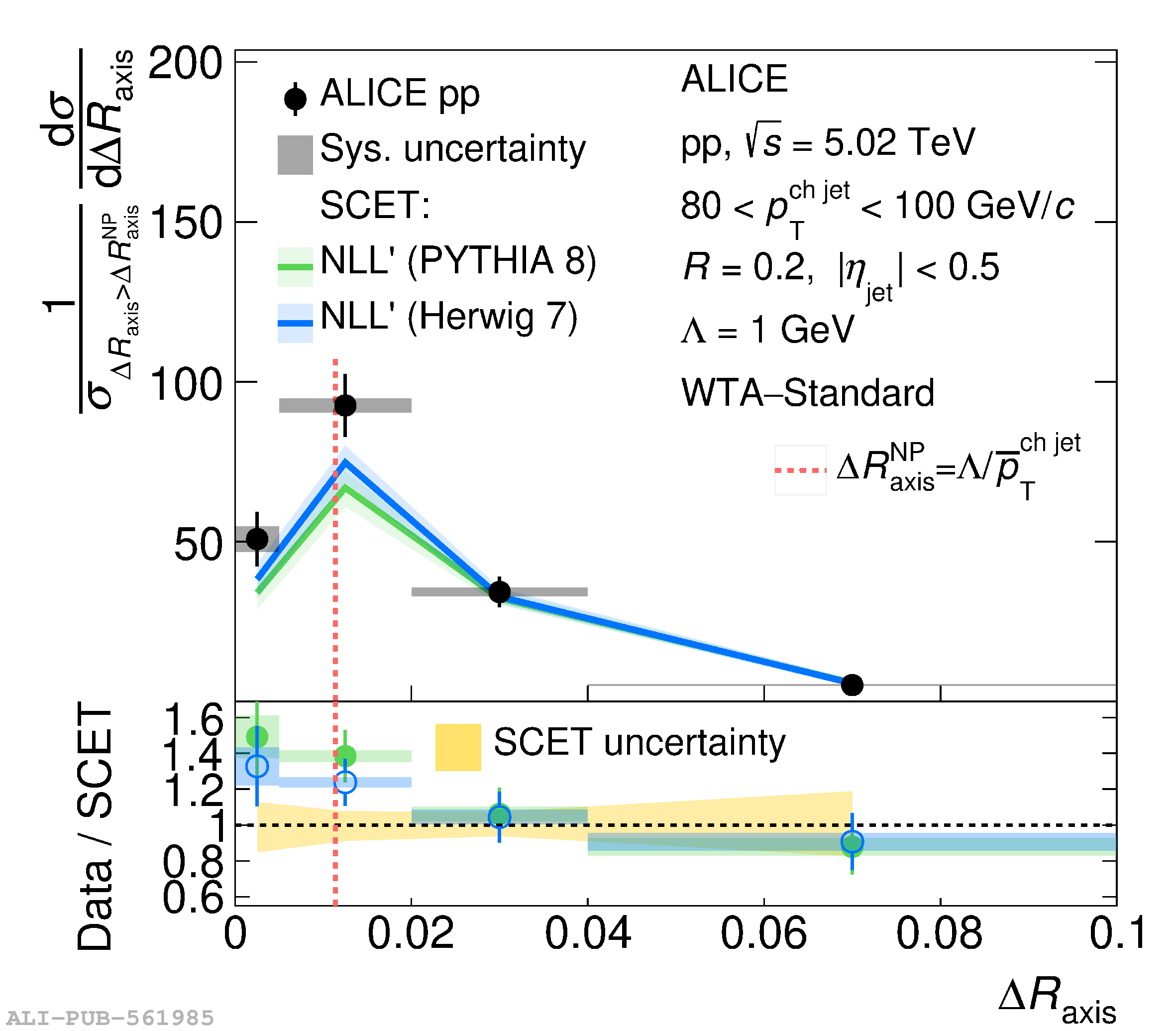
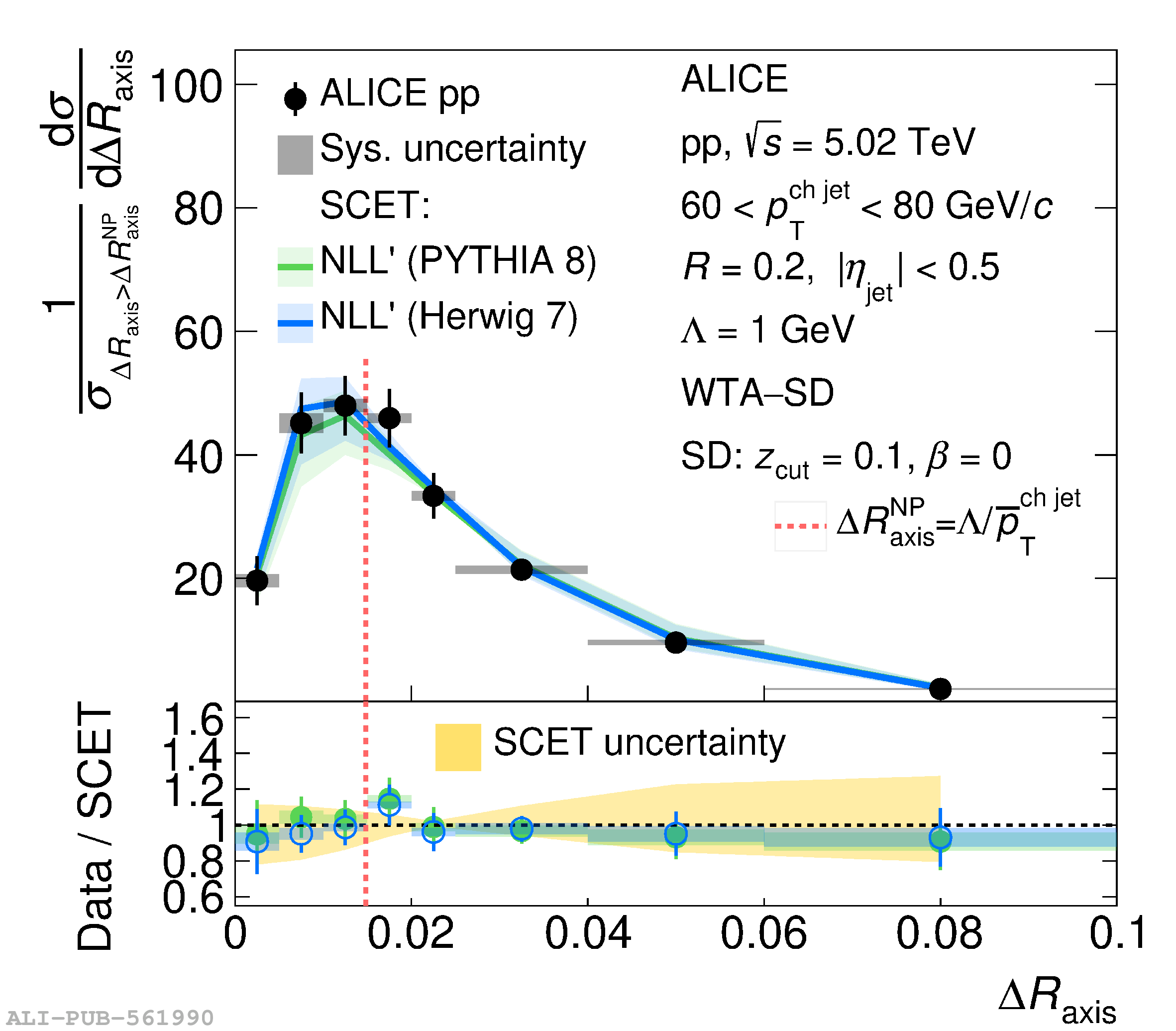
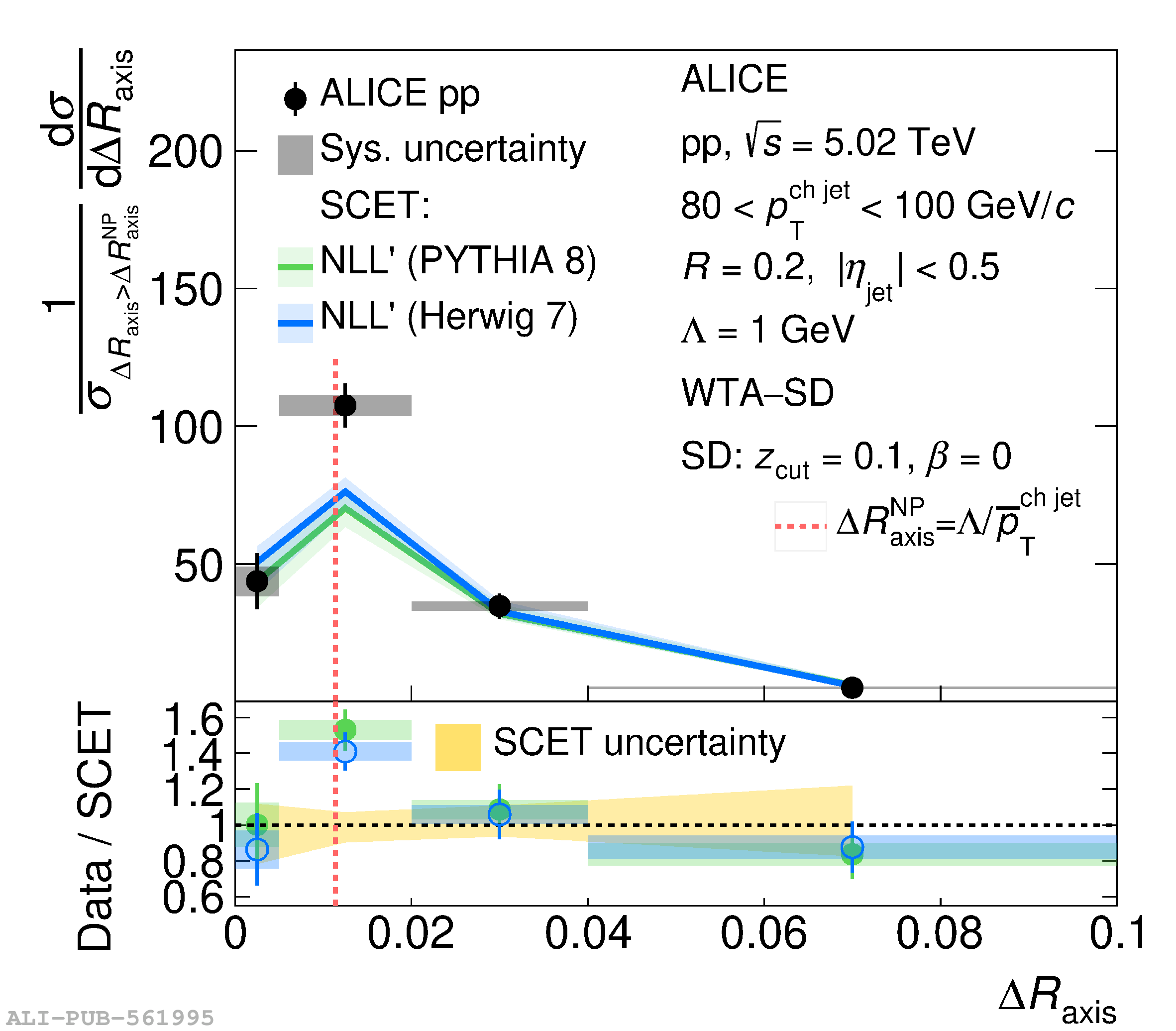
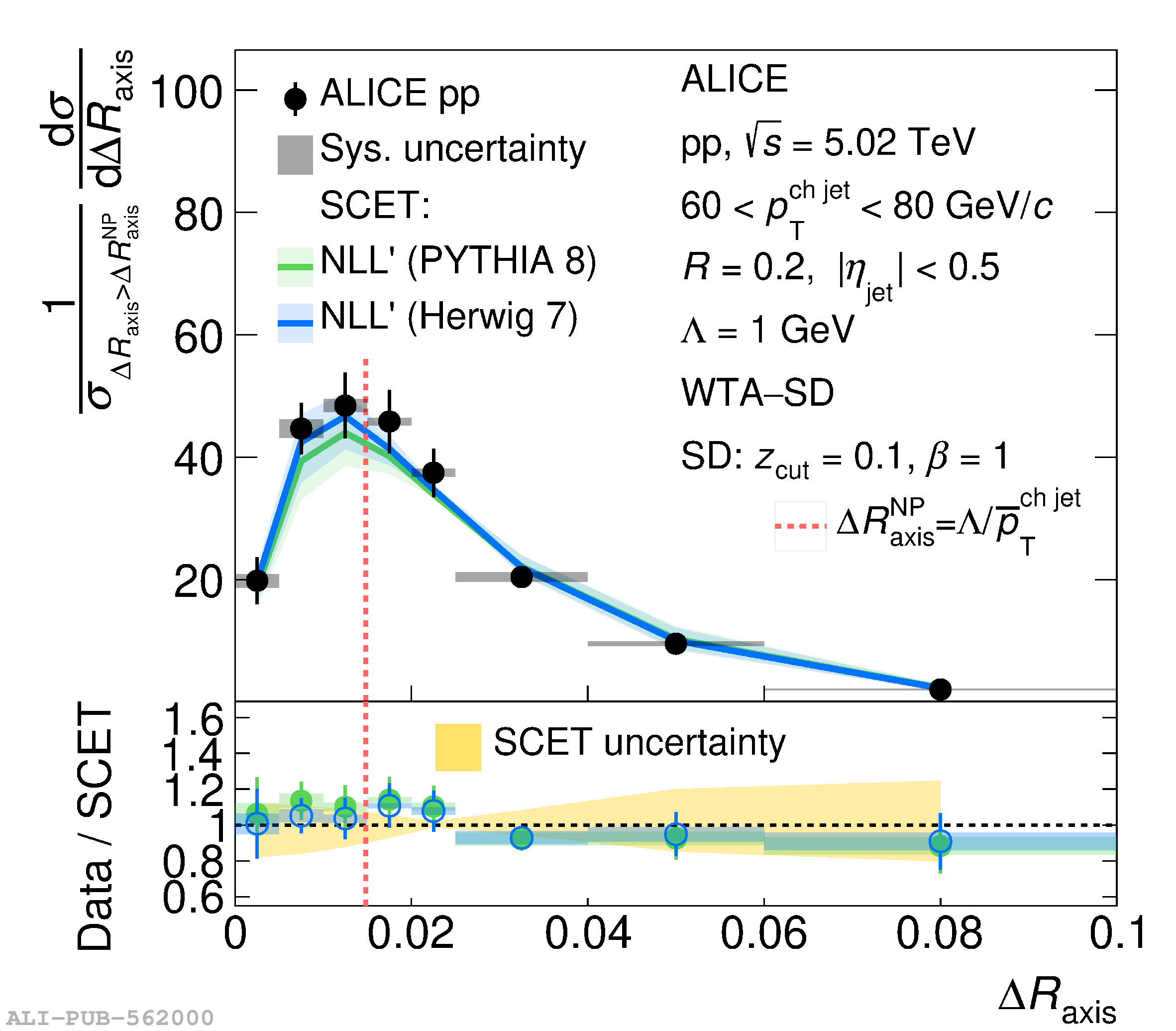
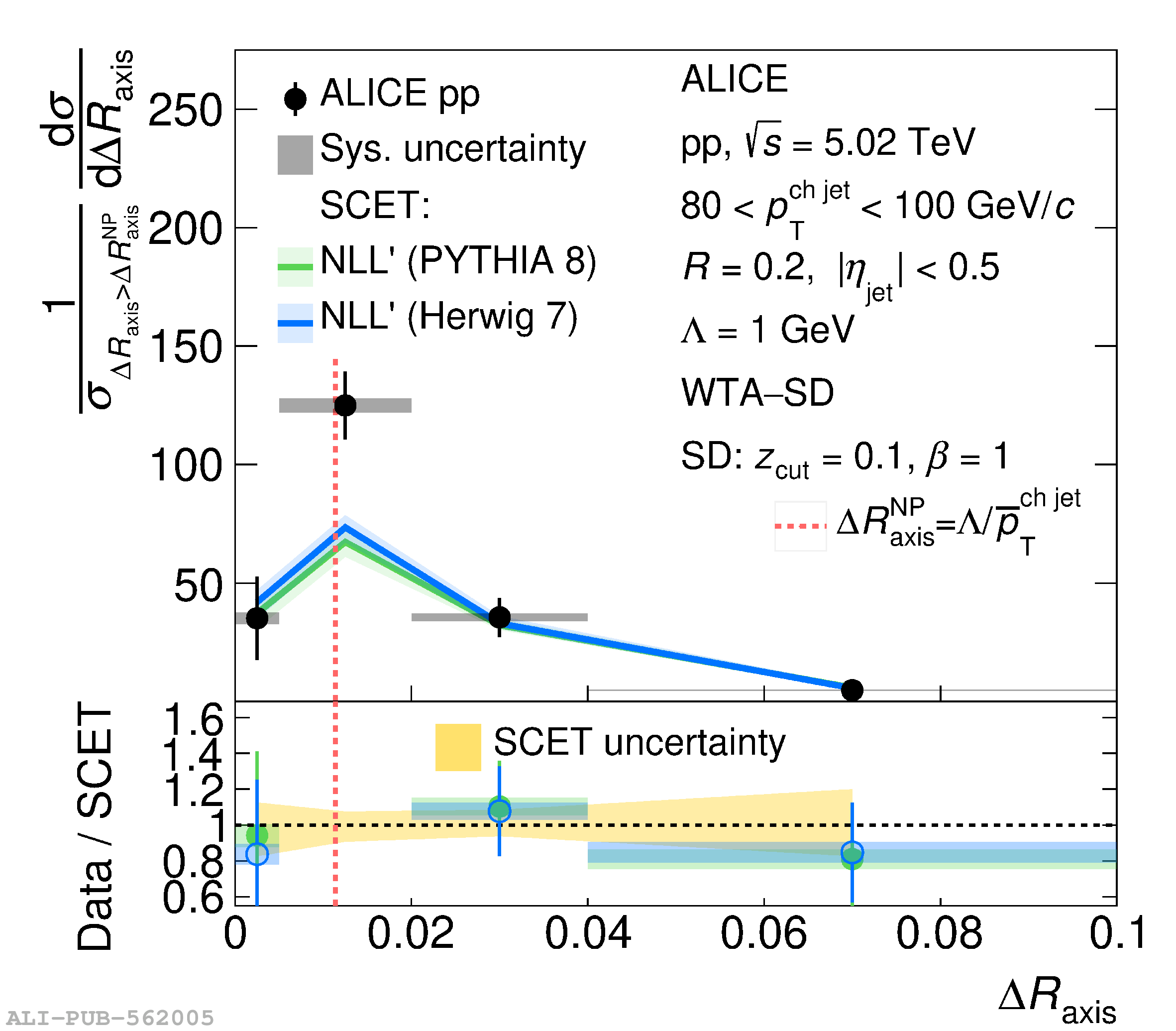
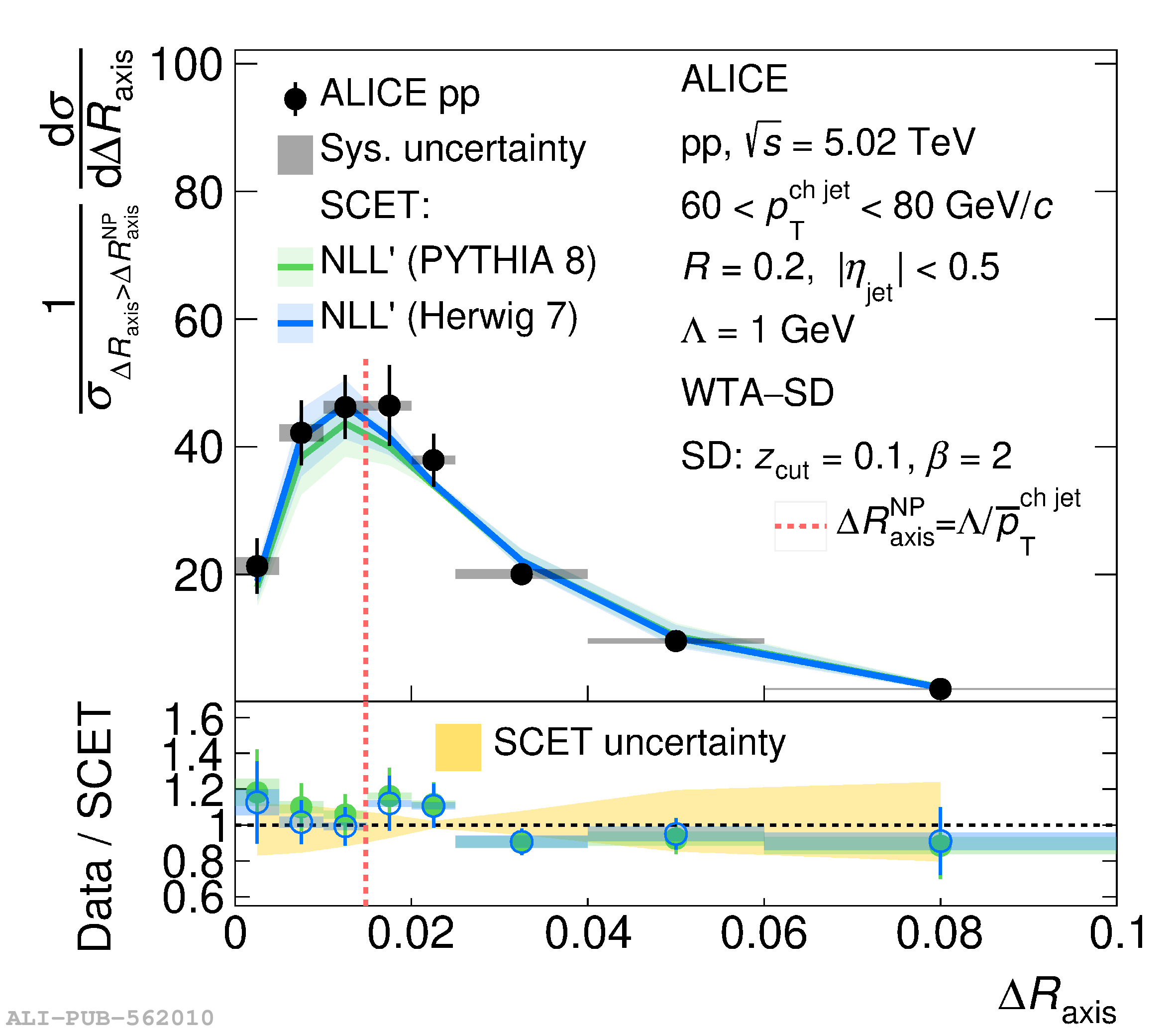
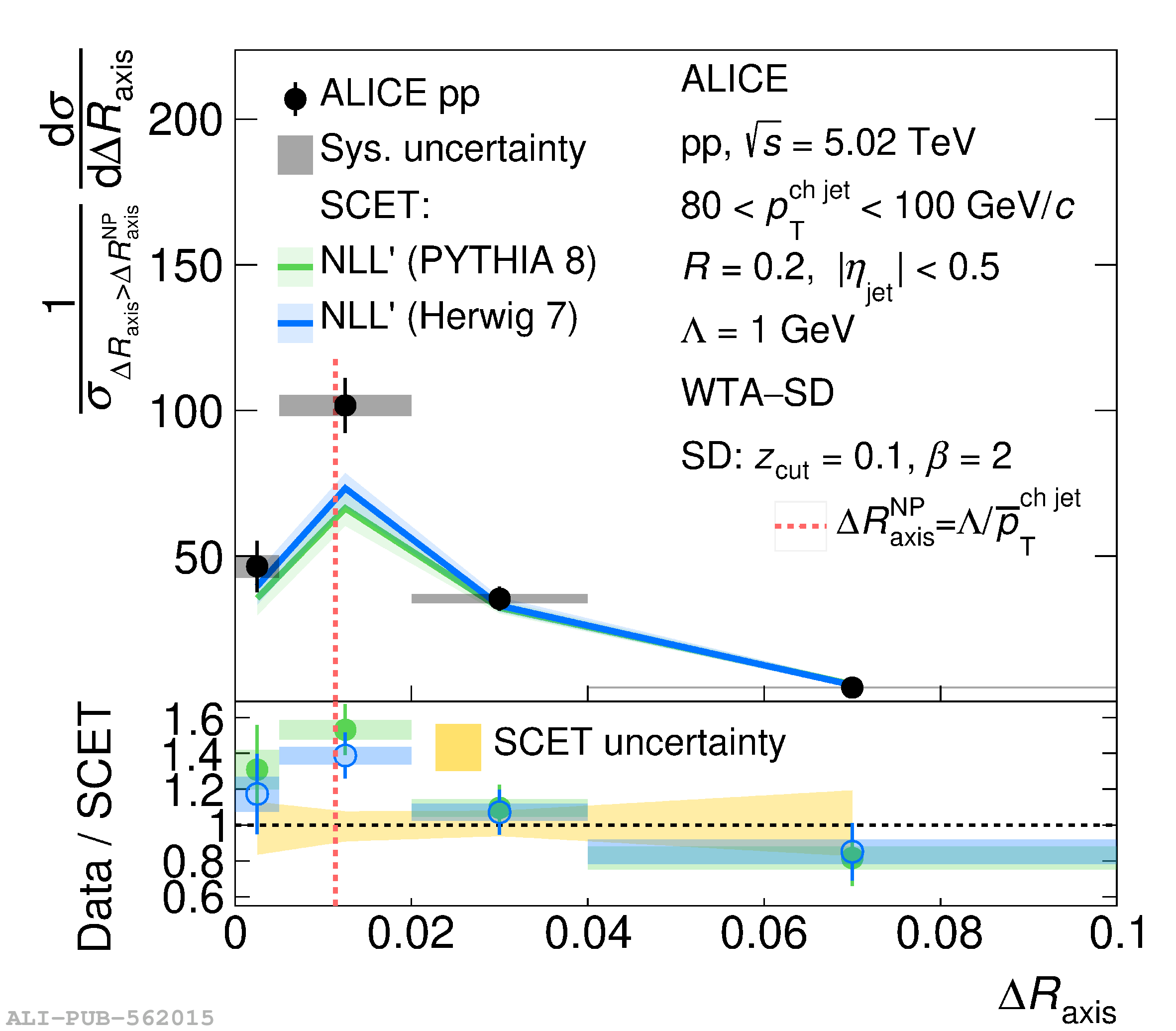
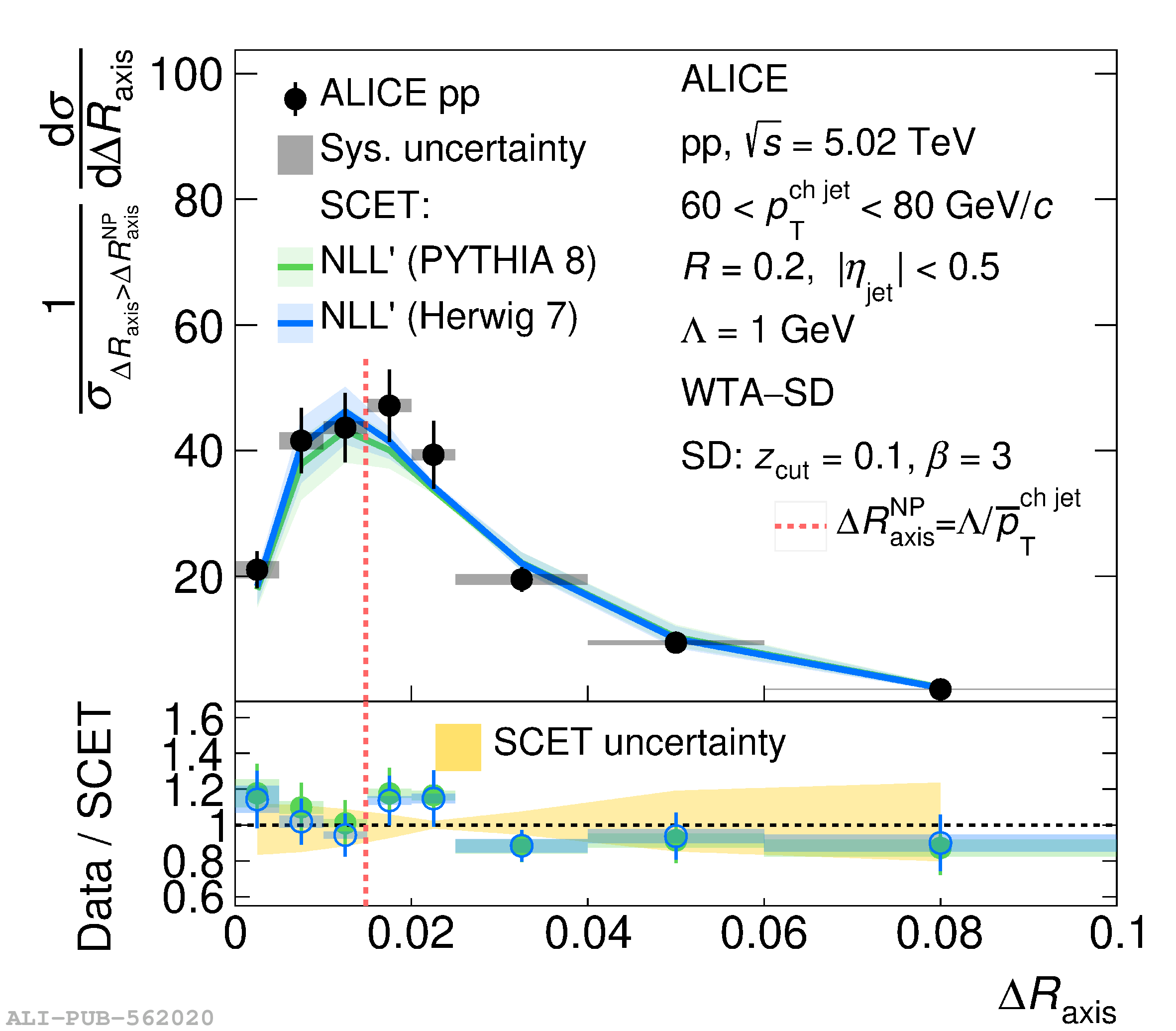
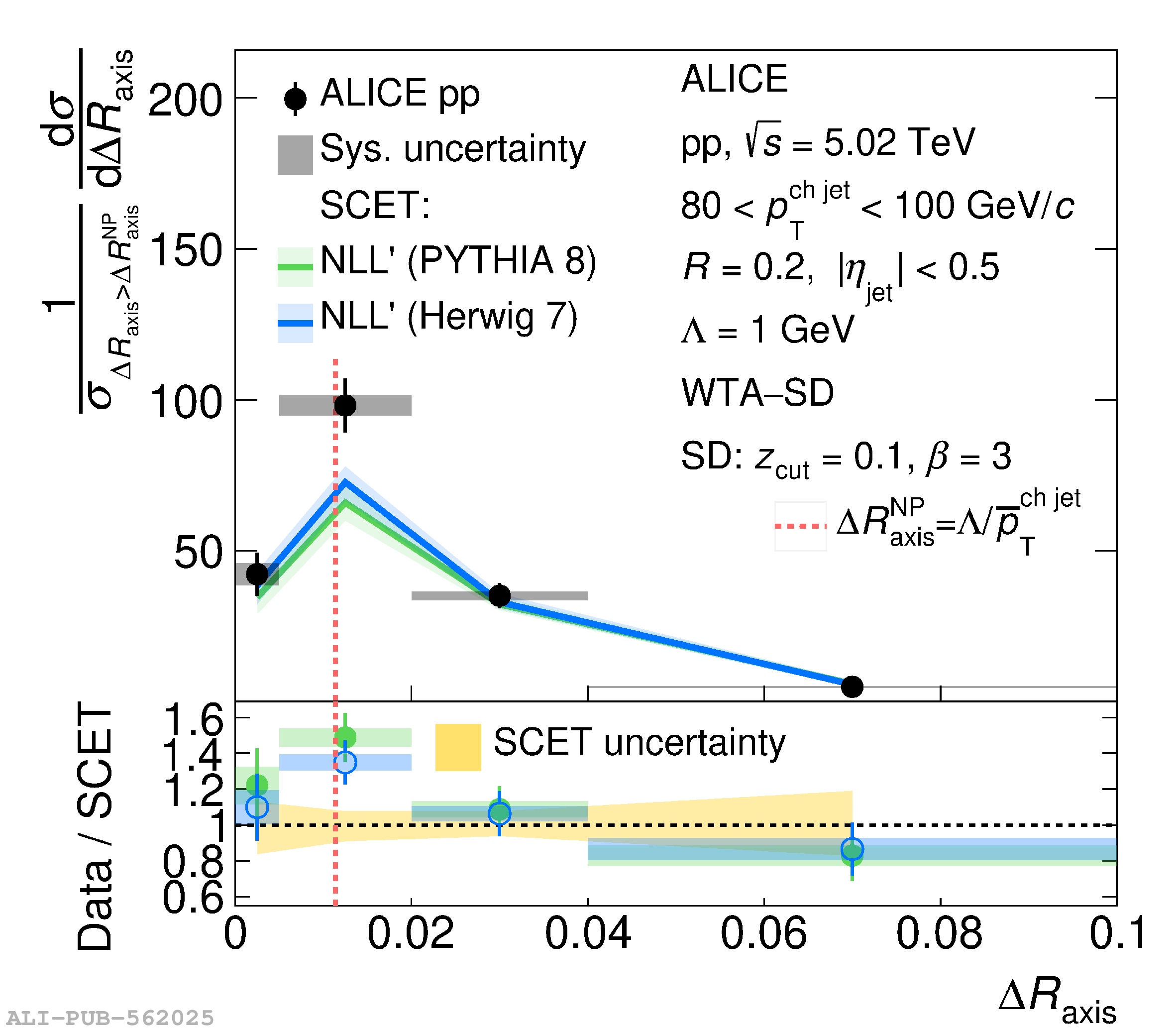
This article reports measurements of the angle between differently defined jet axes in pp collisions at $\sqrt{s} = 5.02$ TeV carried out by the ALICE Collaboration. Charged particles at midrapidity are clustered into jets with resolution parameters $R=0.2$ and 0.4. The jet axis, before and after Soft Drop grooming, is compared to the jet axis from the Winner-Takes-All (WTA) recombination scheme. The angle between these axes, $\Delta R_{\mathrm{axis}}$, probes a wide phase space of the jet formation and evolution, ranging from the initial high-momentum-transfer scattering to the hadronization process. The $\Delta R_{\mathrm{axis}}$ observable is presented for $20 <~ {p_{\mathrm{T}}^{\mathrm{ch\; jet}}}<~ 100$ GeV/$c$, and compared to predictions from the PYTHIA 8 and Herwig 7 event generators. The distributions can also be calculated analytically with a leading hadronization correction related to the non-perturbative component of the Collins$-$Soper$-$Sterman (CSS) evolution kernel. Comparisons to analytical predictions at next-to-leading-logarithmic accuracy with leading hadronization correction implemented from experimental extractions of the CSS kernel in Drell$-$Yan measurements are presented. The analytical predictions describe the measured data within 20% in the perturbative regime, with surprising agreement in the non-perturbative regime as well. These results are compatible with the universality of the CSS kernel in the context of jet substructure.
JHEP 07 (2023) 201
HEP Data
e-Print: arXiv:2211.08928 | PDF | inSPIRE
CERN-EP-2022-242
Figure group