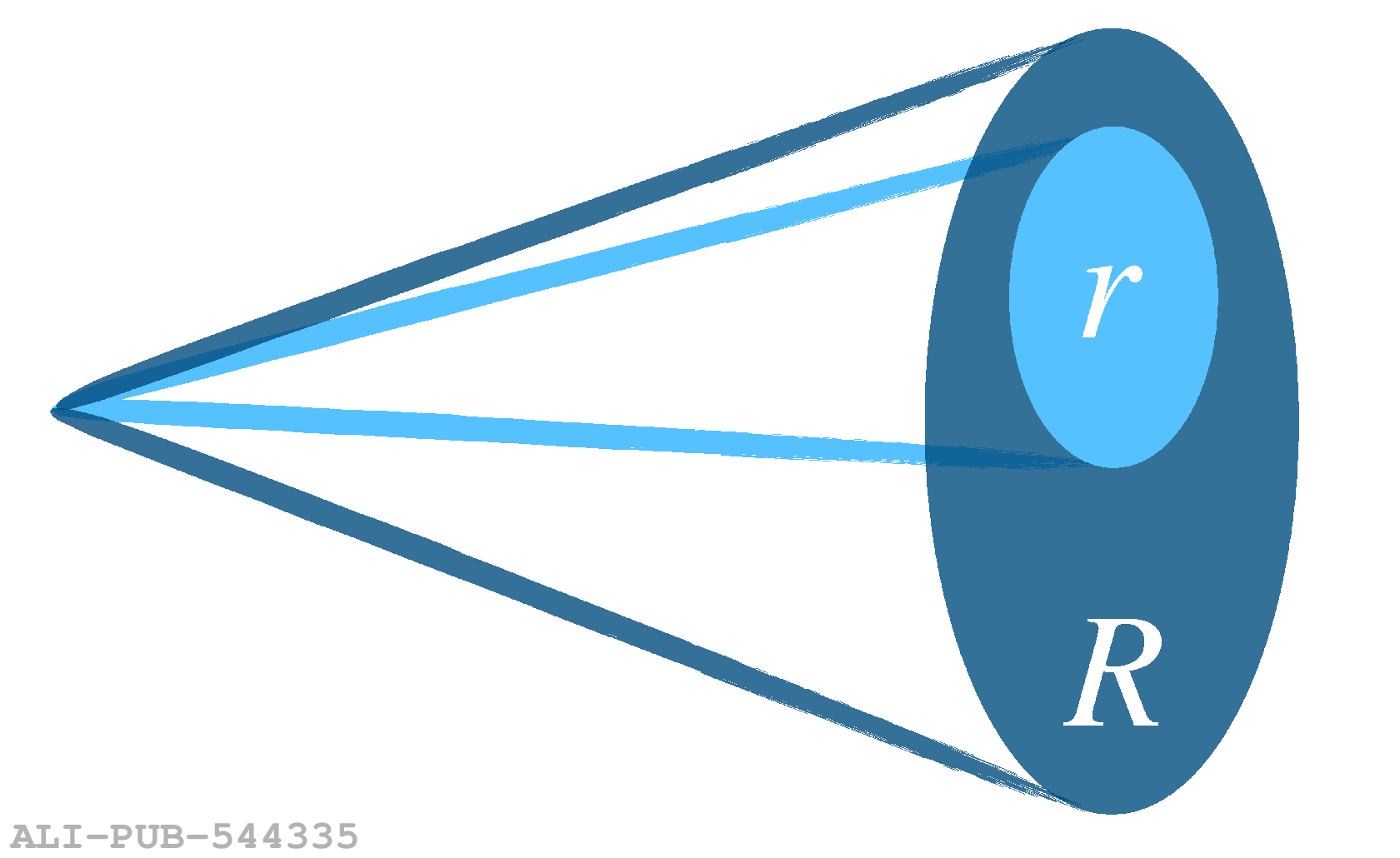
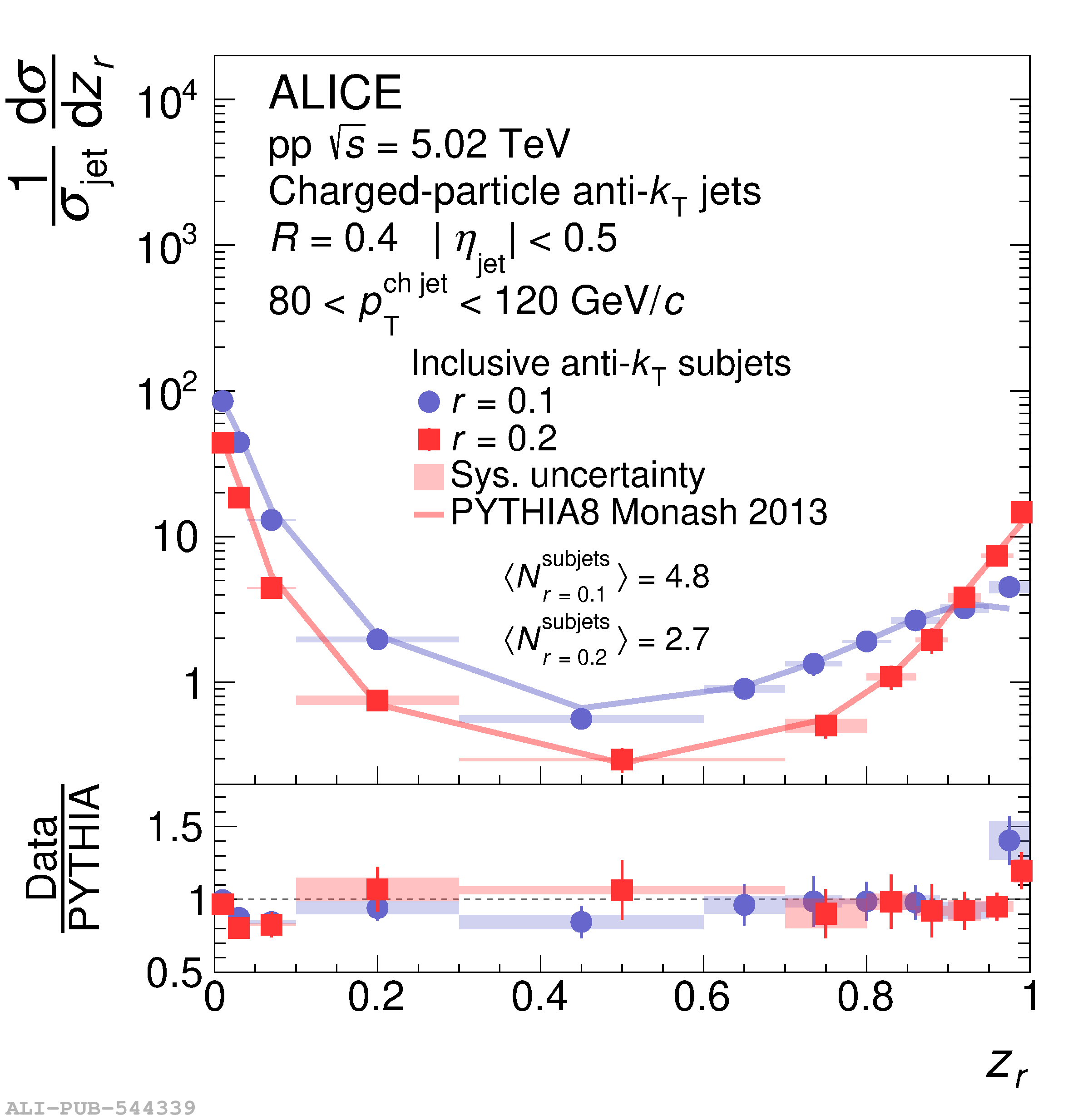
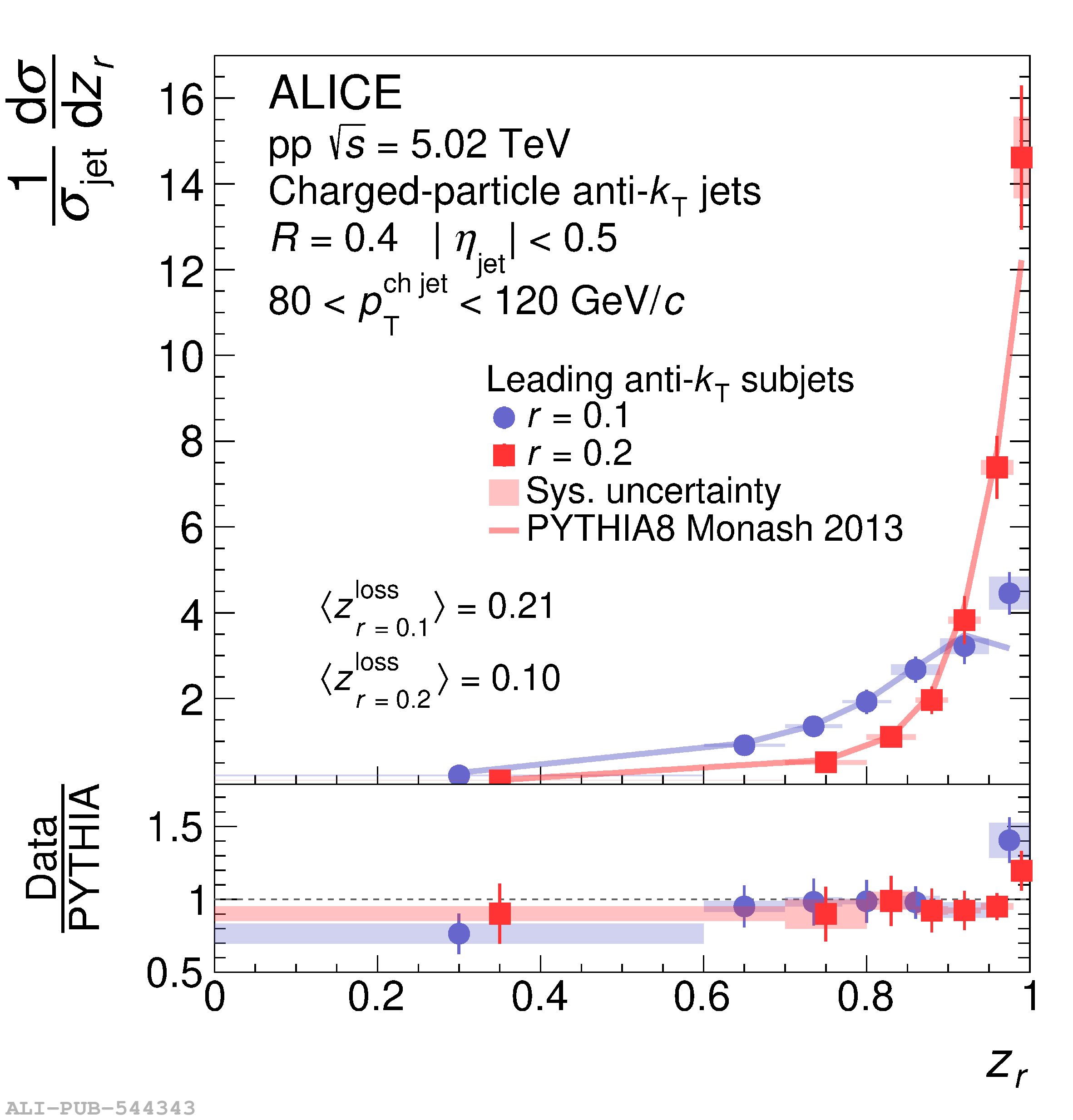
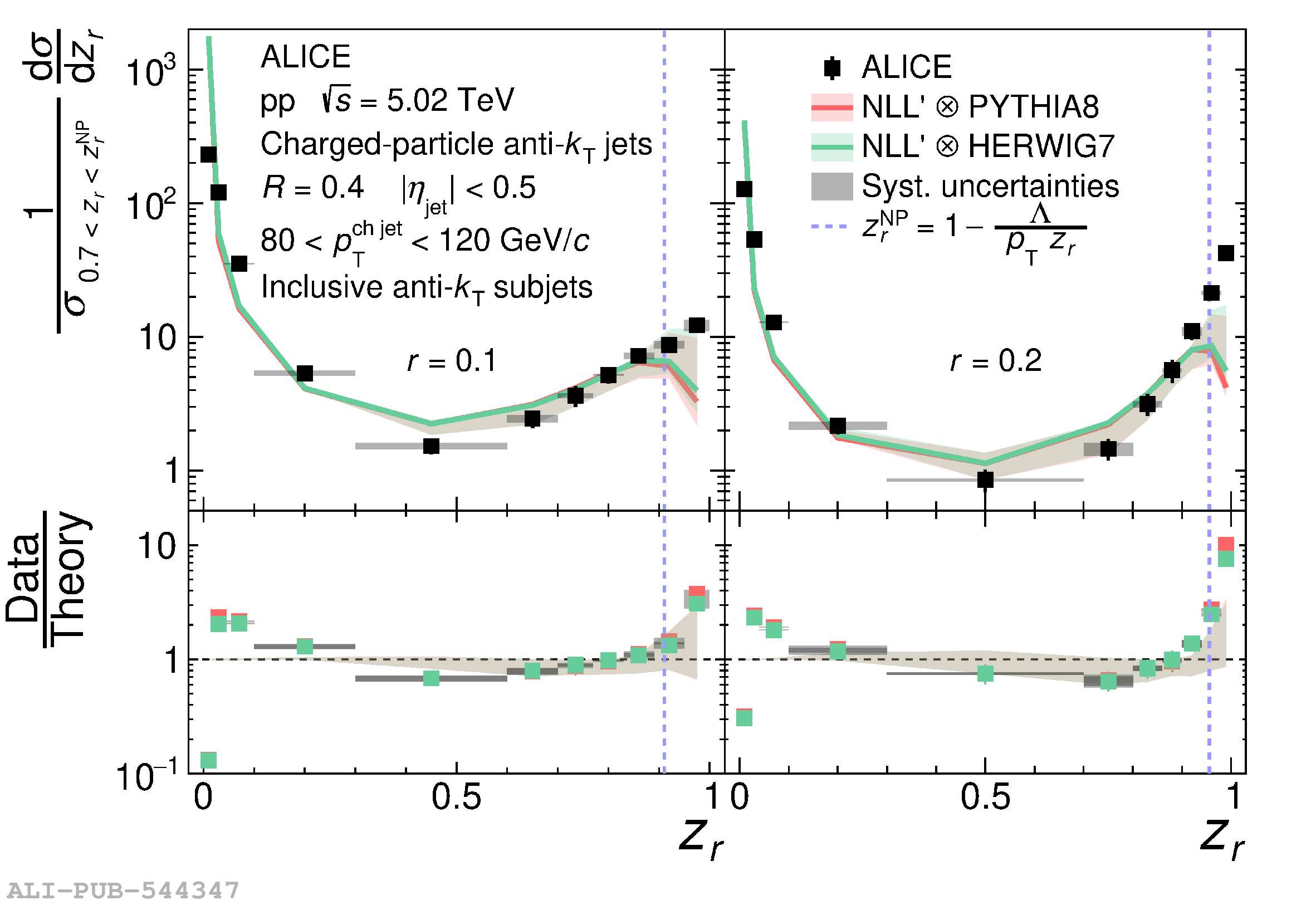
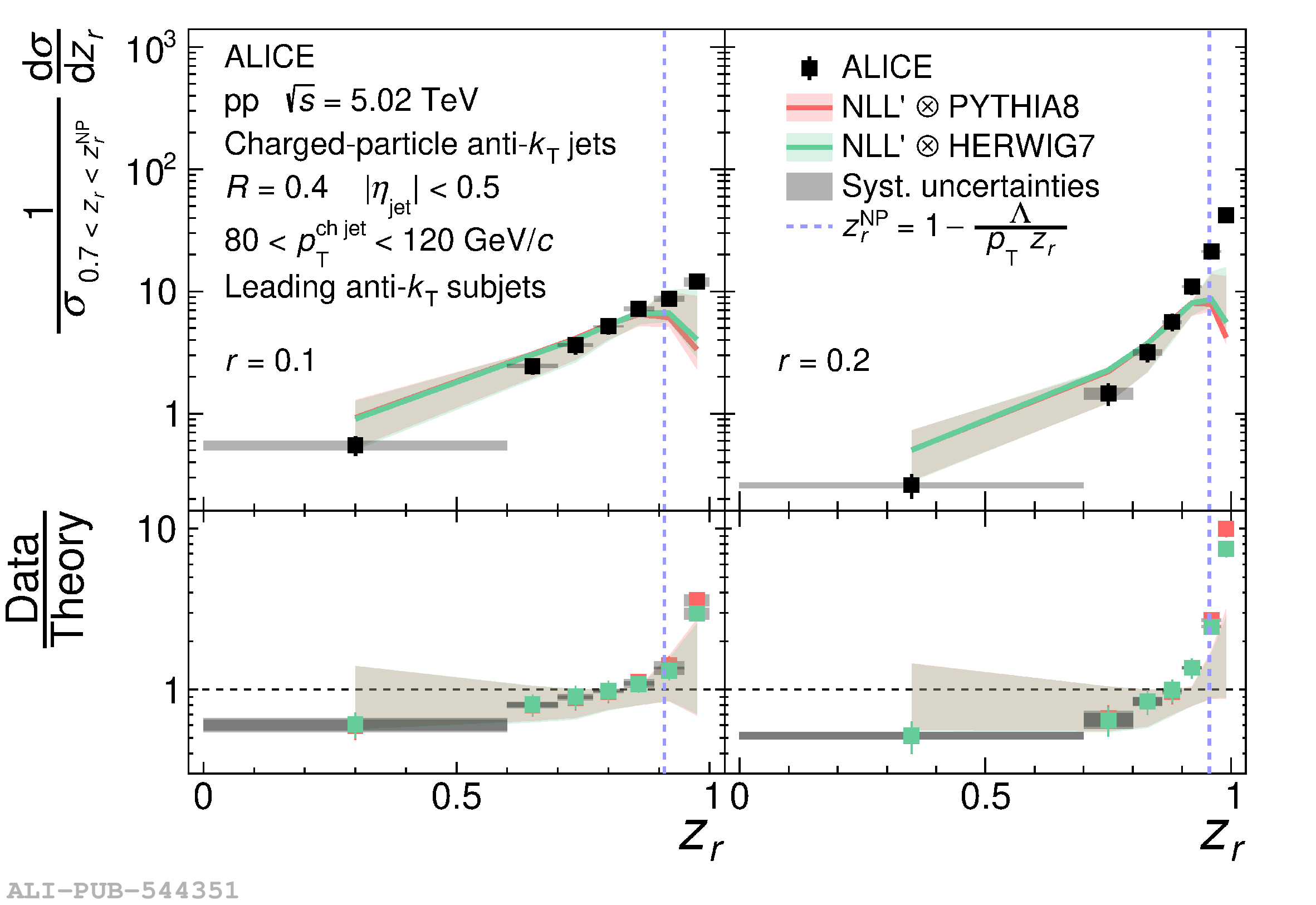
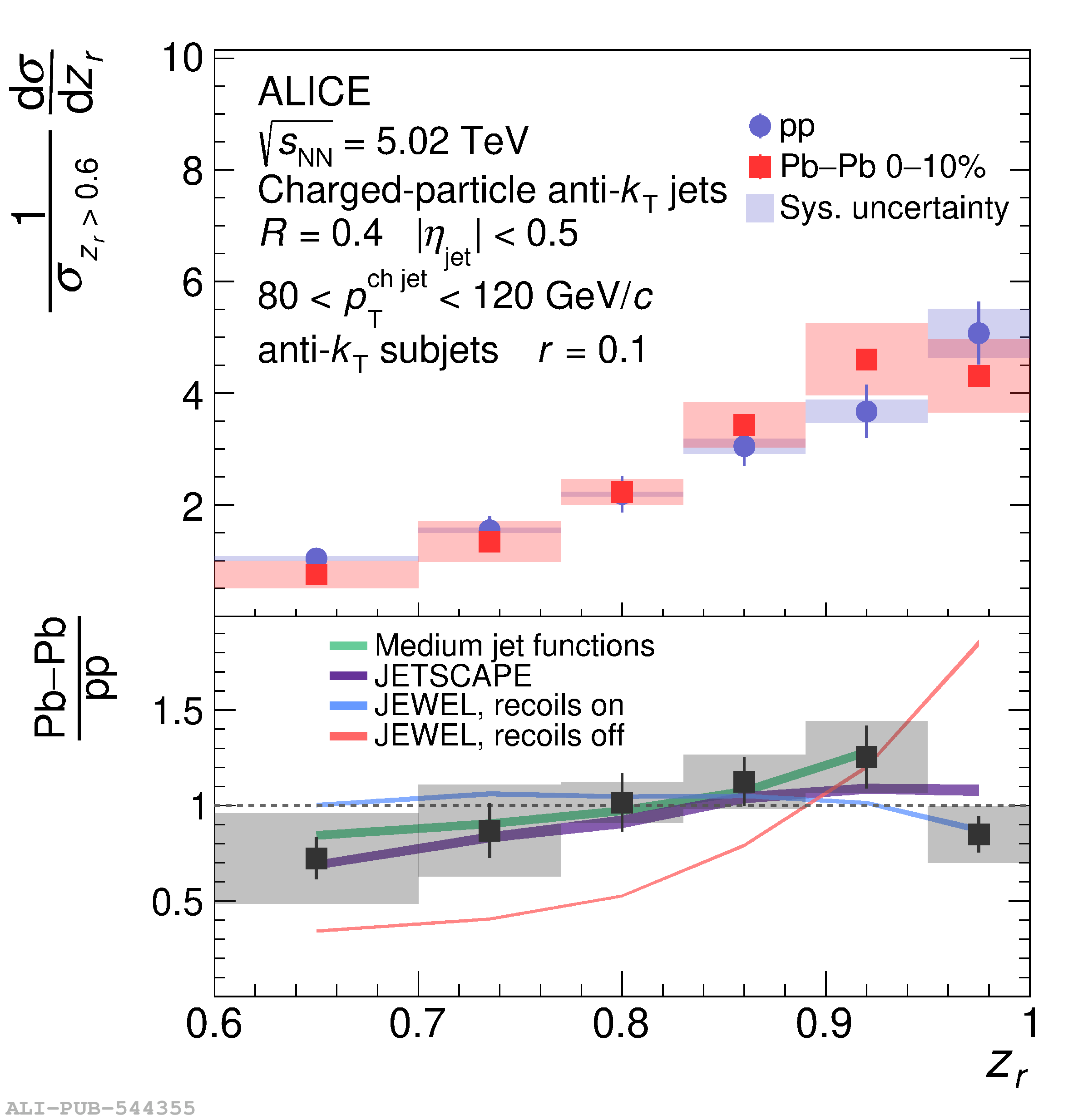
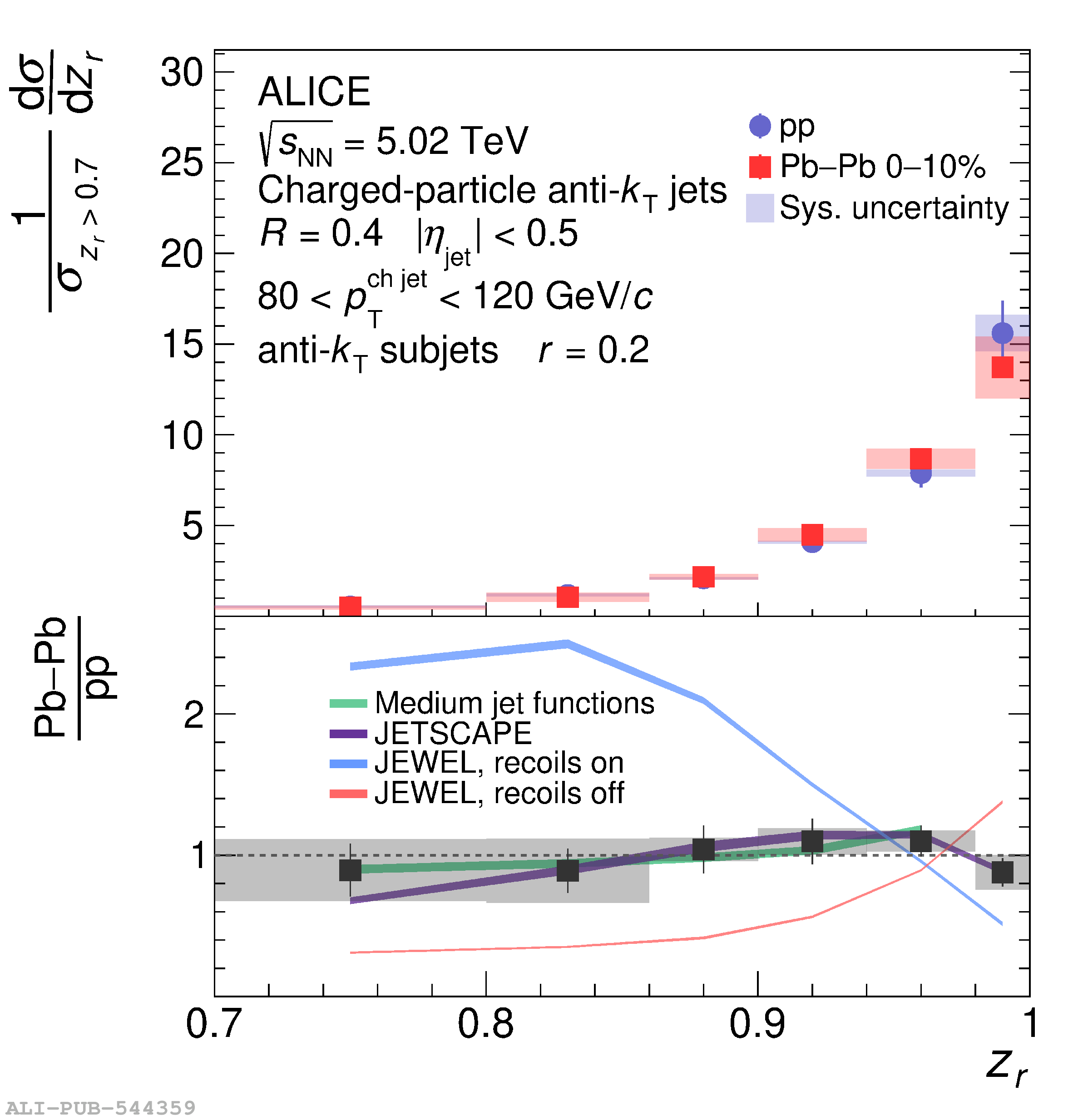
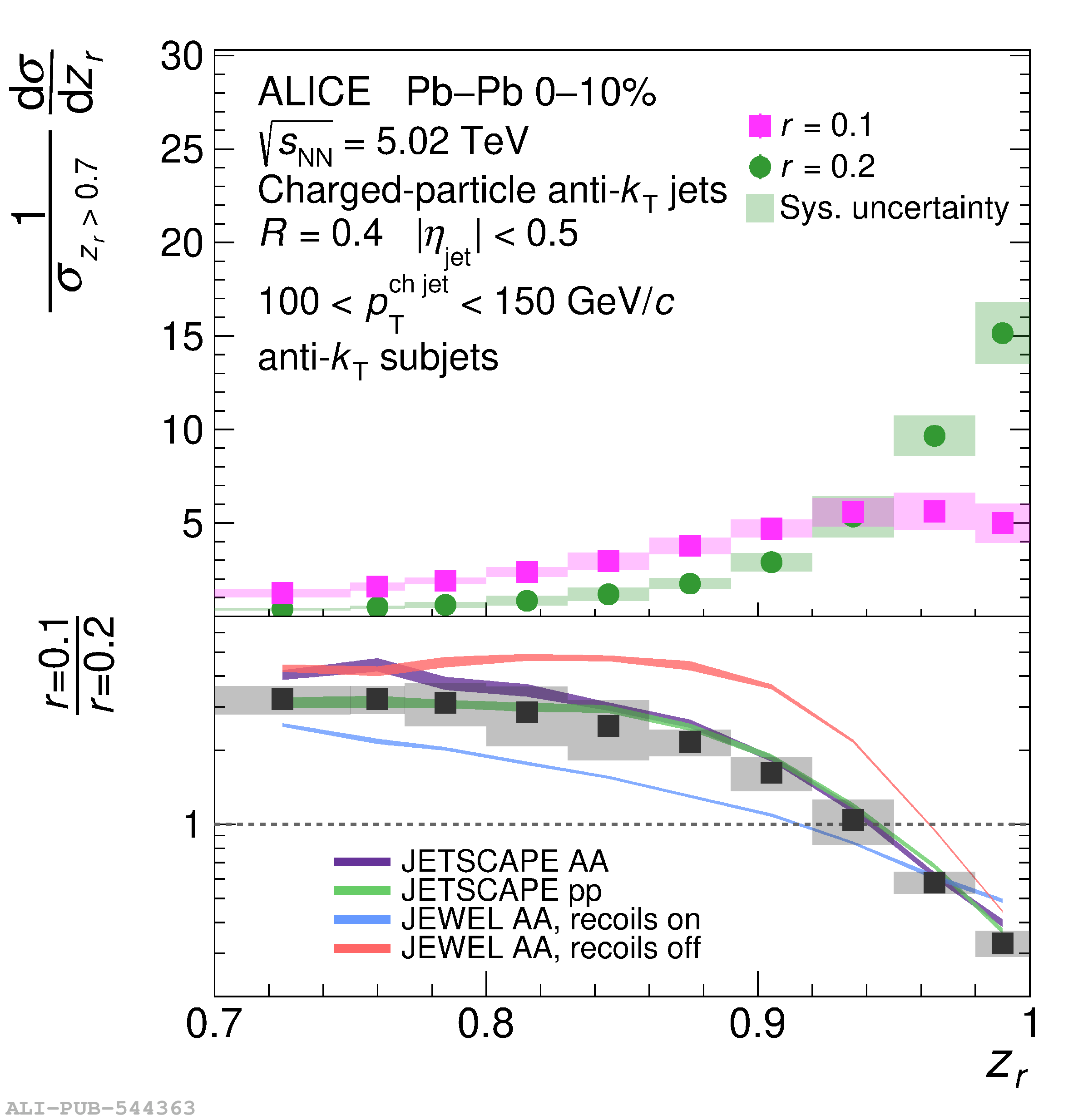
This article presents new measurements of the fragmentation properties of jets in both proton-proton (pp) and heavy-ion collisions with the ALICE experiment at the LHC. We report distributions of the fraction $z_r$ of transverse momentum carried by subjets of radius $r$ within jets of radius $R$. Charged-particle jets are reconstructed at midrapidity using the anti-$k_{\rm{T}}$ algorithm with jet radius $R=0.4$, and subjets are reconstructed by reclustering the jet constituents using the anti-$k_{\rm{T}}$ algorithm with radii $r=0.1$ and $r=0.2$. In pp collisions, we measure both the inclusive and leading subjet distributions. We compare these measurements to perturbative calculations at next-to-leading logarithmic accuracy, which suggest a large impact of threshold resummation and hadronization effects on the $z_r$ distribution. In heavy-ion collisions, we measure the leading subjet distributions, which allow access to a region of harder jet fragmentation than has been probed by previous measurements of jet quenching via hadron fragmentation distributions. The $z_r$ distributions enable extraction of the parton-to-subjet fragmentation function and allow for tests of the universality of jet fragmentation functions in the quark-gluon plasma (QGP). We find no significant modification of $z_r$ distributions in Pb-Pb compared to pp collisions. However, the distributions are also consistent with a hardening trend for $z_r<~0.95$, as predicted by several jet quenching models. As $z_r \rightarrow 1$ our results indicate that any such hardening effects cease, exposing qualitatively new possibilities to disentangle competing jet quenching mechanisms. By comparing our results to theoretical calculations based on an independent extraction of the parton-to-jet fragmentation function, we find consistency with the universality of jet fragmentation and no indication of factorization breaking in the QGP.
JHEP 05 (2023) 245
HEP Data
e-Print: arXiv:2204.10270 | PDF | inSPIRE
CERN-EP-2022-060
Figure group
Figure 4
ALICE measurements of inclusive (top) and leading (bottom) subjet $z_r$ distributions in pp collisions at $\sqrt{s}=5.02$ TeV, compared to NLL$^\prime$ predictions carried out with SCET and corrected for missing neutral-particle energy and multi-parton interaction effects using PYTHIA8 or HERWIG7. The shaded bands denote systematic uncertainty on the NLL$^\prime$ calculations. The distributions are normalized such that the integral of the region defined by $0.7< z_r < z_r^{\rm NP}$ is unity,where $z_r^{\rm NP}$ is denoted by the dashed vertical blue lines. The non-perturbative scale in Eq. 4 is taken to be $\Lambda$ =1 GeV/$c$ In determining the normalization, bins that overlap with the dashed blue line are considered to be in the non-perturbative (right) region. |   |
