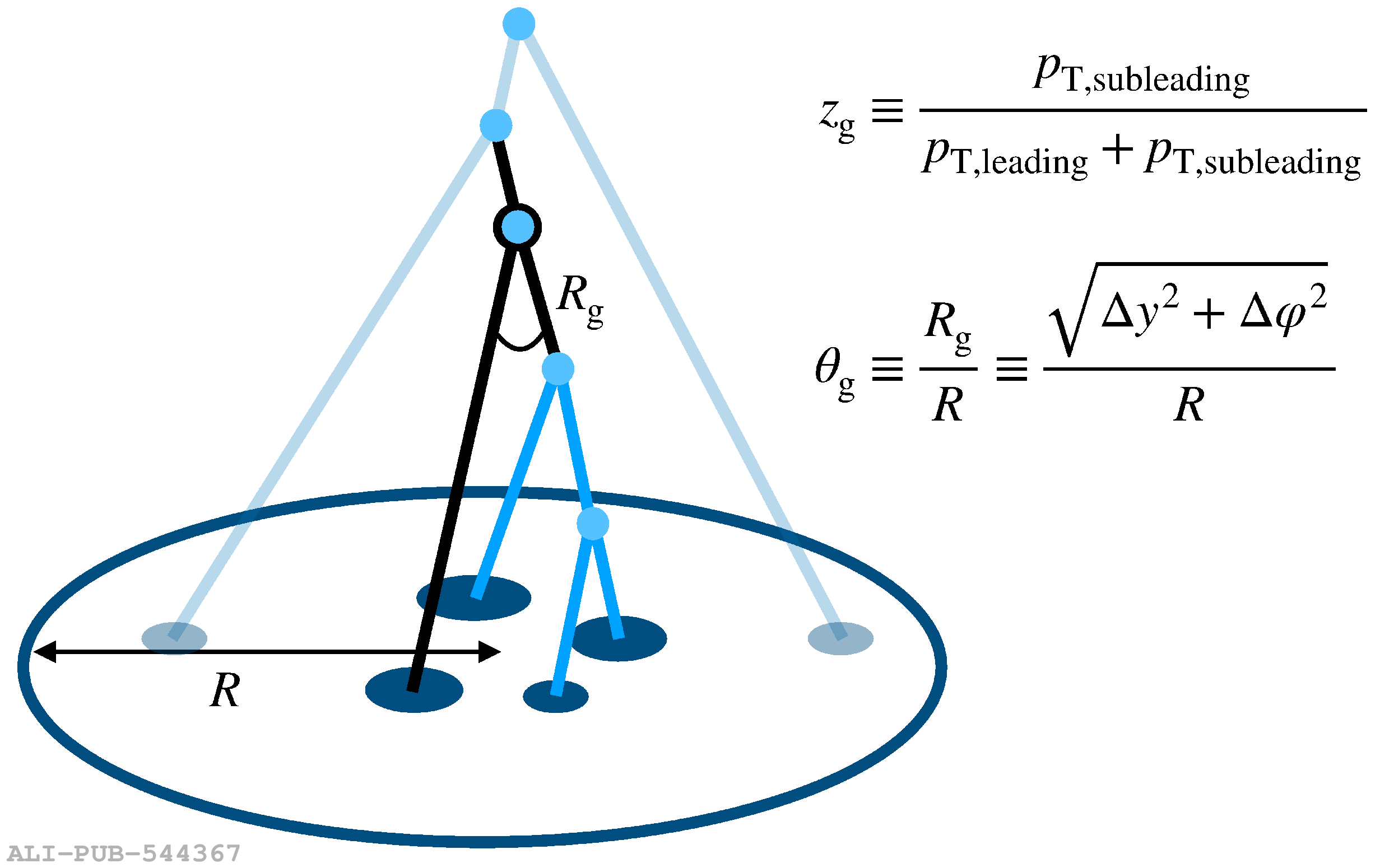
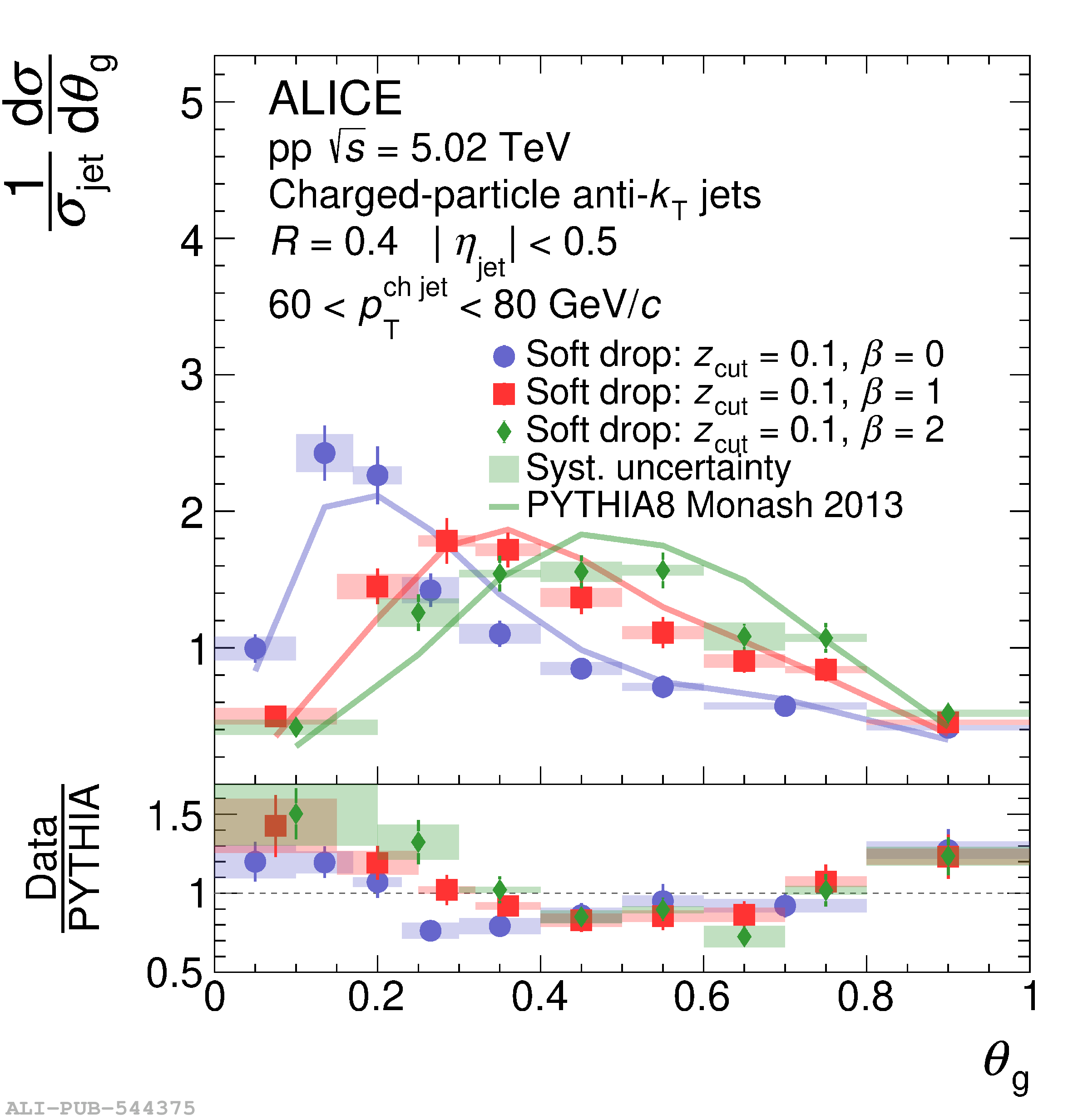
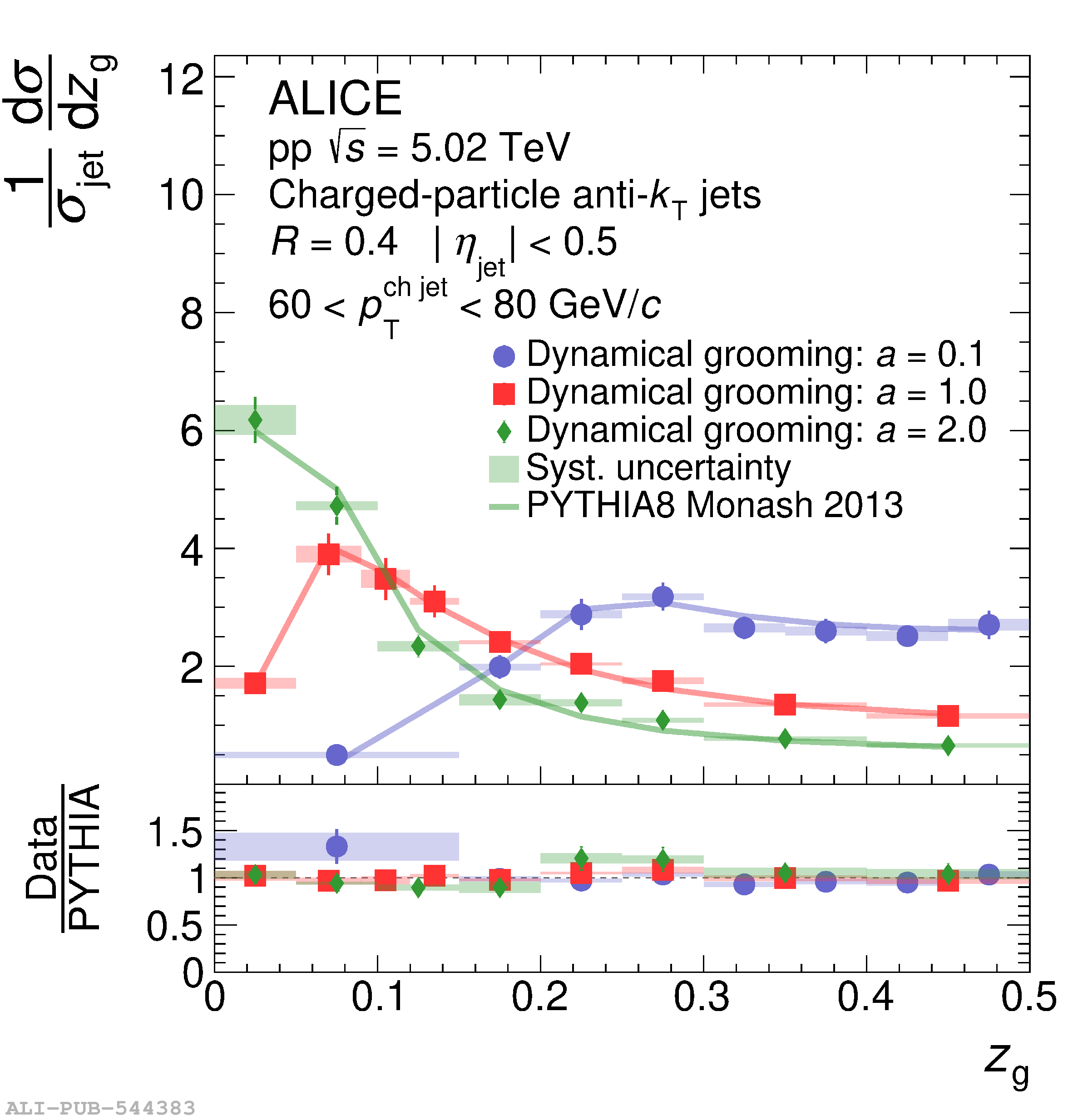
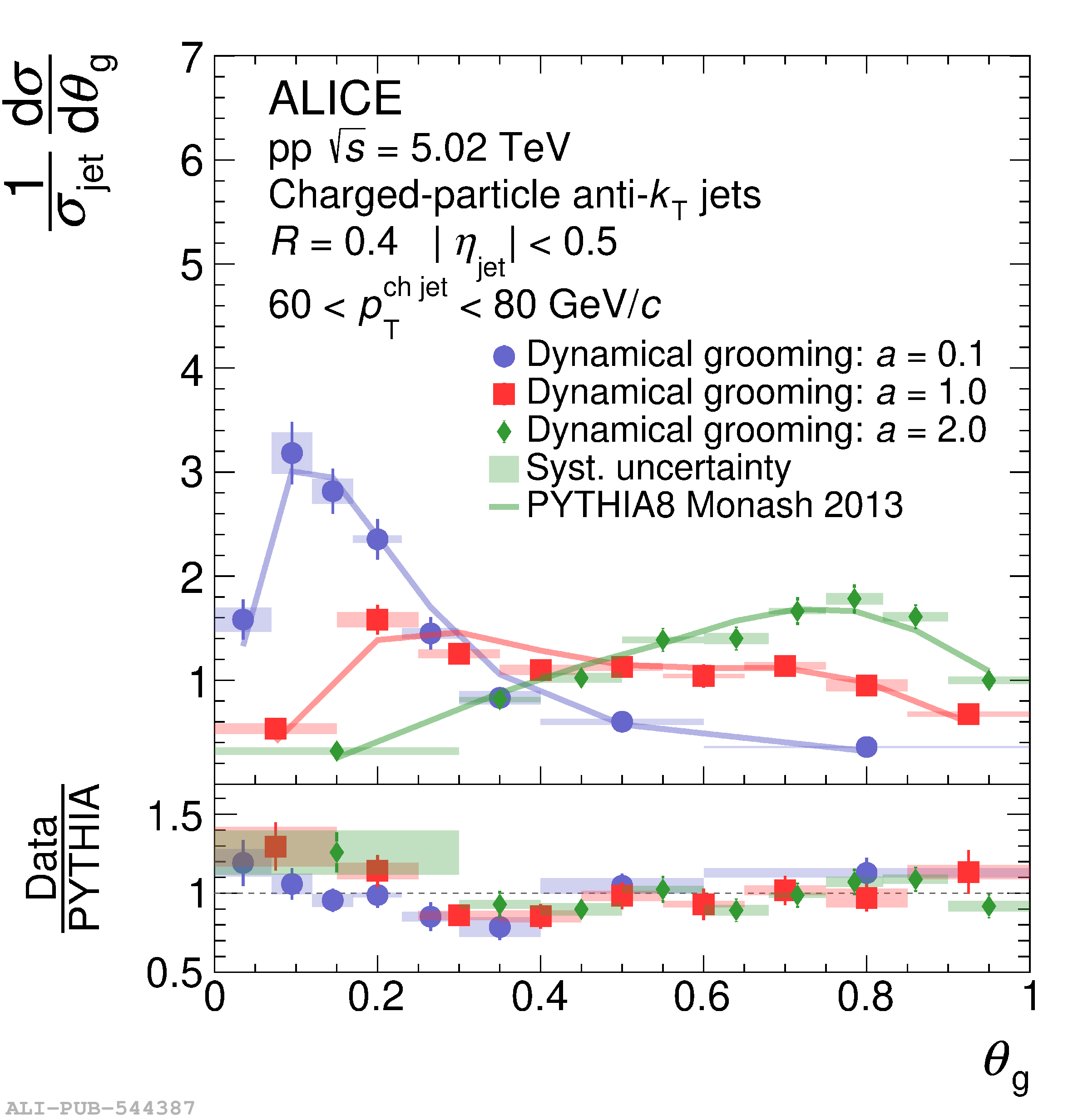
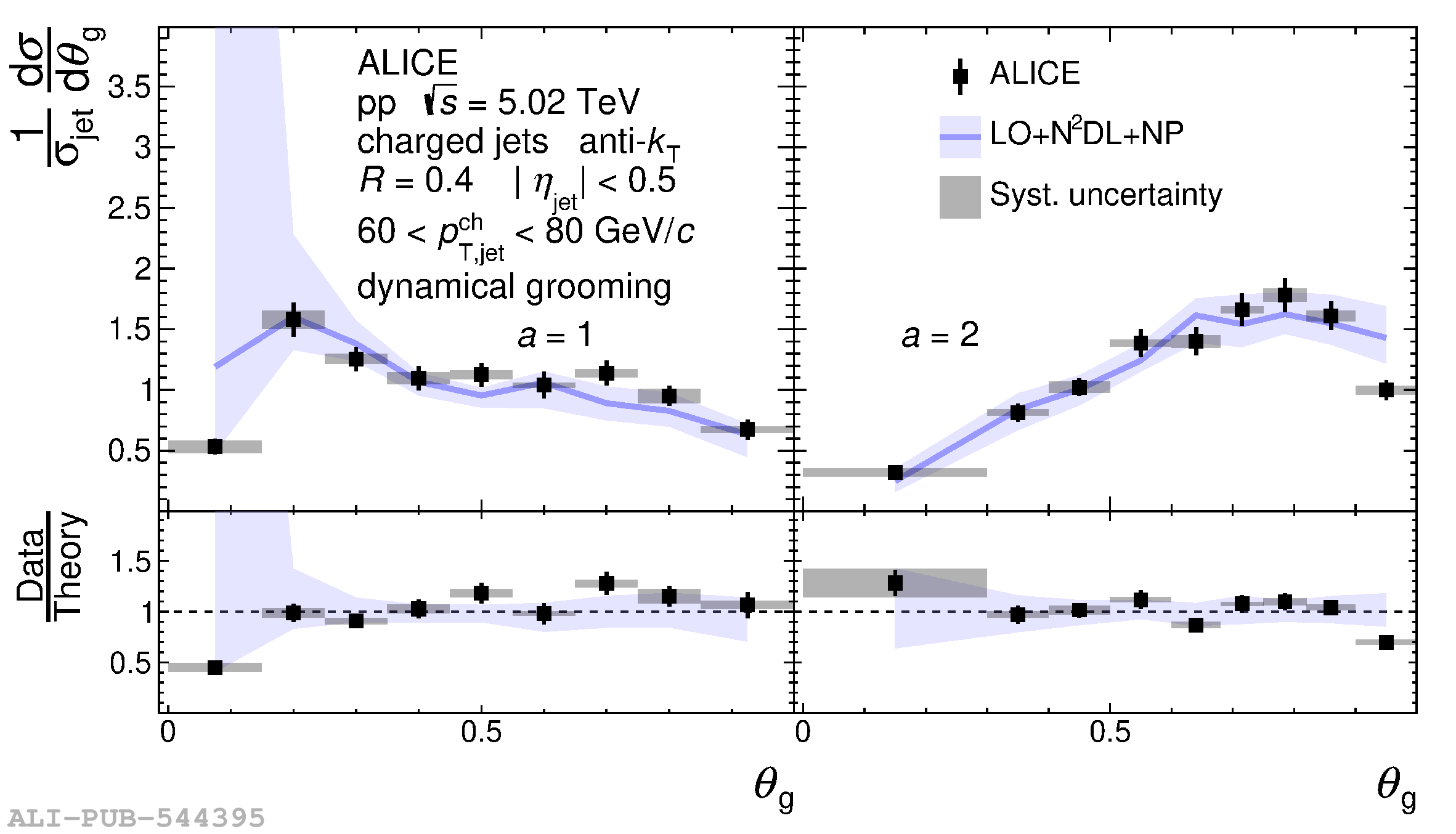
This article presents measurements of the groomed jet radius and momentum splitting fraction in pp collisions at $\sqrt{s}=5.02$ TeV with the ALICE detector at the Large Hadron Collider. Inclusive charged-particle jets are reconstructed at midrapidity using the anti-$k_{\rm{T}}$ algorithm for transverse momentum $60<~ p_{\mathrm{T}}^{\rm{ch\; jet}}<~80$ GeV/$c$. We report results using two different grooming algorithms: soft drop and, for the first time, dynamical grooming. For each grooming algorithm, a variety of grooming settings are used in order to explore the impact of collinear radiation on these jet substructure observables. These results are compared to perturbative calculations that include resummation of large logarithms at all orders in the strong coupling constant. We find good agreement of the theoretical predictions with the data for all grooming settings considered.
JHEP 05 (2023) 244
HEP Data
e-Print: arXiv:2204.10246 | PDF | inSPIRE
CERN-EP-2022-056
Figure group
Figure 4
ALICE measurements of $\theta_{\rm g}$ distributions in pp collisions at $\sqrt{s}=5.02$ TeV withsoft drop, compared with NLL$^\prime$ predictions carried out with SCET and corrected for non-perturbative effects using either PYTHIA8 or Herwig7. The distributions are normalized such that the integral of the perturbative region defined by $\theta_{\rm g} > \theta_{\rm g}^{\rm NP}$ (to the right of the dashed vertical blue line) is unity The non-perturbative scale in Eq. 7 is taken to be $\Lambda$=1 GeV/$c$ In determining the normalization, intervals that overlap with the dashed blue line are considered to be in the non-perturbative (left) region. |  |
