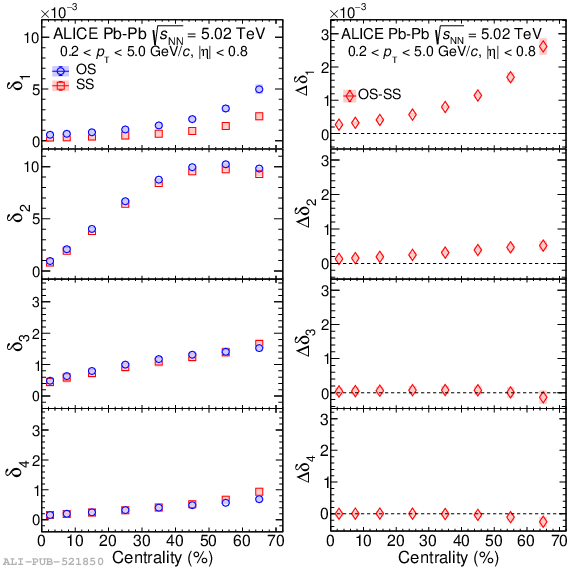
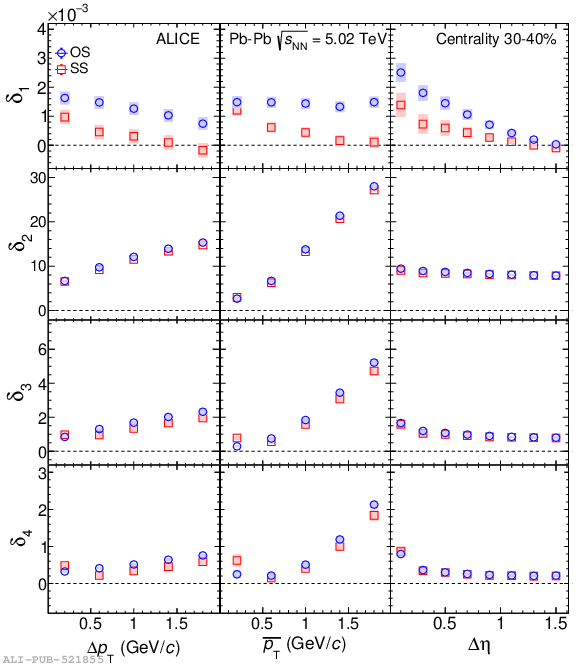
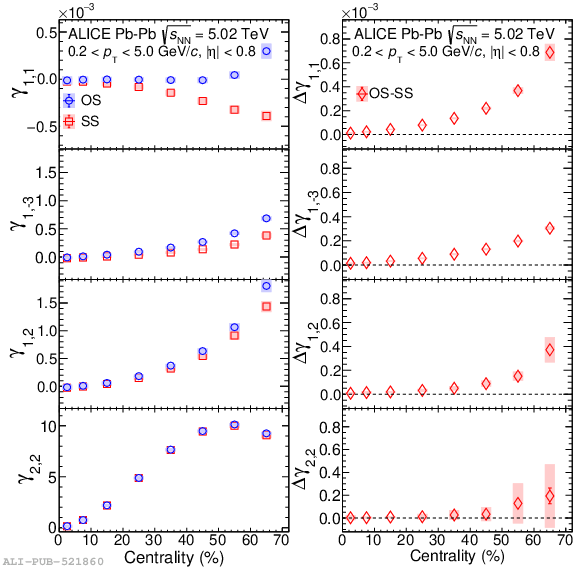
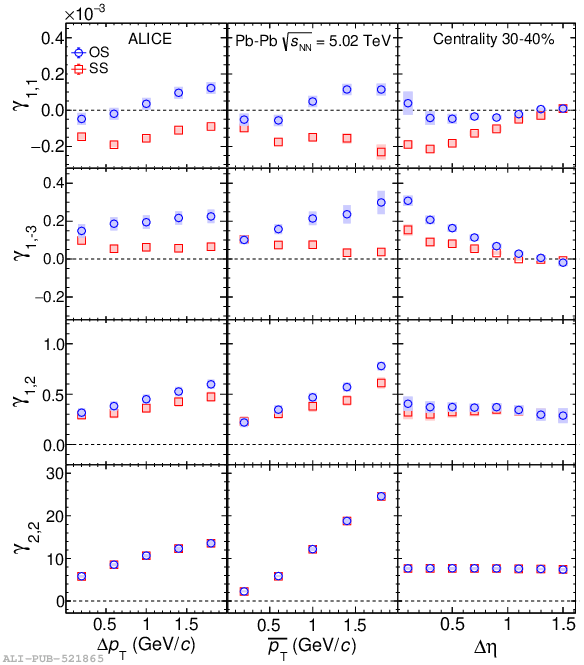
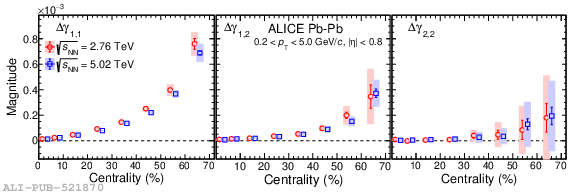
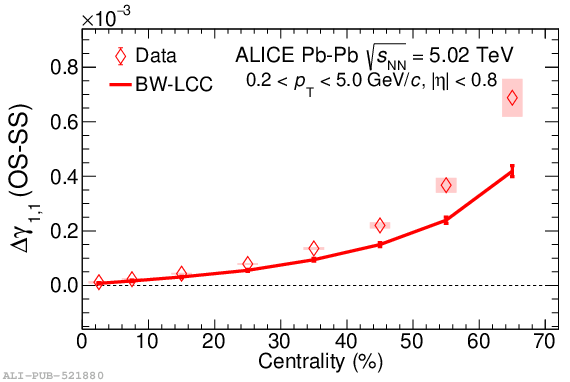
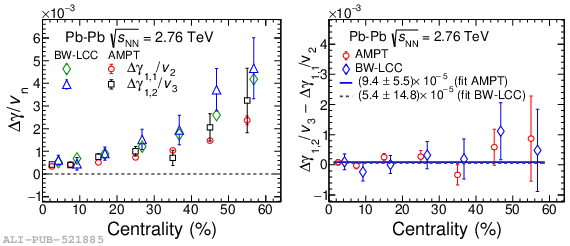
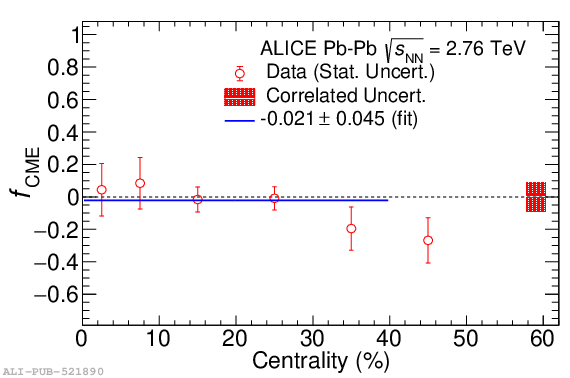
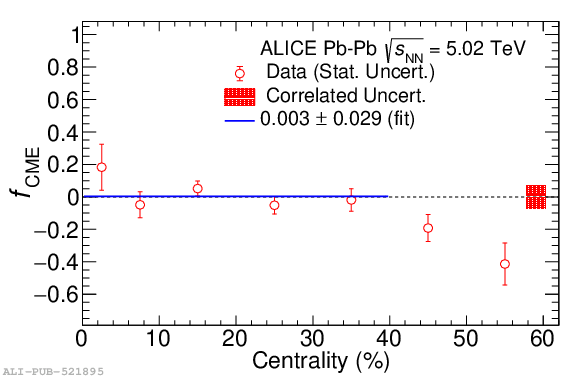
Systematic studies of charge-dependent two- and three-particle correlations in Pb-Pb collisions at $\sqrt{\it{s}_\mathrm{{NN}}} = $ 2.76 and 5.02 TeV used to probe the Chiral Magnetic Effect (CME) are presented. These measurements are performed for charged particles in the pseudorapidity ($\eta$) and transverse momentum ($p_{\rm{T}}$) ranges $\left|\eta \right| <~ 0.8$ and $0.2 <~ p_{\mathrm{T}} <~ 5$ GeV/$c$. A significant charge-dependent signal that becomes more pronounced for peripheral collisions is reported for the CME-sensitive correlators $\gamma_{1,1} = \langle \cos (\varphi_{\alpha} +\varphi_{\beta} - 2\Psi_{2}) \rangle$ and $\gamma_{1,-3} = \langle \cos (\varphi_{\alpha} -3\varphi_{\beta} + 2\Psi_{2}) \rangle$. The results are used to estimate the contribution of background effects, associated with local charge conservation coupled to anisotropic flow modulations, to measurements of the CME. A blast-wave parametrisation that incorporates local charge conservation tuned to reproduce the centrality dependent background effects is not able to fully describe the measured $\gamma_{1,1}$. Finally, the charge and centrality dependence of mixed-harmonics three-particle correlations, of the form $\gamma_{1,2} = \langle \cos (\varphi_{\alpha} +2\varphi_{\beta} - 3\Psi_{3}) \rangle$, which are insensitive to the CME signal, verify again that background contributions dominate the measurement of $\gamma_{1,1}$.
J. High Energ. Phys. 2020, 160 (2020)
HEP Data
e-Print: arXiv:2005.14640 | PDF | inSPIRE
CERN-EP-2020-098
Figure group