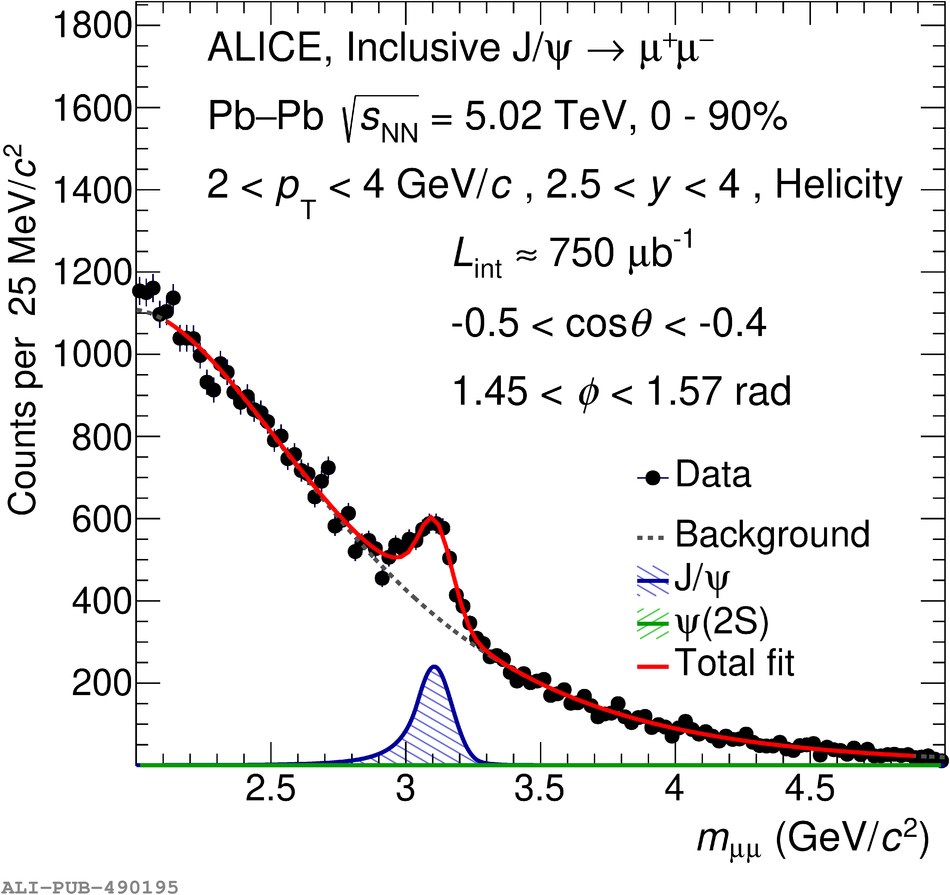
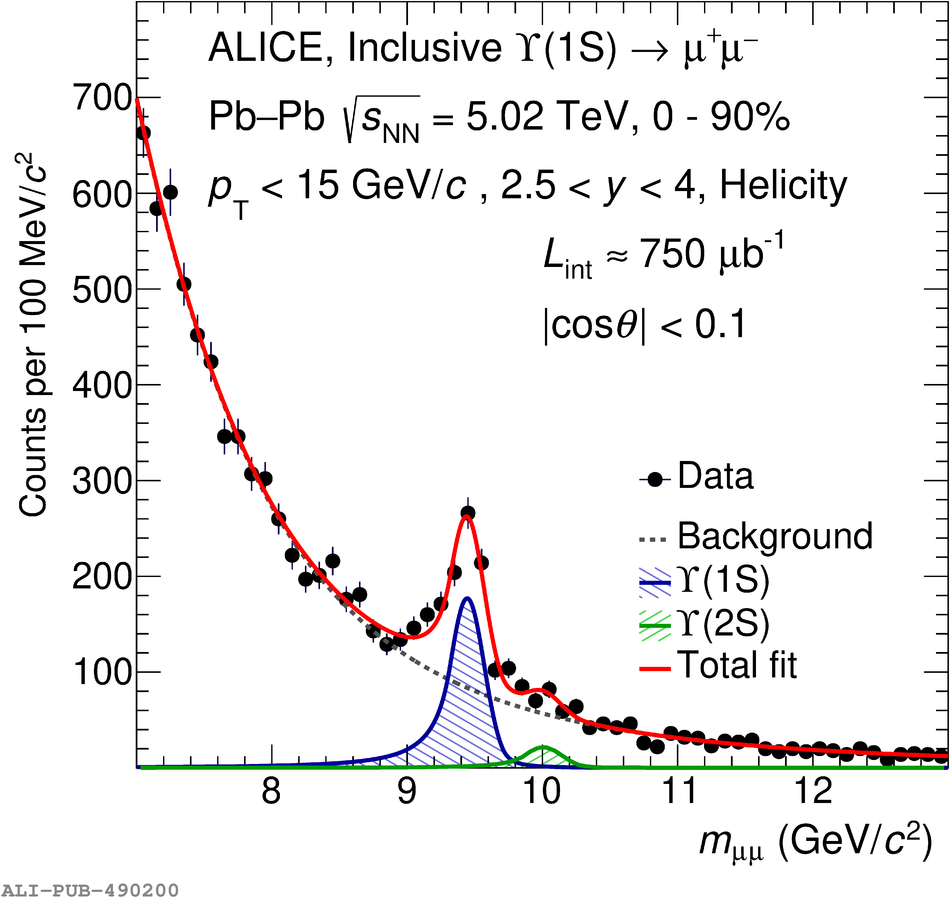
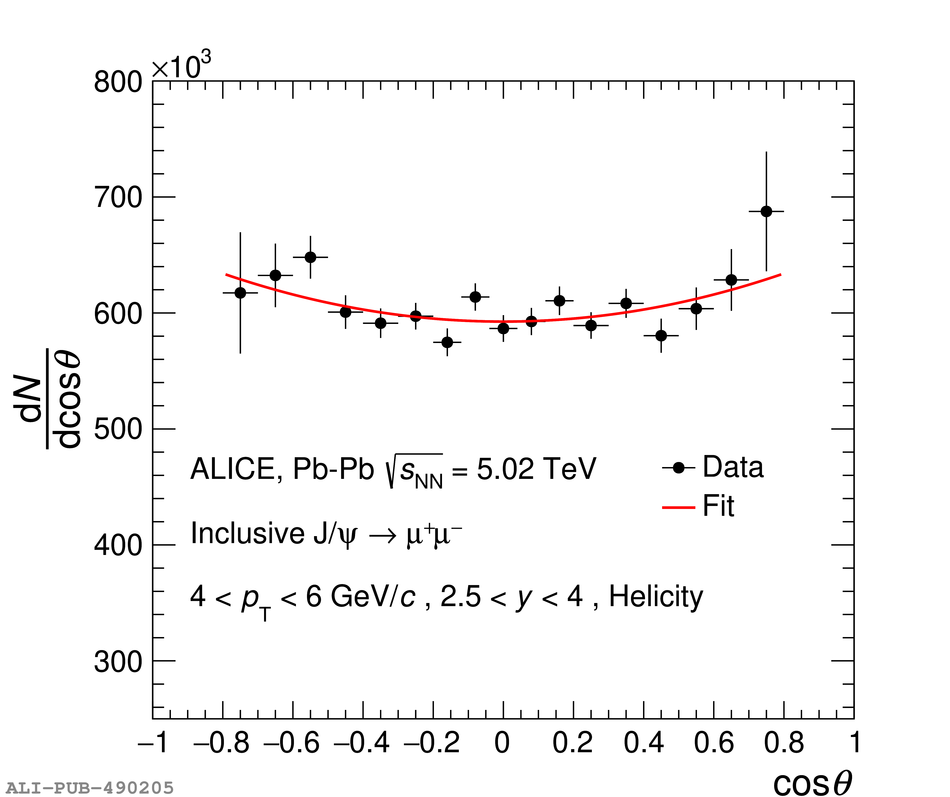
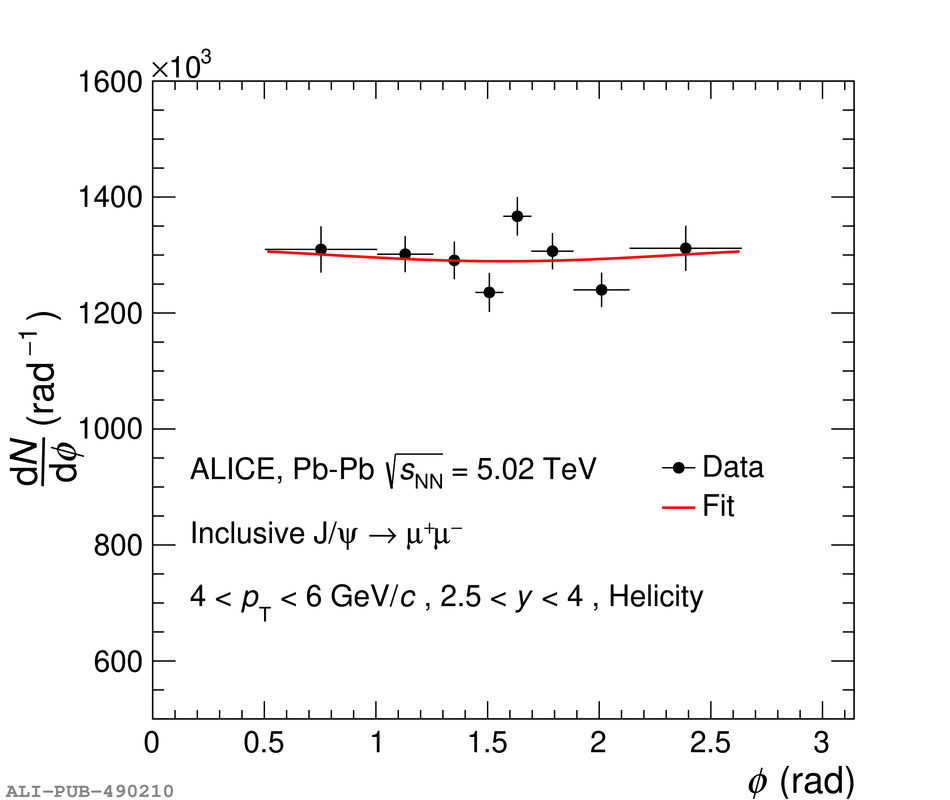
The polarization of inclusive J/$\psi$ and $\Upsilon(1{\rm S})$ produced in Pb-Pb collisions at $\sqrt{s_{\rm{NN}}}=5.02$ TeV at the LHC is measured with the ALICE detector. The study is carried out by reconstructing the quarkonium through its decay to muon pairs in the rapidity region $2.5<~y<~4$ and measuring the polar and azimuthal angular distributions of the muons. The polarization parameters $\lambda_{\theta}$, $\lambda_{\phi}$ and $\lambda_{\theta\phi}$ are measured in the helicity and Collins-Soper reference frames, in the transverse momentum interval $2<~p_{\rm T}<~10$ GeV/$c$ and $p_{\rm T}<~15$ GeV/$c$ for the J/$\psi$ and $\Upsilon(1{\rm S})$, respectively. The polarization parameters for the J/$\psi$ are found to be compatible with zero, within a maximum of about two standard deviations at low $p_{\rm T}$, for both reference frames and over the whole $p_{\rm T}$ range. The values are compared with the corresponding results obtained for pp collisions at $\sqrt{s}=7$ and 8 TeV in a similar kinematic region by the ALICE and LHCb experiments. Although with much larger uncertainties, the polarization parameters for $\Upsilon(1{\rm S})$ production in Pb-Pb collisions are also consistent with zero.
Phys. Lett. B 815 (2021) 136146
HEP Data
e-Print: arXiv:2005.11128 | PDF | inSPIRE
CERN-EP-2020-092