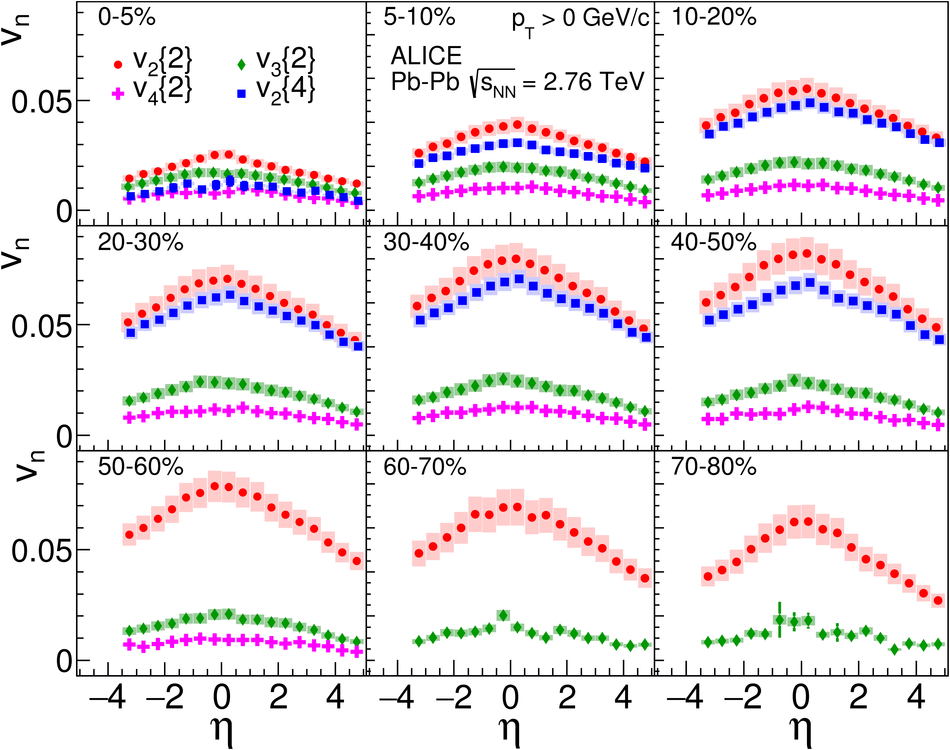
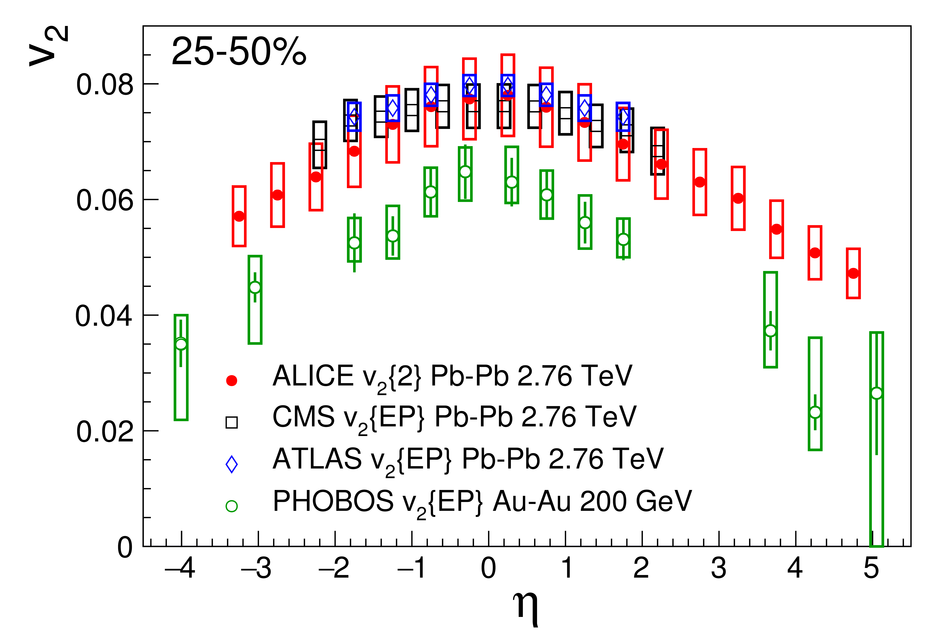
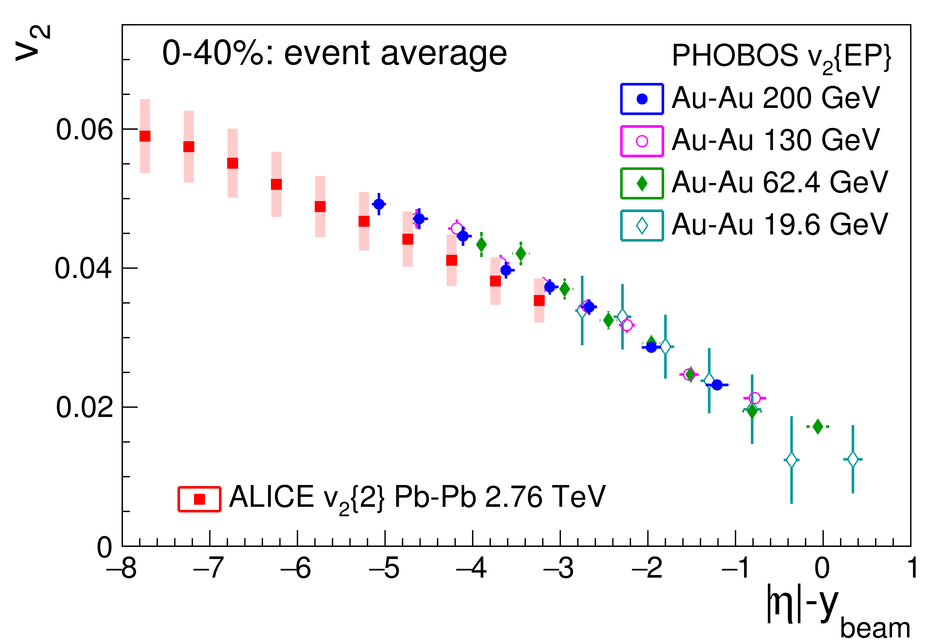
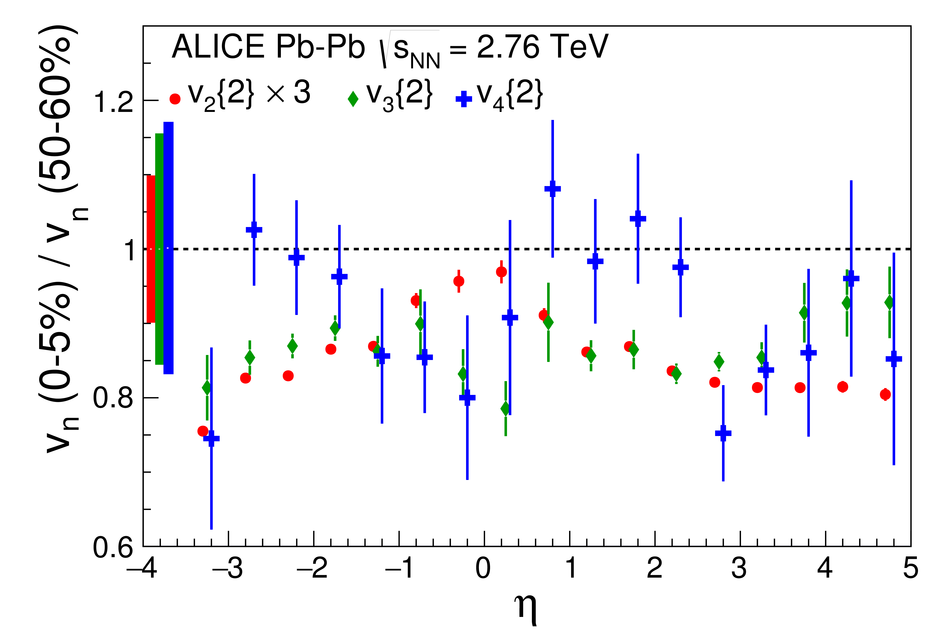
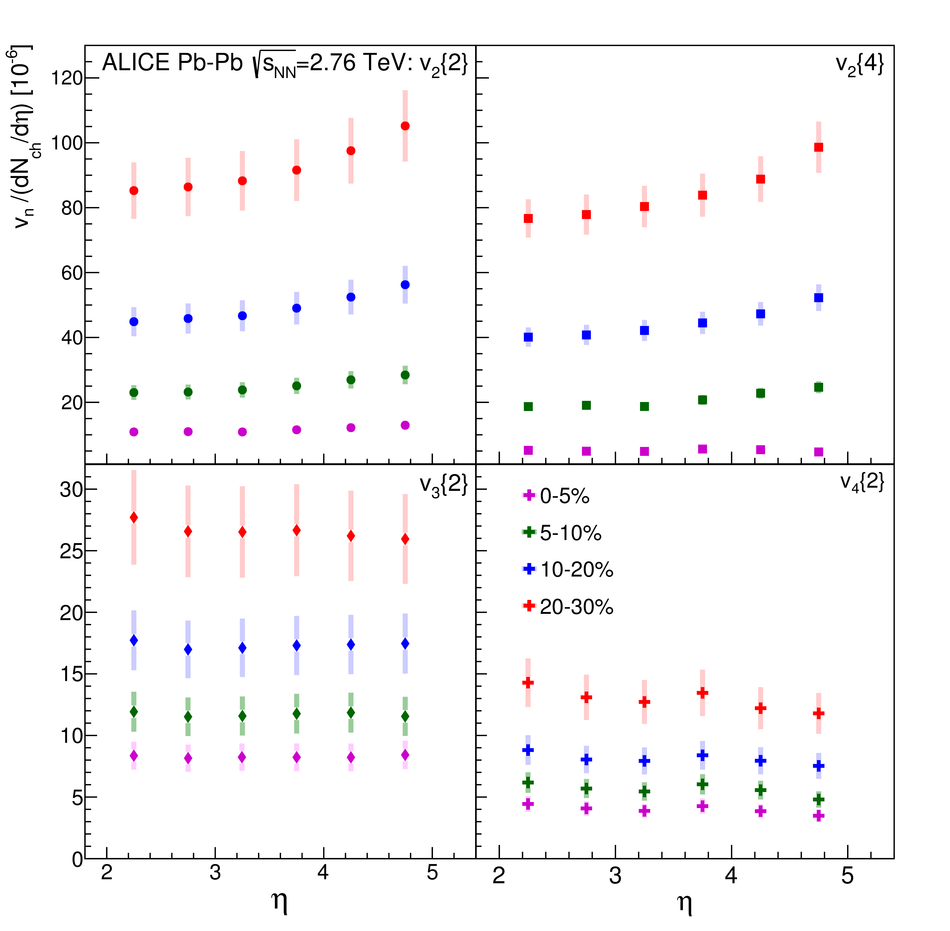
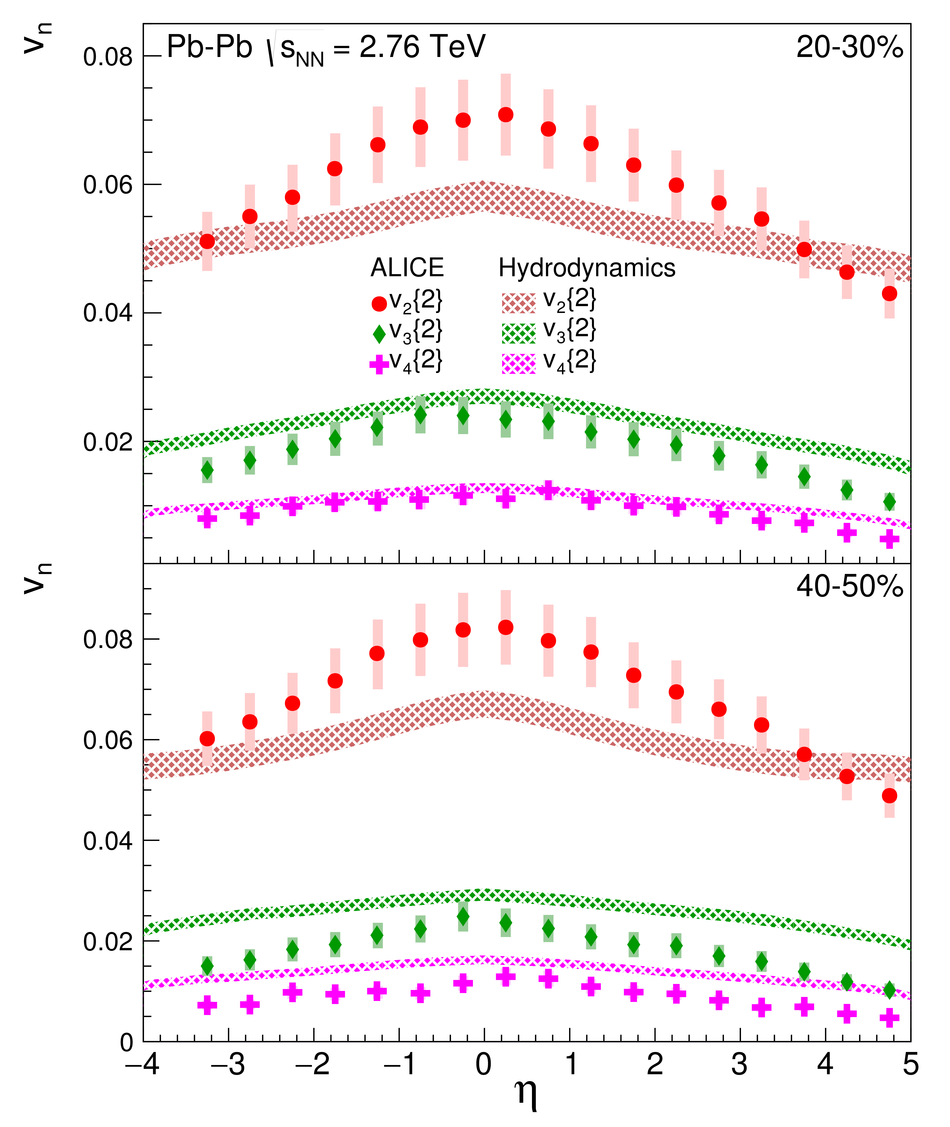
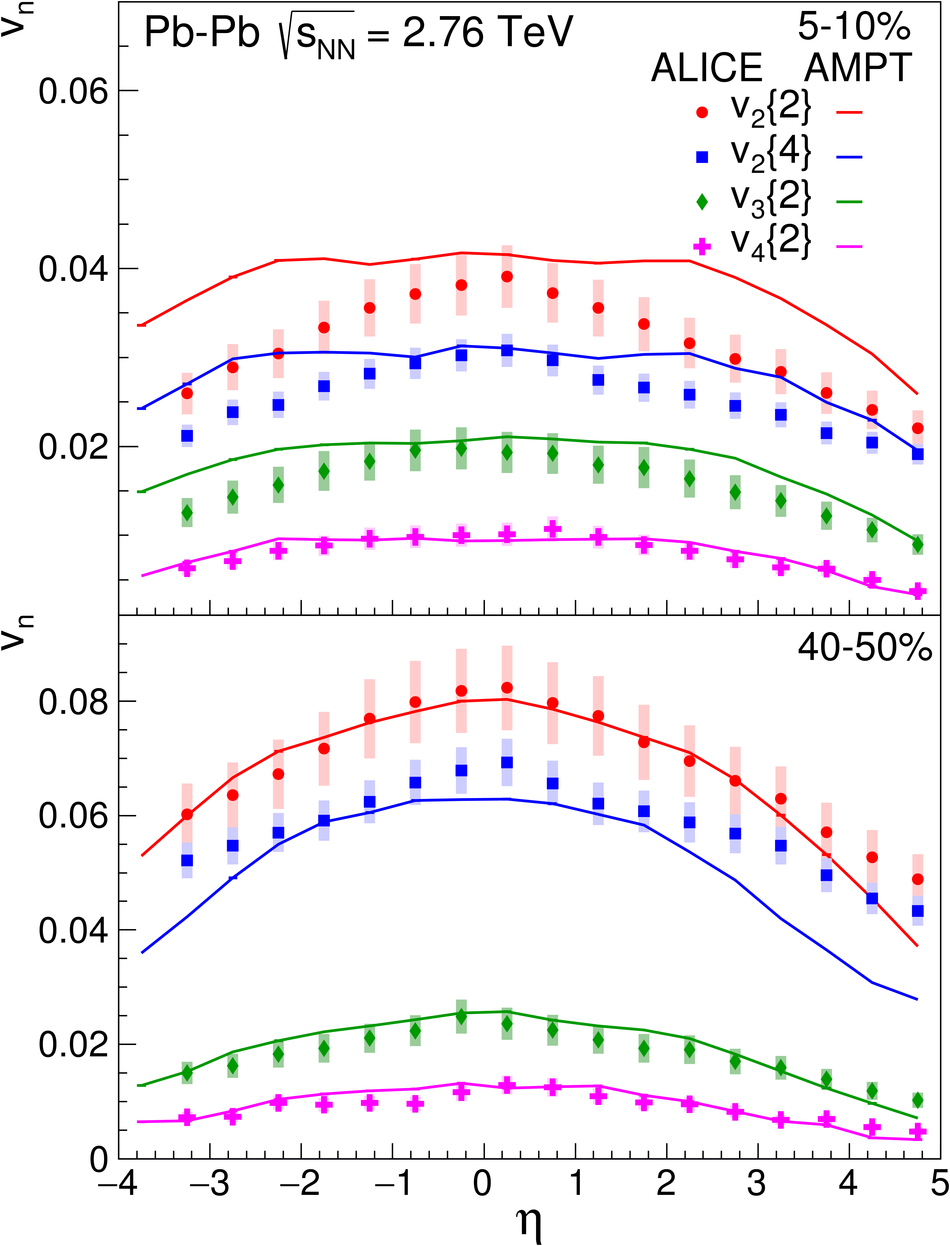
We present measurements of the elliptic ($\mathrm{v}_2$), triangular ($\mathrm{v}_3$) and quadrangular ($\mathrm{v}_4$) anisotropic azimuthal flow over a wide range of pseudorapidities ($-3.5<~ \eta <~ 5$). The measurements are performed with Pb-Pb collisions at $\sqrt{s_{\text{NN}}} = 2.76$ TeV using the ALICE detector at the Large Hadron Collider (LHC). The flow harmonics are obtained using two- and four-particle correlations from nine different centrality intervals covering central to peripheral collisions. We find that the shape of $\mathrm{v}_n(\eta)$ is largely independent of centrality for the flow harmonics $n=2-4$, however the higher harmonics fall off more steeply with increasing $|\eta|$. We assess the validity of extended longitudinal scaling of $\mathrm{v}_2$ by comparing to lower energy measurements, and find that the higher harmonic flow coefficients are proportional to the charged particle densities at larger pseudorapidities. Finally, we compare our measurements to both hydrodynamical and transport models, and find they both have challenges when it comes to describing our data.
Phys. Lett. B 762 (2016) 376-388
HEP Data
e-Print: arXiv:1605.02035 | PDF | inSPIRE
CERN-EP-2016-115