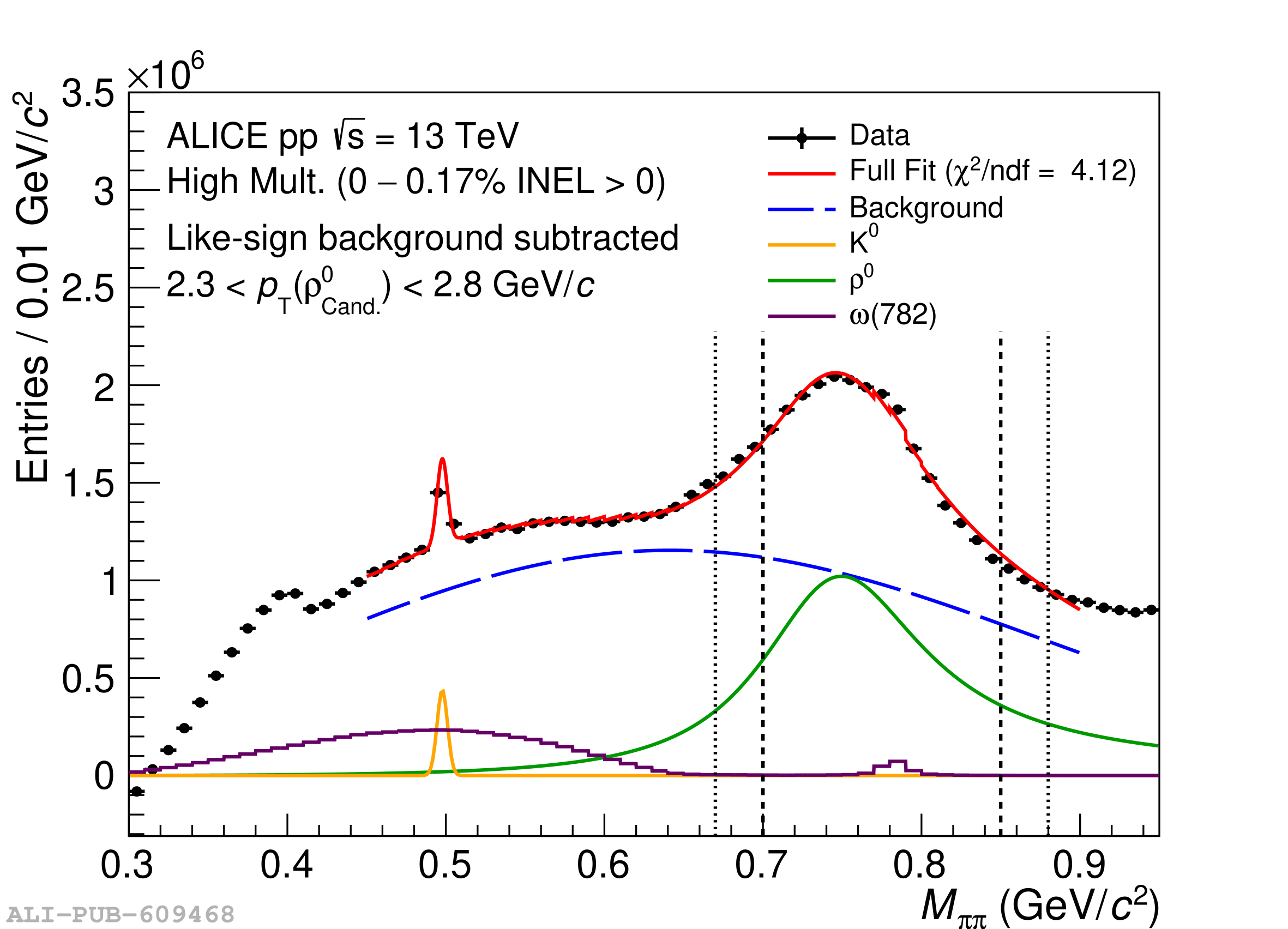
Direct measurements of the $\rho^0$p interaction have remained so far elusive, with most insights derived indirectly from photoproduction or low-energy partial wave analyses. This letter presents the first direct observation of the $\rho^0$p interaction, obtained through two-particle correlations measured in high-multiplicity, ultrarelativistic proton-proton collisions at $\sqrt{s} = 13$ TeV by the ALICE Collaboration at the LHC. Two-particle correlation data, analyzed within chiral effective field theory ($\chi$EFT) using a coupled-channel approach and incorporating recent $\phi$-p data, yield a scattering length of $a_{\rho^0p} = (-0.46 \pm 0.04) + i(0.20 \pm 0.04)$ fm and constrain coupling strengths of two states identified with the N(1958) and N(1700). These findings emphasize the importance of coupled-channel dynamics and dynamically generated states in understanding the $\rho^0$p interaction. The results establish a vacuum baseline for extrapolation studies to high densities, contributing to the foundation for chiral symmetry restoration searches, and offer collider-based insights into the QCD spectrum, complementing traditional low-energy approaches. This work marks a significant advance in correlation studies, extending the exploration of interactions to the most short-lived QCD states.