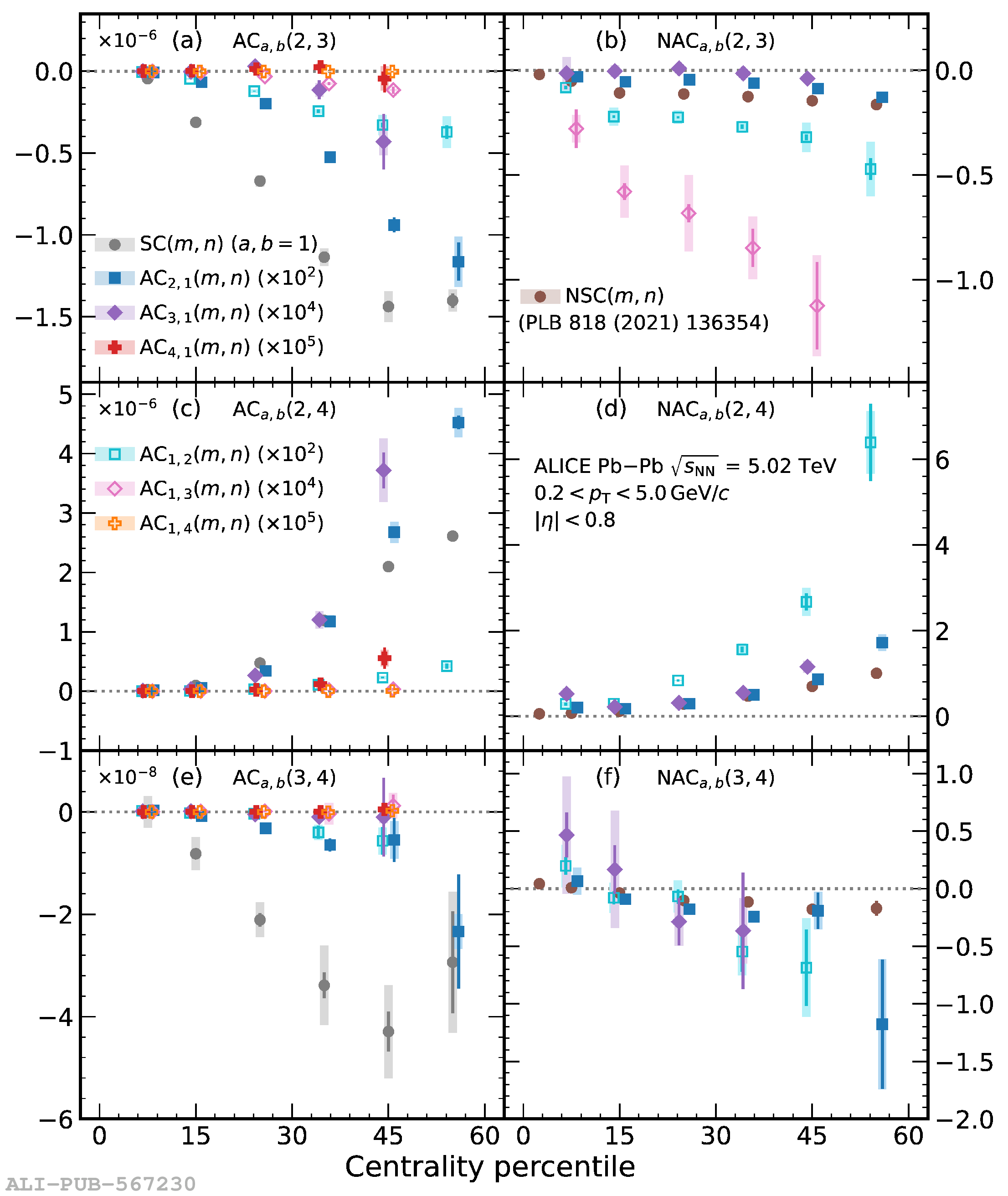
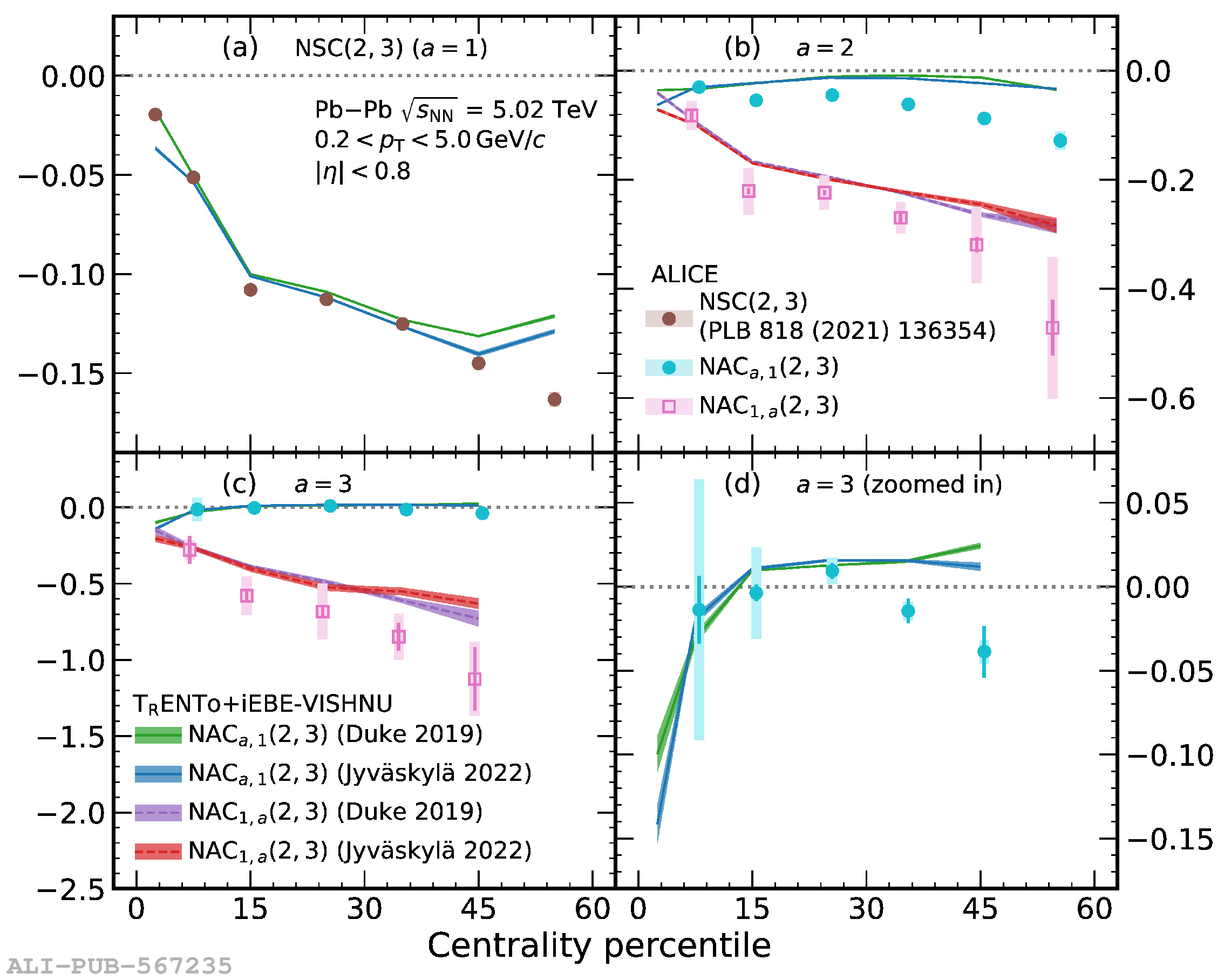
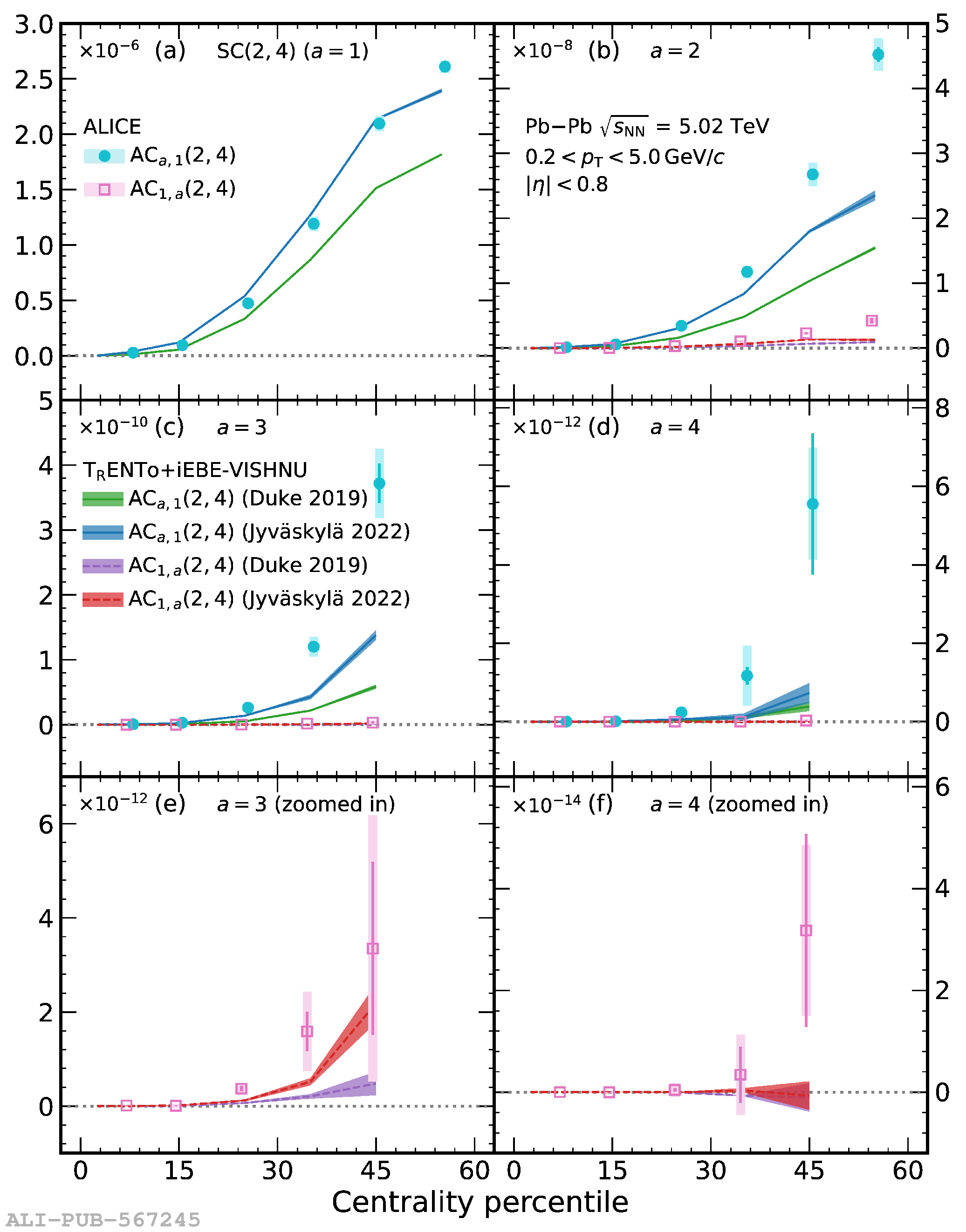
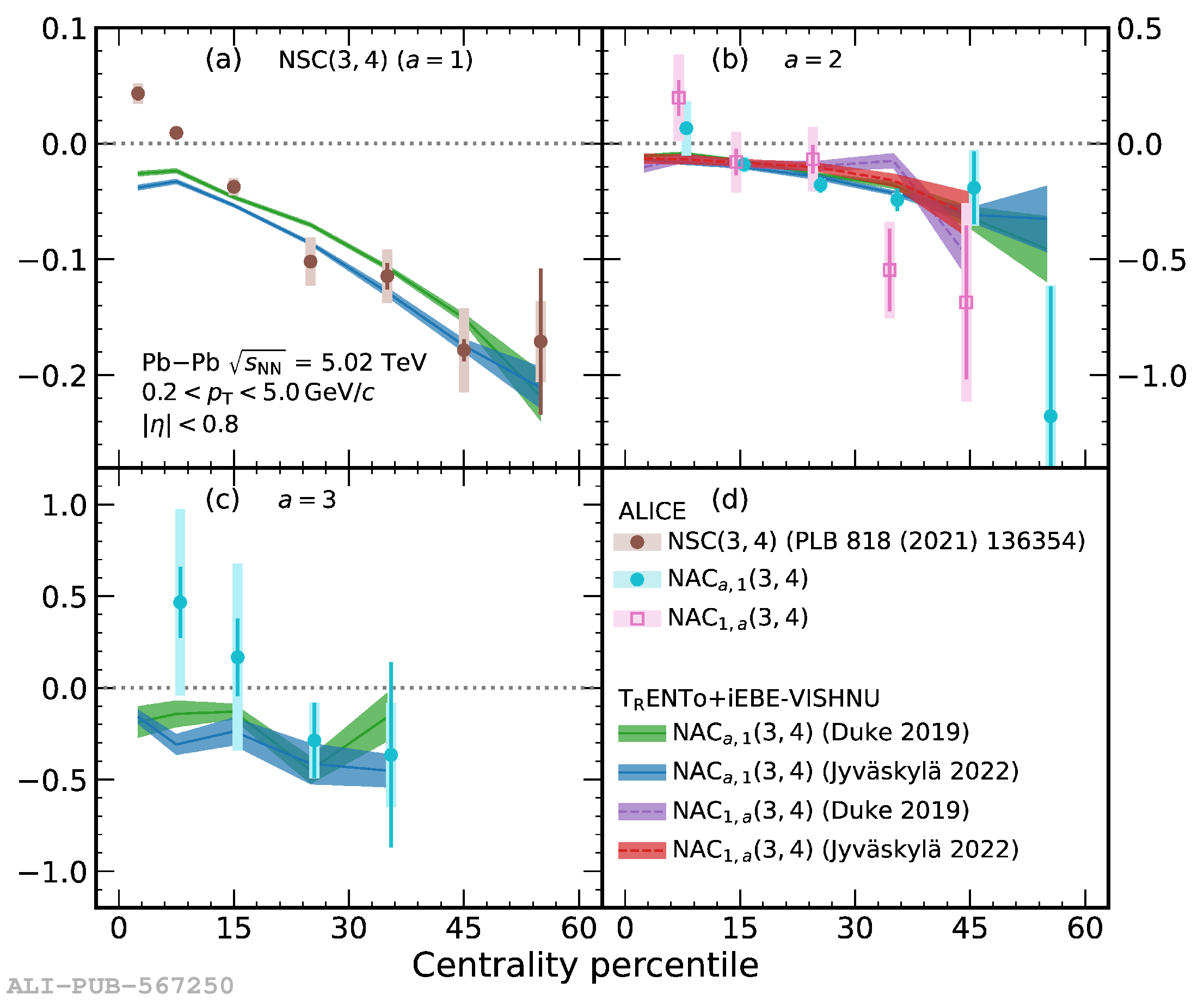
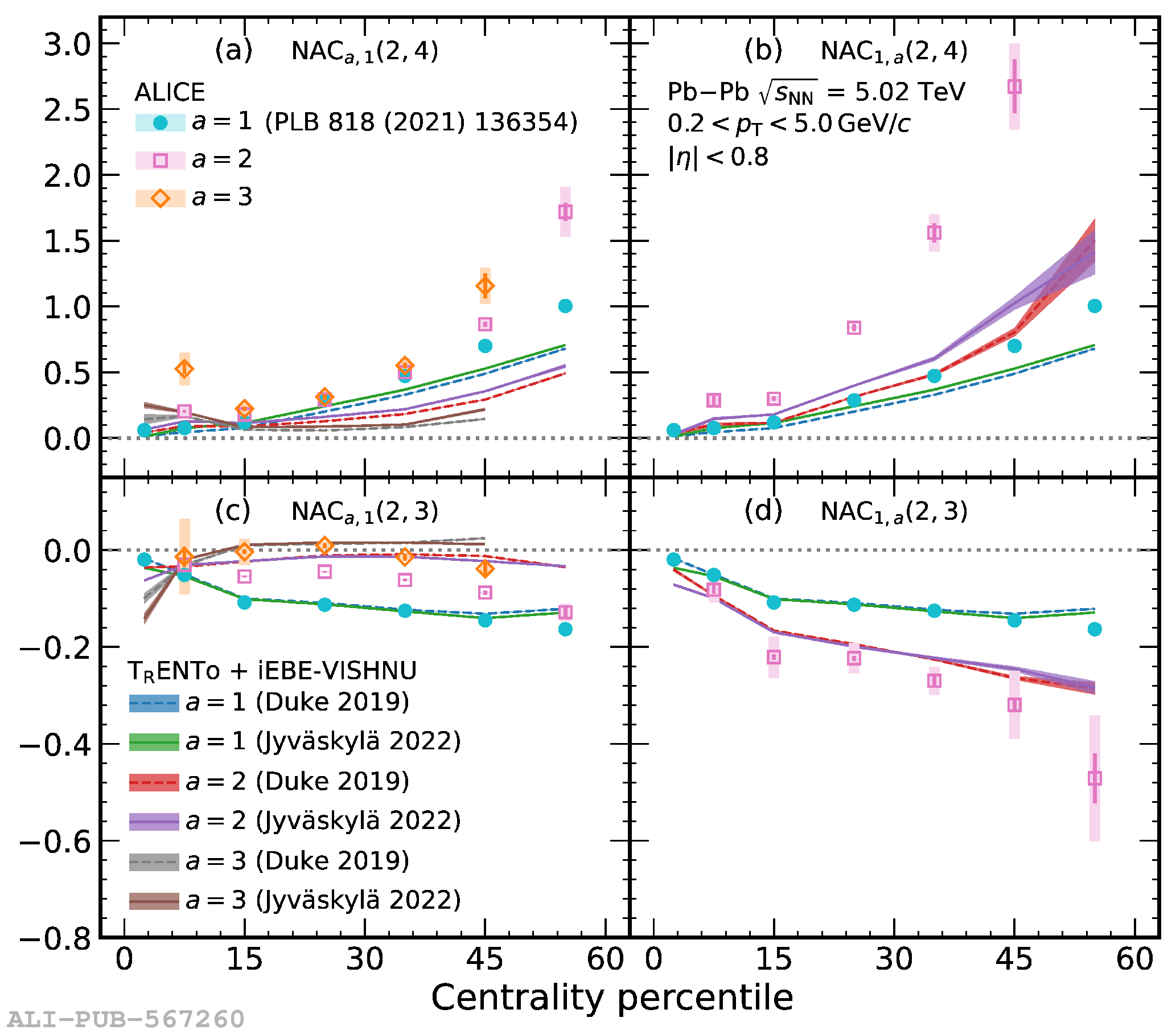
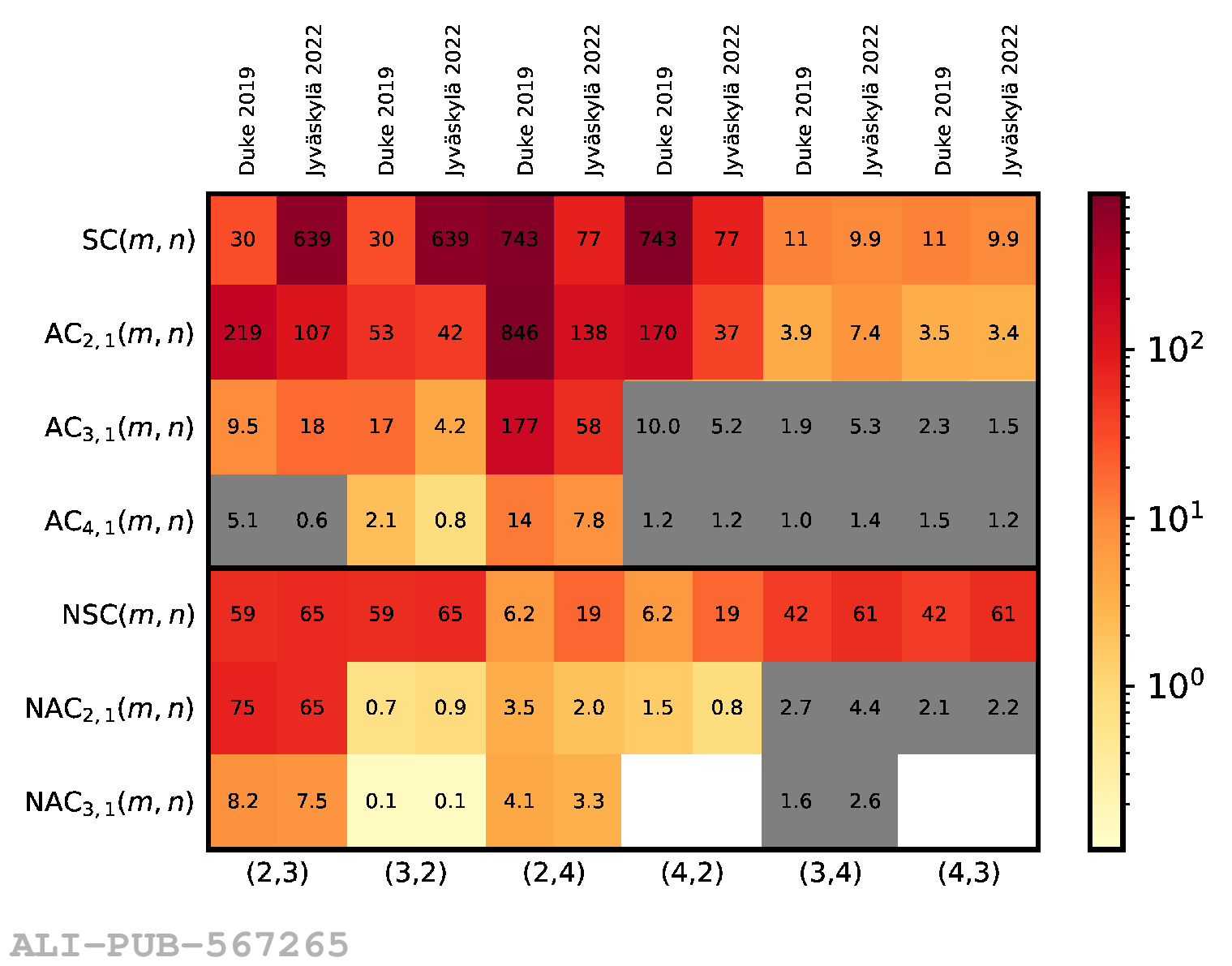
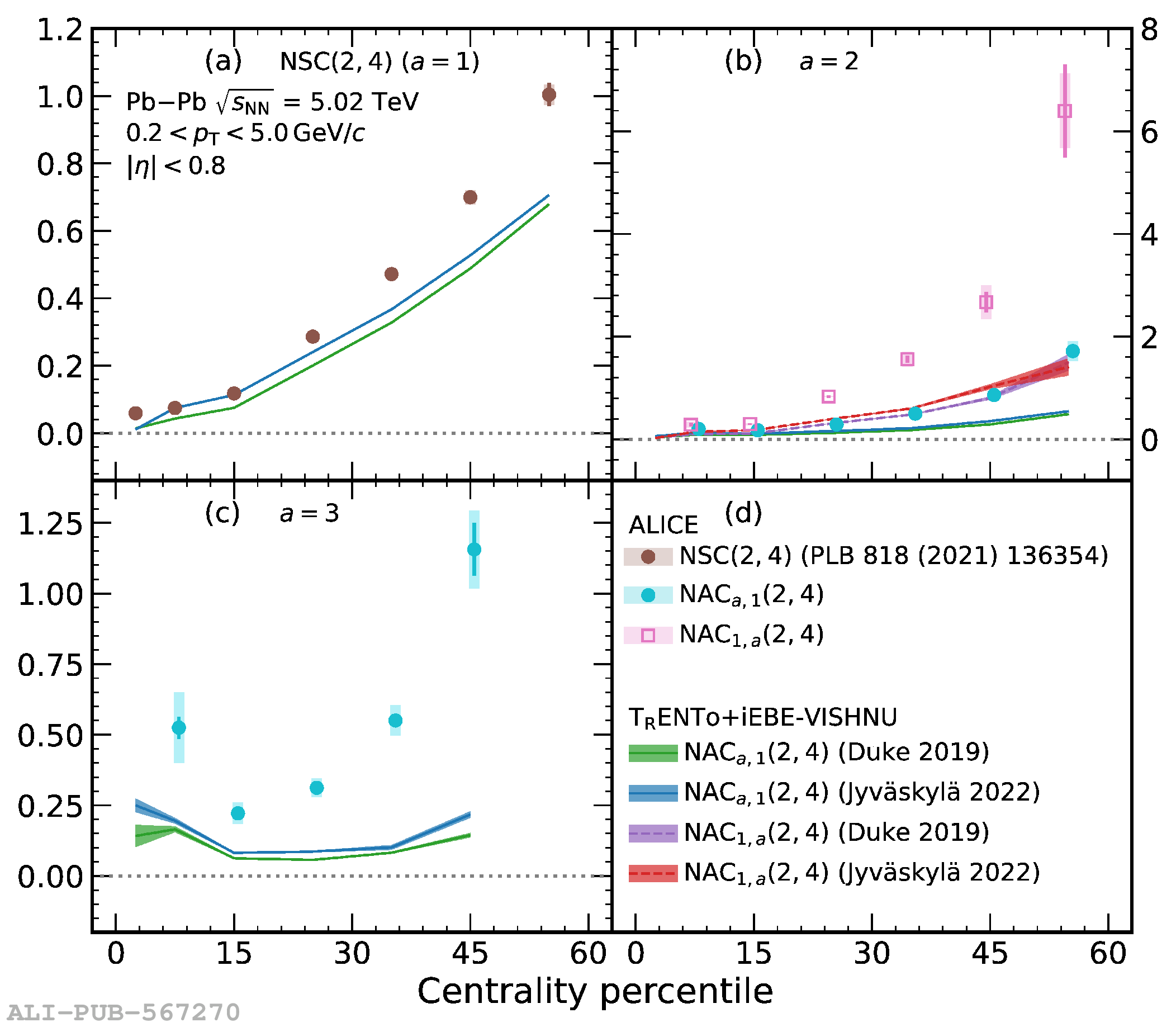
The correlations between different moments of two flow amplitudes, extracted with the recently developed asymmetric cumulants, are measured in Pb$-$Pb collisions at $\sqrt{s_{\rm NN}} = 5.02$ TeV recorded by the ALICE detector at the CERN Large Hadron Collider. The magnitudes of the measured observables show a dependence on the different moments as well as on the collision centrality, indicating the presence of non-linear response in all even moments up to the eighth. Furthermore, the higher-order asymmetric cumulants show different signatures than the symmetric and lower-order asymmetric cumulants. Comparisons with state-of-the-art event generators using two different parametrizations obtained from Bayesian optimization show differences between data and simulations in many of the studied observables, indicating a need for further tuning of the models behind those event generators. These results provide new and independent constraints on the initial conditions and transport properties of the system created in heavy-ion collisions.
Phys. Rev. C 108 (2023) 055203
HEP Data
e-Print: arXiv:2303.13414 | PDF | inSPIRE
CERN-EP-2023-047
Figure group
Figure 1
Centrality dependence of the different orders of AC$_{a,b}(m,n)$ (left) and NAC$_{a,b}(m,n)$ (right) for four pairs of indices ($a,b$) and three pairs of harmonics ($m,n$) in Pb-Pb collisions at $\snn$ = 5.02 TeV. The mirror combinations of AC$_{a,b}(m,n)$ (closed markers), i.e., AC$_{b,a}(m,n)$, are indicated with open markers and similar color scheme. The statistical (systematic) uncertainties are shown with lines (boxes). The data points are shifted horizontally for visibility. |  |
Figure 2
Centrality dependence of the different orders $a = 1,\ldots,3$ of NAC$_{a,1}(2,3)$ (cyan closed circles) and NAC$_{1,a}(2,3)$ (pink open squares) compared with the theoretical predictions from TRENTO+iEBE-VISHNU for the Duke 2019 and Jyvaskyla 2022 parametrizations. Panel (d) shows a close-up of the results of NAC$_{3,1}(2,3)$. The statistical uncertainties in the calculations are indicated by the thicknesses of the colored bands. The data points for NSC$(2,3)$ are taken from Ref. [17]. |  |
Figure 3
Centrality dependence of the different orders $a = 1,\ldots,4$ of AC$_{a,1}(2,4)$ (cyan closed circles) and AC$_{1,a}(2,4)$ (pink open squares) compared with the theoretical predictions from TRENTO+iEBE-VISHNU for the Duke 2019 and Jyvaskyla 2022 parametrizations. Panels (e) and (f) show a close-up of the results of AC$_{1,3}(2,4)$ and AC$_{1,4}(2,4)$, respectively. The statistical uncertainties in the calculations are indicated by the thicknesses of the colored bands. |  |
Figure 4
Centrality dependence of the different orders $a = 1,\ldots,3$ of NAC$_{a,1}(3,4)$ (cyan closed circles) and NAC$_{1,a}(3,4)$ (pink open squares) compared with the theoretical predictions from TRENTO+iEBE-VISHNU for the Duke 2019 and Jyvaskyla 2022 parametrizations. The statistical uncertainties in the calculations are indicated by the thicknesses of the colored bands. The data points for NSC$(3,4)$ are taken from Ref. [17]. |  |
Figure 5
Centrality dependence of the different orders $a = 1,\ldots,3$ of NAC$_{a,1}(m,n)$ and NAC$_{1,a}(m,n)$ compared with the theoretical predictions from TRENTO+iEBE-VISHNU for the Duke 2019 and Jyvaskyla 2022 parametrizations. The last point of NAC$_{1,2}(2,4)$ and the results for NAC$_{1,3}(2,3)$ are not shown for visibility purposes. The statistical uncertainties in the calculations are indicated by the thicknesses of the colored bands. The data points for $a = 1$ are taken from Ref. [17]. |  |
Figure 6
Values for $\chi^2$ test calculated between the data and two different model calculations for all ACs and NACs and all pairs of harmonics presented in this paper. The observables with large uncertainties are indicated with a grey filling, while an absence of observable (see Fig. 1) is shown with a white filling. |  |
Figure A.1
Centrality dependence of the different orders a = 1, . . . , 4 of AC$_{a,1}(2, 3)$ (cyan closed circles) and AC$_{1,a}(2, 3)$ (pink open squares) compared with the theoretical predictions from TRENTo+iEBE-VISHNU for the Duke 2019 [22] and Jyväskylä 2022 [12] parametrizations. The statistical uncertainties in the calculations are indicated by the thicknesses of the colored bands. |  |
Figure A.2
Centrality dependence of the different orders $a = 1,\ldots,3$ of NAC$_{a,1}(2,4)$ (cyan closed circles) and NAC$_{1,a}(2,4)$ (pink open squares) compared with the theoretical predictions from TRENTo+iEBE-VISHNU for the Duke 2019 and Jyvaskyla 2022 parametrizations. The statistical uncertainties in the calculations are indicated by the thicknesses of the colored bands. The data points for NSC$(2,4)$ are taken from Ref. [17]. |  |
Figure A.3
Centrality dependence of the different orders a = 1, . . . , 4 of AC$_{a,1}(3, 4)$ (cyan closed circles) and AC$_{1,a}(3, 4)$ (pink open squares) compared with the theoretical predictions from TRENTo+iEBE-VISHNU for the Duke 2019 [22] and Jyväskylä 2022 [12] parametrizations. The statistical uncertainties in the calculations are indicated by the thicknesses of the colored bands |  |