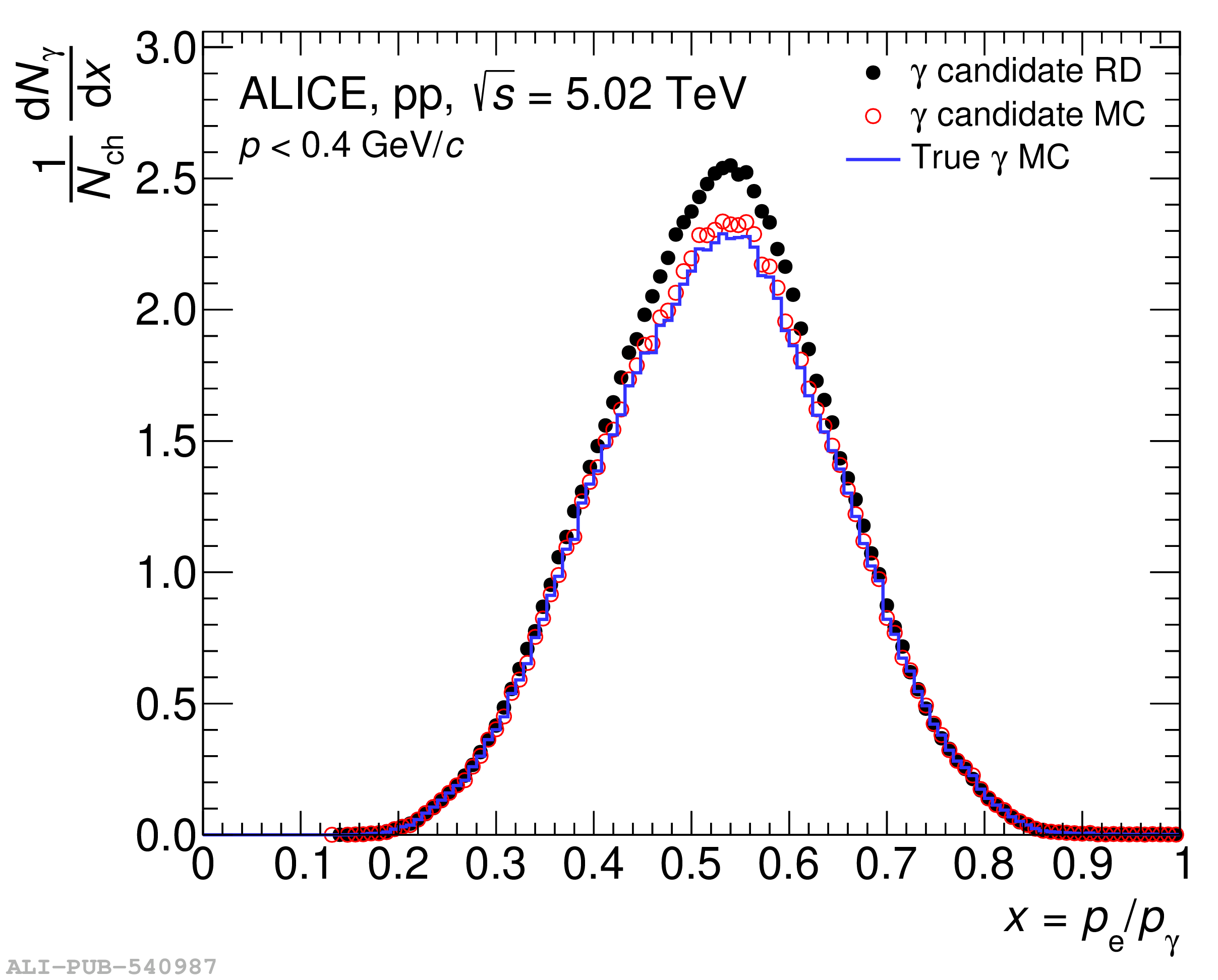
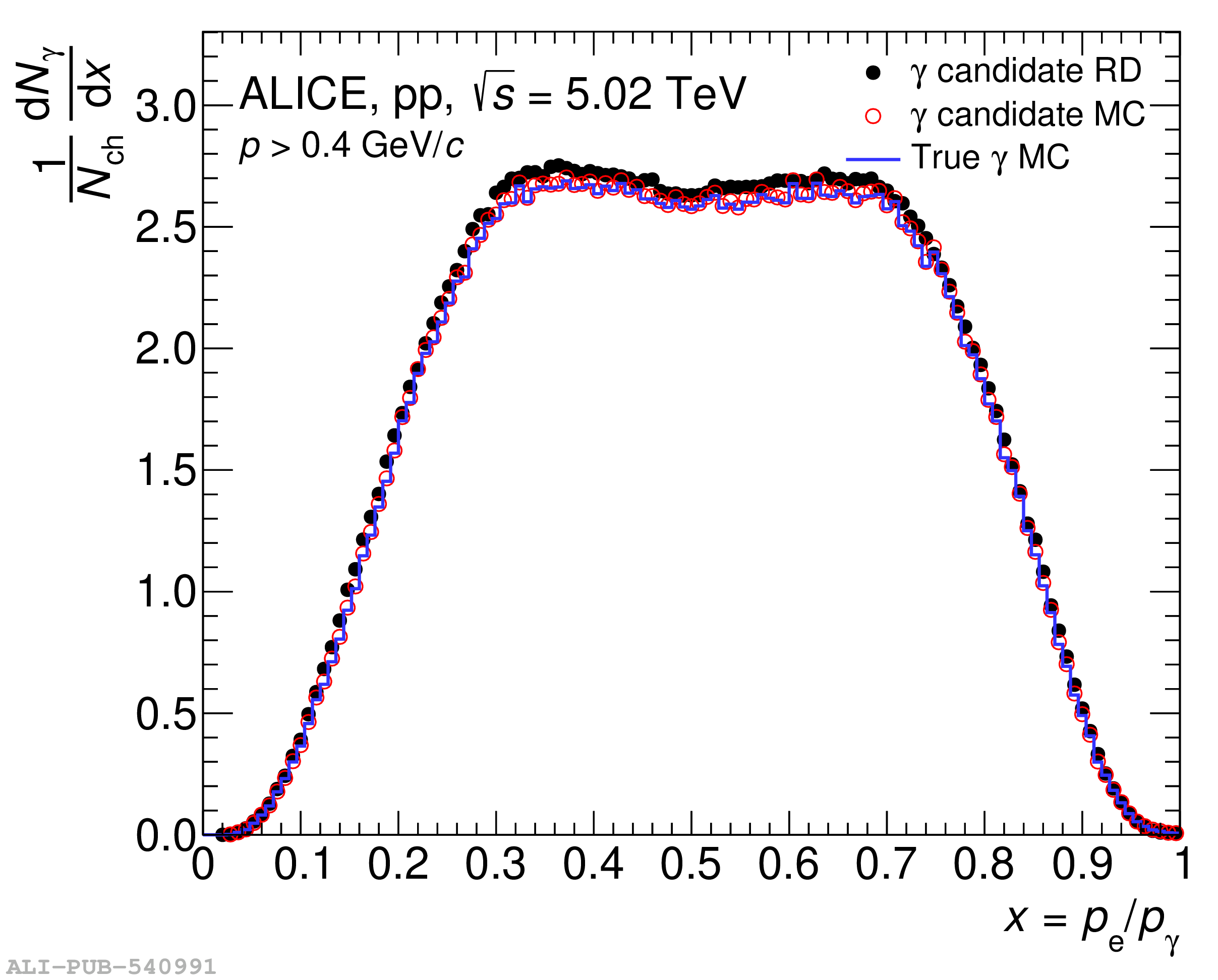
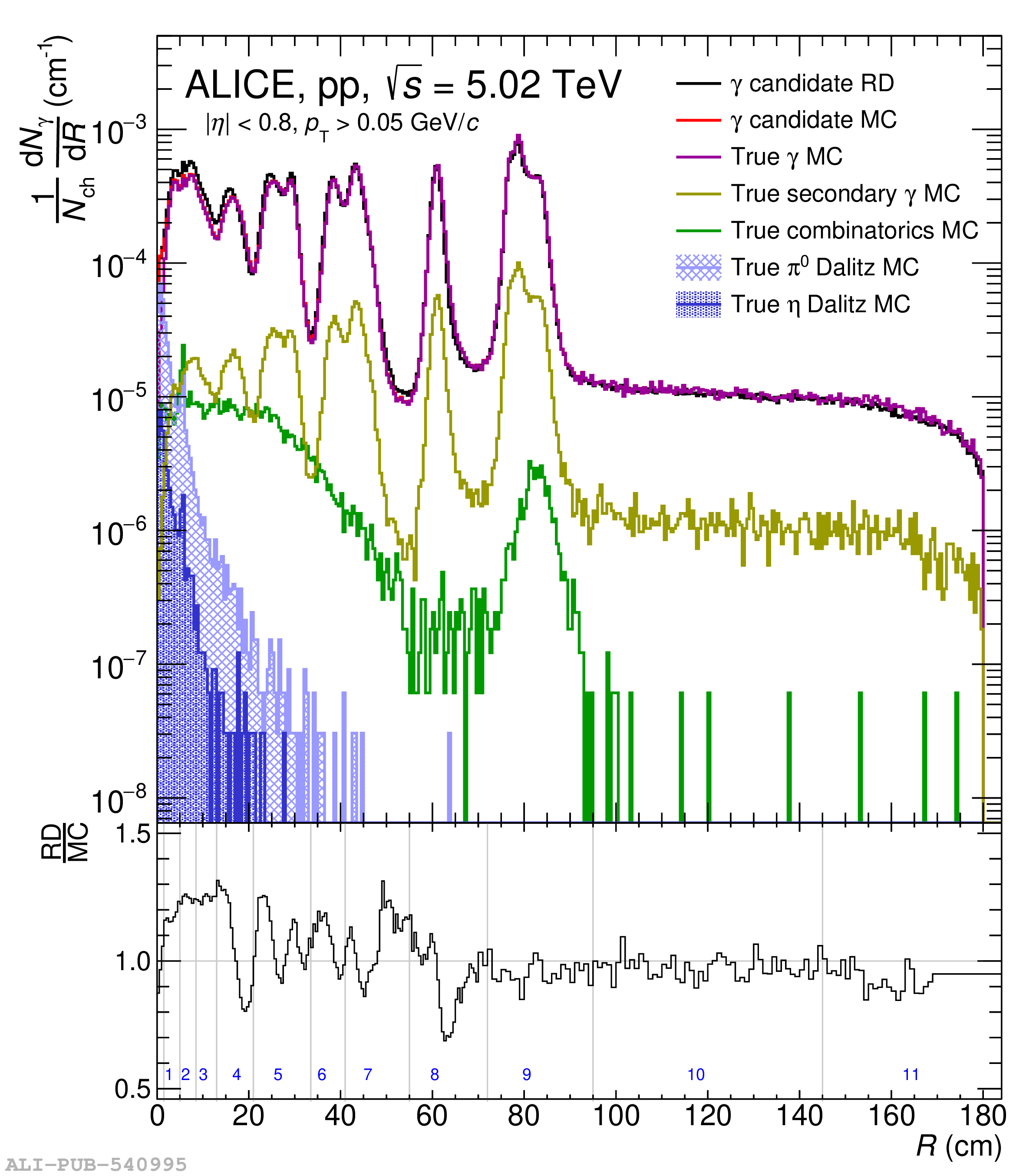
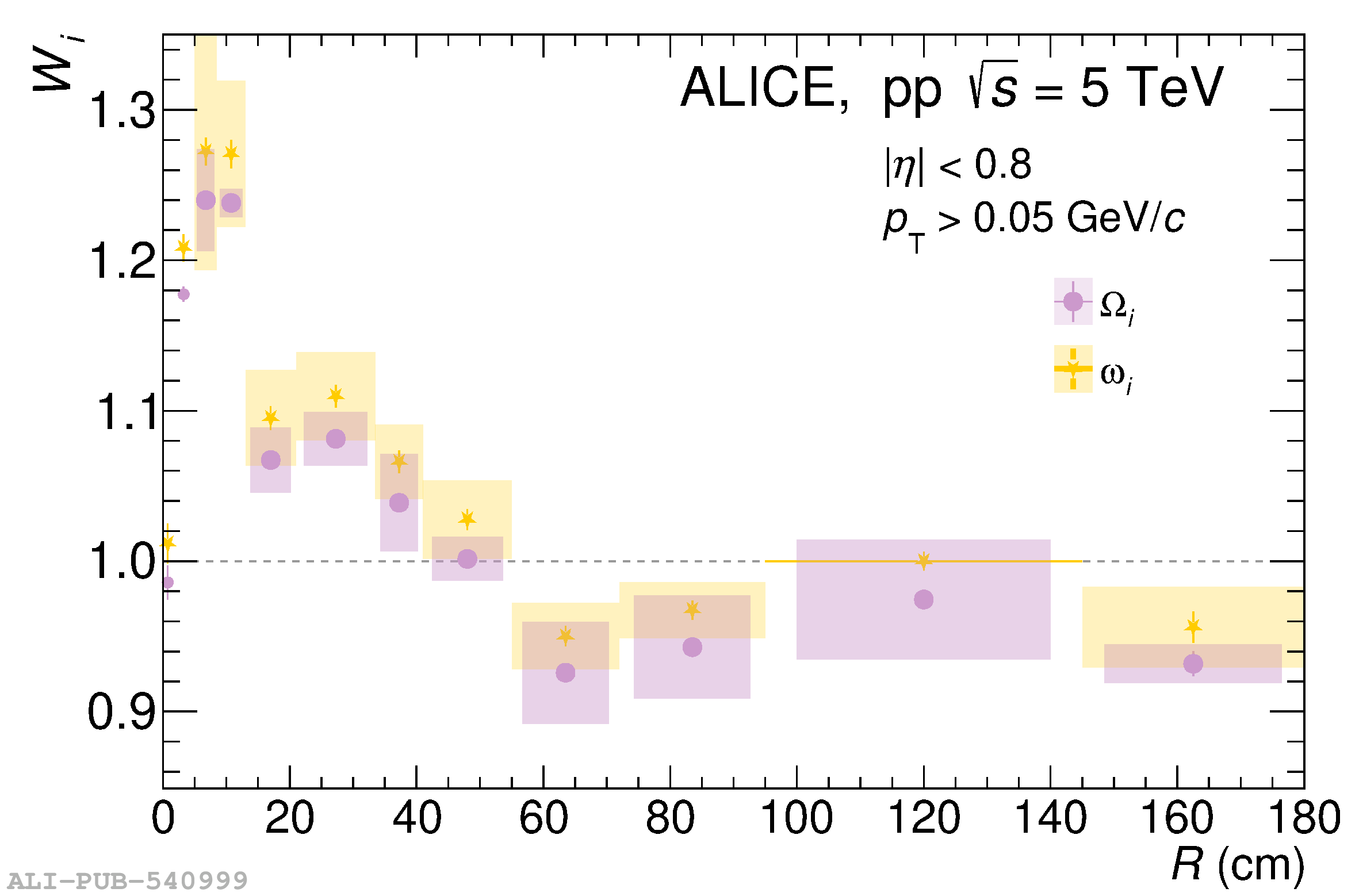
The knowledge of the material budget with a high precision is fundamental for measurements of direct photon production using the photon conversion method due to its direct impact on the total systematic uncertainty. Moreover, it influences many aspects of the charged-particle reconstruction performance. In this article, two procedures to determine data-driven corrections to the material-budget description in ALICE simulation software are developed. One is based on the precise knowledge of the gas composition in the Time Projection Chamber. The other is based on the robustness of the ratio between the produced number of photons and charged particles, to a large extent due to the approximate isospin symmetry in the number of produced neutral and charged pions. Both methods are applied to ALICE data allowing for a reduction of the overall material budget systematic uncertainty from 4.5% down to 2.5%. Using these methods, a locally correct material budget is also achieved. The two proposed methods are generic and can be applied to any experiment in a similar fashion.
JINST 18 (2023) P11032
e-Print: arXiv:2303.15317 | PDF | inSPIRE
CERN-EP-2023-043
Figure group