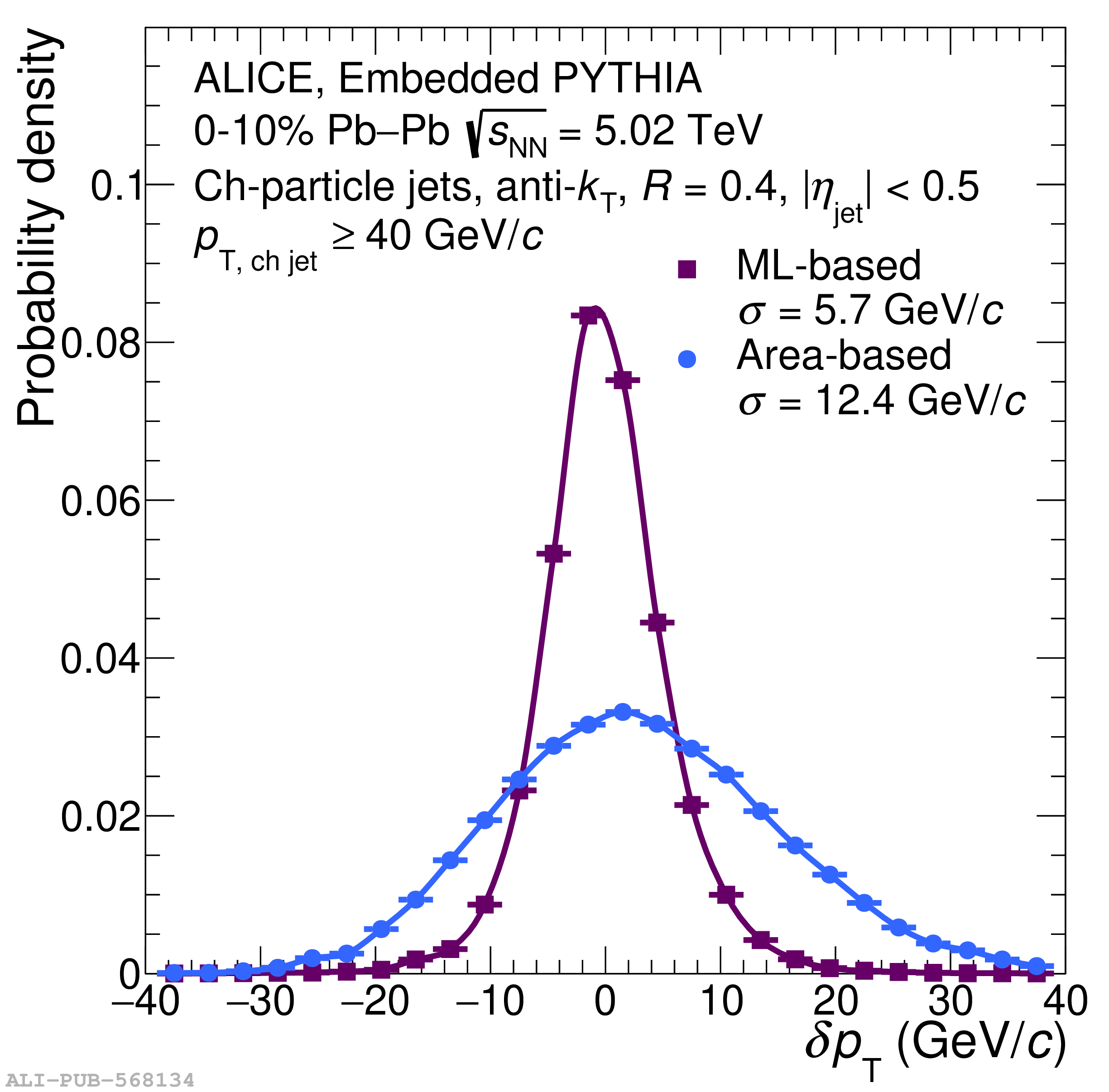
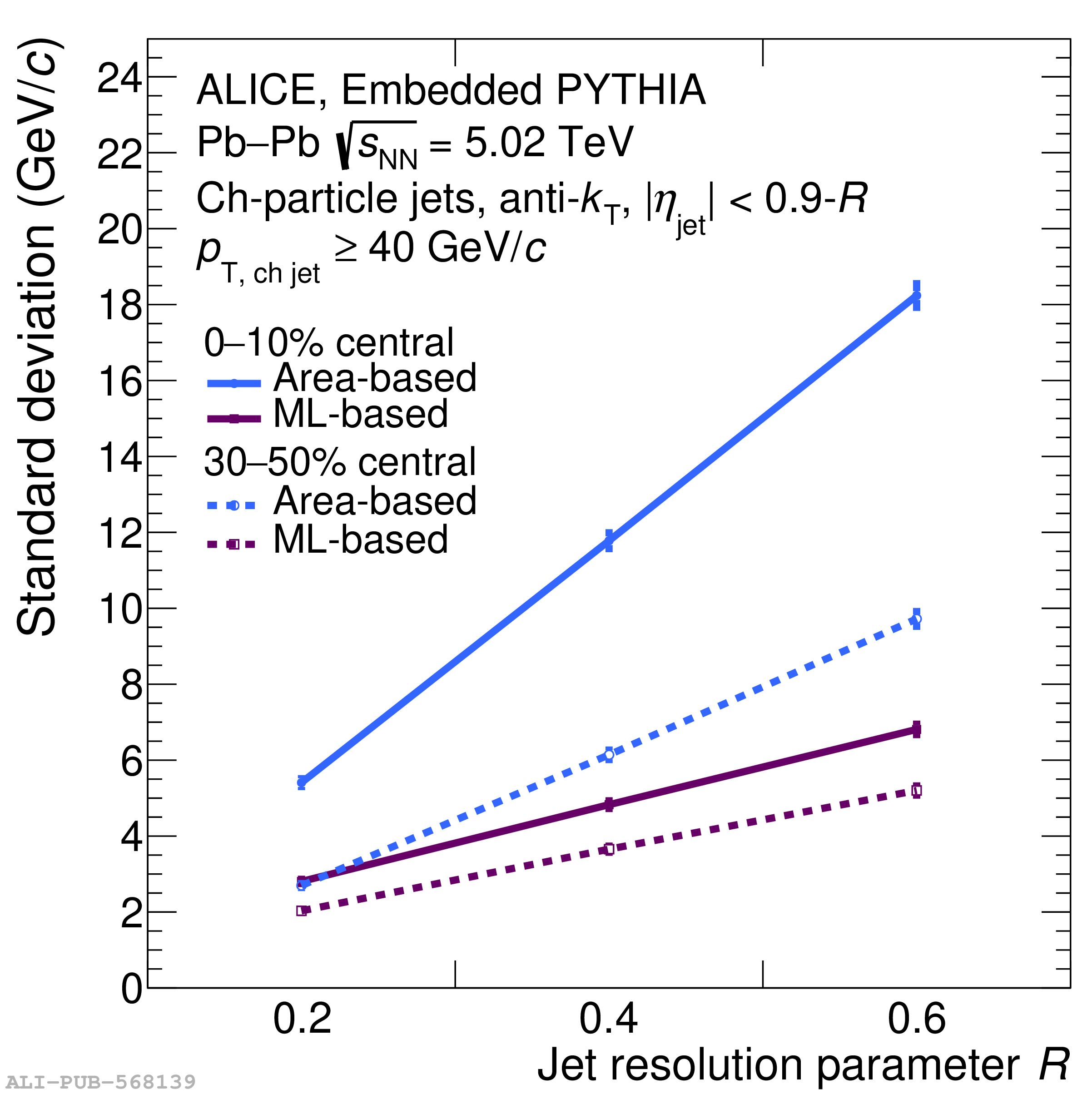
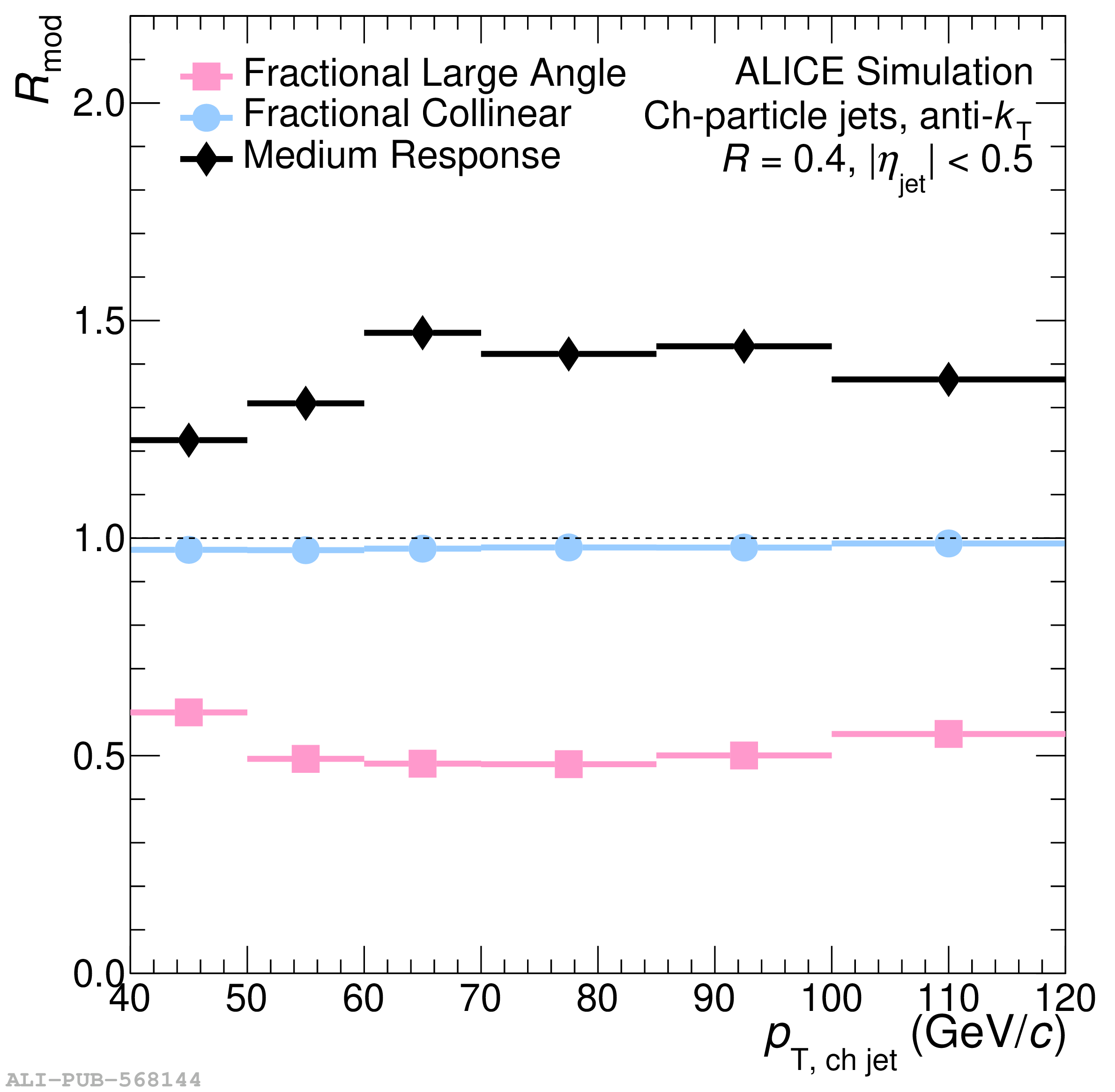
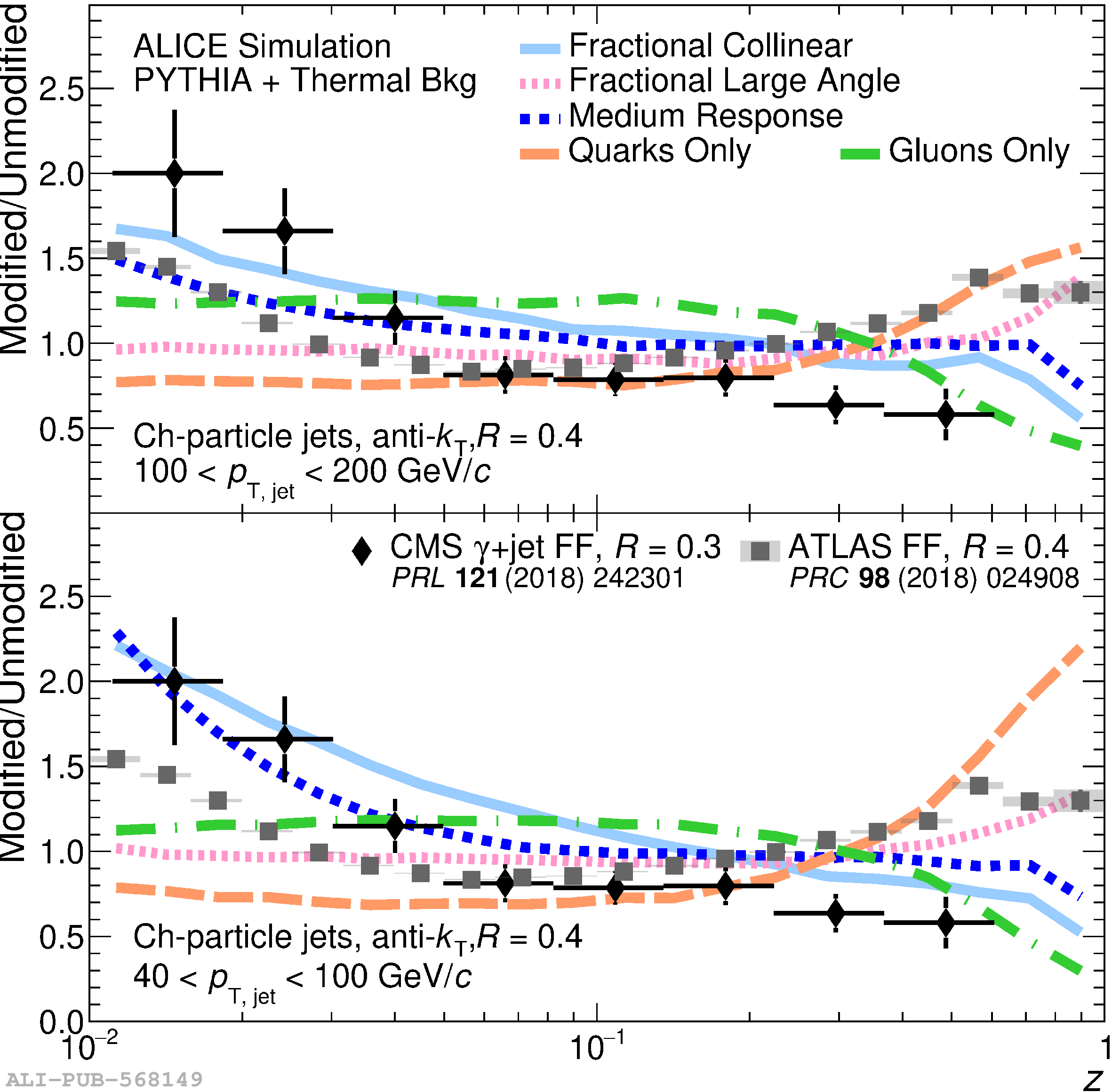
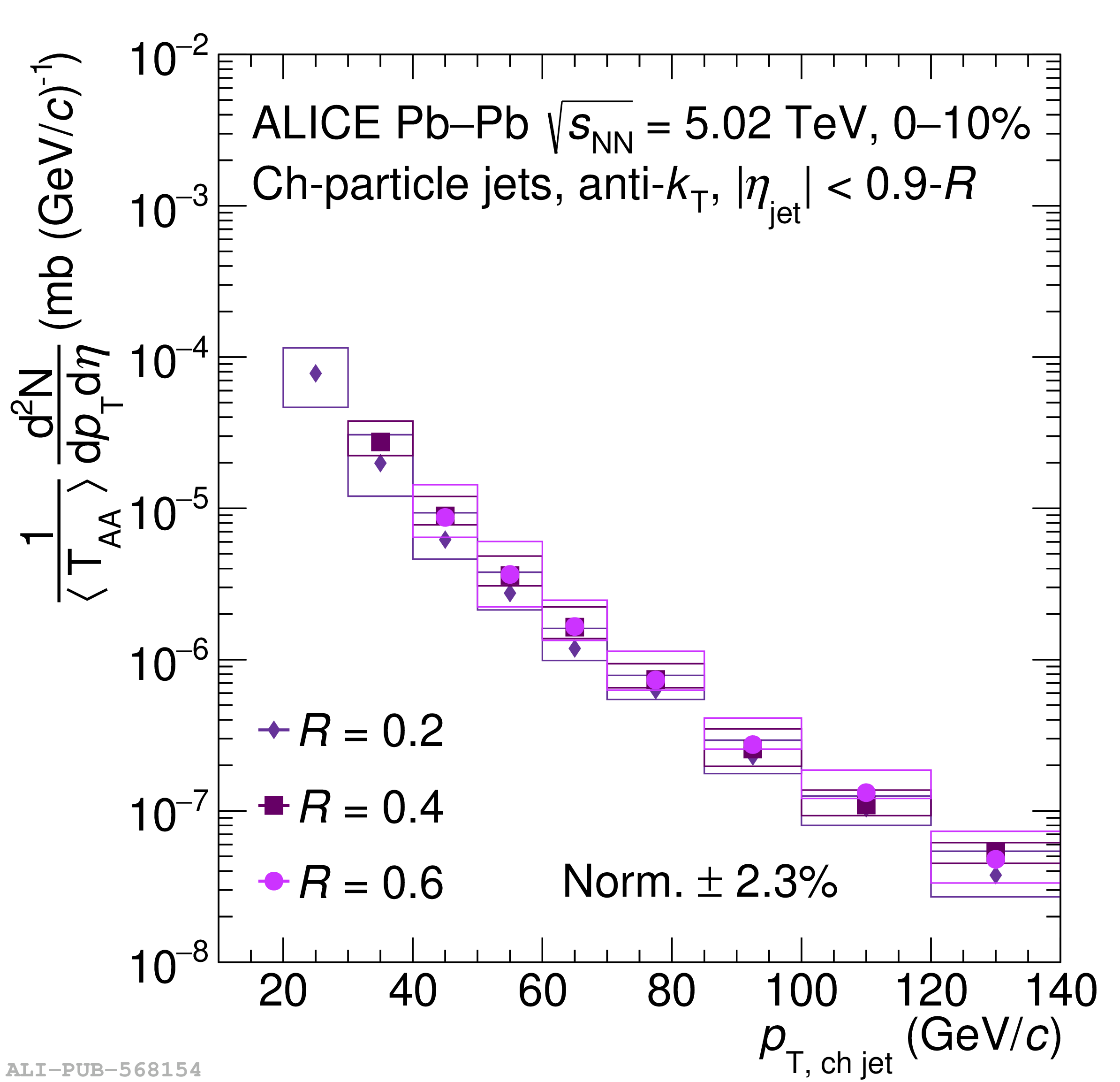
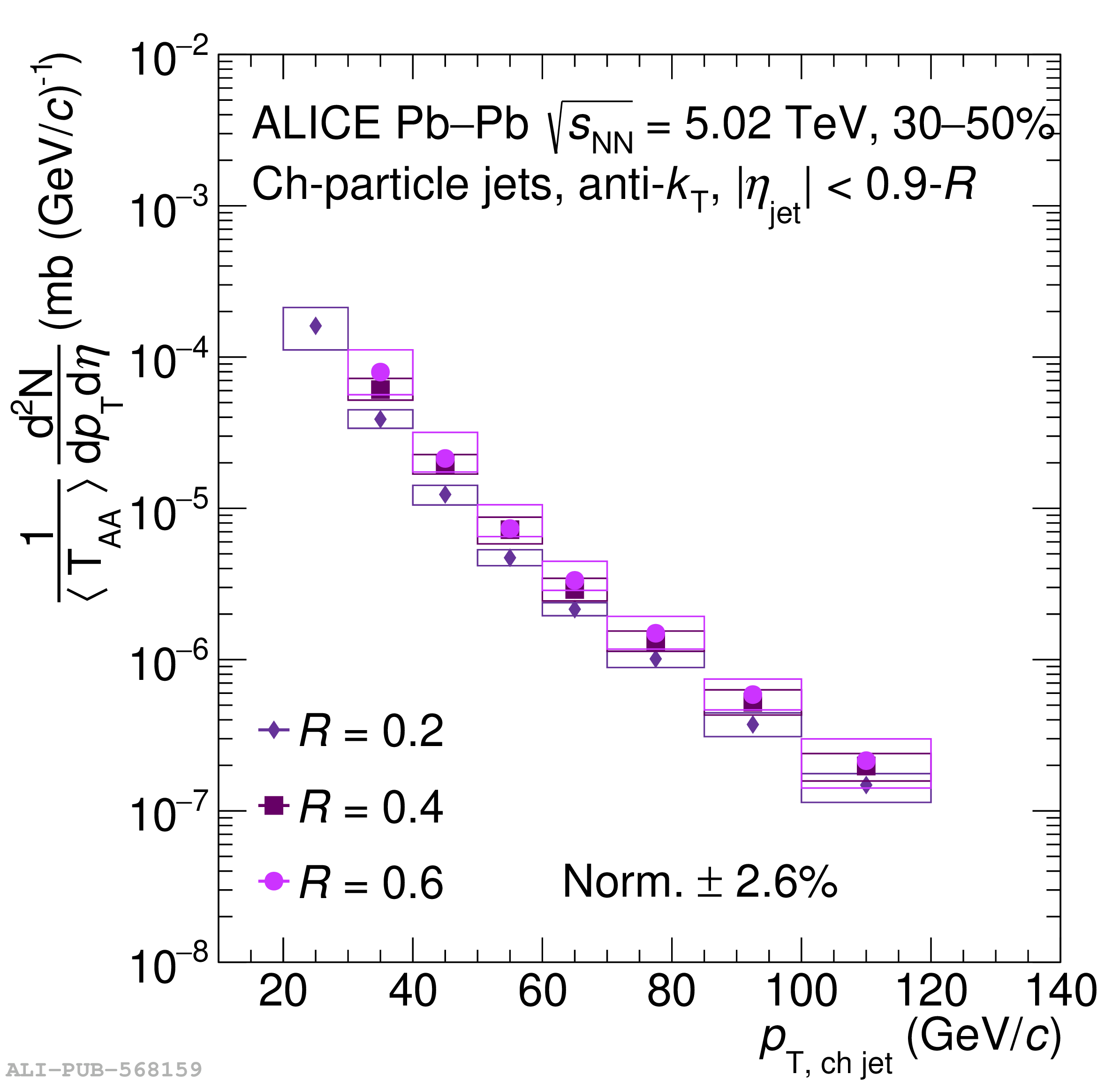
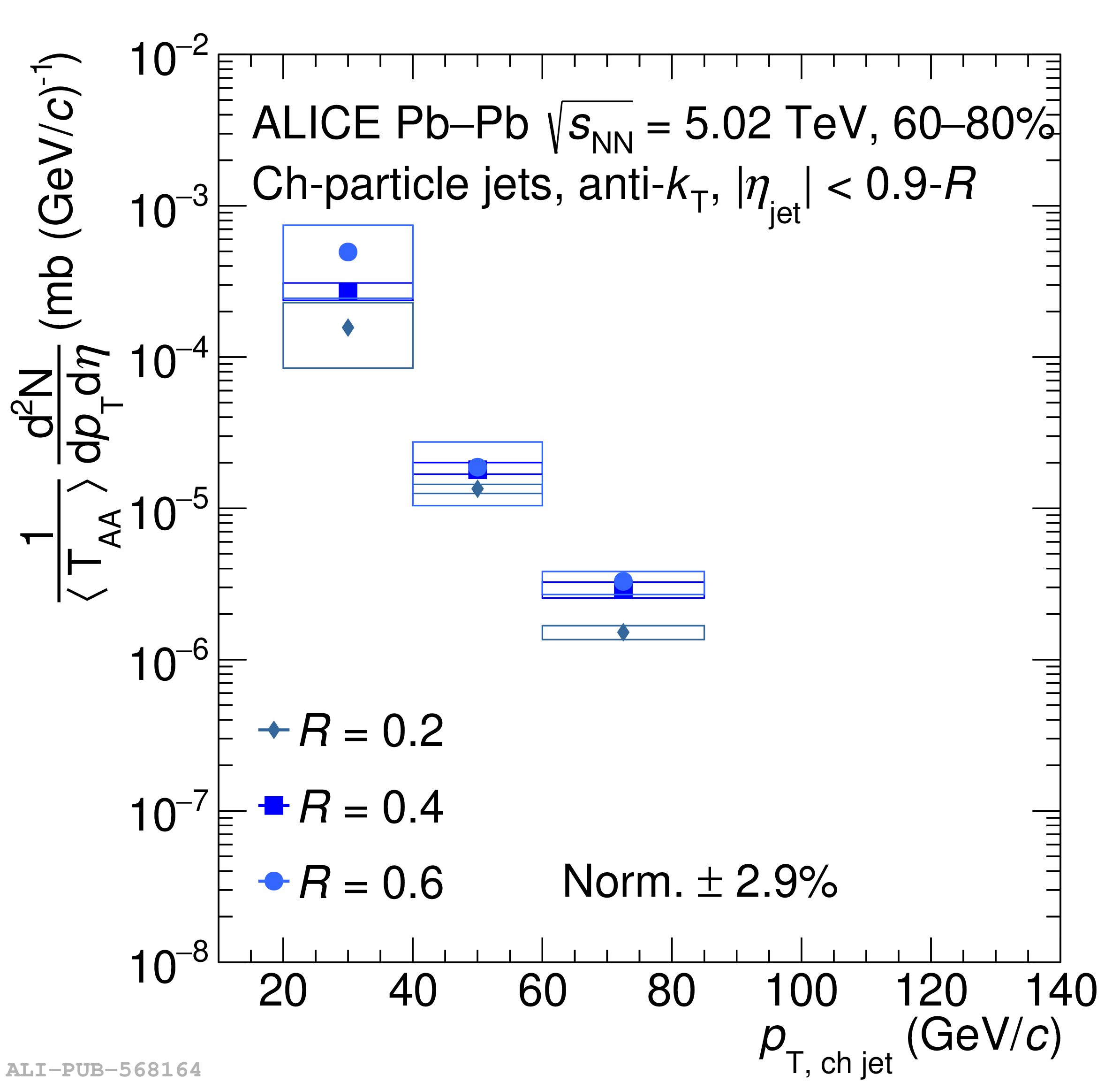
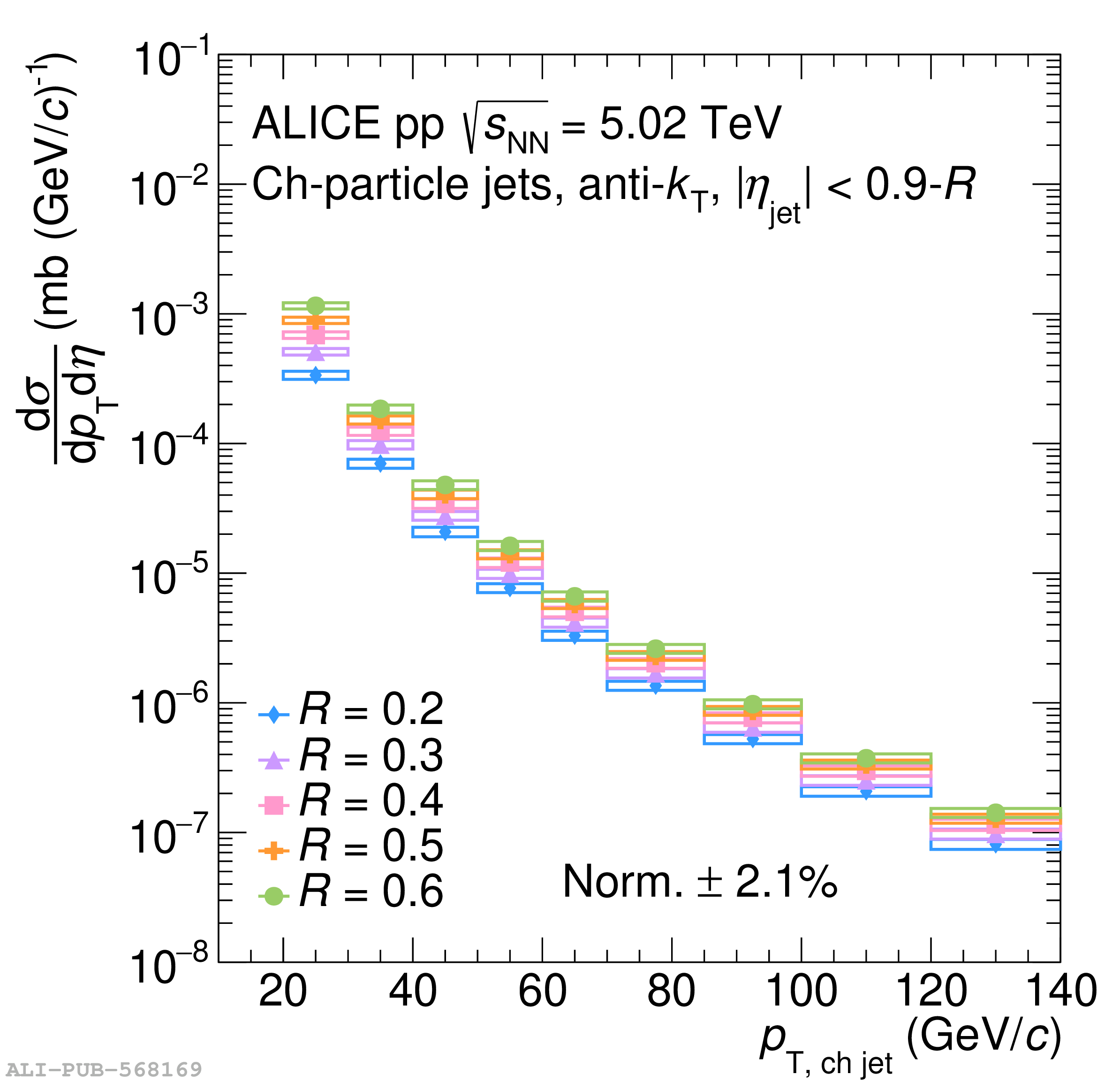
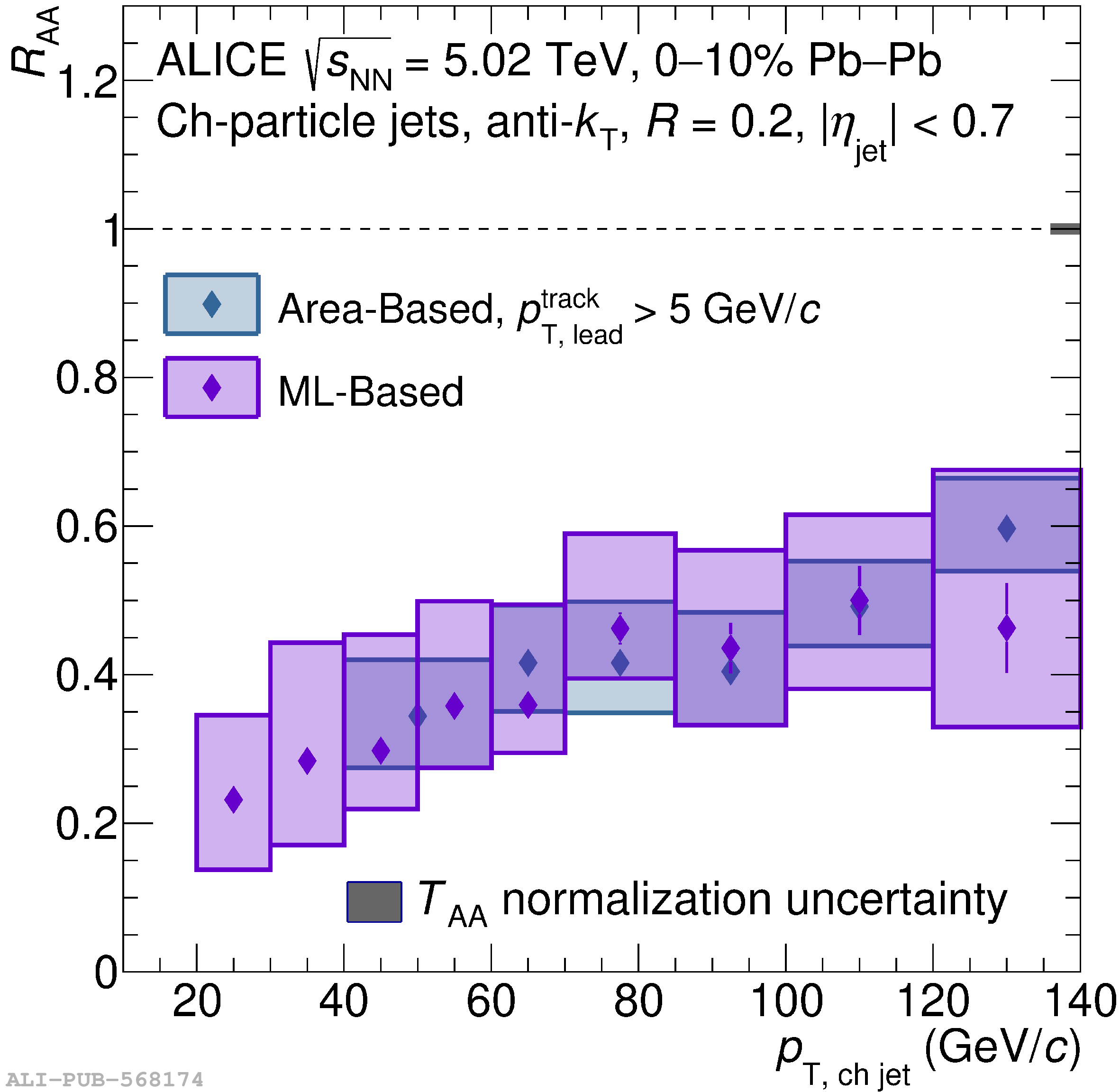
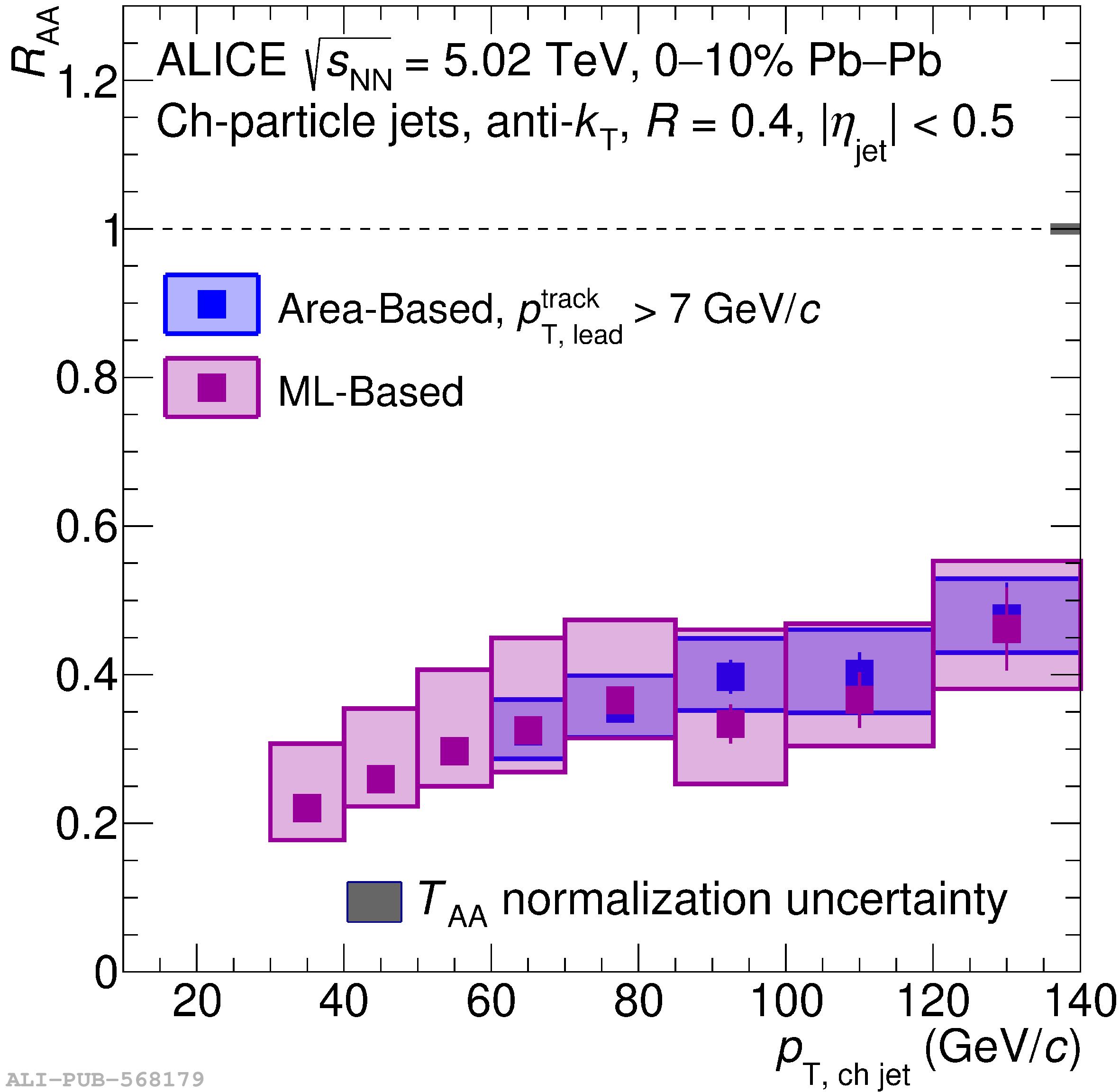
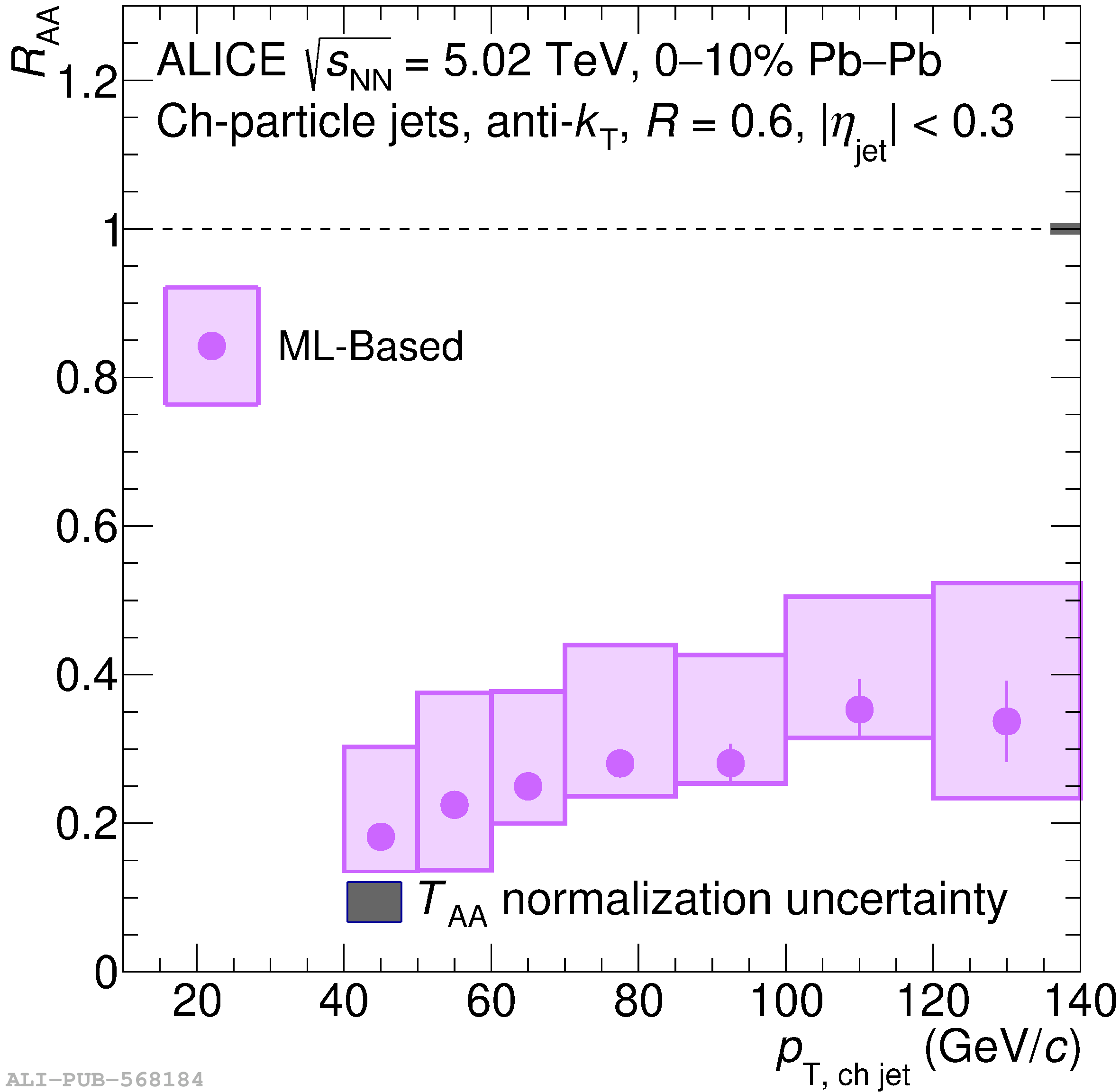
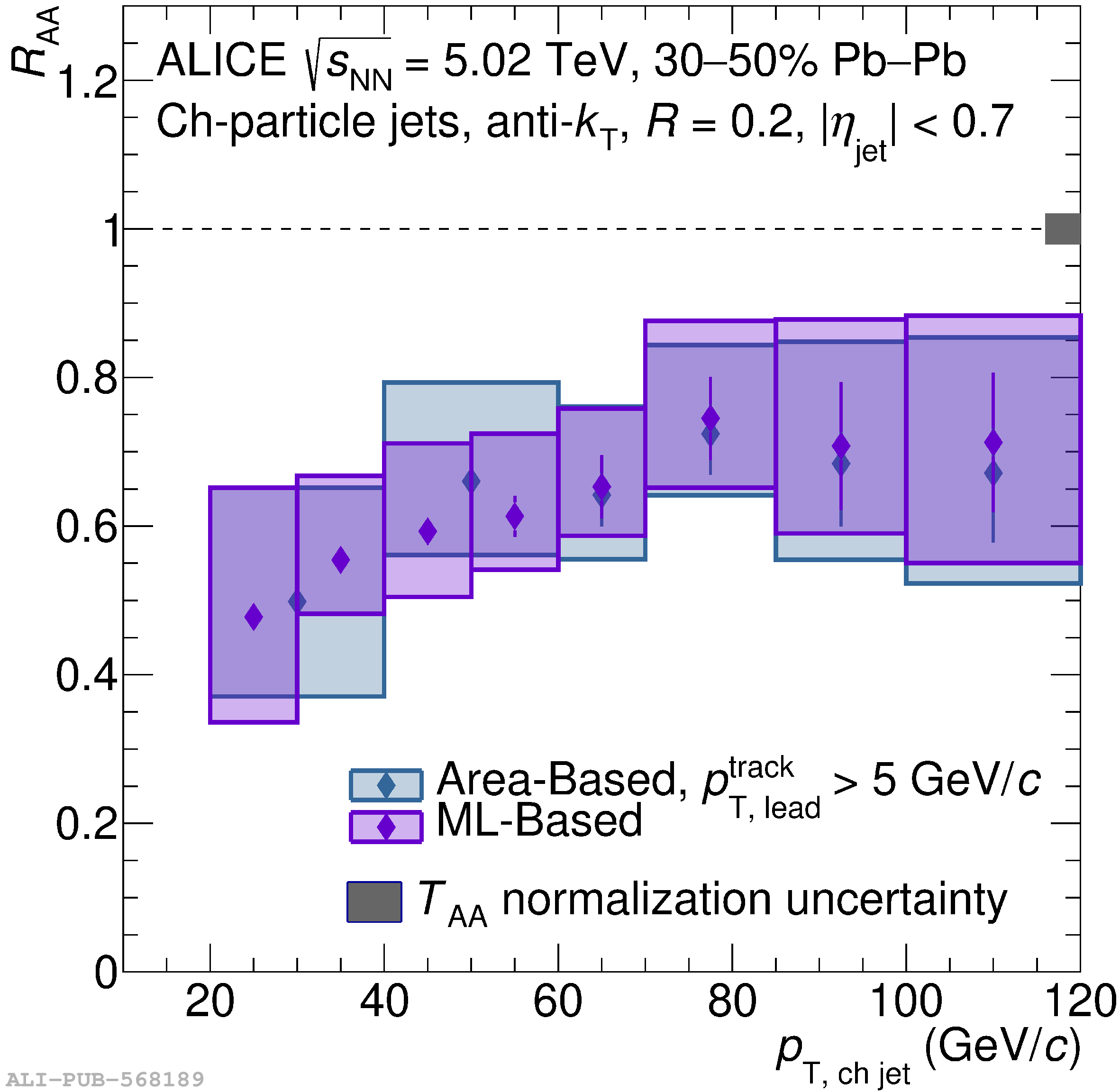
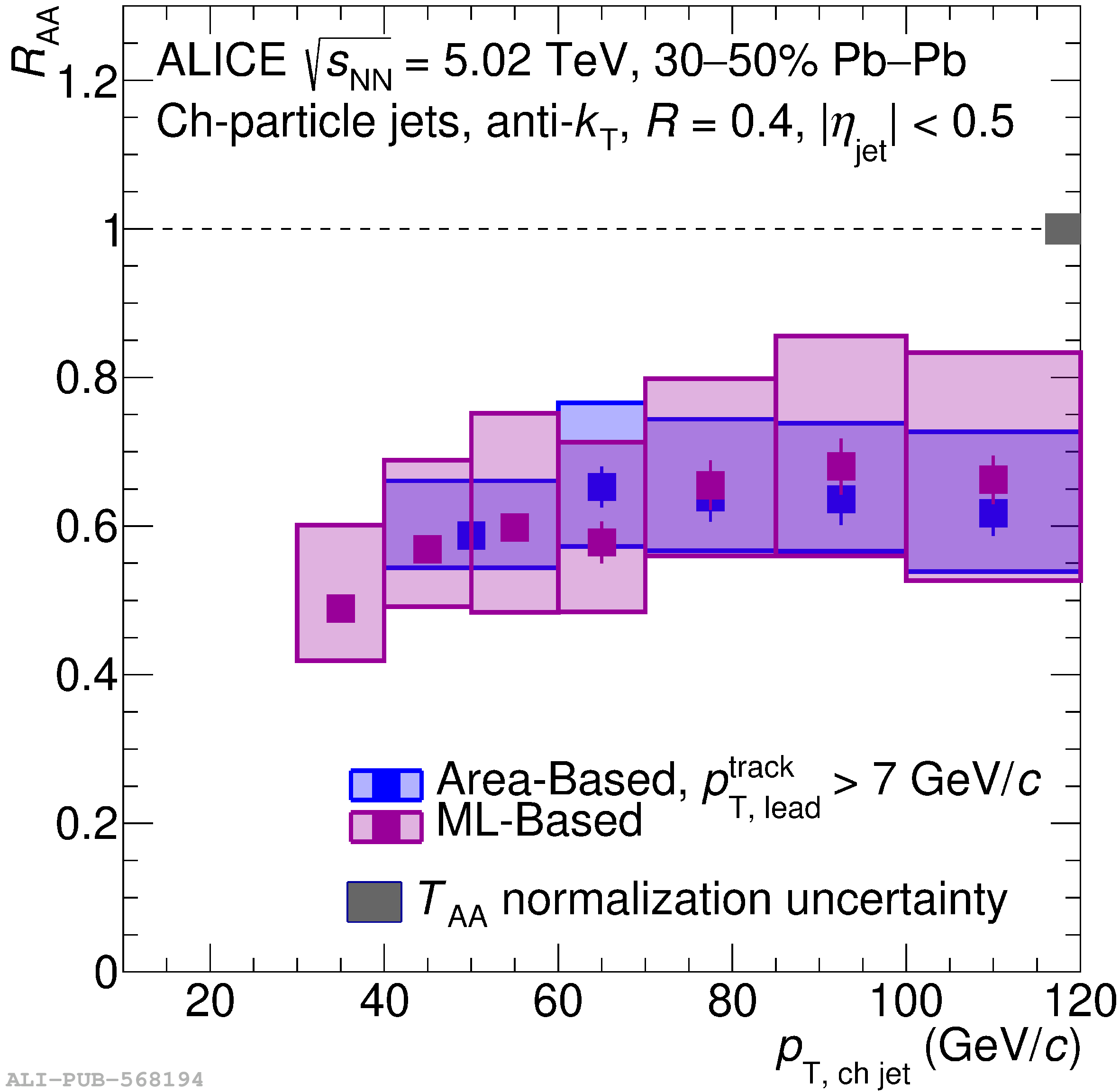
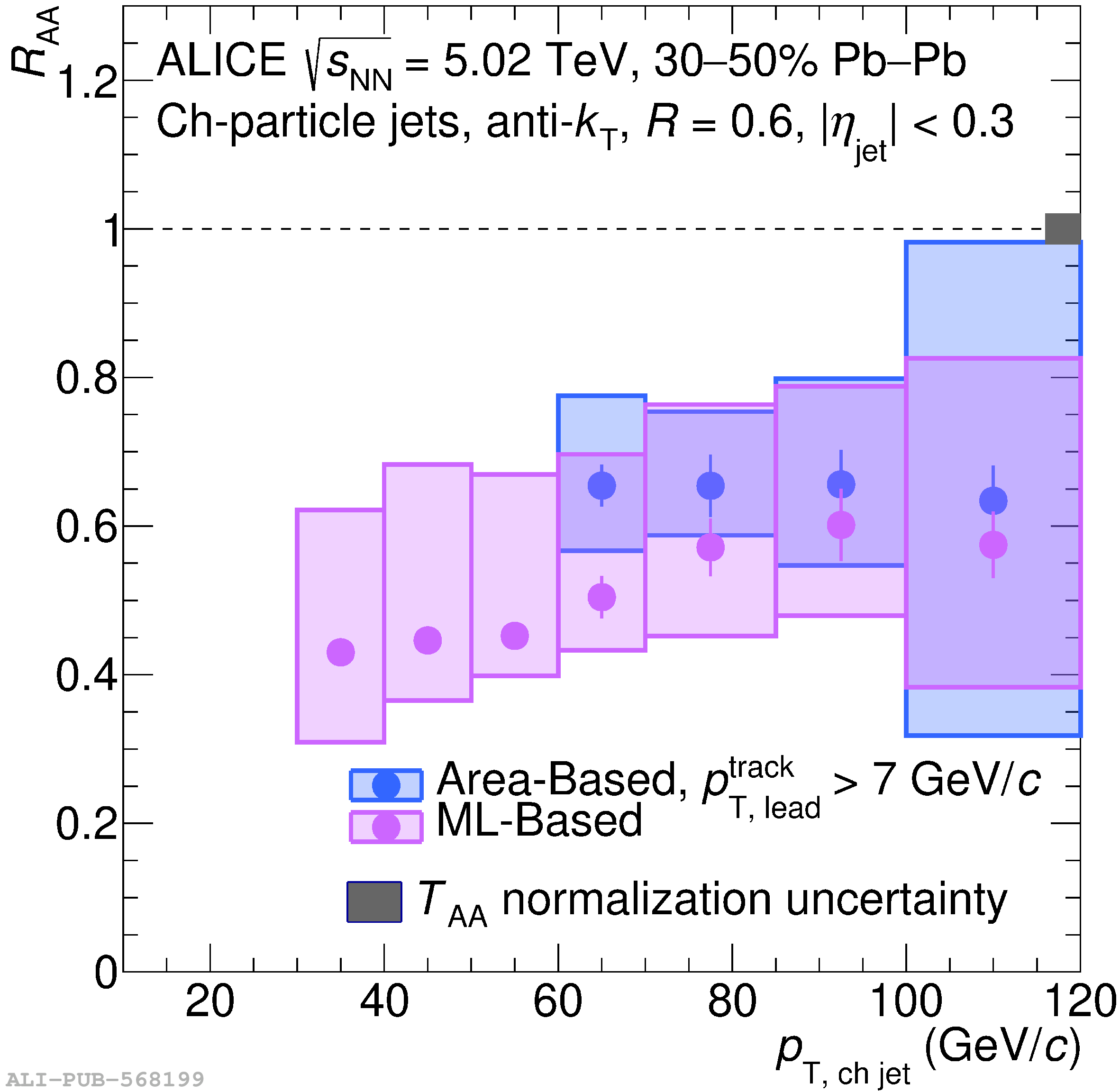
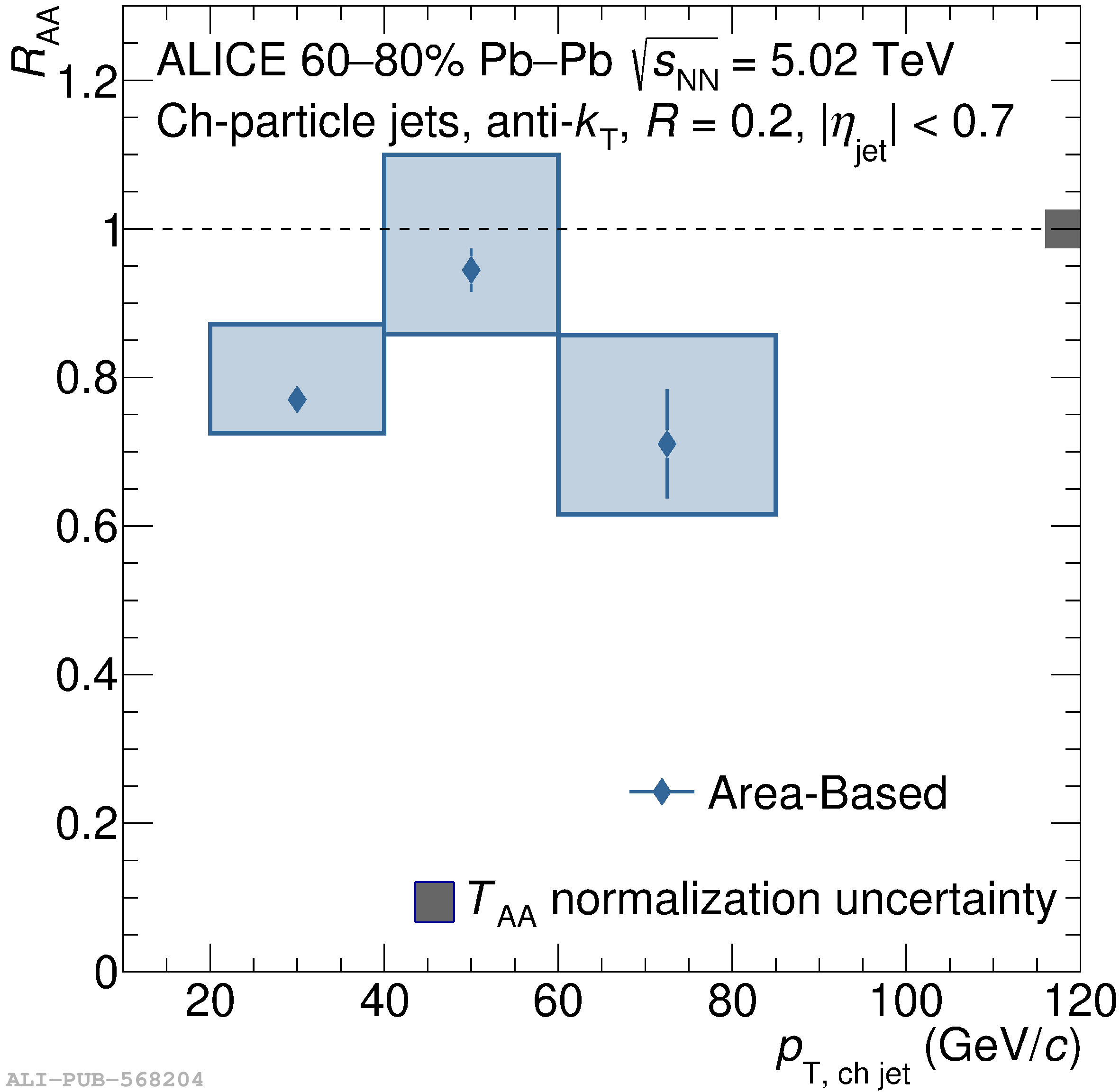
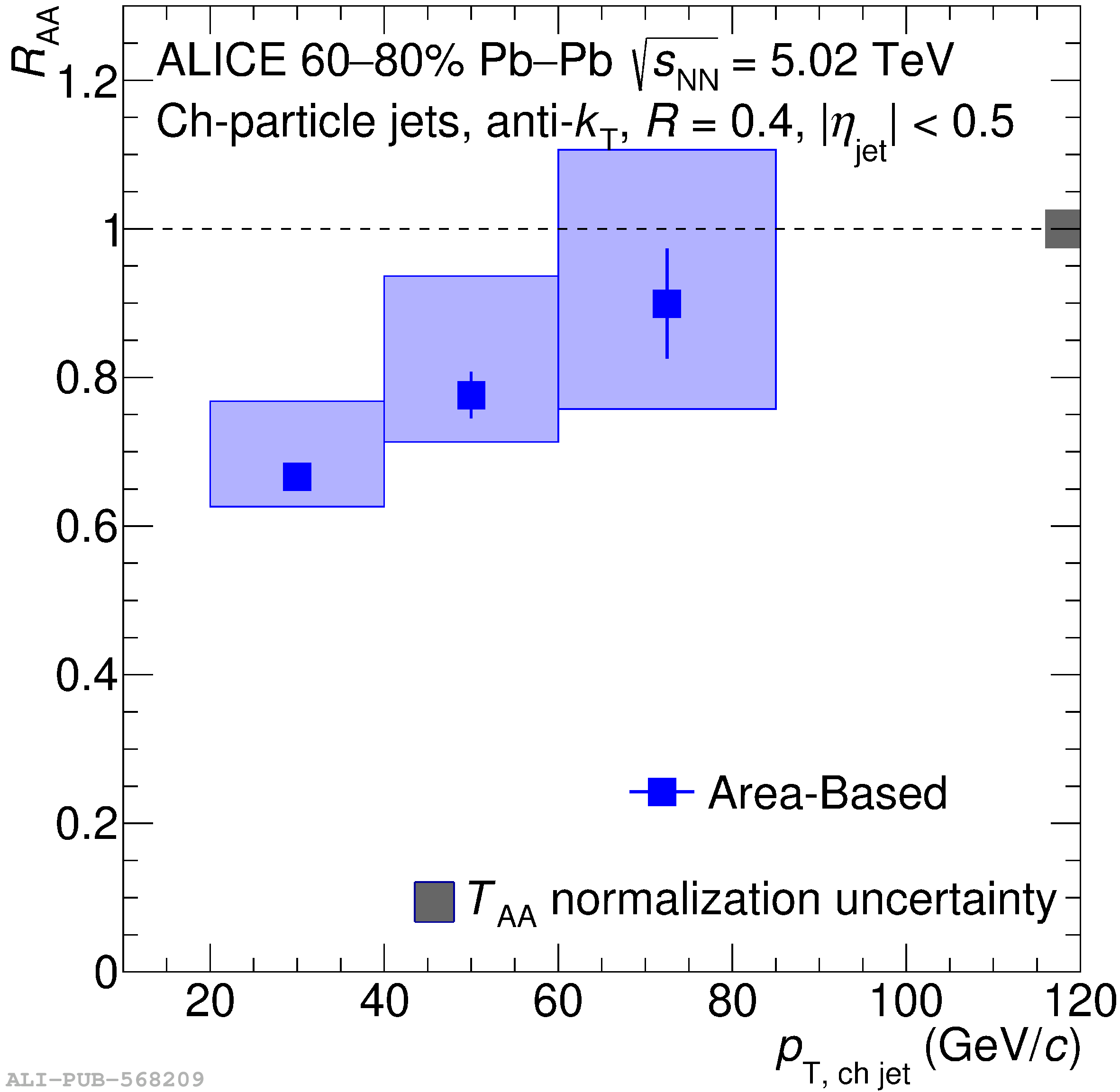
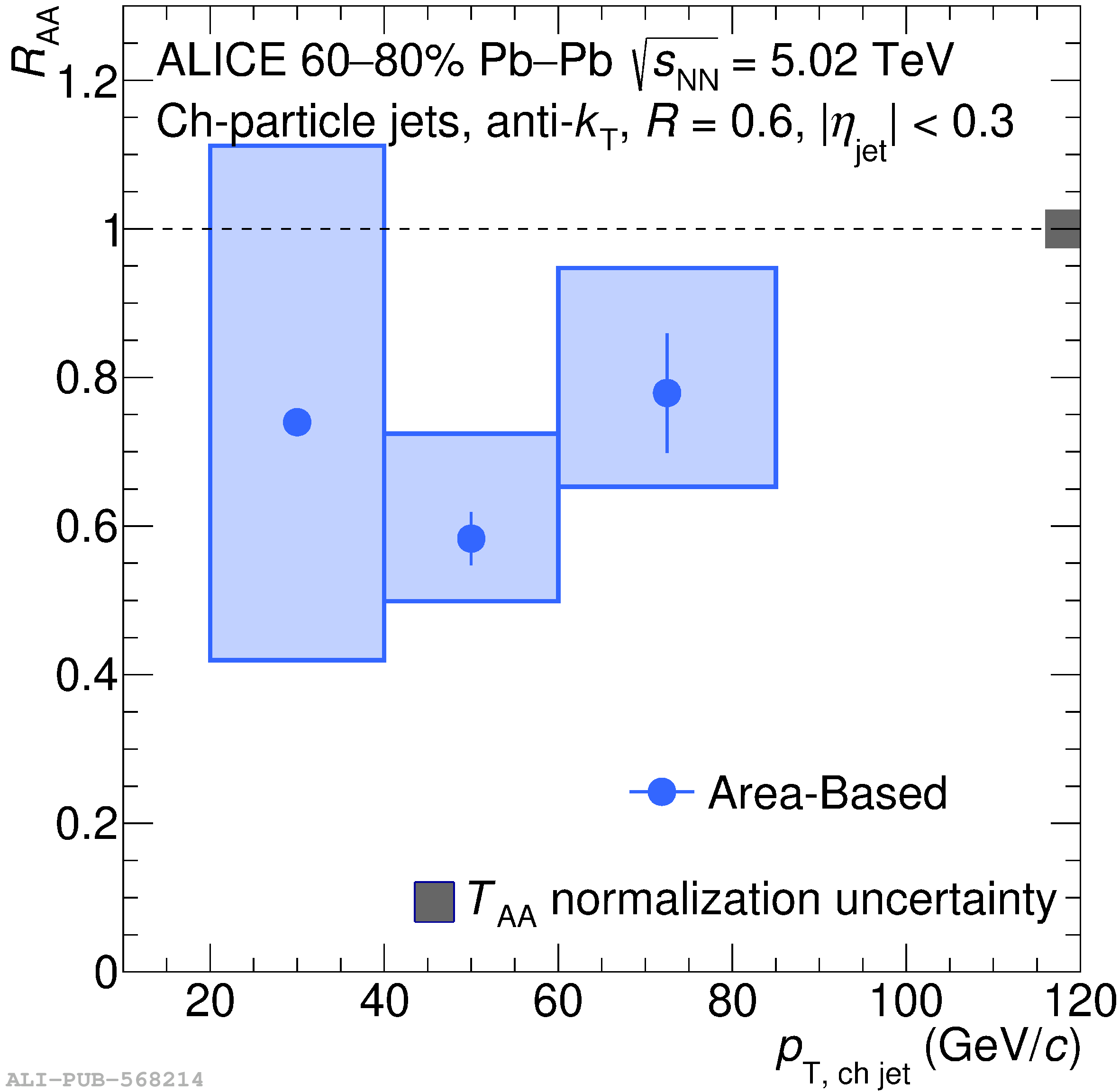
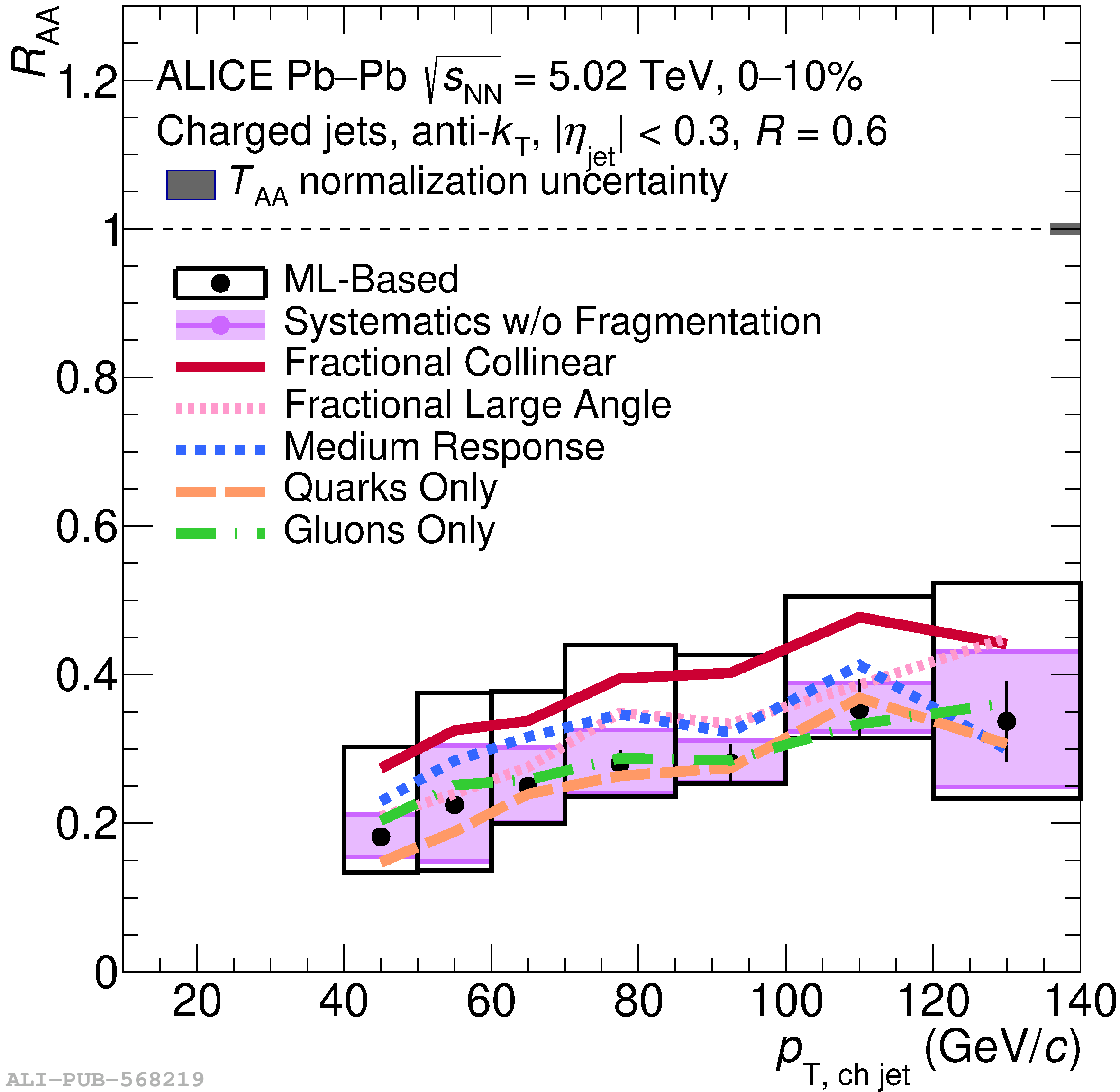
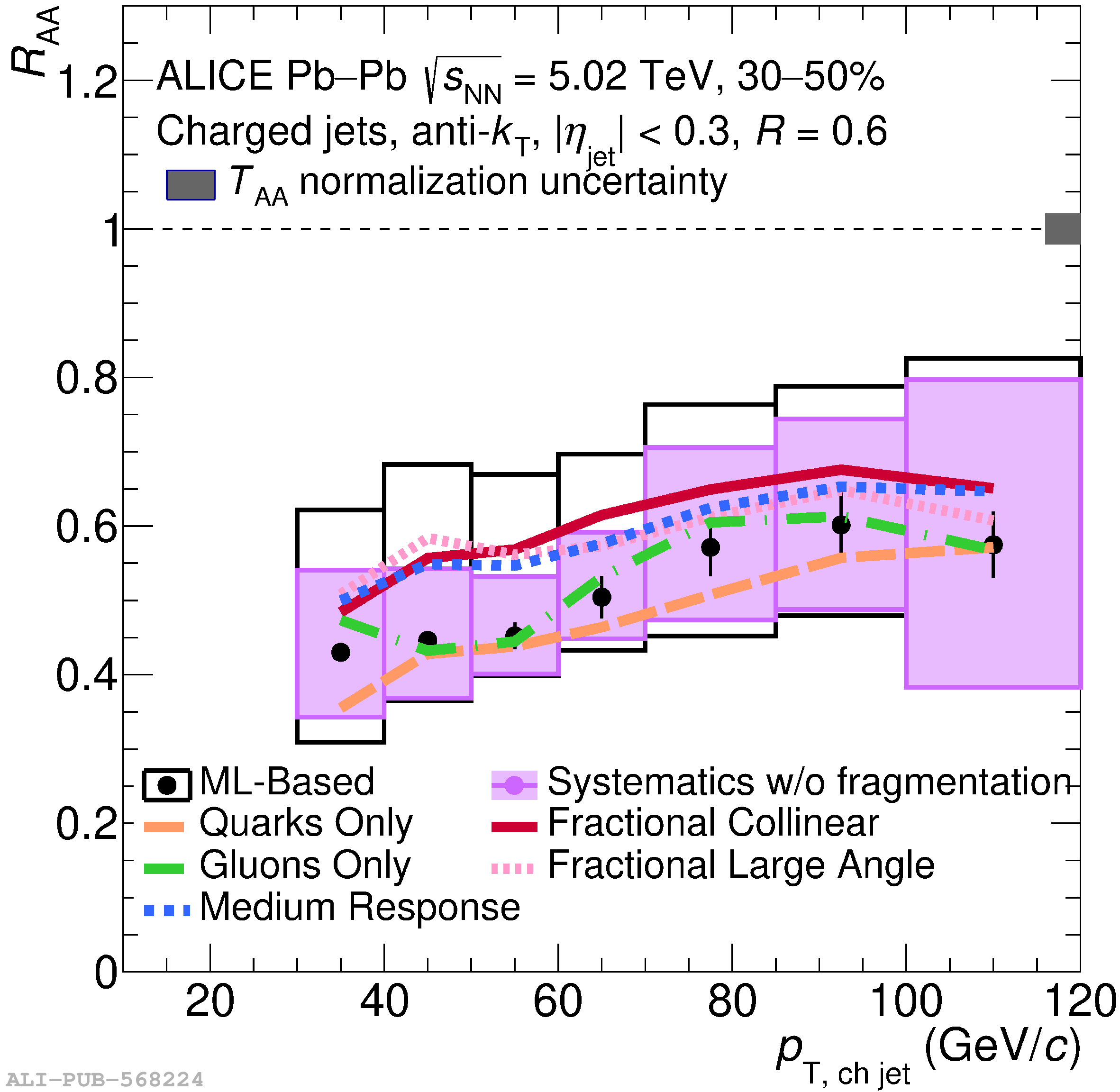
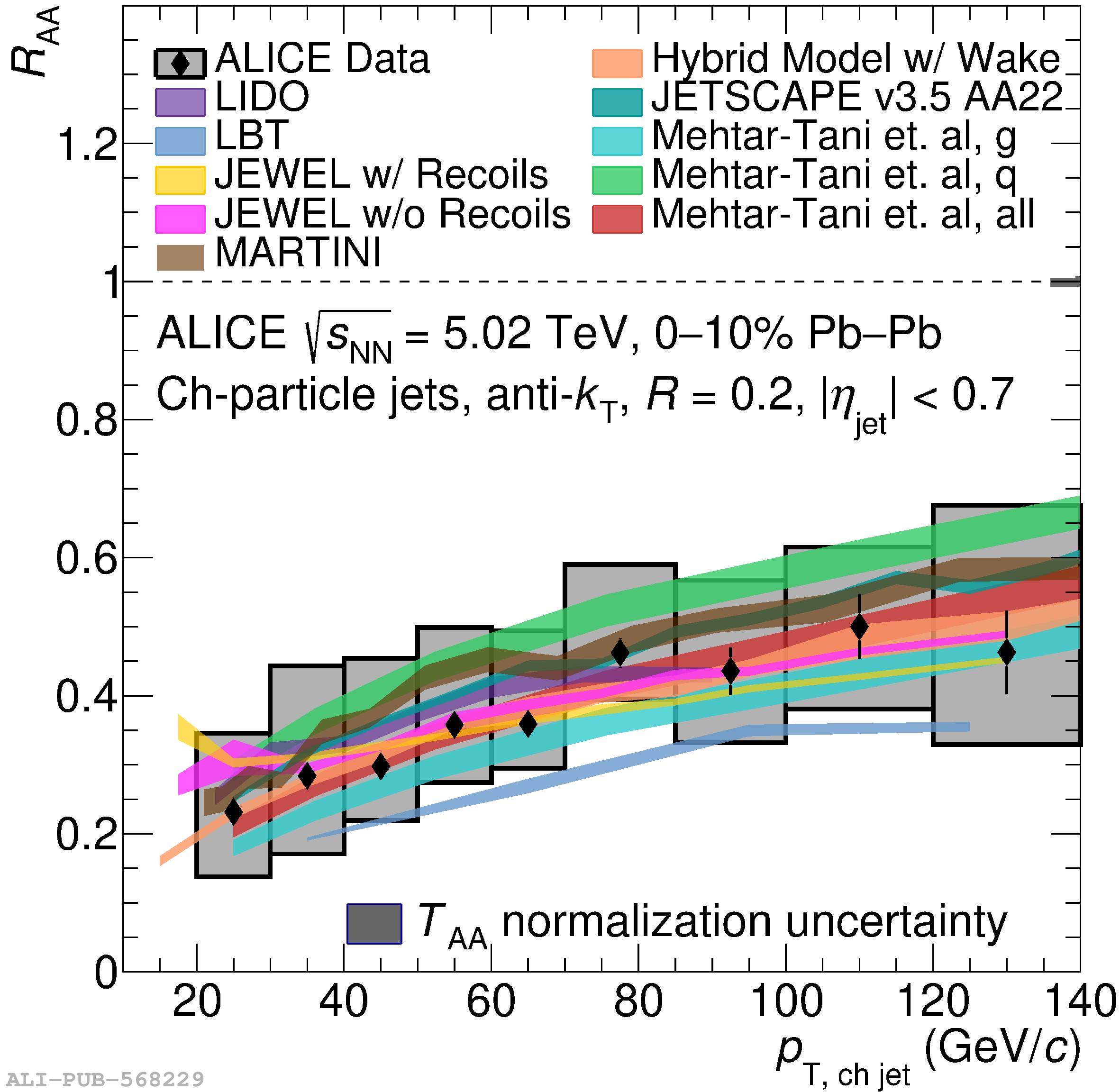
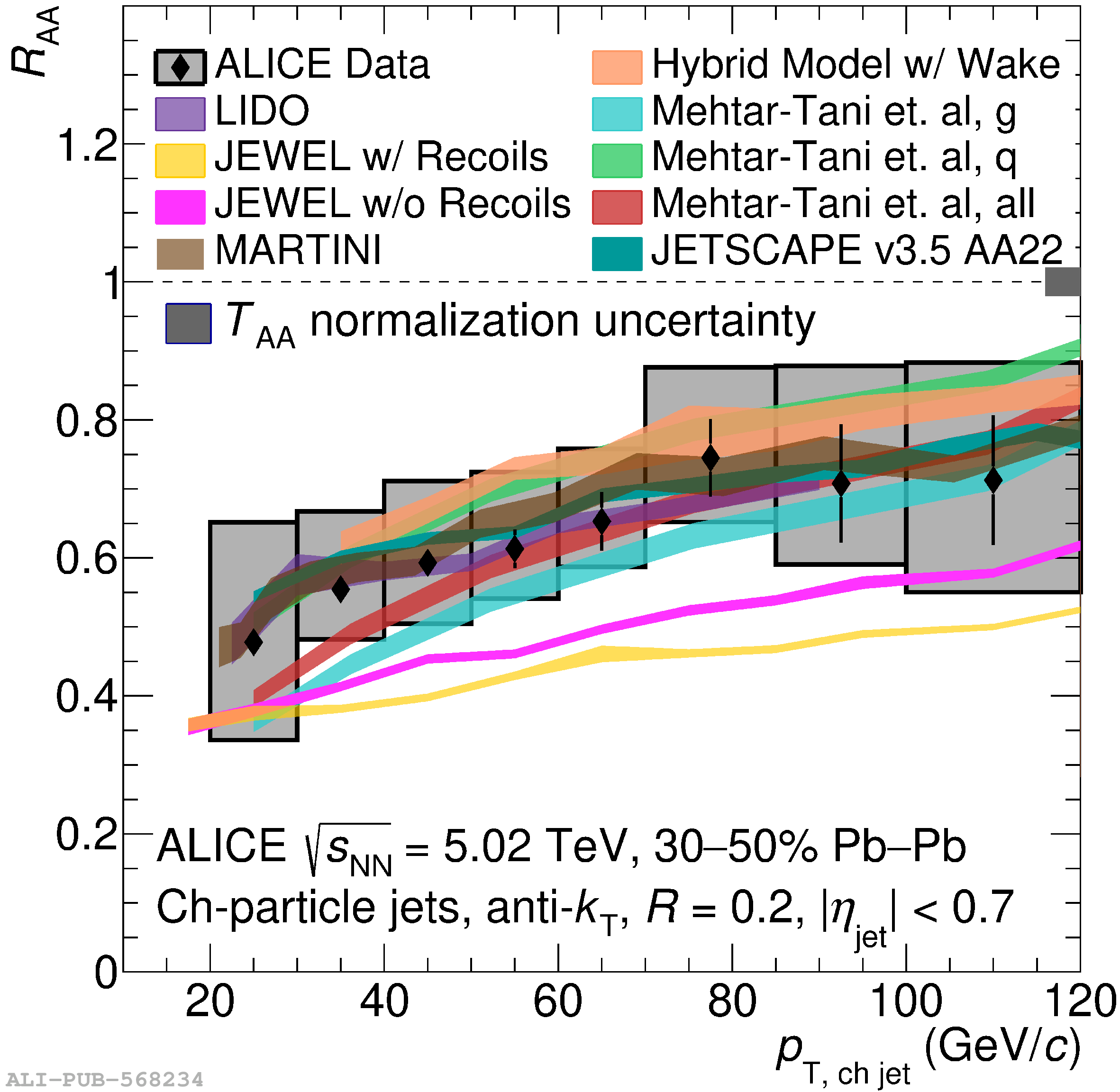
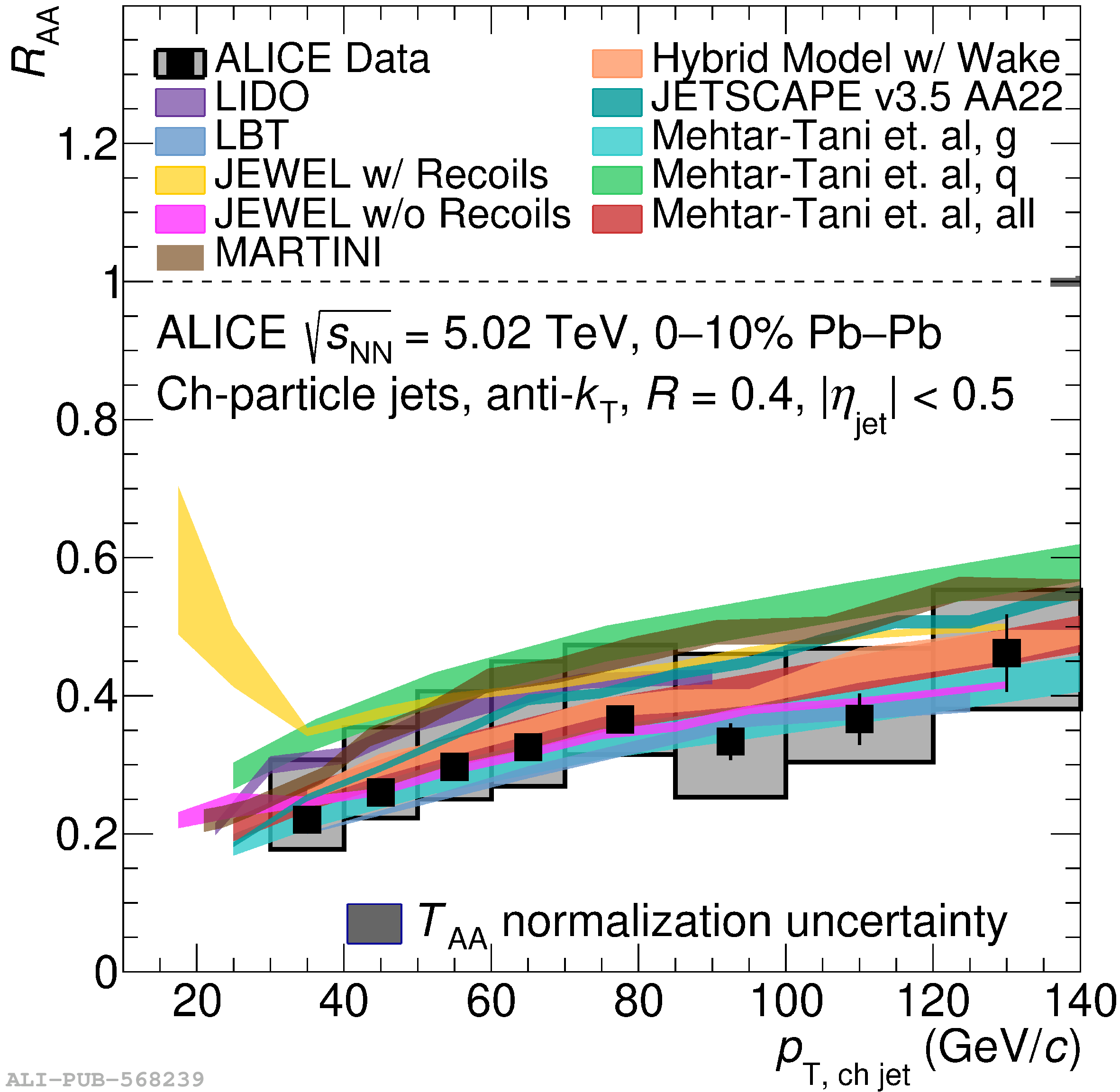
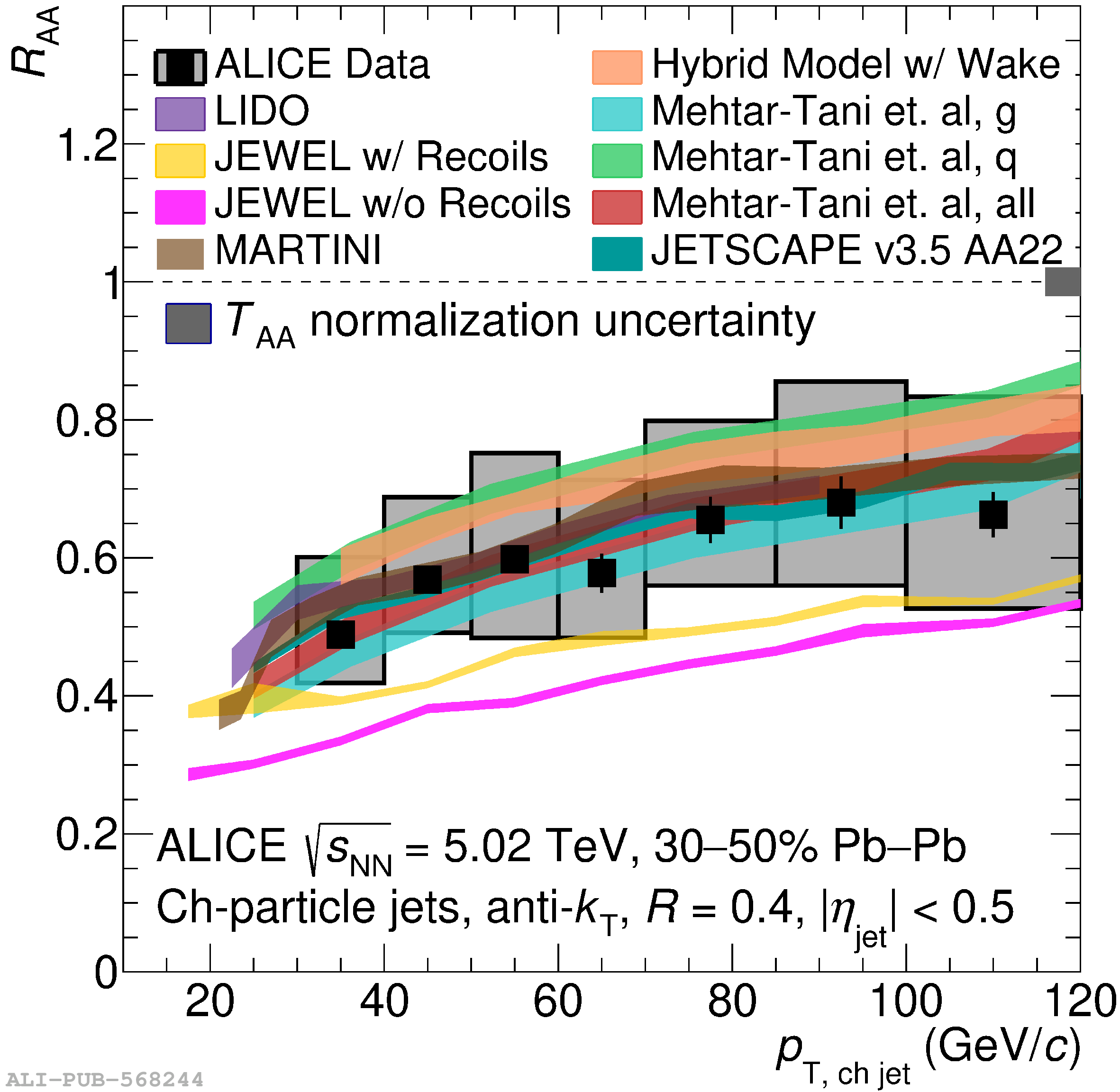
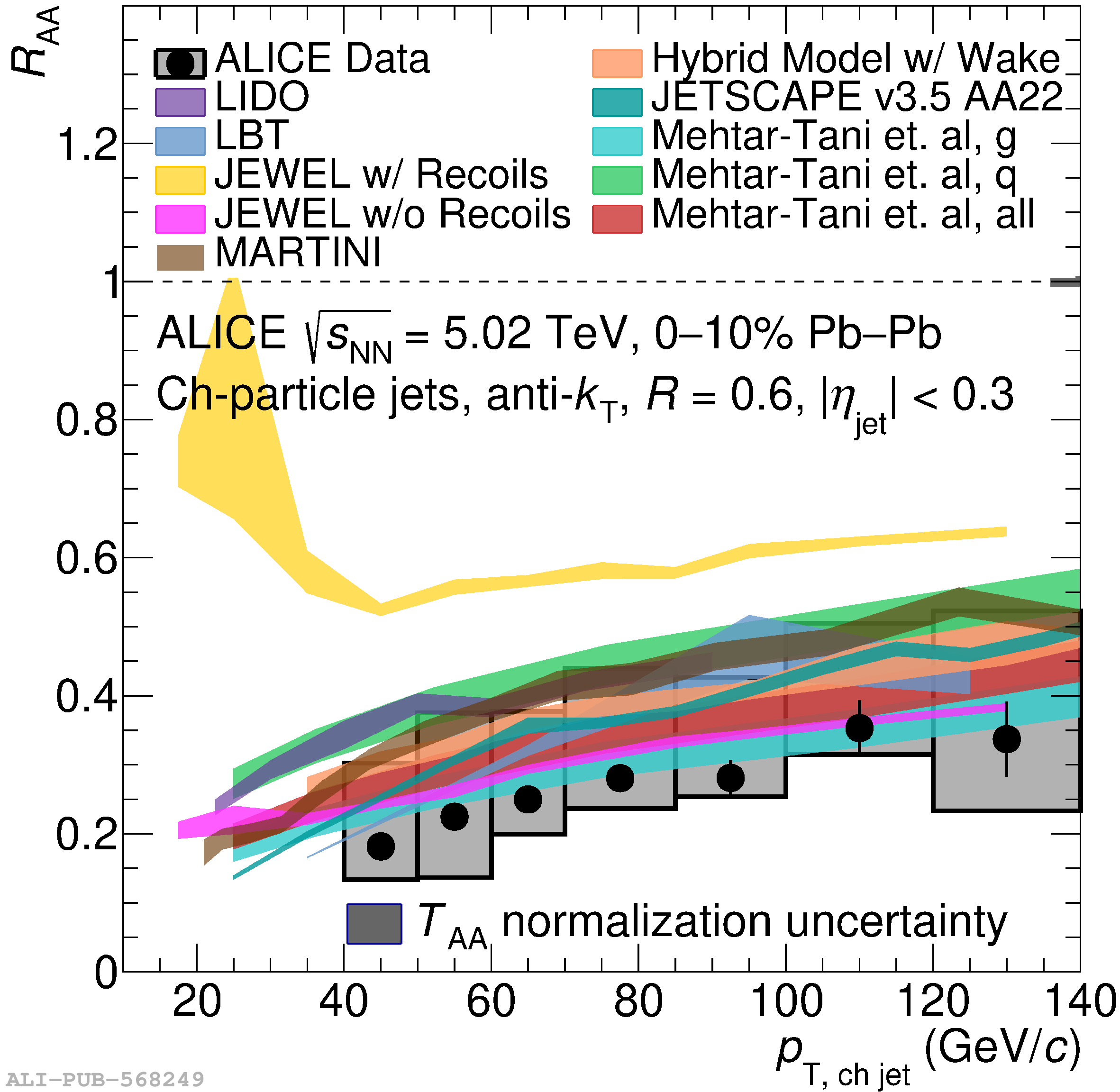
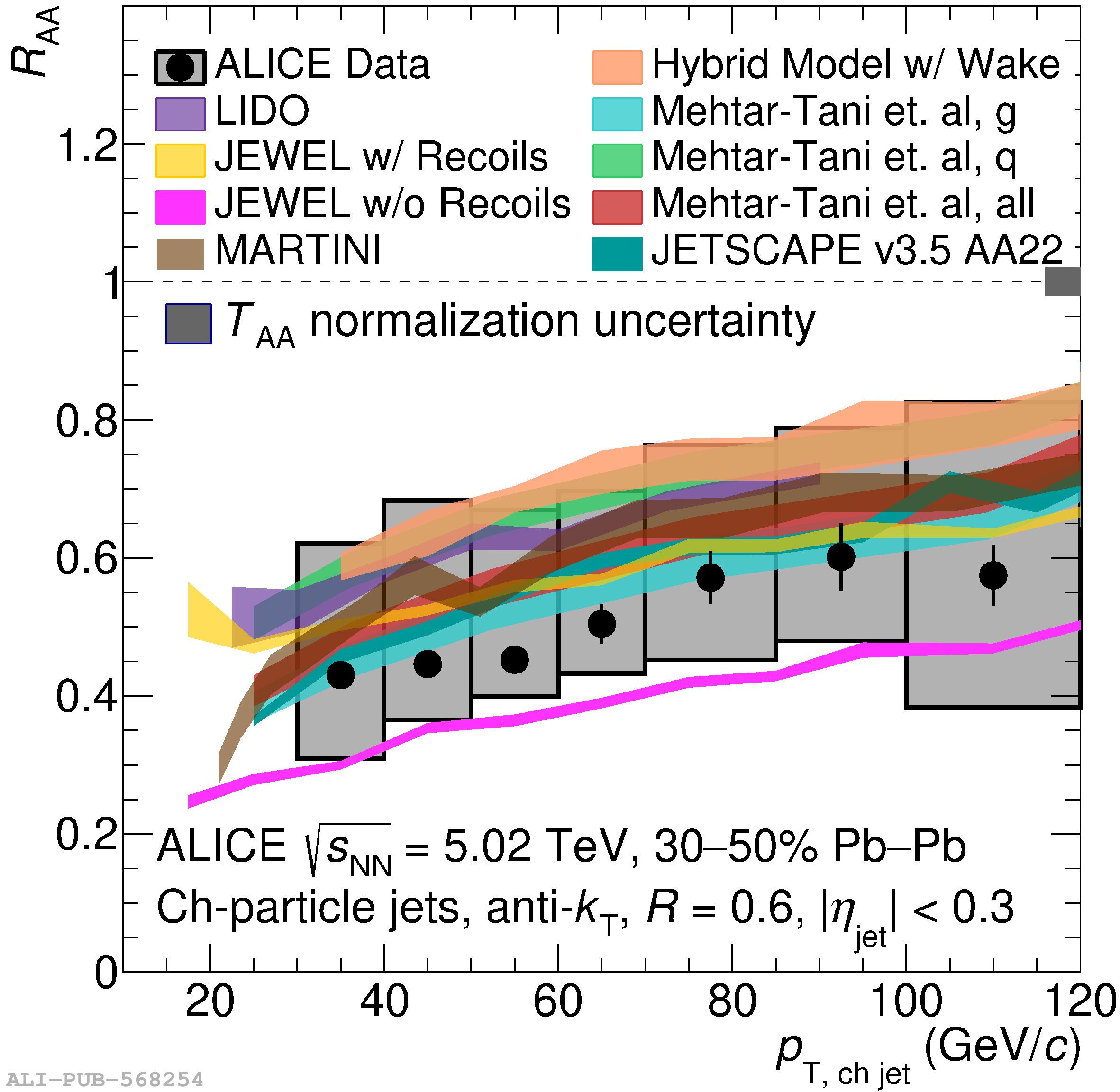
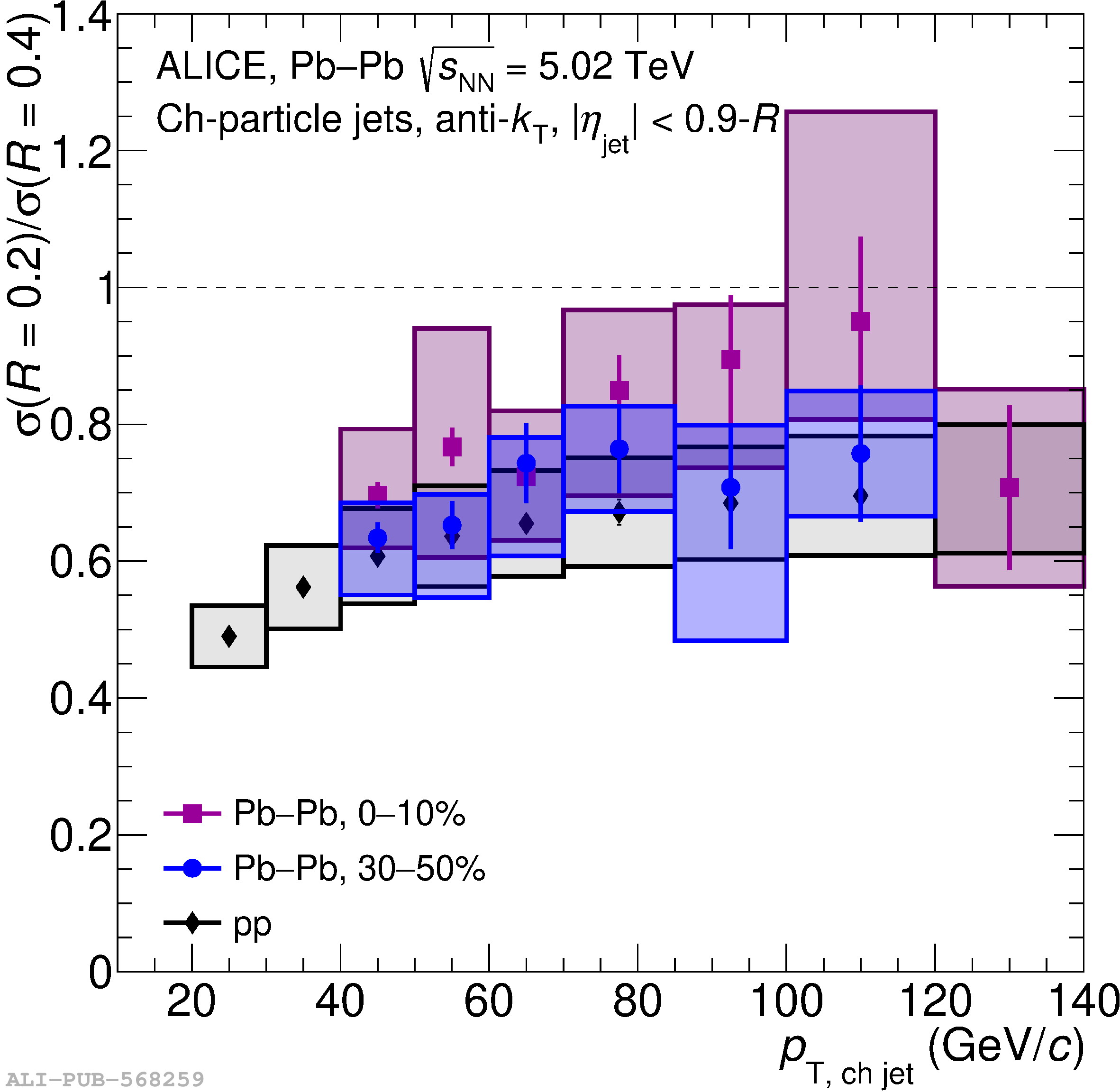
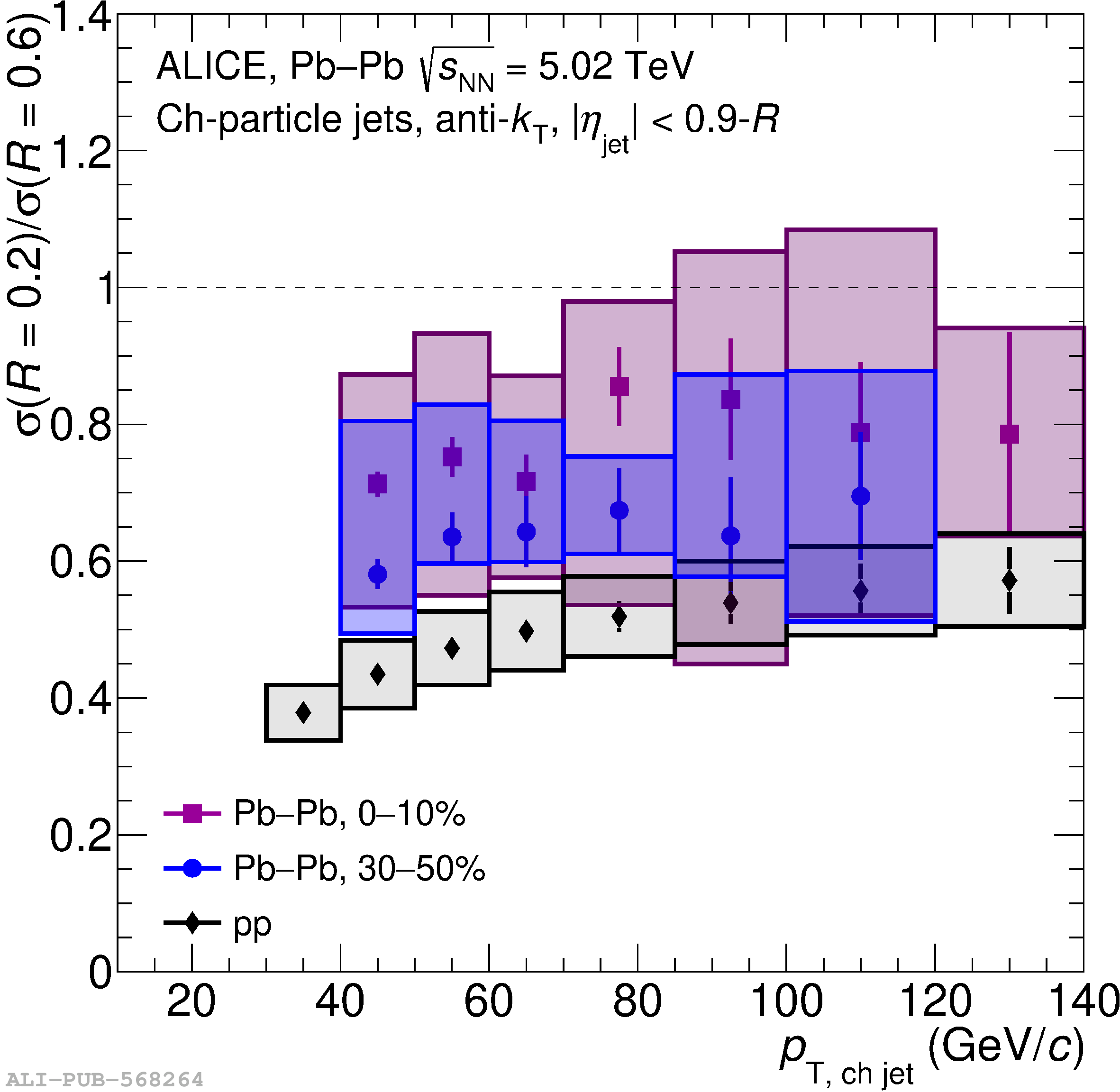
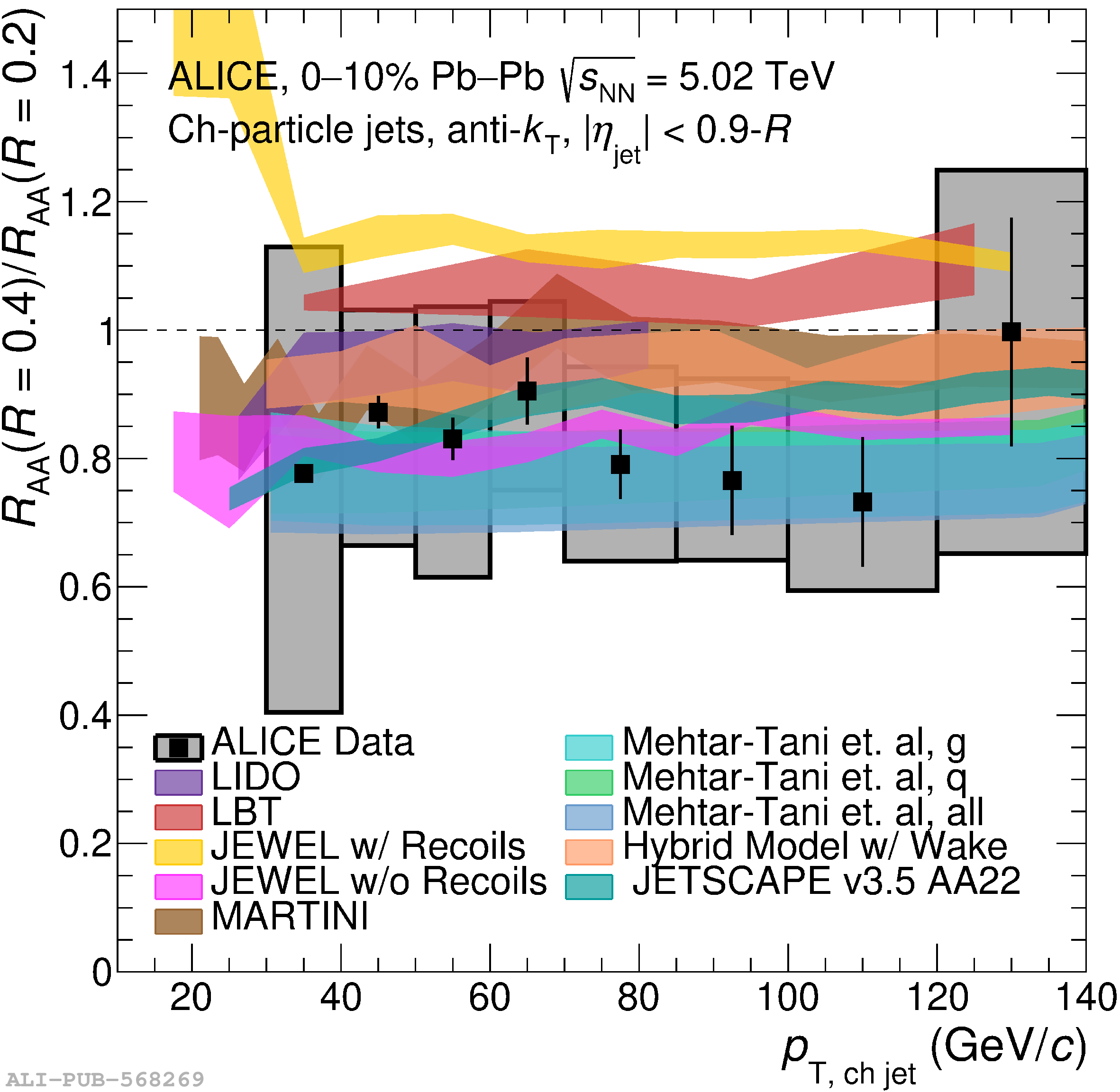
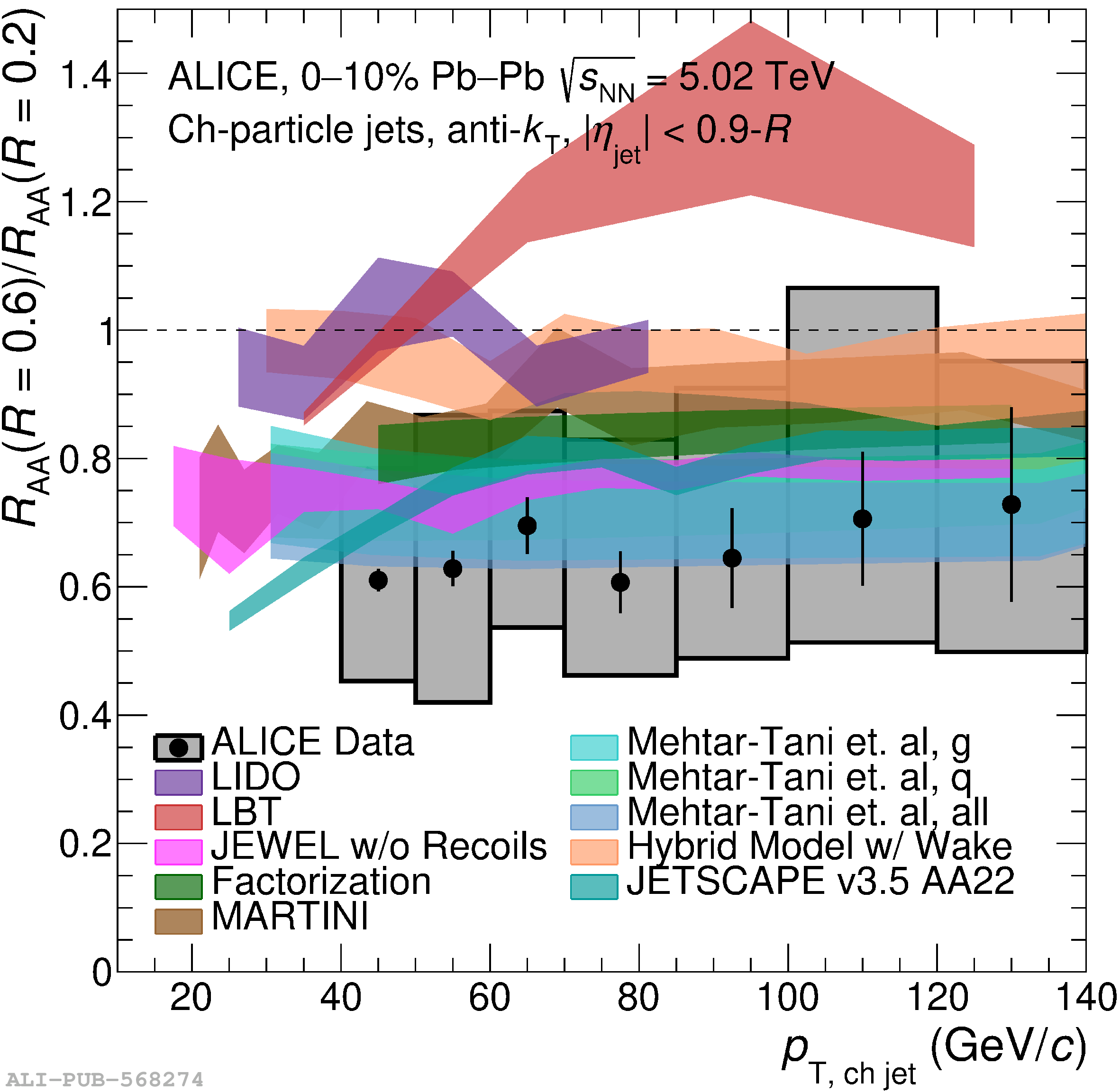
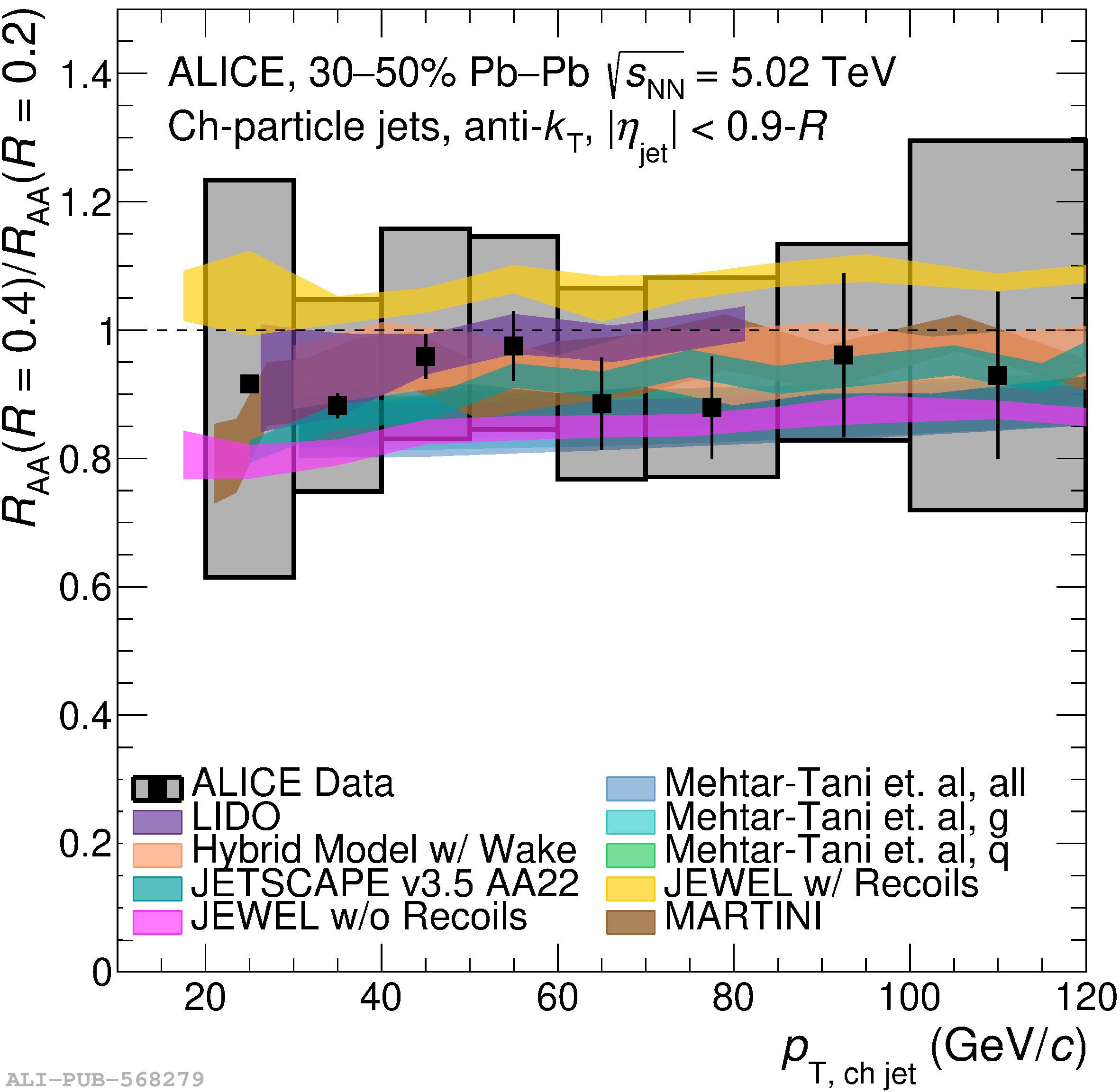
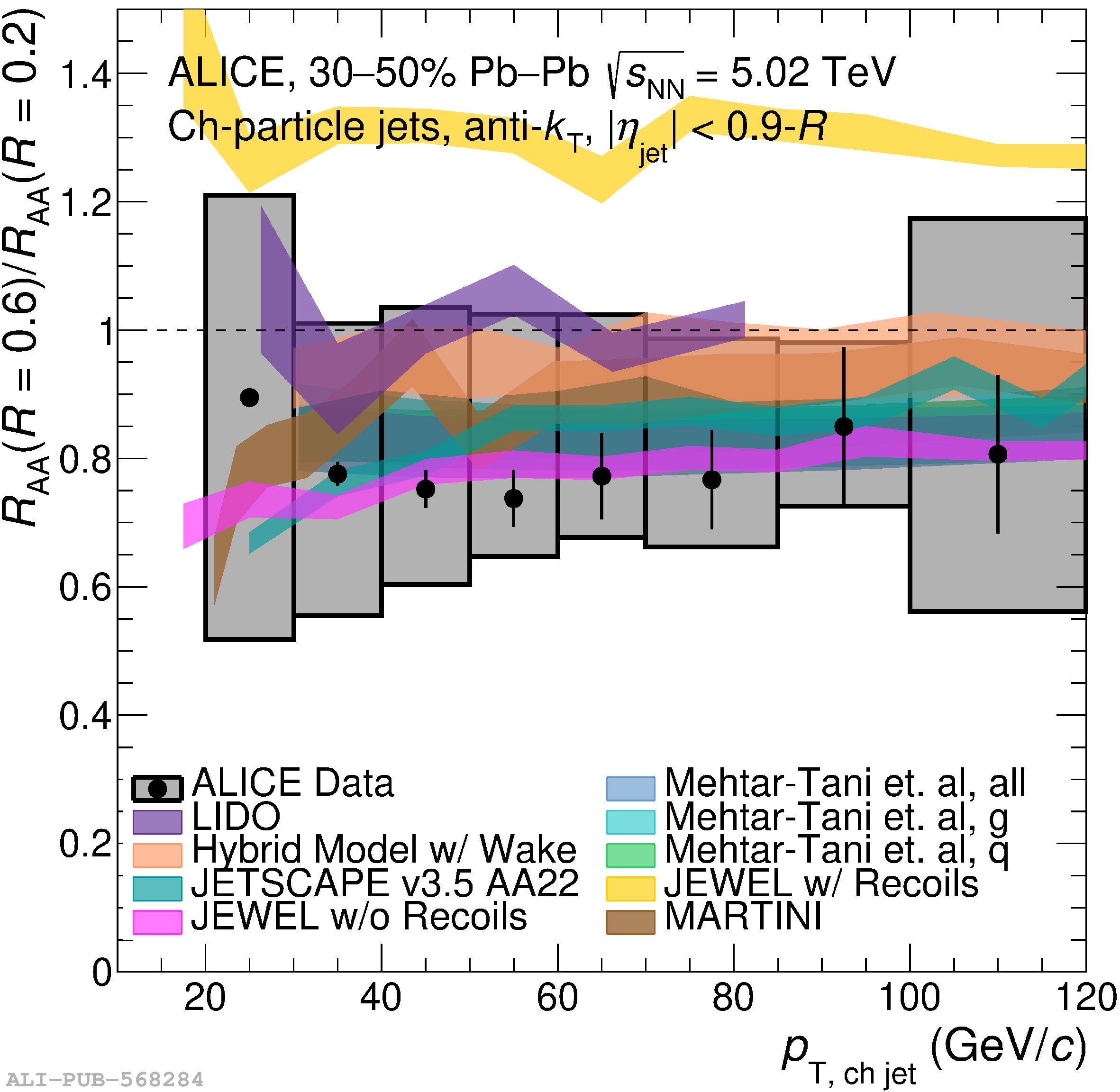
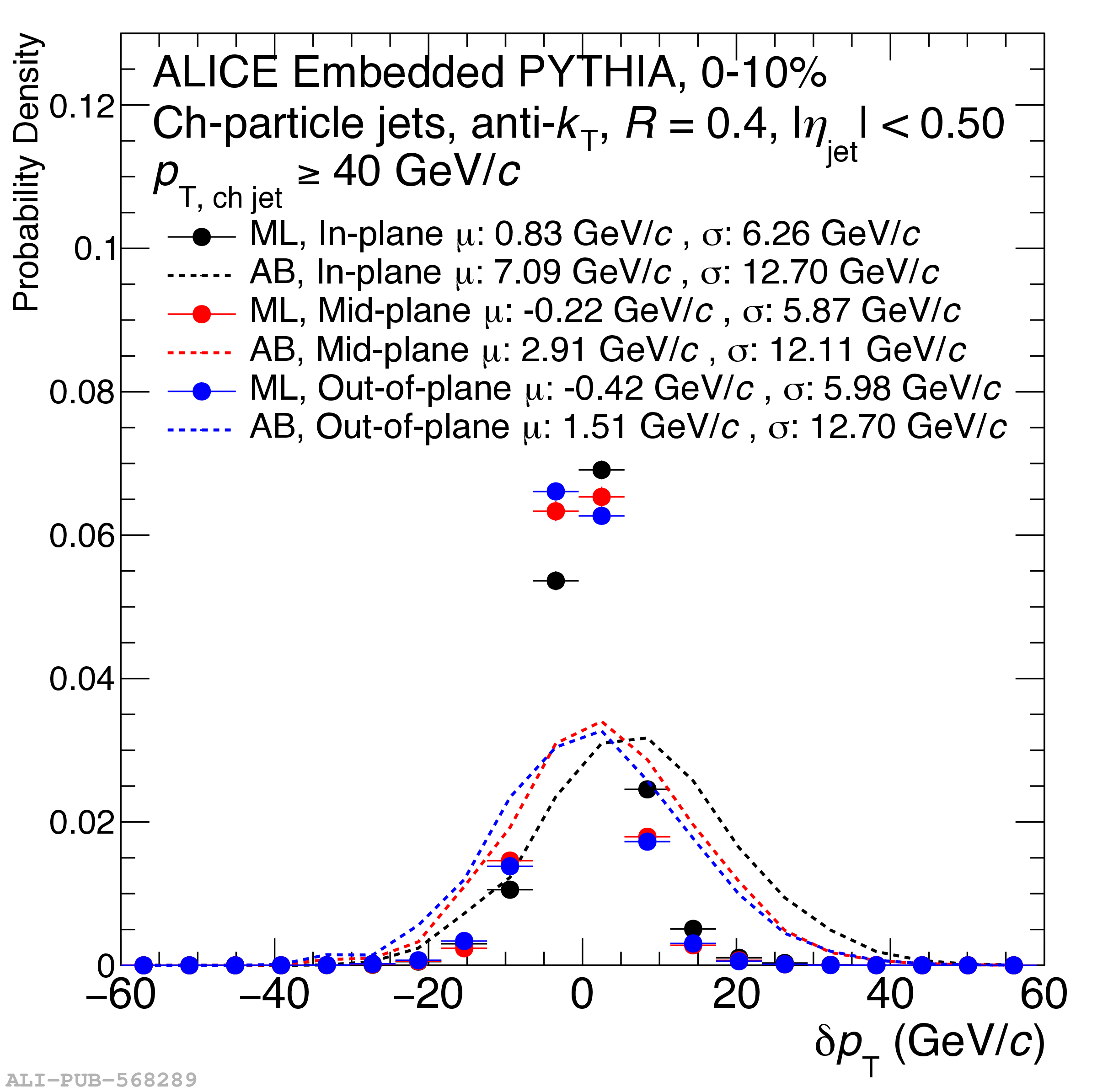
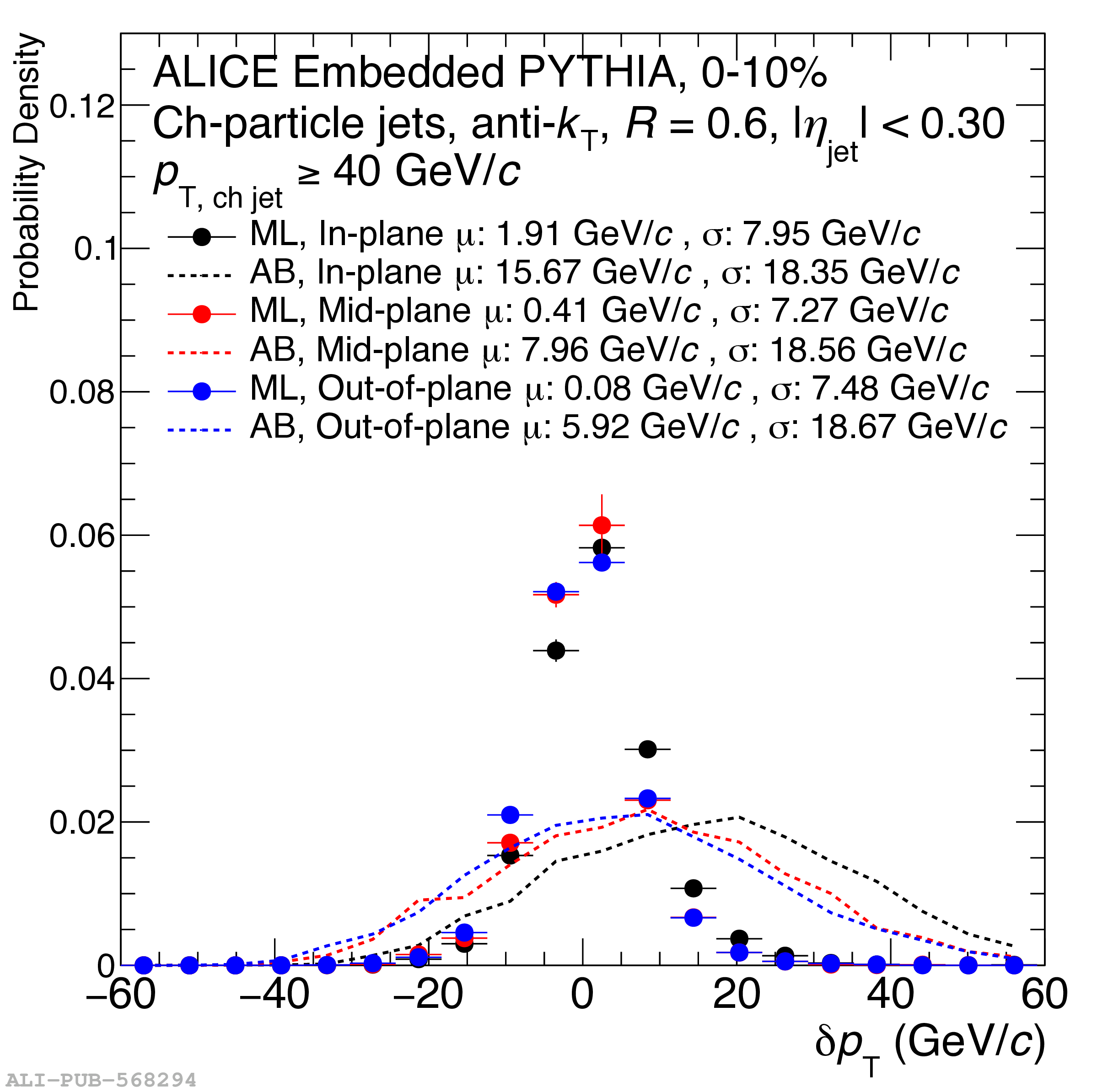
The ALICE Collaboration reports a differential measurement of inclusive jet suppression using pp and Pb$-$Pb collision data at a center-of-mass energy per nucleon-nucleon collision $\sqrt{s_{\rm NN}} = 5.02$ TeV. Charged-particle jets are reconstructed using the anti-$k_{\rm T}$ algorithm with resolution parameters $R =$ 0.2, 0.3, 0.4, 0.5, and 0.6 in pp collisions and $R =$ 0.2, 0.4, 0.6 in central (0$-$10%), semi-central (30$-$50%), and peripheral (60$-$80%) Pb$-$Pb collisions. A novel approach based on machine learning is employed to mitigate the influence of jet background. This enables measurements of inclusive jet suppression in new regions of phase space, including down to the lowest jet $p_{\rm T} \geq 40$ GeV/$c$ at $R = 0.6$ in central Pb$-$Pb collisions. This is an important step for discriminating different models of jet quenching in the quark-gluon plasma. The transverse momentum spectra, nuclear modification factors, derived cross section, and nuclear modification factor ratios for different jet resolution parameters of charged-particle jets are presented and compared to model predictions. A mild dependence of the nuclear modification factor ratios on collision centrality and resolution parameter is observed. The results are compared to a variety of jet-quenching models with varying levels of agreement.
Phys. Lett. B 849 (2024) 138412
HEP Data
e-Print: arXiv:2303.00592 | PDF | inSPIRE
CERN-EP-2023-027
Figure group