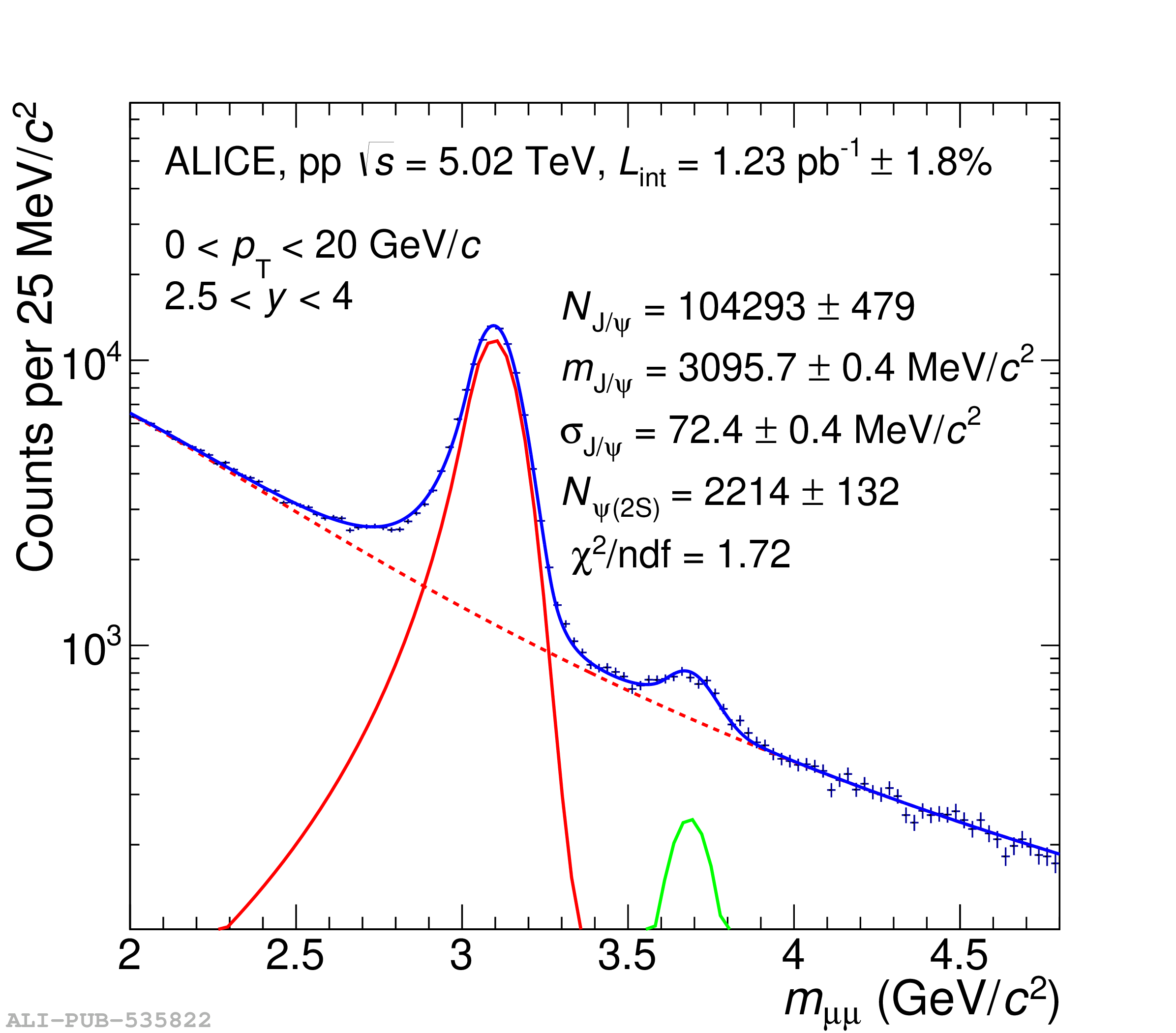
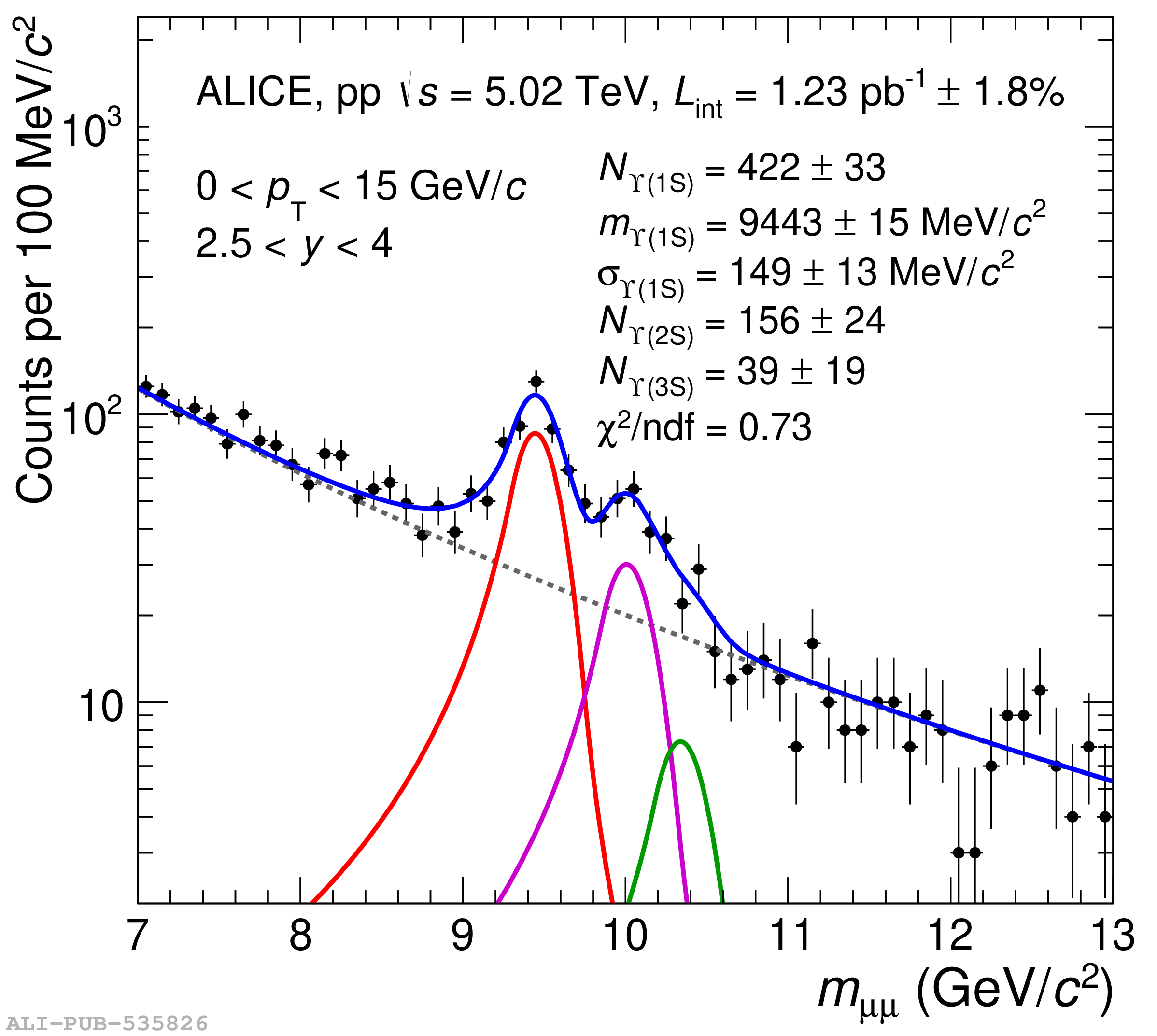
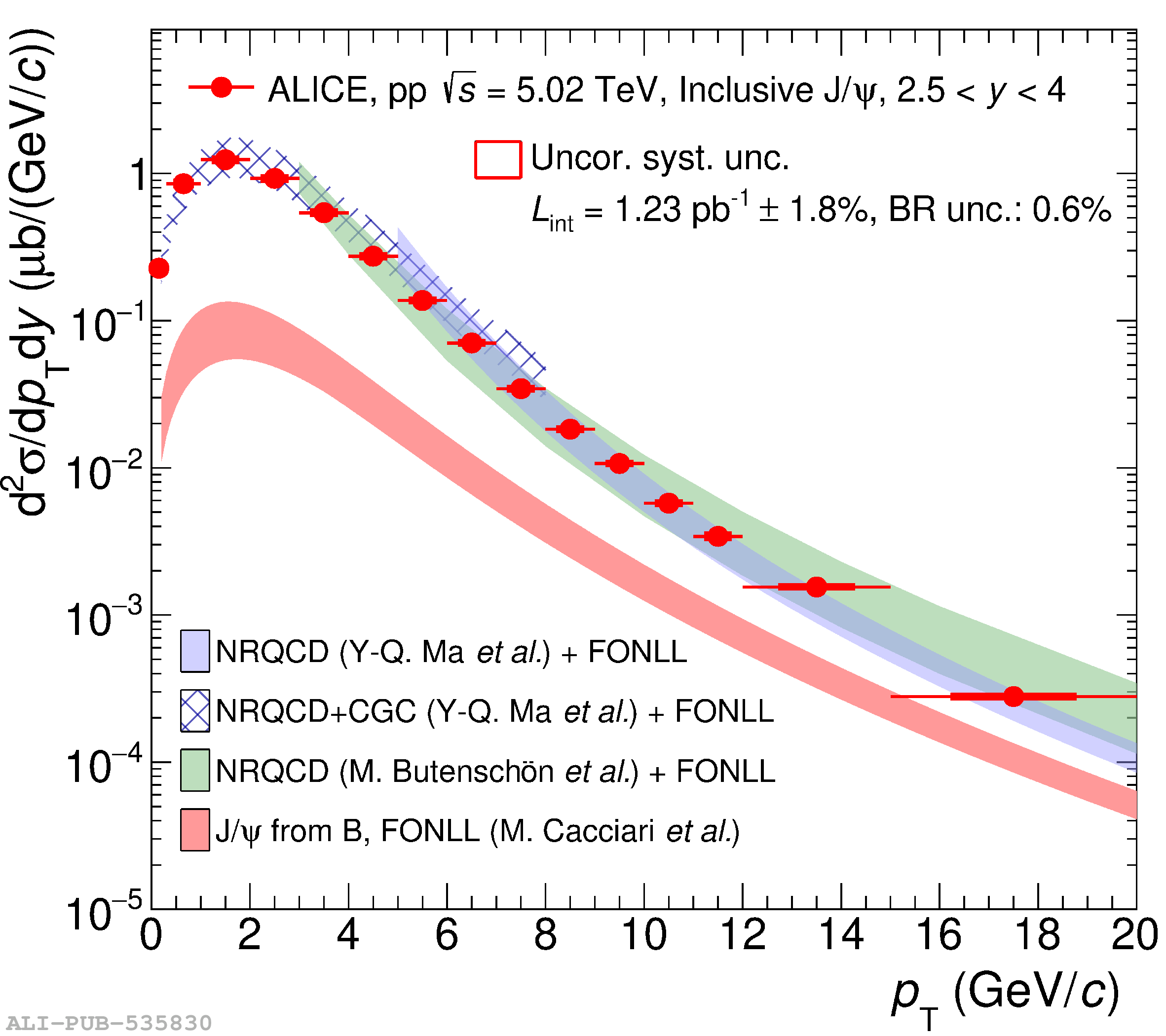
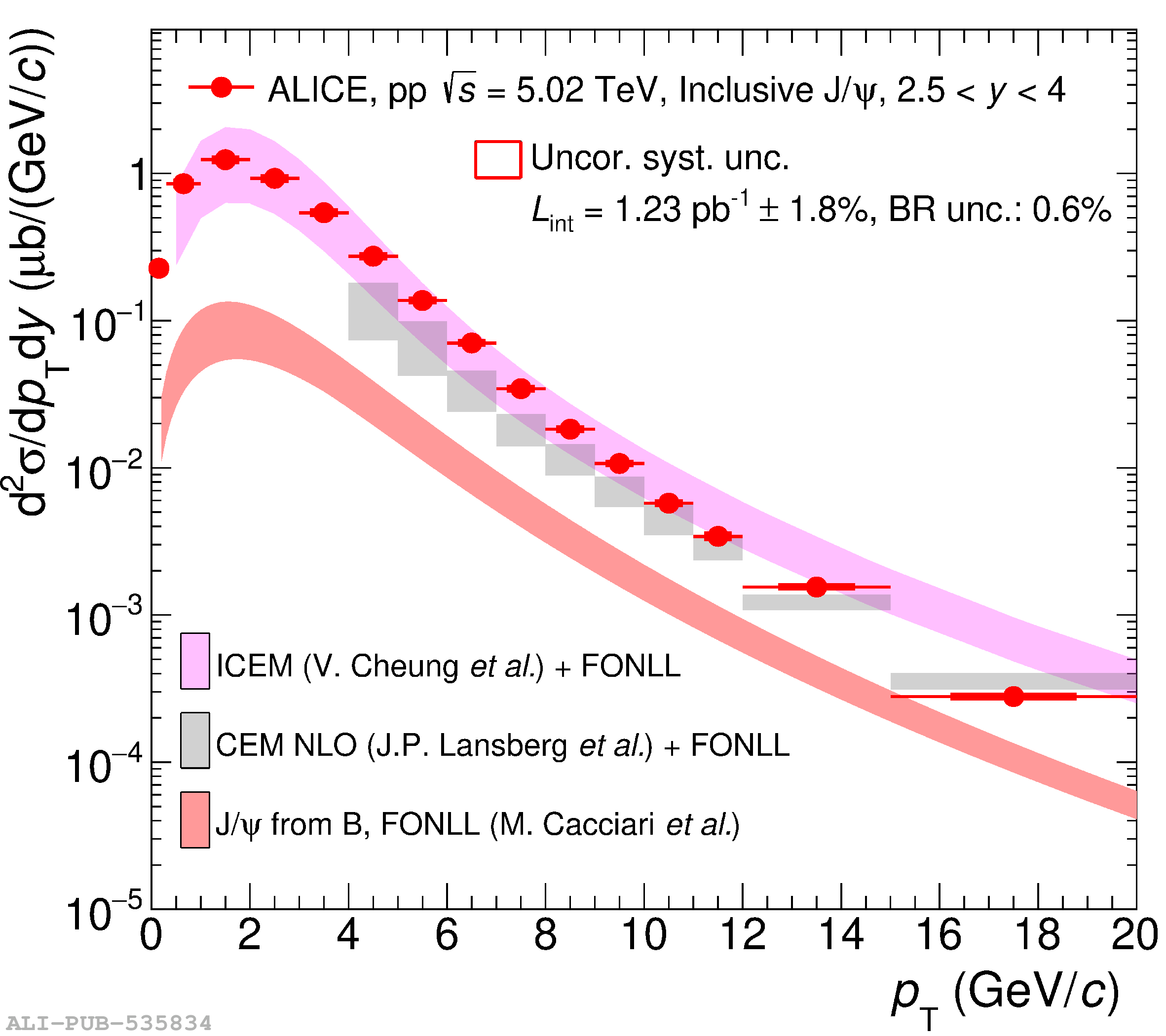
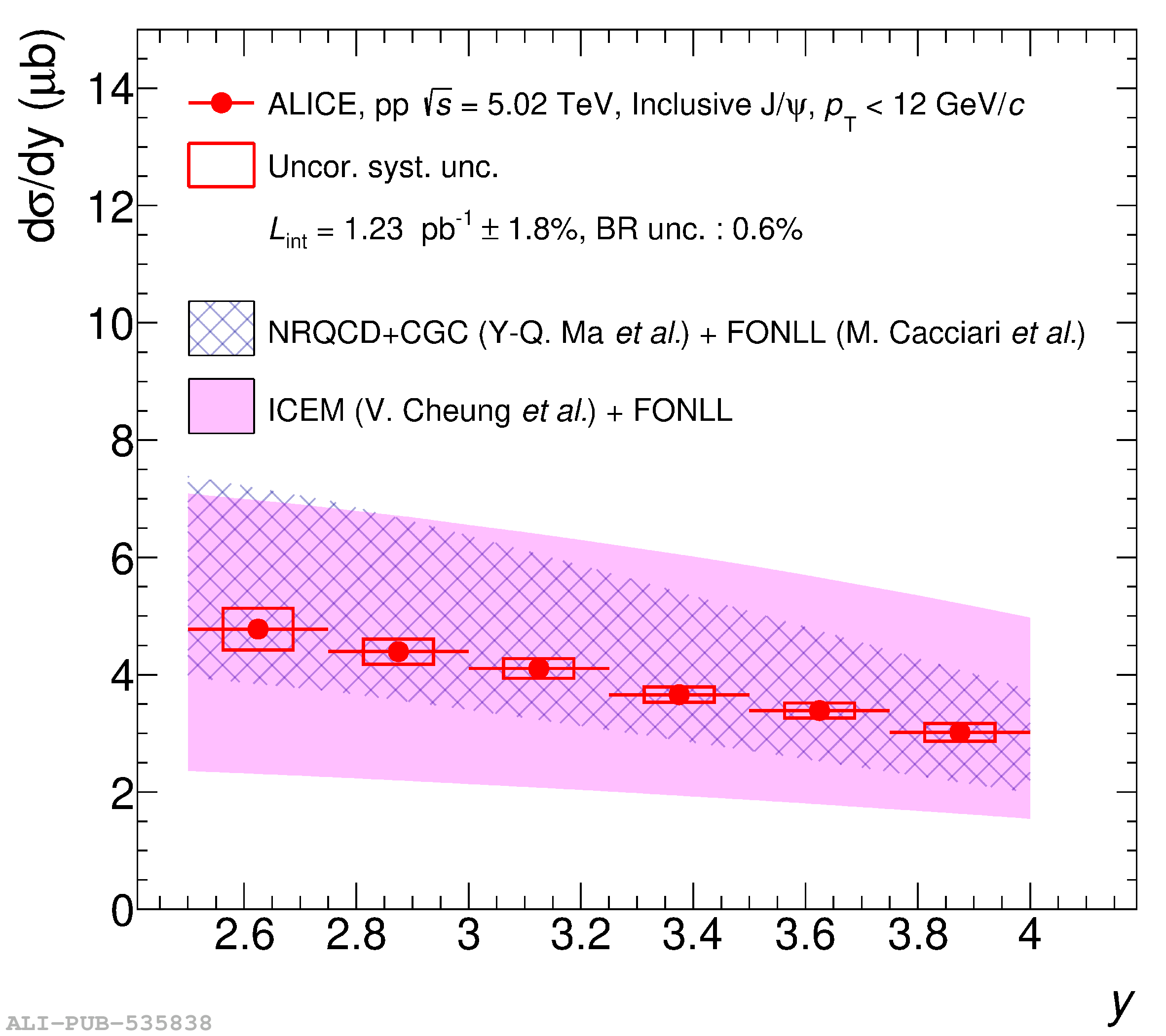
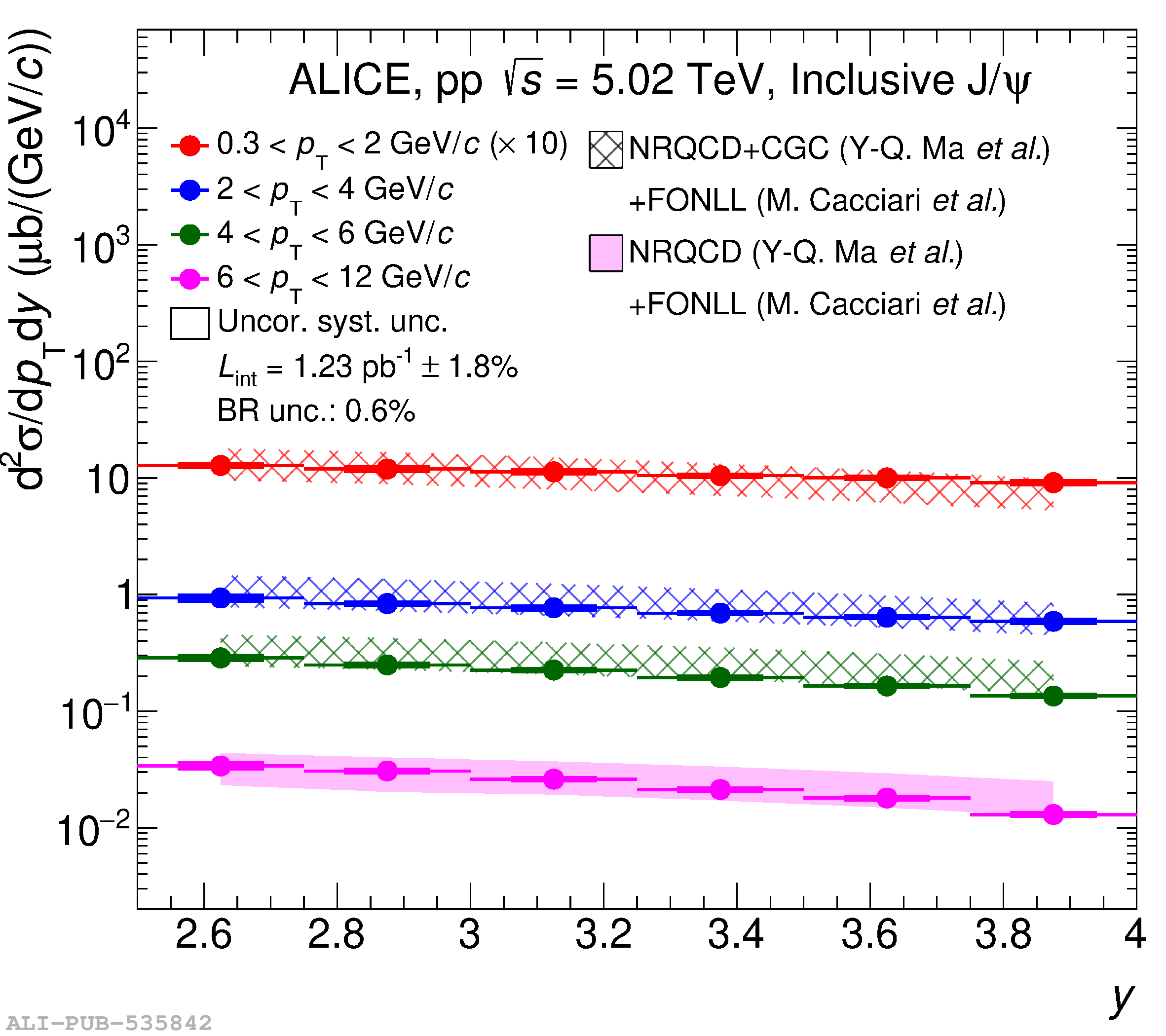
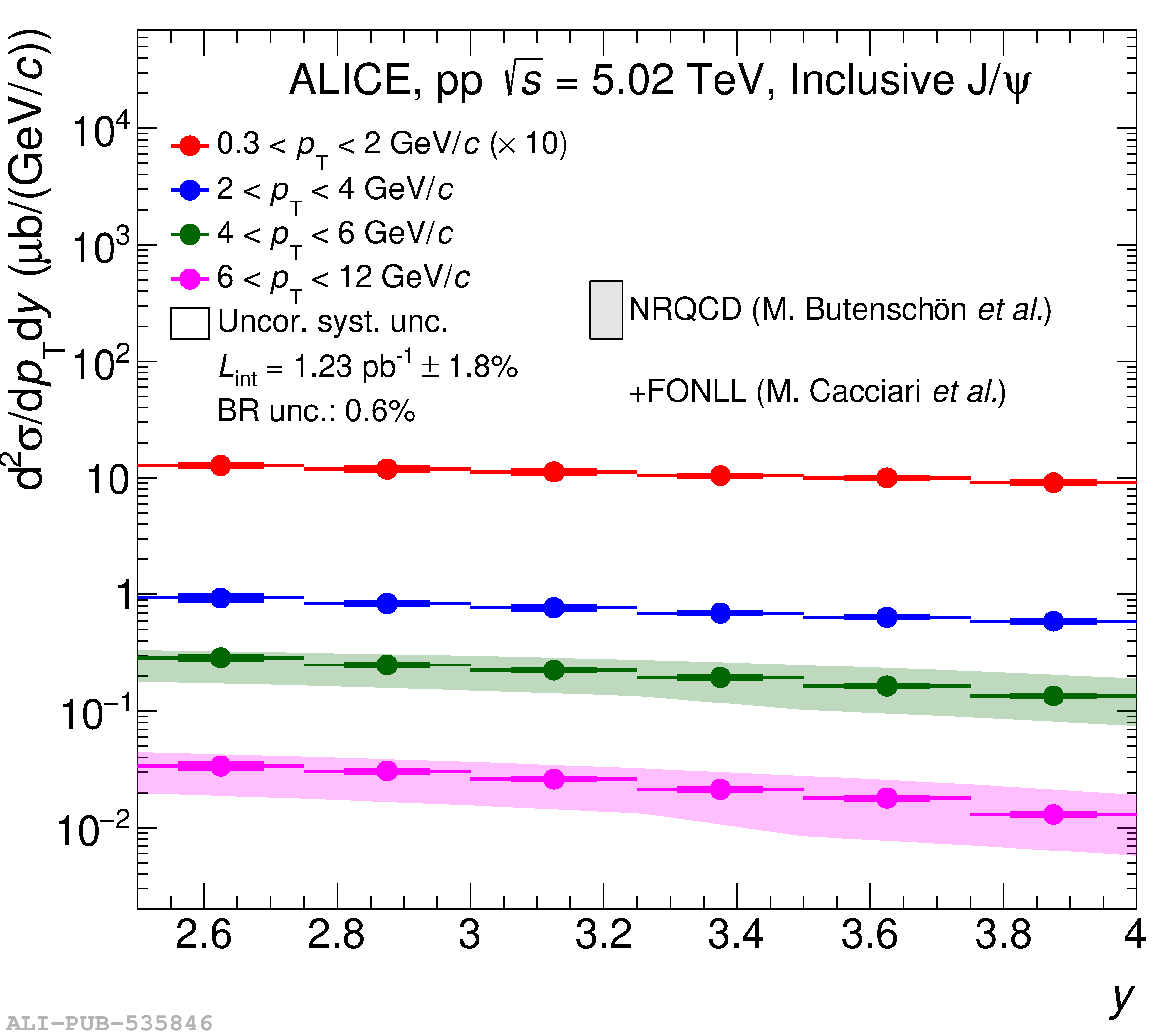
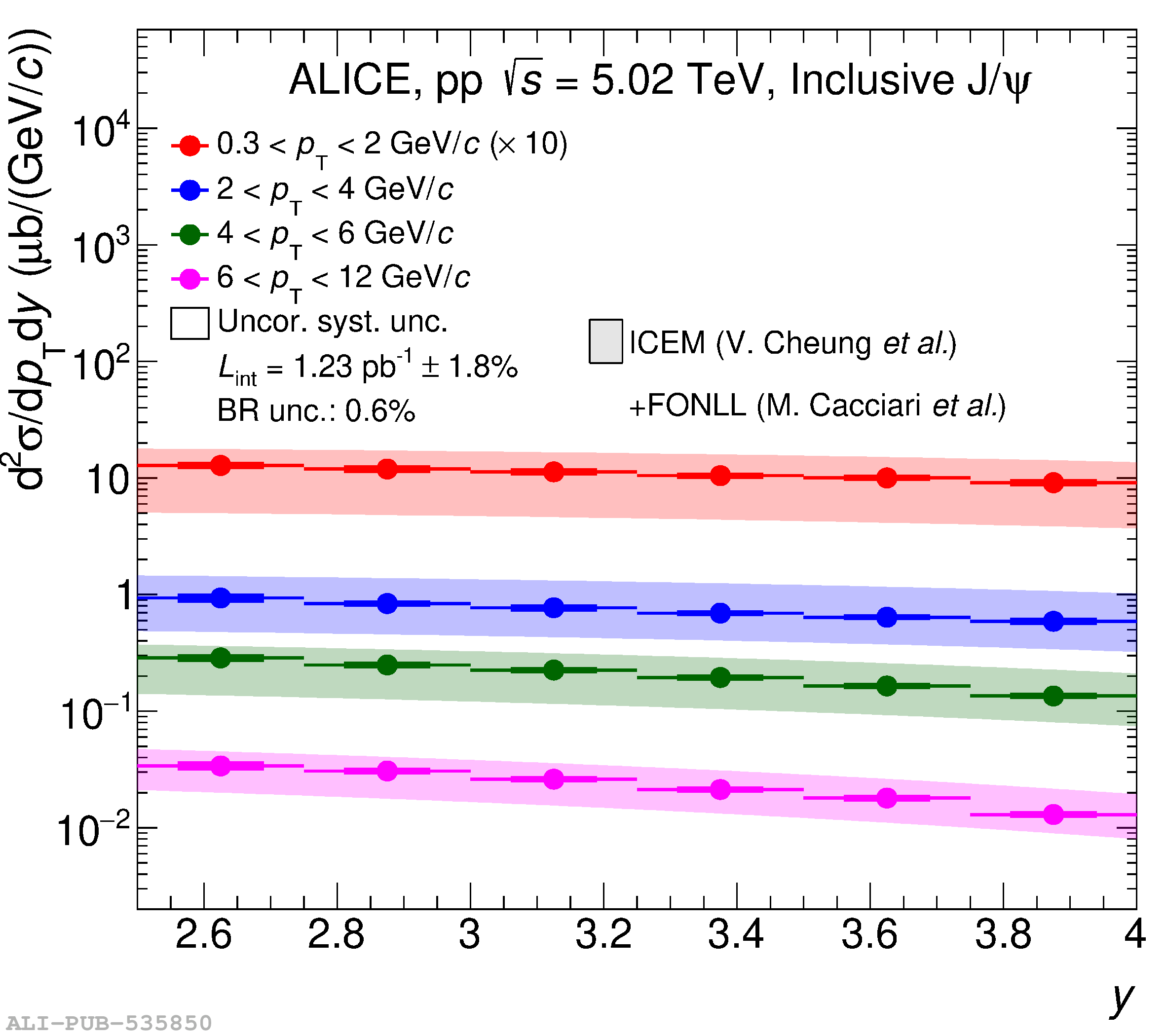
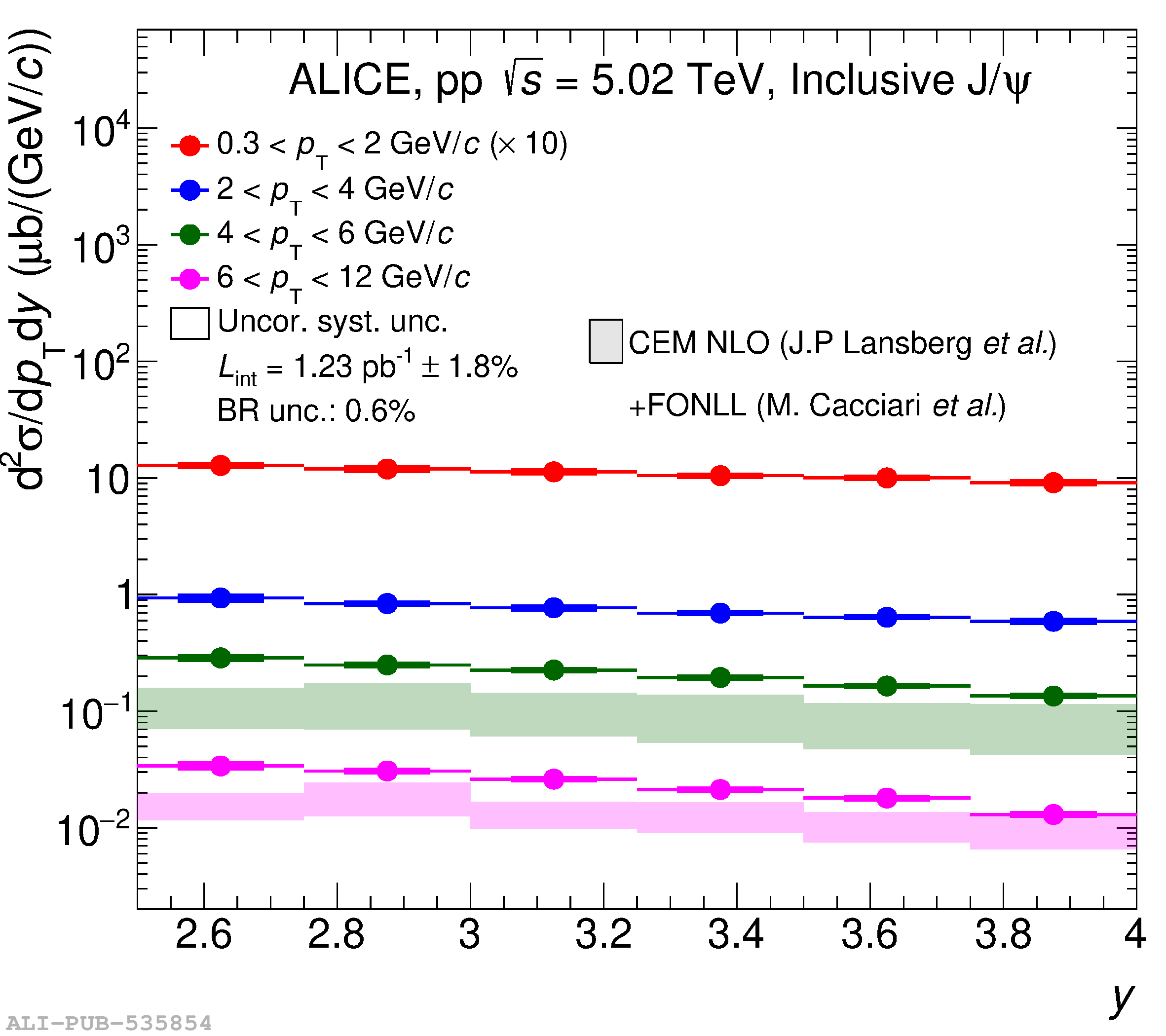
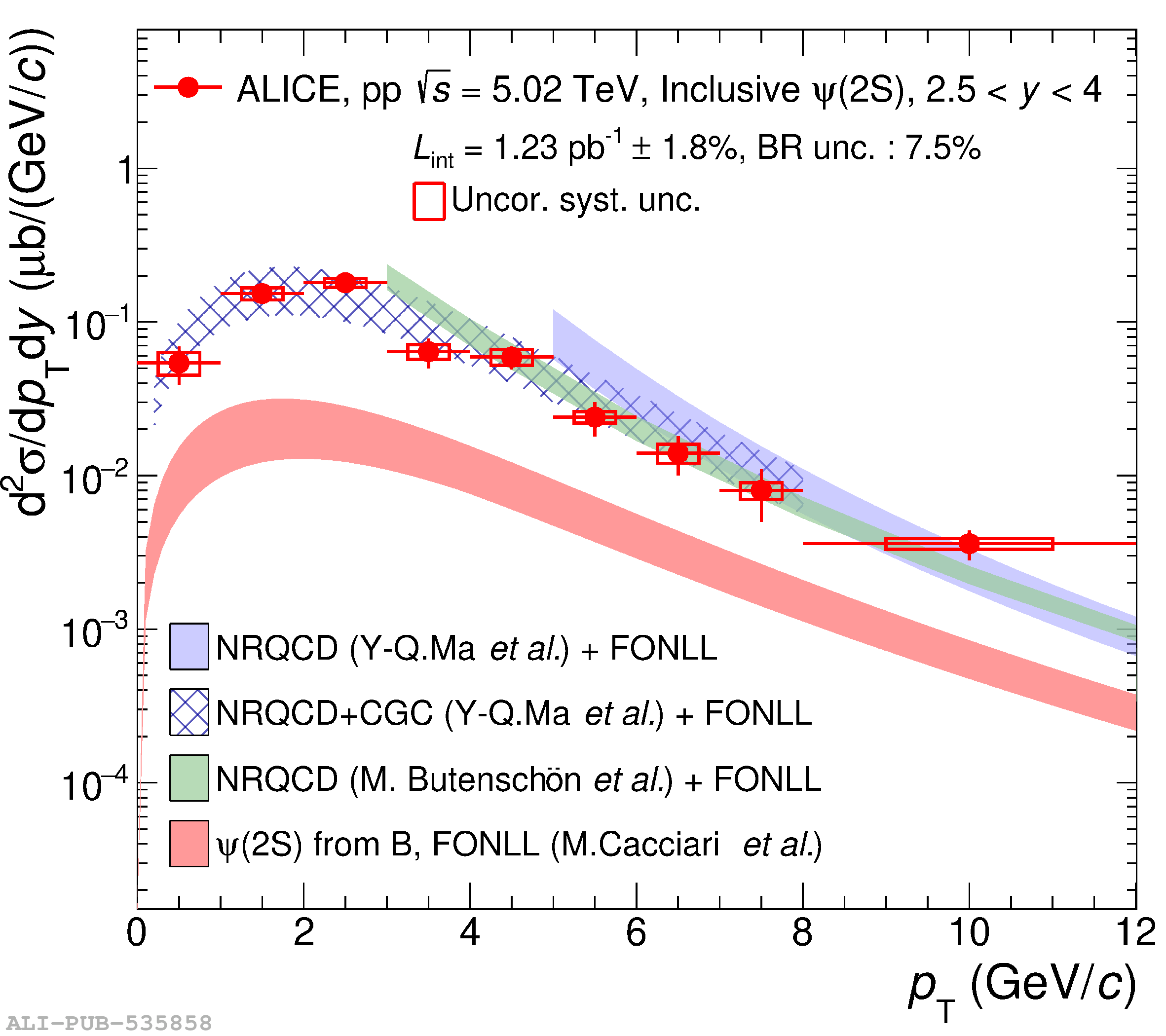
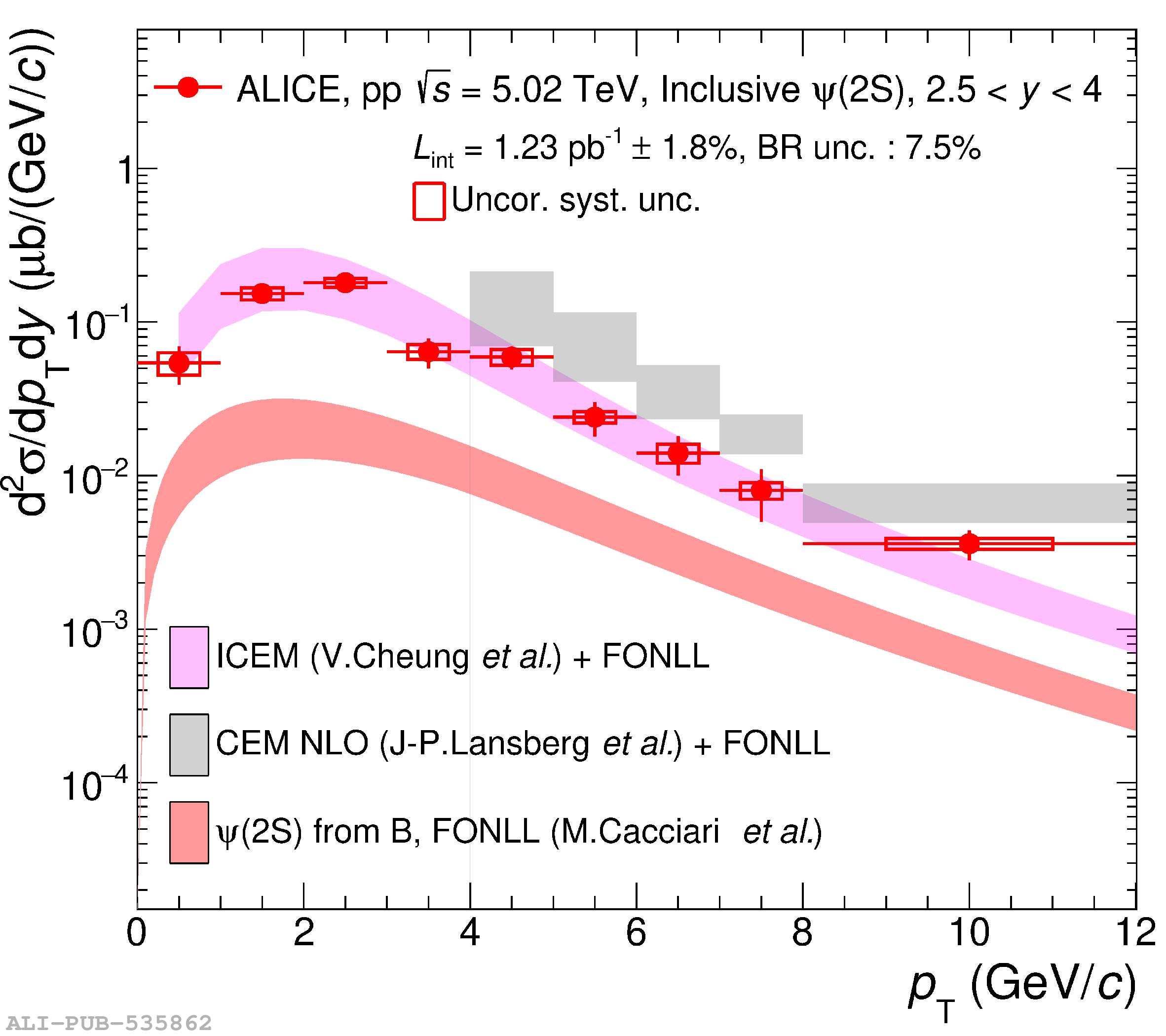
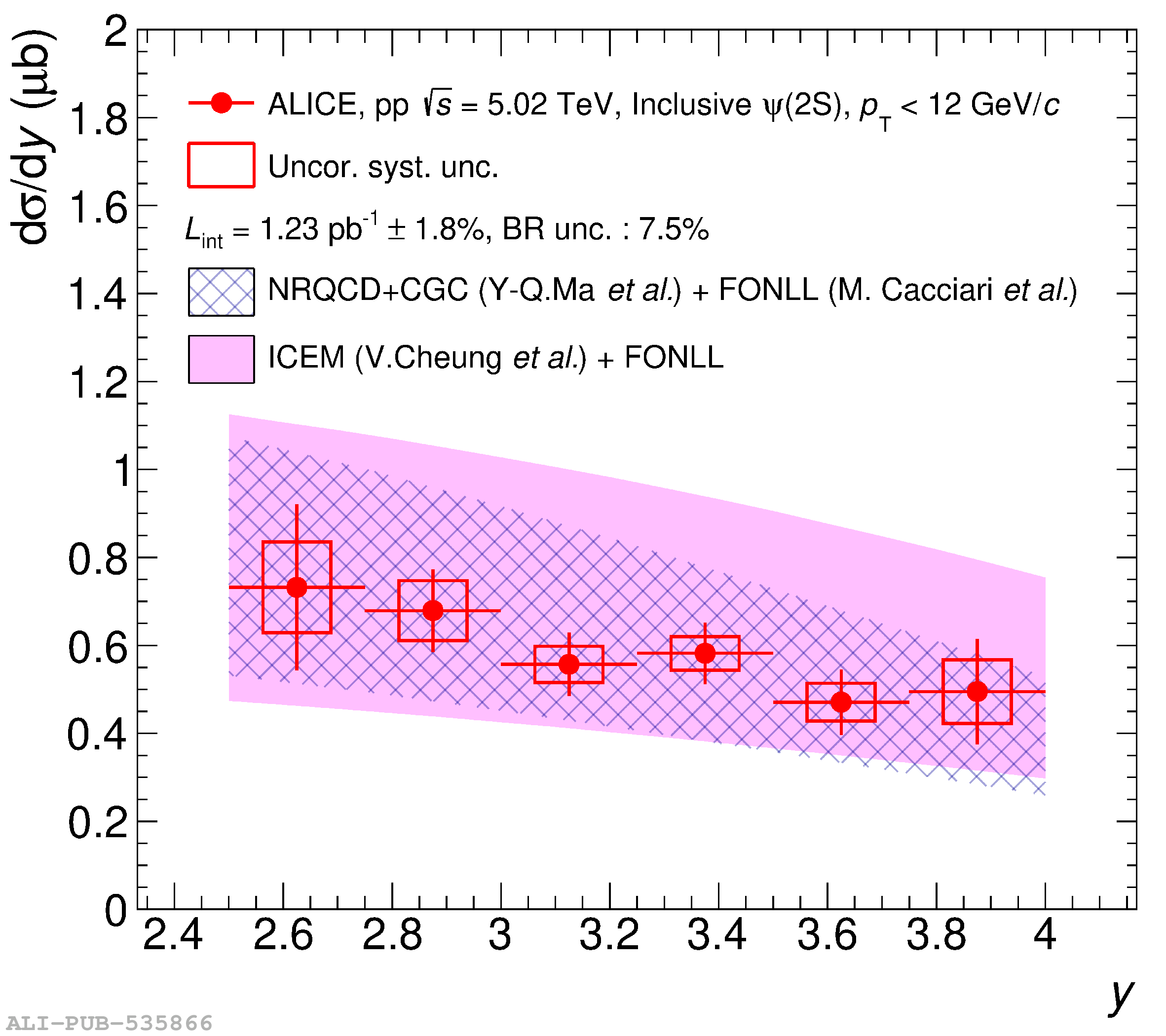
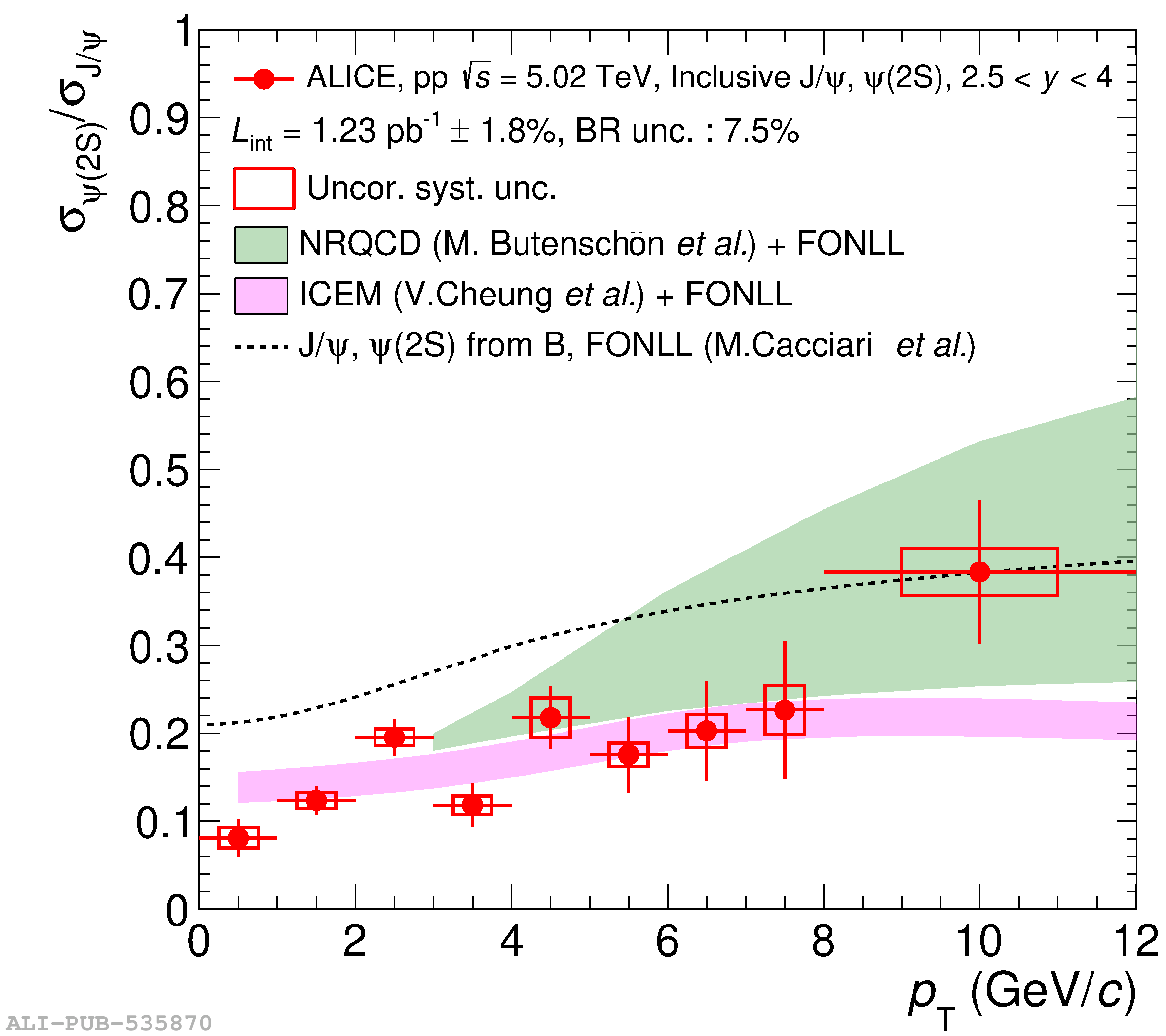
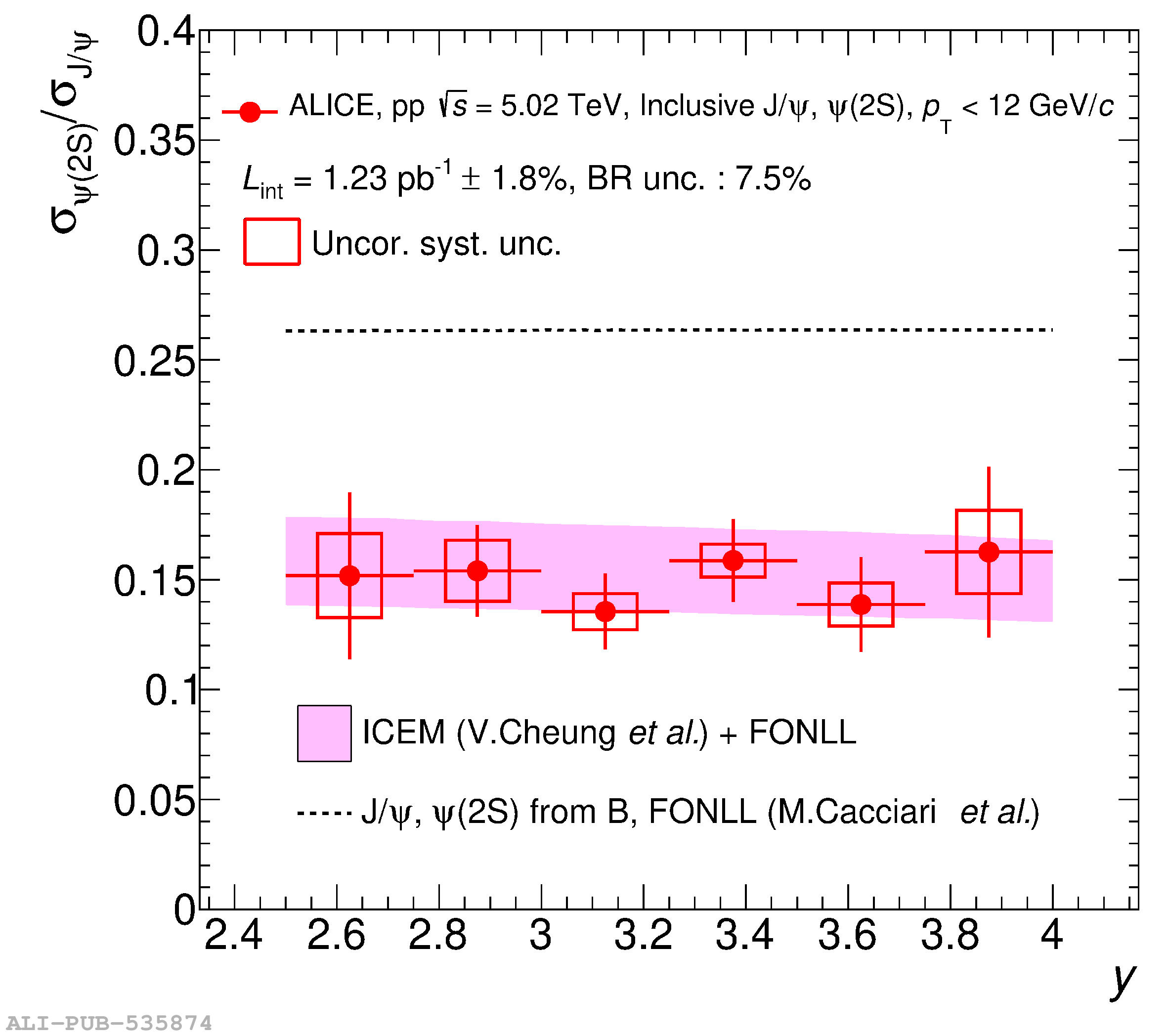
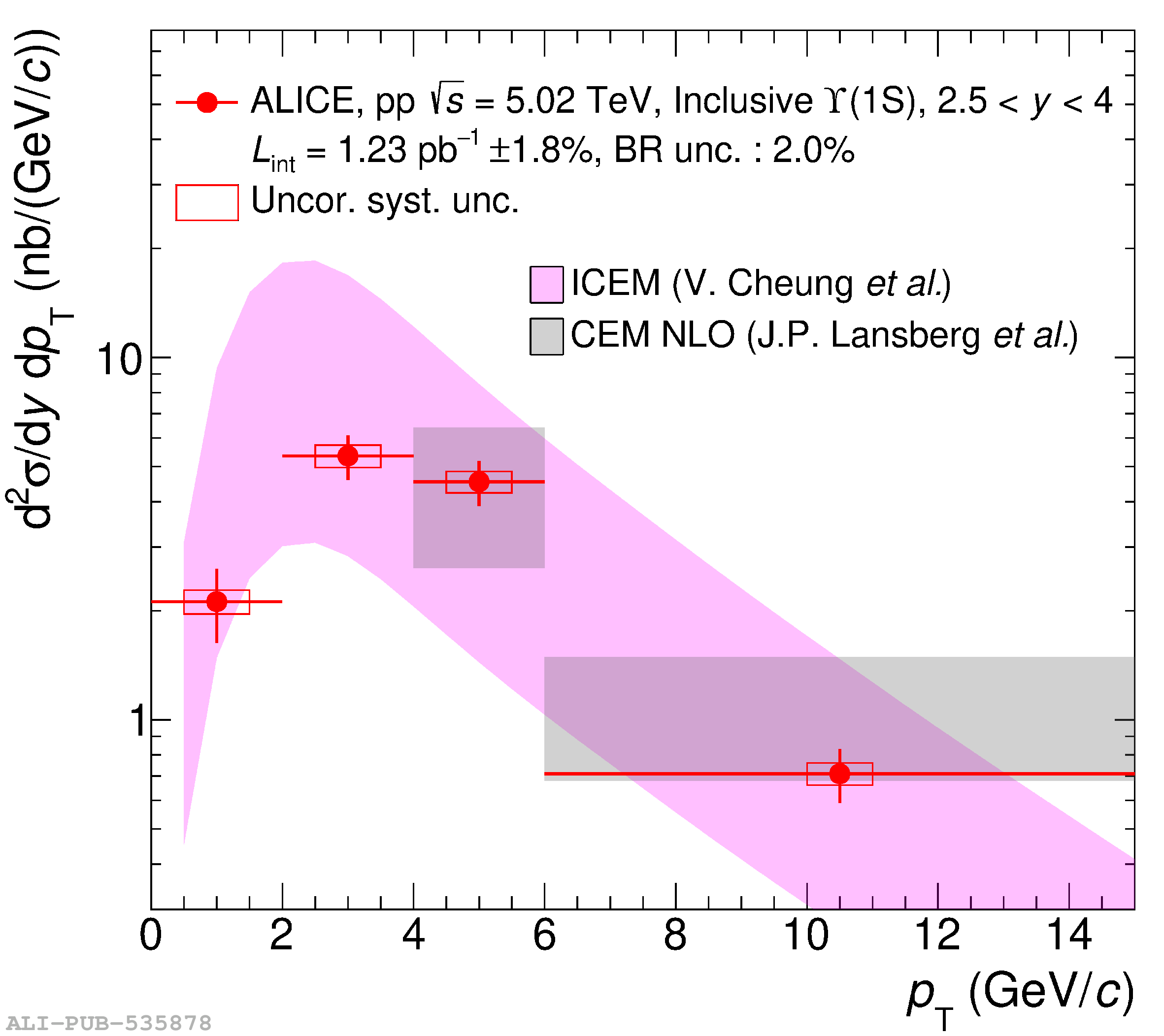
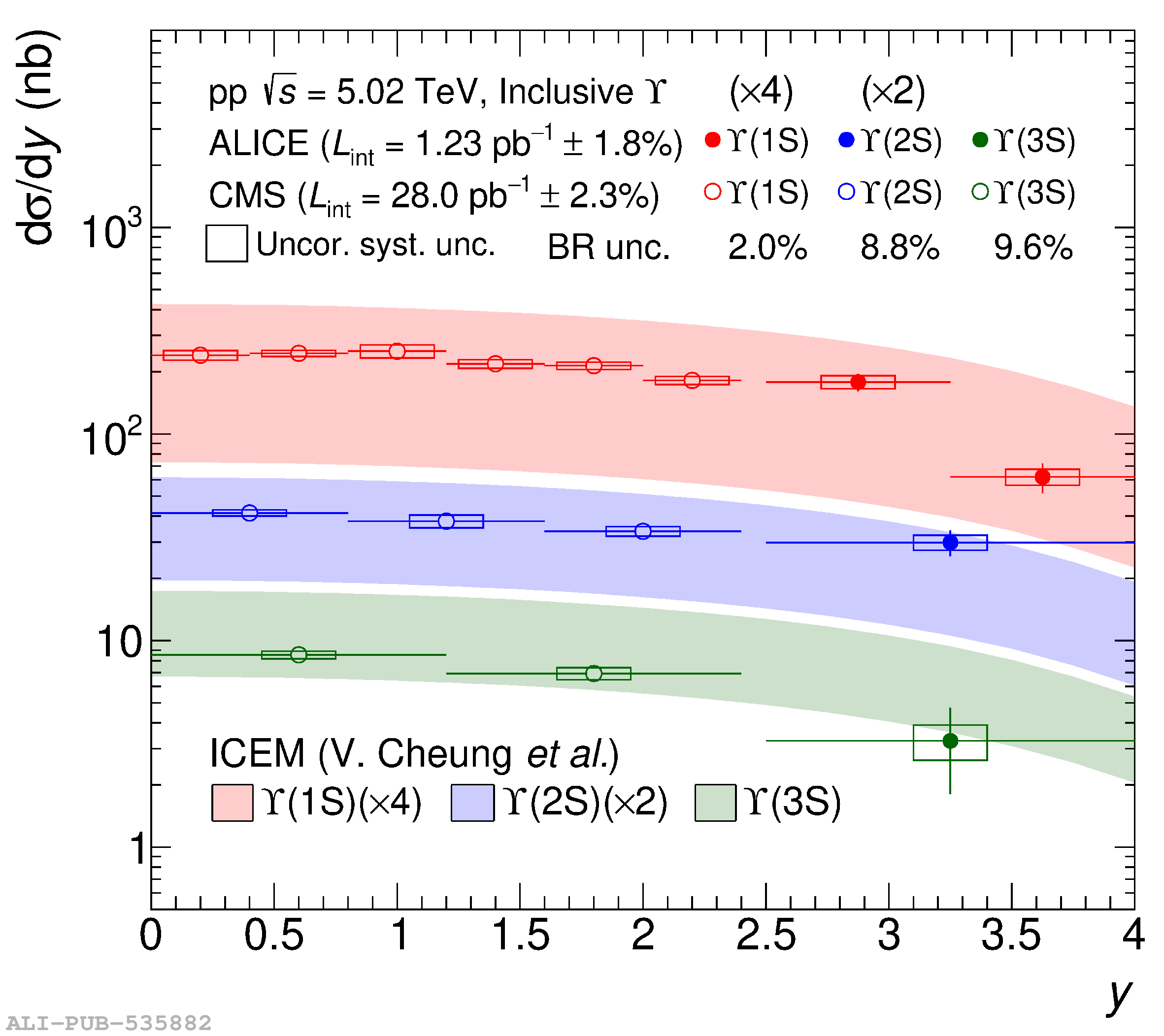
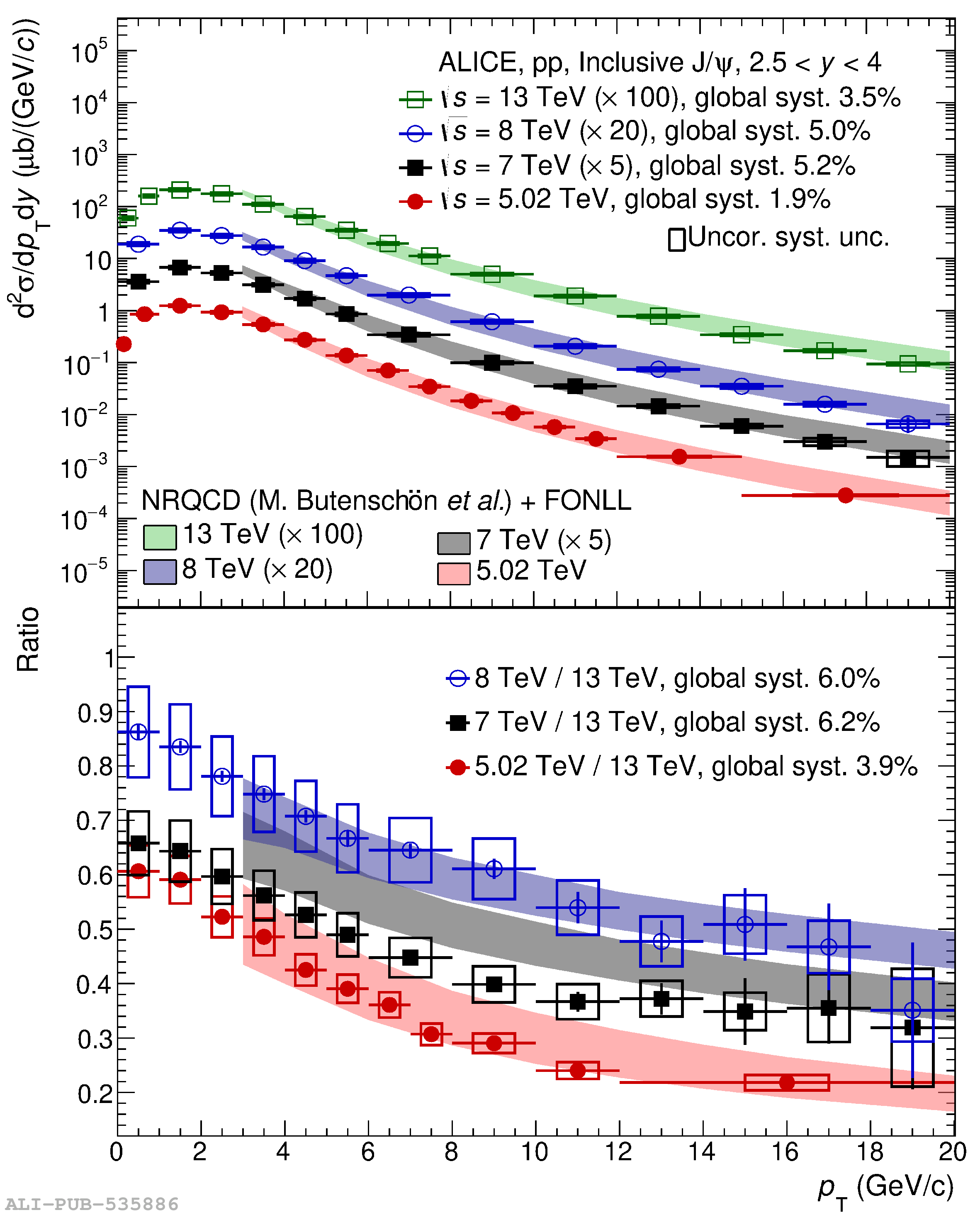
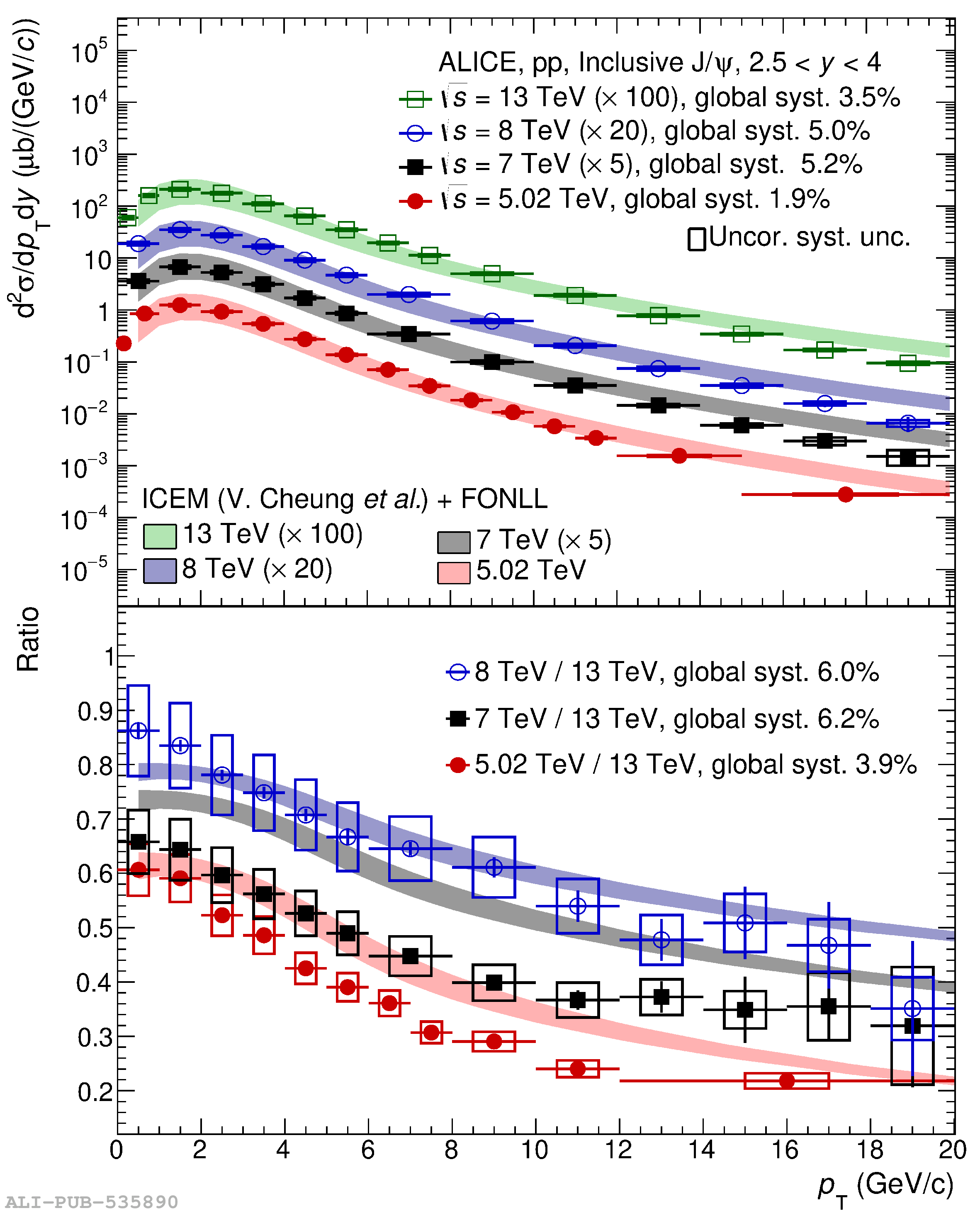
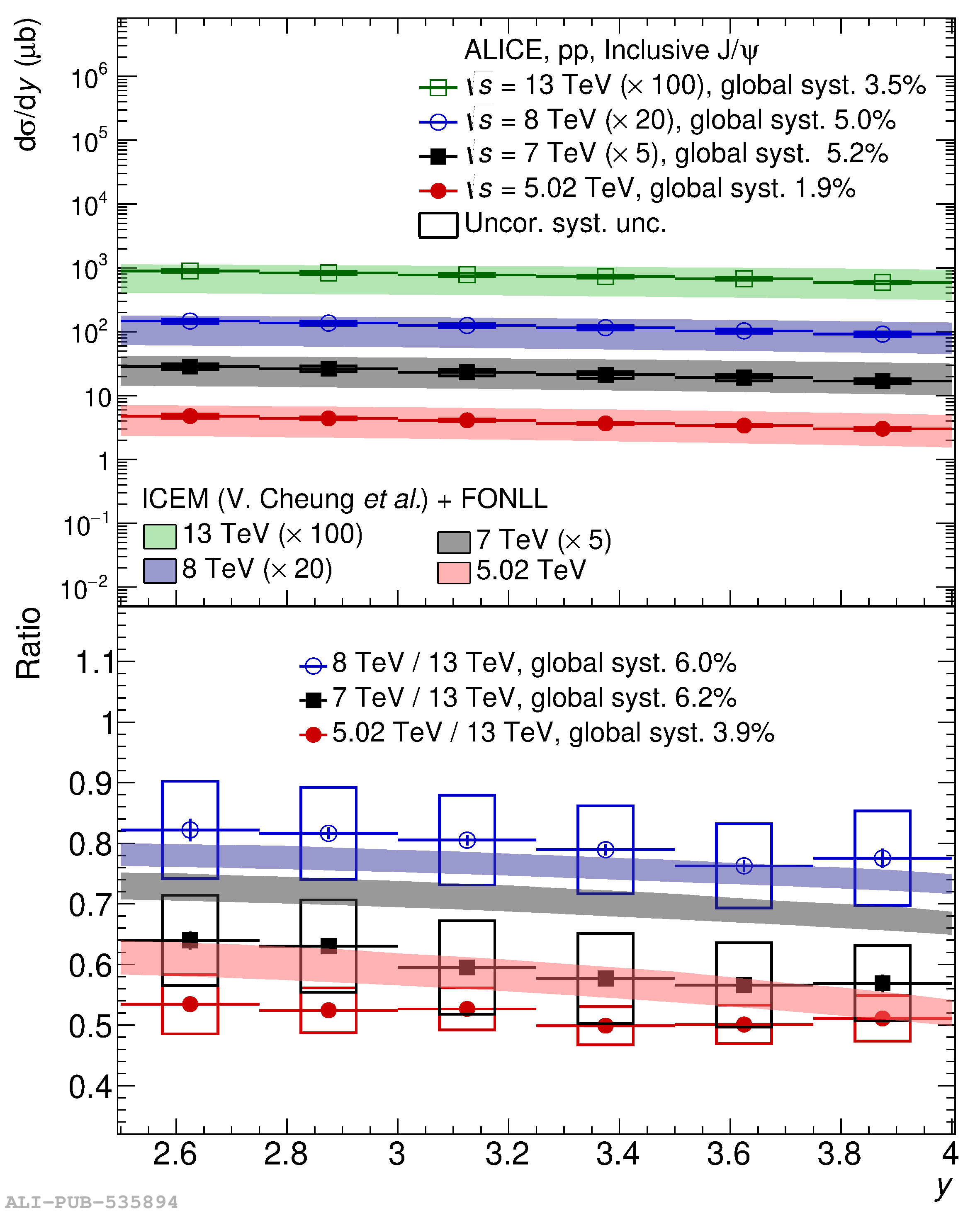
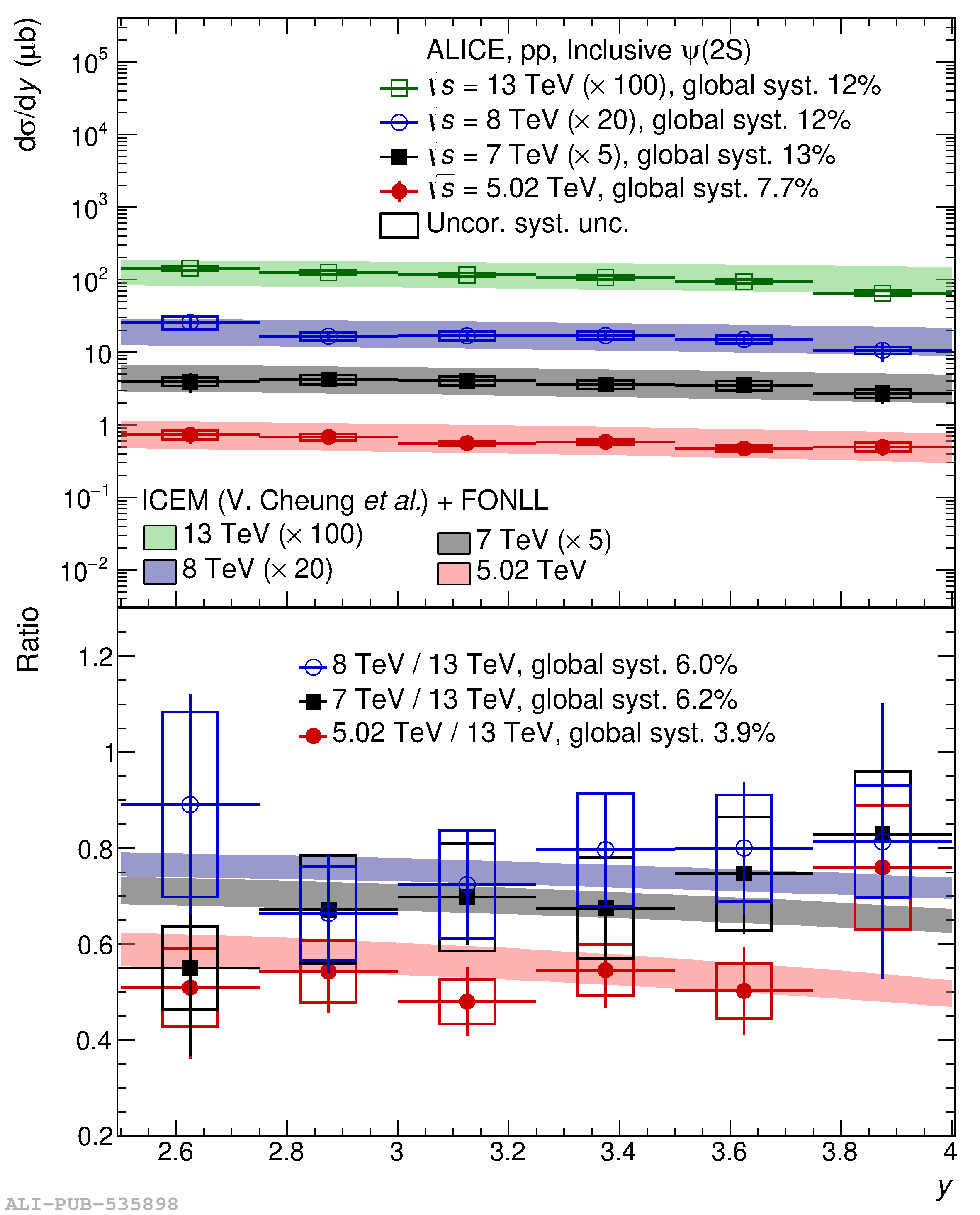
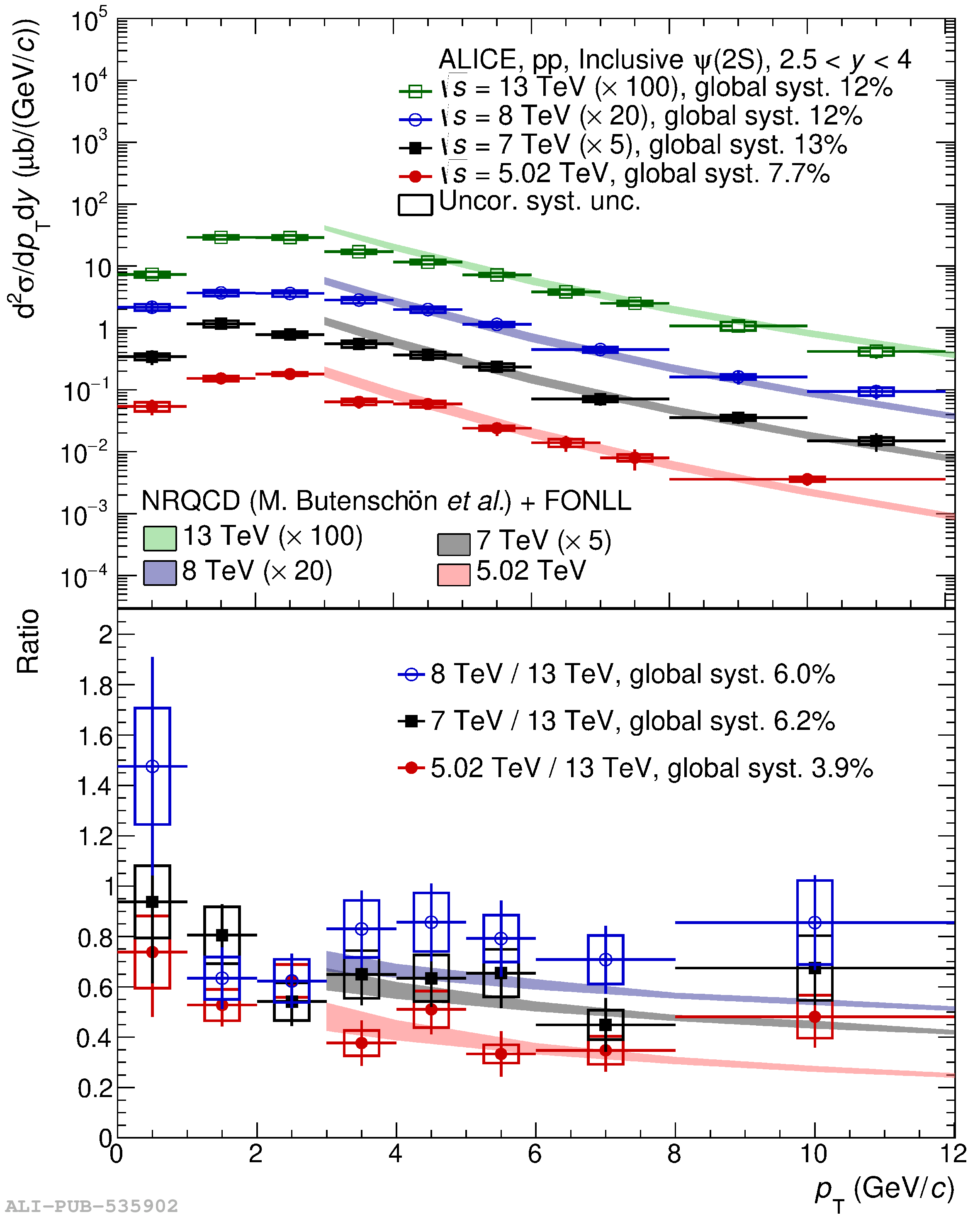
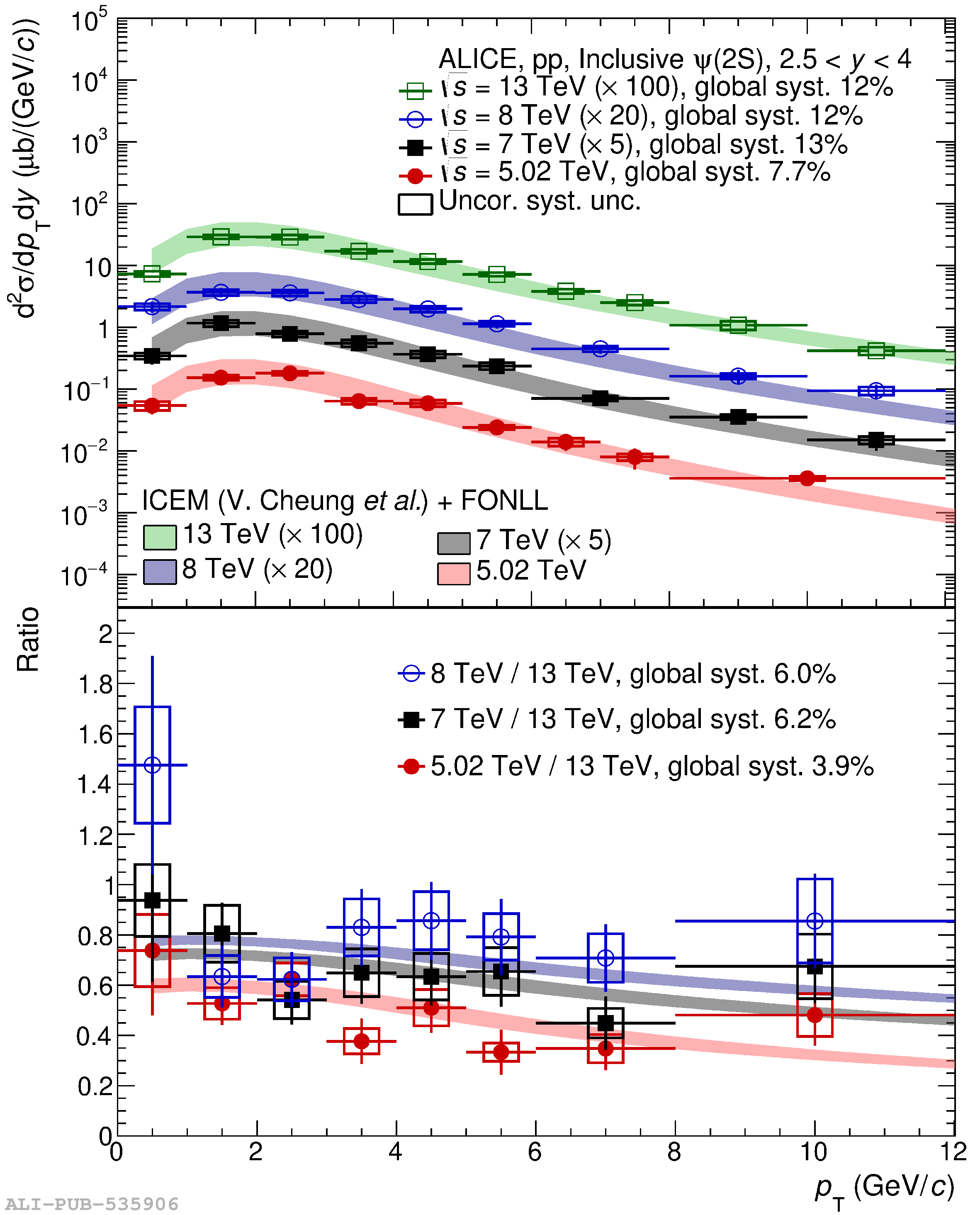
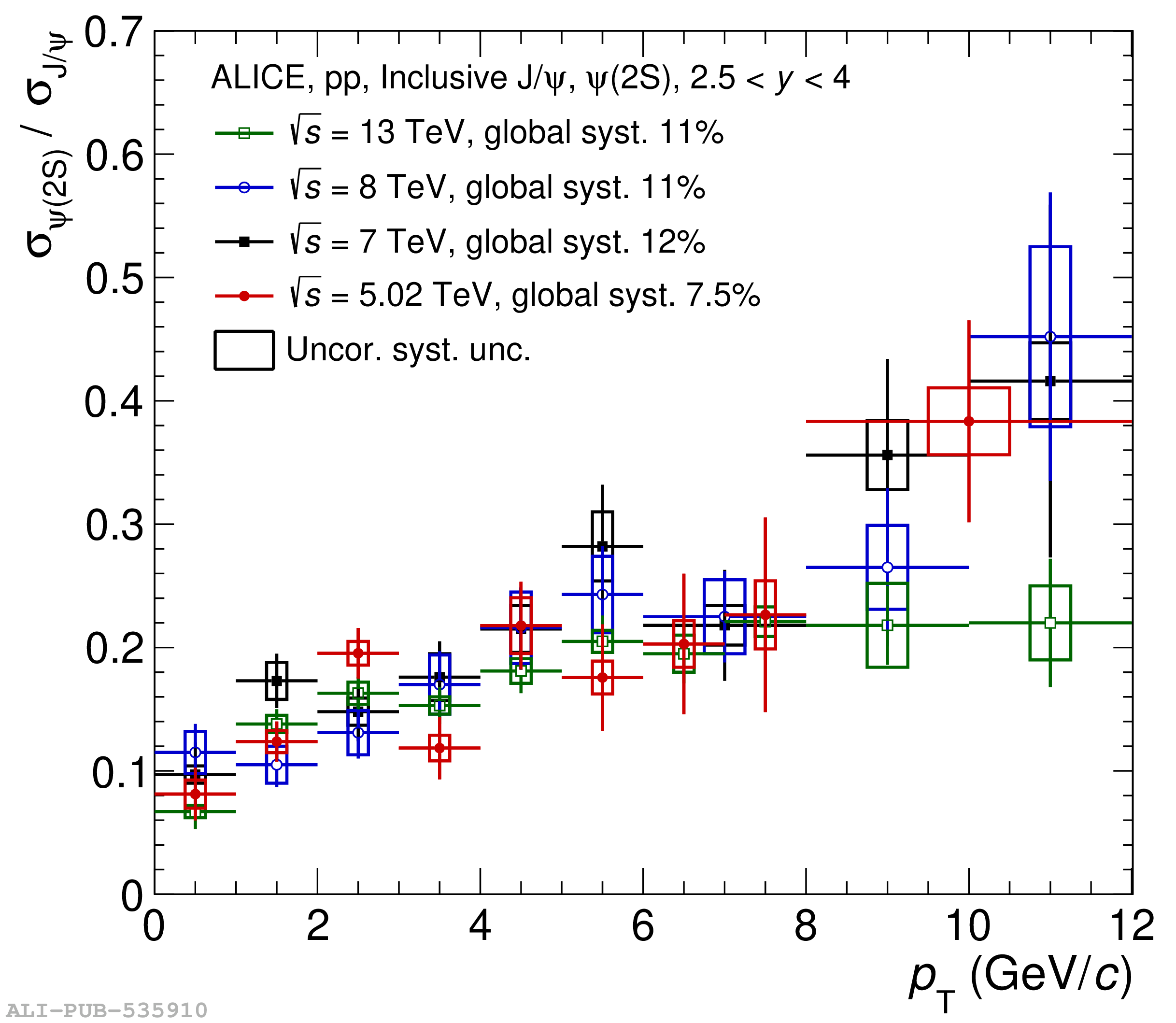
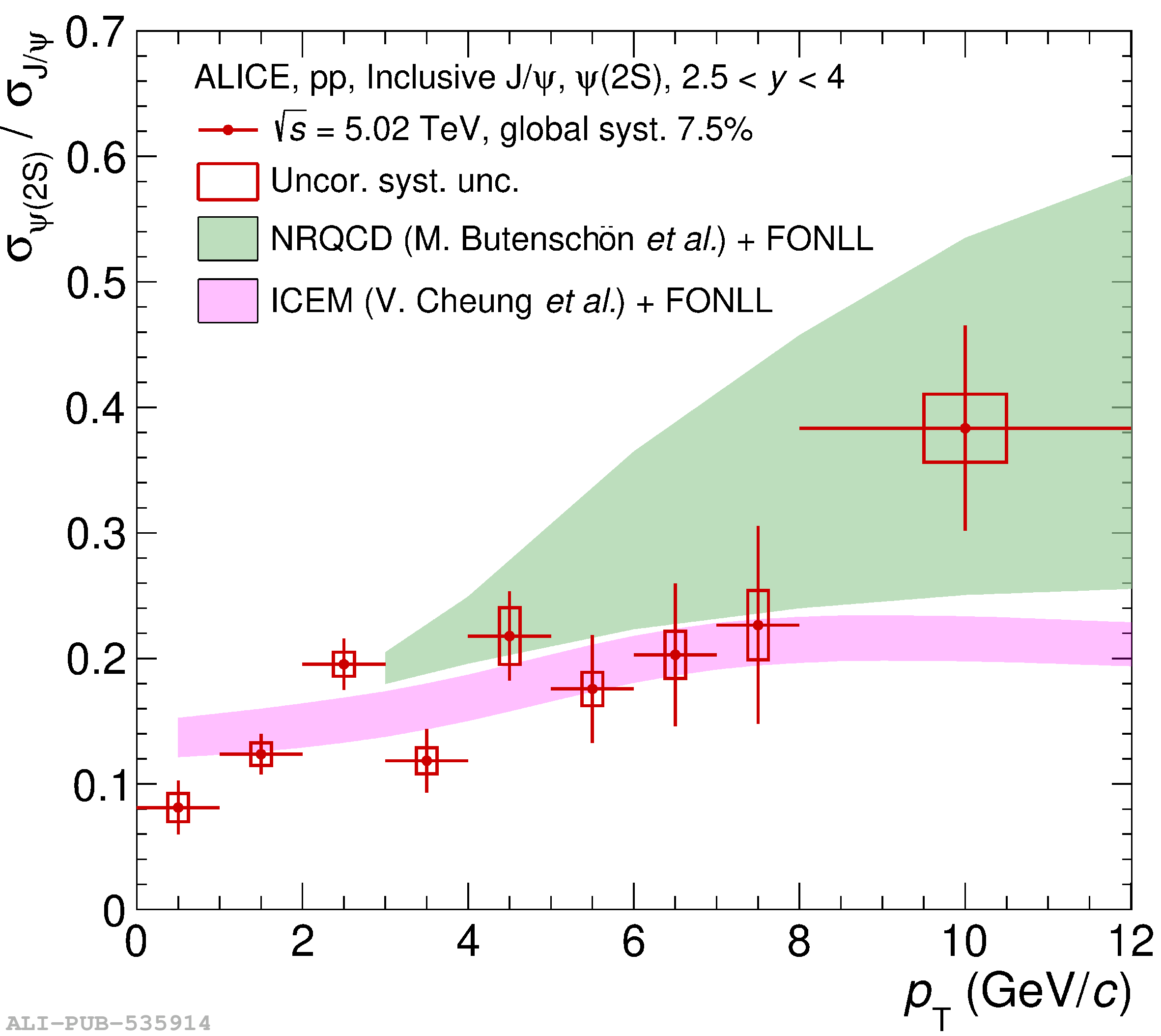
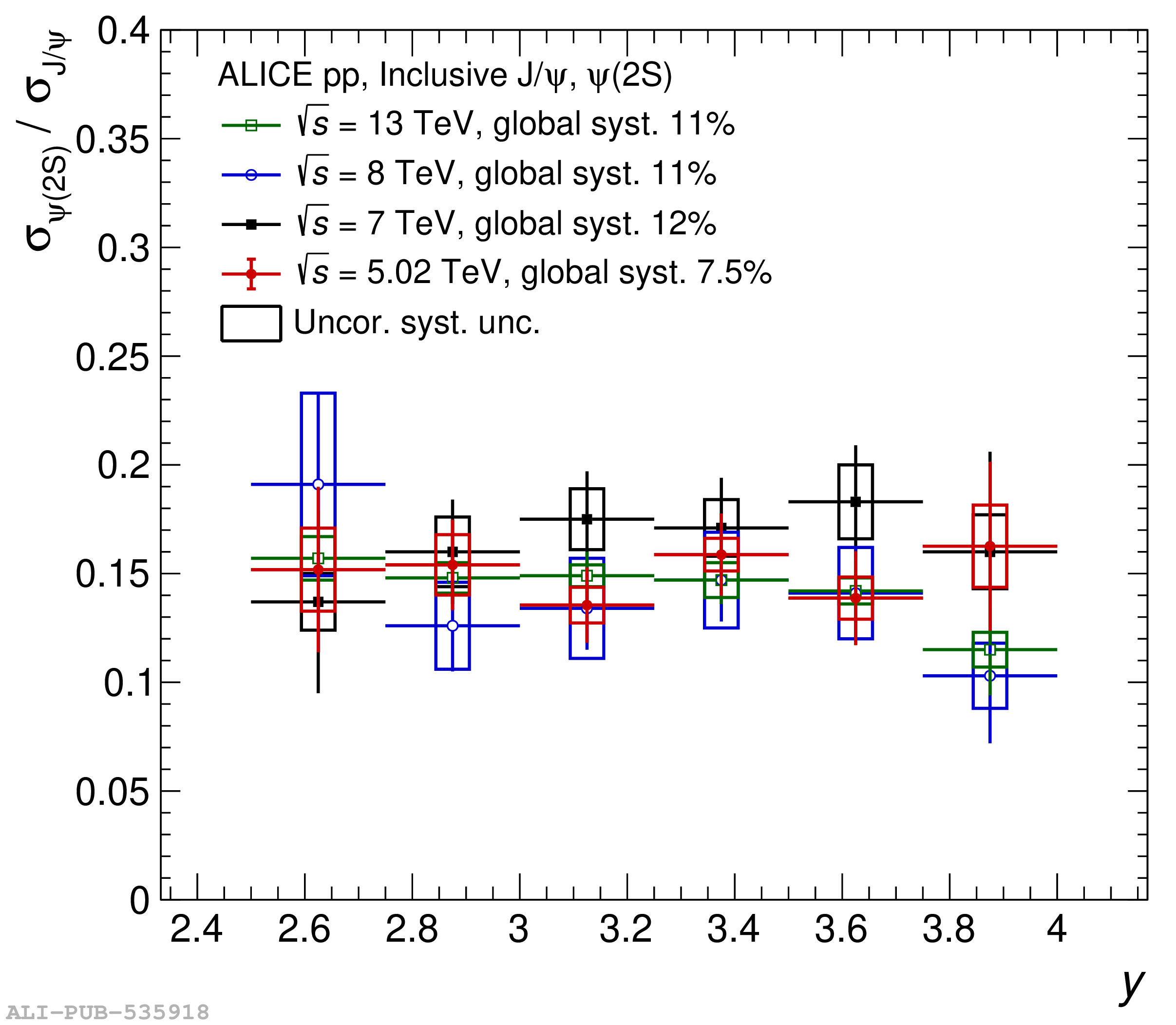
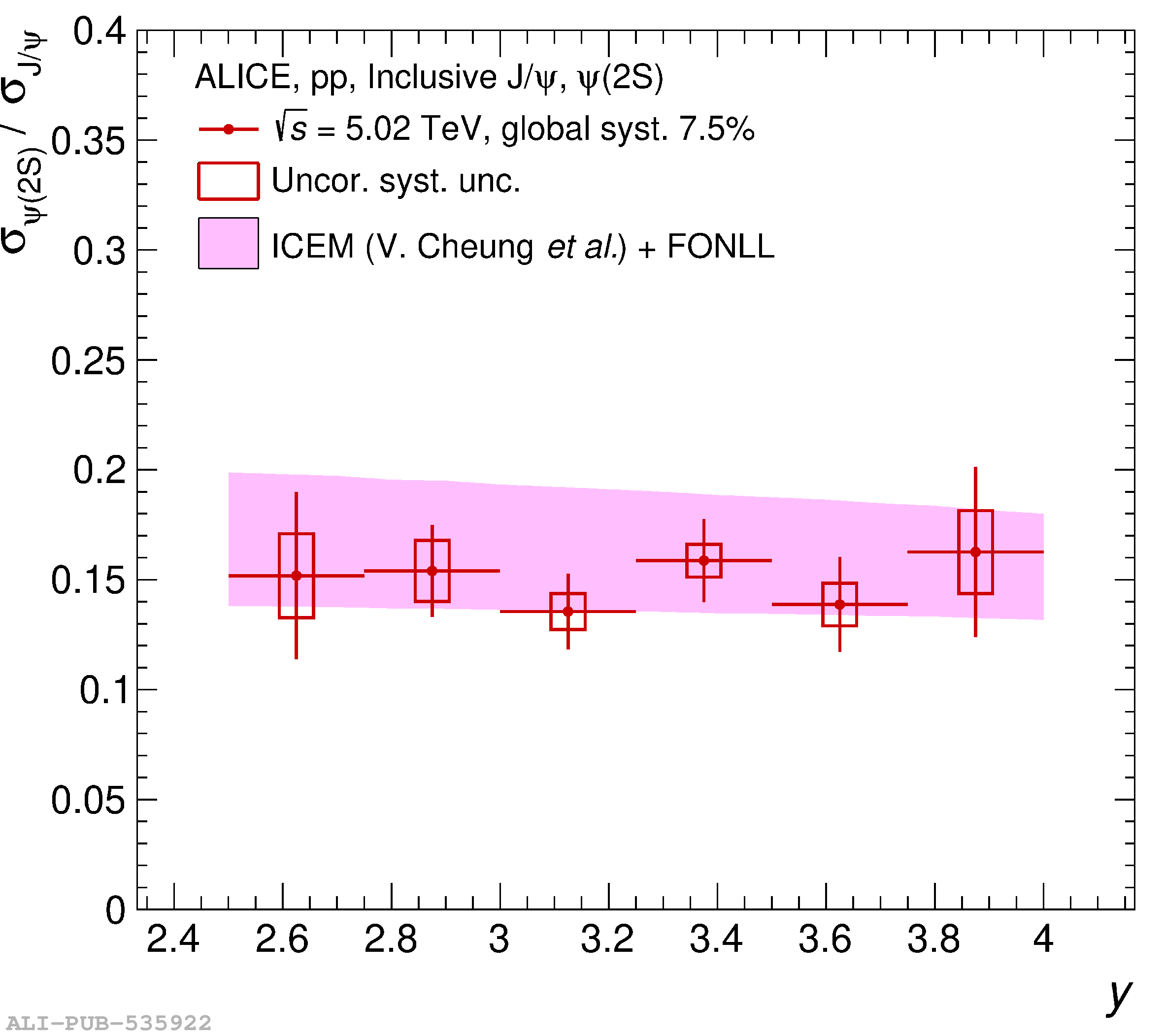
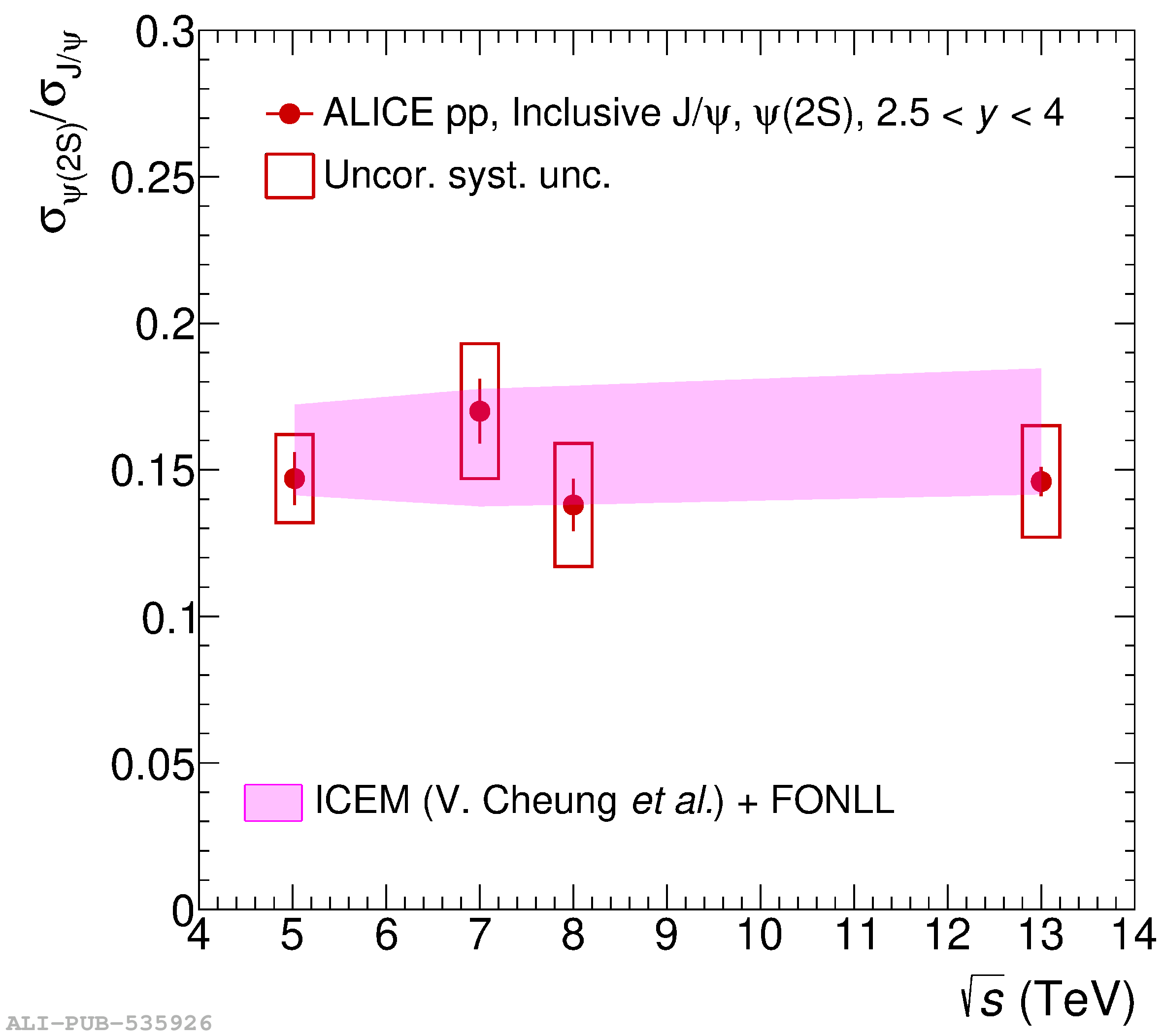
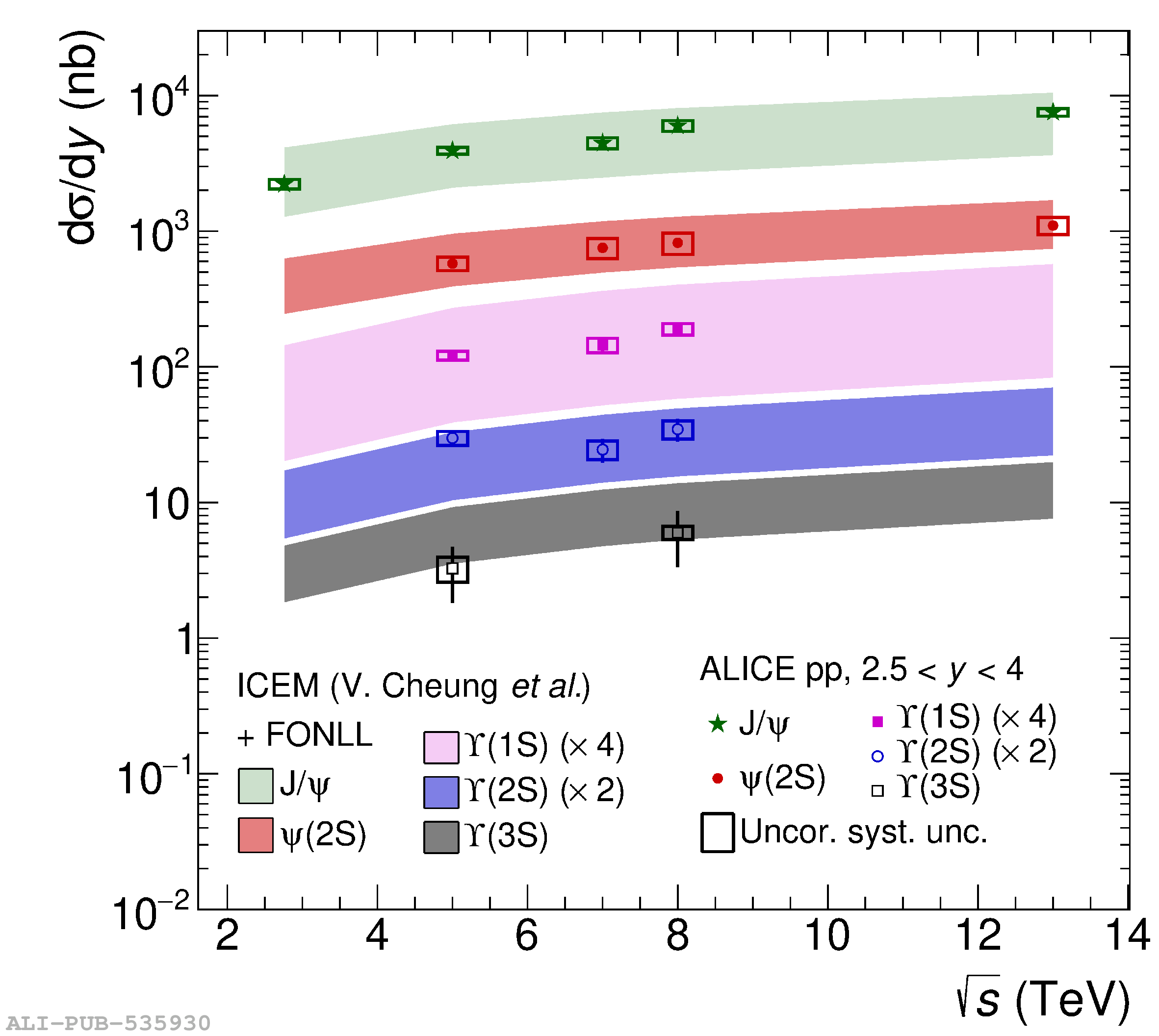
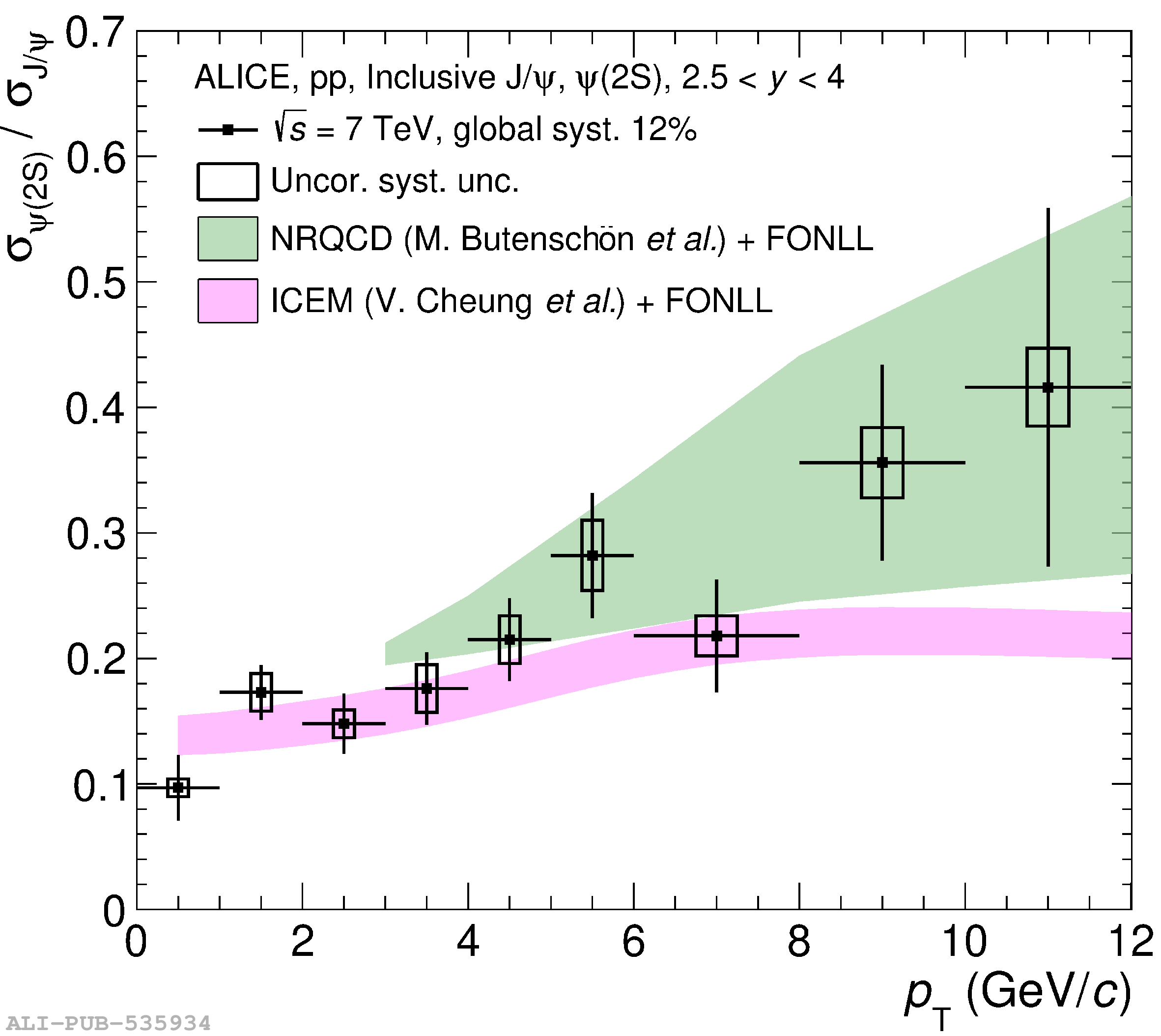
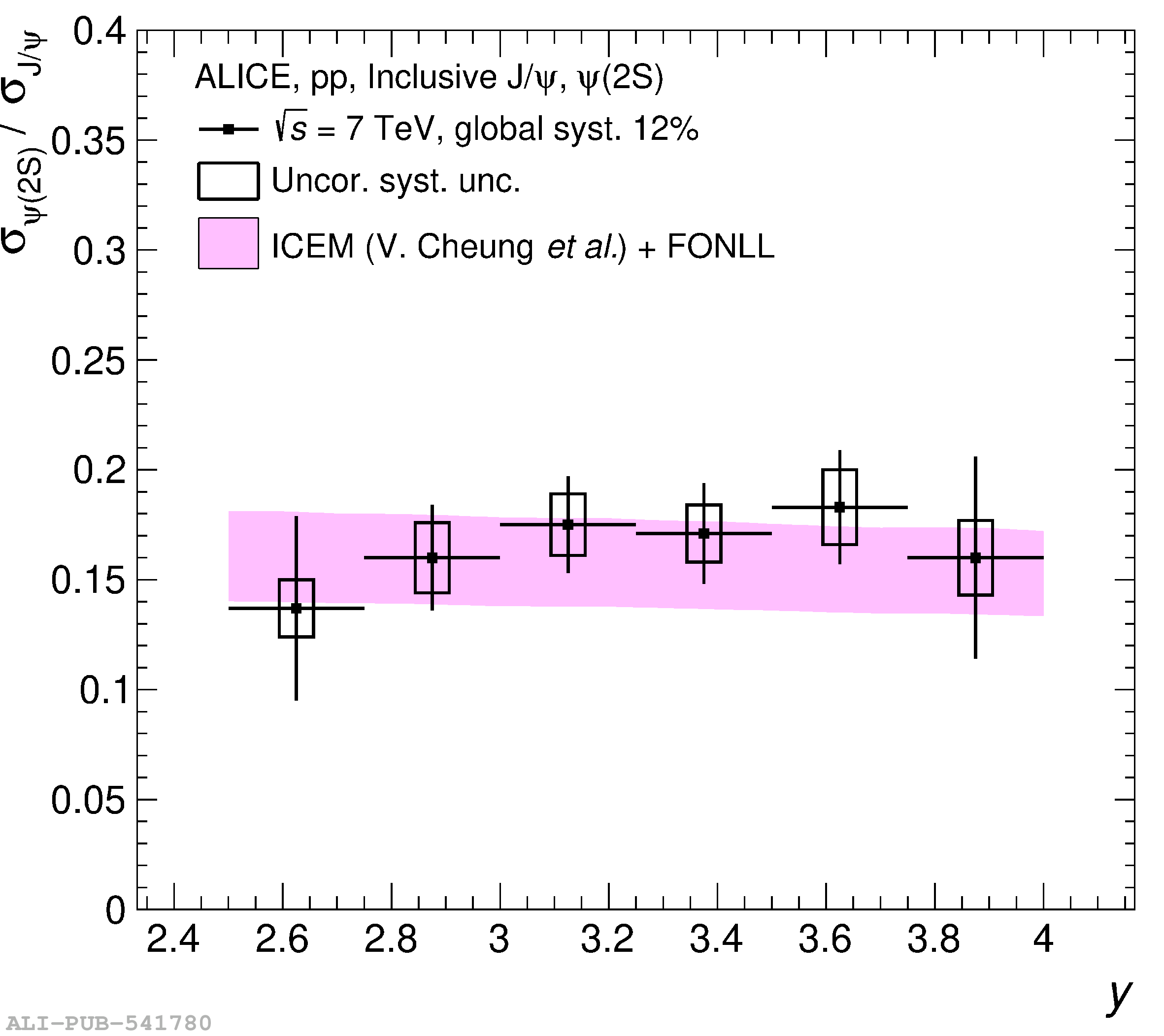
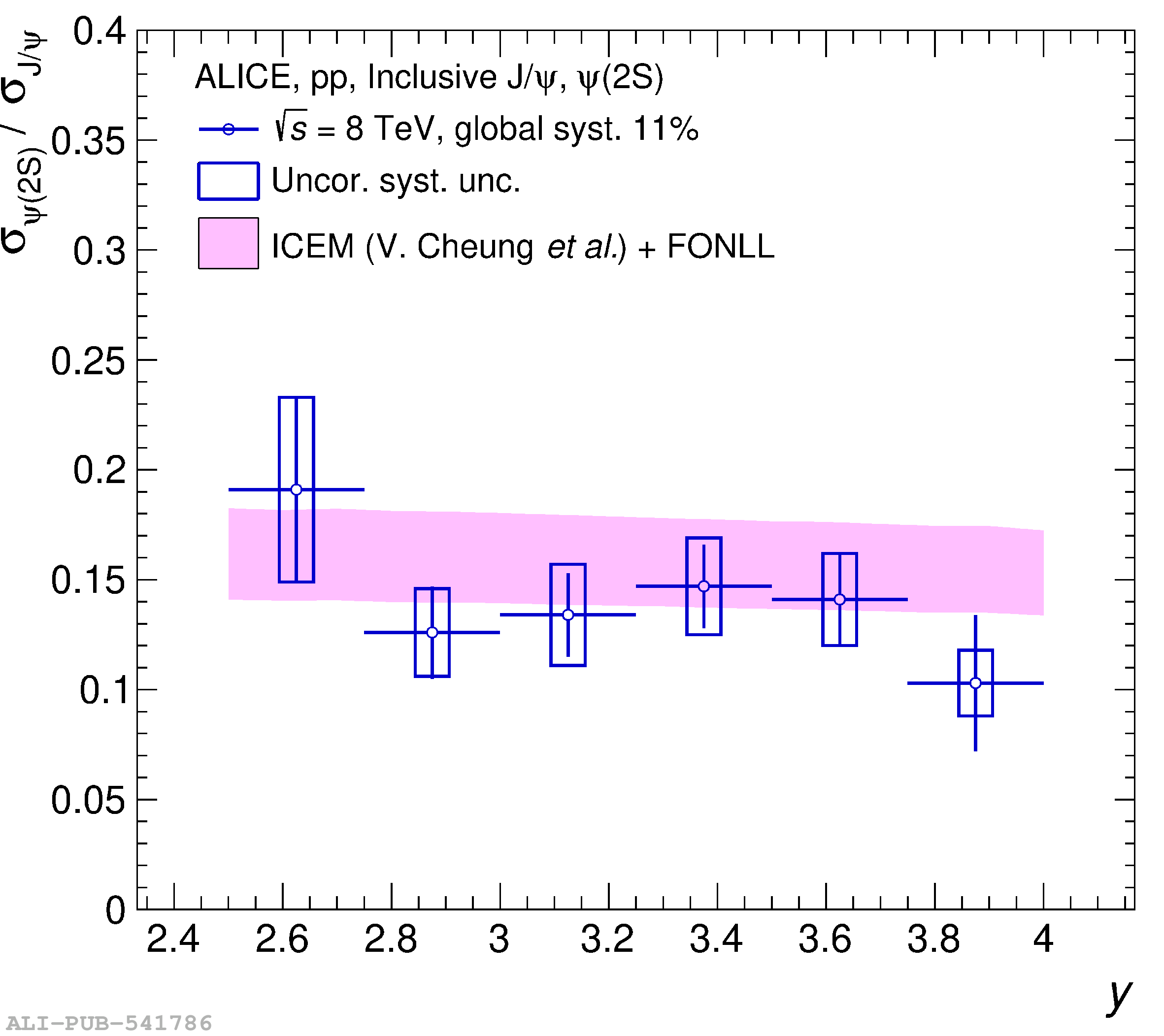
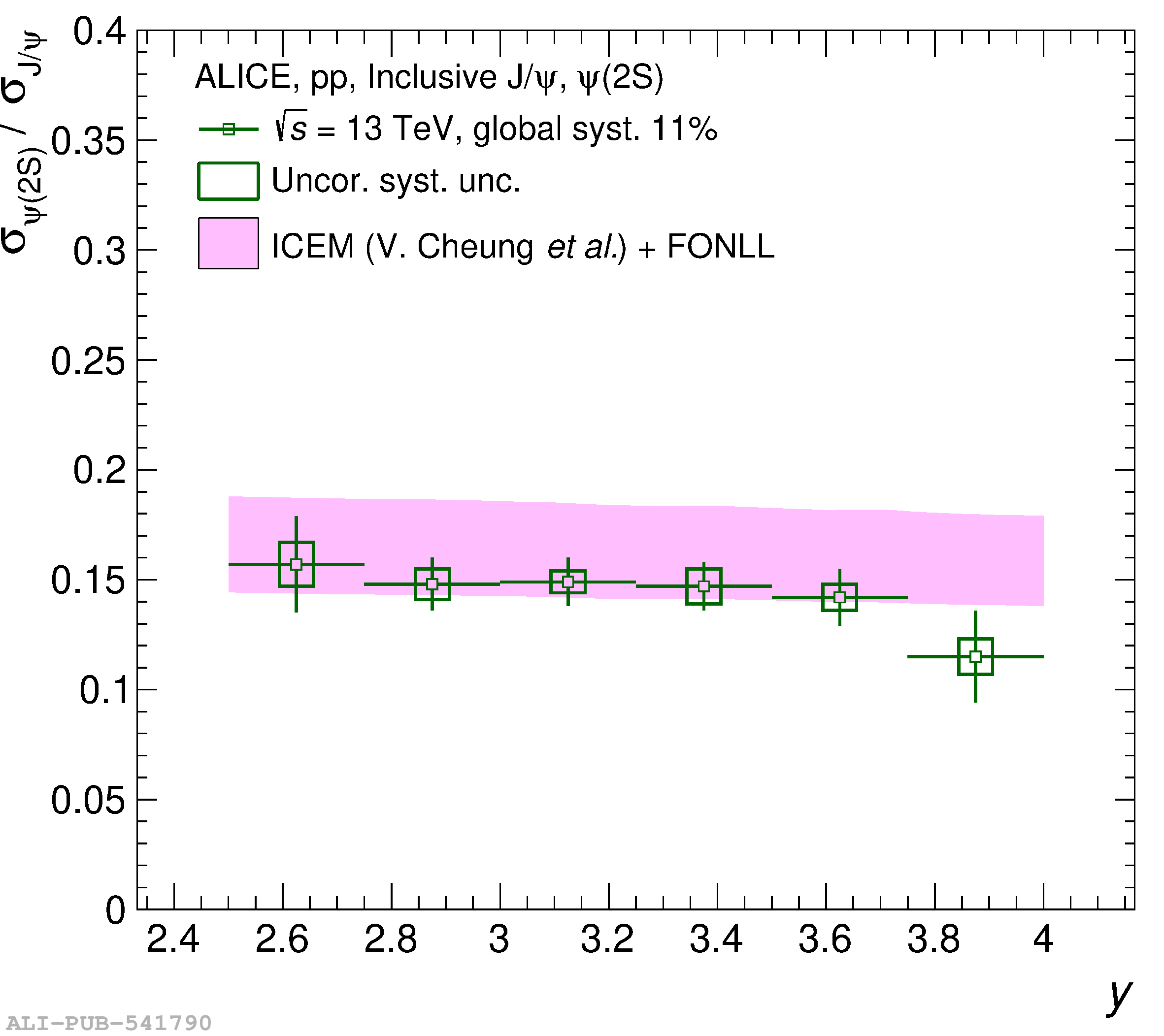
This article reports on the inclusive production cross section of several quarkonium states, $\mathrm{J}/\psi$, $\psi {\rm (2S)}$, $\Upsilon\rm(1S)$, $\Upsilon\rm(2S)$, and $\Upsilon\rm(3S)$, measured with the ALICE detector at the LHC, in pp collisions at $\sqrt{s} = 5.02$ TeV. The analysis is performed in the dimuon decay channel at forward rapidity ($2.5 <~ y <~ 4$). The integrated cross sections and transverse-momentum ($p_{\rm T}$) and rapidity ($y$) differential cross sections for $\mathrm{J}/\psi$, $\psi {\rm (2S)}$, $\Upsilon\rm(1S)$, and the $\psi {\rm (2S)}$-to-$\mathrm{J}/\psi$ cross section ratios are presented. The integrated cross sections, assuming unpolarized quarkonia, are: $\sigma_{\mathrm{J}/\psi}$($p_{\rm T}<~20$ GeV/c) = 5.88 $\pm$ 0.03 $\pm$ 0.34 $\mu$b, $\sigma_{\psi {\rm (2S)}}$($p_{\rm T}<~12$ GeV/c) = 0.87 $\pm$ 0.06 $\pm$ 0.10 $\mu$b, $\sigma_{\Upsilon\rm(1S)}$($p_{\rm T}<~15$ GeV/c) = 45.5 $\pm$ 3.9 $\pm$ 3.5 nb, $\sigma_{\Upsilon\rm(2S)}$($p_{\rm T}<~15$ GeV/c) = 22.4 $\pm$ 3.2 $\pm$ 2.7 nb, and $\sigma_{\Upsilon\rm(3S)}$($p_{\rm T}<~15$ GeV/c) = 4.9 $\pm$ 2.2 $\pm$ 1.0 nb, where the first (second) uncertainty is the statistical (systematic) one. For the first time, the cross sections of the three $\Upsilon$ states, as well as the $\psi {\rm (2S)}$ one as a function of $p_{\rm T}$ and $y$, are measured at $\sqrt{s} = 5.02$ TeV at forward rapidity. These measurements also significantly extend the $\mathrm{J}/\psi$ $p_{\rm T}$ reach and supersede previously published results. A comparison with ALICE measurements in pp collisions at $\sqrt{s} = 2.76$, 7, 8, and 13 TeV is presented and the energy dependence of quarkonium production cross sections is discussed. Finally, the results are compared with the predictions from several production models.
Eur. Phys. J. C 83 (2023) 61
HEP Data
e-Print: arXiv:2109.15240 | PDF | inSPIRE
CERN-EP-2021-197
Figure group