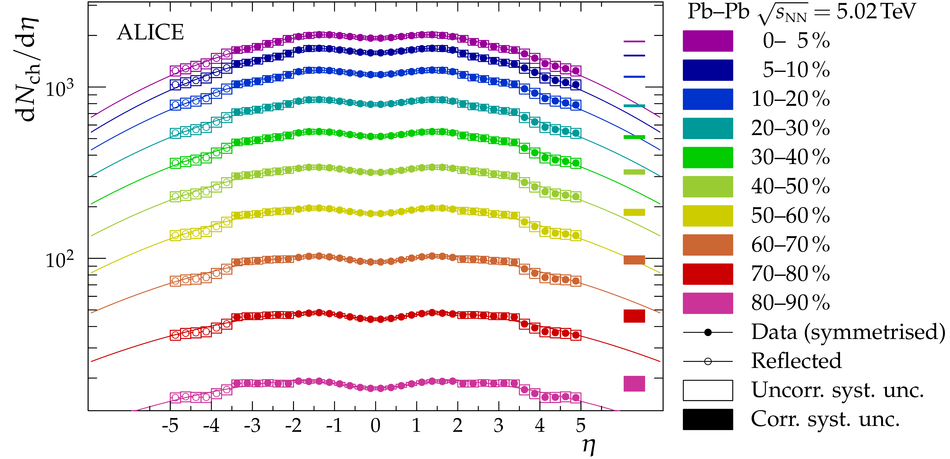
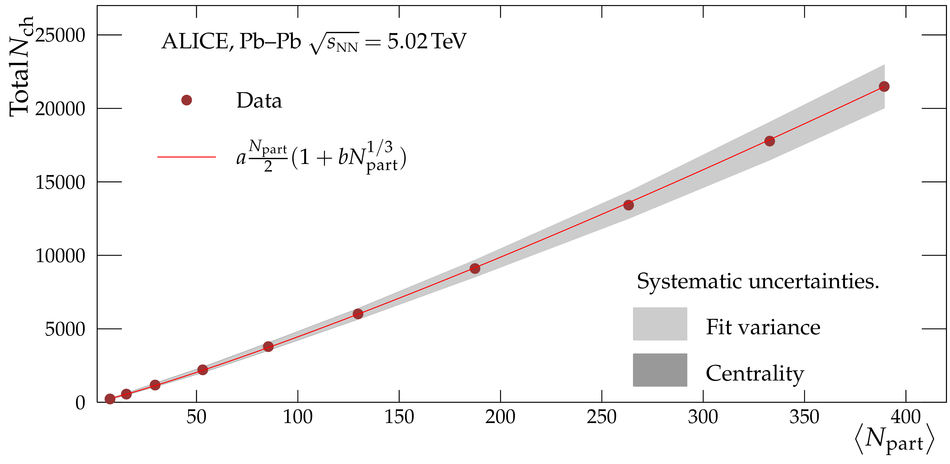
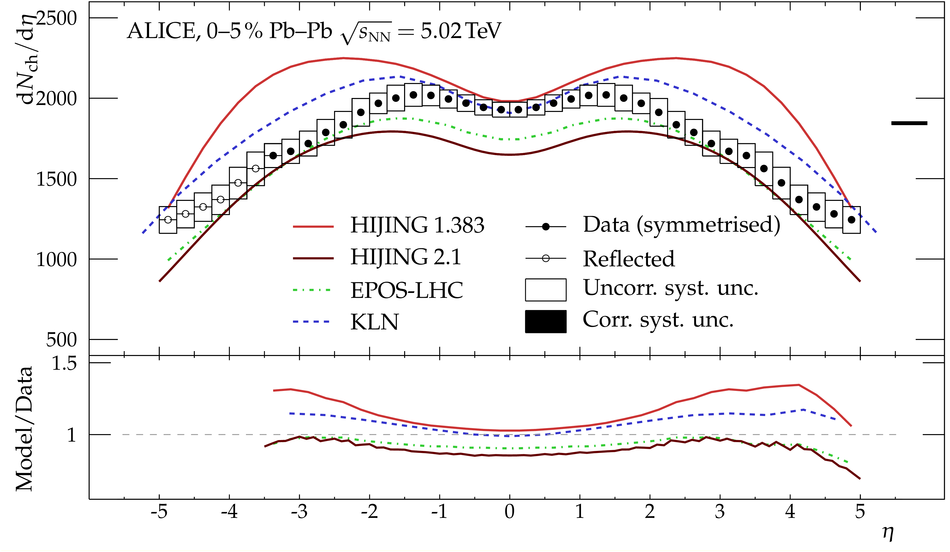
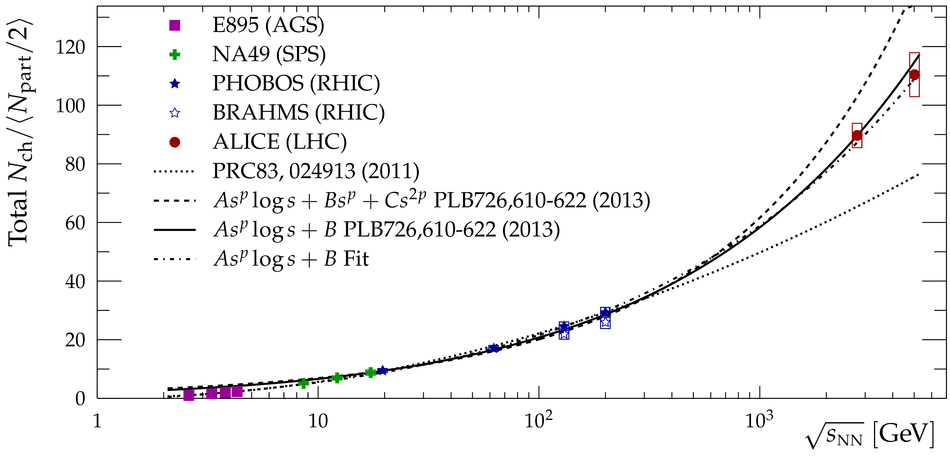
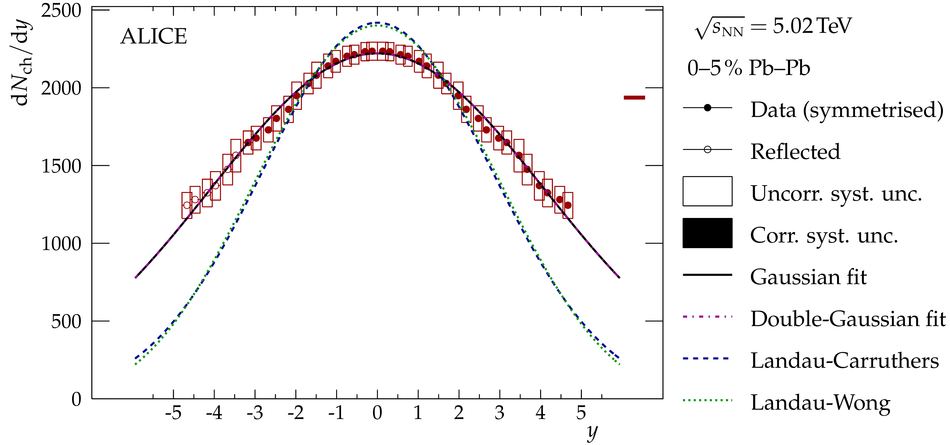
We present the charged-particle pseudorapidity density in Pb-Pb collisions at $\sqrt{s_{\mathrm{NN}}}=5.02\,\mathrm{Te\kern-.25exV}$ in centrality classes measured by ALICE. The measurement covers a wide pseudorapidity range from $-3.5$ to $5$, which is sufficient for reliable estimates of the total number of charged particles produced in the collisions. For the most central (0-5%) collisions we find $21\,400\pm 1\,300$ while for the most peripheral (80-90%) we find $230\pm 38$. This corresponds to an increase of $(27\pm4)\%$ over the results at $\sqrt{s_{\mathrm{NN}}}=2.76\,\mathrm{Te\kern-.25exV}$ previously reported by ALICE. The energy dependence of the total number of charged particles produced in heavy-ion collisions is found to obey a modified power-law like behaviour. The charged-particle pseudorapidity density of the most central collisions is compared to model calculations --- none of which fully describes the measured distribution. We also present an estimate of the rapidity density of charged particles. The width of that distribution is found to exhibit a remarkable proportionality to the beam rapidity, independent of the collision energy from the top SPS to LHC energies.
Phys. Lett. B 772 (2017) 567-577
HEP Data
e-Print: arXiv:1612.08966 | PDF | inSPIRE
CERN-EP-2016-327