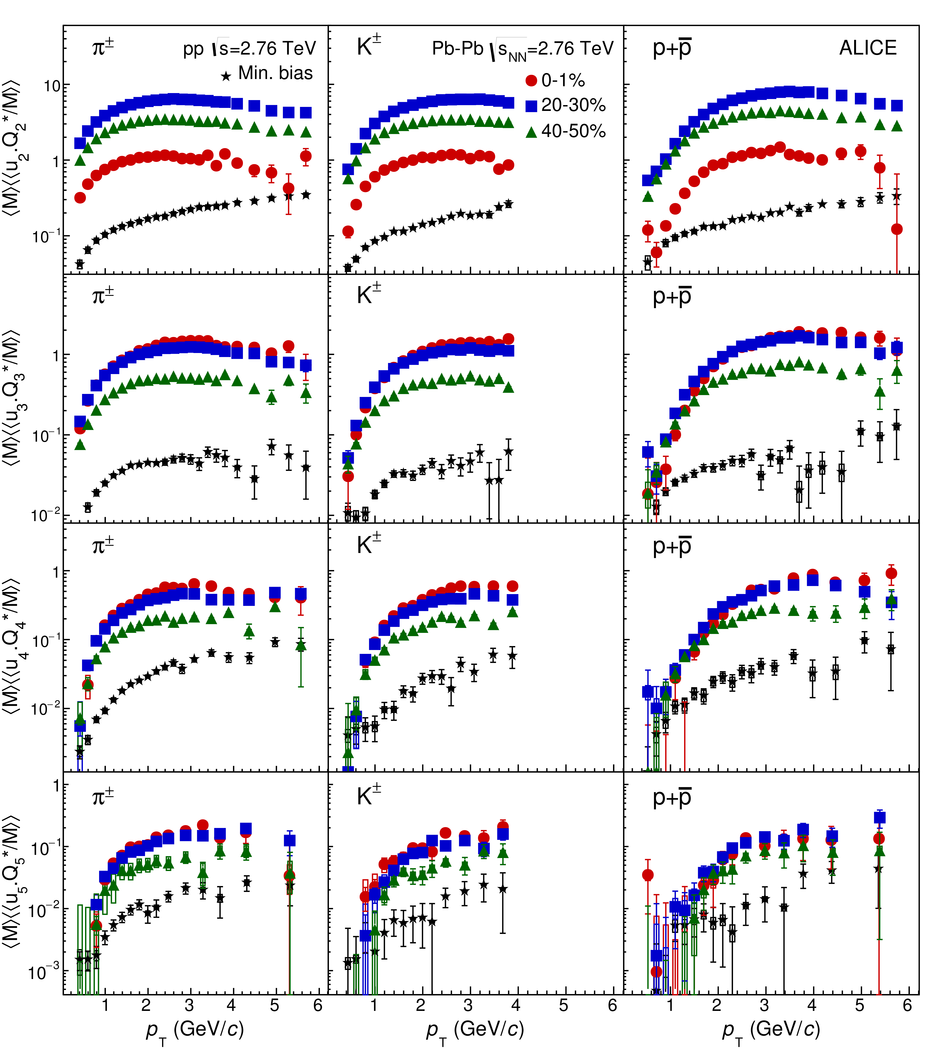
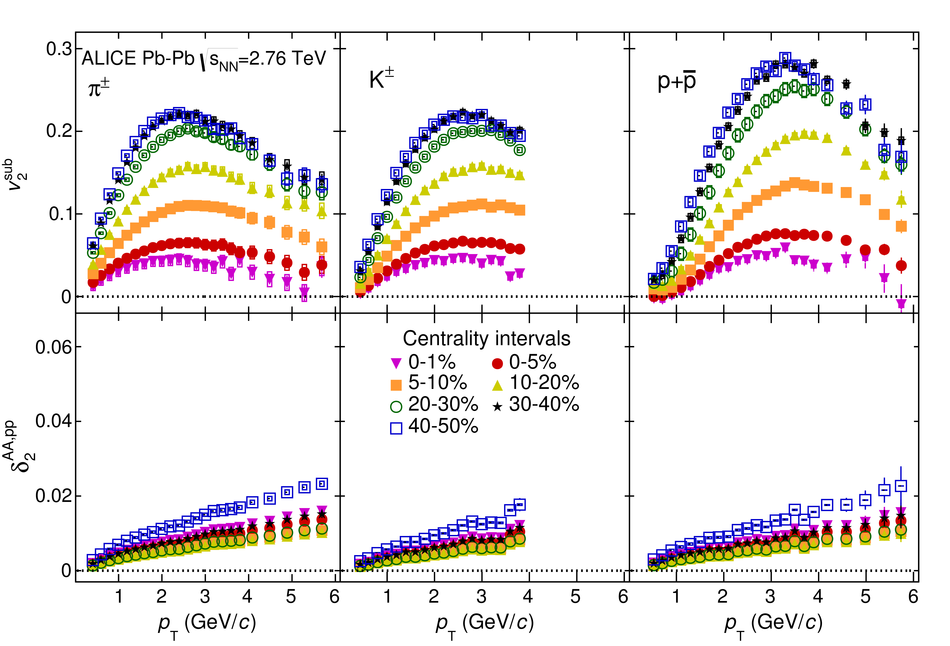
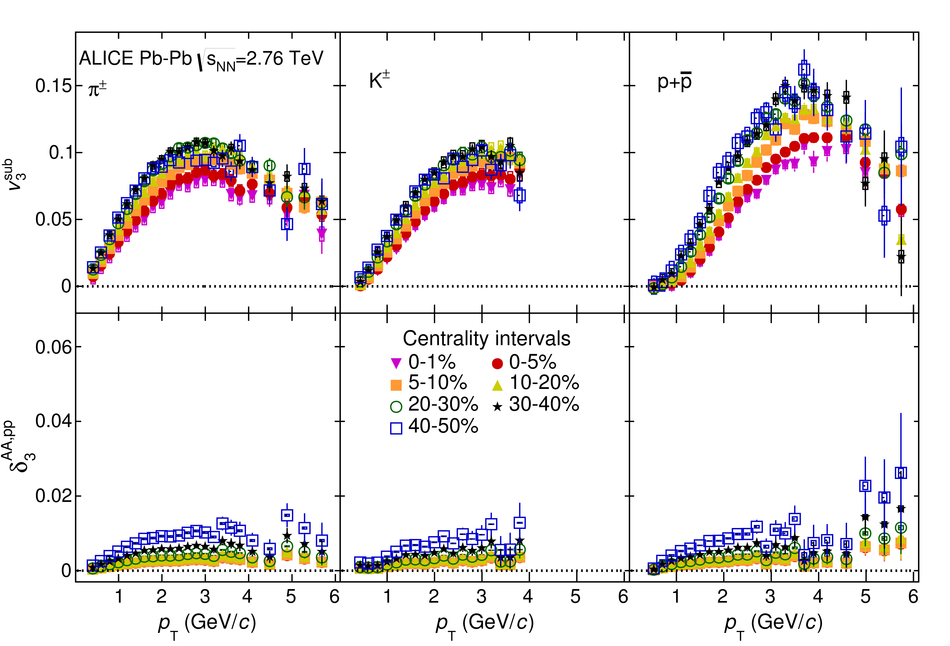
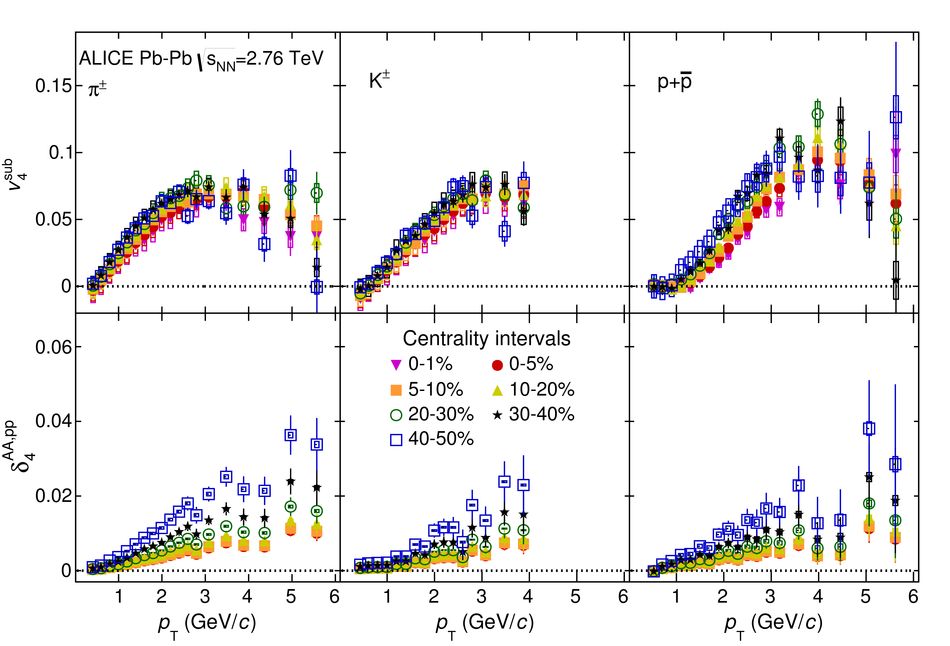
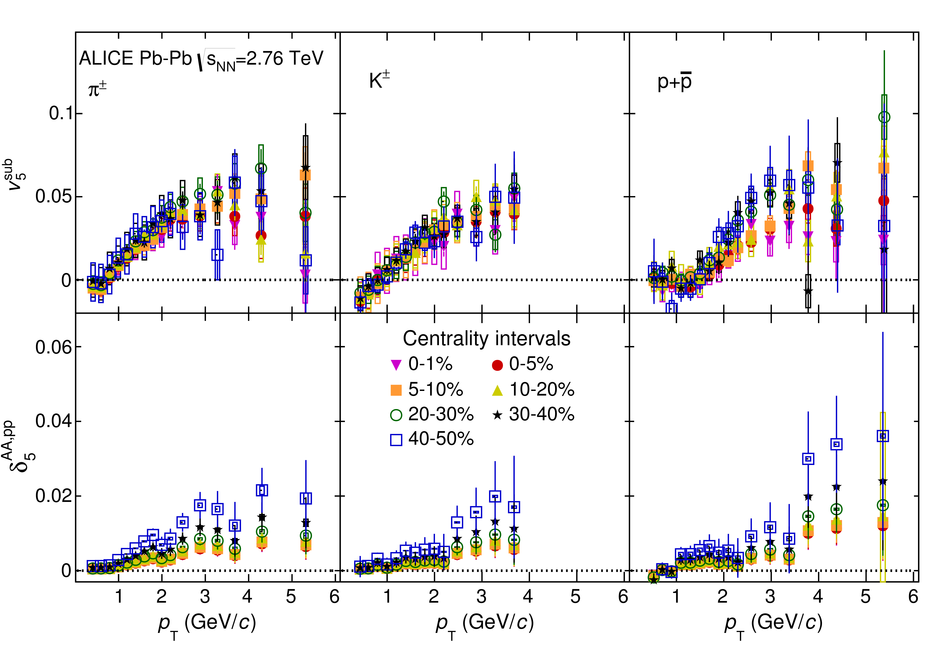
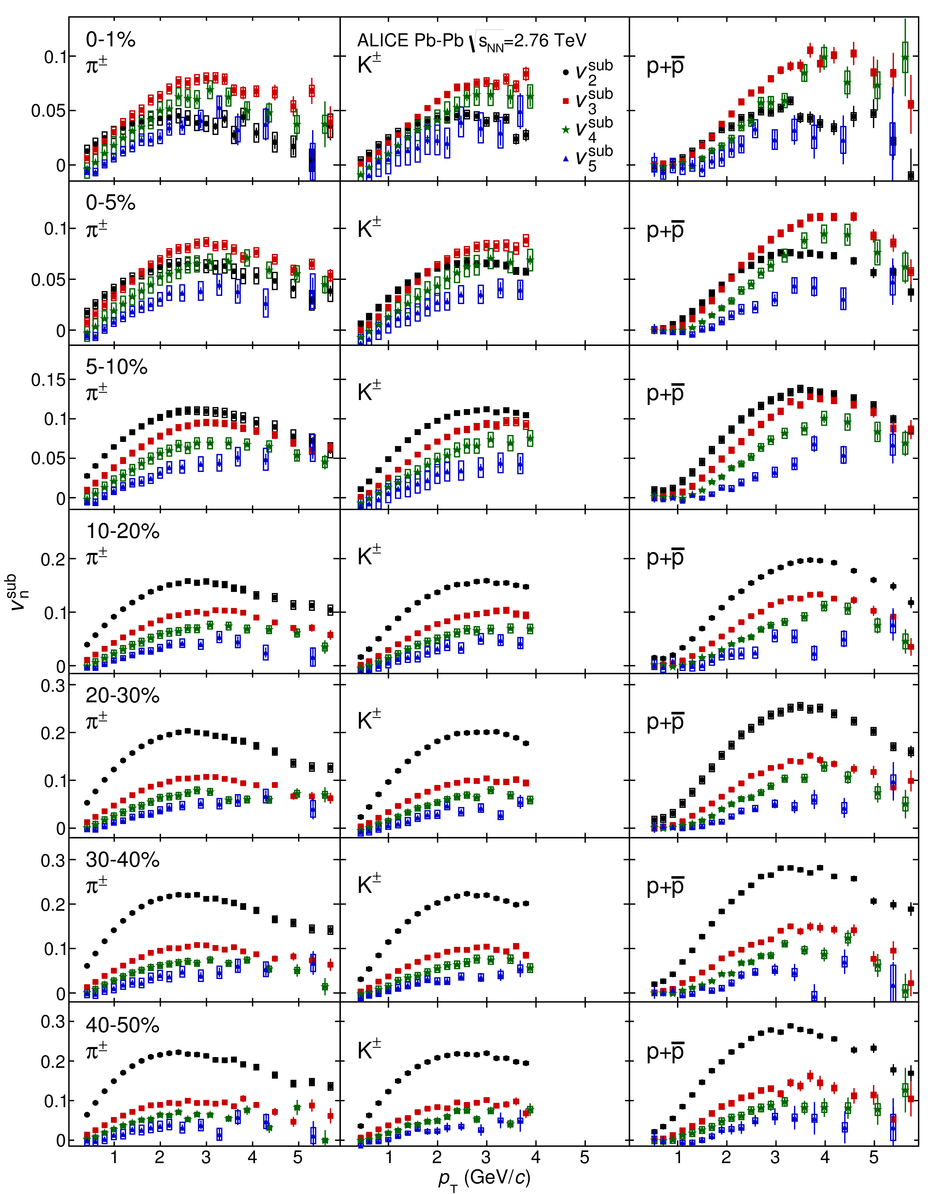
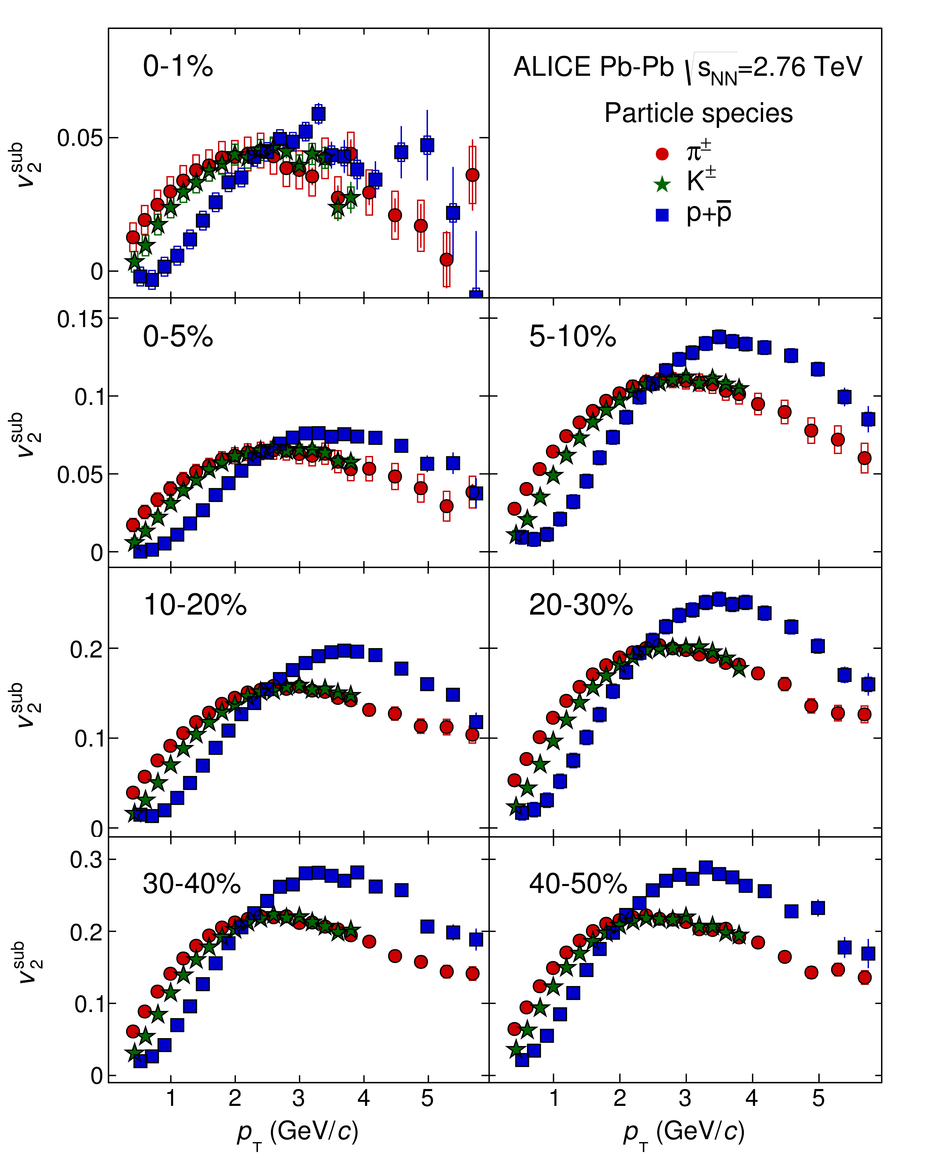
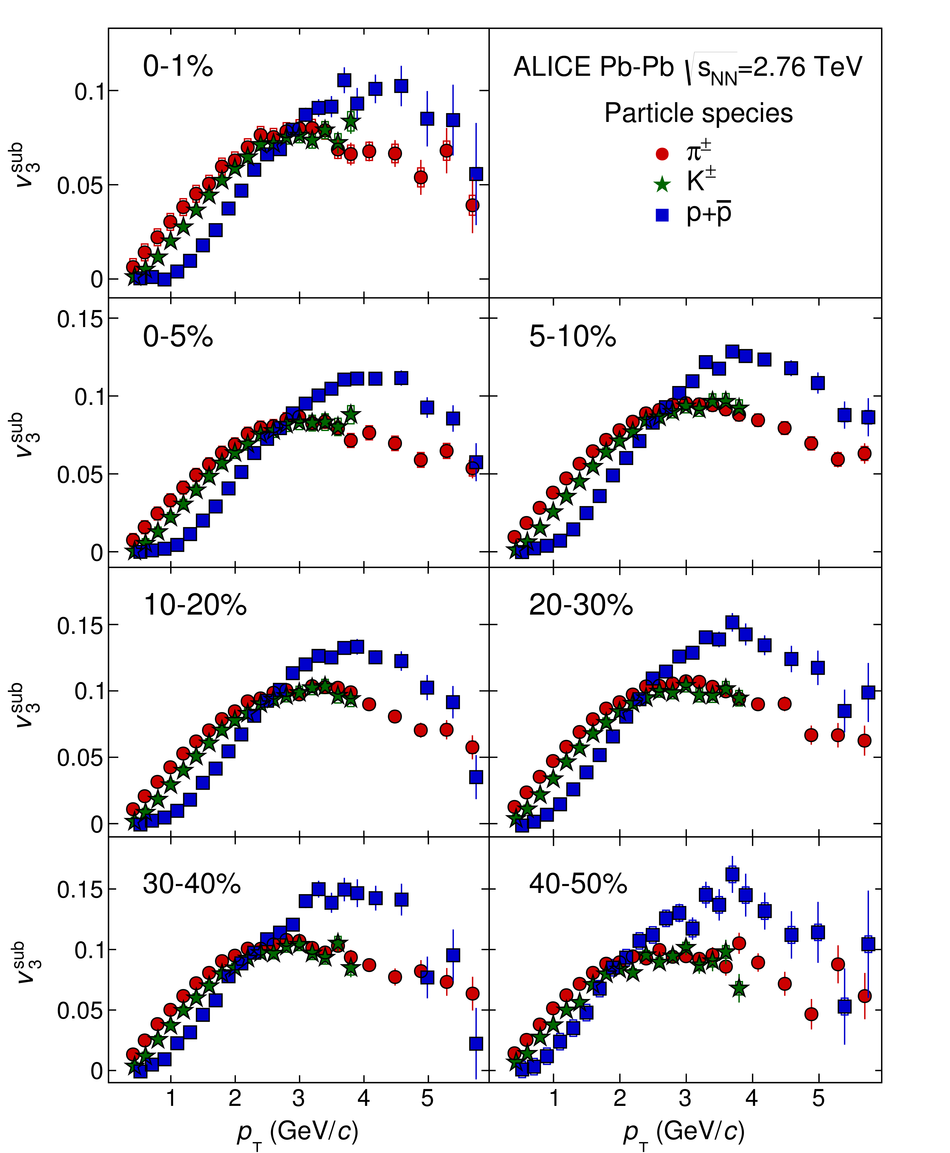
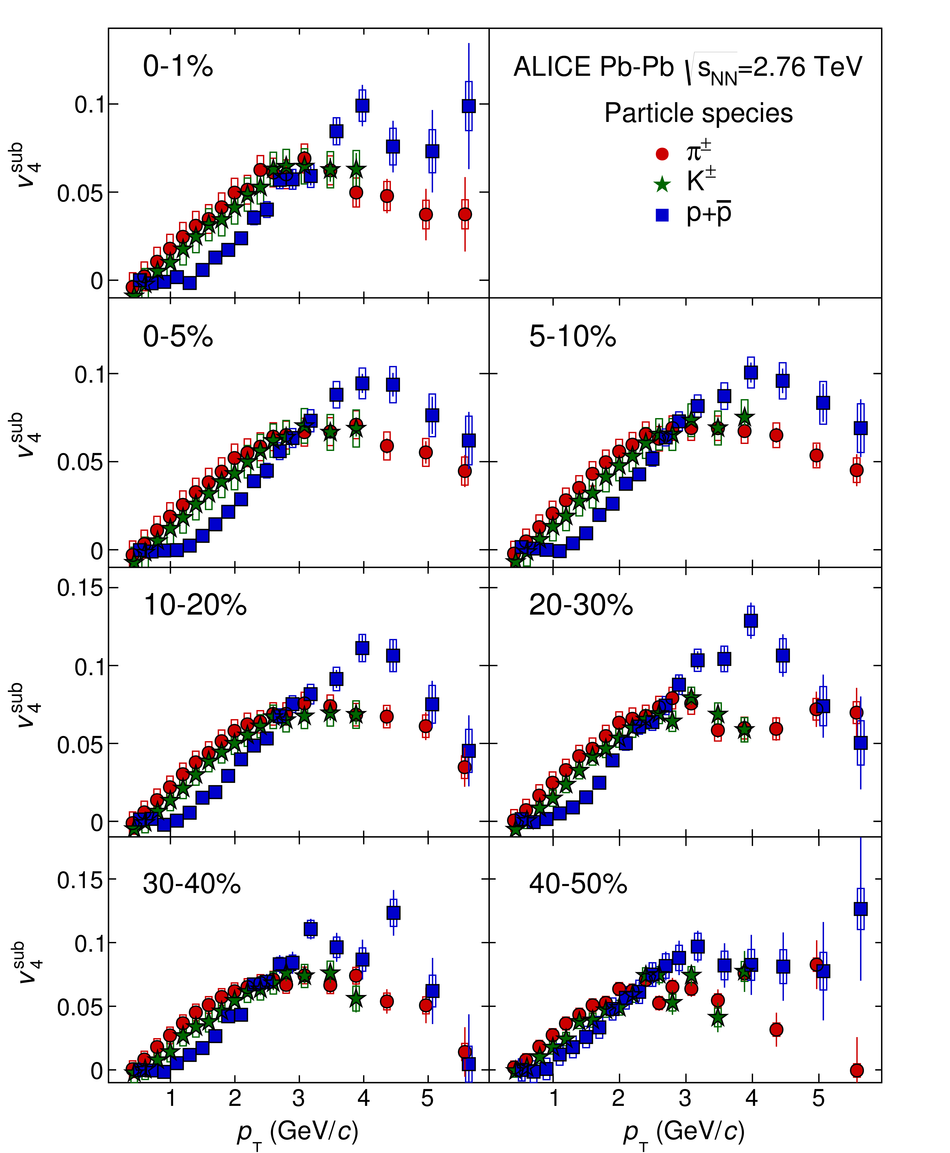
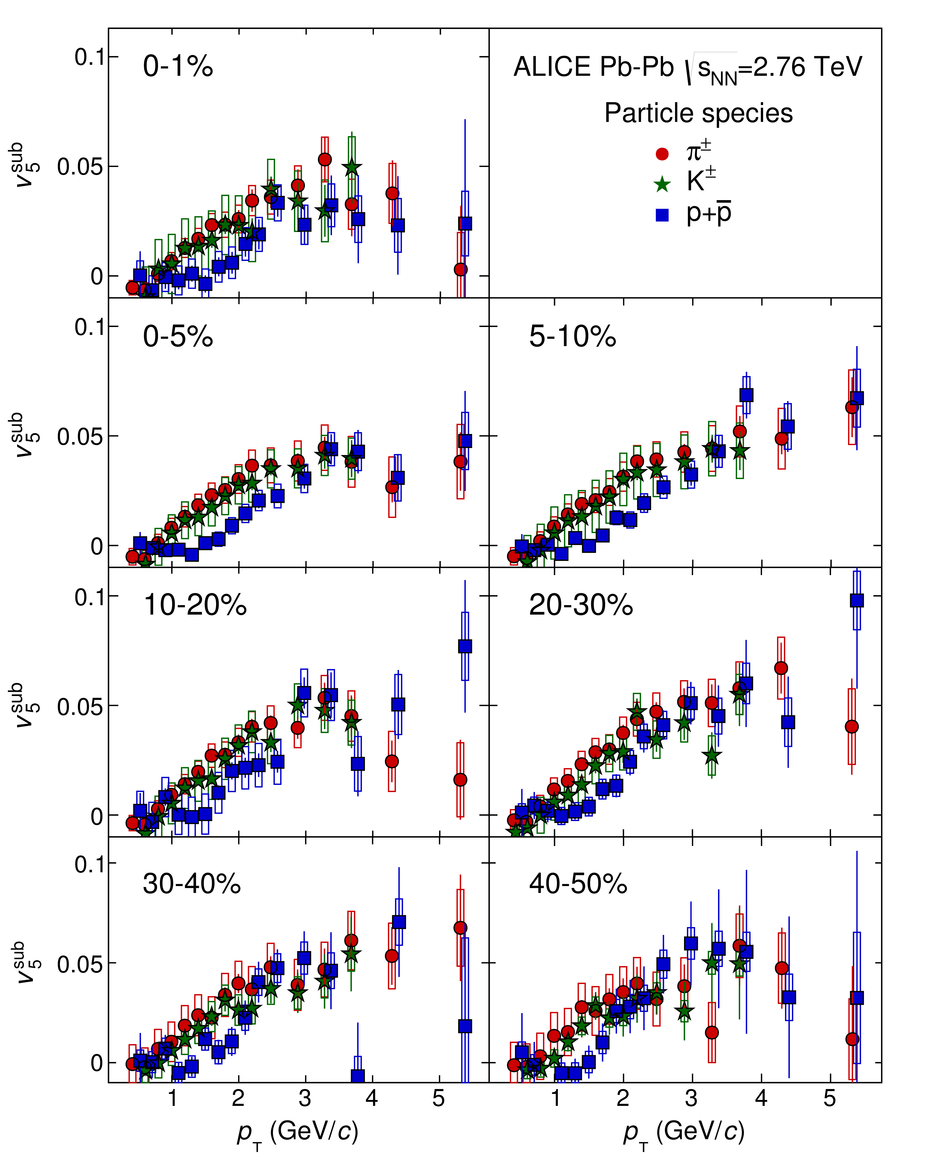
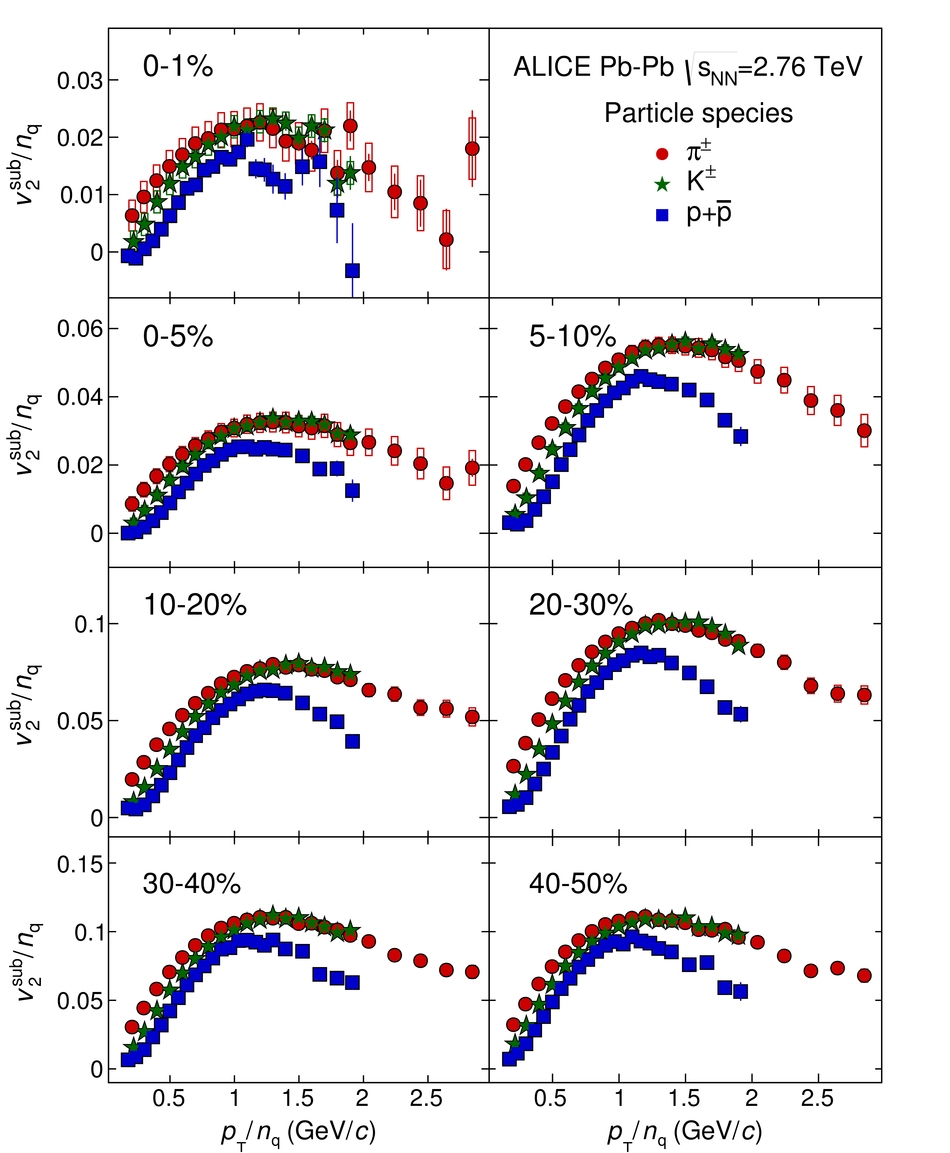
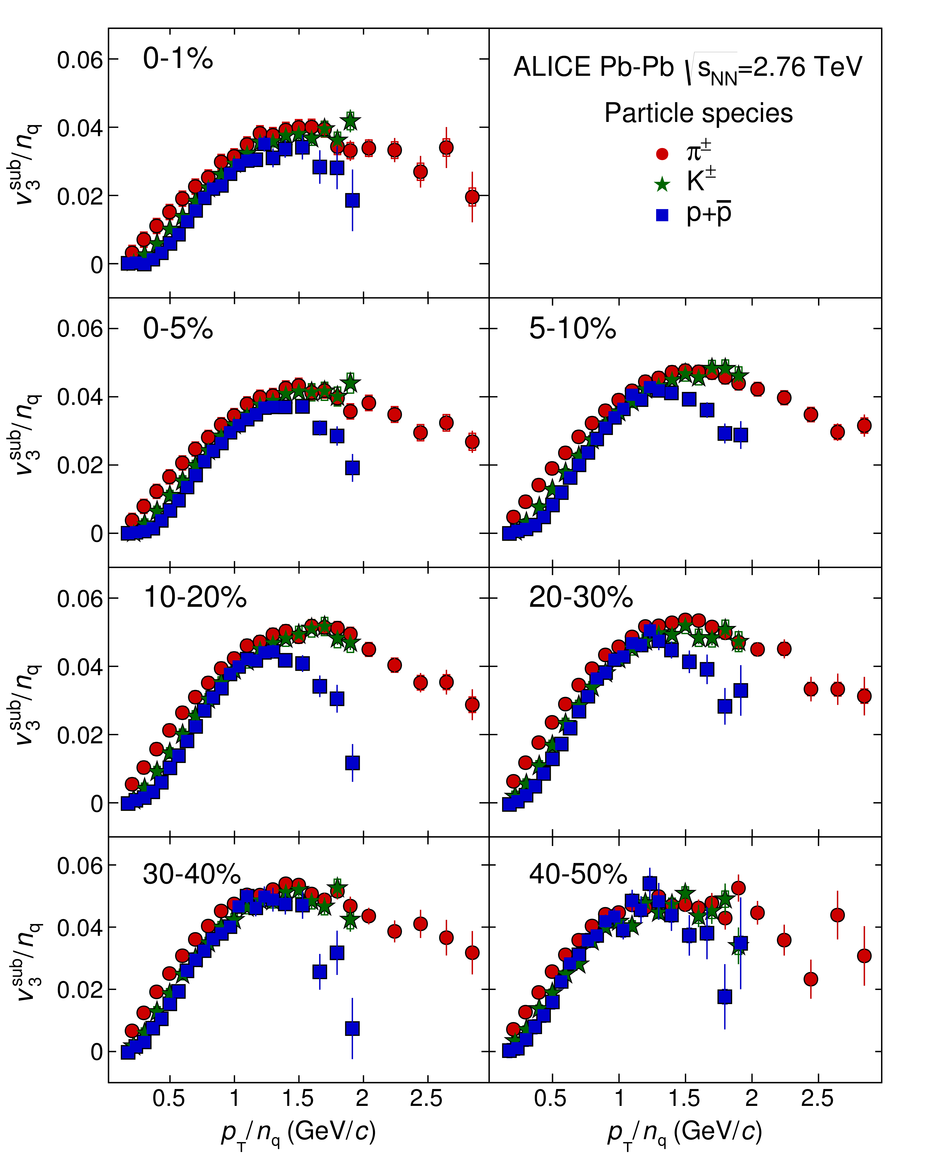
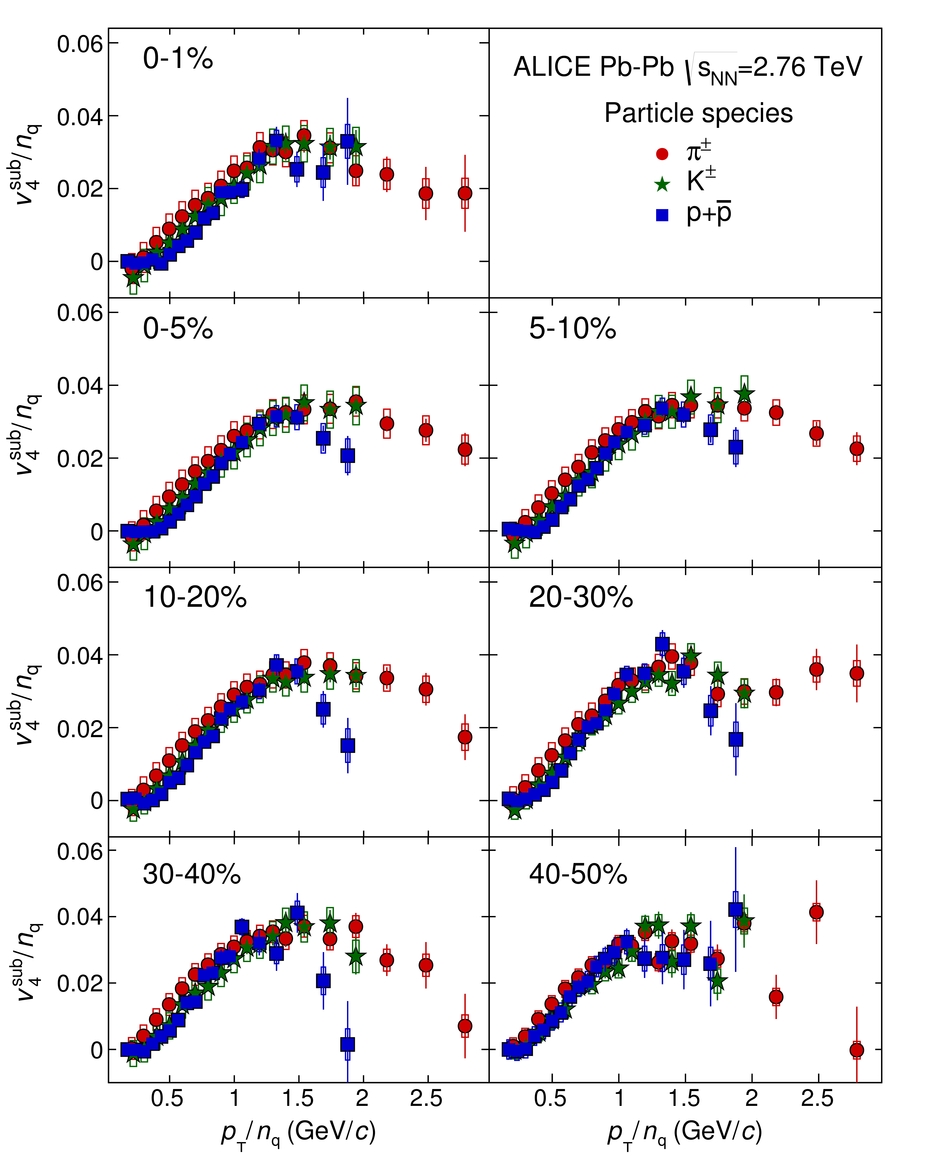
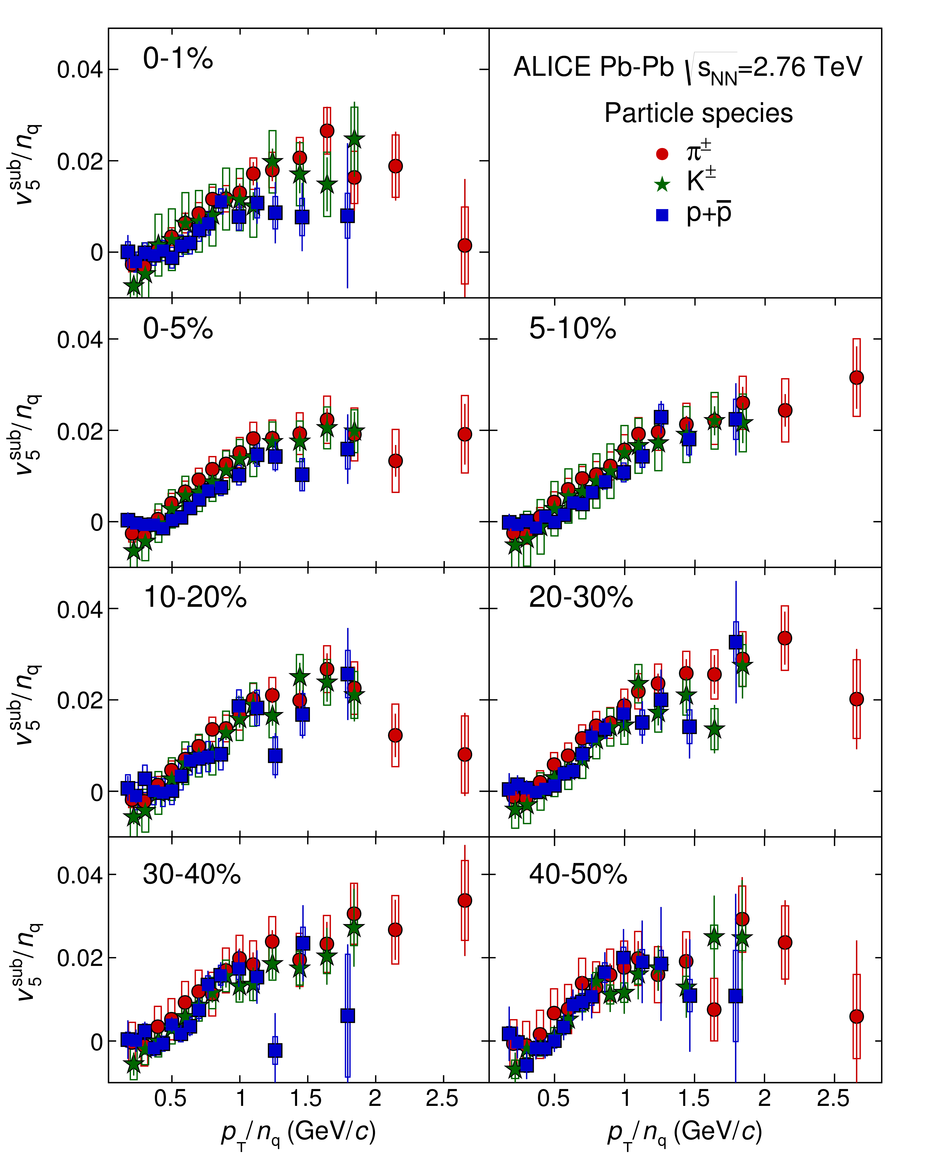
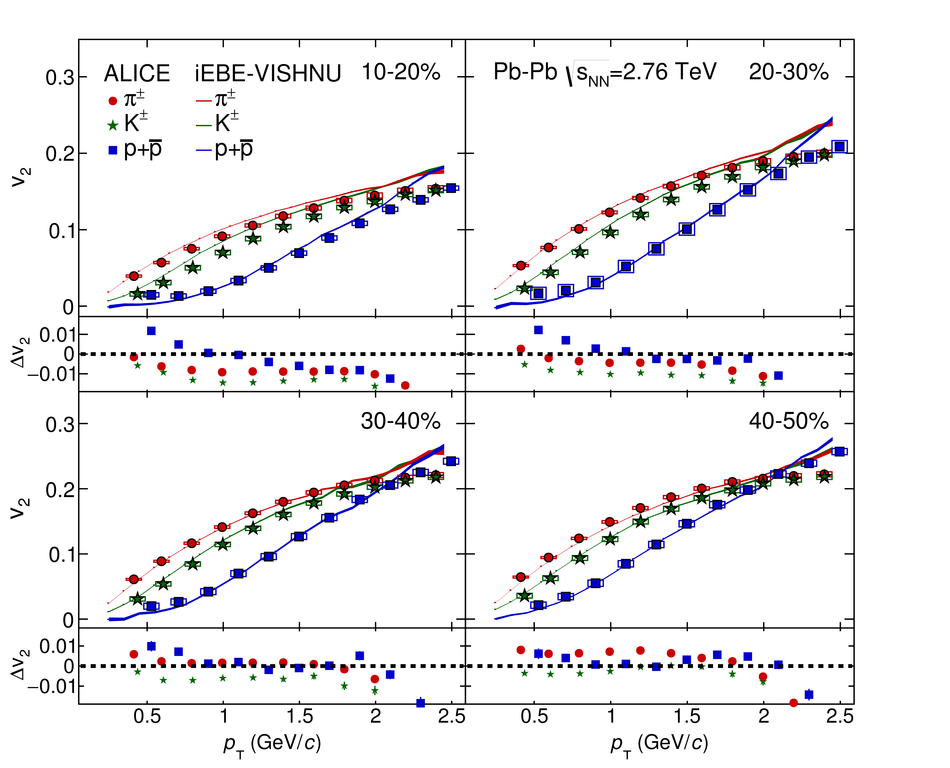
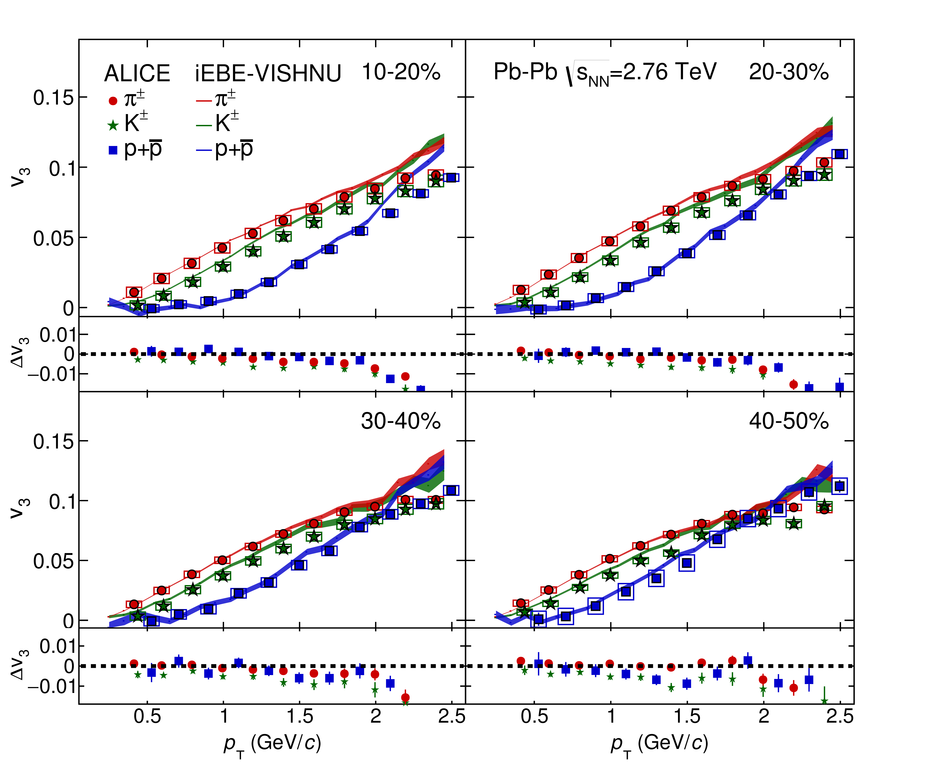
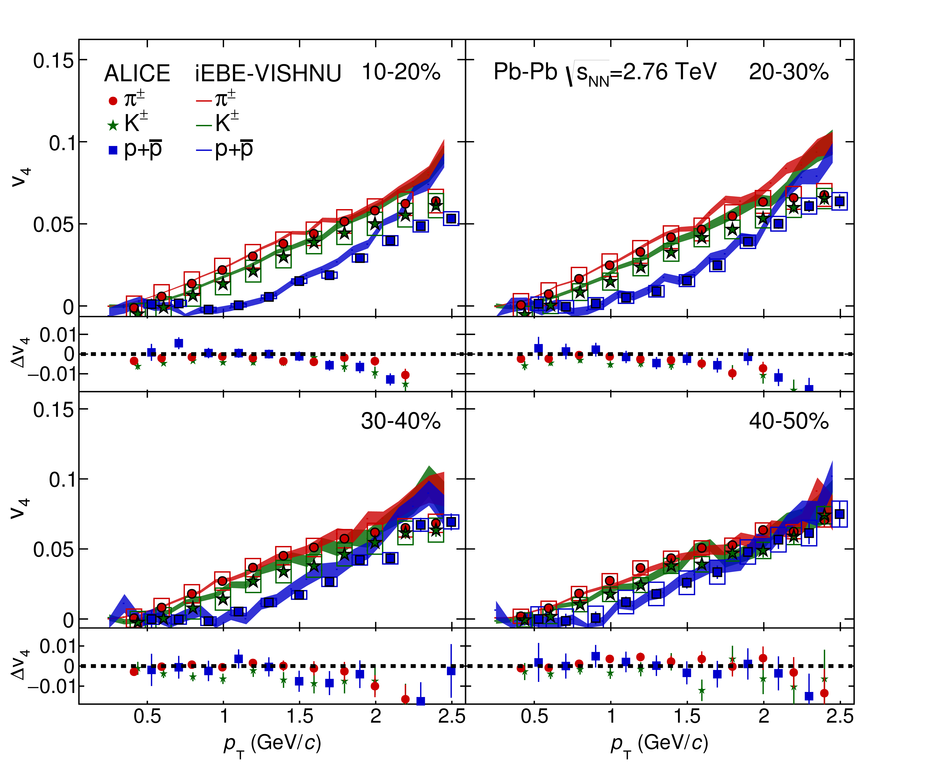
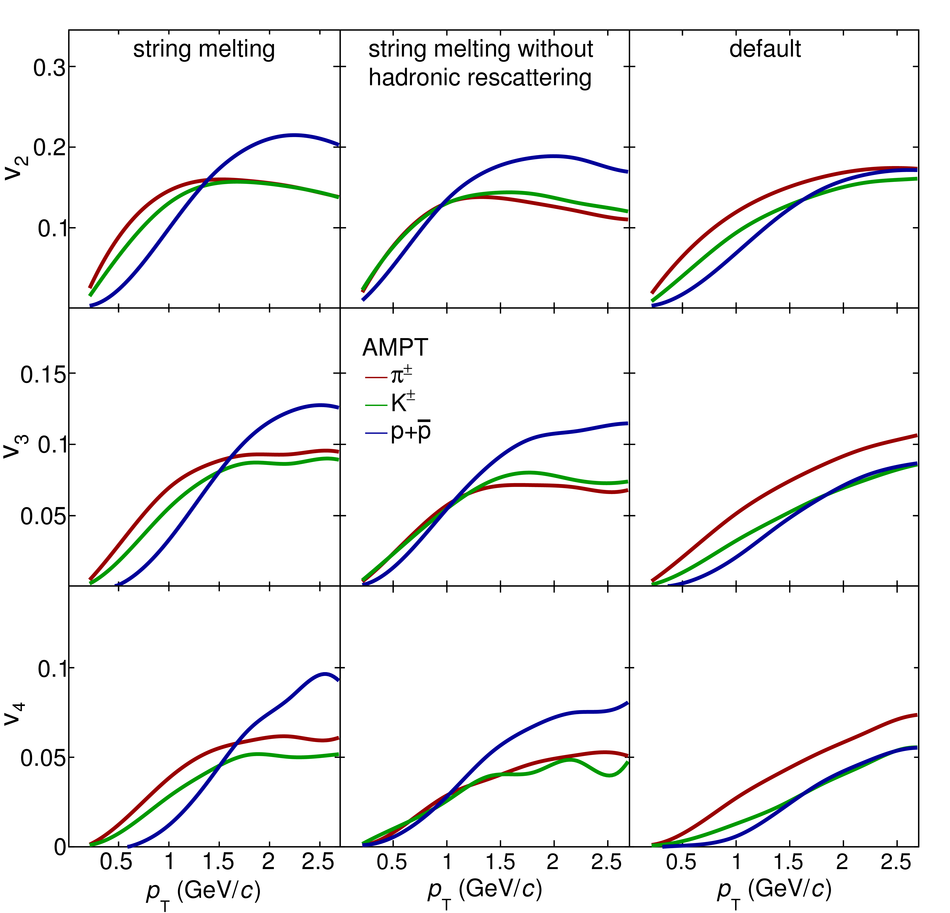
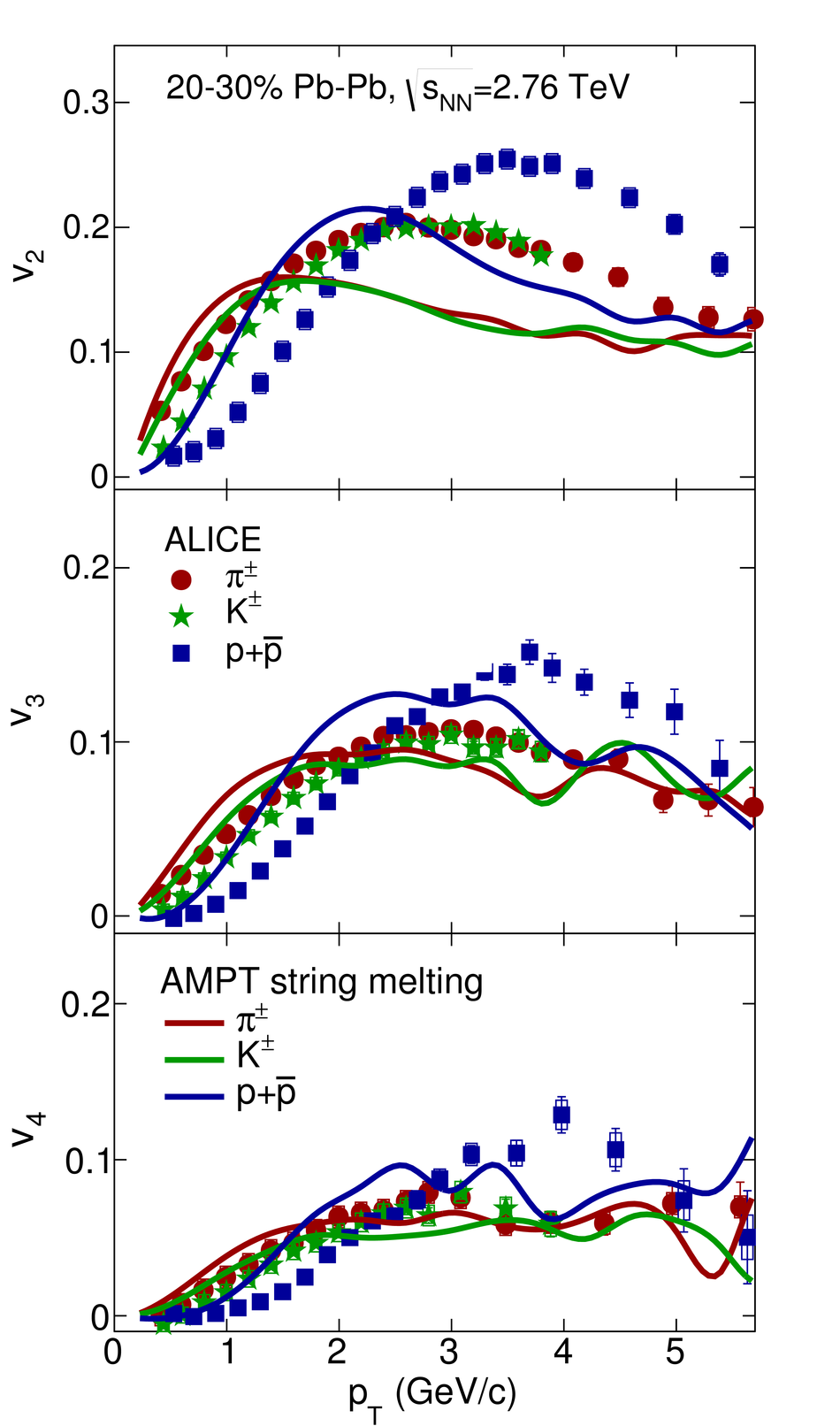
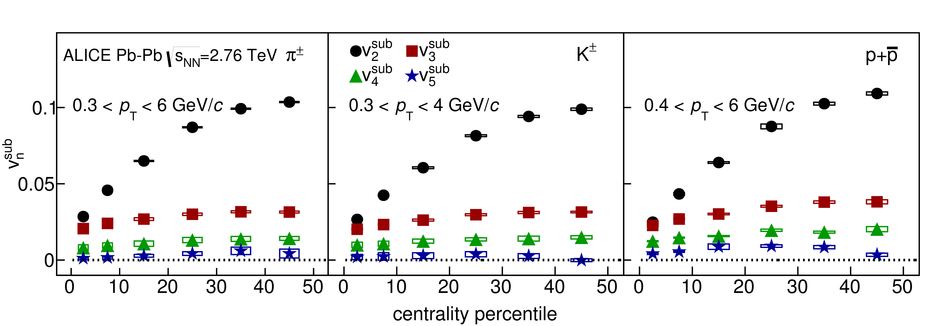
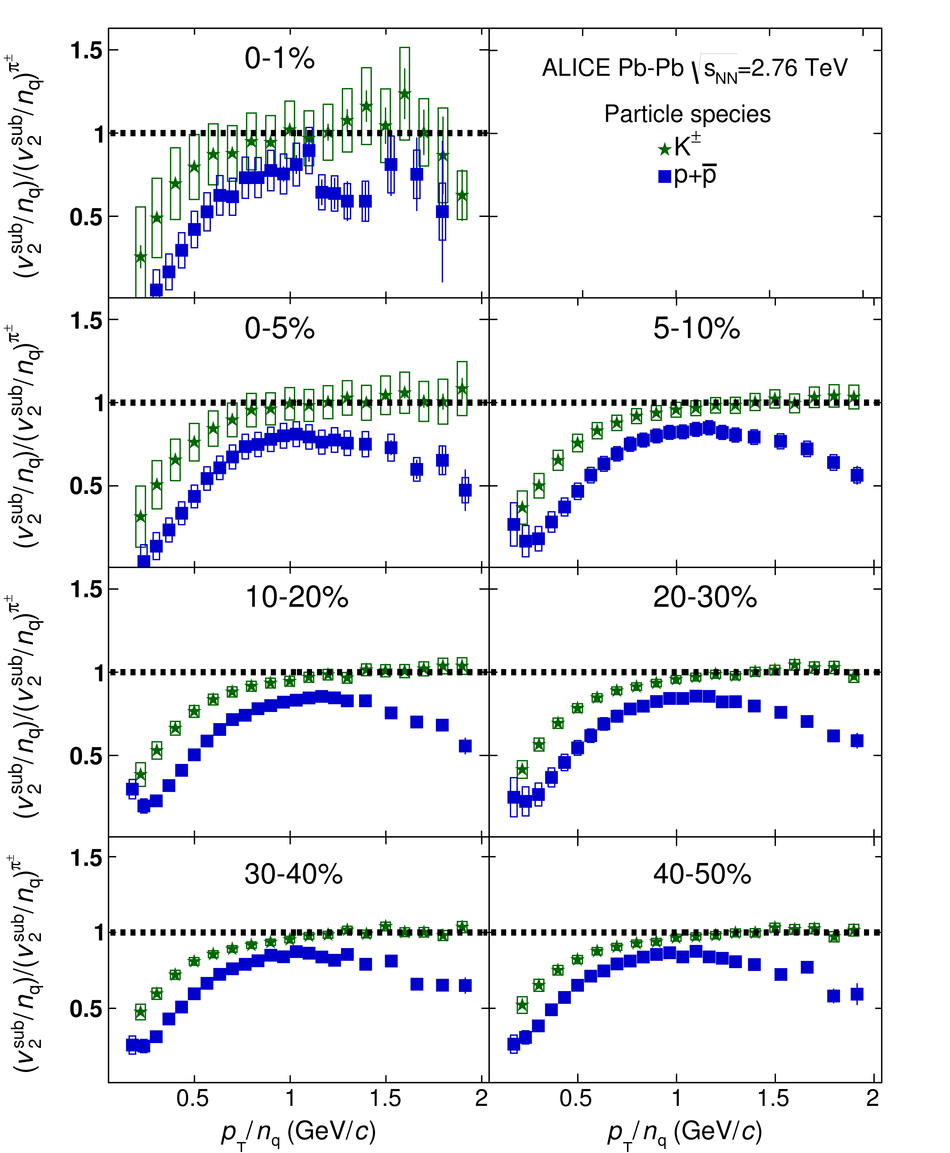
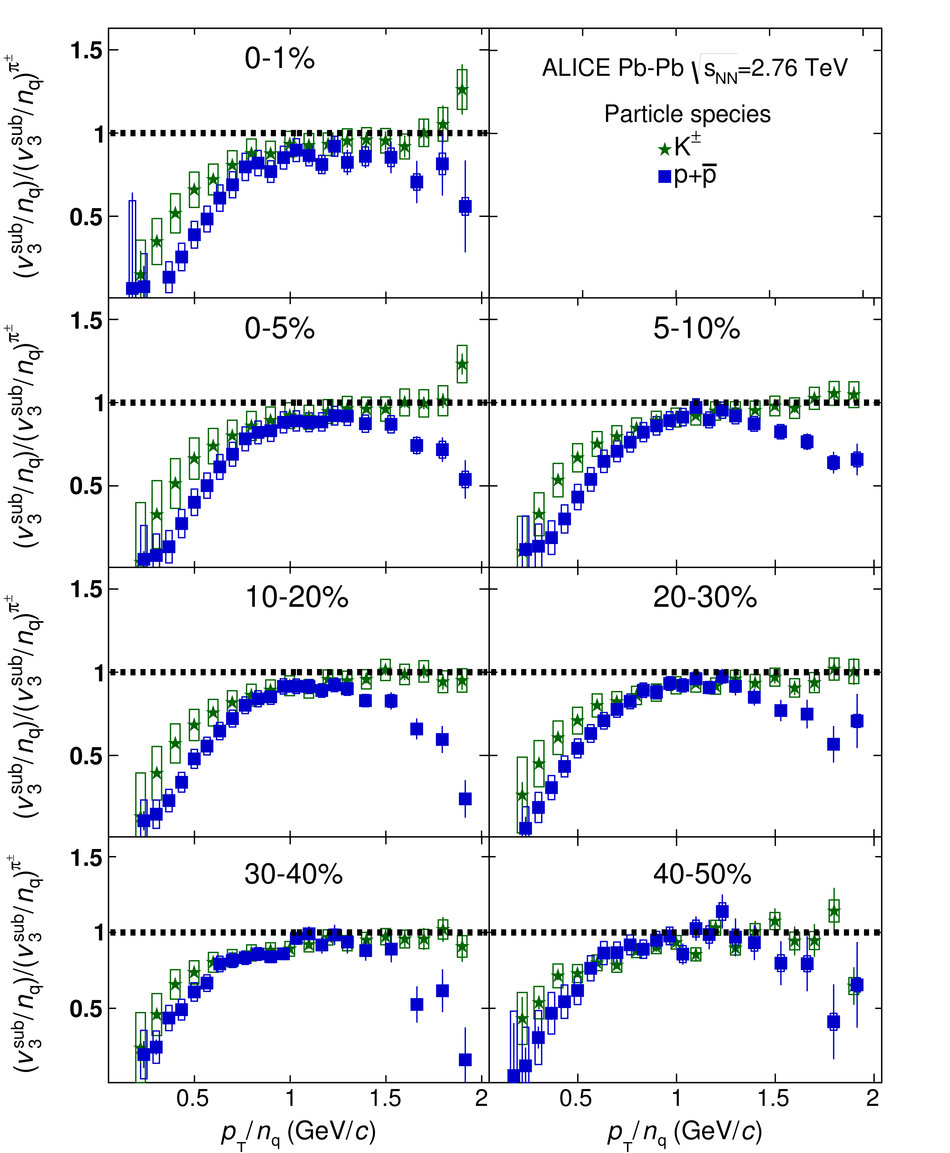
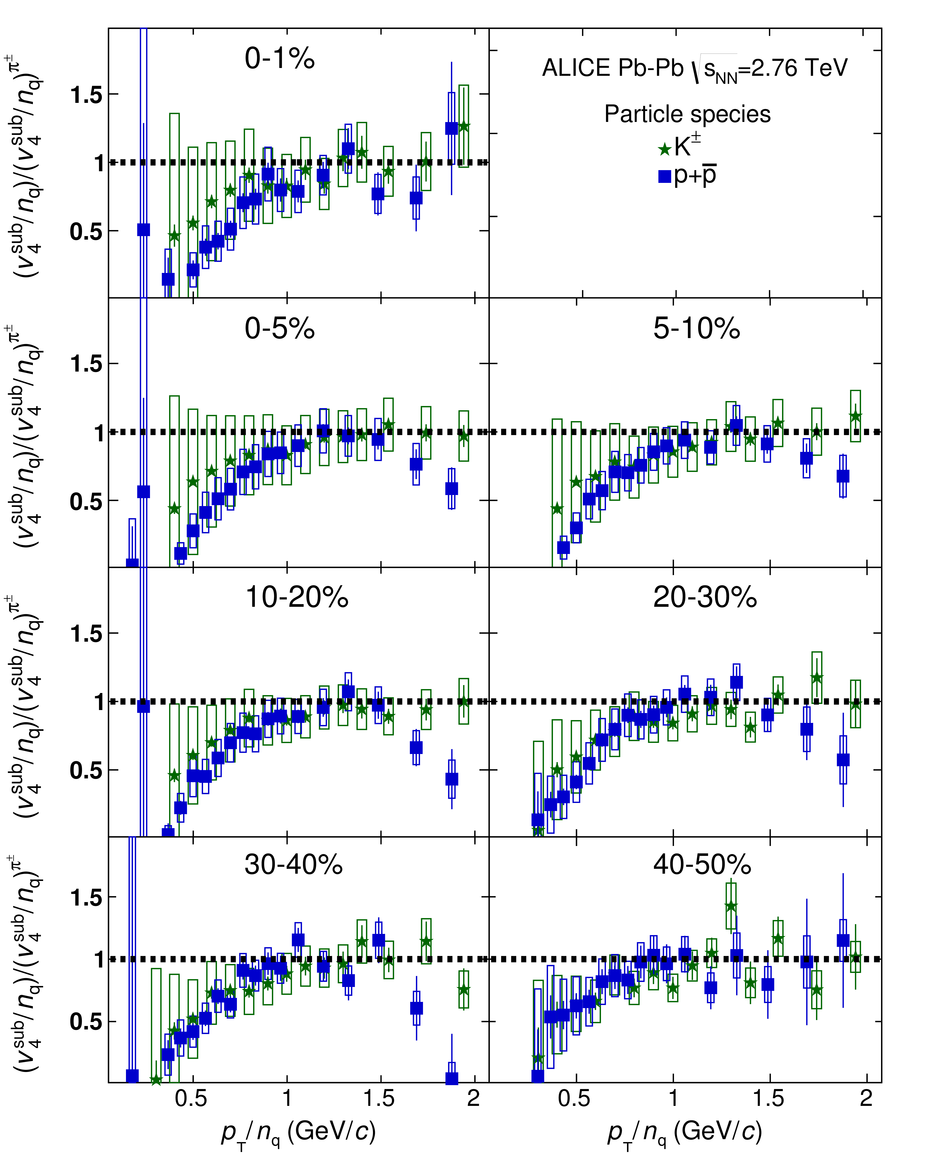
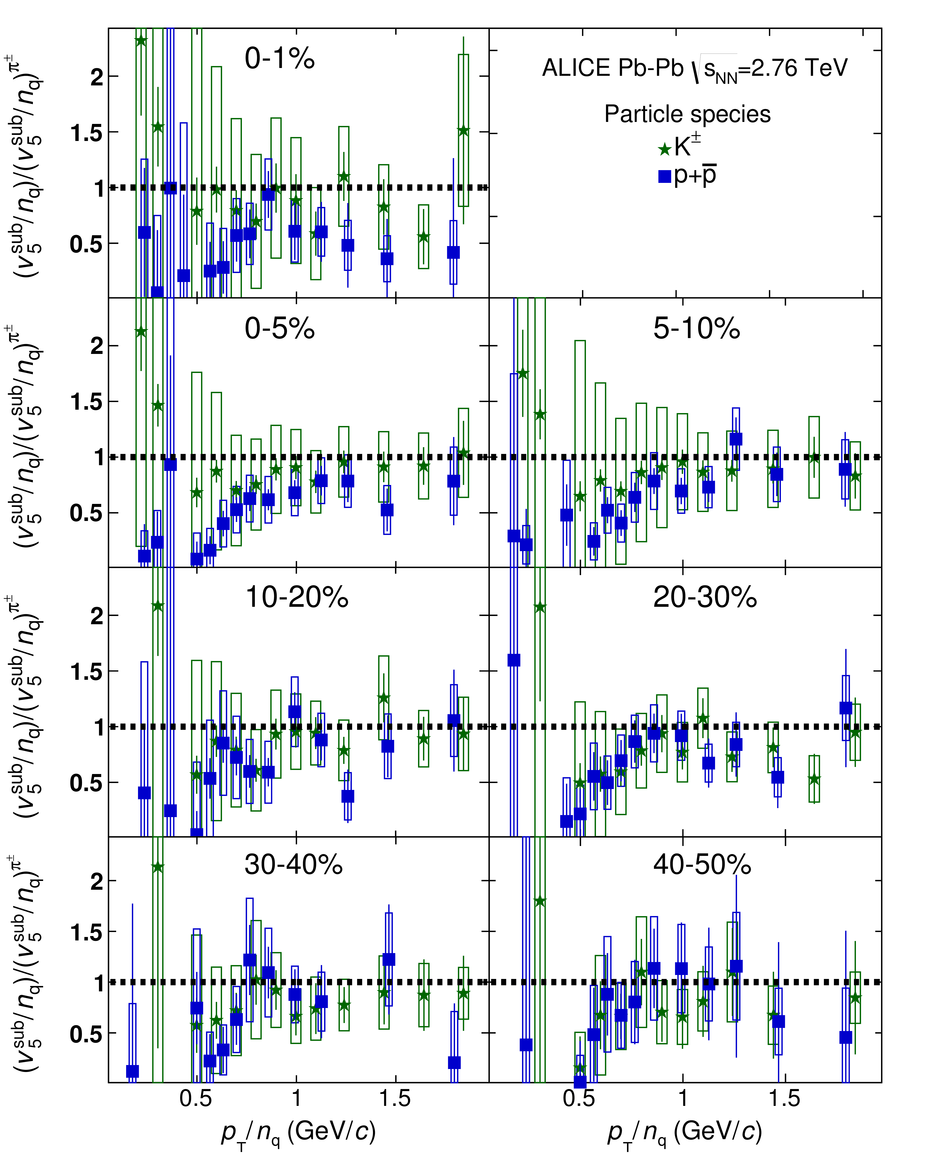
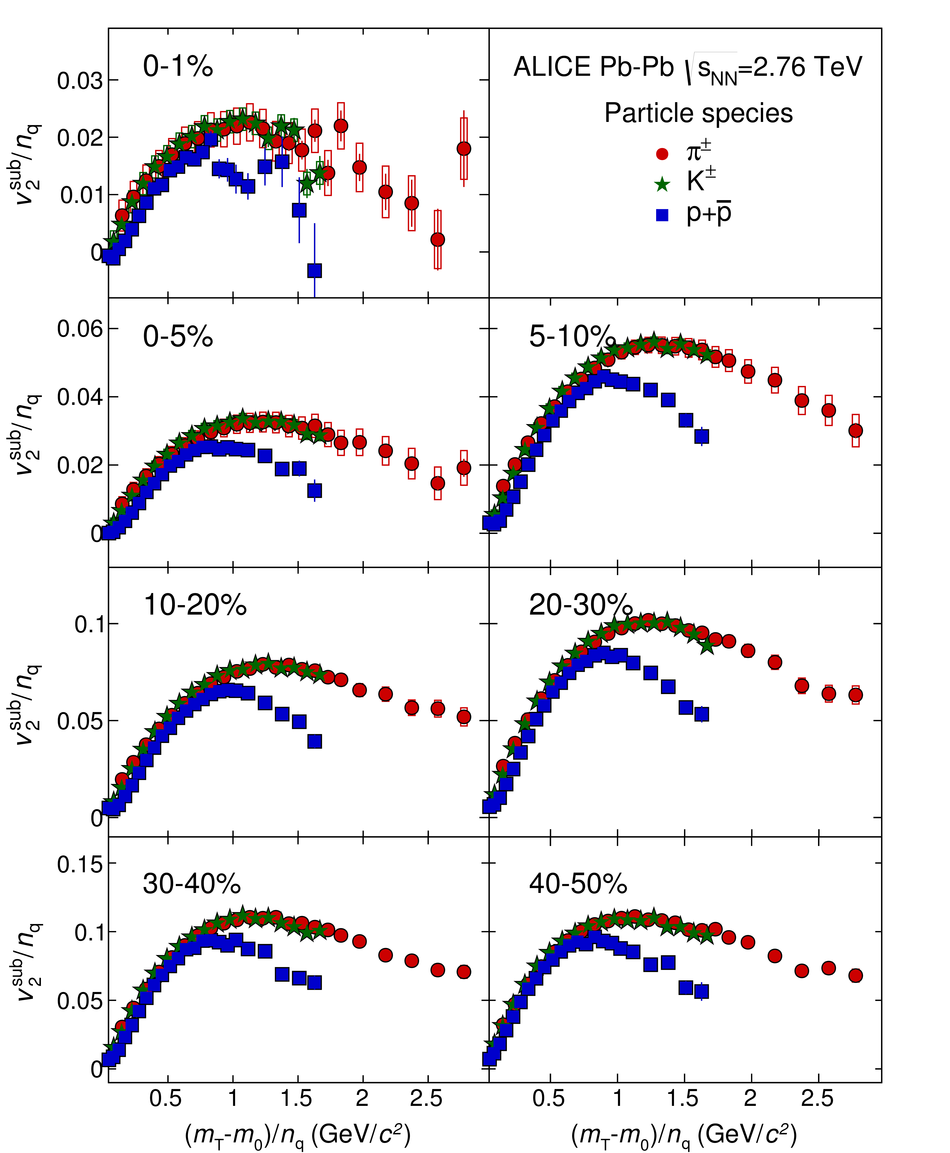
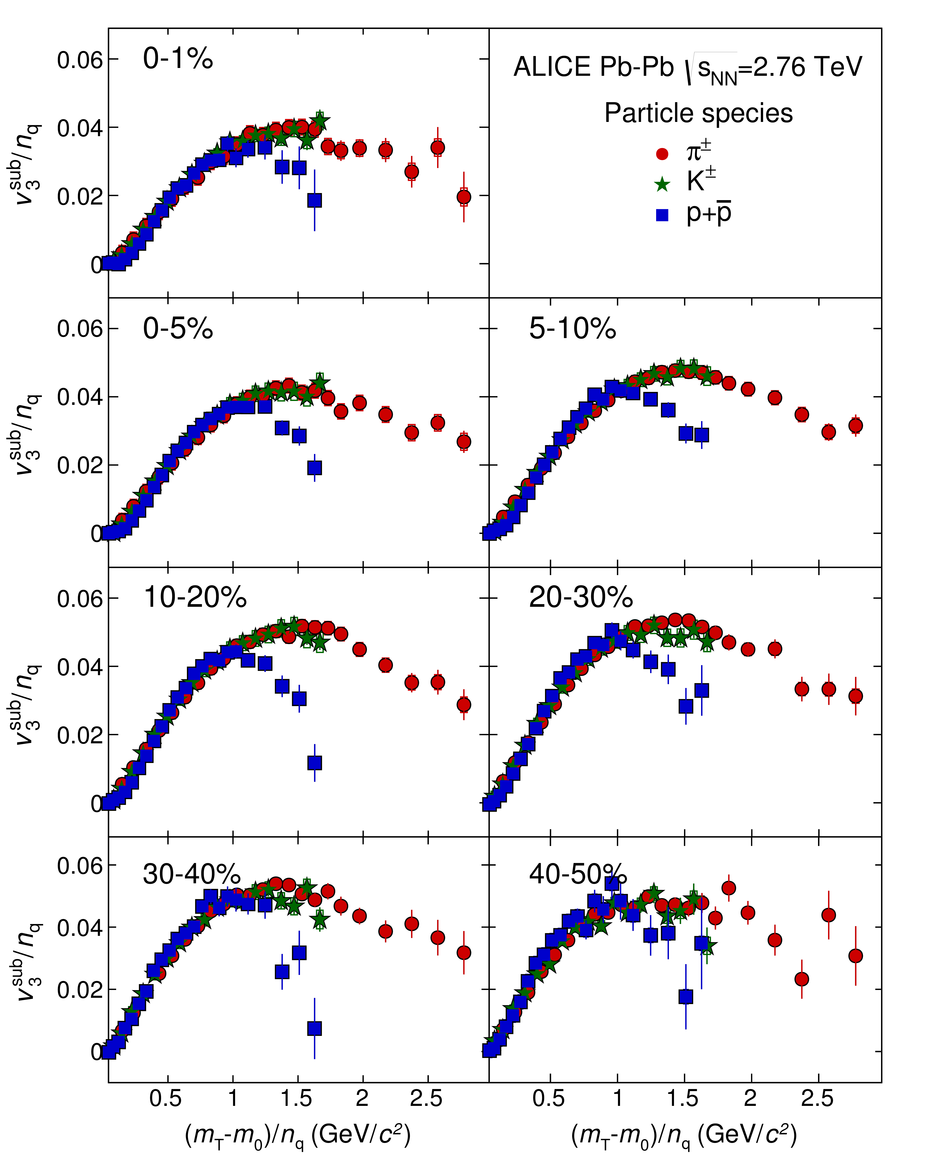
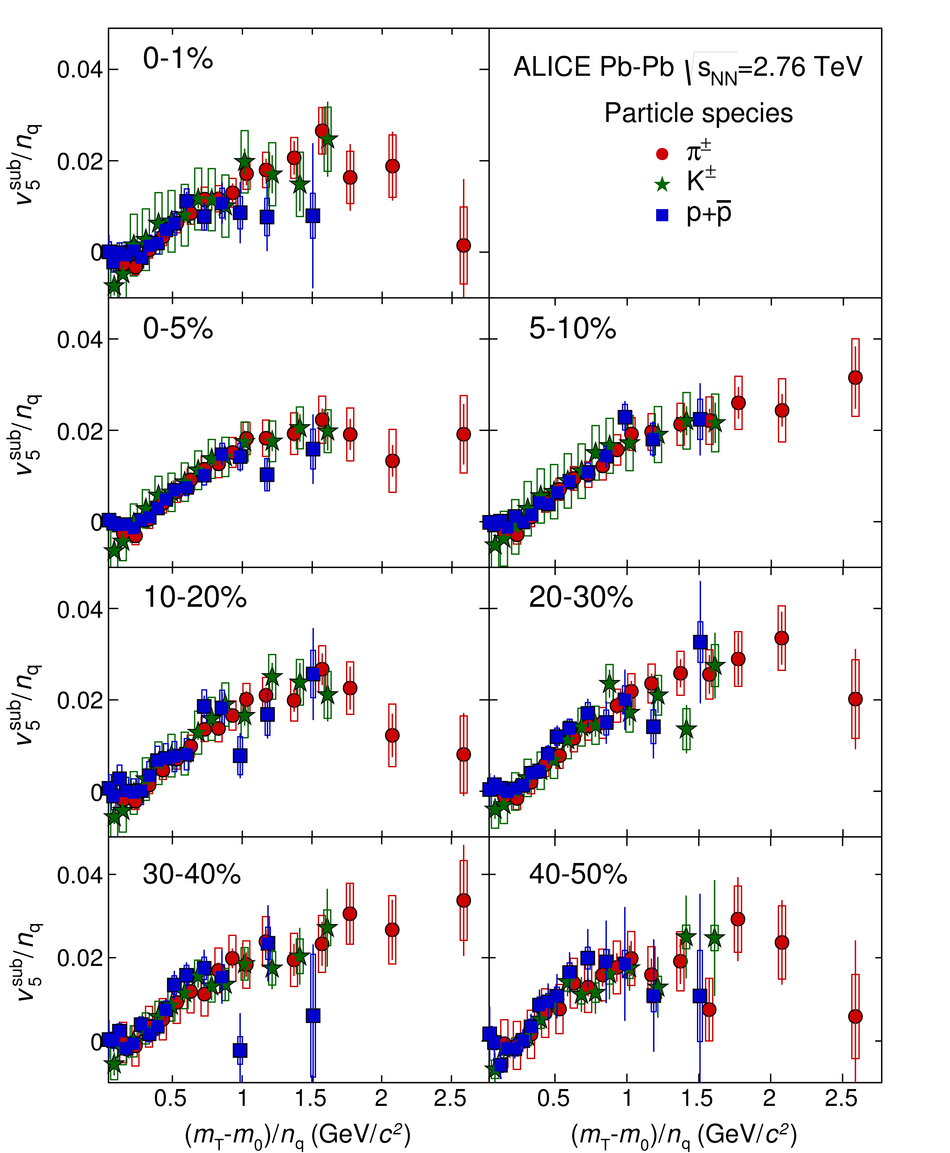
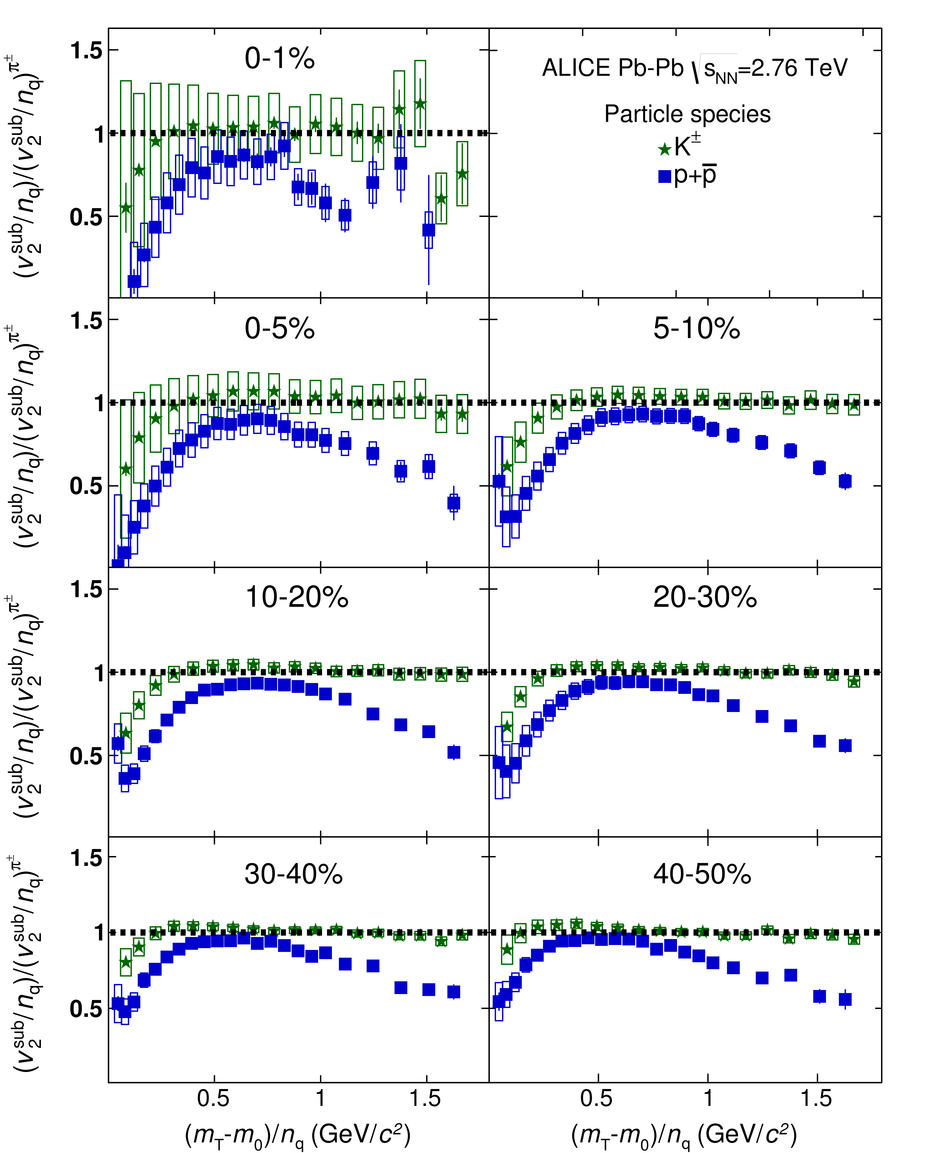
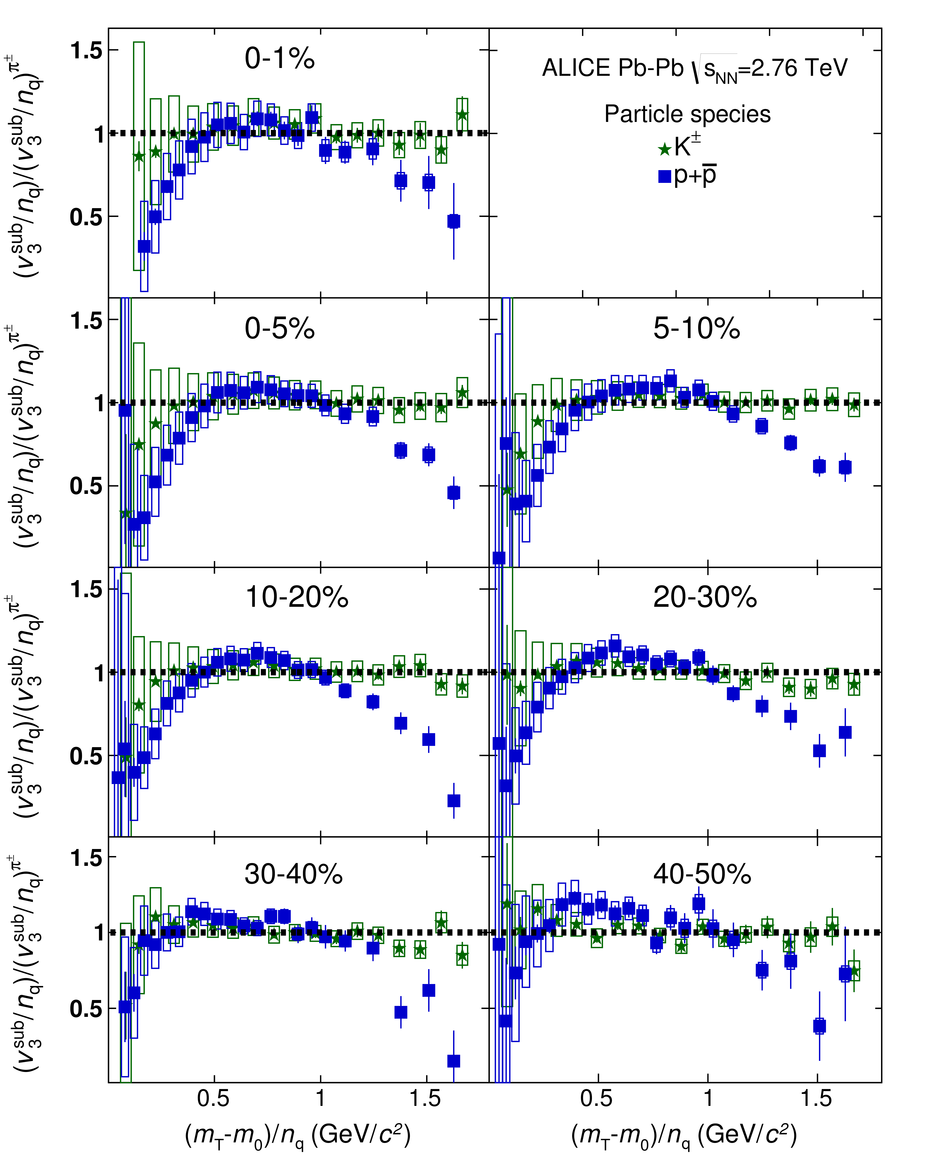
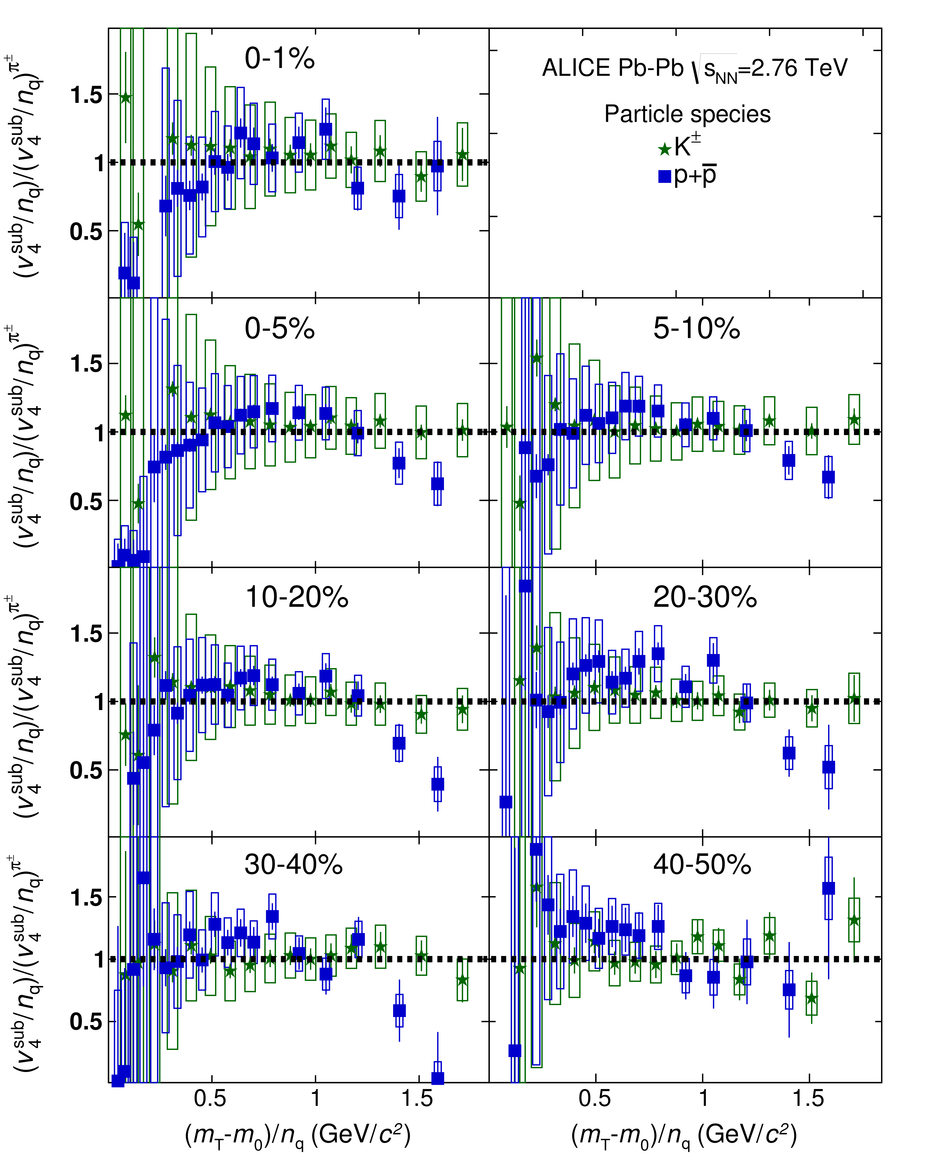
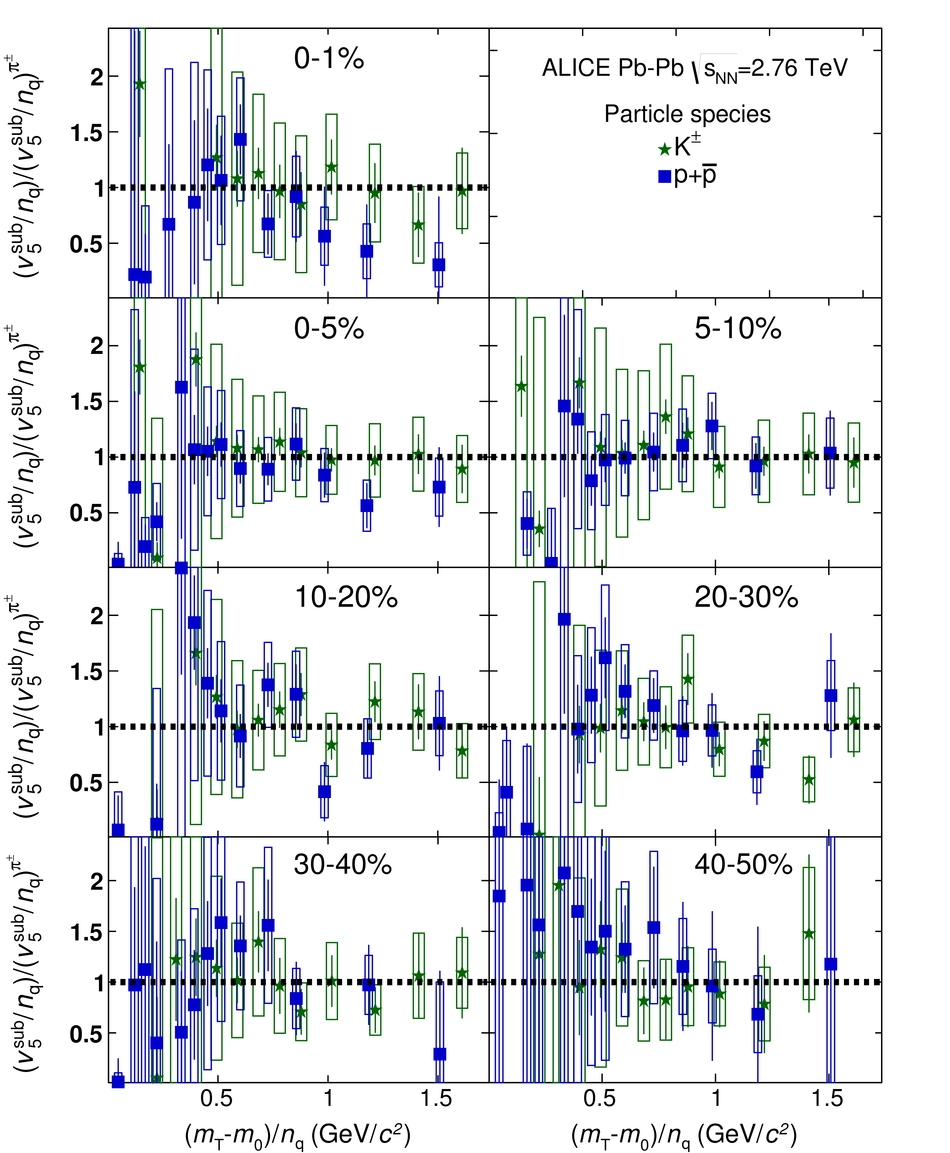
Higher harmonic flow coefficients of identified hadrons in Pb-Pb collisions at $\sqrt{s_{\rm NN}}$ = 2.76 TeV

The elliptic, triangular, quadrangular and pentagonal anisotropic flow coefficients for $\pi^{\pm}$, $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$ in Pb-Pb collisions at $\sqrt{s_\mathrm{{NN}}} = 2.76$ TeV were measured with the ALICE detector at the Large Hadron Collider. The results were obtained with the Scalar Product method, correlating the identified hadrons with reference particles from a different pseudorapidity region. Effects not related to the common event symmetry planes (non-flow) were estimated using correlations in pp collisions and were subtracted from the measurement. The obtained flow coefficients exhibit a clear mass ordering for transverse momentum ($p_{\mathrm{T}}$) values below $\approx$ 3 GeV/$c$. In the intermediate $p_{\mathrm{T}}$ region ($3 <~ p_{\mathrm{T}} <~ 6$ GeV/$c$), particles group at an approximate level according to the number of constituent quarks, suggesting that coalescence might be the relevant particle production mechanism in this region. The results for $p_{\mathrm{T}} <~ 3$ GeV/$c$ are described fairly well by a hydrodynamical model (iEBE-VISHNU) that uses initial conditions generated by A Multi-Phase Transport model (AMPT) and describes the expansion of the fireball using a value of 0.08 for the ratio of shear viscosity to entropy density ($\eta/s$), coupled to a hadronic cascade model (UrQMD). Finally, expectations from AMPT alone fail to quantitatively describe the measurements for all harmonics throughout the measured transverse momentum region. However, the comparison to the AMPT model highlights the importance of the late hadronic rescattering stage to the development of the observed mass ordering at low values of $p_{\mathrm{T}}$ and of coalescence as a particle production mechanism for the particle type grouping at intermediate values of $p_{\mathrm{T}}$ for all harmonics.

 

JHEP 1609 (2016) 164
HEP Data
e-Print: arXiv:1606.06057 | PDF | inSPIRE
CERN-EP-2016-159

Figures

Figure 1

The $\pT$-differential $\langle{M}\rangle\langle{\langle{\vec{u}_{n}\cdot\frac{\vec{Q}^{*}_{n}}{M}}\rangle}\rangle$ of pions (left column), kaons (middle column) and protons (right column) for minimum bias pp and 0-1%, 20-30% and 40-50% centralities in Pb-Pb collisions at $\sNN$. The rows represent different harmonics.
[png] [eps]

Figure 2

The $\pT$-differential $v_{2}^{\mathrm{sub}}$ (top row) and $\delta_{2}^{\textrm{AA,pp}}$ (bottom row) for different centralities in Pb-Pb collisions at $\sNN$ grouped by particle species.
[png] [eps]

Figure 3

The $\pT$-differential $v_{3}^{\mathrm{sub}}$ (top row) and $\delta_{3}^{\textrm{AA,pp}}$ (bottom row) for different centralities in Pb-Pb collisions at $\sNN$ grouped by particle species.
[png] [eps]

Figure 4

The $\pT$-differential $v_{4}^{\mathrm{sub}}$ (top row) and $\delta_{4}^{\textrm{AA,pp}}$ (bottom row) for different centralities in Pb-Pb collisions at $\sNN$ grouped by particle species.
[png] [eps]

Figure 5

The $\pT$-differential $v_{5}^{\mathrm{sub}}$ (top row) and $\delta_{4}^{\textrm{AA,pp}}$ (bottom row) for different centralities in Pb-Pb collisions at $\sNN$ grouped by particle species.
[png] [eps]

Figure 6

The evolution of the $\pT$-differential $v_{n}^{\mathrm{sub}}$ for $\pi^{\pm}$, $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$, in the left, middle and right columns, respectively, grouped by centrality interval in Pb-Pb collisions at $\sNN$.
[png] [eps]

Figure 7

The $\pT$-differential $v_{2}^{\mathrm{sub}}$ (top figure) and $v_{3}^{\mathrm{sub}}$ (bottom figure) for different particle species grouped by centrality class in Pb-Pb collisions at $\sNN$.
[png] [eps]
[png] [eps]

Figure 8

The $\pT$-differential $v_{4}^{\mathrm{sub}}$ (top figure) and $v_{5}^{\mathrm{sub}}$ (bottom figure) for different particle species grouped by centrality class in Pb-Pb collisions at $\sNN$.
[png] [eps]
[png] [eps]

Figure 9

The $p_{\mathrm{T}}/n_{q}$ dependence of $v_{2}^{\mathrm{sub}}/n_{q}$ (left figure) and $v_{3}^{\mathrm{sub}}/n_{q}$ (right figure) for $\pi^{\pm}$, $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$ for Pb-Pb collisions in various centrality intervals at $\sNN$.
[png] [eps]
[png] [eps]

Figure 10

The $p_{\mathrm{T}}/n_{q}$ dependence of $v_{4}^{\mathrm{sub}}/n_{q}$ (top figure) and $v_{5}^{\mathrm{sub}}/n_{q}$ (bottom figure) for $\pi^{\pm}$, $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$ for Pb-Pb collisions in various centrality intervals at $\sNN$.
[png] [eps]
[png] [eps]

Figure 11

The $\pT$-differential $v_{2}^{\mathrm{sub}}$ for pions, kaons and protons measured with the Scalar Product method in Pb-Pb collisions at $\sNN$ compared to $v_{2}$ measured with iEBE-VISHNU. The upper panels present the comparison for 10-20% up to 40-50% centrality intervals. The thickness of the curves reflect the uncertainties of the hydrodynamical calculations. The differences between $v_{2}^{\mathrm{sub}}$ from data and $v_{2}$ from iEBE-VISHNU are presented in the lower panels.
[png] [eps]

Figure 12

The $\pT$-differential $v_{3}^{\mathrm{sub}}$ for pions, kaons and protons measured with the Scalar Product method in Pb-Pb collisions at $\sNN$ compared to $v_{3}$ measured with iEBE-VISHNU. The upper panels present the comparison for 10-20% up to 40-50% centrality intervals. The thickness of the curves reflect the uncertainties of the hydrodynamical calculations. The differences between $v_{3}^{\mathrm{sub}}$ from data and $v_{3}$ from iEBE-VISHNU are presented in the lower panels
[png] [eps]

Figure 13

The $\pT$-differential $v_{4}^{\mathrm{sub}}$ for pions, kaons and protons measured with the Scalar Product method in Pb-Pb collisions at $\sNN$ compared to $v_{4}$ measured with iEBE-VISHNU. The upper panels present the comparison for 10-20% up to 40-50% centrality intervals. The thickness of the curves reflect the uncertainties of the hydrodynamical calculations. The differences between $v_{4}^{\mathrm{sub}}$ from data and $v_{4}$ from iEBE-VISHNU are presented in the lower panels.
[png] [eps]

Figure 14

The $v_{2}^{\mathrm{AA}}$($\pT$), $v_{3}^{\mathrm{AA}}$($\pT$) and $v_{4}^{\mathrm{AA}}$($\pT$) in 20-30% central Pb-Pb collisions at $\sNN$, obtained using the string melting, with (left) and without (middle) hadronic rescattering, and the default (right) versions.
[png] [eps]

Figure 15

The $v_{2}^{\mathrm{sub}}$($\pT$), $v_{3}^{\mathrm{sub}}$($\pT$) and $v_{4}^{\mathrm{sub}}$($\pT$) for $\pi^{\pm}$, $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$ measured in Pb-Pb collisions at $\sNN$ compared to AMPT (with the string melting option) in the 20-30% centrality range.
[png] [eps]

Figure 16

The $v_{2}$, $v_{3}$ and $v_{4}$ integrated over the $\pT$ range $0.3< \pT< 6 \GeV$ for $\pi^{\pm}$ (left), $0.3< \pT< 4 \GeV$ for $\mathrm{K}^{\pm}$ (middle) and $0.4< \pT< 6 \GeV$ for p+$\overline{\mathrm{p}}$ (right) as a function of centrality intervals in Pb-Pb collisions at $\sNN$.
[png] [eps]

Figure 17

Top: the $p_{\mathrm{T}}/n_{q}$ dependence of the double ratio of $v_{2}^{\mathrm{sub}}/n_{q}$ for $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$ relative to a fit to $v_{2}^{\mathrm{sub}}/n_{q}$ of $\pi^{\pm}$ for Pb-Pb collisions in various centrality intervals at $\sNN$. Bottom: the same for $v_{3}^{\mathrm{sub}}/n_{q}$.
[png] [eps]
[png] [eps]

Figure 18

Top: the $p_{\mathrm{T}}/n_{q}$ dependence of the double ratio of $v_{4}^{\mathrm{sub}}/n_{q}$ for $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$ relative to a fit to $v_{4}^{\mathrm{sub}}/n_{q}$ of $\pi^{\pm}$ for Pb-Pb collisions in various centrality intervals at $\sNN$. Bottom: the same for $v_{5}^{\mathrm{sub}}/n_{q}$.
[png] [eps]
[png] [eps]

Figure 19

The $(m_{\mathrm{T}}-m_{0})/n_{q}$-dependence of $v_{2}^{\mathrm{sub}}/n_{q}$ (top) and $v_{3}^{\mathrm{sub}}/n_{q}$ (bottom) for $\pi^{\pm}$, $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$ for Pb-Pb collisions in various centrality intervals at $\sNN$.
[png] [eps]
[png] [eps]

Figure 20

The $(m_{\mathrm{T}}-m_{0})/n_{q}$-dependence of $v_{4}^{\mathrm{sub}}/n_{q}$ (left) and $v_{5}^{\mathrm{sub}}/n_{q}$ (right) for $\pi^{\pm}$, $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$ for Pb-Pb collisions in various centrality intervals at $\sNN$.
[png] [eps]
[png] [eps]

Figure 21

Top: the $(m_{\mathrm{T}}-m_{0})/n_{q}$ dependence of the double ratio of $v_{2}^{\mathrm{sub}}/n_{q}$ for $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$ relative to a fit to $v_{2}^{\mathrm{sub}}/n_{q}$ of $\pi^{\pm}$ for Pb-Pb collisions in various centrality intervals at $\sNN$. Bottom: the same for $v_{3}^{\mathrm{sub}}/n_{q}$.
[png] [eps]
[png] [eps]

Figure 22

Top: the $(m_{\mathrm{T}}-m_{0})/n_{q}$ dependence of the double ratio of $v_{4}^{\mathrm{sub}}/n_{q}$ for $\mathrm{K}^{\pm}$ and p+$\overline{\mathrm{p}}$ relative to a fit to $v_{4}^{\mathrm{sub}}/n_{q}$ of $\pi^{\pm}$ for Pb-Pb collisions in various centrality intervals at $\sNN$. Bottom: the same for $v_{5}^{\mathrm{sub}}/n_{q}$.
[png] [eps]
[png] [eps]