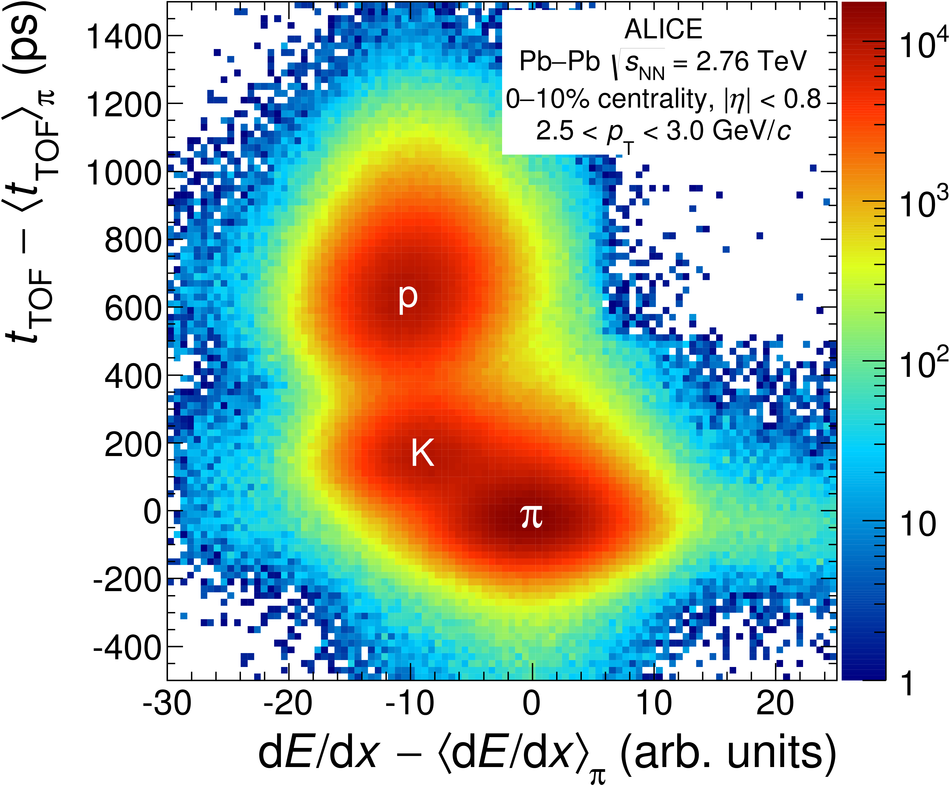
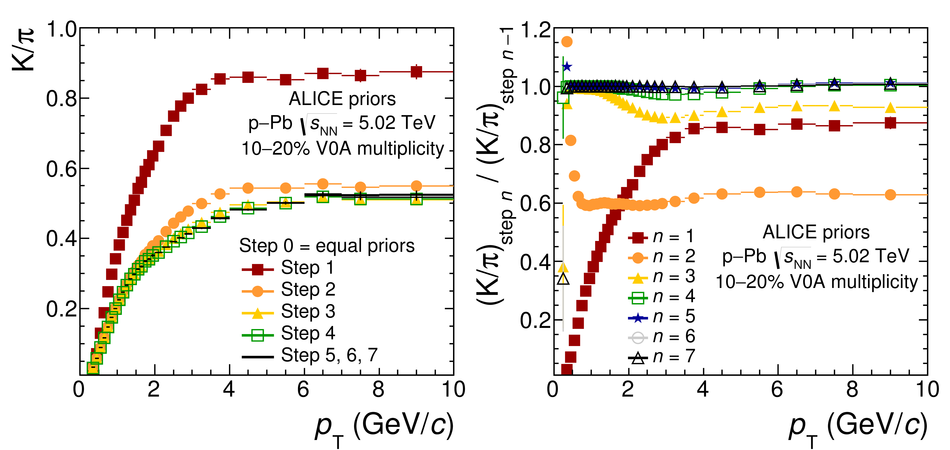
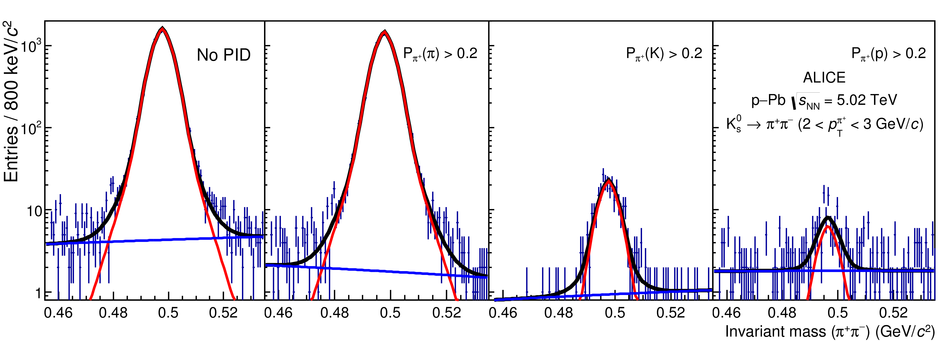
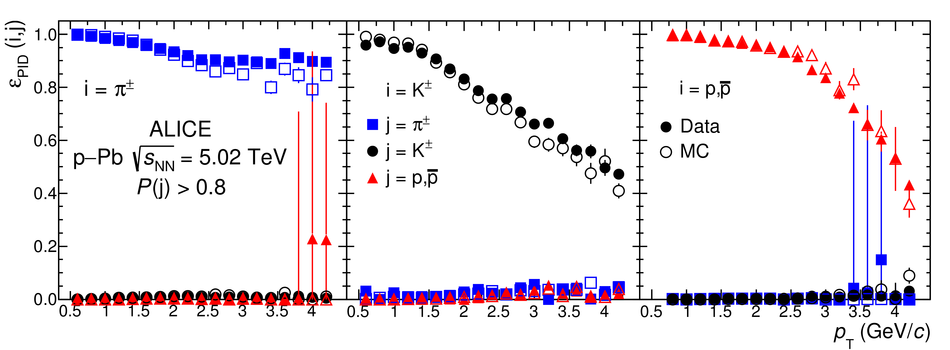
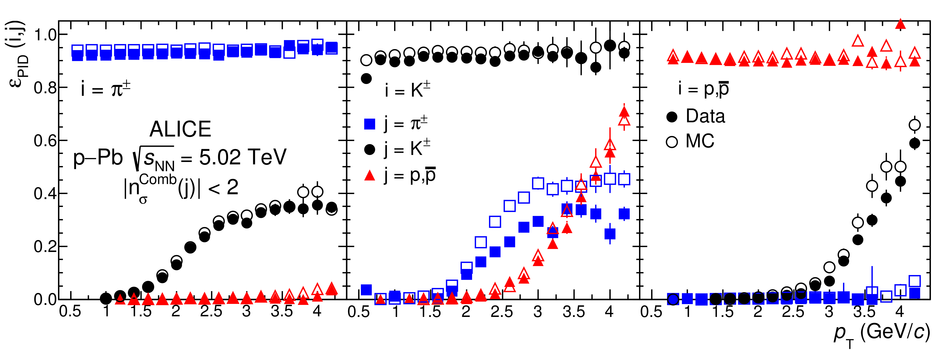
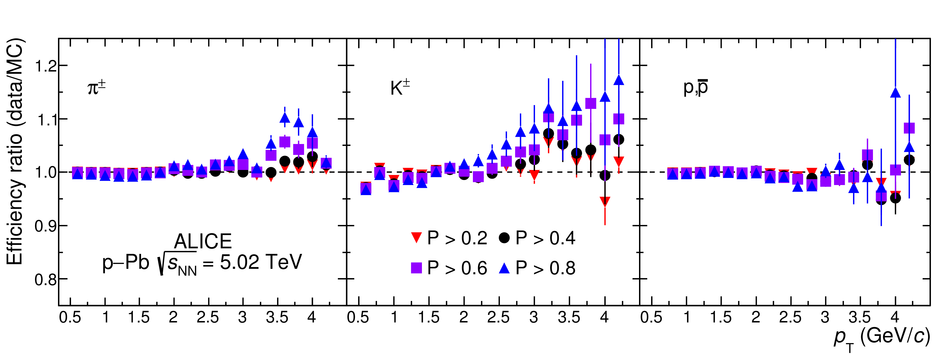
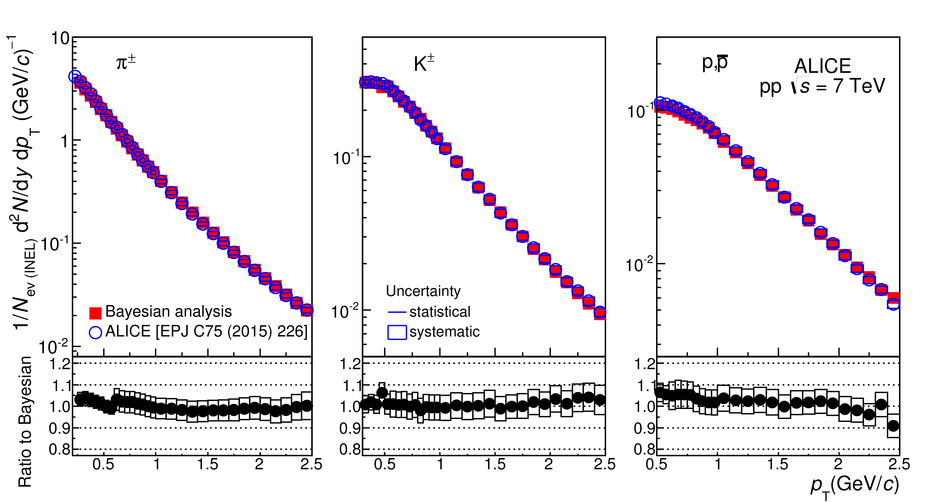
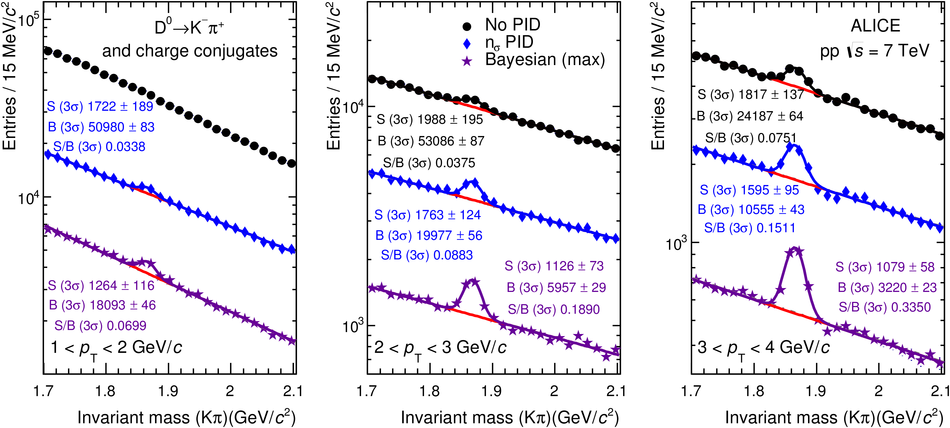
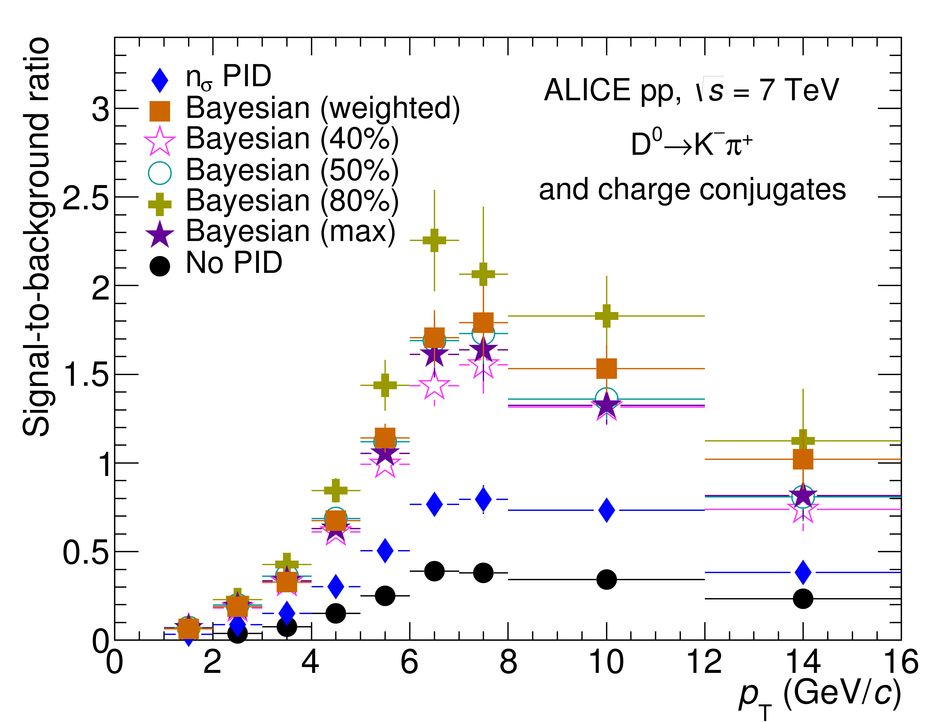
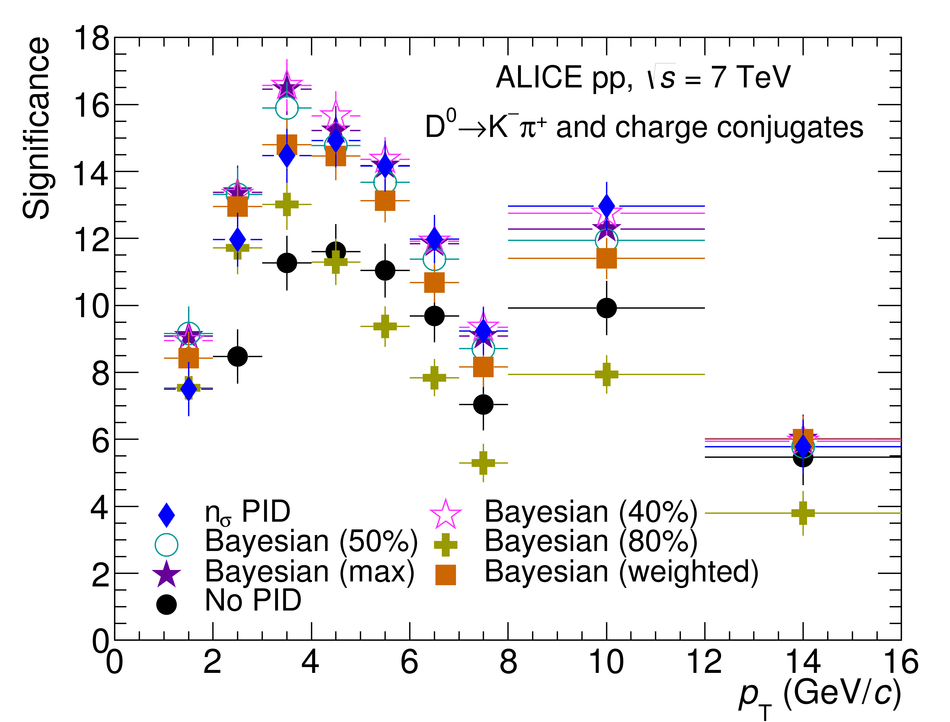
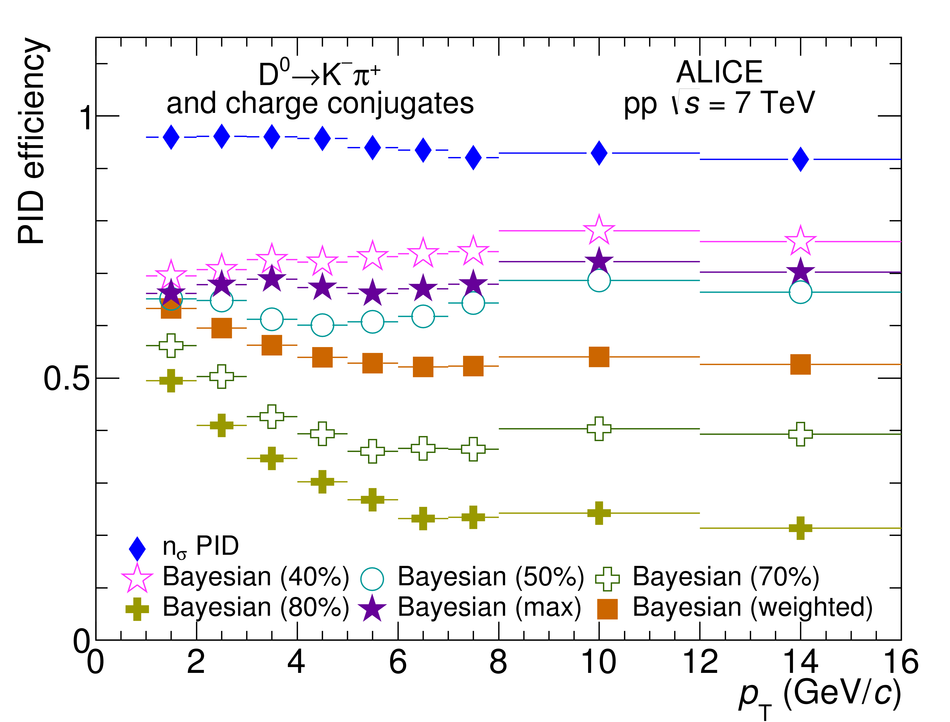
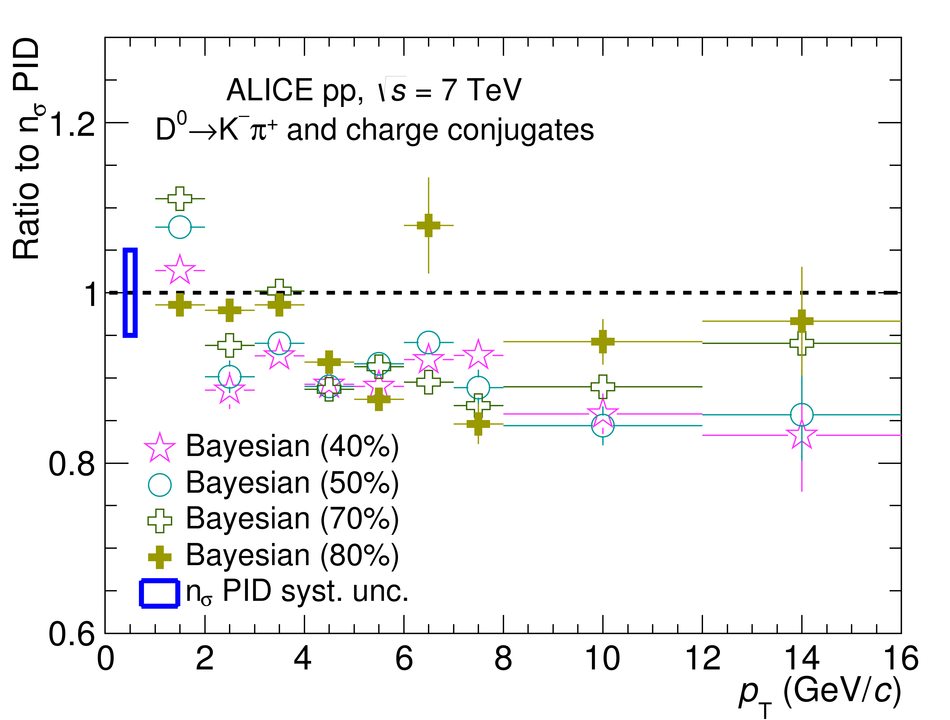
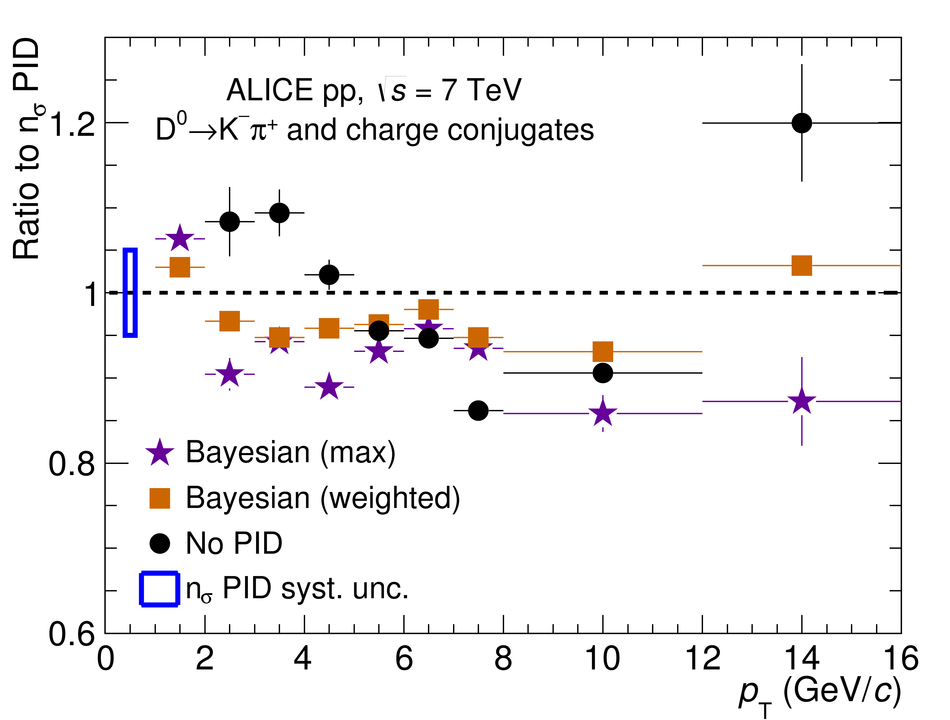
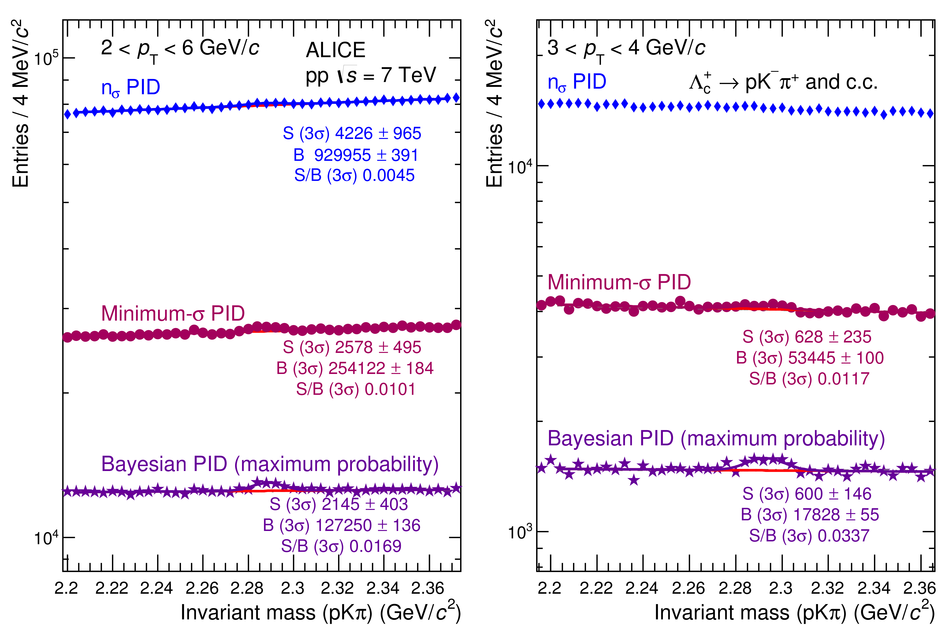
We present a Bayesian approach to particle identification (PID) within the ALICE experiment. The aim is to more effectively combine the particle identification capabilities of its various detectors. After a brief explanation of the adopted methodology and formalism, the performance of the Bayesian PID approach for charged pions, kaons and protons in the central barrel of ALICE is studied. PID is performed via measurements of specific energy loss ($\mathrm{d}E/\mathrm{d}x$) and time-of-flight. PID efficiencies and misidentification probabilities are extracted and compared with Monte Carlo simulations using high-purity samples of identified particles in the decay channels ${\rm K}^0_S \rightarrow \pi^-\pi^+$, $\phi \rightarrow {\rm K}^-{\rm K}^+$, and $\Lambda \rightarrow {\rm p}\pi^-$ in p-Pb collisions at $\sqrt{s_{\rm NN}}=5.02$ TeV. In order to thoroughly assess the validity of the Bayesian approach, this methodology was used to obtain corrected $p_{\rm T}$ spectra of pions, kaons, protons, and D$^0$ mesons in pp collisions at $\sqrt{s}=7$ TeV. In all cases, the results using Bayesian PID were found to be consistent with previous measurements performed by ALICE using a standard PID approach. For the measurement of D$^0 \rightarrow {\rm K}^-\pi^+$, it was found that a Bayesian PID approach gave a higher signal-to-background ratio and a similar or larger statistical significance when compared with standard PID selections, despite a reduced identification efficiency. Finally, we present an exploratory study of the measurement of $\Lambda_{\rm c}^{+}\rightarrow {\rm p} {\rm K}^-\pi^+$ in pp collisions at $\sqrt{s}=7$ TeV, using the Bayesian approach for the identification of its decay products.
Eur. Phys. J. Plus 131 (2016) 168
e-Print: arXiv:1602.01392 | PDF | inSPIRE
CERN-EP-2016-023