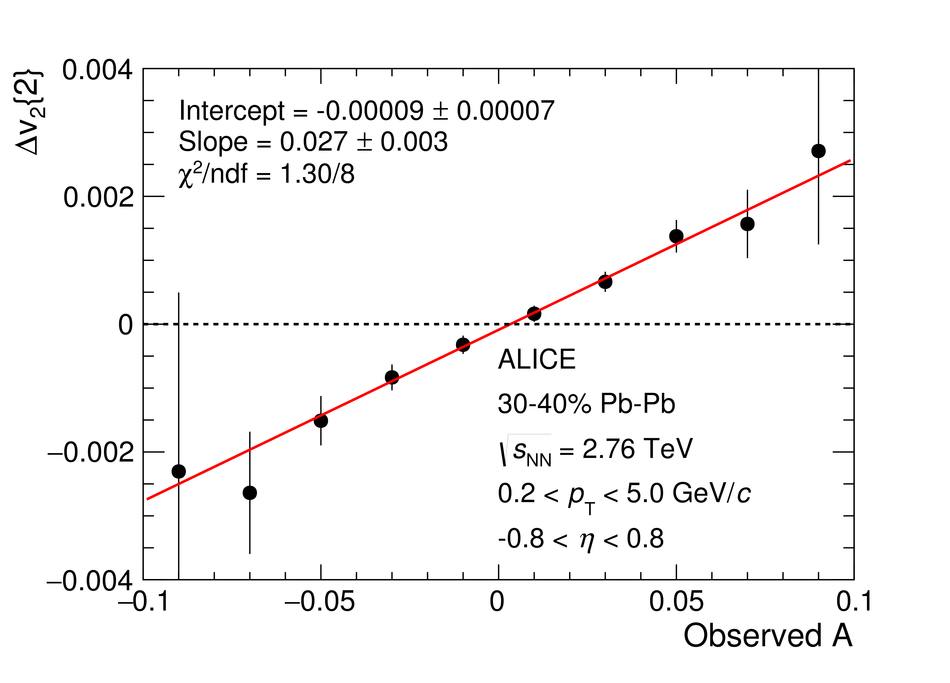
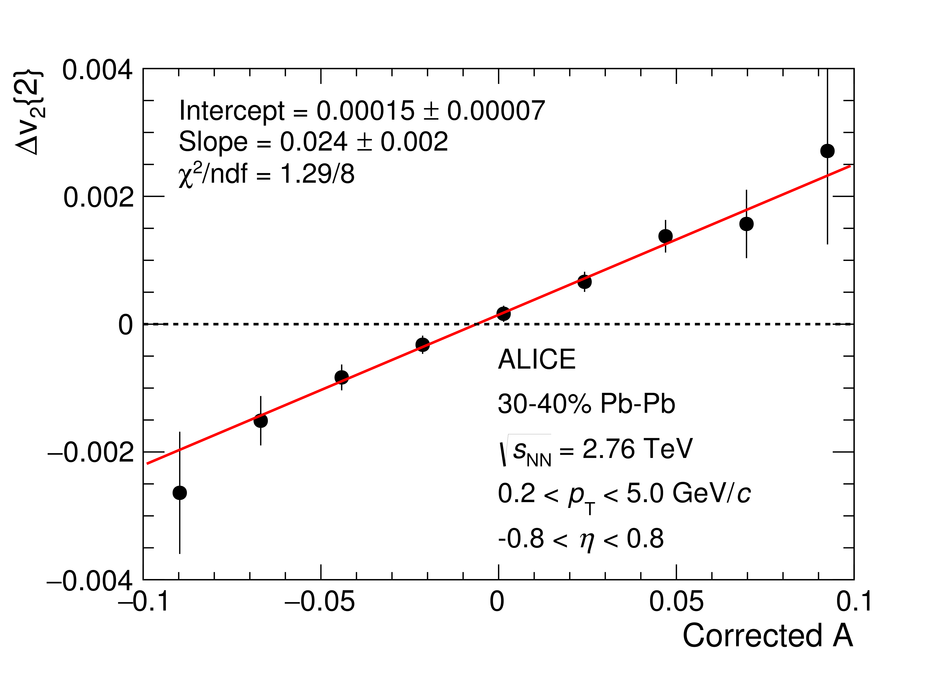
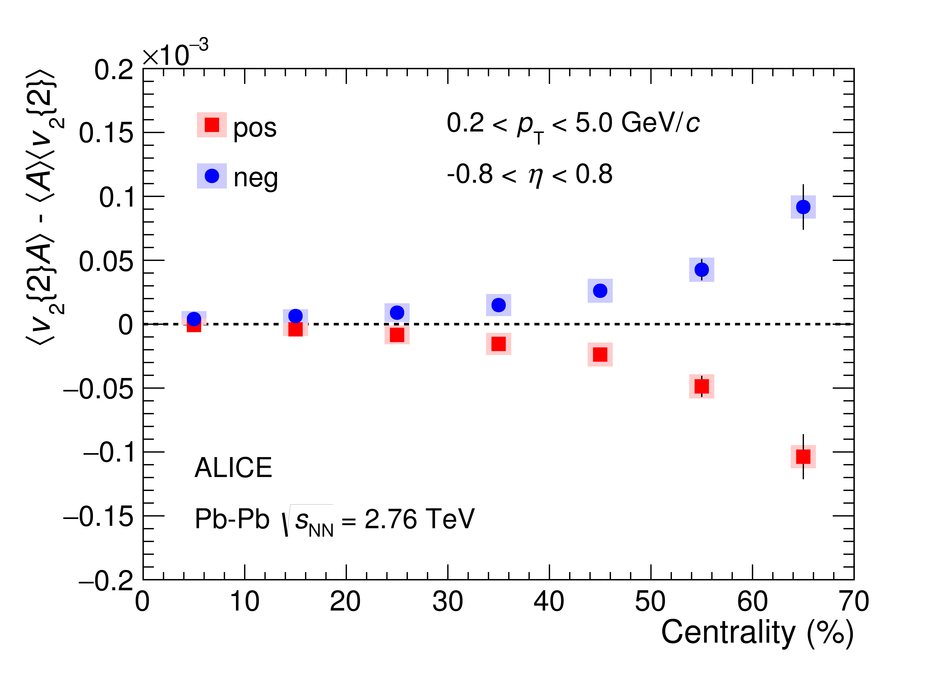
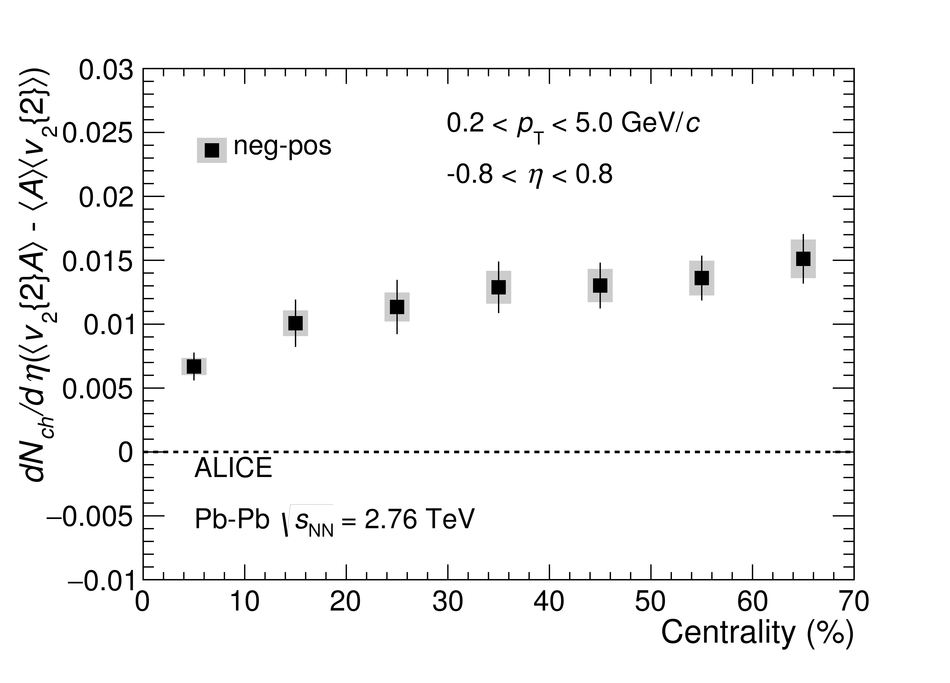
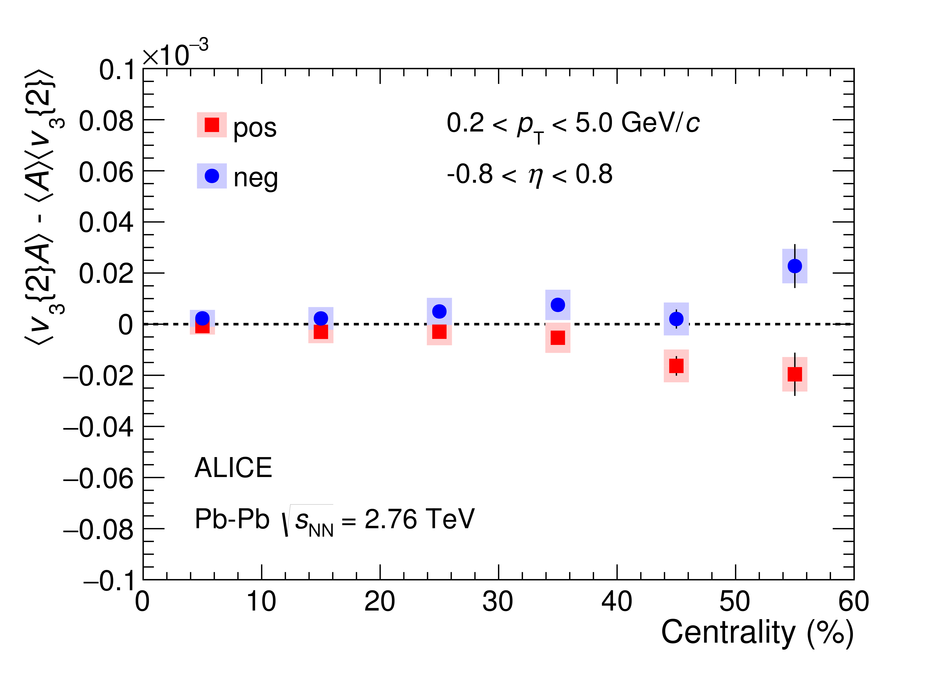
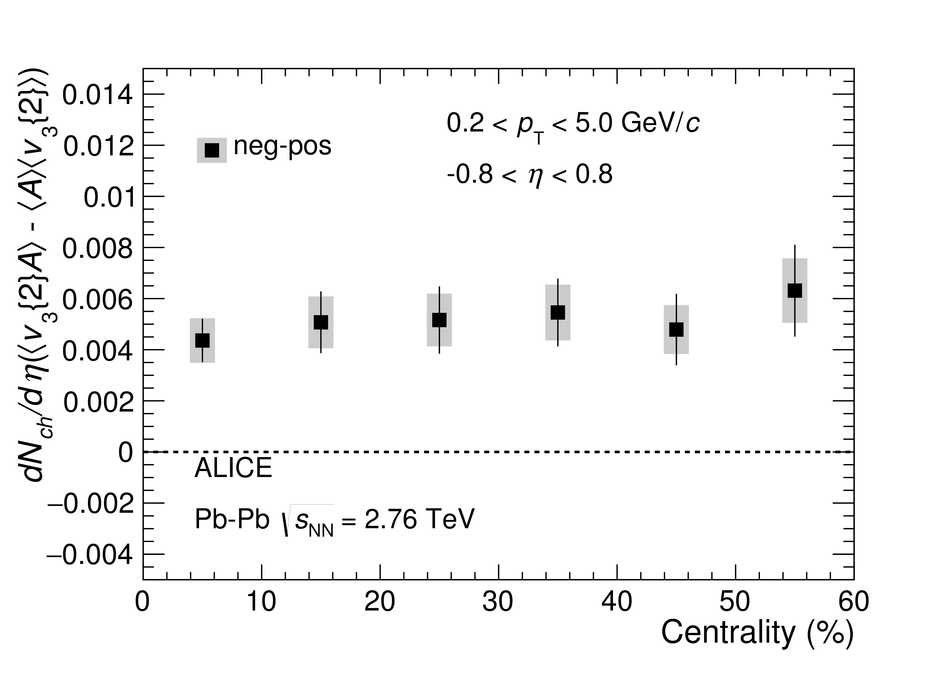
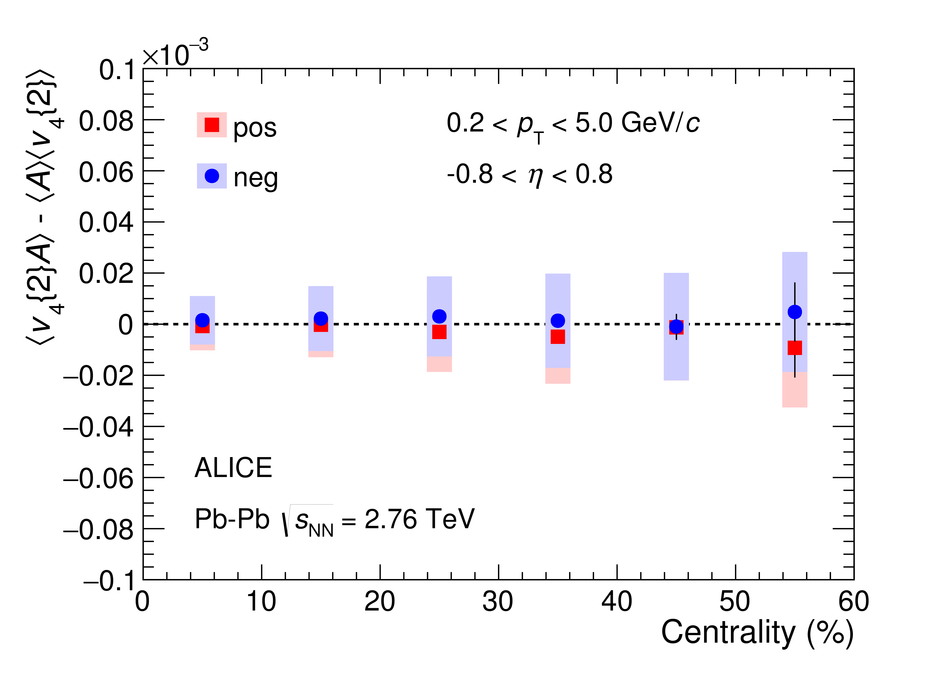
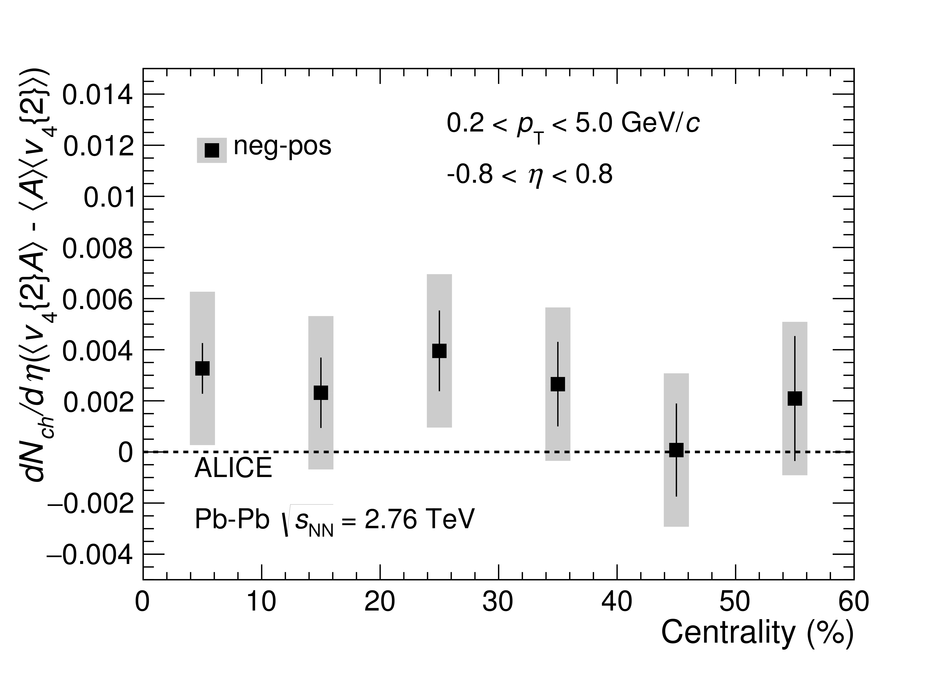
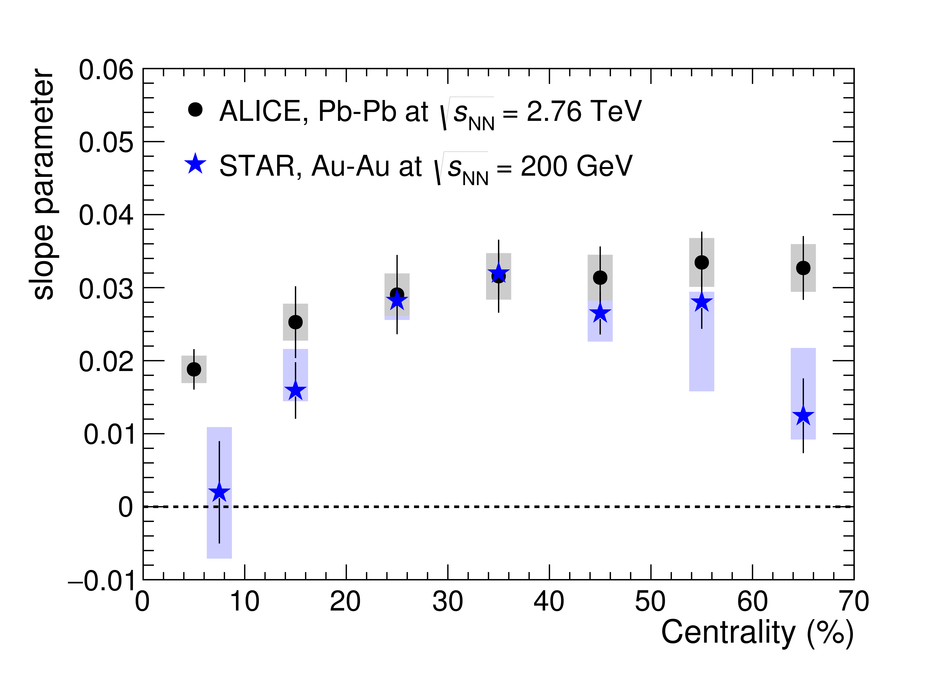
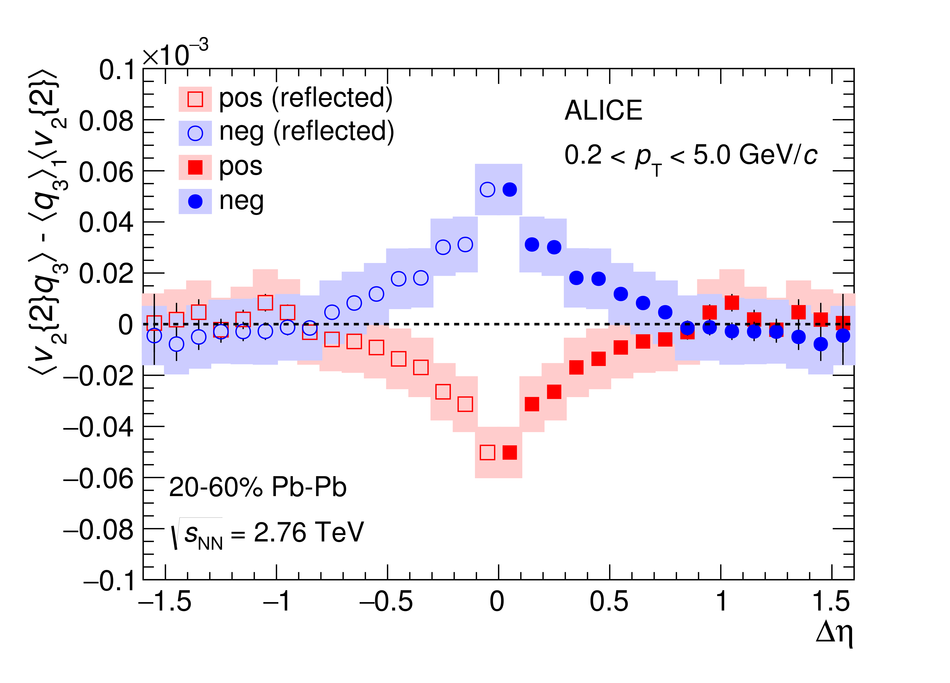
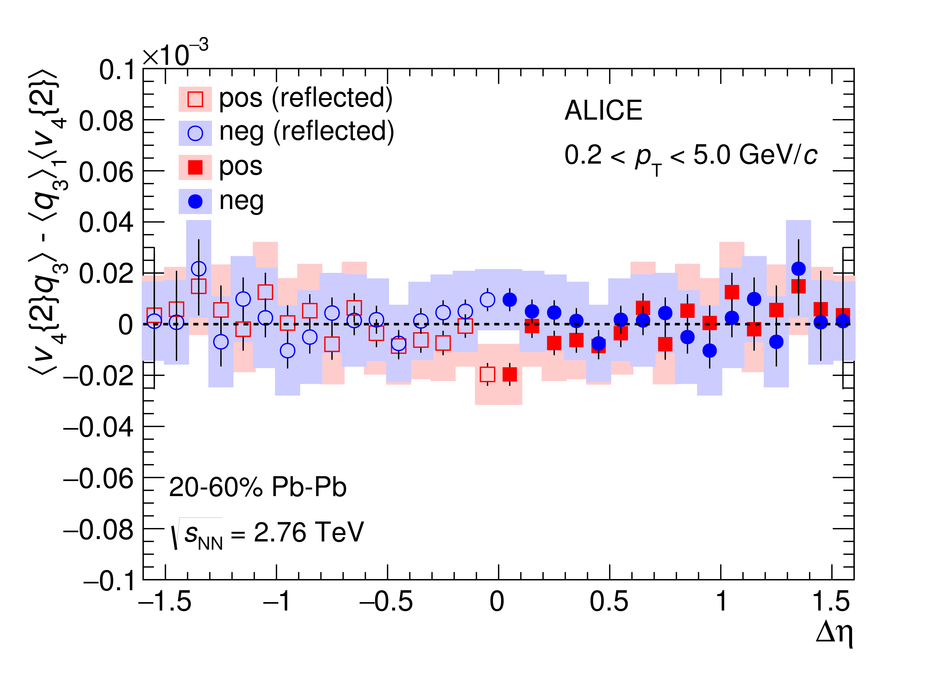
Charge-dependent flow and the search for the Chiral Magnetic Wave in Pb-Pb collisions at $\sqrt{s_{\rm NN}}$ = 2.76 TeV

We report on measurements of a charge-dependent flow using a novel three-particle correlator with ALICE in Pb-Pb collisions at the LHC, and discuss the implications for observation of local parity violation and the Chiral Magnetic Wave (CMW) in heavy-ion collisions. Charge-dependent flow is reported for different collision centralities as a function of the event charge asymmetry. While our results are in qualitative agreement with expectations based on the CMW, the nonzero signal observed in higher harmonics correlations indicates a possible significant background contribution. We also present results on a differential correlator, where the flow of positive and negative charges is reported as a function of the mean charge of the particles and their pseudorapidity separation. We argue that this differential correlator is better suited to distinguish the differences in positive and negative charges expected due to the CMW and the background effects, such as local charge conservation coupled with strong radial and anisotropic flow.

 

Phys. Rev. C 93 (2016) 044903
HEP Data
e-Print: arXiv:1512.05739 | PDF | inSPIRE
CERN-PH-EP-2015-316

Figures

Figure 1

Harmonic coefficients $v_2^+$ (red squares) and $v_2^-$ (blue circles) as a function of the observed event charge asymmetry $A$ in the 30--40\% centrality class. Statistical uncertainties only.
[png] [eps]

Figure 2

$\Delta v_2 = v_2^--v_2^+$ as a function of the observed (left) and corrected (right) event charge asymmetry $A$ in the 30--40\% centrality class Statistical uncertainties only.
[png] [eps]
[png] [eps]

Figure 3

Three-particle correlator for positive (red squares) and negative (blue circles) particles for the second harmonic as a function of centrality Statistical (systematic) uncertainties are indicated by vertical bars (shaded boxes).
[png] [eps]

Figure 4

Charge difference of the three-particle correlator for the second harmonic as a function of centrality, multiplied by $\dndeta$ . Statistical (systematic) uncertainties are indicated by vertical bars (shaded boxes).
[png] [eps]

Figure 5

Three-particle correlator for the third harmonic (left panel) for positive (red squares) and negative (blue circles) particles, and the charge difference multiplied by $\dndeta$ (right panel). Statistical (systematic) uncertainties are indicated by vertical bars (shaded boxes).
[png] [eps]
[png] [eps]

Figure 6

Three-particle correlator for the fourth harmonic (left panel) for positive (red squares) and negative (blue circles) particles, and the charge difference multiplied by $\dndeta$ (right panel). Statistical (systematic) uncertainties are indicated by vertical bars (shaded boxes).
[png] [eps]
[png] [eps]

Figure 7

Slope parameter $r$ as a function of centrality, including points from STAR . Statistical (systematic) uncertainties are indicated by vertical bars (shaded boxes).
[png] [eps]

Figure 8

Correlation between the charge of the first particle $q_1$ and the charge of the third particle $q_3$. Statistical uncertainties only.
[png] [eps]

Figure 9

Three-particle correlator for the second harmonic, for positive (red squares) and negative (blue circles) particles. Statistical (systematic) uncertainties are indicated by vertical bars (shaded boxes).
[png] [eps]

Figure 10

Three-particle correlator for the third (left panel) and fourth (right panel) harmonics, for positive (red squares) and negative (blue circles) particles. Statistical (systematic) uncertainties are indicated by vertical bars (shaded boxes).
[png] [eps]
[png] [eps]