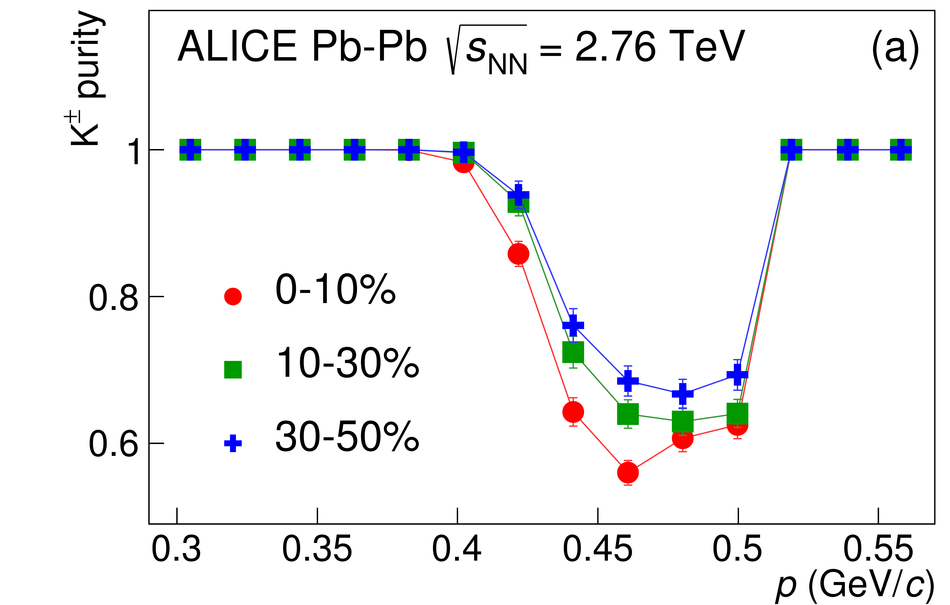
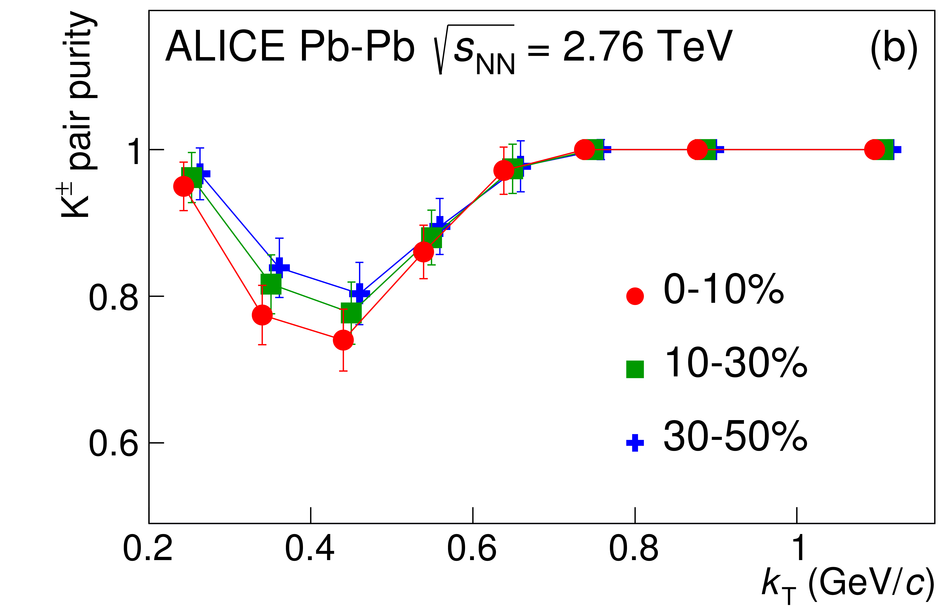
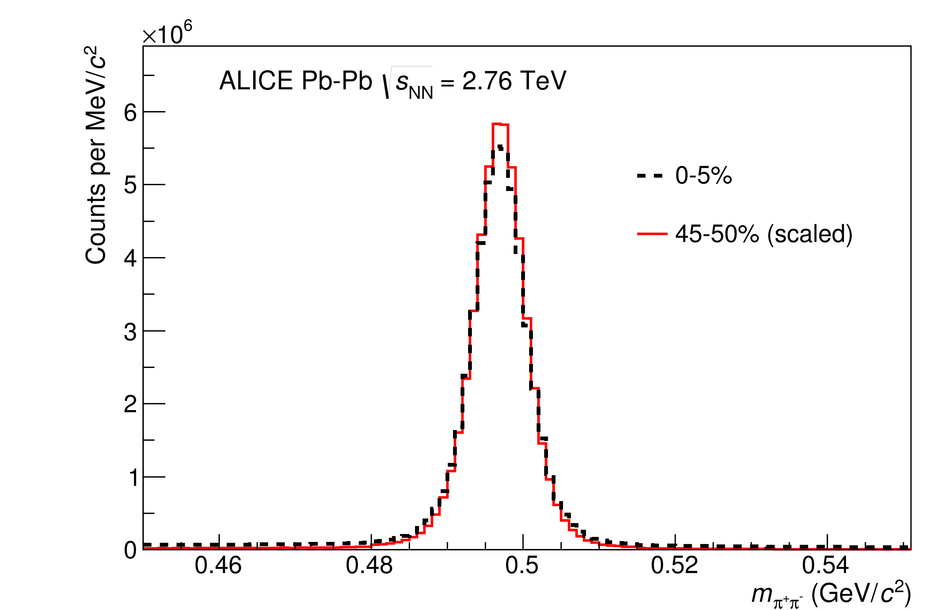
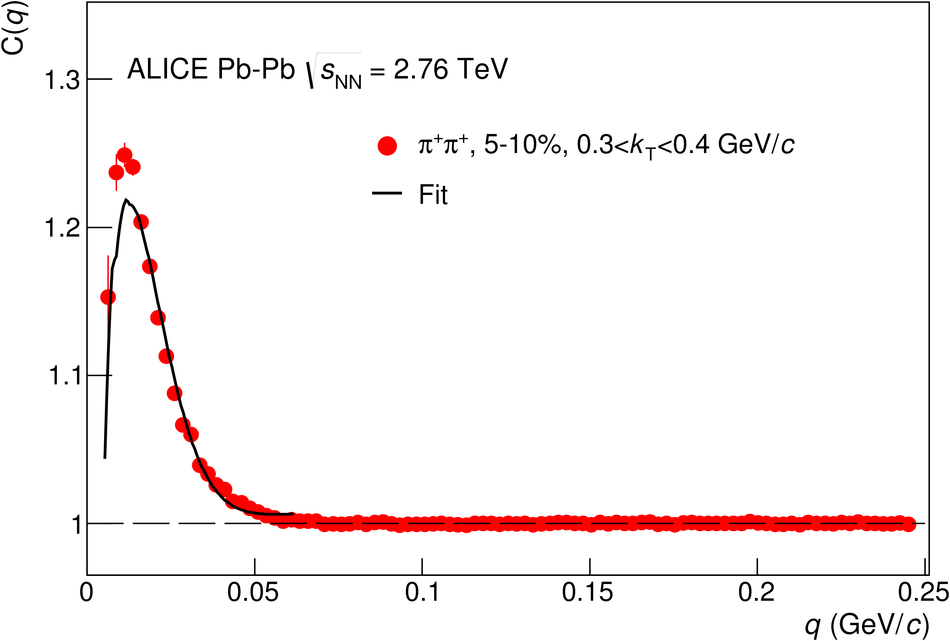
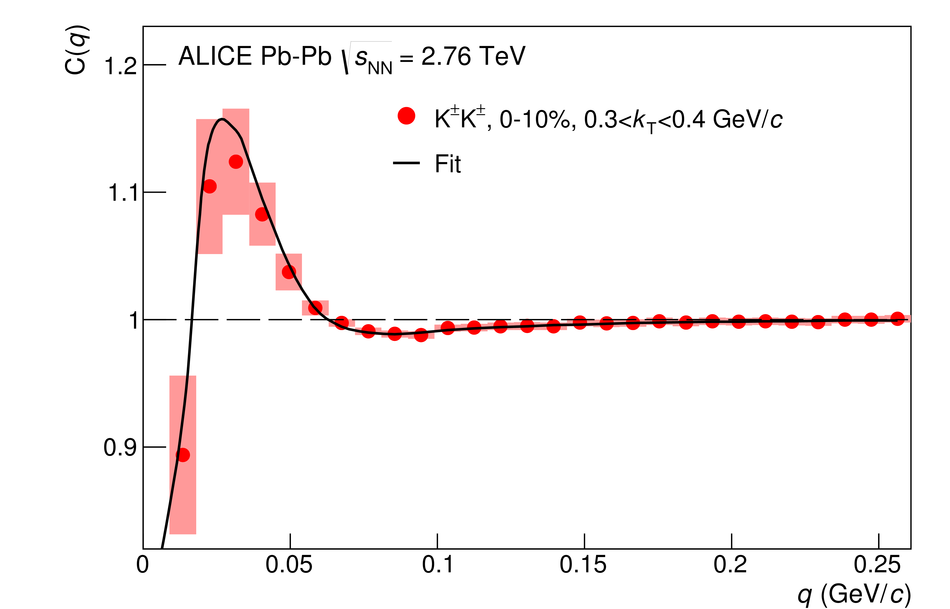
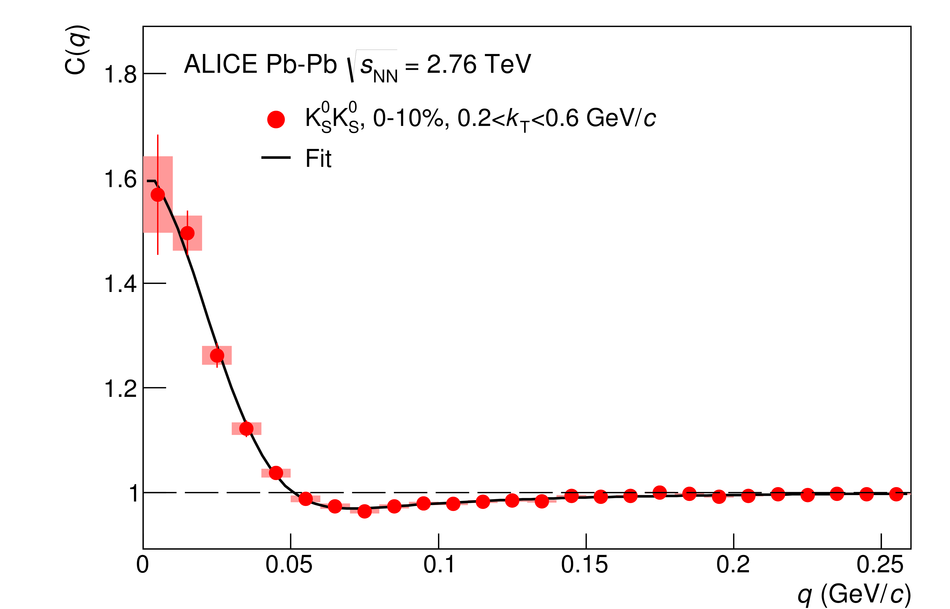
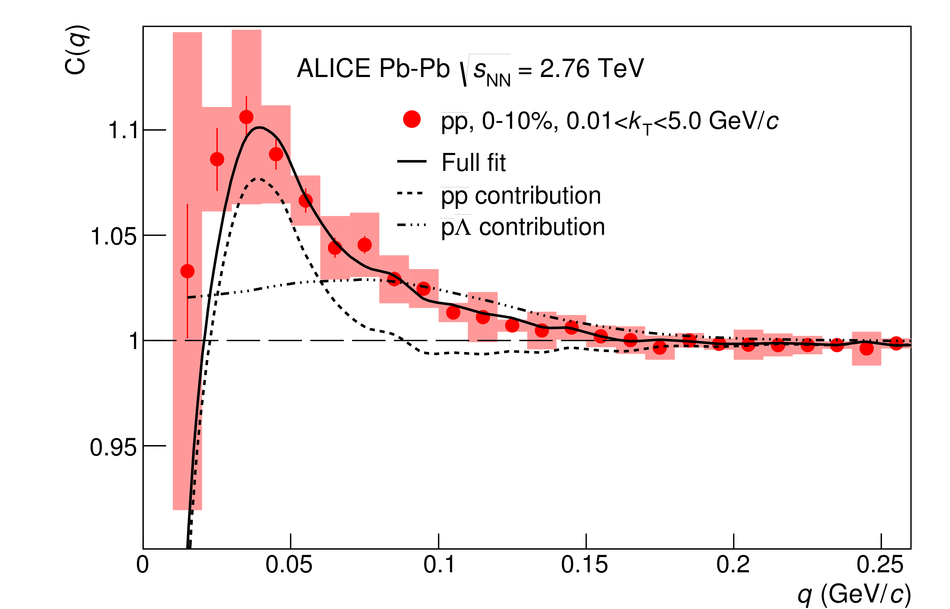
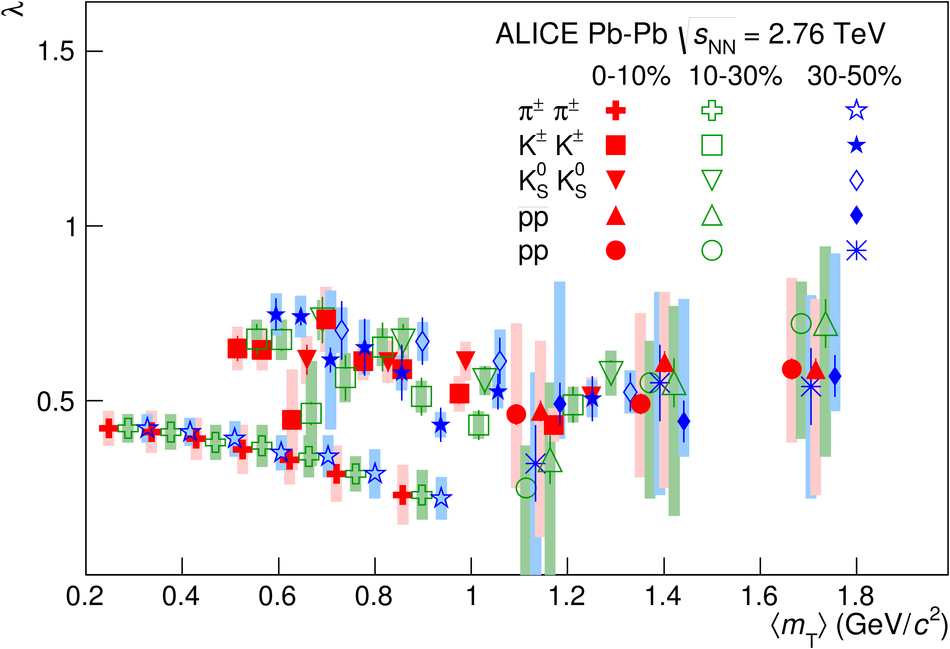
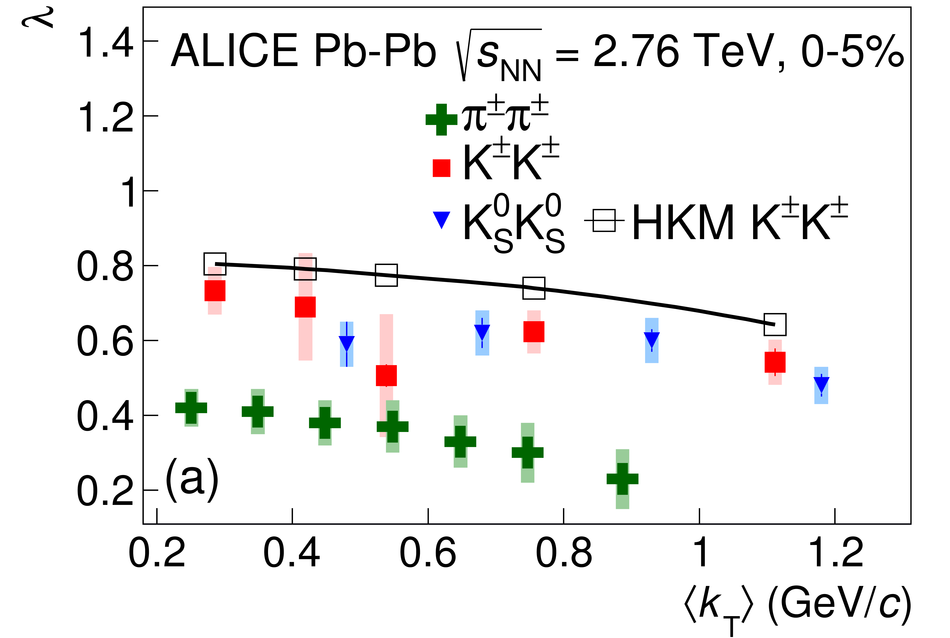
One-dimensional pion, kaon, and proton femtoscopy in Pb-Pb collisions at $\sqrt{s_{\rm {NN}}}$ =2.76 TeV

The size of the particle emission region in high-energy collisions can be deduced using the femtoscopic correlations of particle pairs at low relative momentum. Such correlations arise due to quantum statistics and Coulomb and strong final state interactions. In this paper, results are presented from femtoscopic analyses of $\pi^{\pm}\pi^{\pm}$, ${\rm K}^{\pm}{\rm K}^{\pm}$, ${\rm K}^{0}_S{\rm K}^{0}_S$, ${\rm pp}$, and ${\rm \overline{p}}{\rm \overline{p}}$ correlations from Pb-Pb collisions at $\sqrt{s_{\mathrm {NN}}}=2.76$ TeV by the ALICE experiment at the LHC. One-dimensional radii of the system are extracted from correlation functions in terms of the invariant momentum difference of the pair. The comparison of the measured radii with the predictions from a hydrokinetic model is discussed. The pion and kaon source radii display a monotonic decrease with increasing average pair transverse mass $m_{\rm T}$ which is consistent with hydrodynamic model predictions for central collisions. The kaon and proton source sizes can be reasonably described by approximate $m_{\rm T}$-scaling.

Phys. Rev. C 92 (2015) 054908
HEP Data
e-Print: arXiv:1506.07884 | PDF | inSPIRE
CERN-PH-EP-2015-106

Figures

Figure 1

Single $\rm K^{\pm}$ purity (a) and $\rm K^{\pm}$ pair purity (b) for different centralities. In (b) the $k_{\rm T}$ values for different centrality intervals are slightly offset for clarity.

[png] [pdf]

Figure 2

Invariant mass distribution of $\pi^+\pi^-$ pairs showing the $\Kzs$ peak for two centrality intervals The 45-50% centrality is scaled so that both distributions have the same integral in the range $0.480 < m_{\pi^+ \pi^-} < 0.515$ GeV/${\rm c}^2$.

[png] [pdf]

Figure 3

Example correlation function with fit for $\pi^+\pi^+$ for centrality 5-10% and $\left < k_{\rm T} \right > = 0.35$ GeV/$c$. Statistical uncertainties are shown as thin lines.

[png] [pdf]

Figure 4

Example correlation function with fit for $\rm K^{\pm}\rm K^{\pm}$ for centrality 0-10% and $\left < k_{\rm T} \right > = 0.35$ GeV/$c$. Systematic uncertainties (boxes) are shown; statistical uncertainties are within the data markers. The main sources of systematic uncertainty are the momentum resolution correction and PID selection.

[png] [pdf]

Figure 5

Example correlation function with fit for $\Kzs\Kzs$ for centrality 0-10% and $\left < k_{\rm T} \right > = 0.48$ GeV/$c$. Statistical (thin lines) and systematic (boxes) uncertainties are shown. The main source of systematic uncertainty is the variation of single-particle cuts

[png] [pdf]

Figure 6

Example correlation function with fit for $\overline{\rm p}\overline{\rm p}$ for centrality 0-10% and $\left < k_{\rm T} \right > = 1.0$ GeV/$c$. Statistical (thin lines) and systematic (boxes) uncertainties are shown. The main source of systematic uncertainty is the variation of two-track cuts.

[png] [pdf]

Figure 7

$\lambda$ parameters ($\lambda_{\rm {p}\rm {p}}+\lambda_{\rm {p}\Lambda}$ in case of (anti)proton pairs) vs. $m_{\rm T}$ for the three centralities considered for $\pi^{\pm}\pi^{\pm}$, $\rm K^{\pm}\rm K^{\pm}$,$\Kzs\Kzs$, $\rm {p}\rm {p}$, and $\overline{\rm p}\overline{\rm p}$. Statistical (thin lines) and systematic (boxes) uncertainties are shown. The $m_{\rm T}$ values for different centrality intervals are slightlyoffset for clarity.

[png] [pdf]

Figure 8

$R_{\rm inv}$ parameters vs. $m_{\rm T}$ for the three centralities considered for $\pi^{\pm}\pi^{\pm}$, $\rm K^{\pm}\rm K^{\pm}$,$\Kzs\Kzs$, $\rm {p}\rm {p}$, and $\overline{\rm p}\overline{\rm p}$. Statistical (thin lines) and systematic (boxes) uncertainties are shown.

[png] [pdf]

Figure 9

Comparison of the HKM model (see text)with measured kaon $\lambda$ (a) and $R_{\rm inv}$ (b) parameters for 0-5% centrality. Statistical (thin lines) and systematic (boxes) uncertainties are shown.

[png] [pdf]