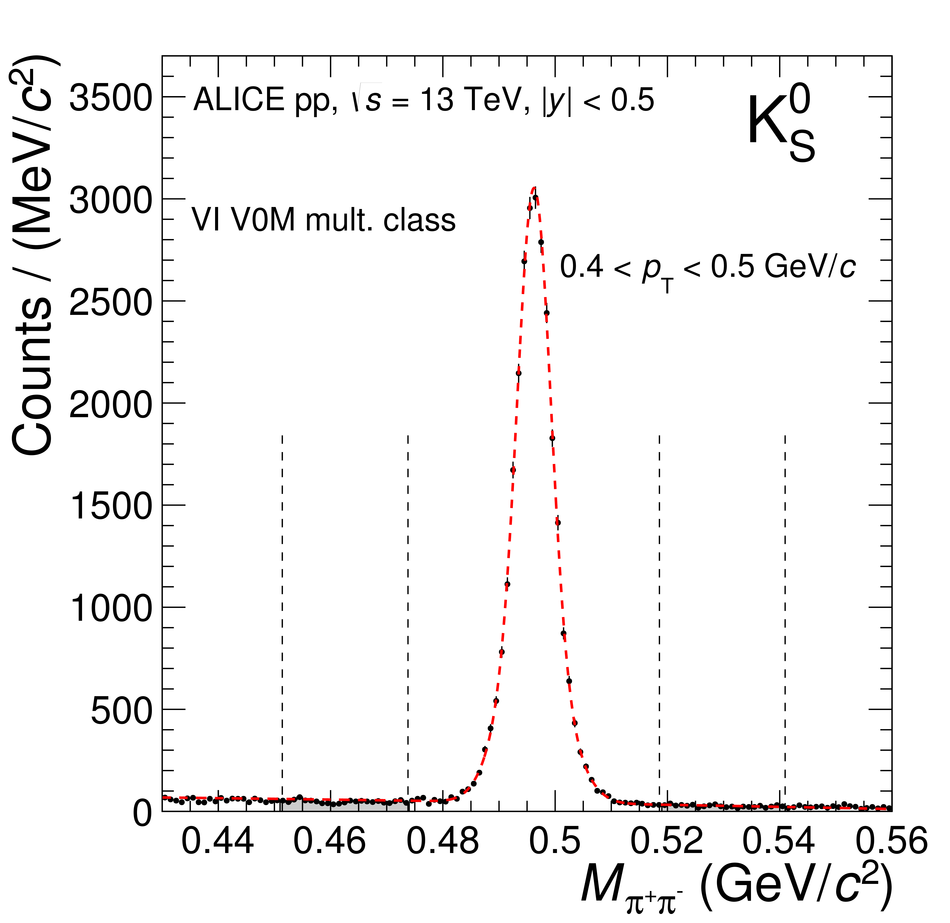
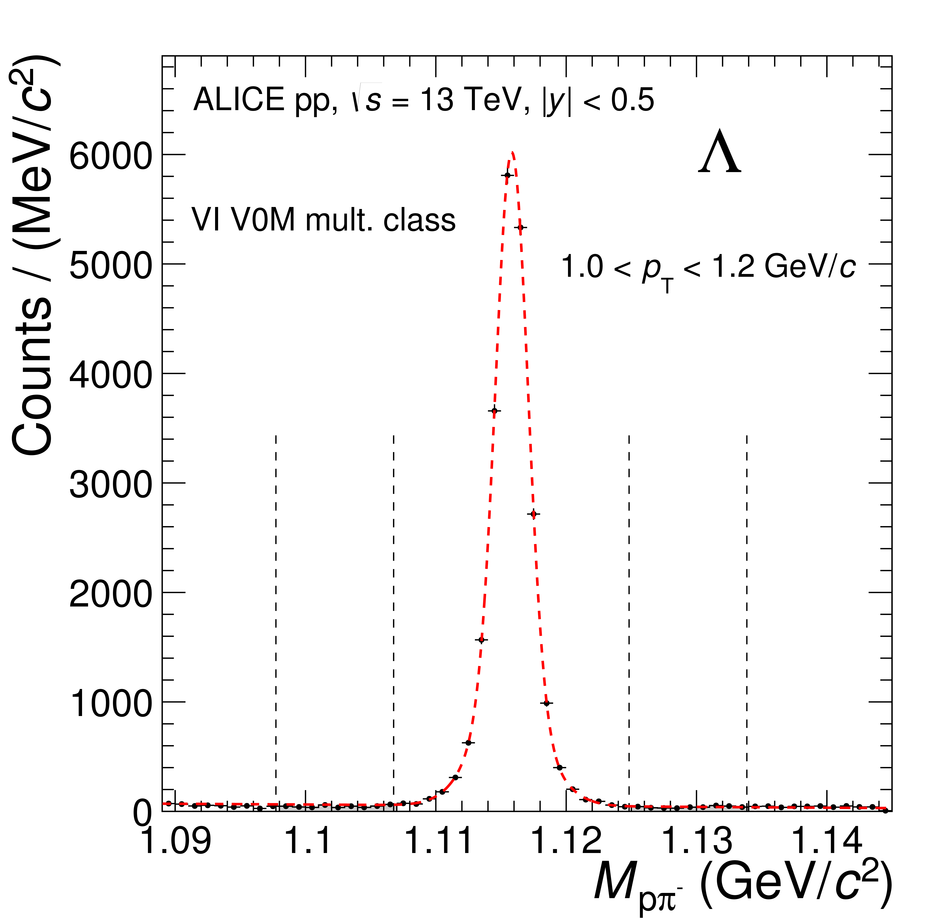
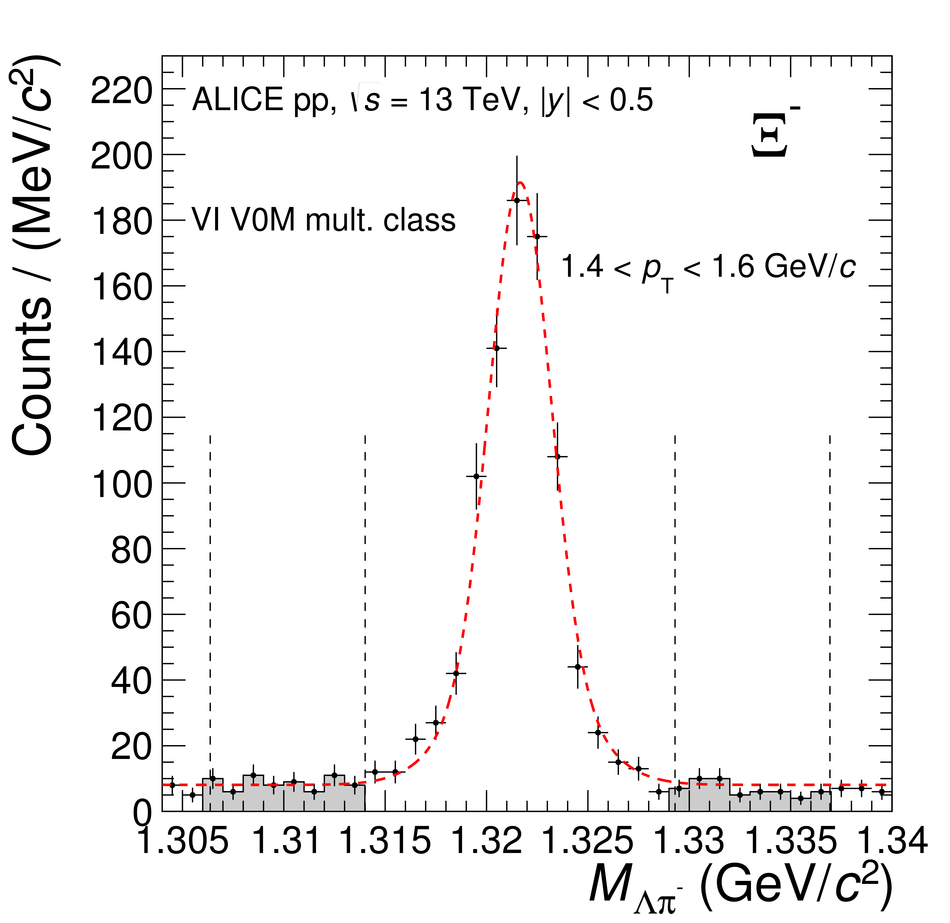
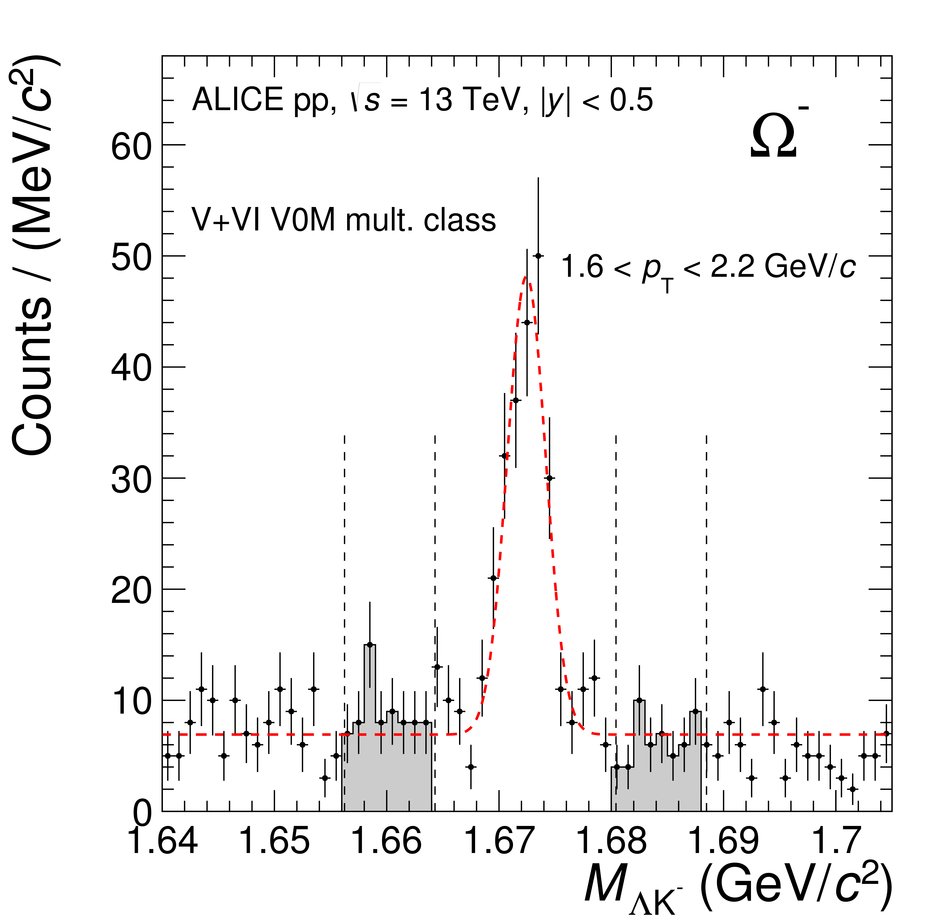
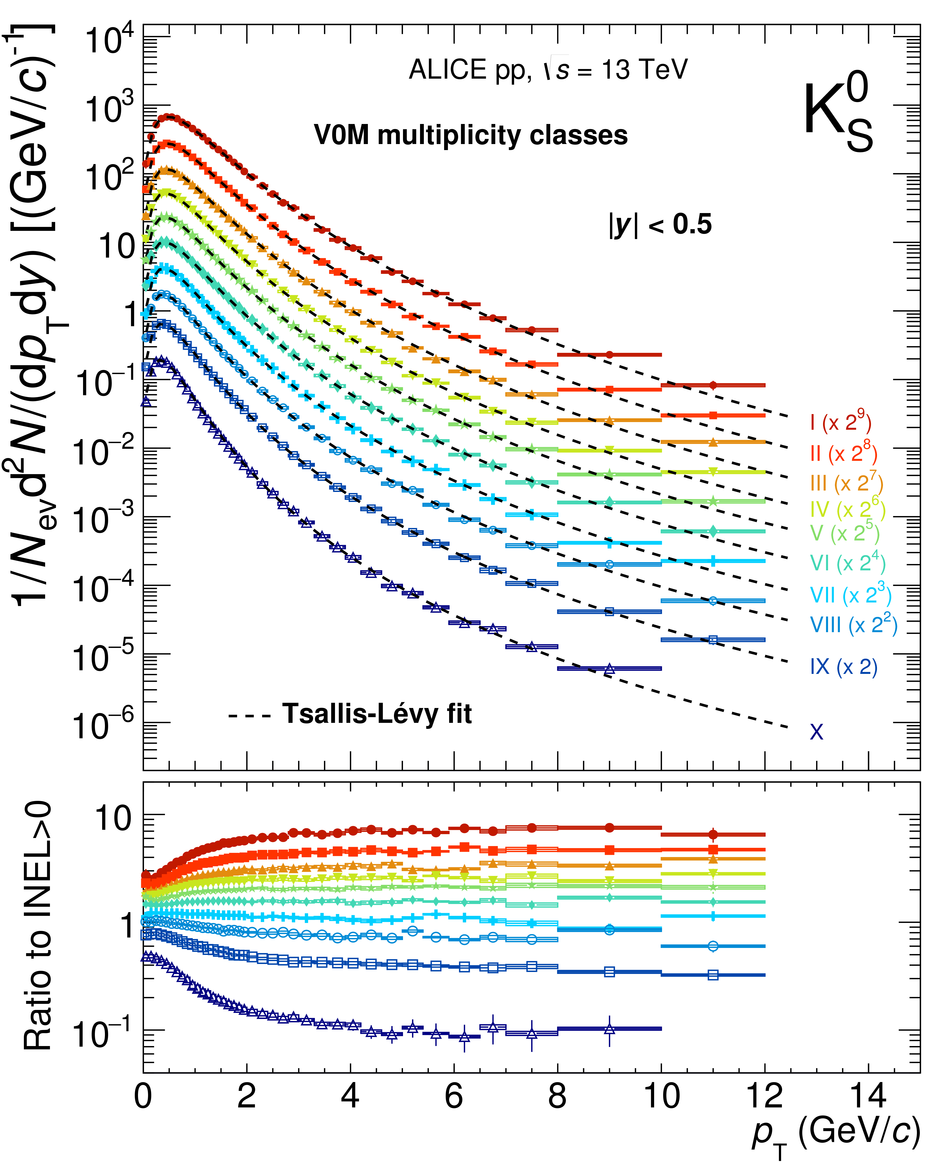
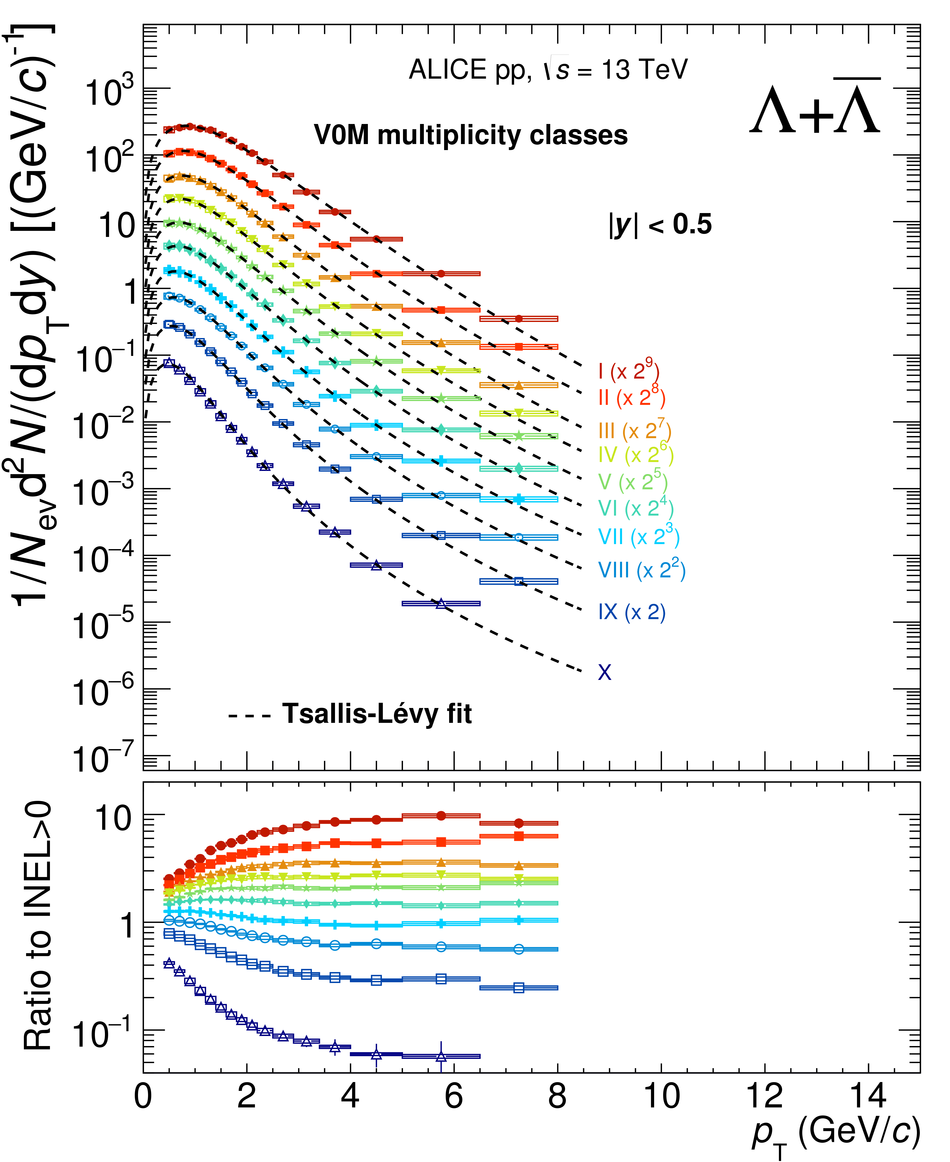
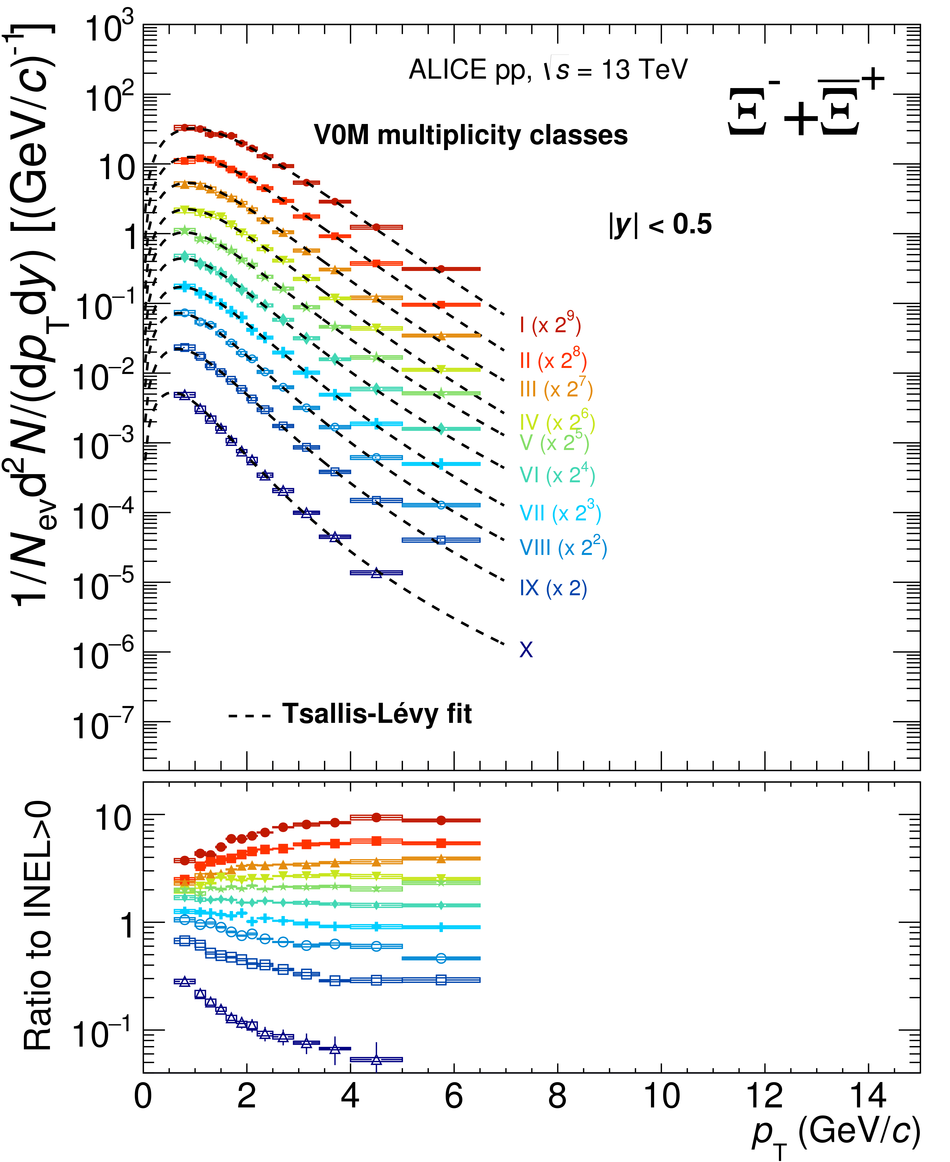
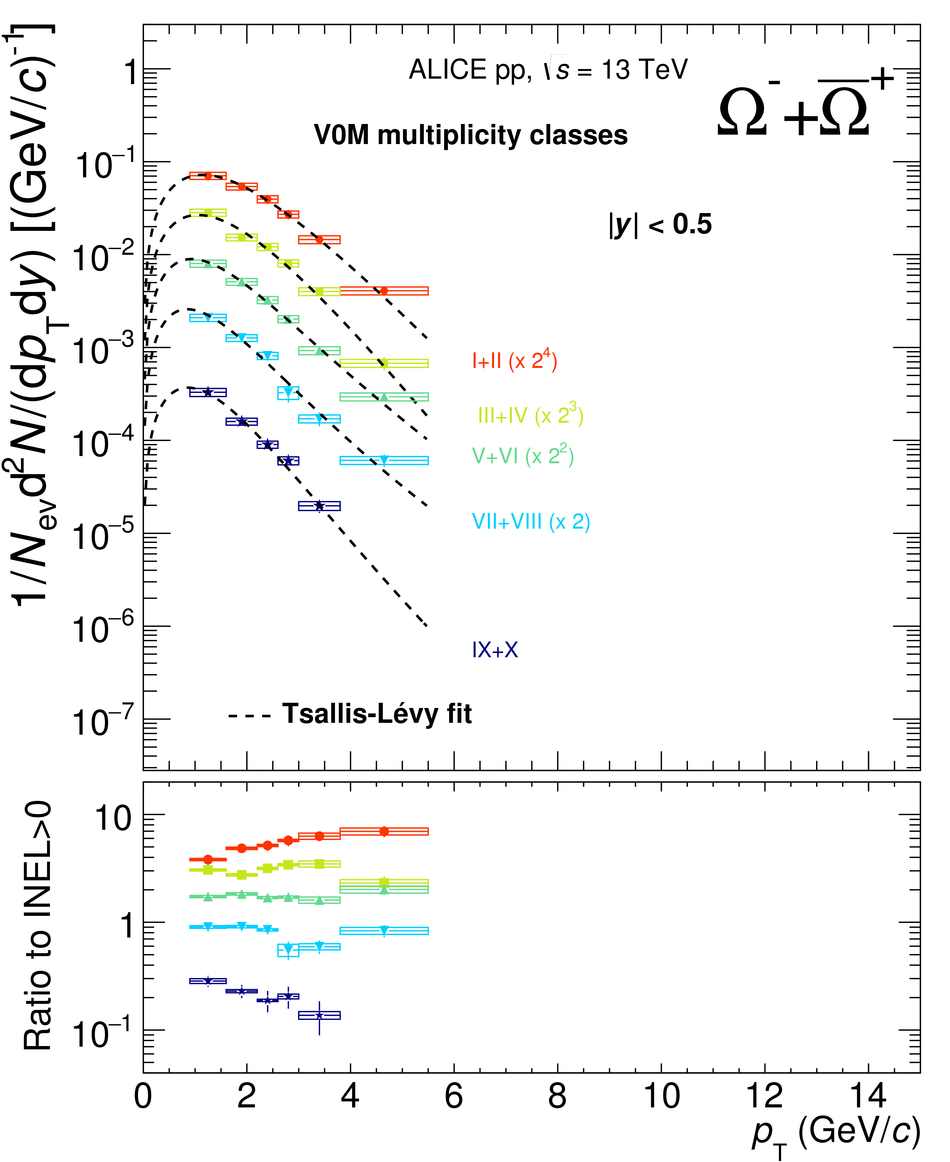
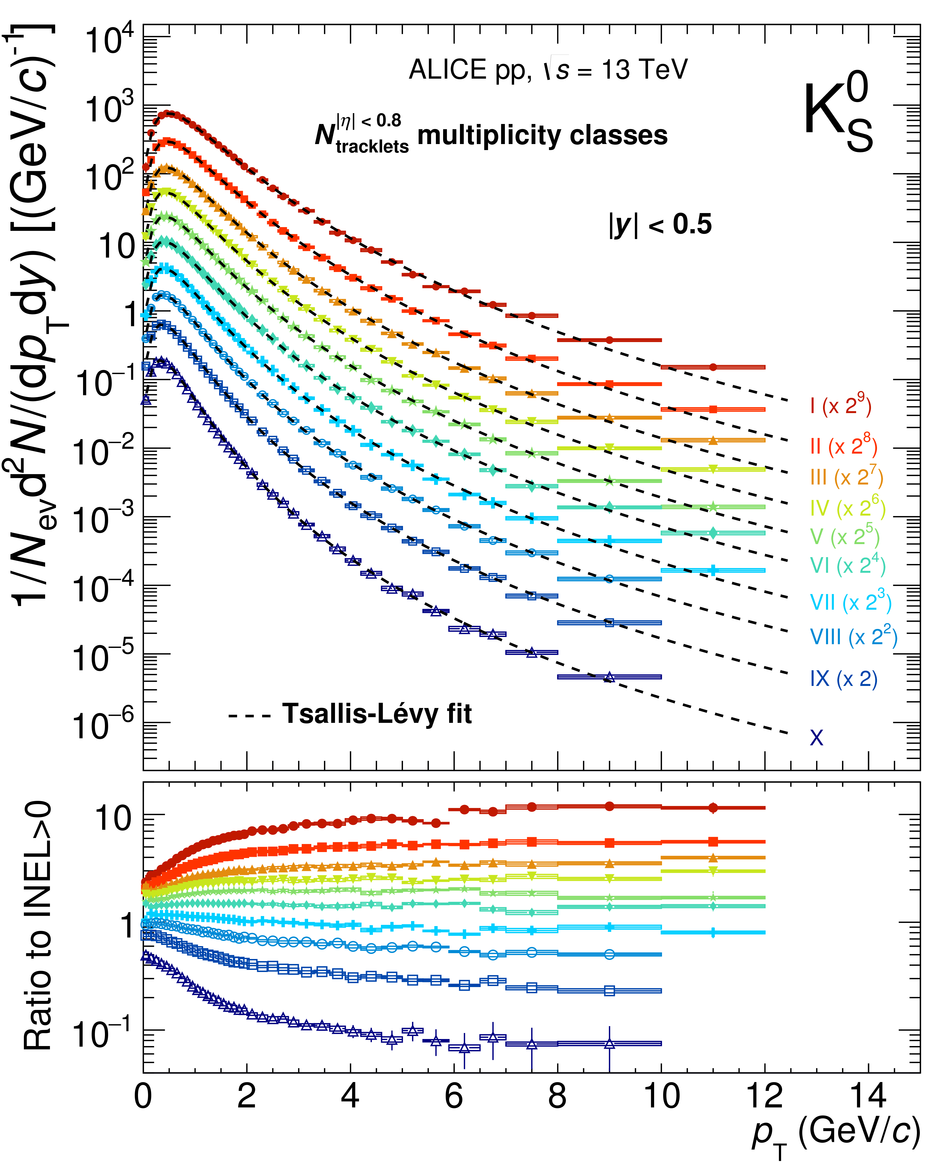
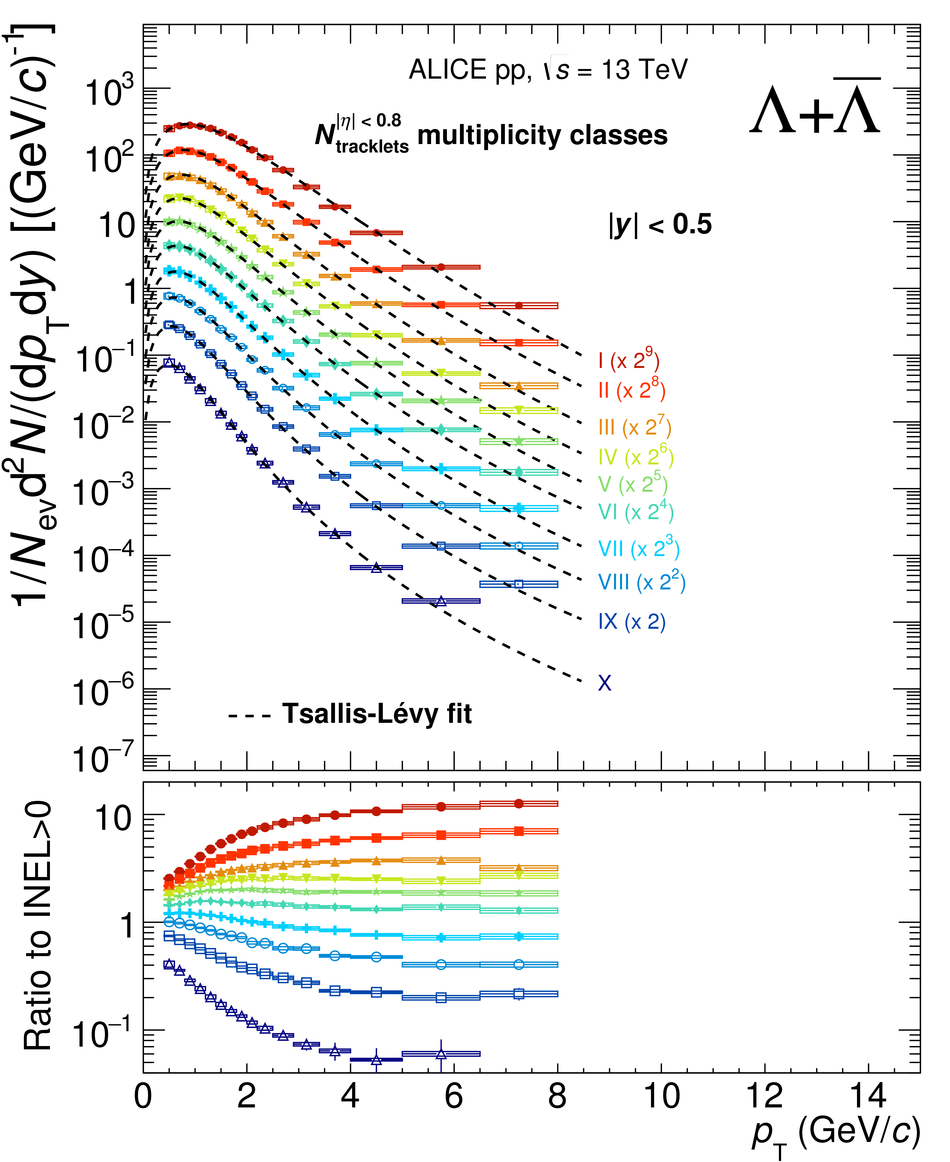
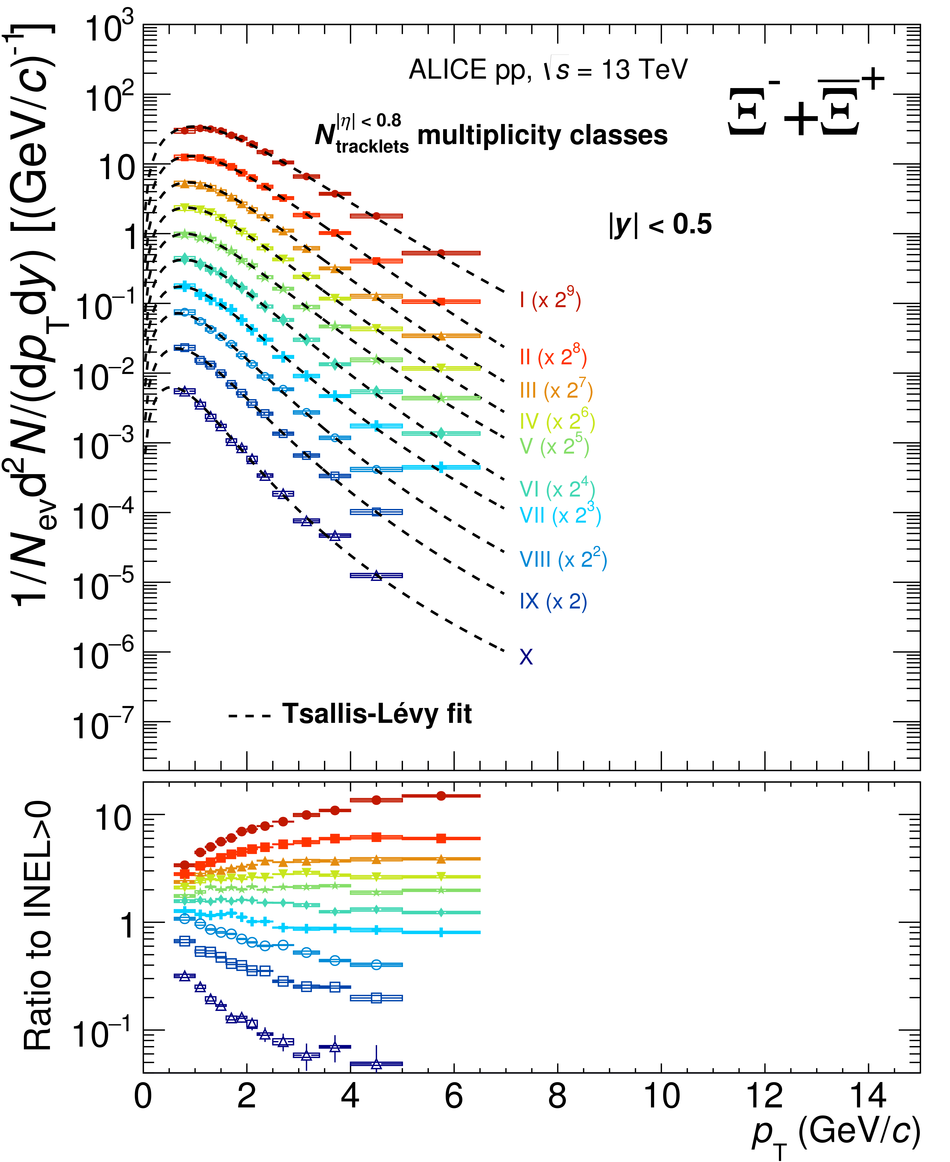
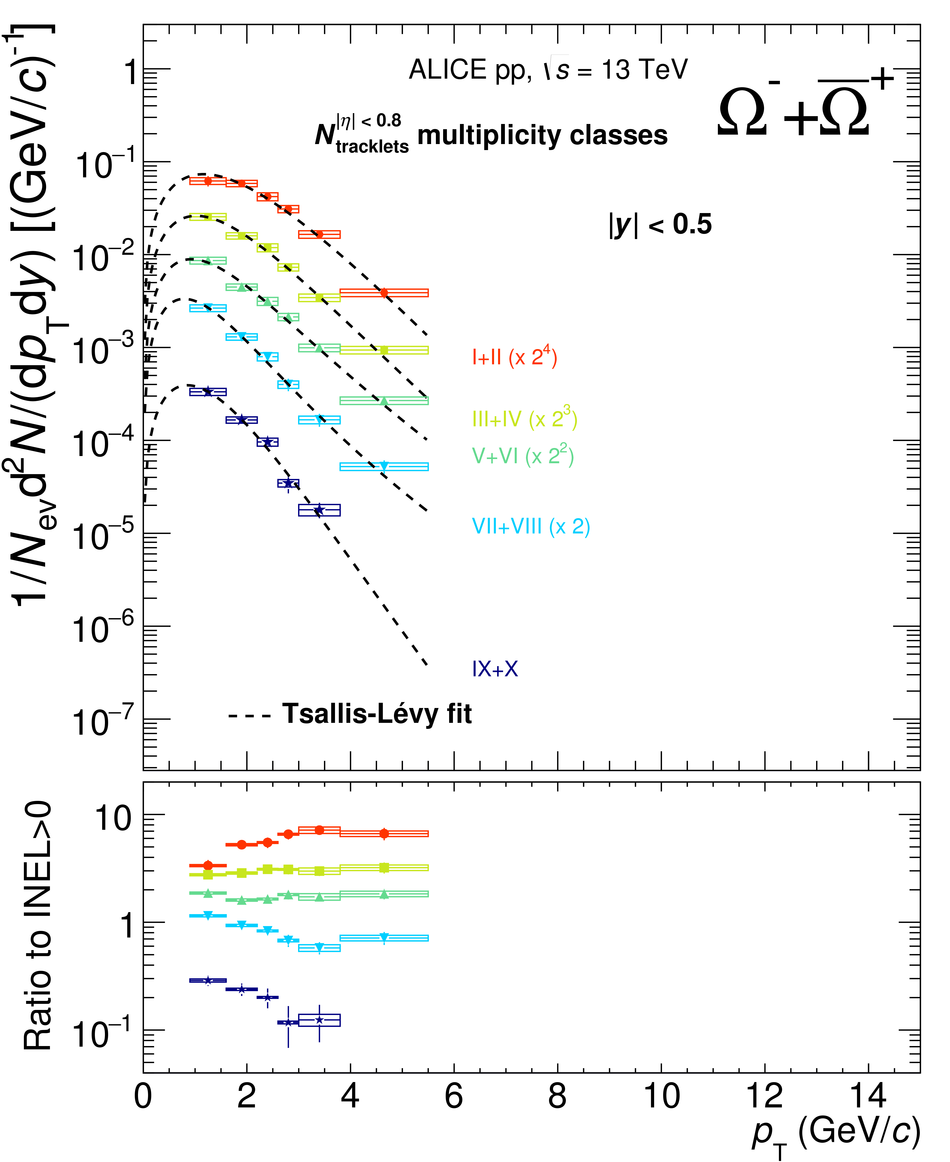
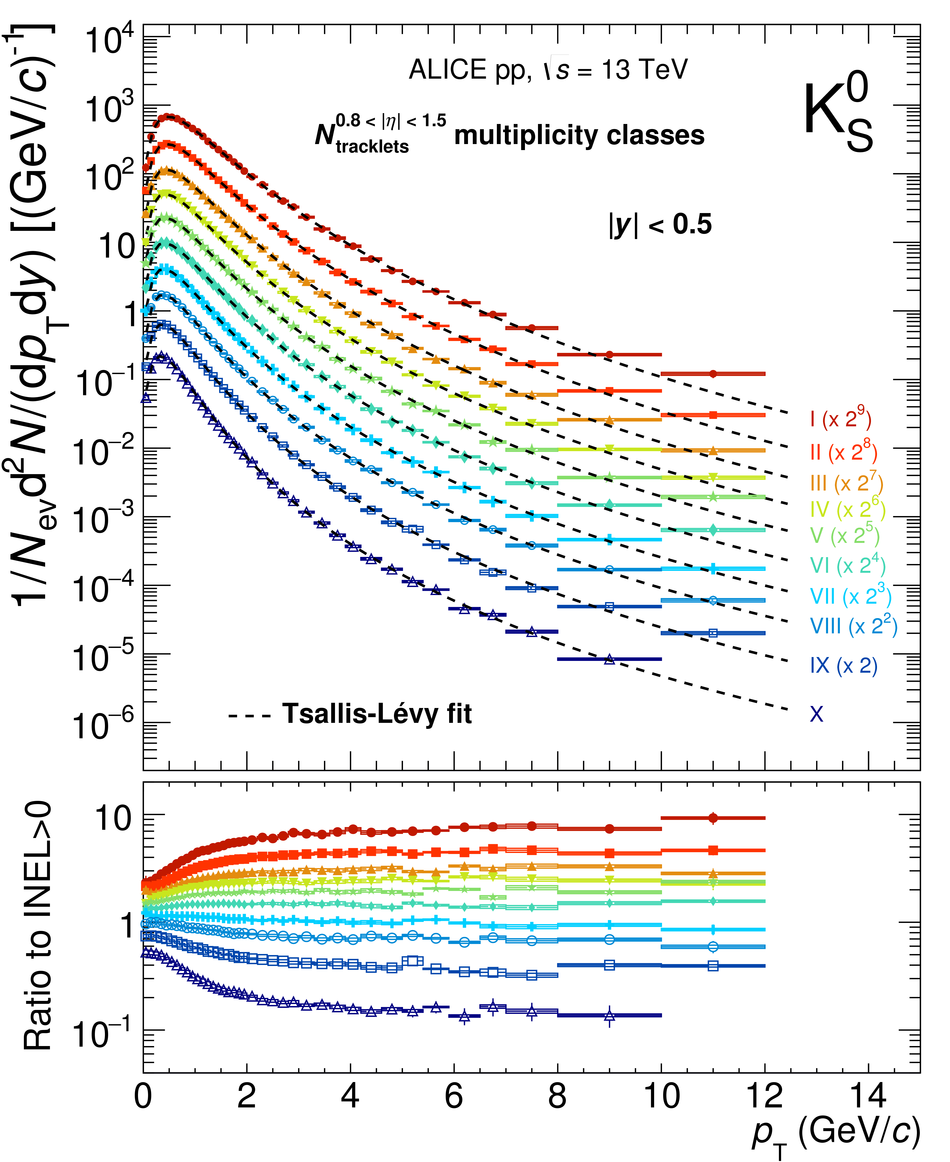
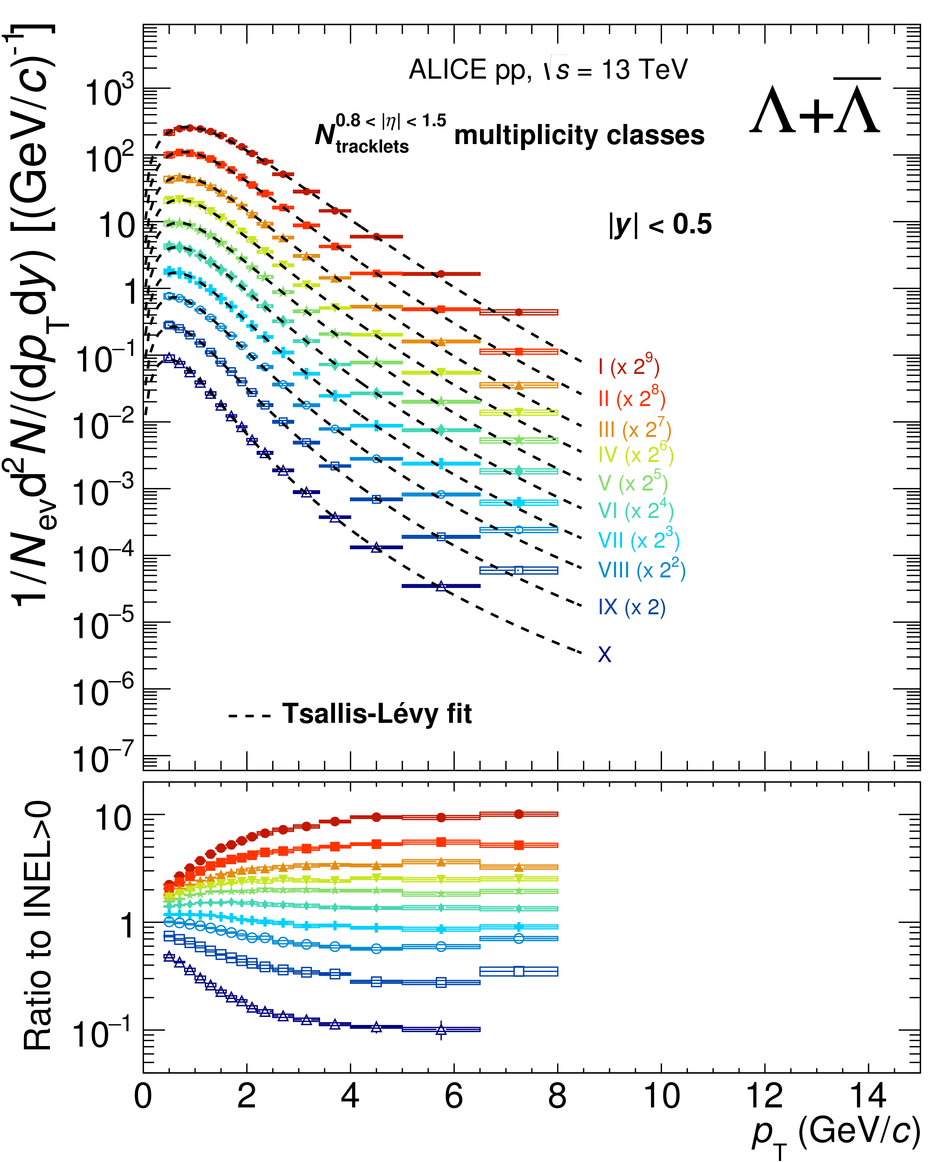
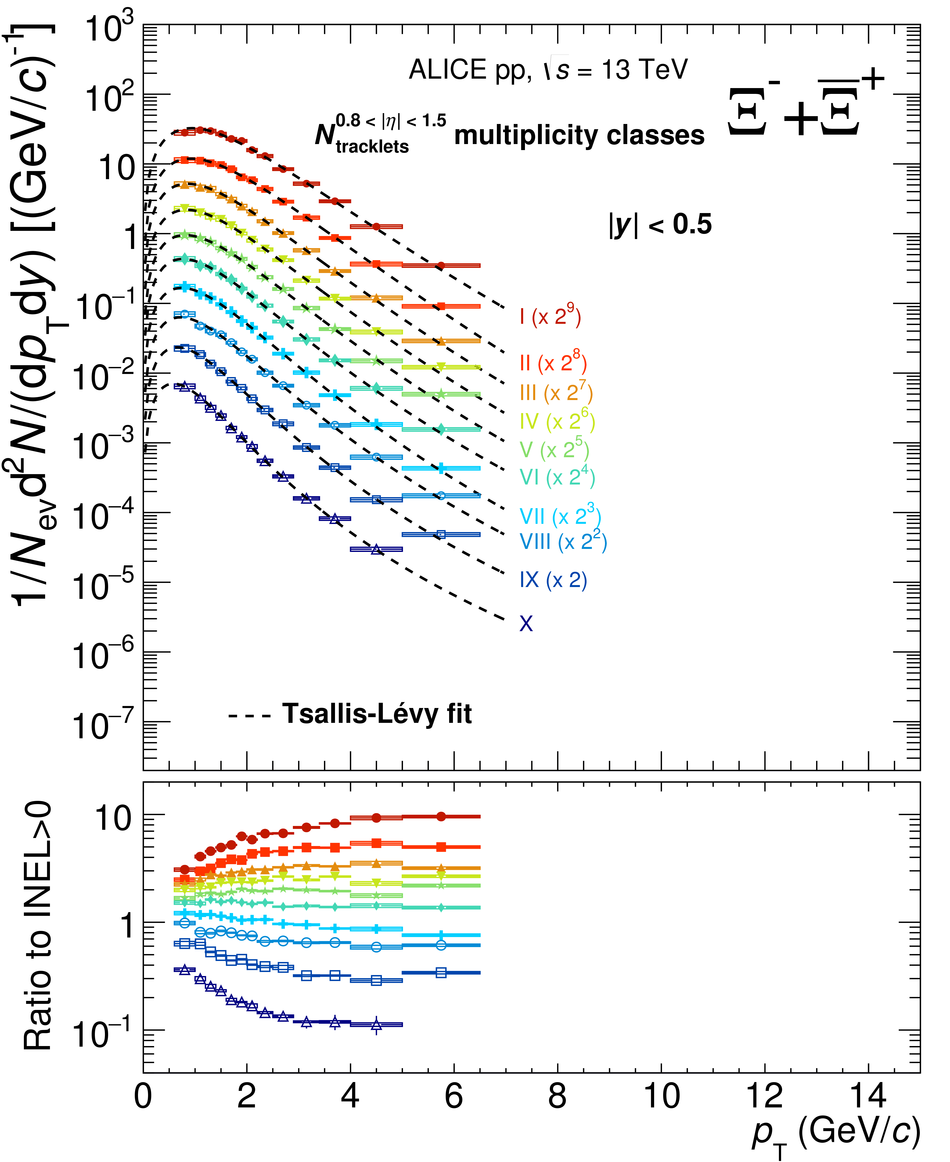
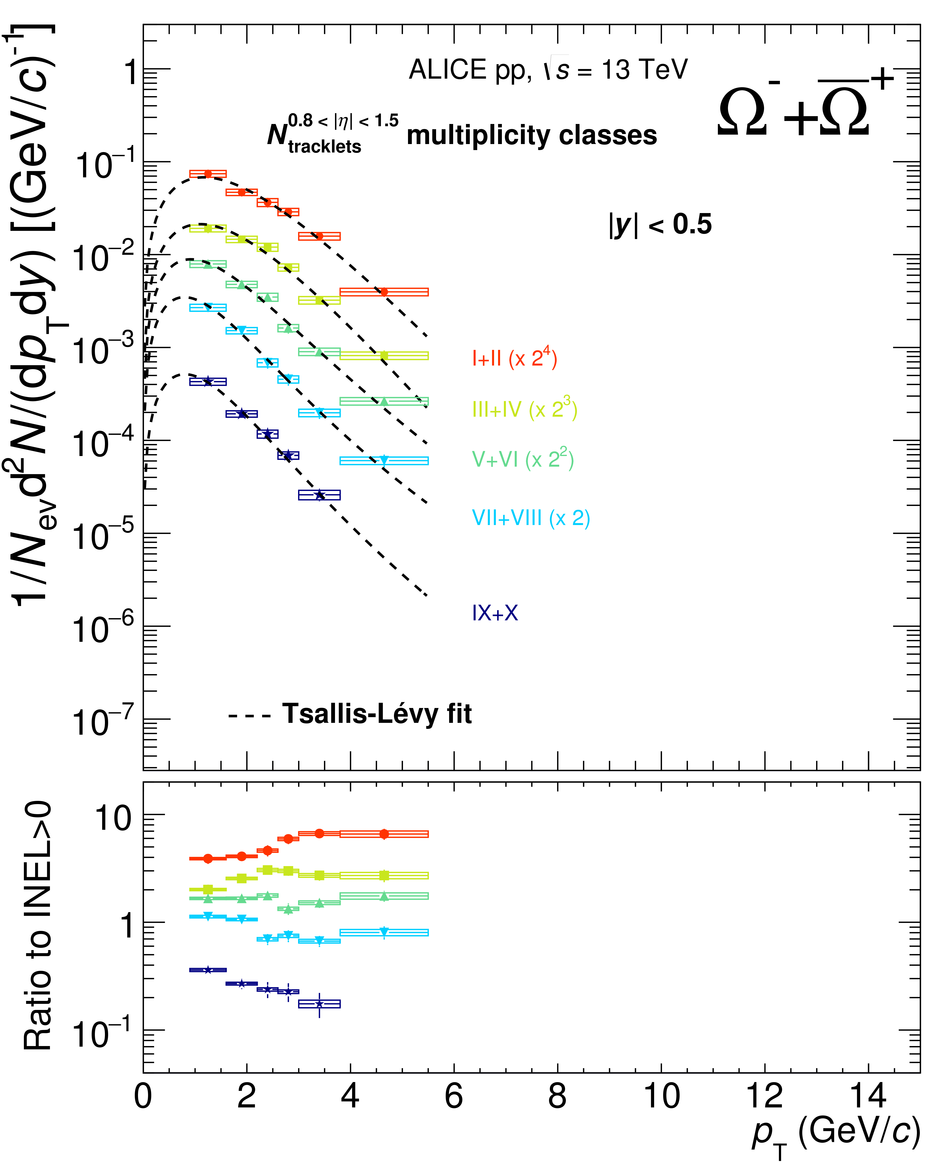
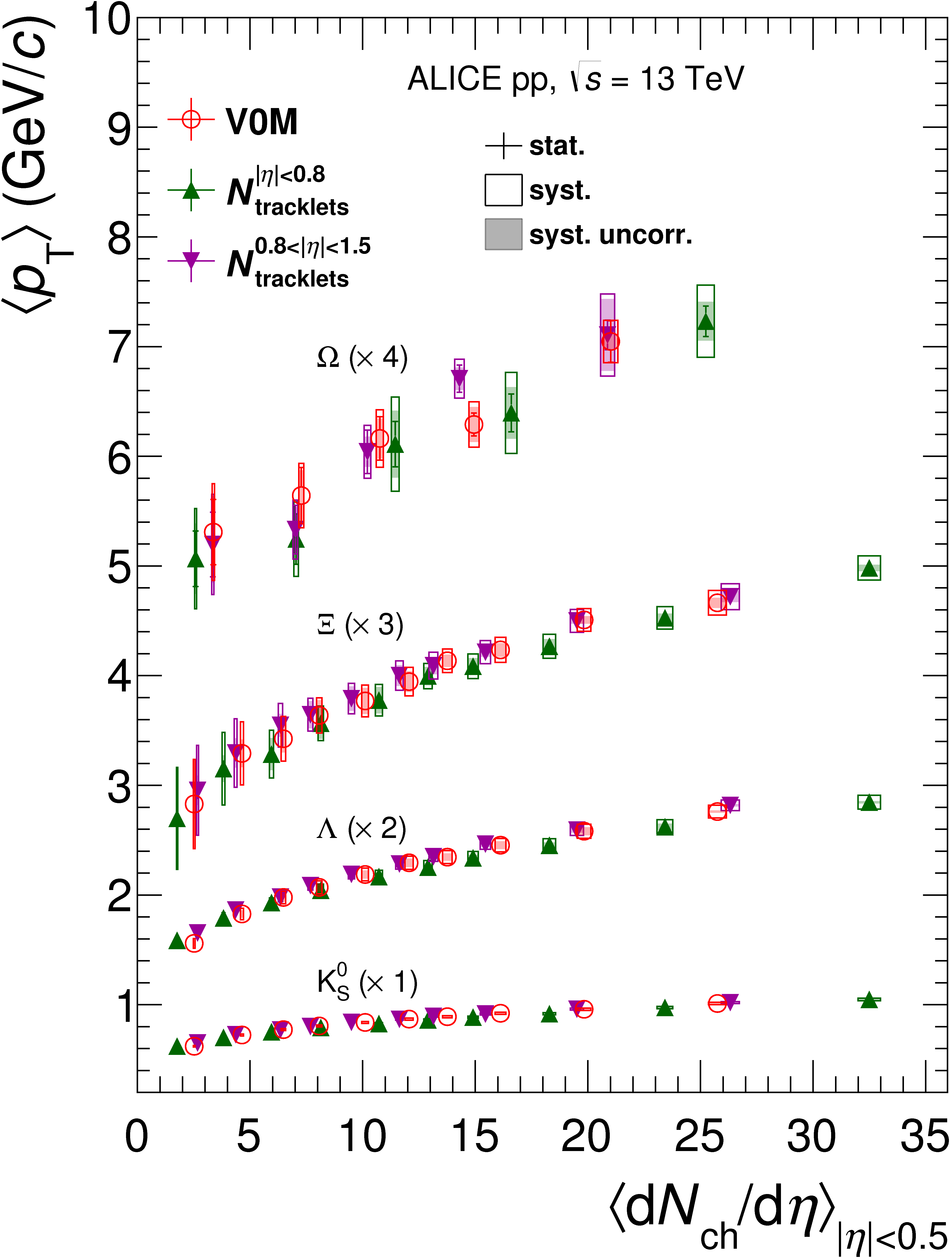
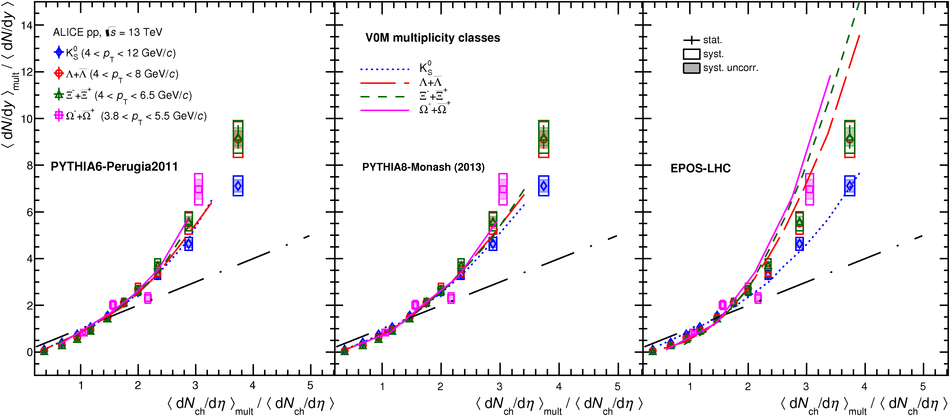
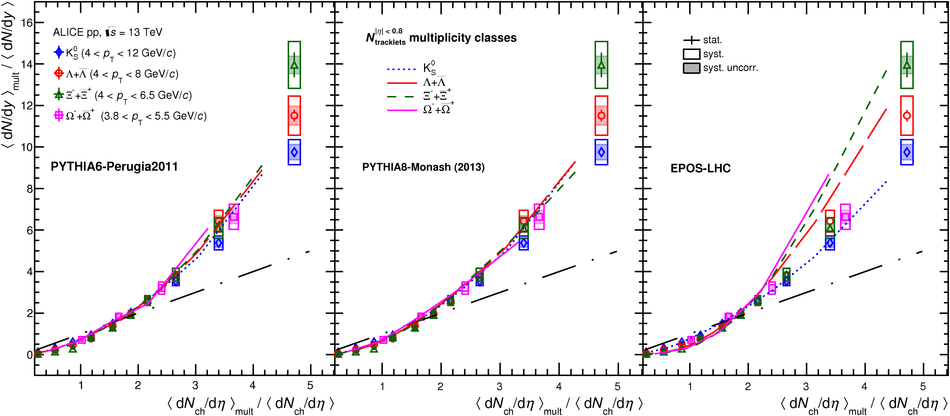
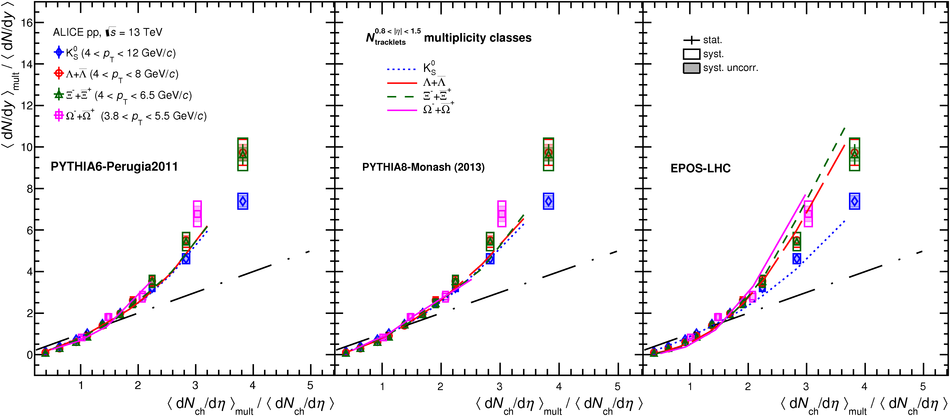
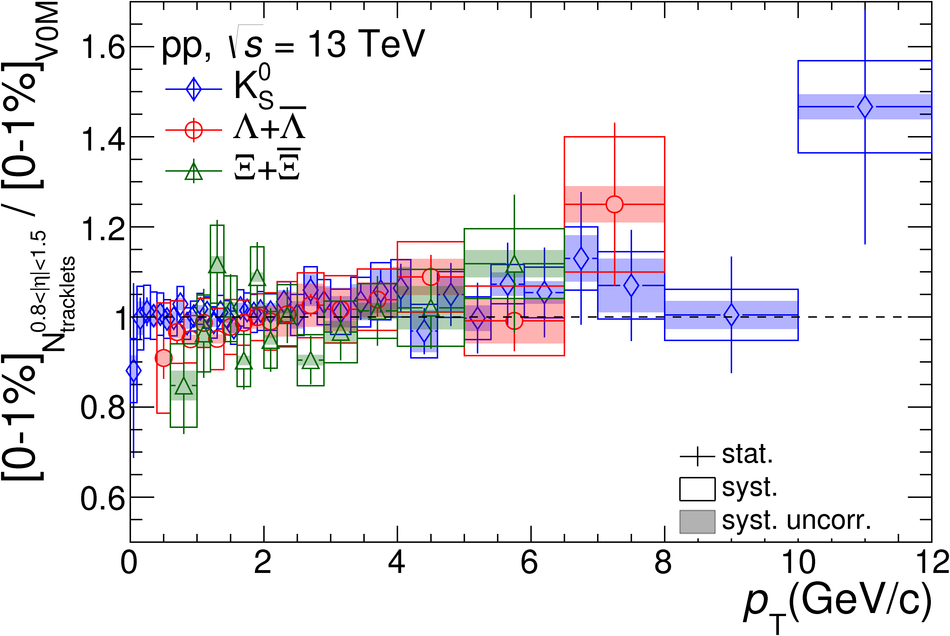
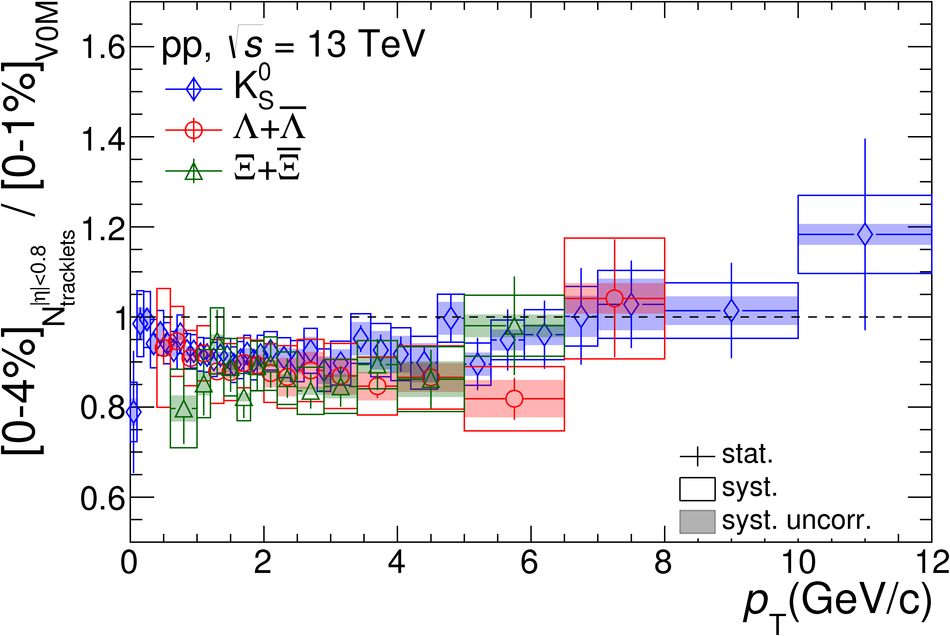
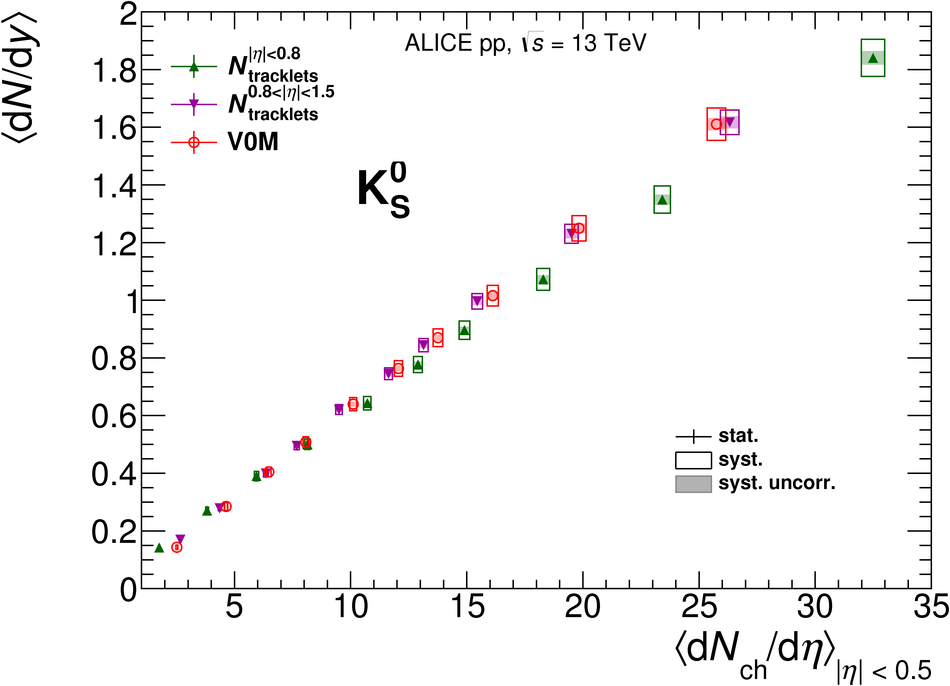
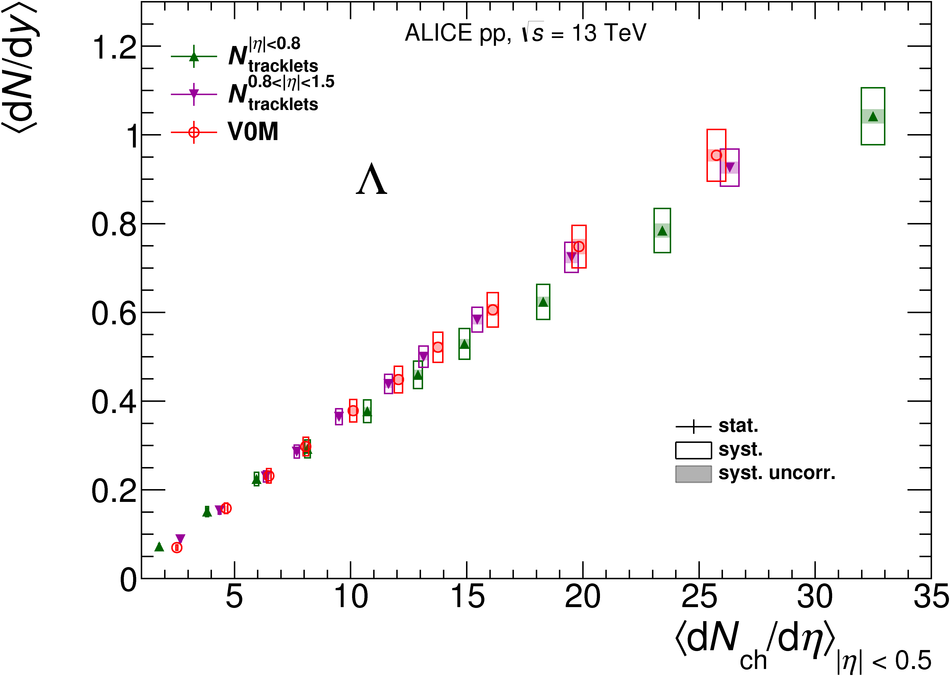
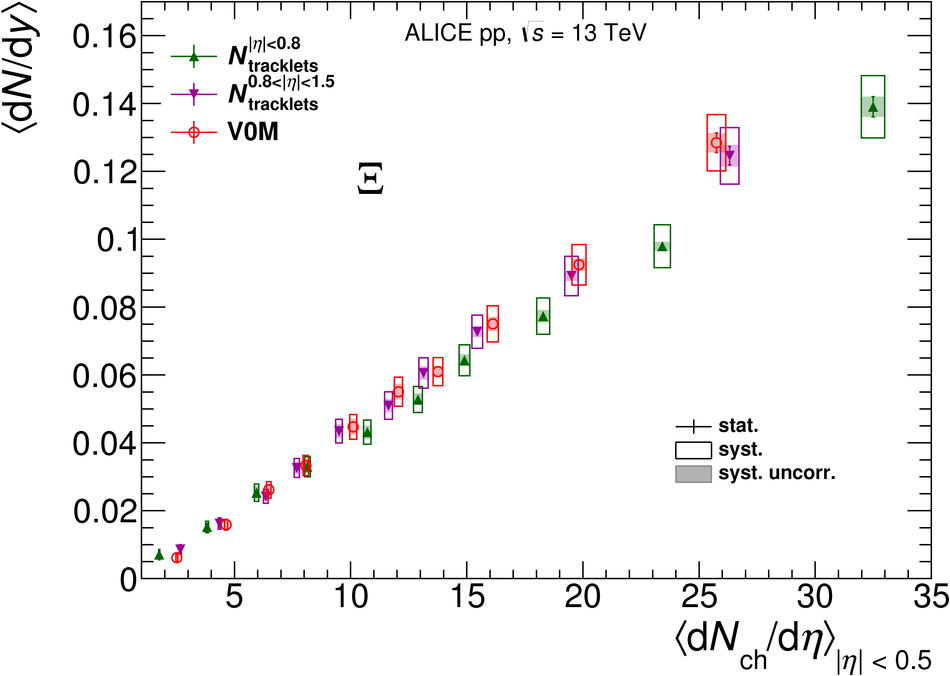
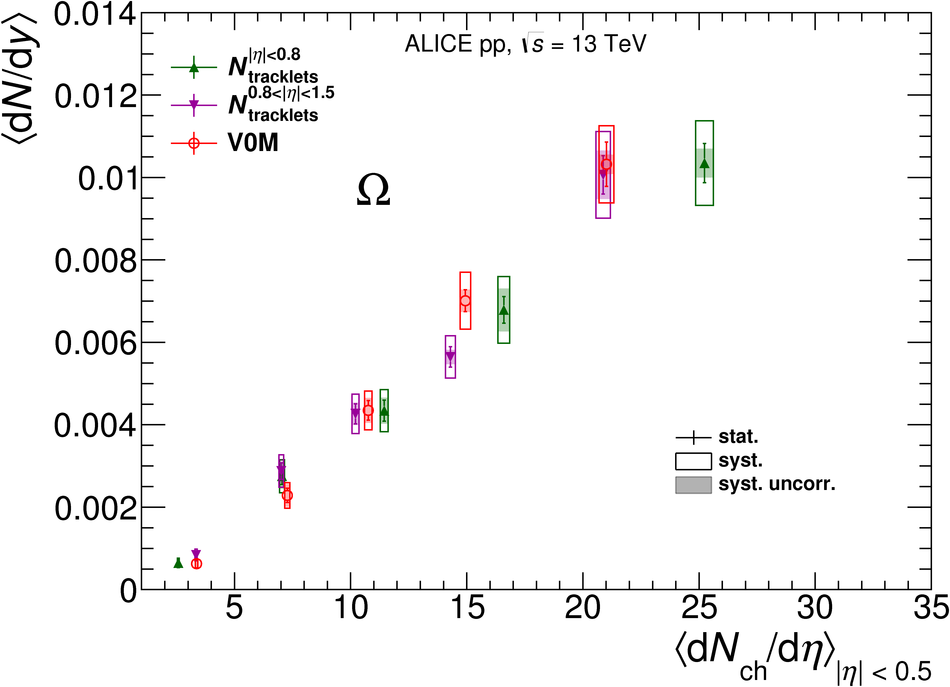
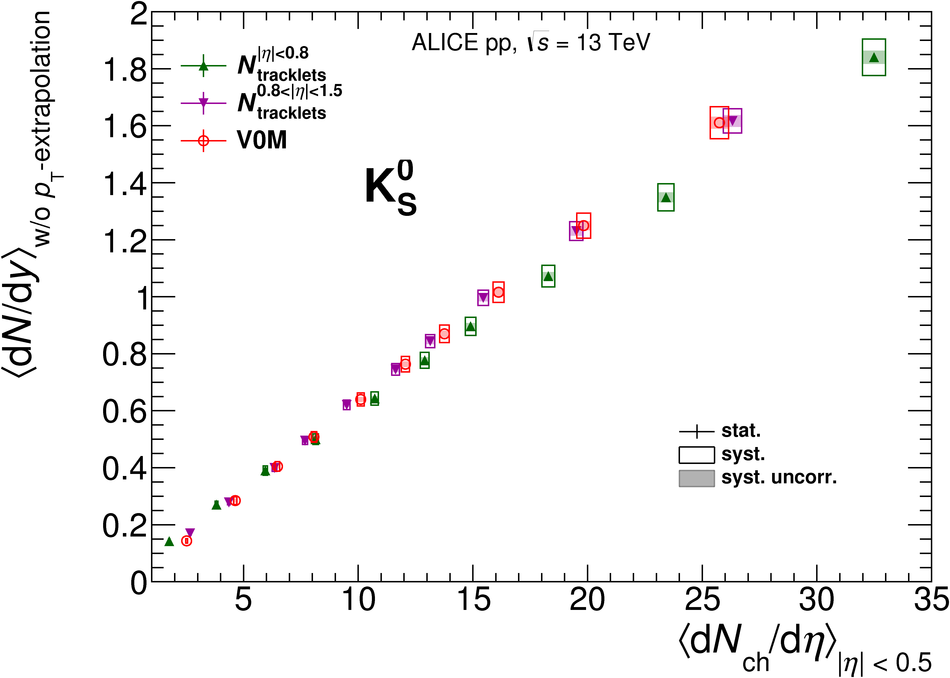
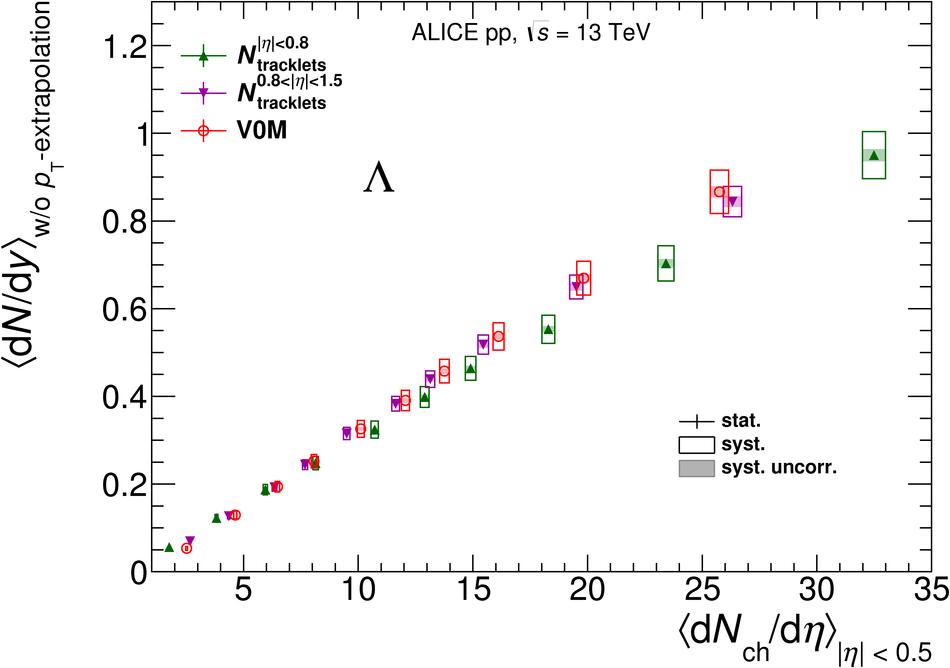
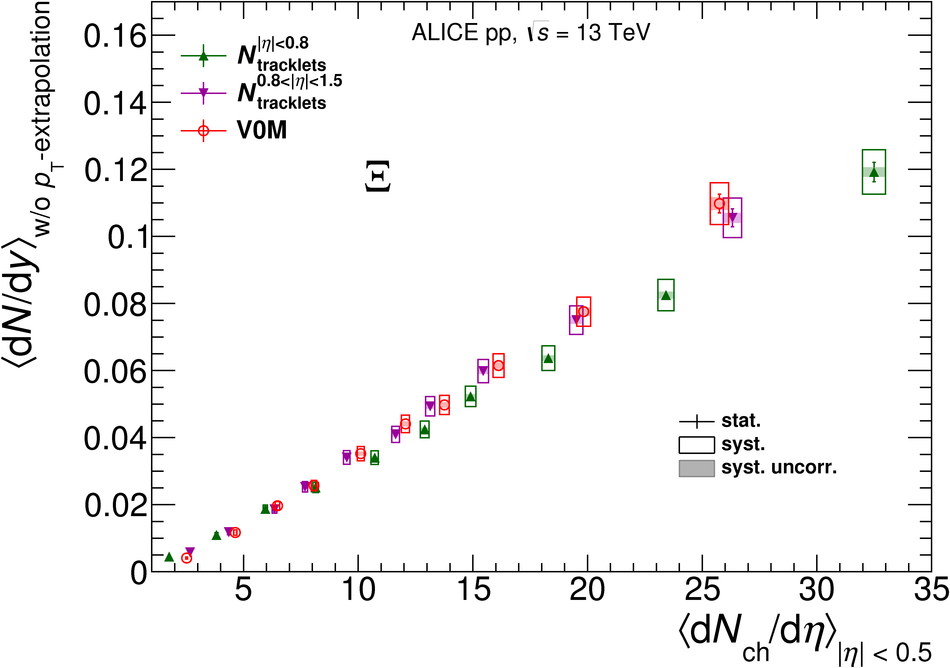
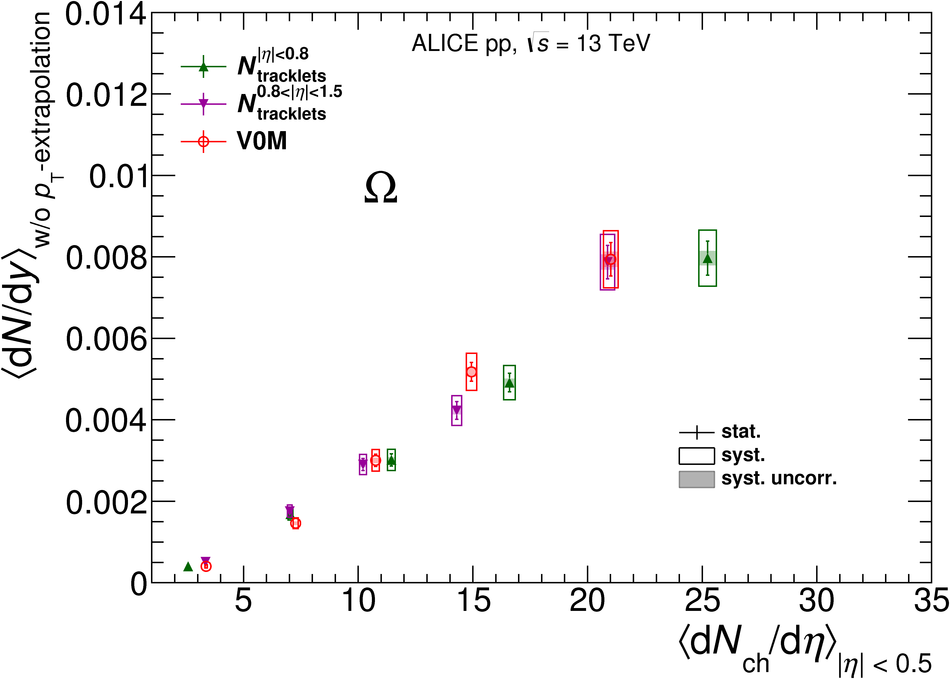
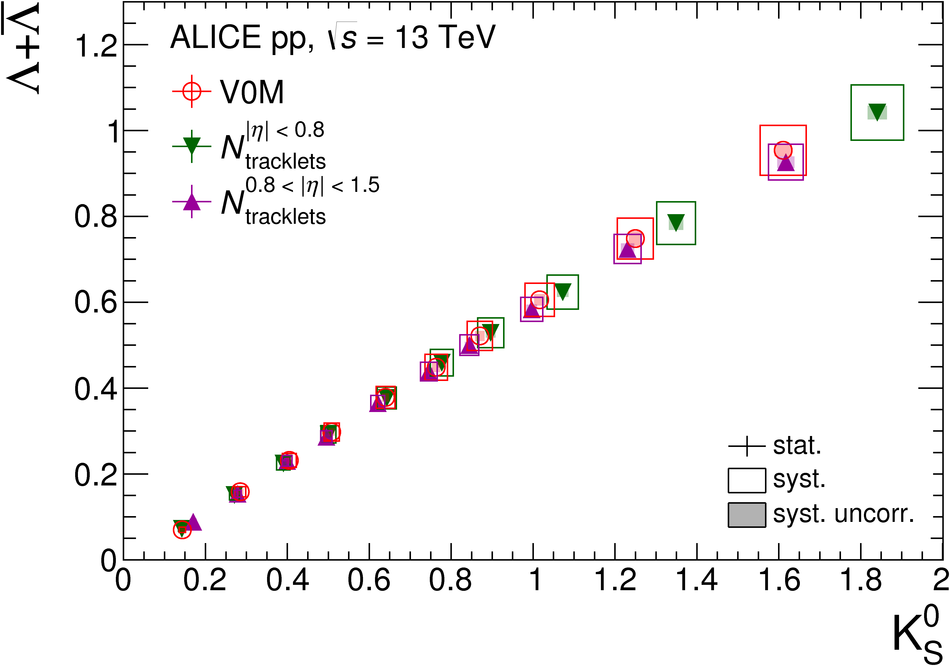
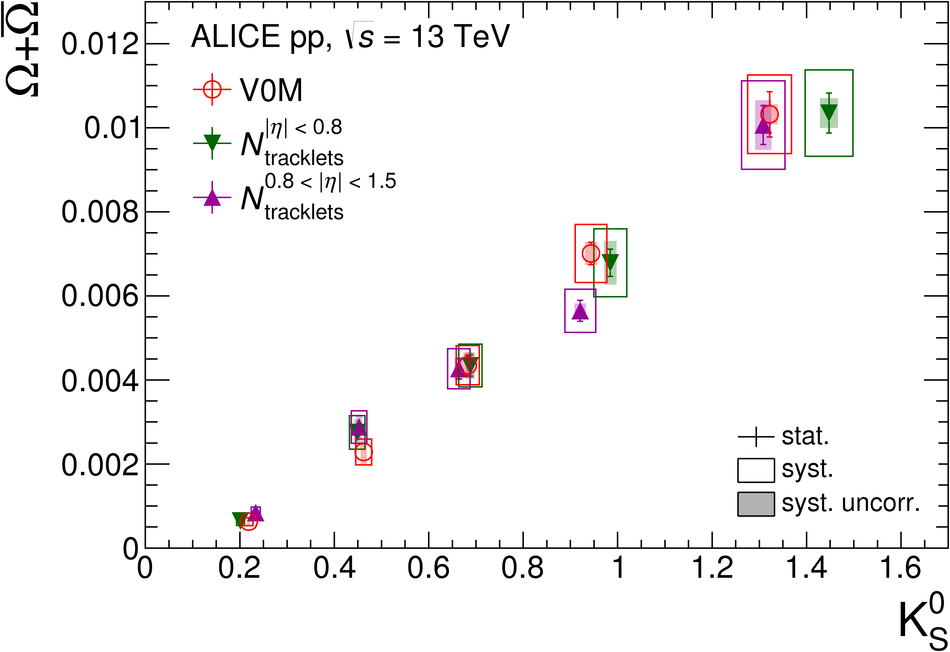
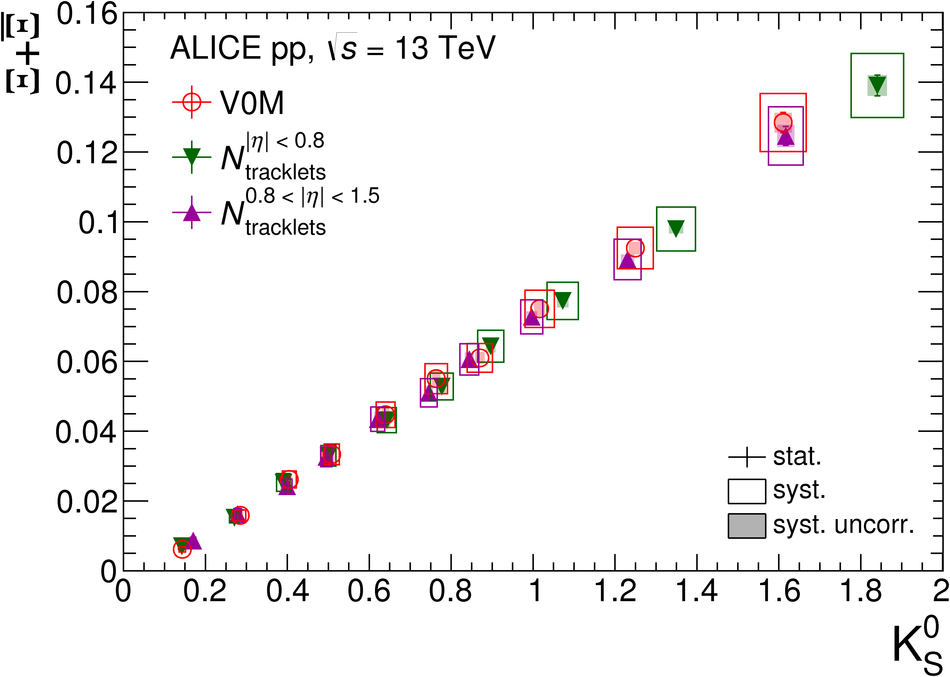
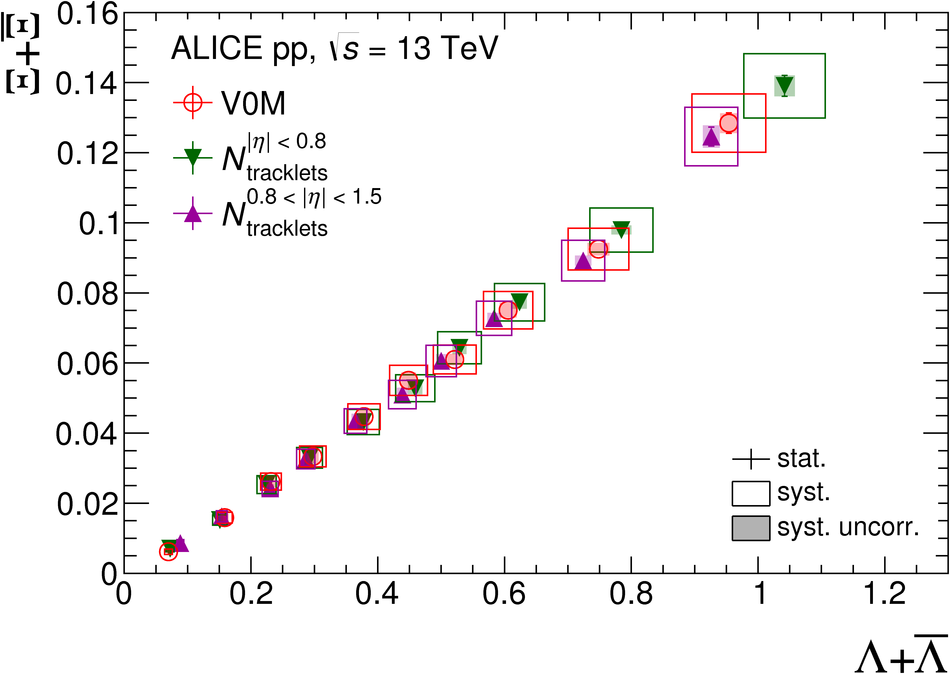
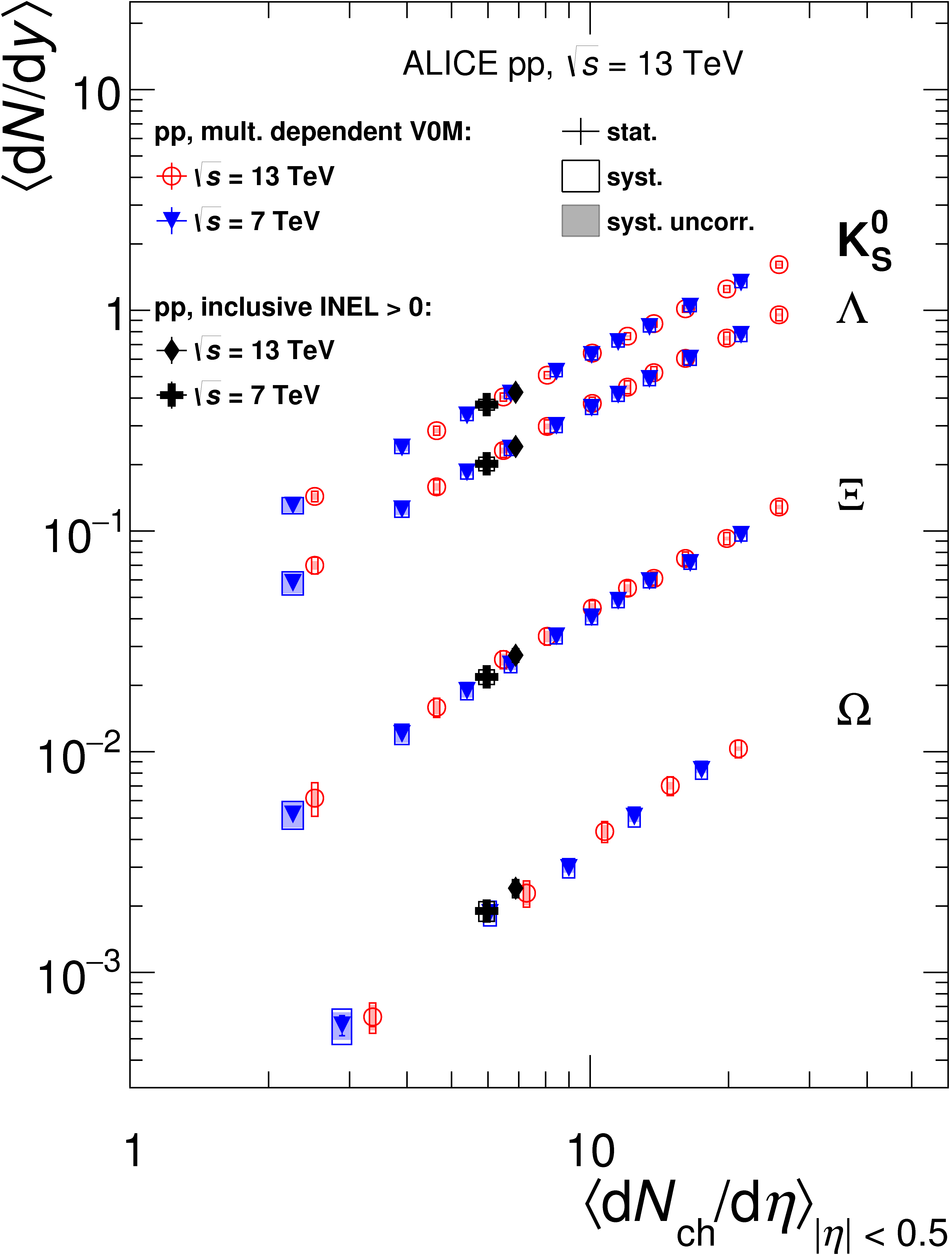
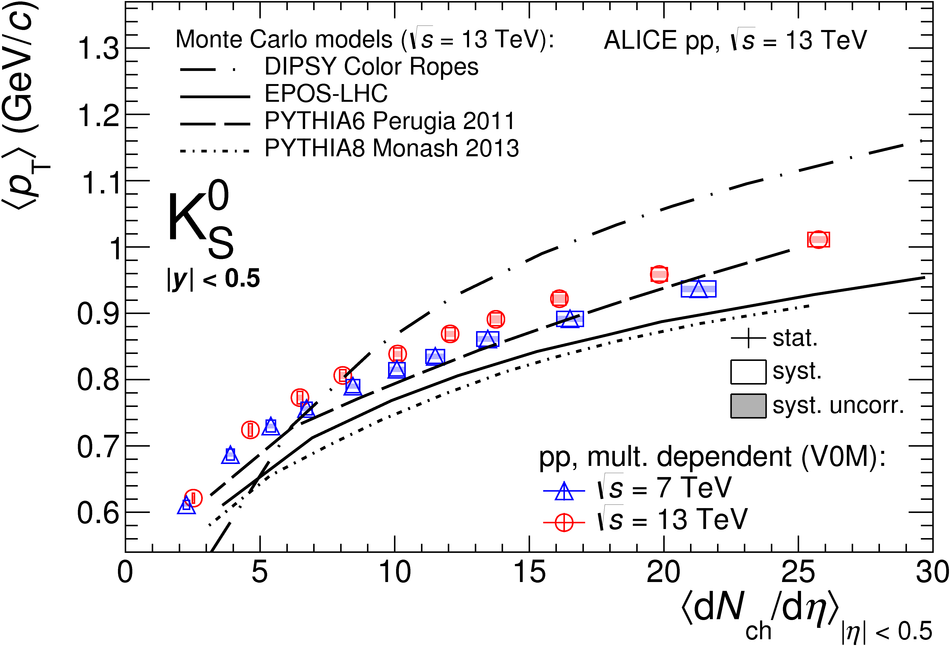
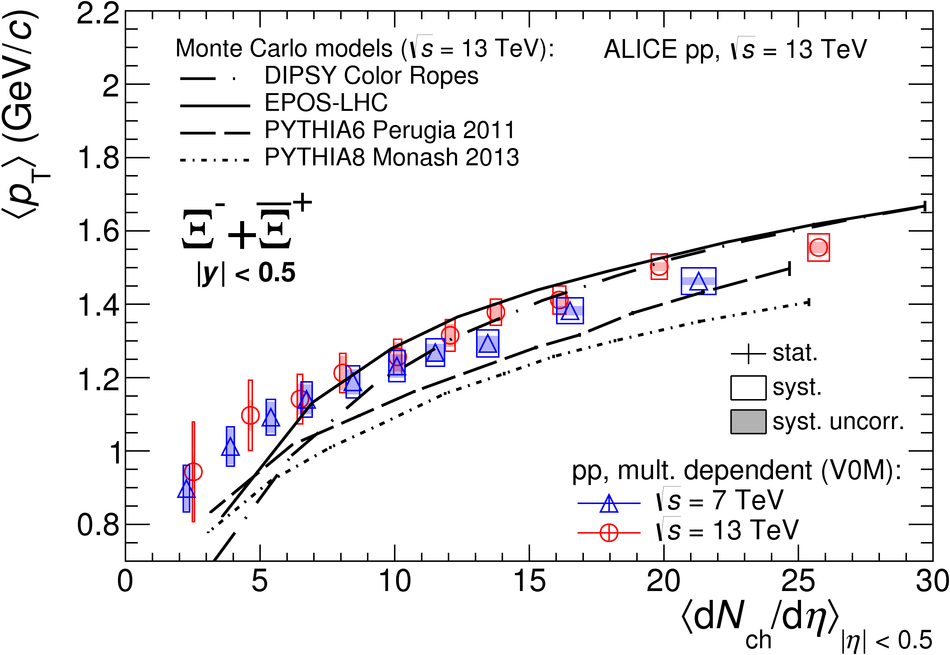
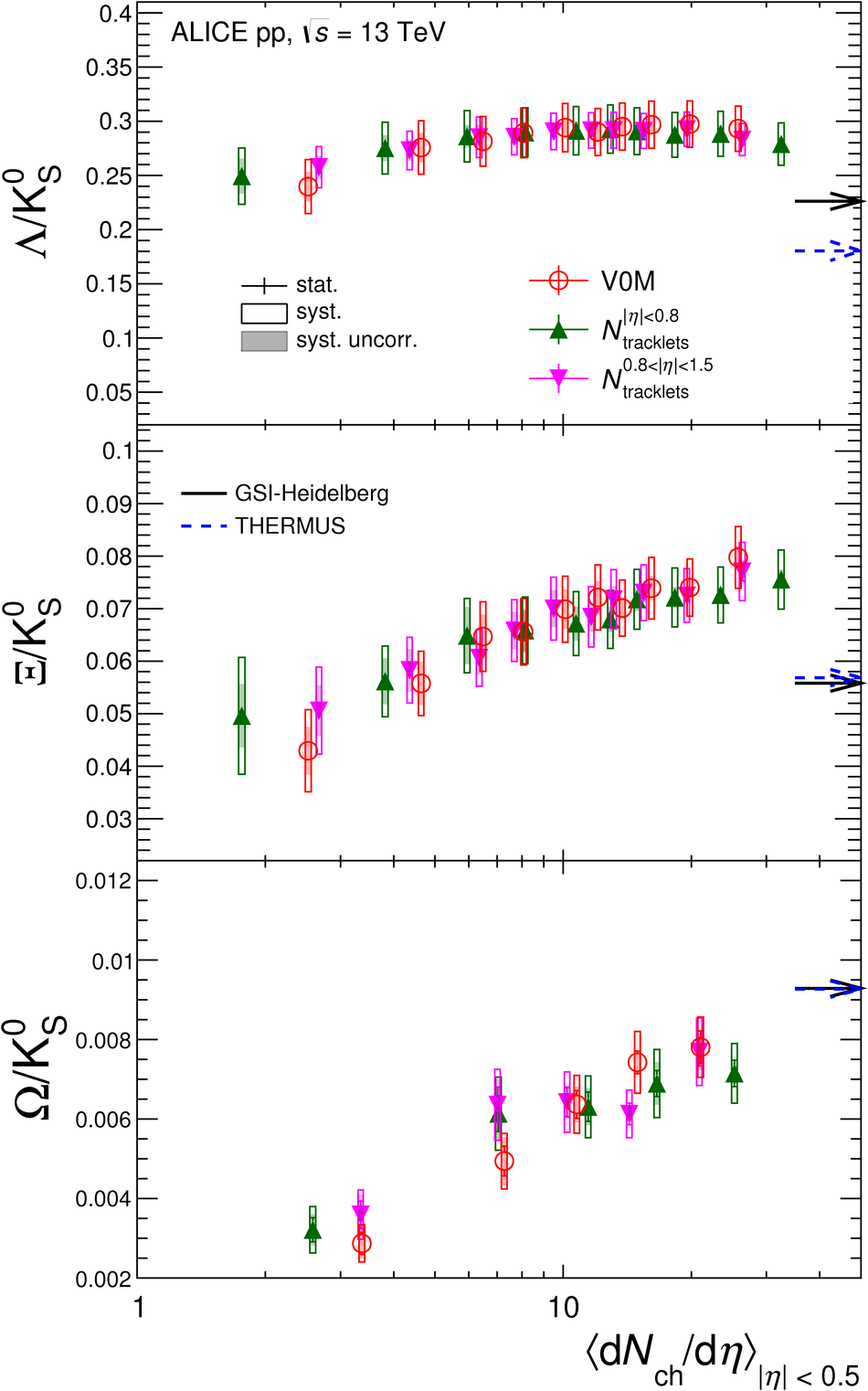
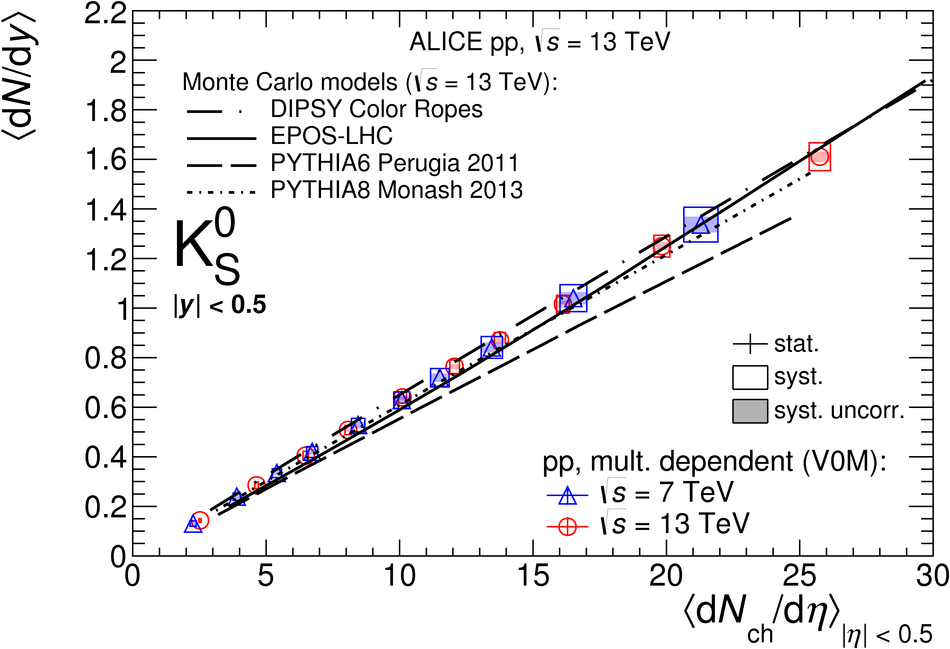
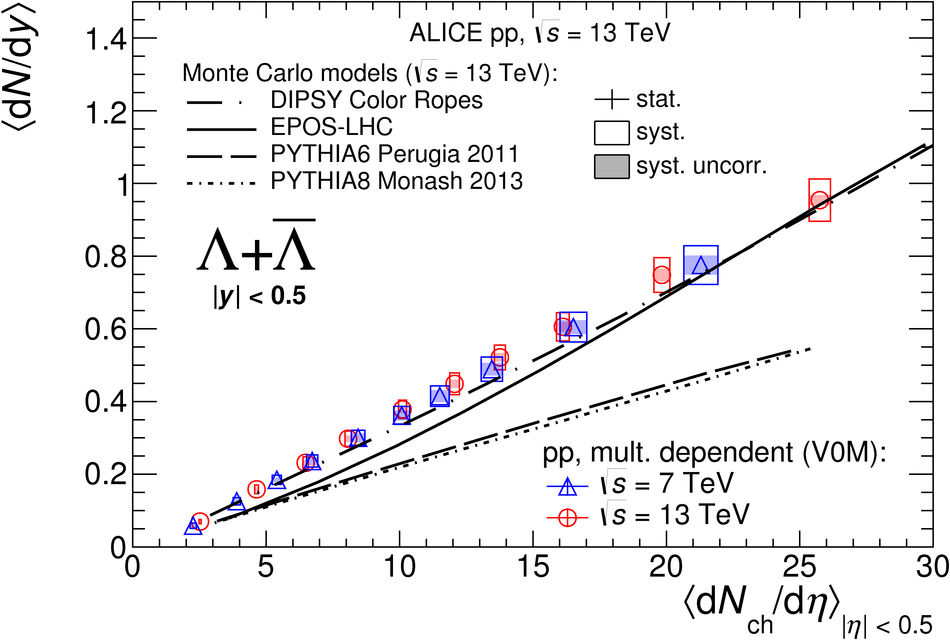
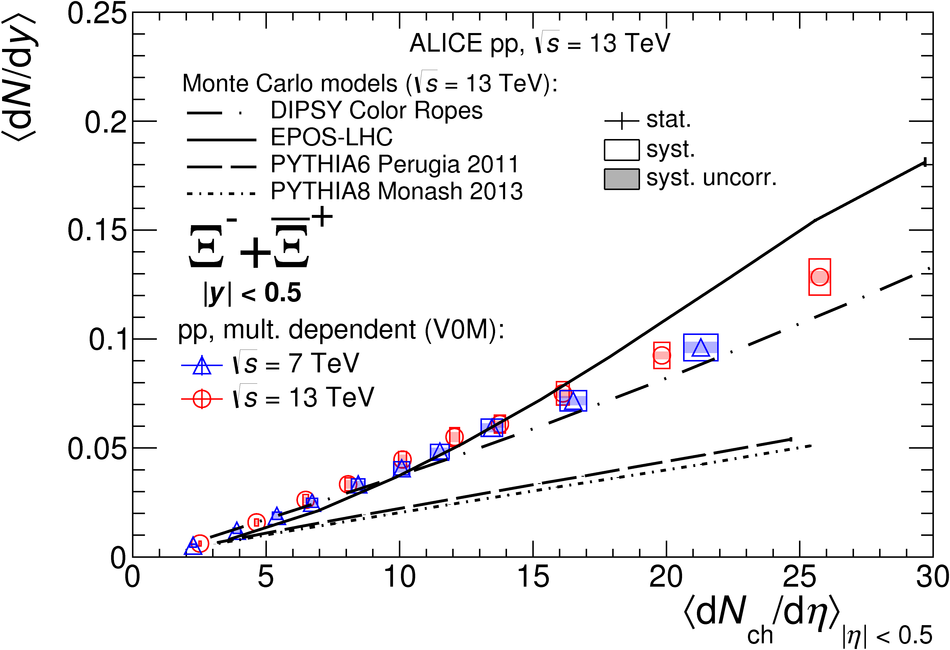
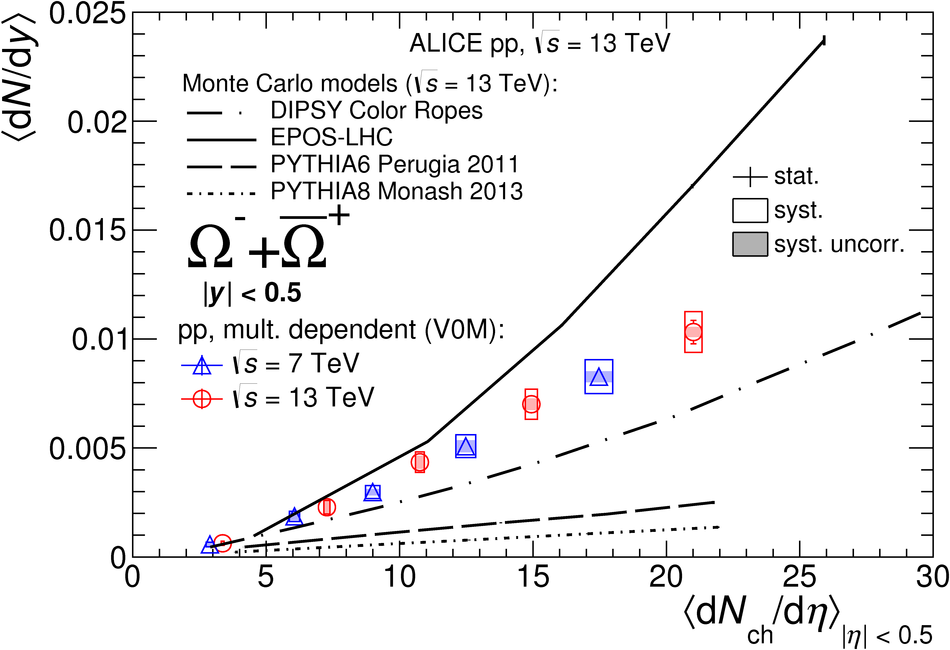
The production rates and the transverse momentum distribution of strange hadrons at mid-rapidity ($\ |y\ | <~ 0.5$) are measured in proton-proton collisions at $\sqrt{s}$ = 13 TeV as a function of the charged particle multiplicity, using the ALICE detector at the LHC. The production rates of $\rm{K}^{0}_{S}$, $\Lambda$, $\Xi$, and $\Omega$ increase with the multiplicity faster than what is reported for inclusive charged particles. The increase is found to be more pronounced for hadrons with a larger strangeness content. Possible auto-correlations between the charged particles and the strange hadrons are evaluated by measuring the event-activity with charged particle multiplicity estimators covering different pseudorapidity regions. When comparing to lower energy results, the yields of strange hadrons are found to depend only on the mid-rapidity charged particle multiplicity. Several features of the data are reproduced qualitatively by general purpose QCD Monte Carlo models that take into account the effect of densely-packed QCD strings in high multiplicity collisions. However, none of the tested models reproduce the data quantitatively. This work corroborates and extends the ALICE findings on strangeness production in proton-proton collisions at 7 TeV.
Eur. Phys. J. C 80, 167 (2020)
HEP Data
e-Print: arXiv:1908.01861 | PDF | inSPIRE
CERN-EP-2019-168