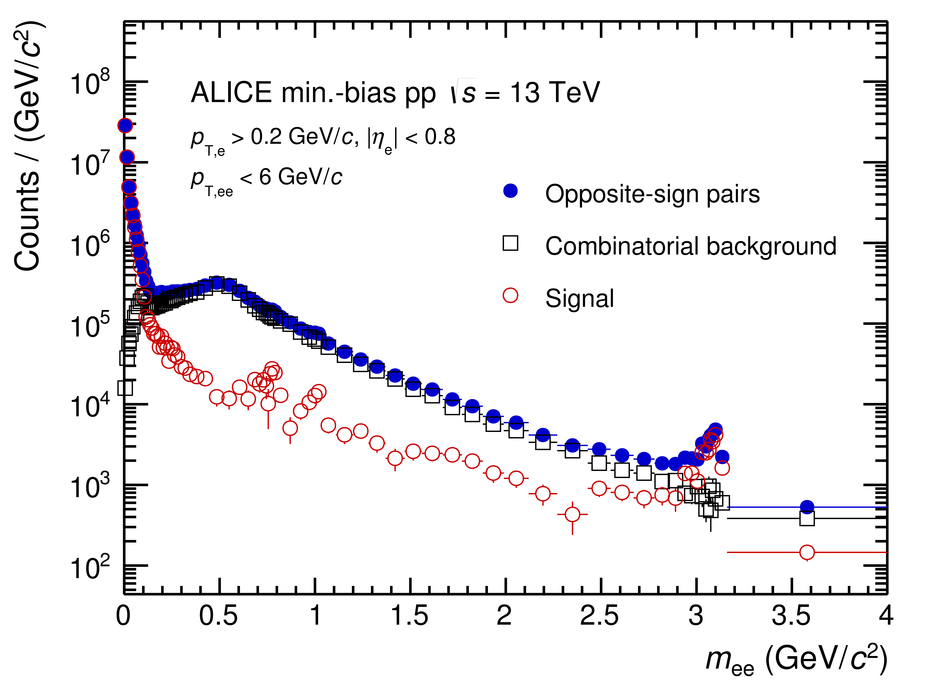
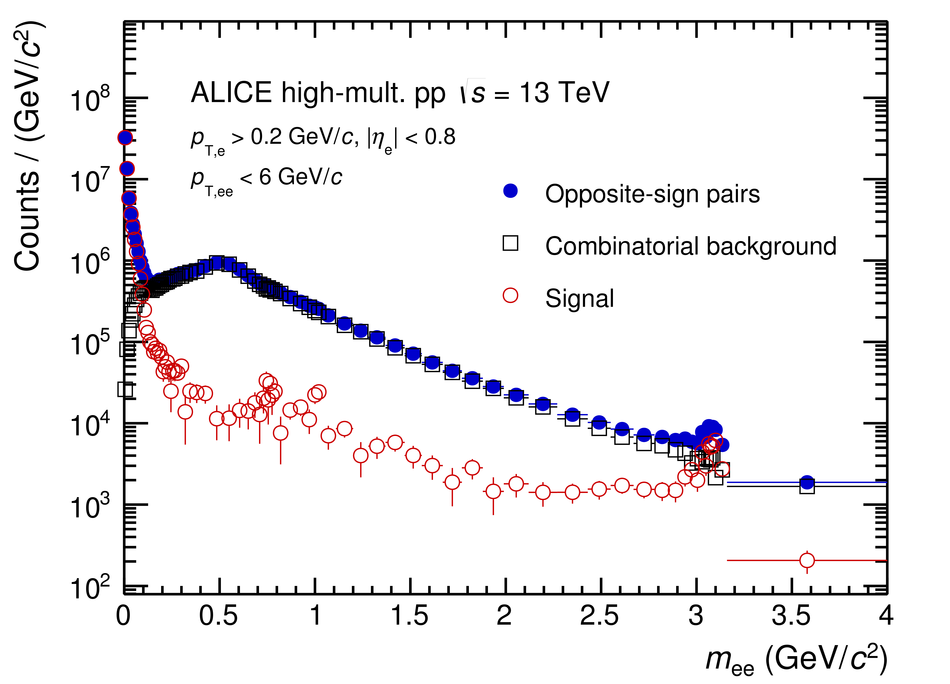
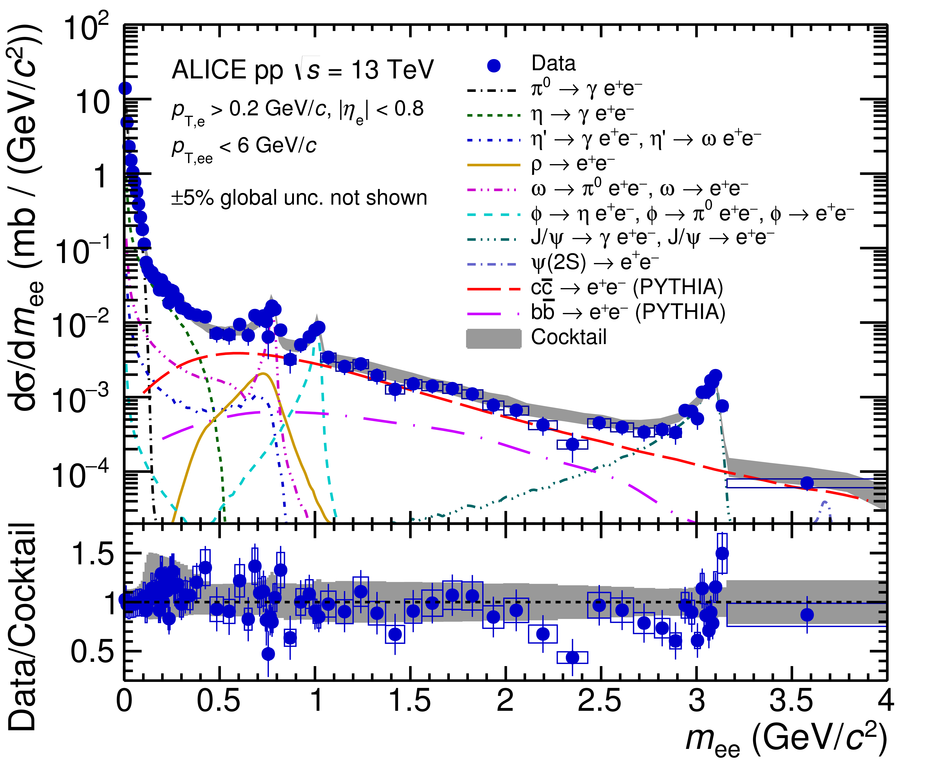
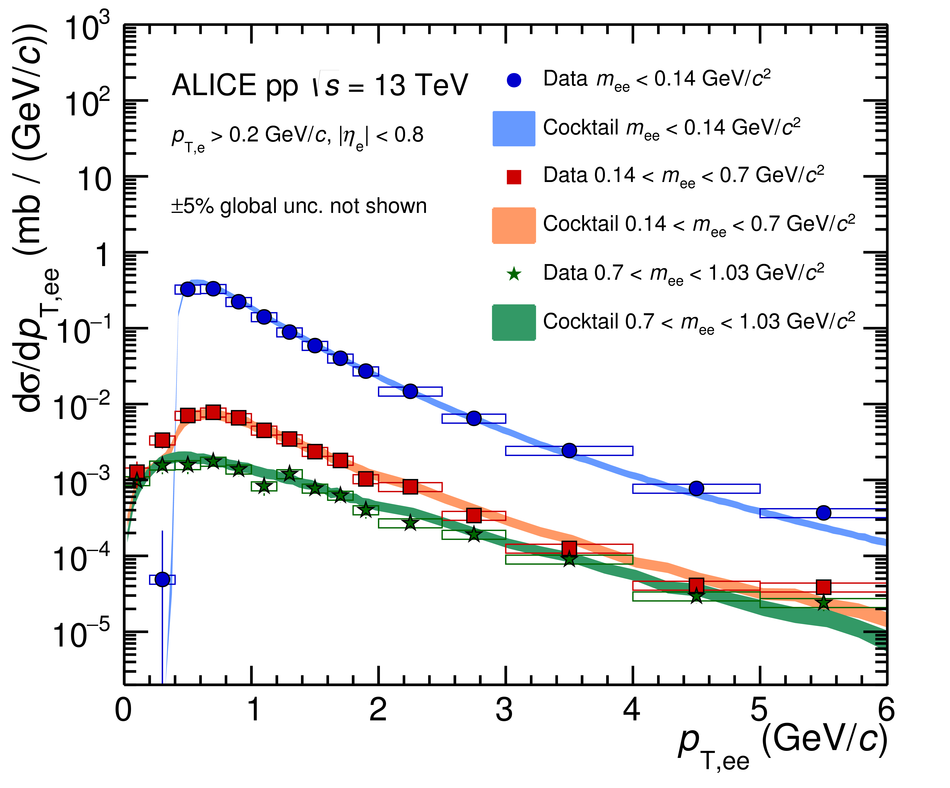
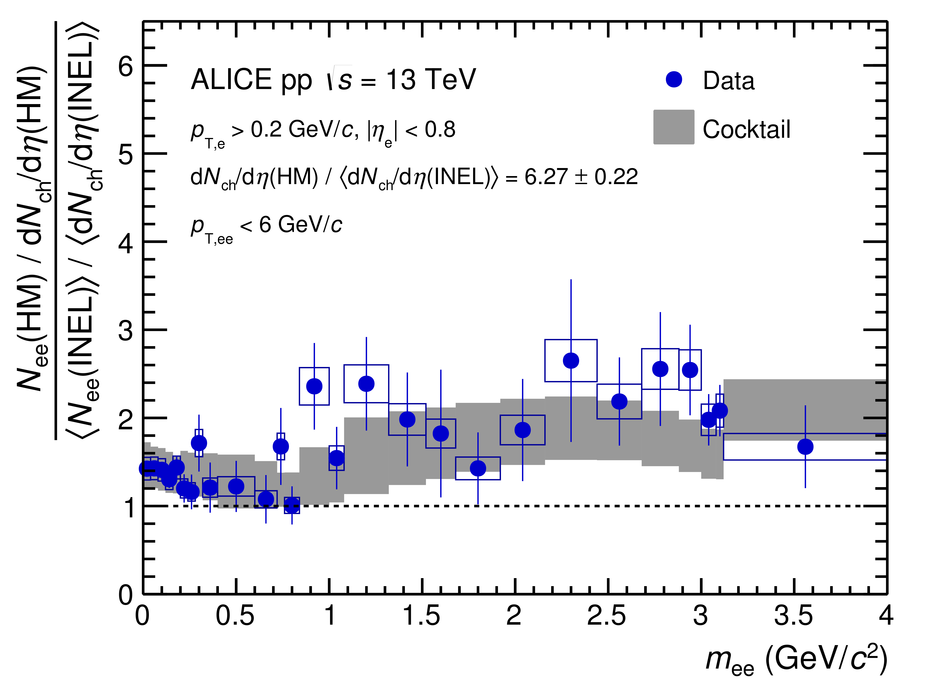
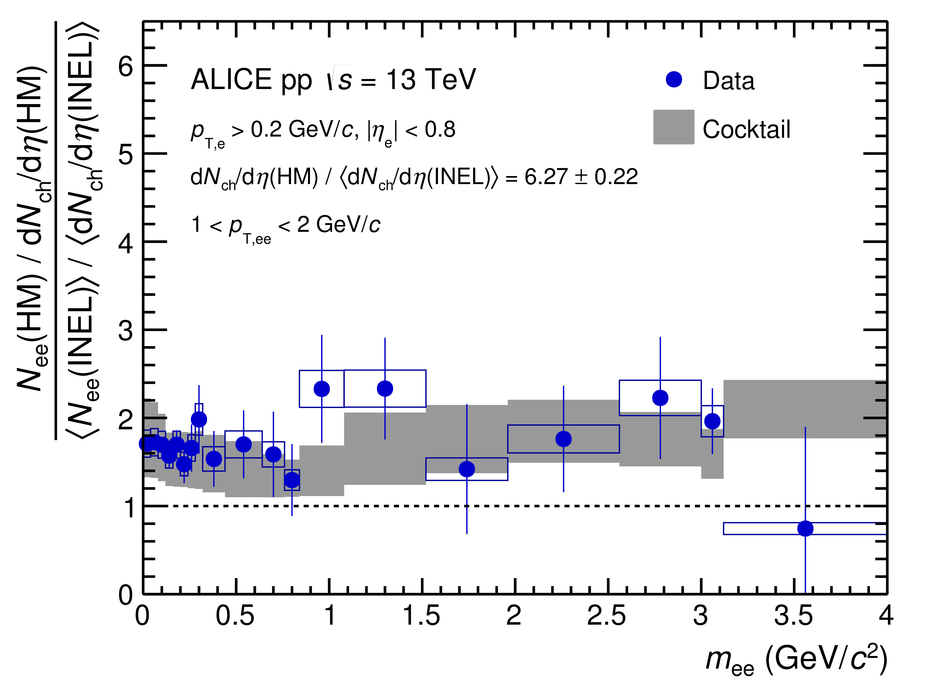
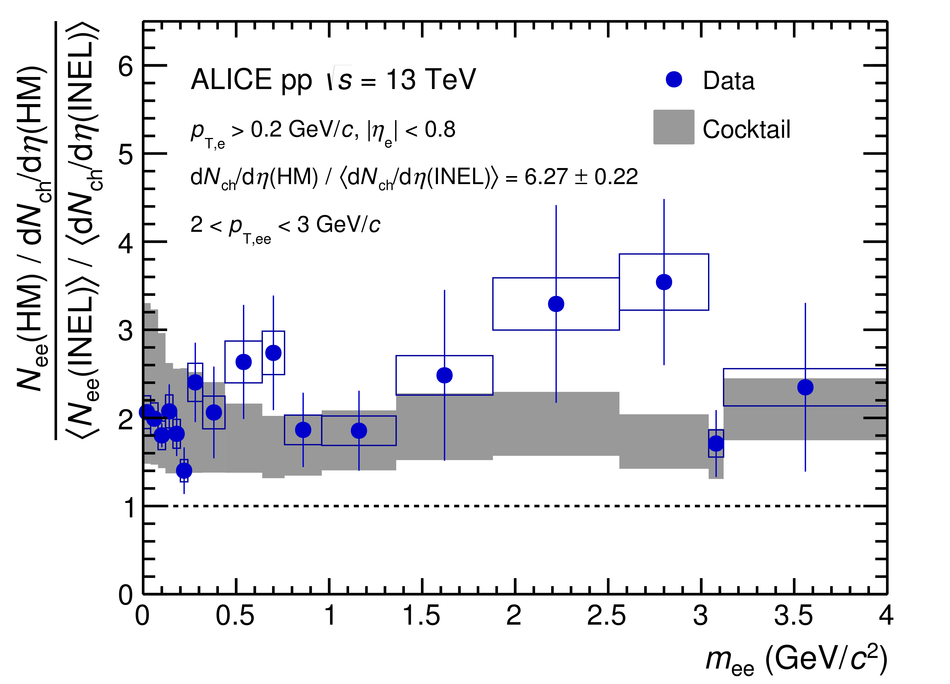
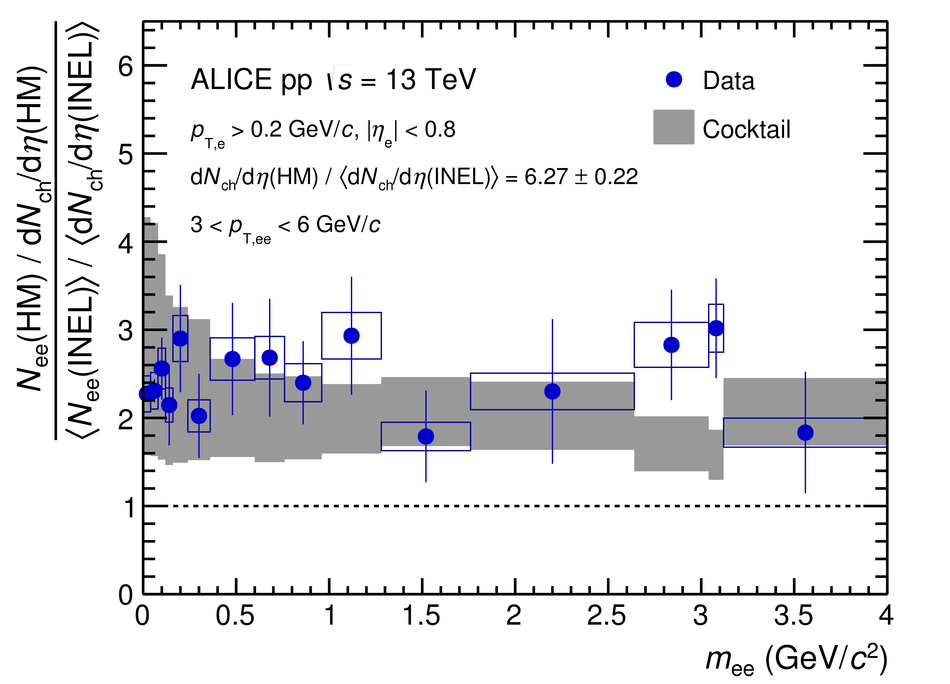
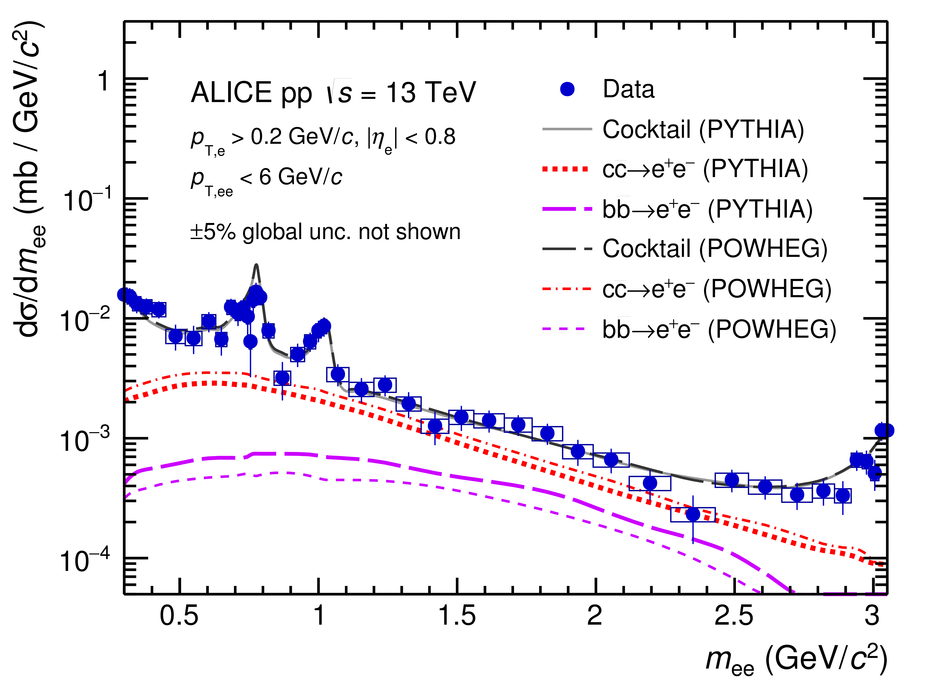
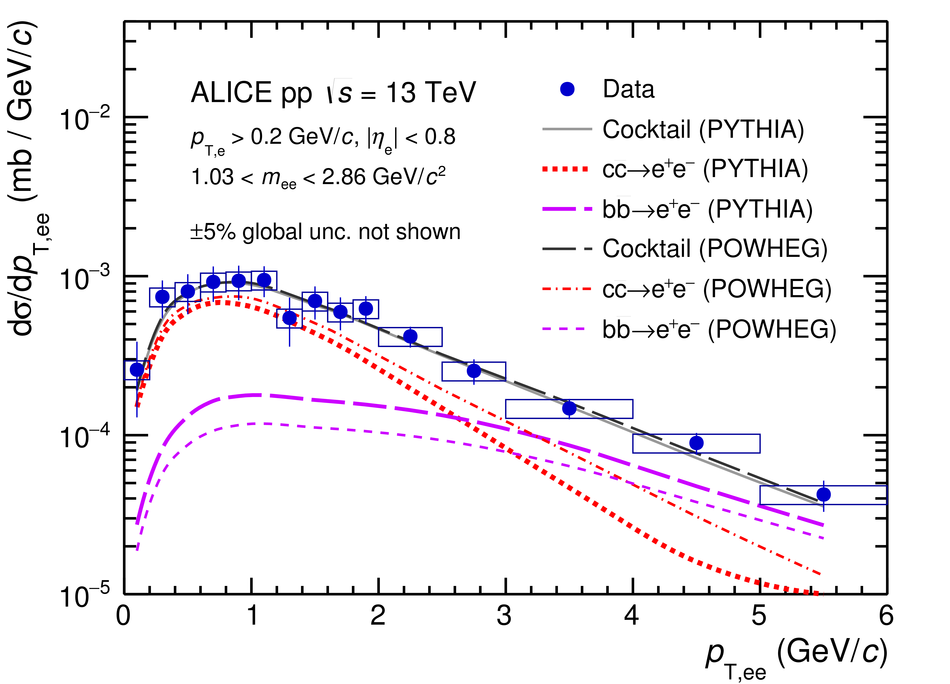
The measurement of dielectron production is presented as a function of invariant mass and transverse momentum ($p_{\rm T}$) at midrapidity ($|y_{\rm e}|<~0.8$) in proton-proton (pp) collisions at a centre-of-mass energy of $\sqrt{s}=13$ TeV. The contributions from light-hadron decays are calculated from their measured cross sections in pp collisions at $\sqrt{s}=7$ TeV or 13 TeV. The remaining continuum stems from correlated semileptonic decays of heavy-flavour hadrons. Fitting the data with templates from two different MC event generators, PYTHIA and POWHEG, the charm and beauty cross sections at midrapidity are extracted for the first time at this collision energy: ${\rm d}\sigma_{\rm c\bar{c}}/{\rm d}y|_{y=0}=974\pm138(\rm{stat.})\pm140(\rm{syst.})~\mu{\rm b}$ and ${\rm d}\sigma_{\rm b\bar{b}}/{\rm d}y|_{y=0}=79\pm14(\rm{stat.})\pm11(\rm{syst.})~\mu{\rm b}$ using PYTHIA simulations and ${\rm d}\sigma_{\rm c\bar{c}}/{\rm d}y|_{y=0}=1417\pm184(\rm{stat.})\pm204(\rm{syst.})~\mu{\rm b}$ and ${\rm d}\sigma_{\rm b\bar{b}}/{\rm d}y|_{y=0}=48\pm14(\rm{stat.})\pm7(\rm{syst.})~\mu{\rm b}$ for POWHEG. These values, whose uncertainties are fully correlated between the two generators, are consistent with extrapolations from lower energies. The different results obtained with POWHEG and PYTHIA imply different kinematic correlations of the heavy-quark pairs in these two generators. Furthermore, comparisons of dielectron spectra in inelastic events and in events collected with a trigger on high charged-particle multiplicities are presented in various $p_{\rm T}$ intervals. The differences are consistent with the already measured scaling of light-hadron and open-charm production at high charged-particle multiplicity as a function of $p_{\rm T}$. Upper limits for the contribution of virtual direct photons are extracted at 90% confidence level and found to be in agreement with pQCD calculations.
Phys. Lett. B 788 (2019) 505
HEP Data
e-Print: arXiv:1805.04407 | PDF | inSPIRE
CERN-EP-2018-122