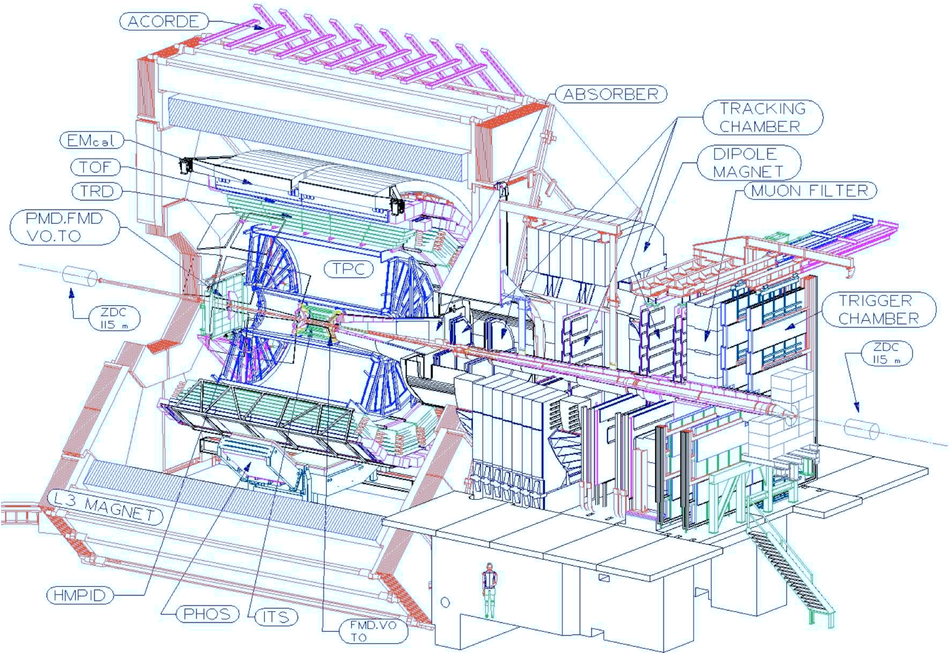
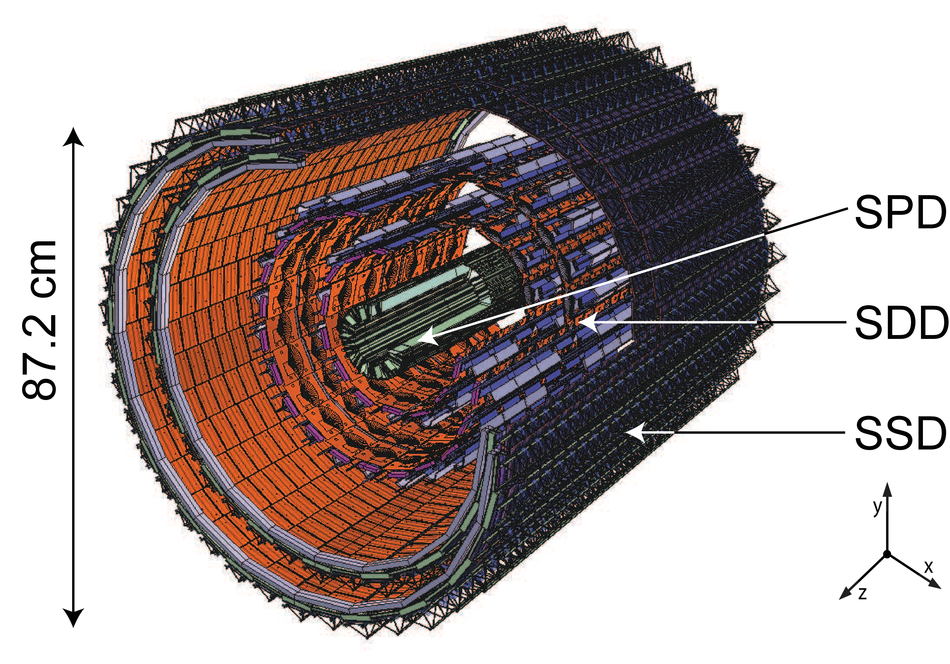
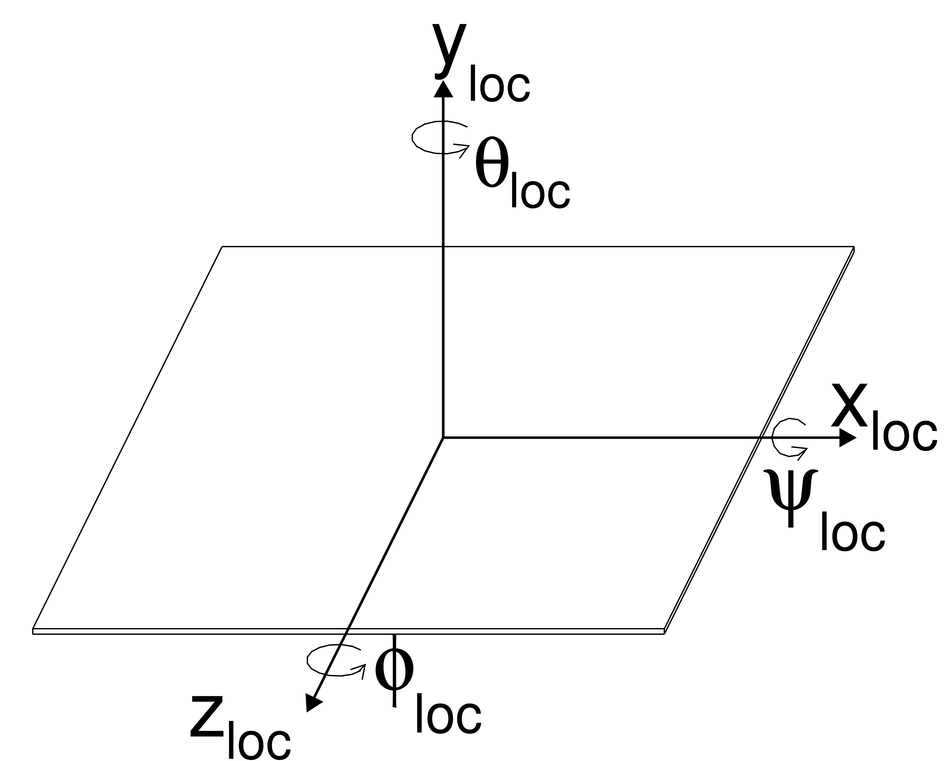
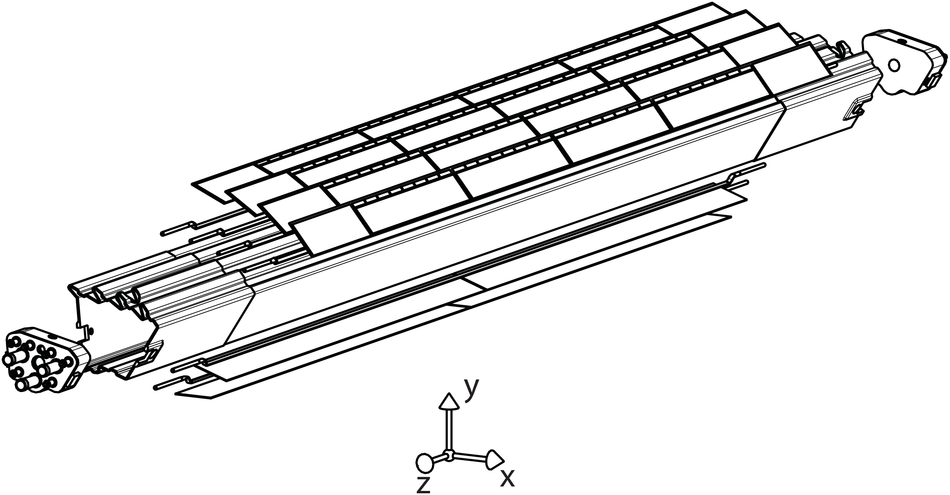
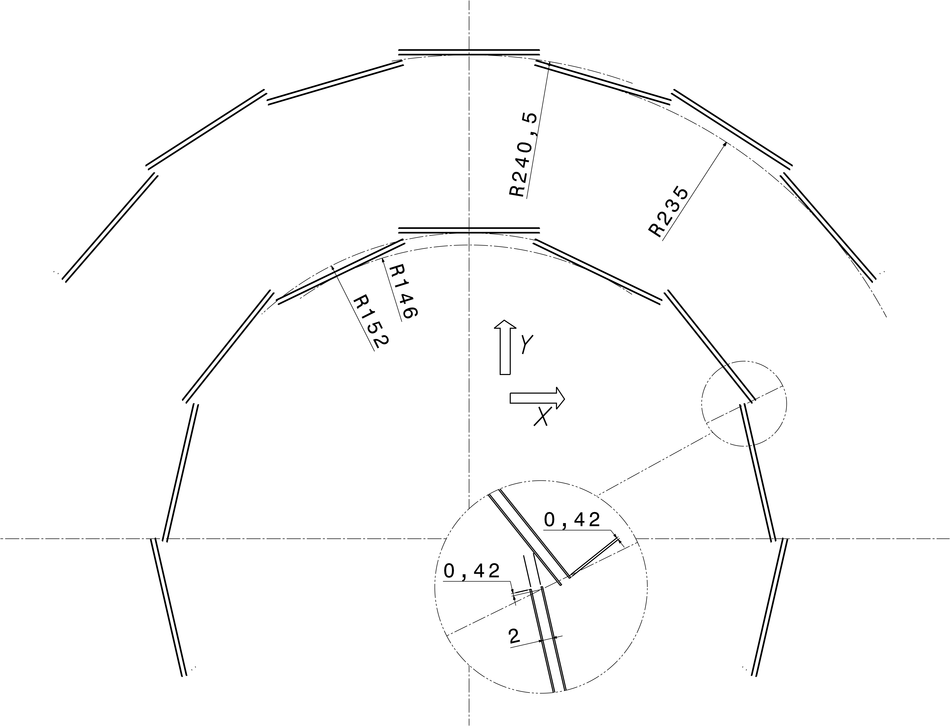
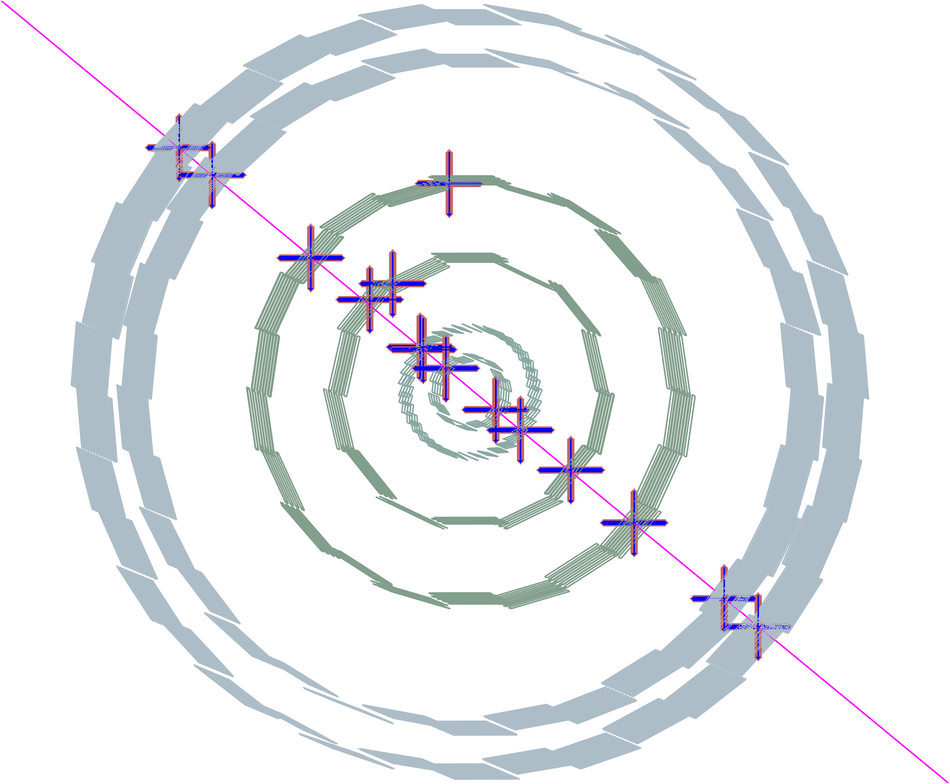
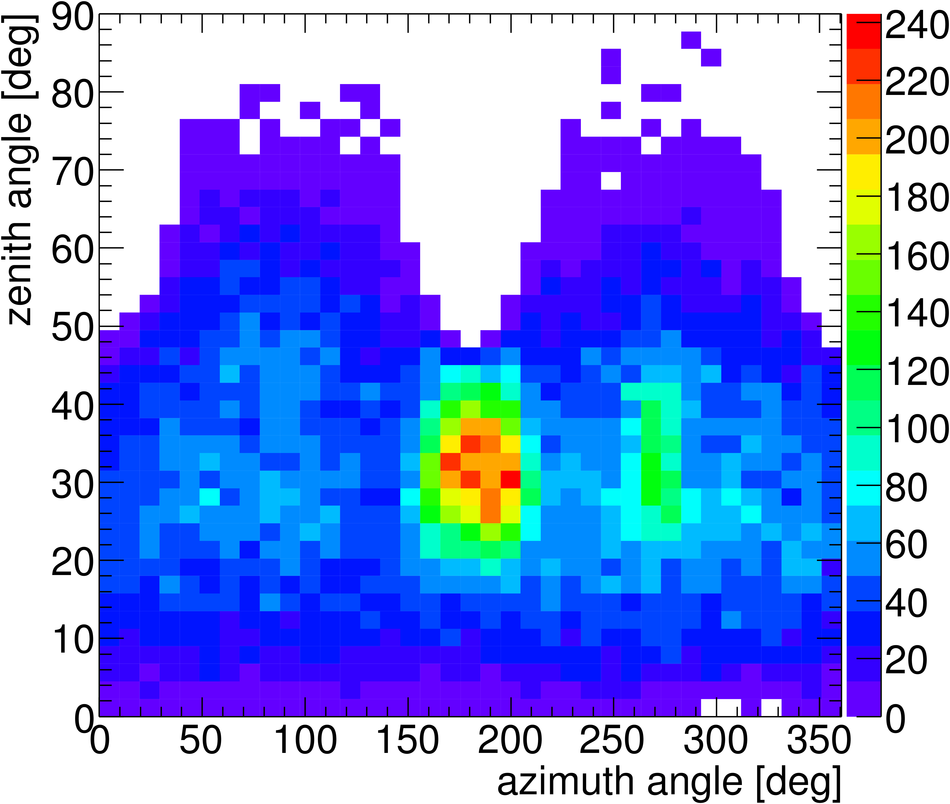
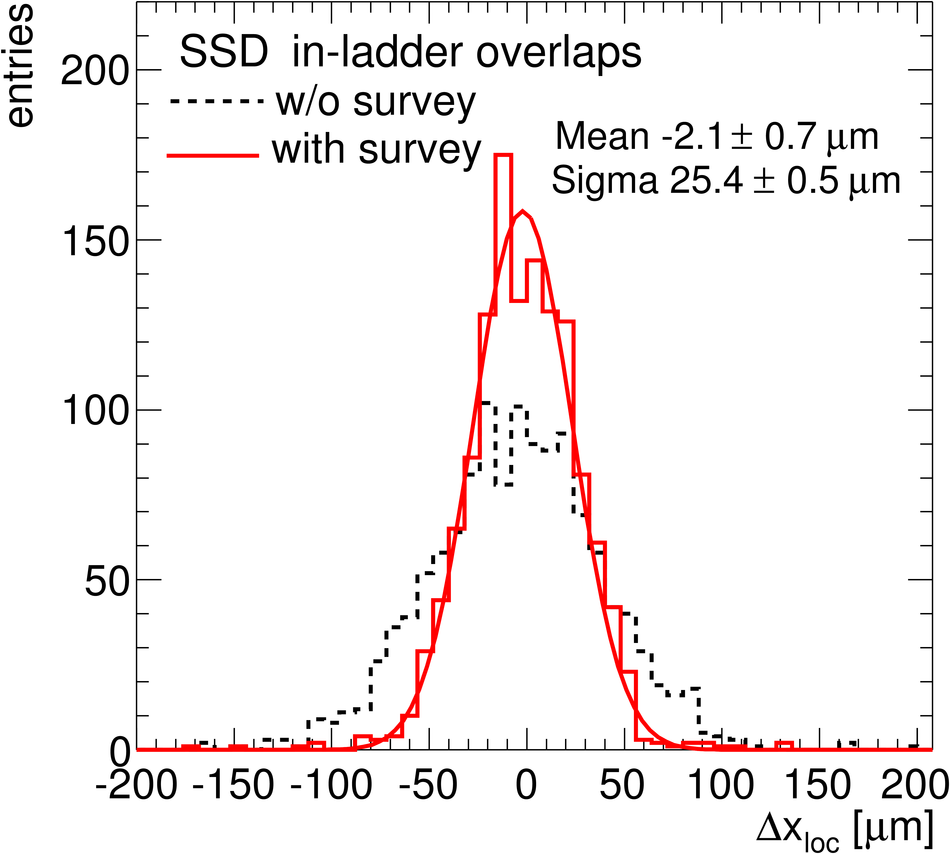
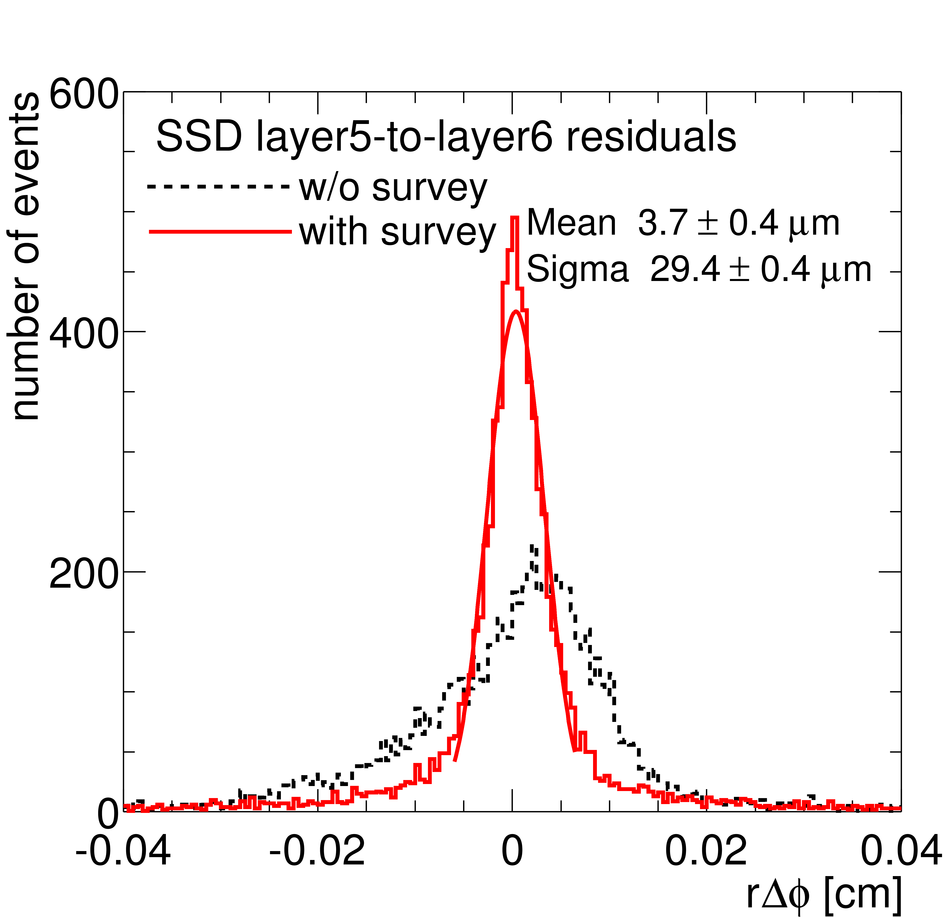
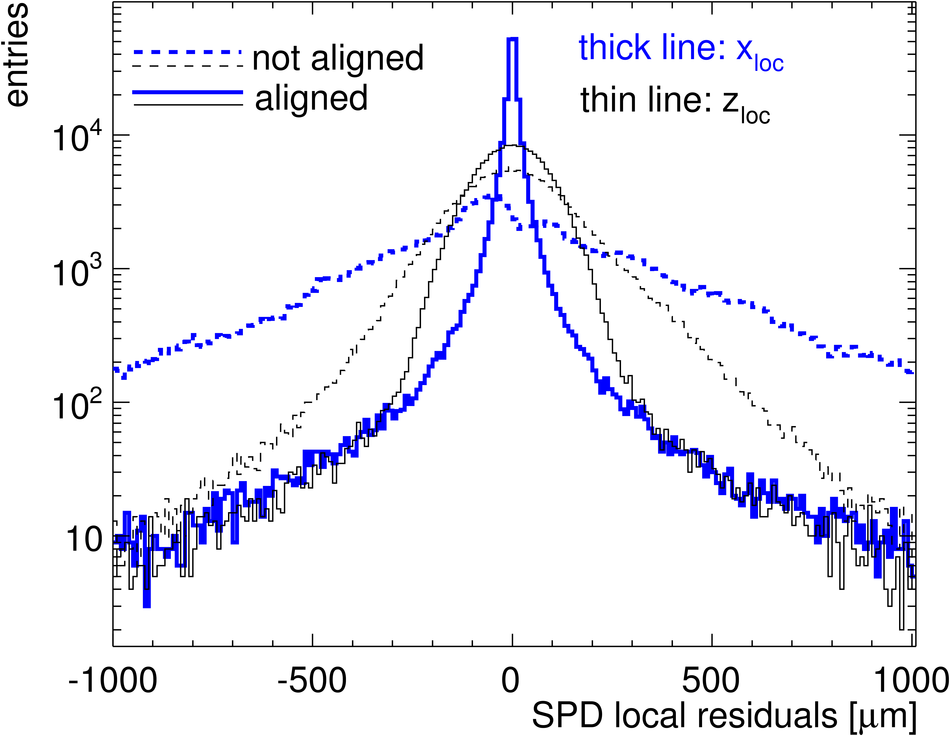
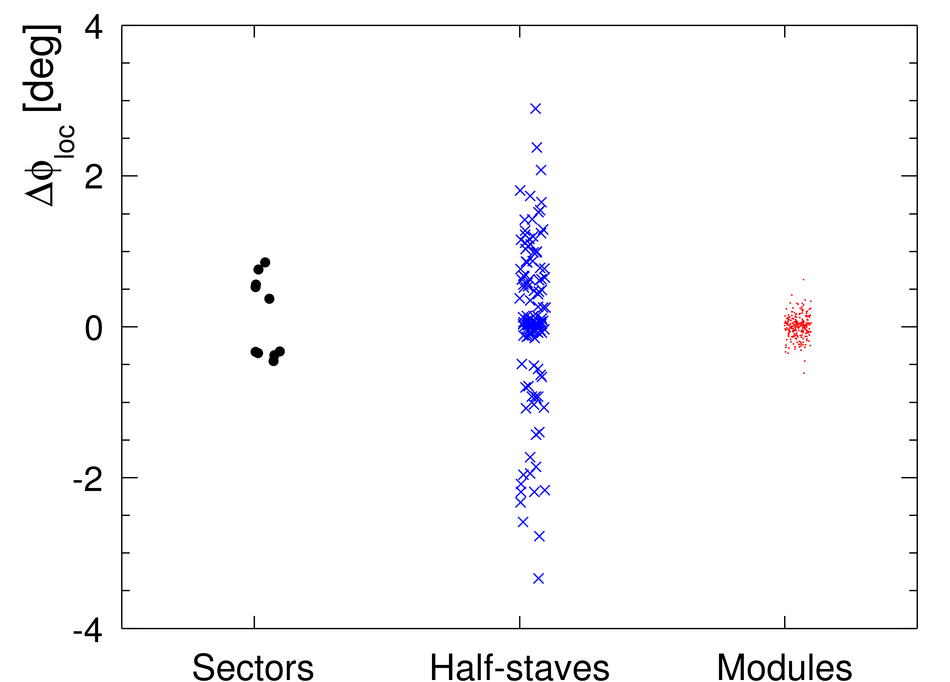
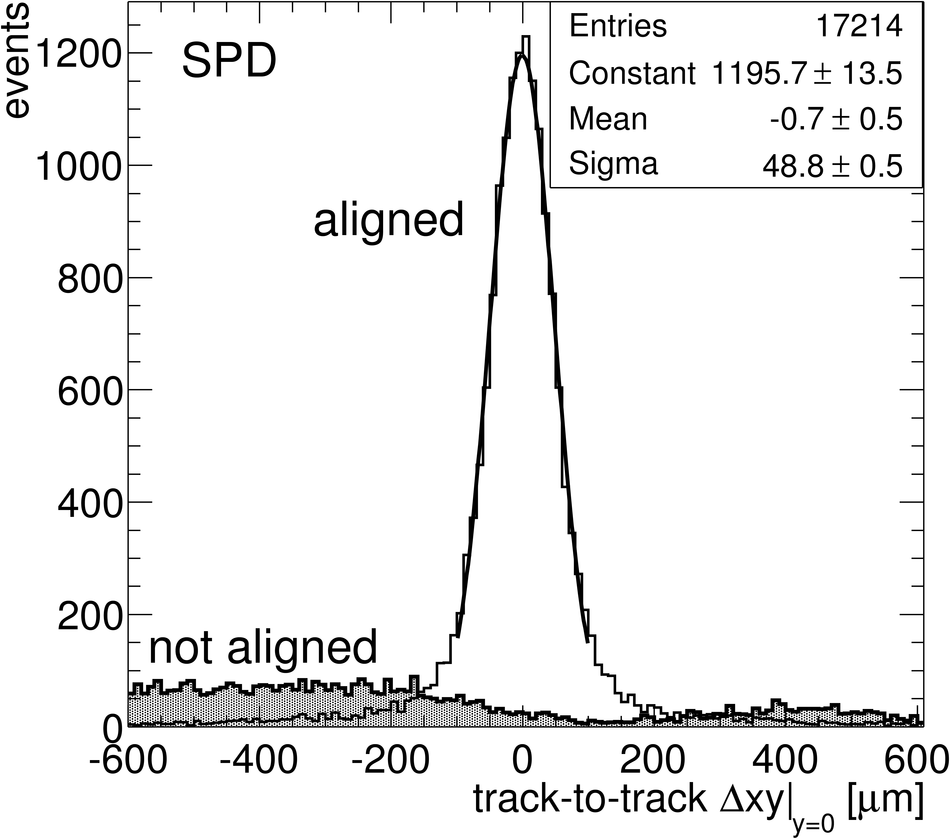
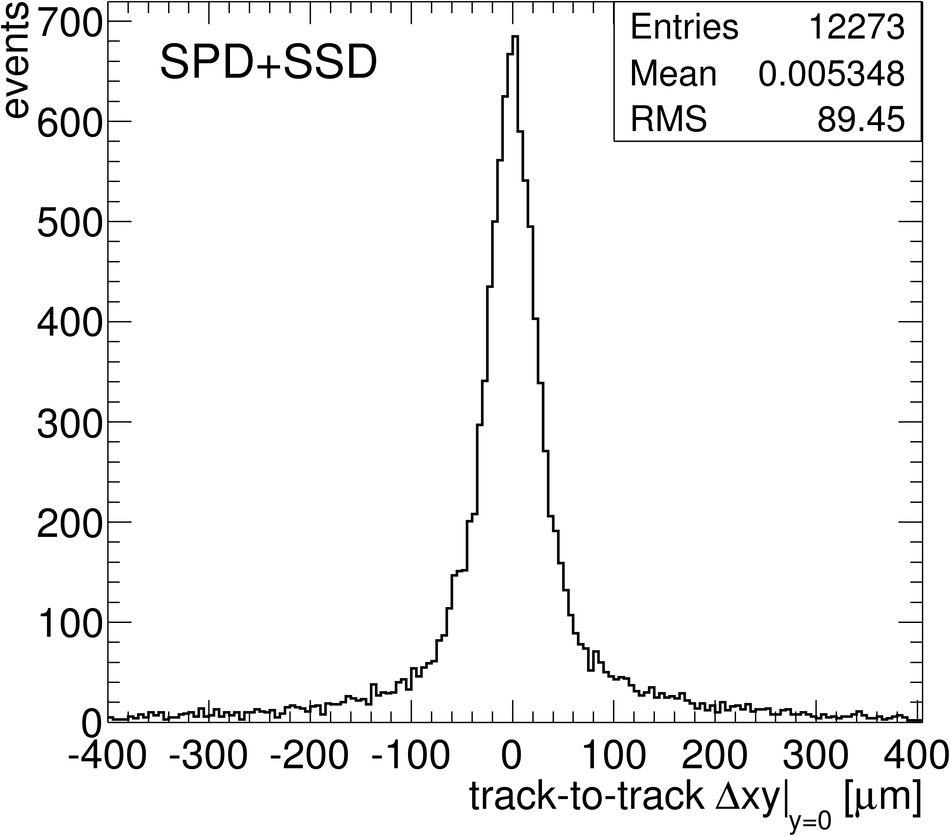
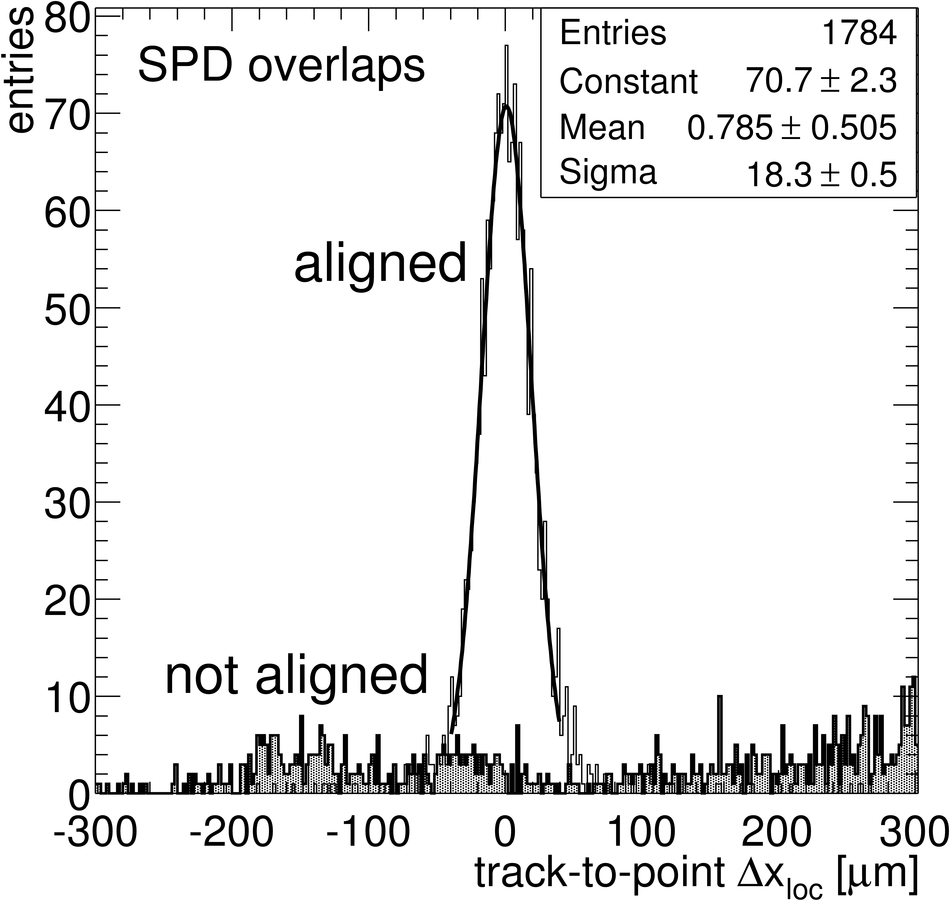
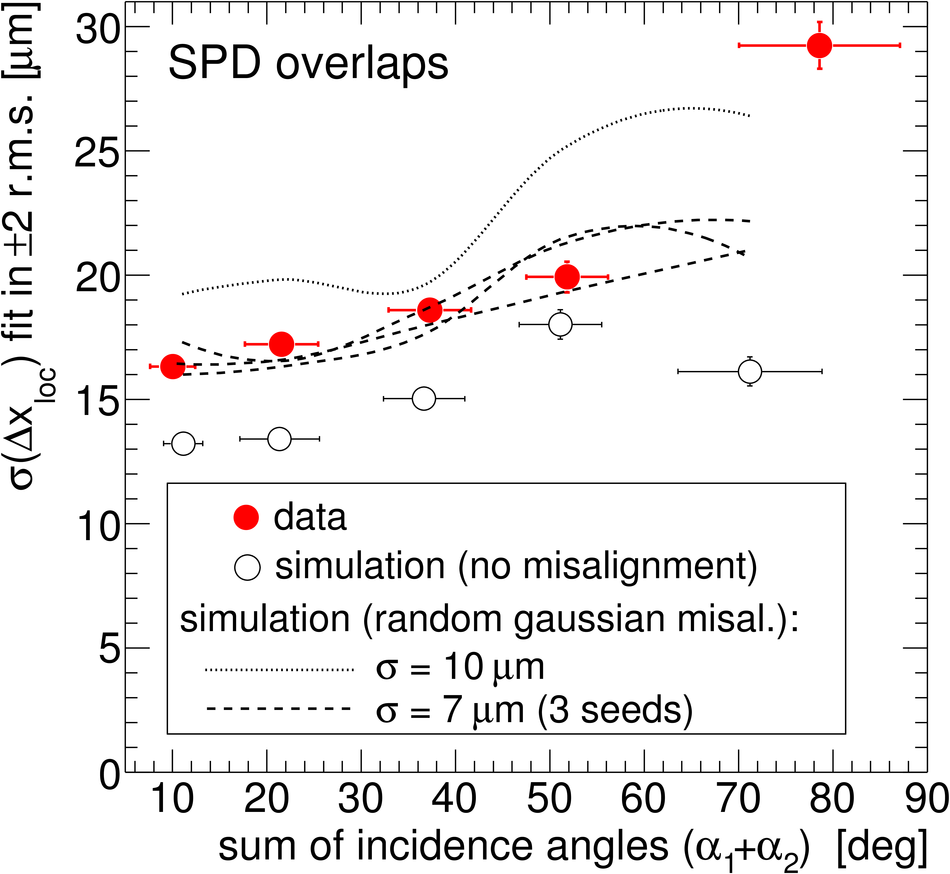
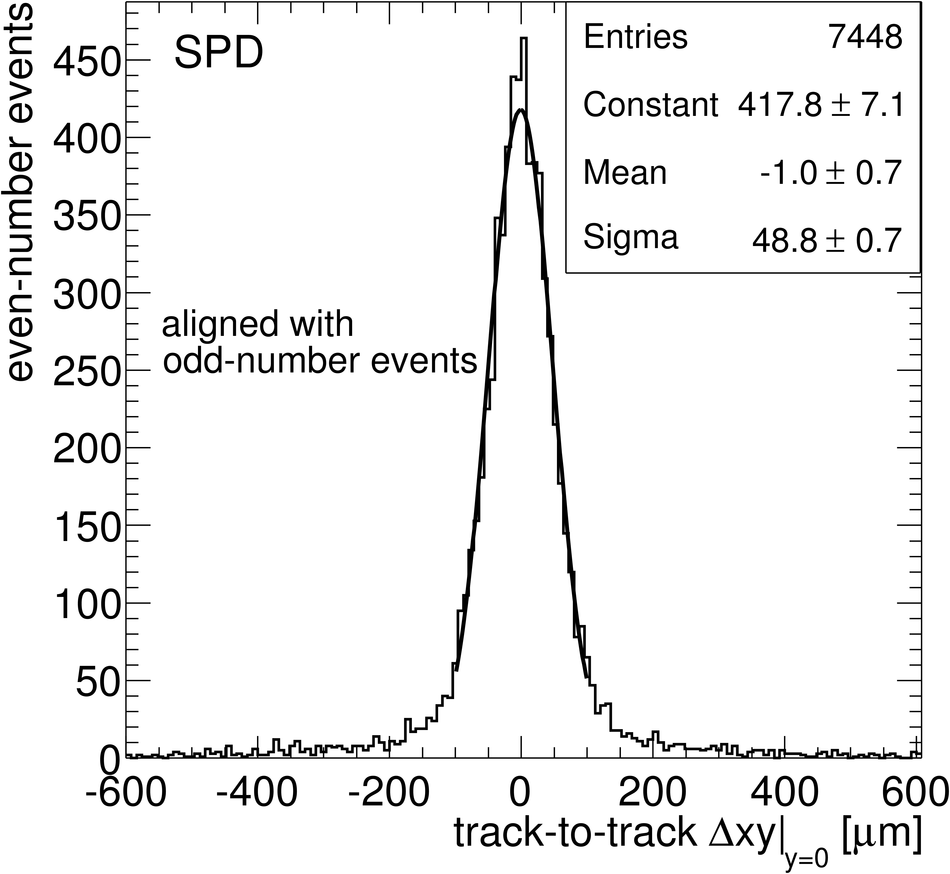
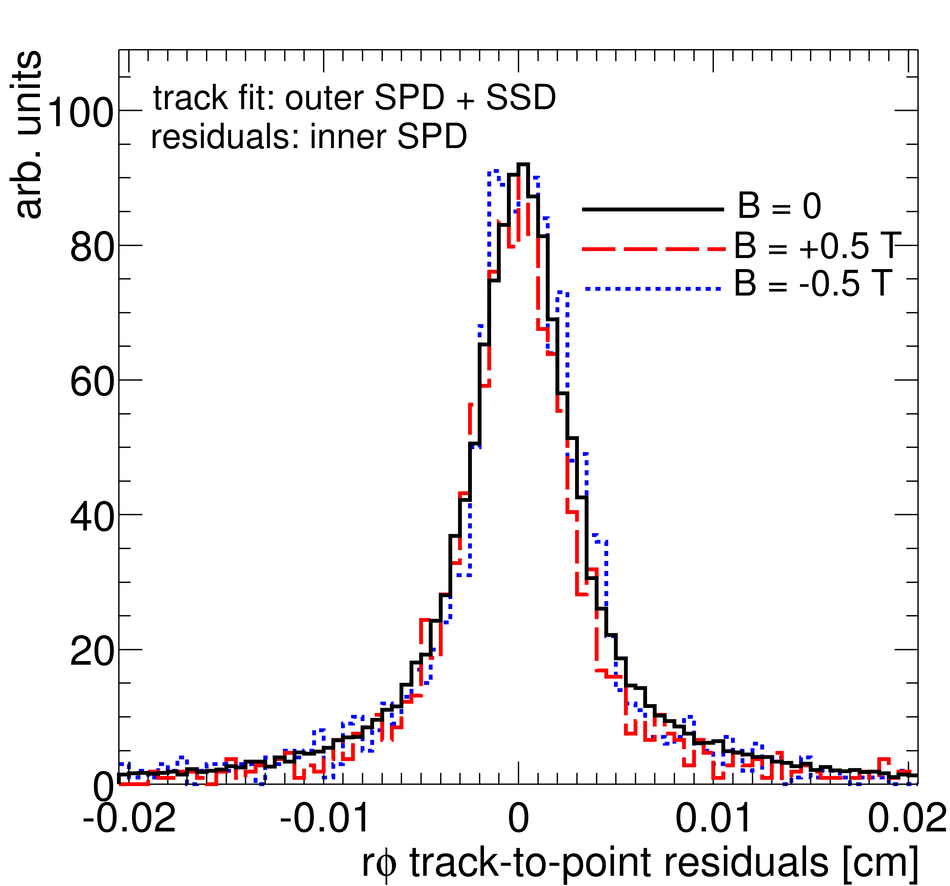
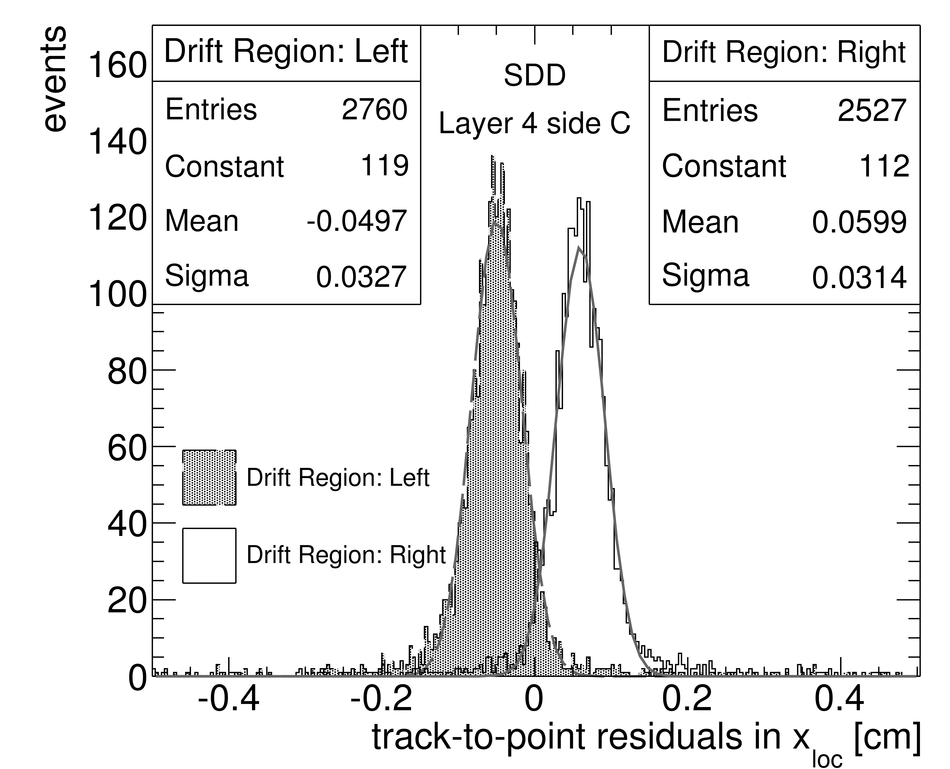
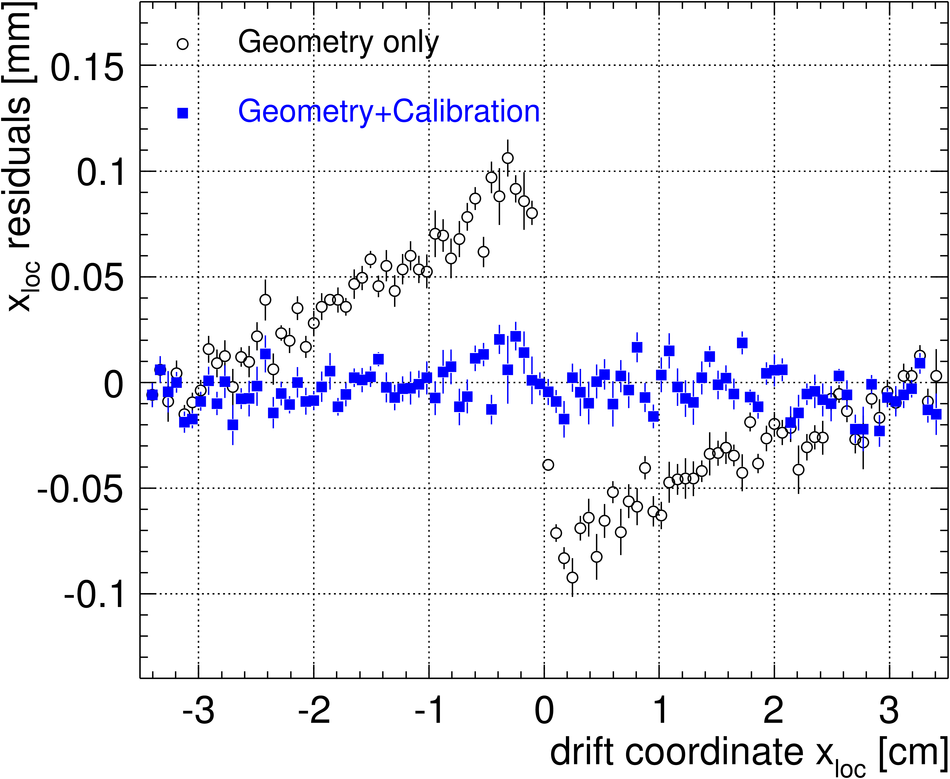
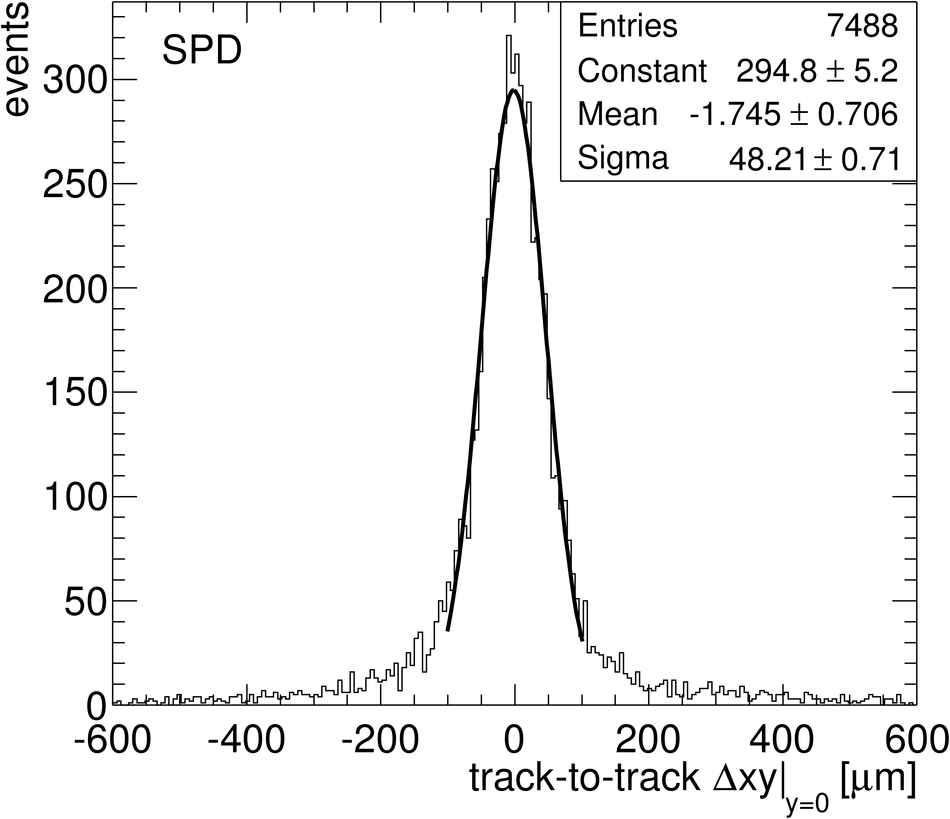
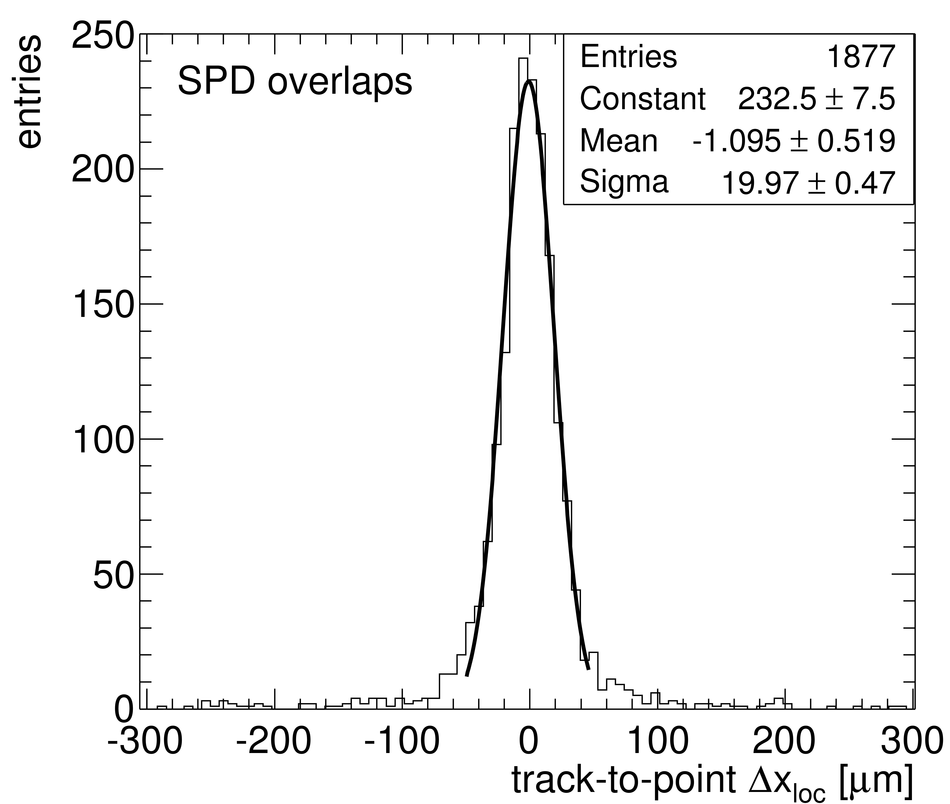
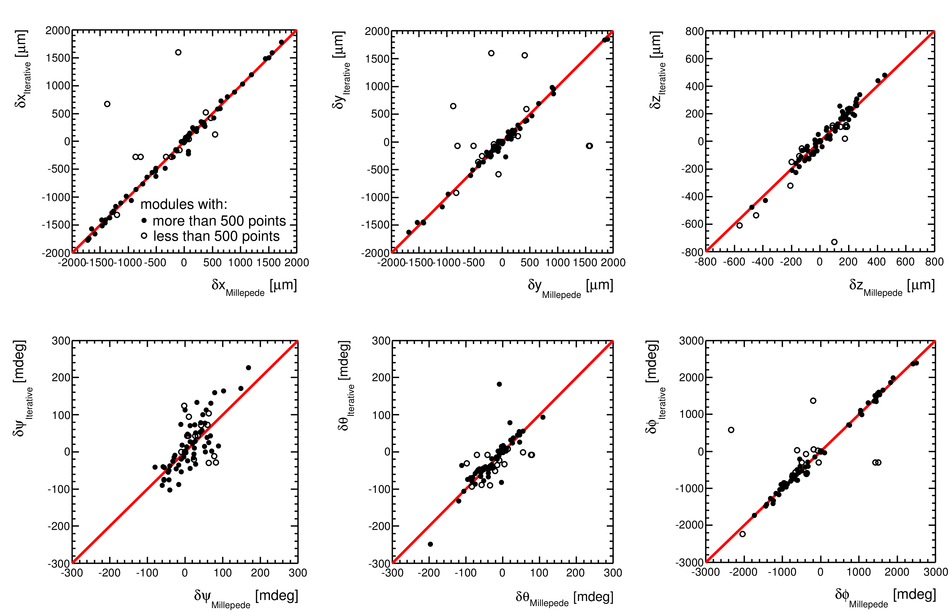
ALICE (A Large Ion Collider Experiment) is the LHC (Large Hadron Collider) experiment devoted to investigating the strongly interacting matter created in nucleus-nucleus collisions at the LHC energies. The ALICE ITS, Inner Tracking System, consists of six cylindrical layers of silicon detectors with three different technologies; in the outward direction: two layers of pixel detectors, two layers each of drift, and strip detectors. The number of parameters to be determined in the spatial alignment of the 2198 sensor modules of the ITS is about 13,000. The target alignment precision is well below 10 micron in some cases (pixels). The sources of alignment information include survey measurements, and the reconstructed tracks from cosmic rays and from proton-proton collisions. The main track-based alignment method uses the Millepede global approach. An iterative local method was developed and used as well. We present the results obtained for the ITS alignment using about 10$^5$ charged tracks from cosmic rays that have been collected during summer 2008, with the ALICE solenoidal magnet switched off.
JINST 5 (2010) P03003
e-Print: arXiv:1001.0502 | PDF | inSPIRE
CERN Record