Distribution of the test statistic $t$ for the direct-photon excess $R_\gamma$ in 0.9 $< p_T < $ 2.1 GeV/$c$ in the 0-20%, 20-40% $\&$ 40-80% classes for pseudo-experiments performed under the null hypothesis that there is no direct photon excess The model of the measurement of the direct-photon excess $R_\gamma$ is based on the type A, B, C systematic uncertainties. It is assumed that the actual measurement can be described by certain values of nuisance parameters $\varepsilon_B$ and $\varepsilon_C$. Our limited knowledge of the actual values of these parameters is parameterized by Gaussian distributions with mean $\mu=0$ and standard deviations $\sigma = 1$ ($N_{0,1}$), i.e., $\varepsilon_B$ and $\varepsilon_C$ are deviations from a central value in units of the standard deviation. We now perform pseudo-experiments by randomly drawing $\varepsilon_B$ and $\varepsilon_C$ from $N_{0,1}$. Suppose that $R_0$ is the true value of the photon excess. The actual measurement in the $p_T$ interval $i$ will now fluctuate around$R_{\mathrm{mod},i} = R_0 (1 + \varepsilon_B \sigma_{B,i,rel}) (1 + \varepsilon_C \sigma_{C,rel})$as given by the statistical and type A systematic uncertainties added in quadrature. The uncertainties $\sigma_{B,i,rel}$ are the relative systematic type B uncertainties and $\sigma_{C,rel}$ is the relative normalization uncertainty. A given pseudo data point in the $p_T$ interval $i$ is denoted by $R_{pd,i}$. The test statistic is defined by the following sum over pseudo-measurements in the different $p_T$ intervals $i$:$t = \sum_{i=1}^{n_\mathrm{data\;points}} \left( \frac{R_{pd,i}-R_0}{\sigma_{0,i}}\right)^2\quad \mathrm{where} \quad R_{0} = 1,\;\sigma_{0,i} = R_{\mathrm{mod},i} \sigma_{i,stat+A,rel} $. The line indicates the value $t_\mathrm{data}$ of the test statistic for the real data (Photon Conversion Method and PHOS combined). The $p\mbox{-values}$ (number of pseudo-experiments with $t>t_\mathrm{data}$ divided by the total number of pseudo-experiments) is indicated in the plot. The $p\mbox{-value}$ is expressed in terms of the significance in units of the standard deviation of a Gaussian ($a\cdot\sigma$) by solving $2 \int_{a}^{\infty} N_{0,1}(x) \, \mathrm{d} x = p\mbox{-value} $ for $a$ (two-tailed test)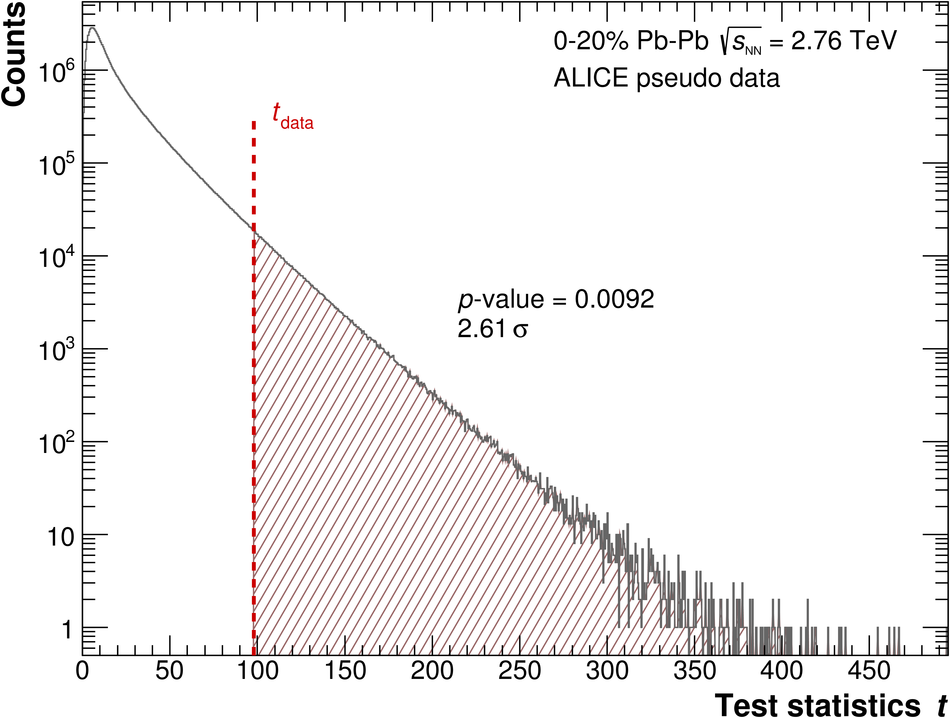