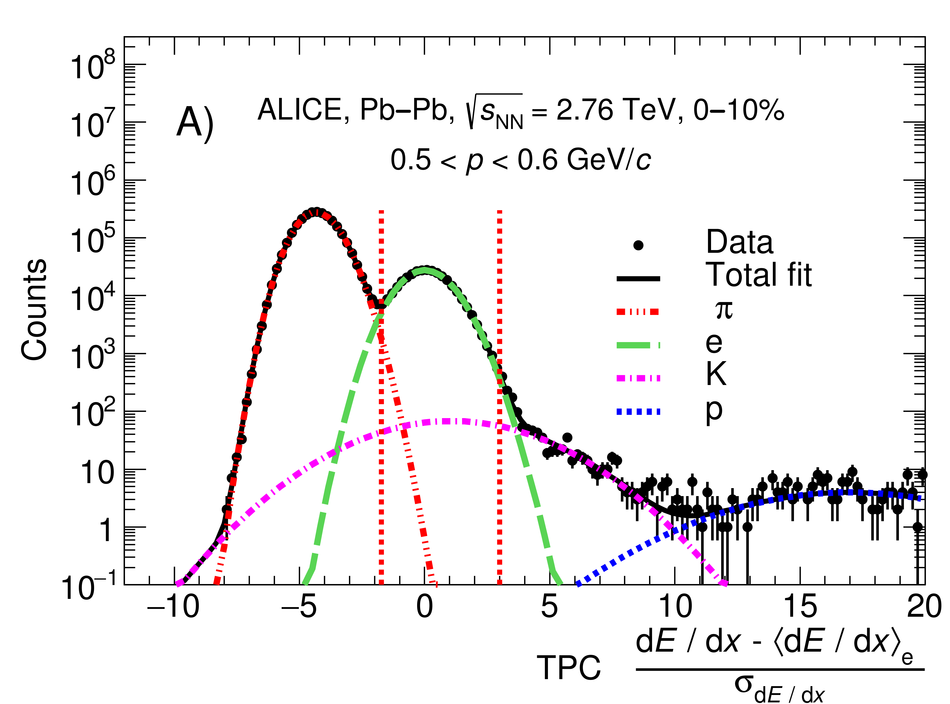
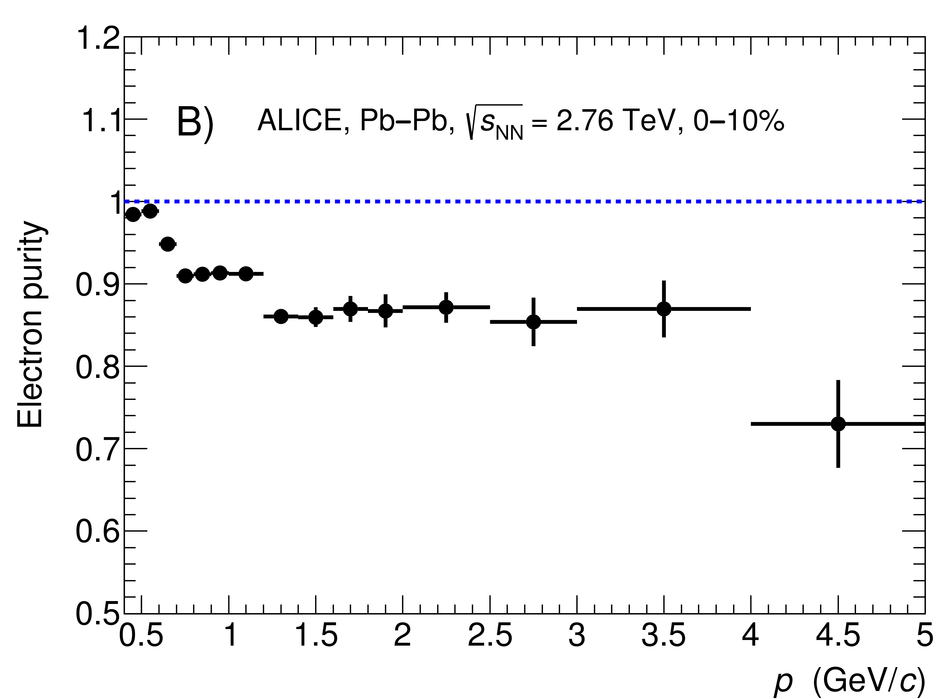
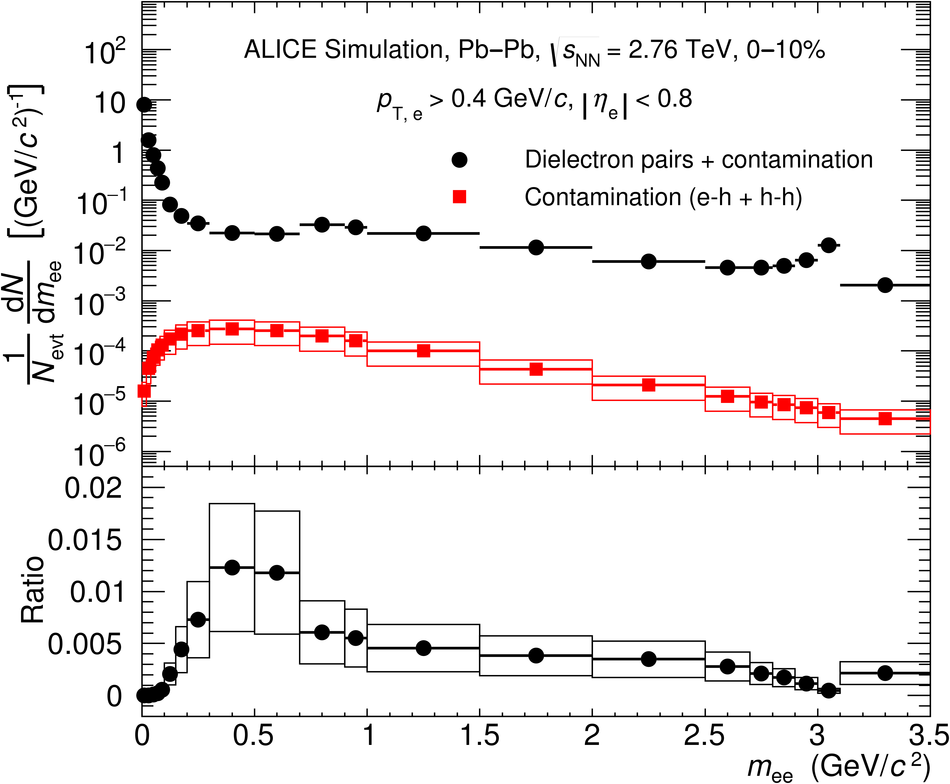
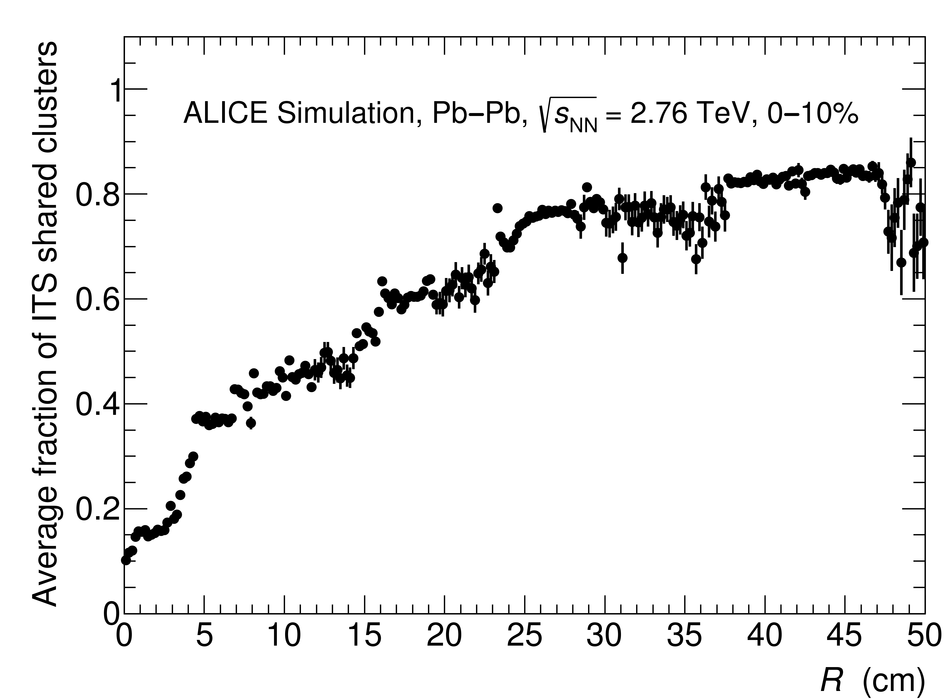
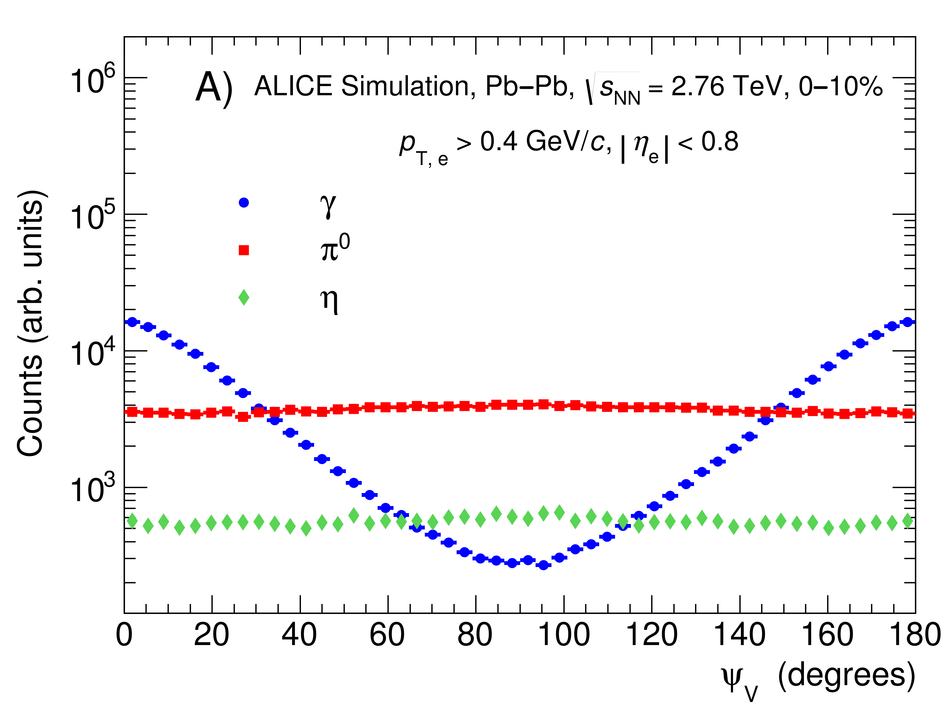
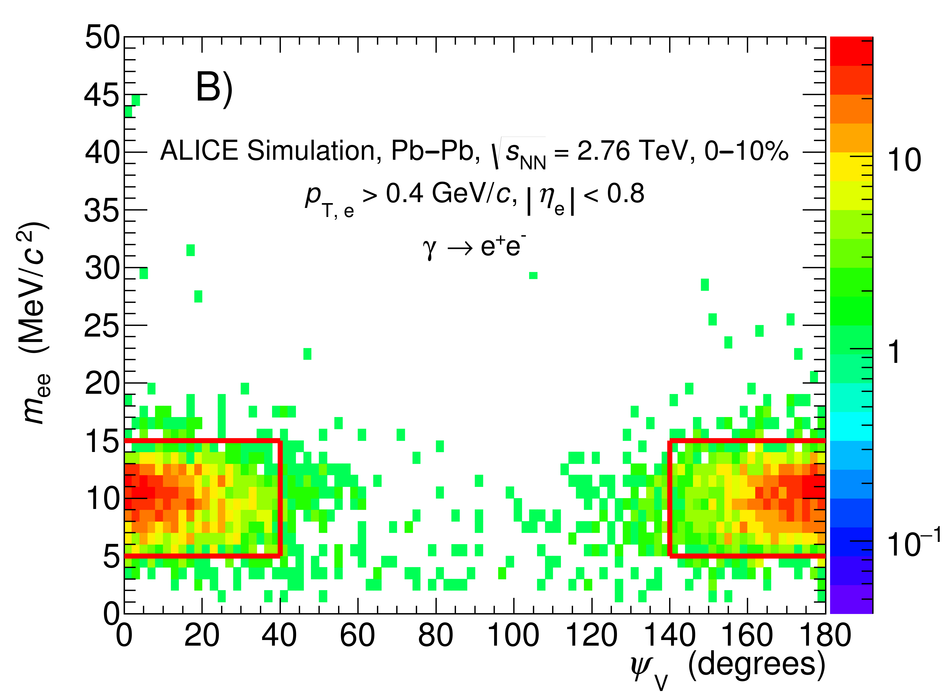
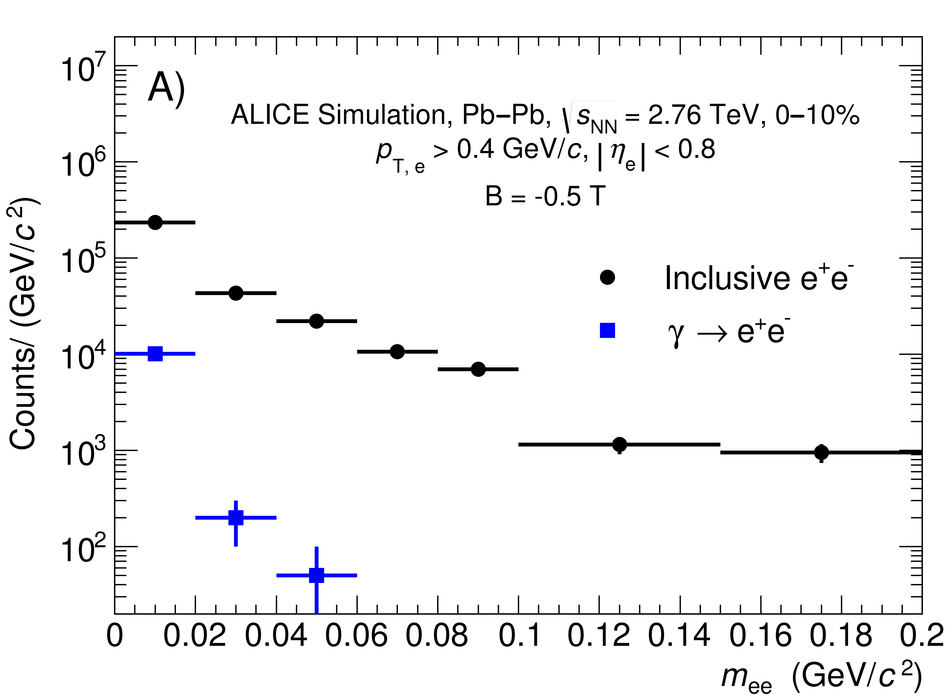
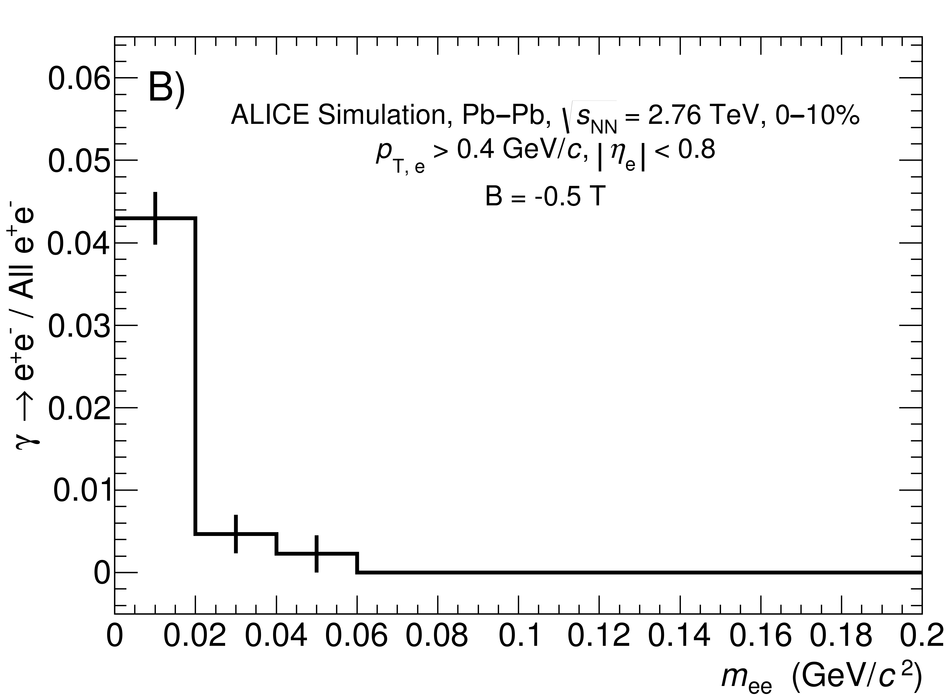
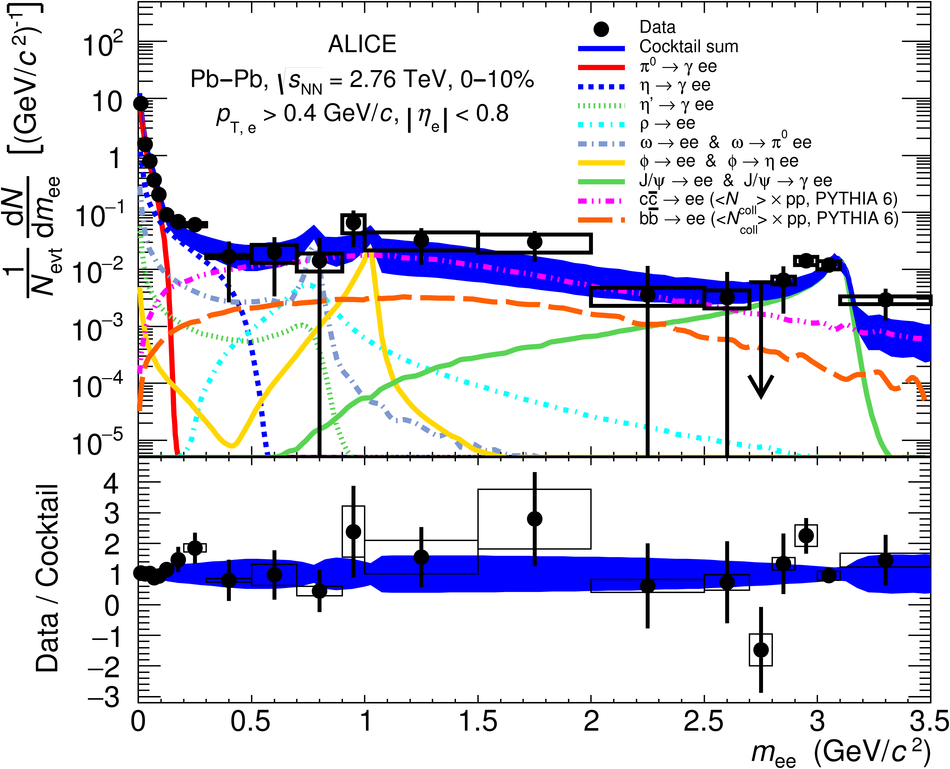
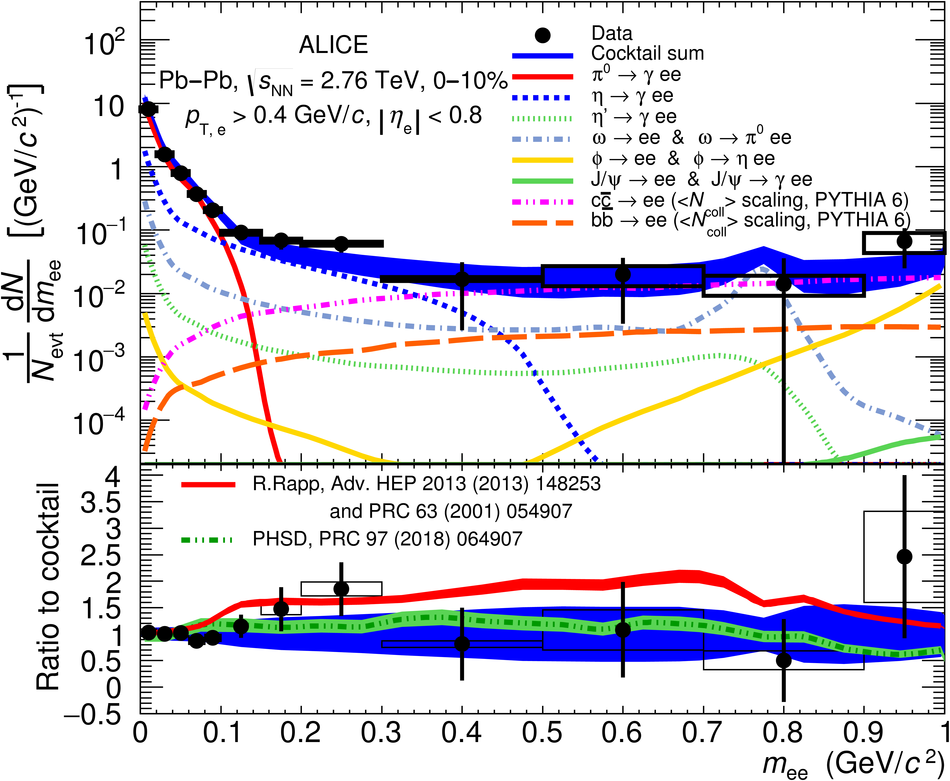
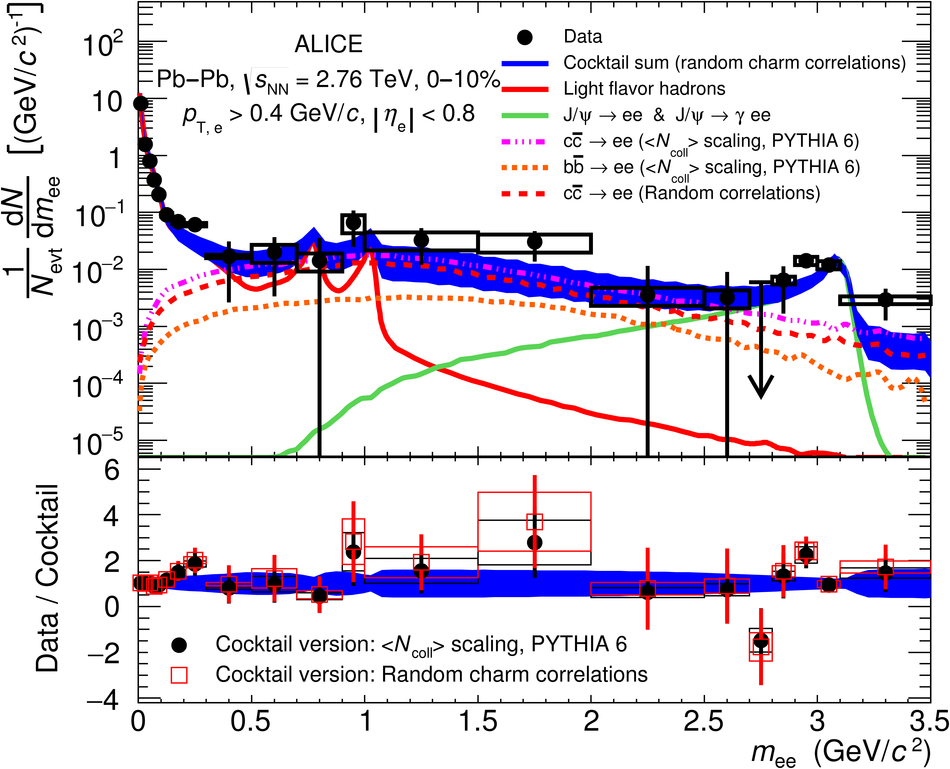
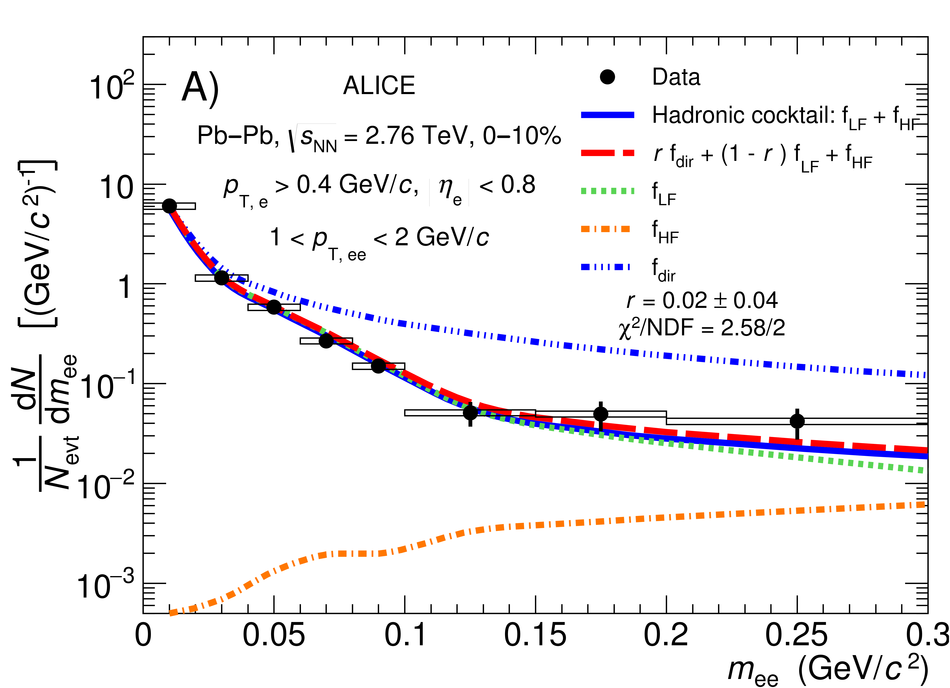
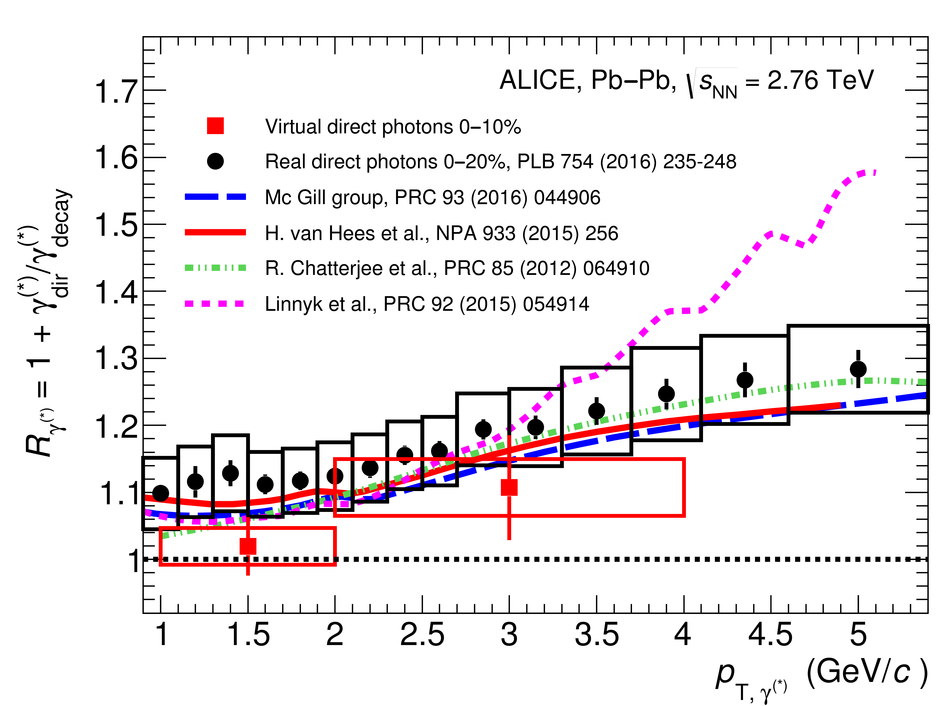
The first measurement of dielectron ($\mathrm{e}^{+}\mathrm{e}^{-}$) production in central (0$-$10$\%$) Pb-Pb collisions at $\mathbf{\sqrt{{\textit{s}}_{\mathrm{NN}}}}$ = 2.76 TeV at the LHC is presented. The dielectron invariant-mass spectrum is compared to the expected contributions from hadron decays in the invariant-mass range $0 <~ m_{\mathrm{ee}}<~3.5\ \mathrm{GeV}/\textit{c}^{2}$. The ratio of data and the cocktail of hadronic contributions without vacuum $\rho^{0}$ is measured in the invariant-mass range $0.15 <~ m_{\mathrm{ee}}<~0.7\ \mathrm{GeV}/\textit{c}^{2}$, where an excess of dielectrons is observed in other experiments, and its value is $1.40 \pm 0.28\ (\mathrm{stat.}) \pm 0.08\ (\mathrm{syst.}) \pm 0.27\ (\mathrm{cocktail})$. The dielectron spectrum measured in the invariant mass range $0 <~ m_{\mathrm{ee}}<~1\ \mathrm{GeV}/\textit{c}^{2}$ is consistent with the predictions from two theoretical model calculations that include thermal dielectron production from both partonic and hadronic phases with in-medium broadened $\rho^{0}$ meson. The fraction of direct virtual photons over inclusive virtual photons is extracted for dielectron pairs with invariant mass $0.1 <~ m_{\mathrm{ee}}<~0.3\ \mathrm{GeV}/\textit{c}^{2}$, and in the transverse-momentum intervals $1<~p_{\mathrm{T}, \mathrm{ee}}<~2\ \mathrm{GeV}/\textit{c}$ and $2<~p_{\mathrm{T}, \mathrm{ee}}<~4\ \mathrm{GeV}/\textit{c}$. The measured fraction of virtual direct photons is consistent with the measurement of real direct photons by ALICE and with the expectations from previous dielectron measurements at RHIC within the experimental uncertainties.
Phys. Rev. C 99, 024002
HEP Data
e-Print: arXiv:1807.00923 | PDF | inSPIRE