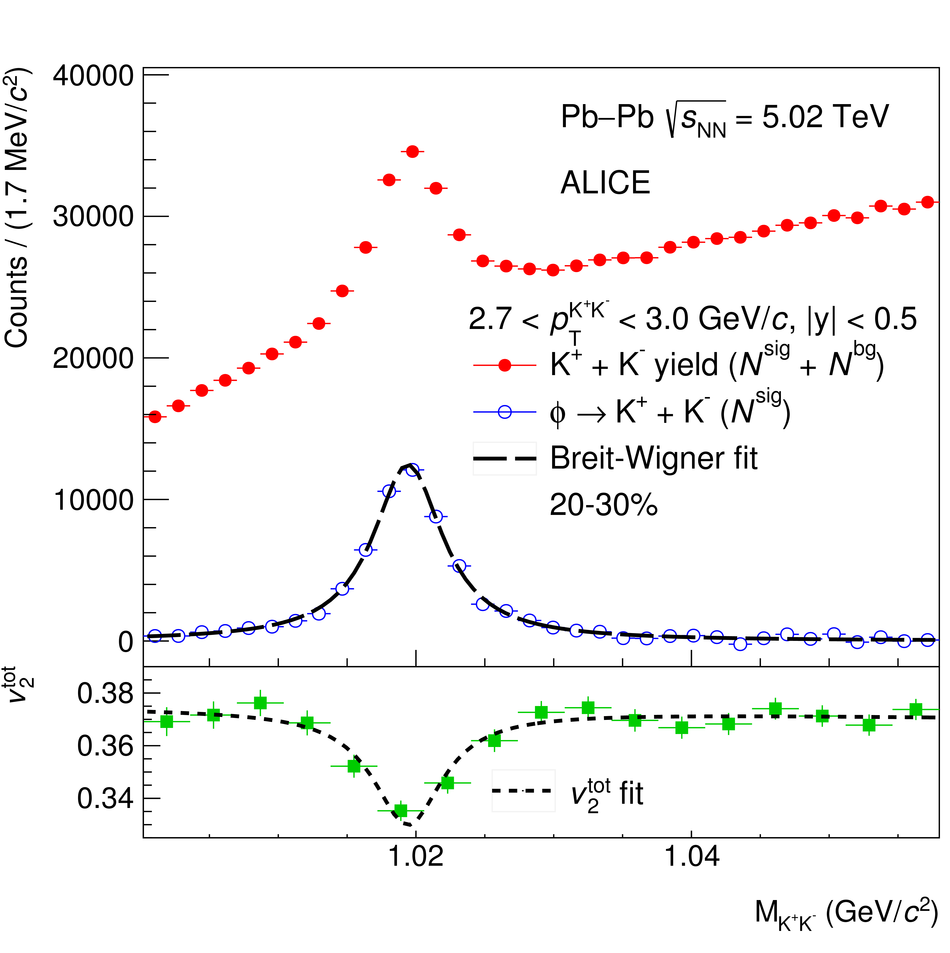
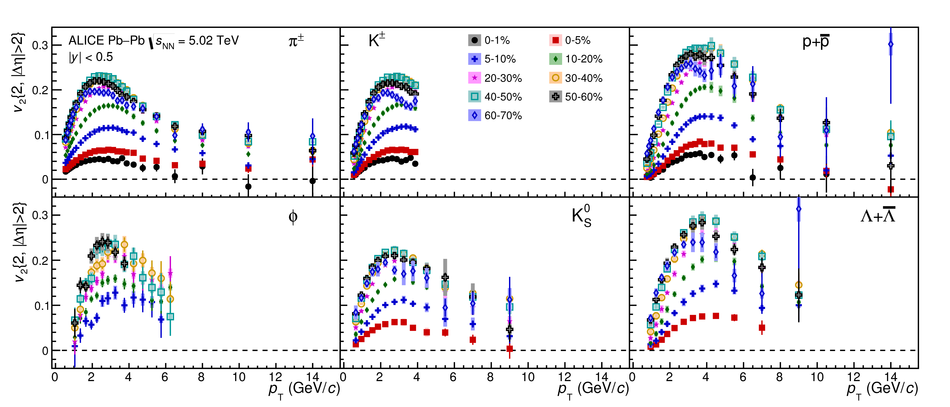
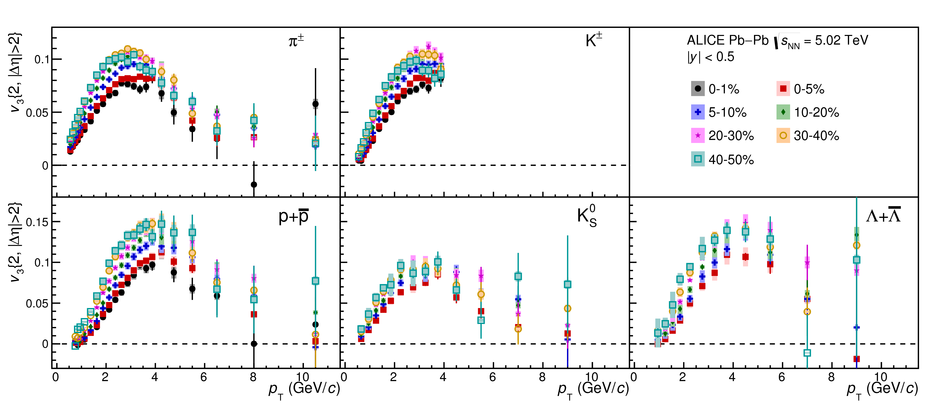
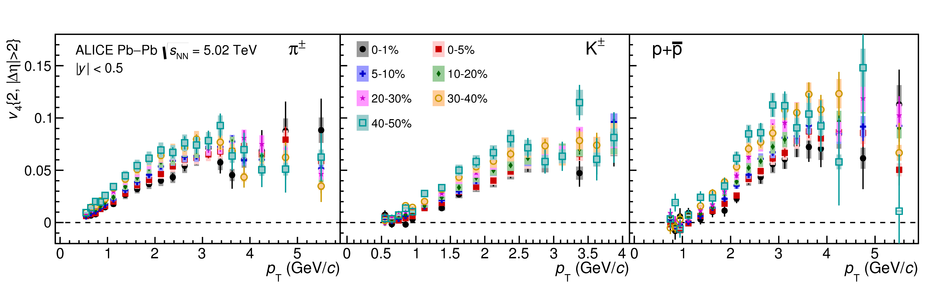
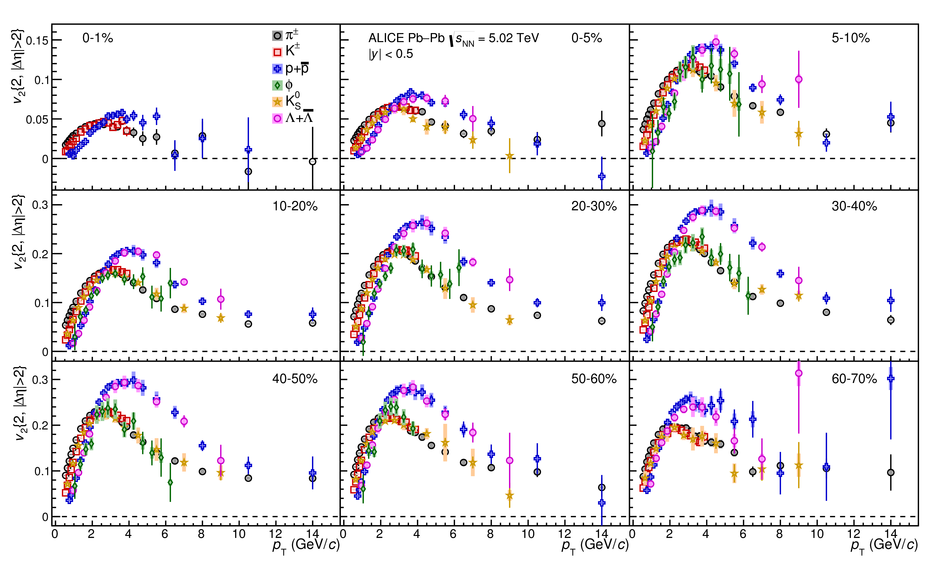
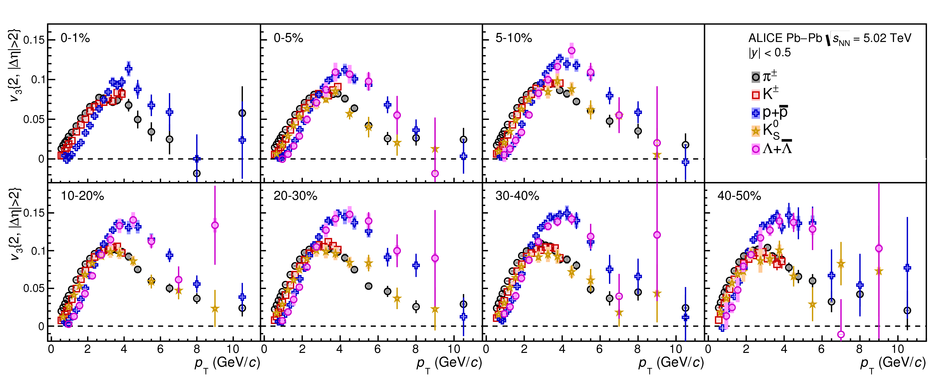
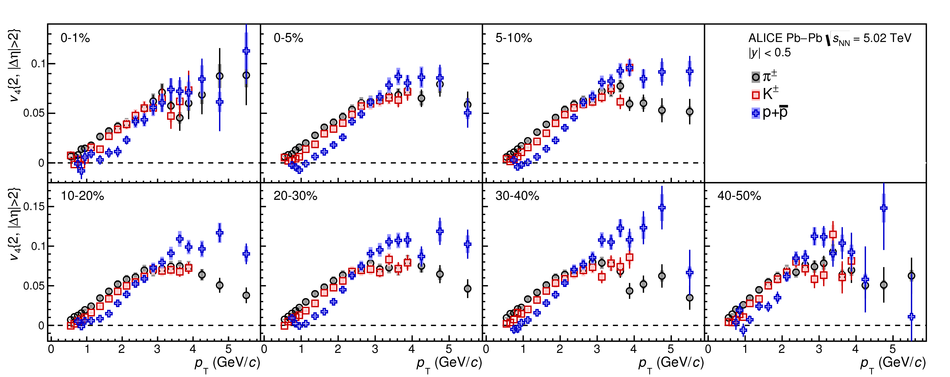
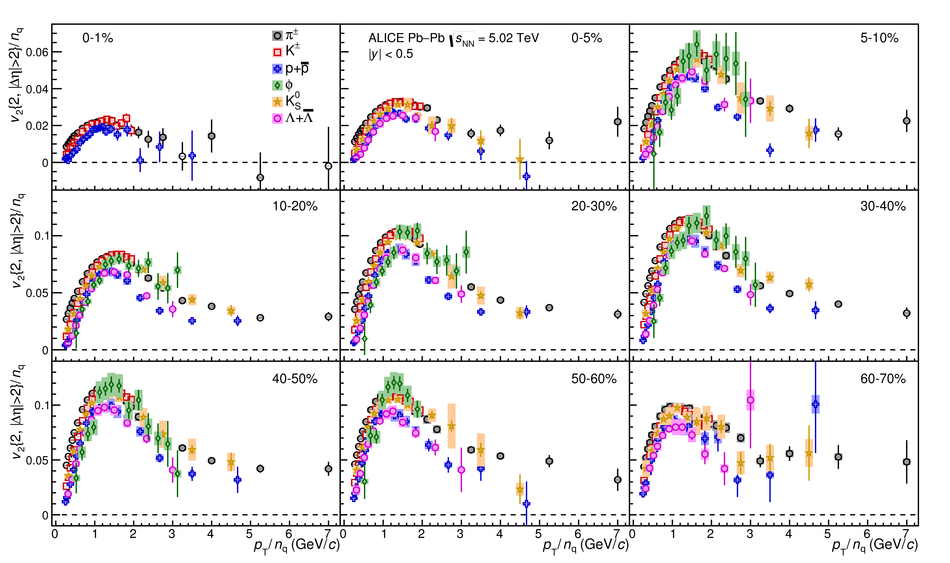
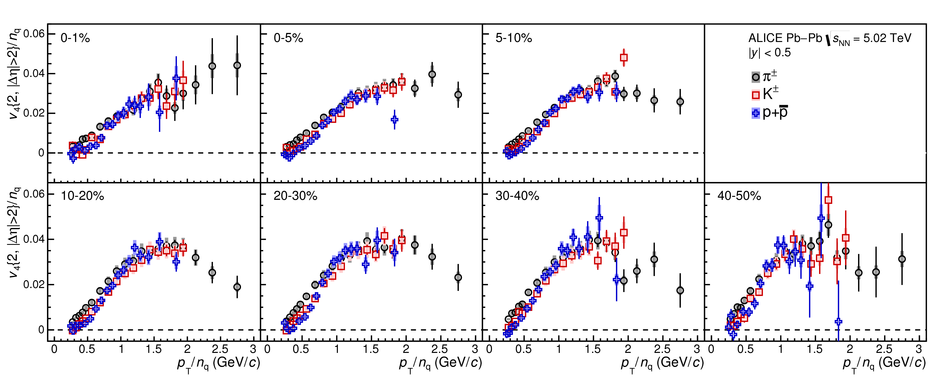
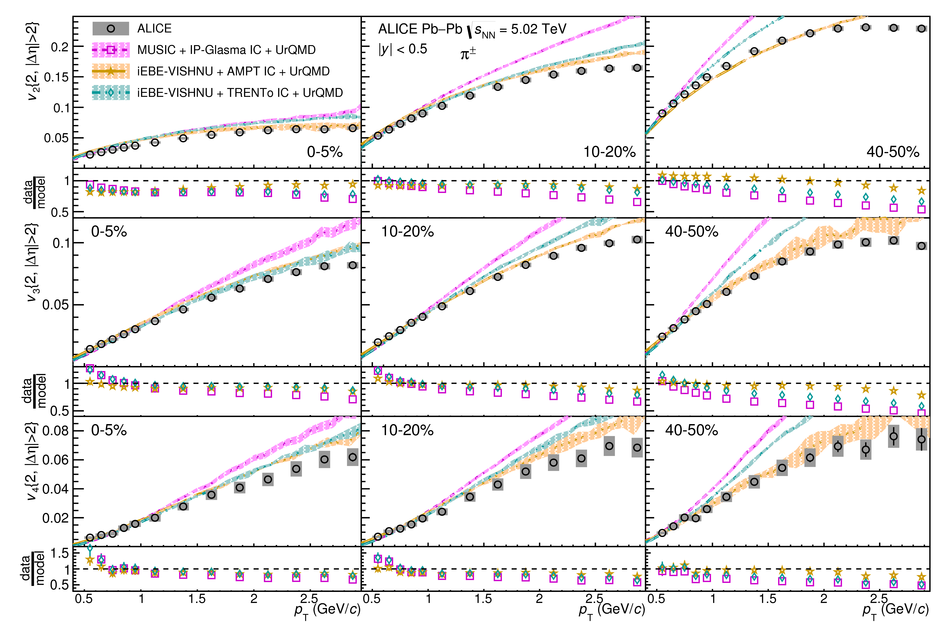
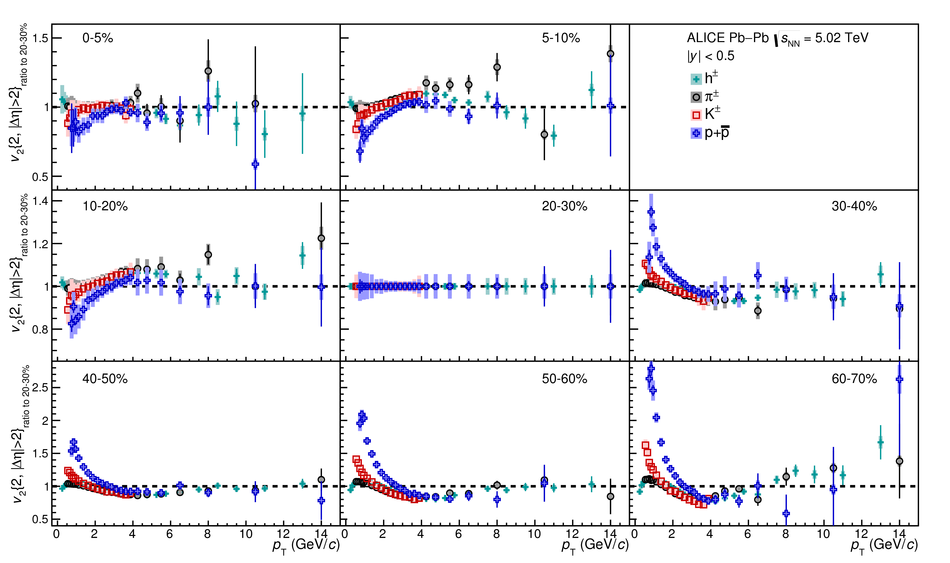
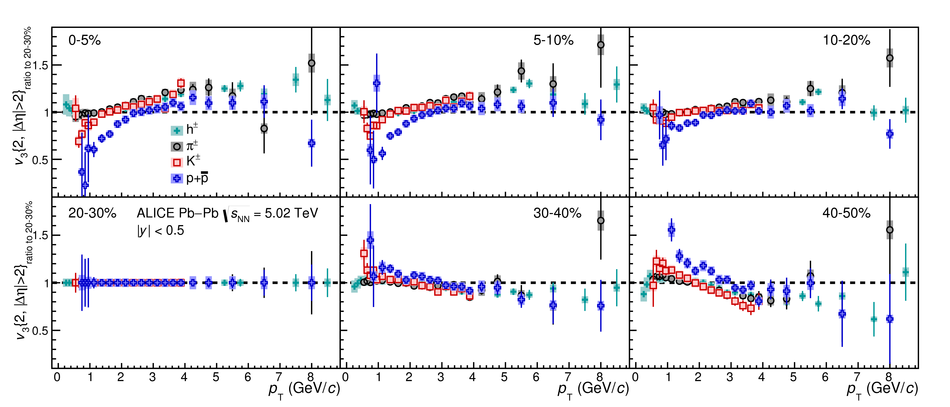
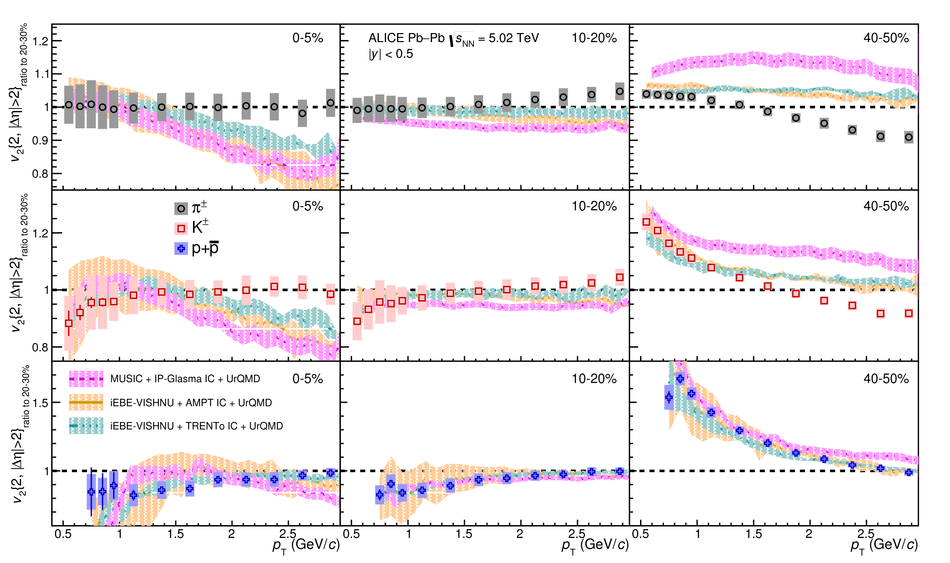
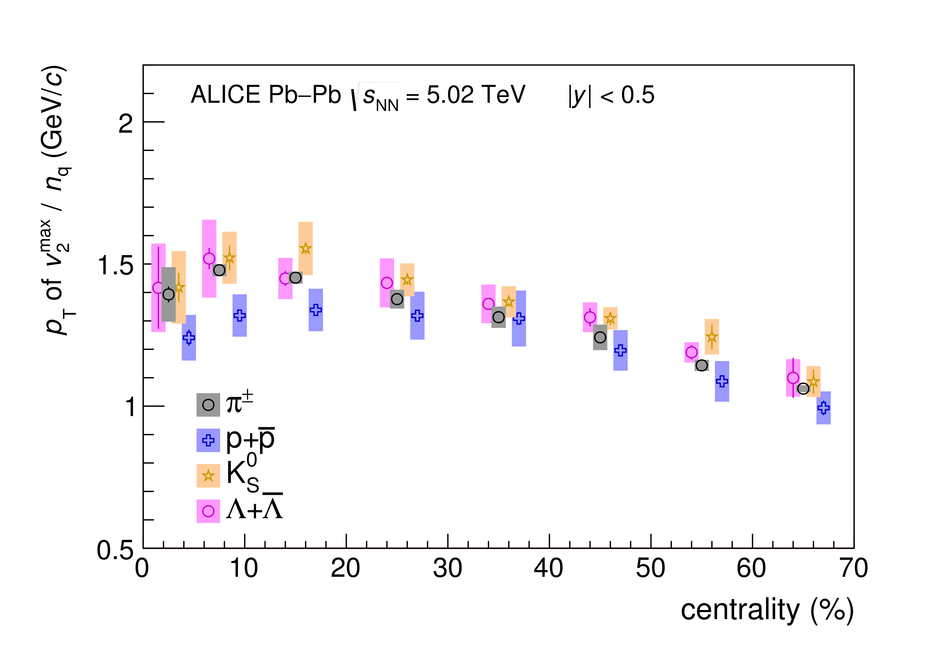
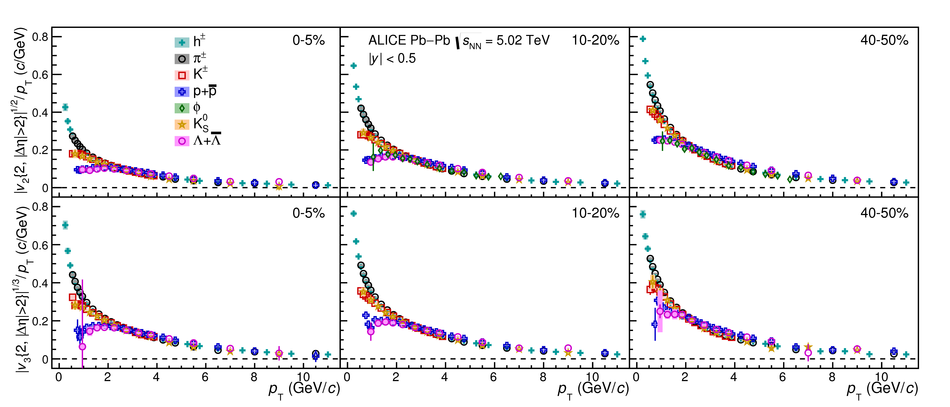
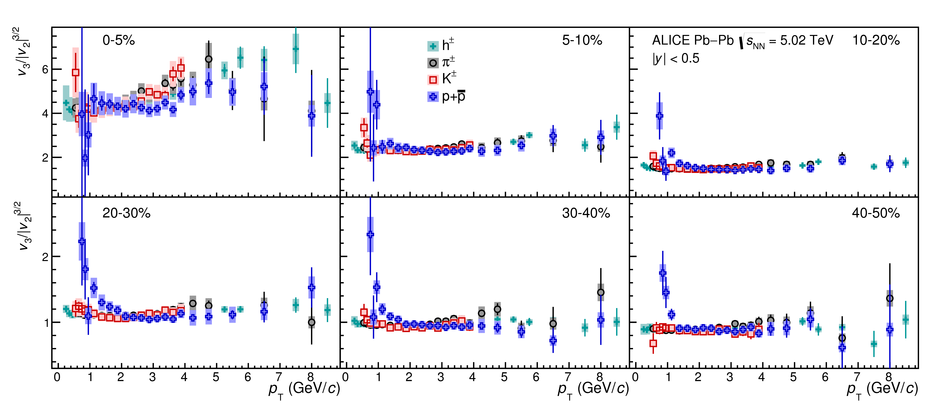
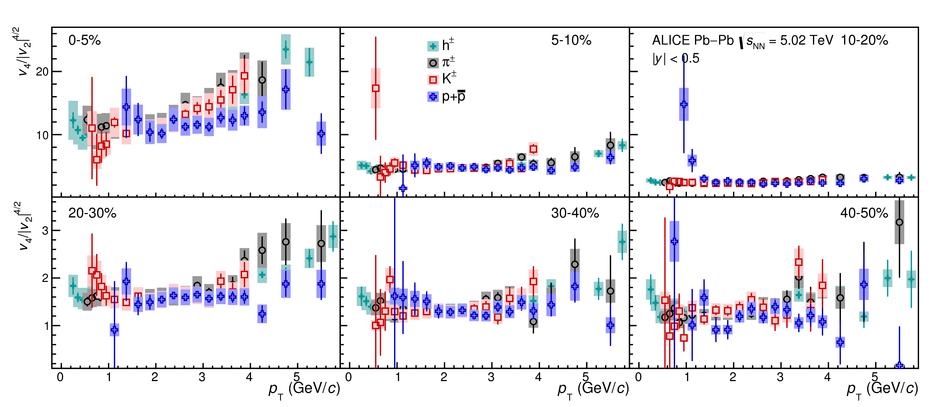
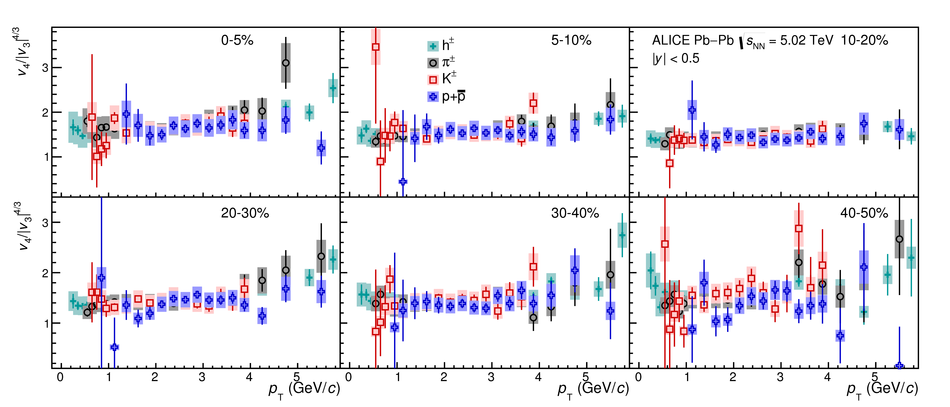
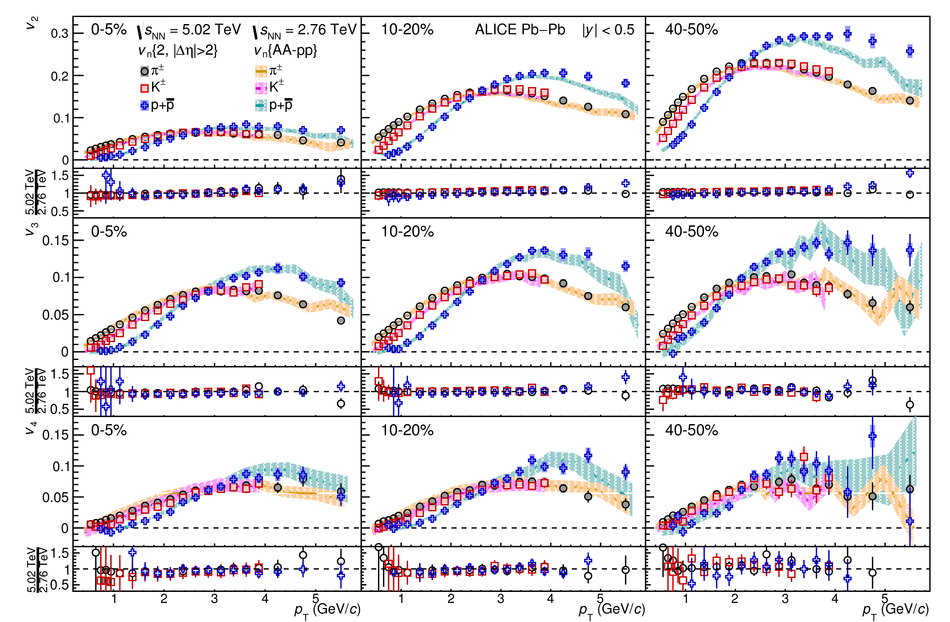
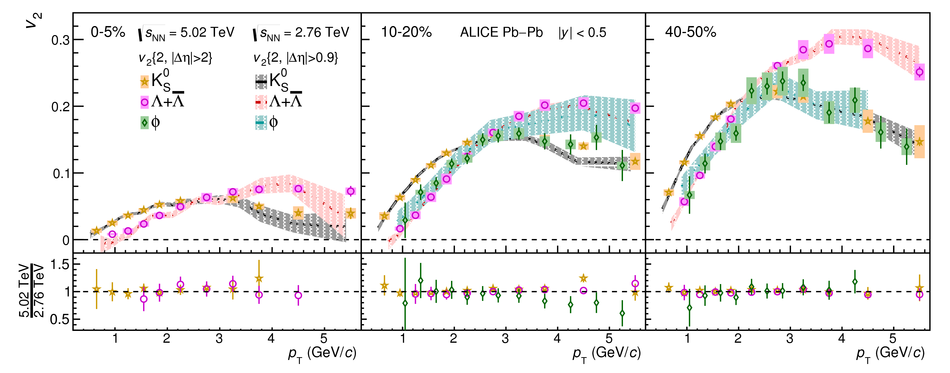
The elliptic ($v_2$), triangular ($v_3$), and quadrangular ($v_4$) flow coefficients of $\pi^{\pm}$, ${\rm K}^{\pm}$, ${\rm p+\overline{p}}$, ${\Lambda+\overline{\Lambda}}$, ${\rm K}^{\rm 0}_{\rm S}$, and the $\phi$-meson are measured in Pb-Pb collisions at $\sqrt{s_{\rm NN}}=5.02$ TeV. Results obtained with the scalar product method are reported for the rapidity range $\vert y \vert <~$ 0.5 as a function of transverse momentum, $p_\text{T}$, at different collision centrality intervals between 0-70%, including ultra-central (0-1%) collisions for $\pi^{\pm}$, ${\rm K}^{\pm}$, and ${\rm p+\overline{p}}$. For $p_\text{T} <~ 3$ GeV$\kern-0.05em/\kern-0.02em c$, the flow coefficients exhibit a particle mass dependence. At intermediate transverse momenta ($3<~p_\text{T}<~$~8-10 GeV$\kern-0.05em/\kern-0.02em c$), particles show an approximate grouping according to their type (i.e., mesons and baryons). The $\phi$-meson $v_2$, which tests both particle mass dependence and type scaling, follows ${\rm p+\overline{p}}$ $v_2$ at low $p_\text{T}$ and $\pi^{\pm}$ $v_2$ at intermediate $p_\text{T}$. The evolution of the shape of $v_{\rm n}(p_{\mathrm{T}})$ as a function of centrality and harmonic number $n$ is studied for the various particle species. Flow coefficients of $\pi^{\pm}$, ${\rm K}^{\pm}$, and ${\rm p+\overline{p}}$ for $p_\text{T}<~3$ GeV$\kern-0.05em/\kern-0.02em c$ are compared to iEBE-VISHNU and MUSIC hydrodynamical calculations coupled to a hadronic cascade model (UrQMD). The iEBE-VISHNU calculations describe the results fairly well for $p_\text{T} <~ 2.5$ GeV$\kern-0.05em/\kern-0.02em c$, while MUSIC calculations reproduce the measurements for $p_\text{T} <~ 1$ GeV$\kern-0.05em/\kern-0.02em c$. A comparison to $v_{\rm n}$ coefficients measured in Pb-Pb collisions at $\sqrt{s_{\rm NN}}$ = 2.76 TeV is also provided.
JHEP09 (2018) 006
HEP Data
e-Print: arXiv:1805.04390 | PDF | inSPIRE