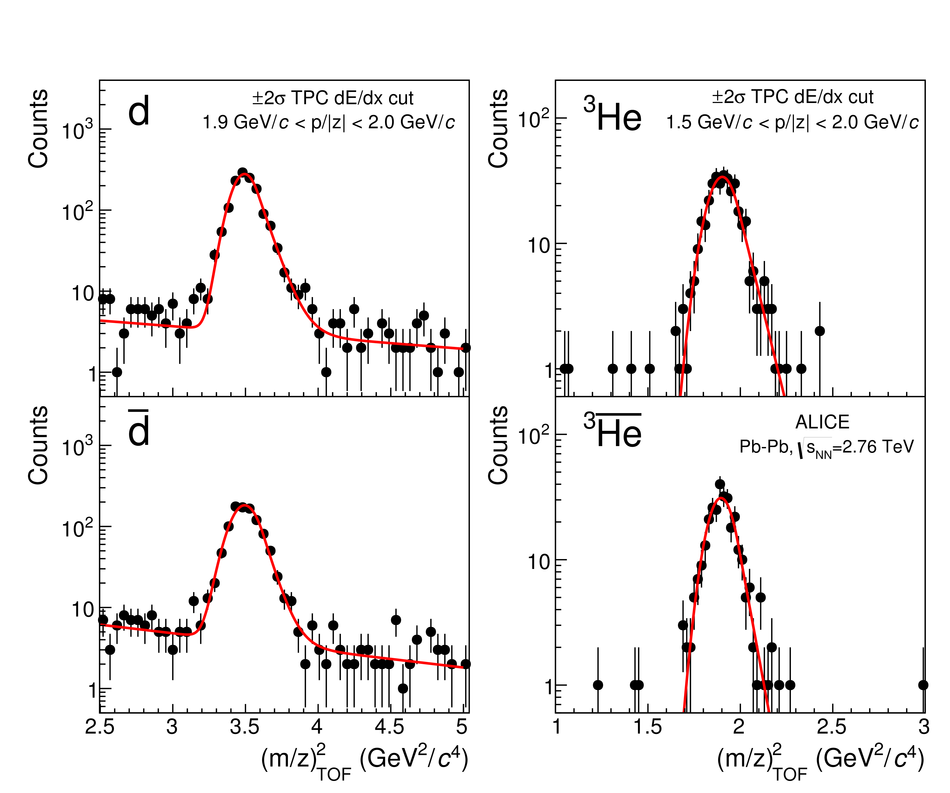
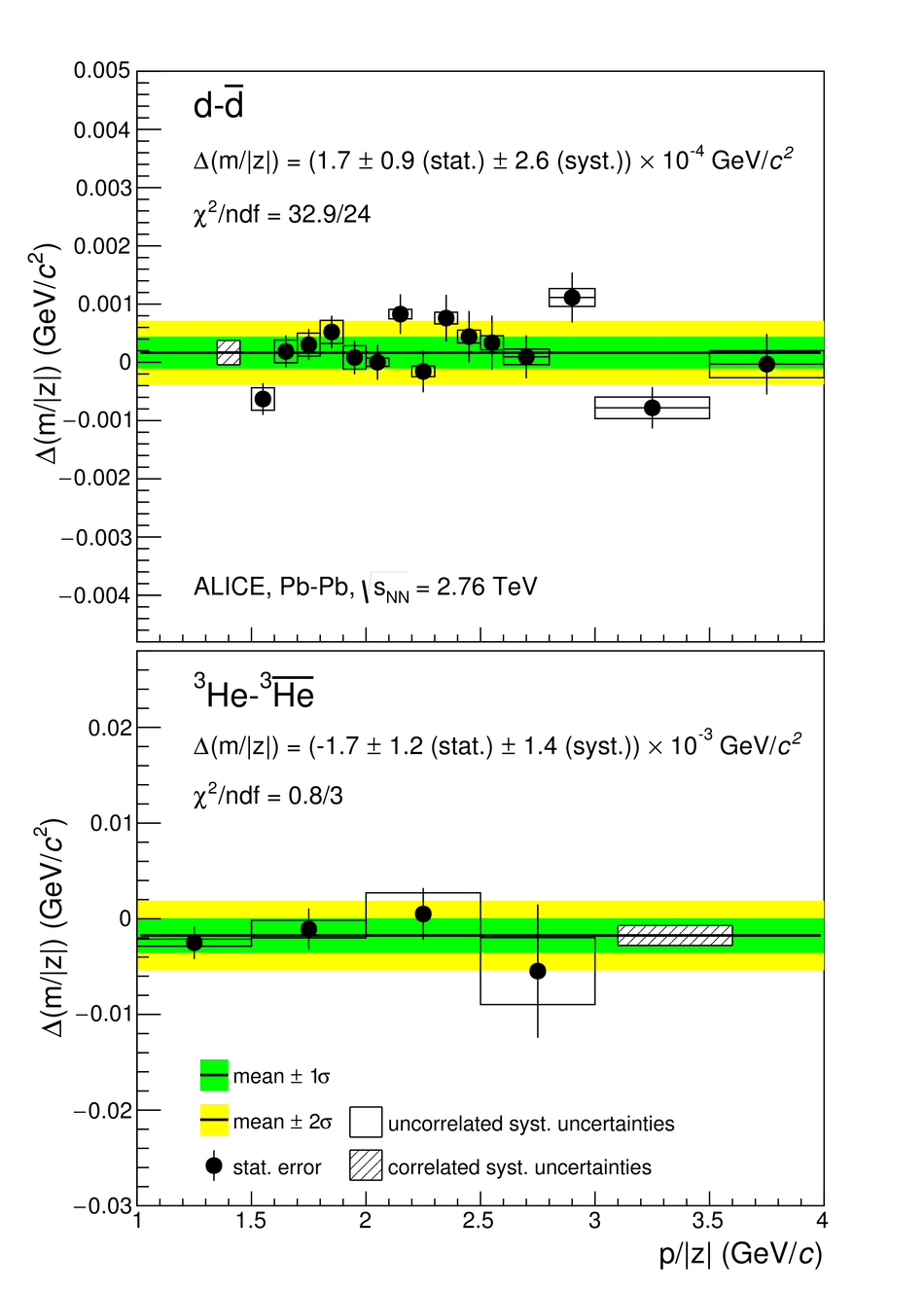
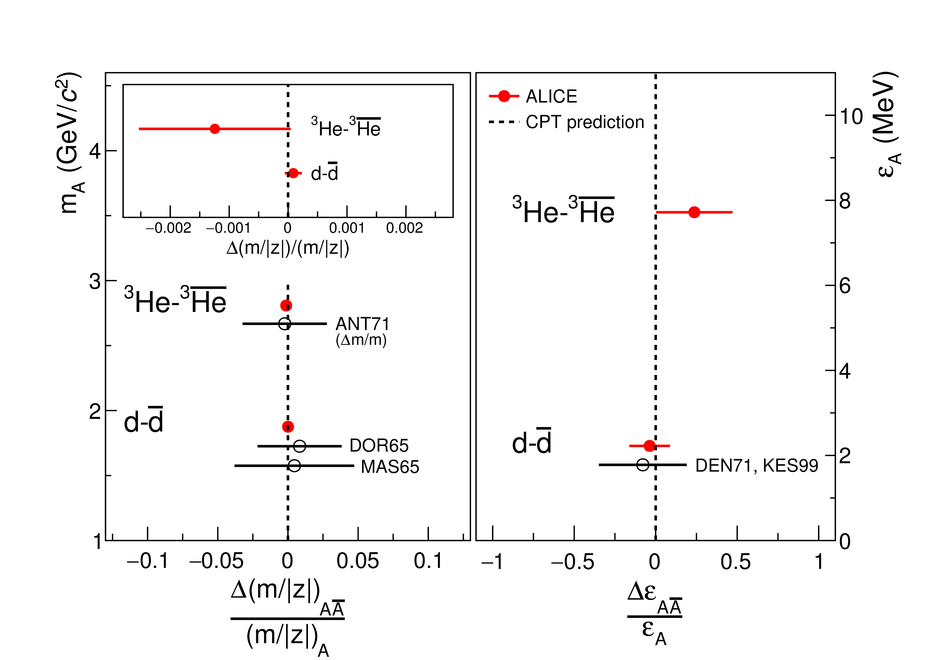
The measurement of the mass differences for systems bound by the strong force has reached a very high precision with protons and anti-protons. The extension of such measurement from (anti-)baryons to (anti-)nuclei allows one to probe any difference in the interactions between nucleons and anti-nucleons encoded in the (anti-)nuclei masses. This force is a remnant of the underlying strong interaction among quarks and gluons and can be described by effective theories, but cannot yet be directly derived from quantum chromodynamics. Here we report a measurement of the difference between the ratios of the mass and charge of deuterons and anti-deuterons, and $^{3}{\rm He}$ and $^3\overline{\rm He}$ nuclei carried out with the ALICE (A Large Ion Collider Experiment) detector in Pb-Pb collisions at a centre-of-mass energy per nucleon pair of 2.76 TeV. Our direct measurement of the mass-over-charge differences confirm CPT invariance to an unprecedented precision in the sector of light nuclei. This fundamental symmetry of nature, which exchanges particles with anti-particles, implies that all physics laws are the same under the simultaneous reversal of charge(s) (charge conjugation C), reflection of spatial coordinates (parity transformation P) and time inversion (T).
Nature Physics 11 (2015) 811-814
e-Print: arXiv:1508.03986 | PDF | inSPIRE
CERN-PH-EP-2015-035